| Transition Temperature | 58 K |
|---|---|
| Experiment Temperature | 7 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | P21/n (#14) |
| Magnetic Space Group | P-1 (#2.4) |
| Magnetic Point Group | -1 (2.1.3) |
| Lattice Parameters | 5.9715(3) 5.9709(3) 8.4761(3) 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1039/b003629n |
| Reference | Y. Izumiyama, Y. Doi', M. Wakeshima, Y. Hinatsu, K. Oikawa, Y. Shimojo, Y. Morii, J. Mater. Chem. (2000) 10 2364 - 2367 |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Nd1_1 | Nd | 1.63 | -1.63 | 0.0 | 2.31 |
| Nd1_2 | Nd | -1.63 | 1.63 | 0.0 | 2.31 |
| Ru1_1 | Ru | -1.56 | 1.56 | 0.0 | 2.21 |
| Ru1_2 | Ru | 1.56 | -1.56 | 0.0 | 2.21 |
Magnetic and neutron diffraction studies of the ordered perovskite \( Ba_{2}NdRuO_{6} \) \( ^{\dagger} \)
Yuki Izumiyama, \( ^{a} \) Yoshihiro Doi, \( ^{a} \) Makoto Wakeshima, \( ^{a} \) Yukio Hinatsu, \( ^{a} \) Kenichi Oikawa, \( ^{b} \) Yutaka Shimojo \( ^{b} \) and Yukio Mori \( ^{b} \)
\( ^{a} \) Division of Chemistry, Graduate School of Science, Hokkaido University, Sapporo 060-0810, Japan
\( ^{b} \) Japan Atomic Energy Research Institute, Tokai-nura, Ibaraki, 319-1195, Japan
Received 8th May 2000, Accepted 5th July 2000 First published as an Advanced Article on the web 4th September 2000
The magnetic properties of the ordered perovskite compound \( Ba_{2}NdRuO_{6} \) are reported. Powder neutron diffraction measurements were performed at 100, 35 and 7 K to determine its crystal structure and magnetic properties. Refinement of the data collected at 100 K showed that this compound has monoclinic symmetry, space group \( P2_{1}/n \) with \( a=5.9888(2) \) , \( b=5.9916(2) \) , \( c=8.4667(2) \) Å and \( \beta=90.026(3)^{\circ} \) , and that the structure is that of a perovskite with a 1:1 ordered arrangement of \( Ru^{5+} \) and \( Nd^{3+} \) over the 6-coordinate sites. From the data collected at 35 and 7 K, it was found that there is a long range antiferromagnetic ordering in the \( Ba_{2}NdRuO_{6} \) . The magnetic structure is of type I and the magnetic moments of \( Nd^{3+} \) and \( Ru^{3+} \) ions are in the same direction in the ab plane.
1 Introduction
Ordered perovskite-type oxides, \( A_{2}LnMO_{6} \) (A = alkaline-earth element; Ln = lanthanide element; M = 4d or 5d transition element), in which the Ln and M elements are regularly ordered show a variety of magnetic behaviors at low temperature. We are particularly interested in such compounds containing pentavalent ruthenium ions. The electronic structure of \( Ru^{5+} \) is \( [Kr]4d^{3} \) ([Kr]: krypton core). Such highly oxidized cations from the second transition series sometimes show quite unusual magnetic behavior. When the Ln ion is diamagnetic (e.g. \( Y^{3+} \) , \( La^{3+} \) and \( Lu^{3+} \) ), such \( A_{2}LnRuO_{6} \) compounds are suitable for studying the behavior of \( Ru^{5+} \) ions, since only the \( Ru^{5+} \) ions are responsible for their magnetic properties. \( ^{1,2} \) Battle et al. investigated the crystal structures and magnetic properties of \( Ba_{2}LnRuO_{6} \) (Ln = Y, La and Lu), and reported that these compounds show antiferromagnetic transitions at ca. 15–30 K. The crystal structures of \( Ba_{2}YRuO_{6} \) and \( Ba_{2}LuRuO_{6} \) are both cubic at room temperature, space group Fm3m, and they exhibit Type I antiferromagnetism at low temperature. \( ^{3} \) They also demonstrated that the crystal structure of \( Ba_{2}LaRuO_{6} \) adopts triclinic symmetry at room temperature, space group \( P\bar{T} \) , and that the magnetic structure at 2 K is a type III antiferromagnetic arrangement.
We have turned our attention to the crystal structures and magnetic properties of the ordered perovskites \( A_{2}NdRuO_{6} \) , in which both \( Nd^{3+} \) and \( Ru^{5+} \) ions are responsible for its magnetic behavior. It was reported that the Nd cation in the \( Ca_{2}NdRuO_{6} \) occupies only the A site of the \( ABO_{3} \) perovskite and that the \( Nd^{3+} \) and \( Ca^{2+} \) ions are disordered on the A site, i.e. the formulation \( \mathrm{CaNd[CaRu]O_{6}} \) is more appropriate for this compound. \( ^{5} \) Doi and Hinatsu reported that, although they tried to prepare \( Sr_{2}NdRuO_{6} \) , its preparation was unsuccessful due to the large size of the \( Nd^{3+} \) ion compared with that of \( Sr^{2+} \) , and that even a compound in which the Nd cation occupies the A site of the perovskite was not prepared. \( ^{6} \) In this study, we have successfully prepared \( Ba_{2}NdRuO_{6} \) , which is the only obtainable ordered perovskite-type compound in the \( A_{2}NdRuO_{6} \) family. Through magnetic susceptibility, heat capacity and neutron diffraction measurements, it has been found that this compound shows an antiferromagnetic transition at ca. 58 K. Herein, we will report these experimental results and discuss the magnetic properties of \( Ba_{2}NdRuO_{6} \) .
2 Experimental
A polycrystalline sample of \( Ba_{2}NdRuO_{6} \) was synthesized by heating stoichiometric amounts of \( BaCO_{3} \) , \( Nd_{2}O_{3} \) and \( RuO_{2} \) , first at \( 900\;^{\circ}C \) for 12 h and then \( 1300\;^{\circ}C \) for 60 h, in air with frequent grinding. X-Ray diffraction measurements were performed with \( Cu-K\alpha \) radiation on a Rigaku RINT 2100 diffractometer equipped with a curved graphite monochromator.
Powder neutron diffraction measurements were performed at 100, 35 and 7 K using the high resolution powder diffractometer (HRPD) at the JRR-3M reactor (Japan Atomic Energy Research Institute), with a Ge(331) monochromator ( \( \lambda=1.8230 \) Å). The collimators used were 6'-20'-6' and were placed before and after the monochromator, and between the sample and each detector. The set of 64 detectors and collimators, which were placed every 2.5°, rotate around the sample. Crystal and magnetic structures were determined by the Rietveld technique, using the RIETAN program. \( ^{7} \)
The temperature dependence of the magnetic susceptibility was measured in the temperature range 2–300 K in a magnetic field of 0.1 T with a SQUID magnetometer (Quantum Design, Model MPMS); the susceptibility data were collected both after cooling the sample from room temperature to 2 K in zero-field (ZFC) and after cooling in an applied field of 0.1 T (FC).
The heat capacity measurements were carried out using a relaxation technique supplied by a commercial heat capacity measurement system (Quantum Design, Model PPMS) in the temperature range from 2 to 300 K. The sample, in the form of a pellet (ca. 10 mg), was mounted on an aluminium plate with Apiezon grease for better thermal contact.

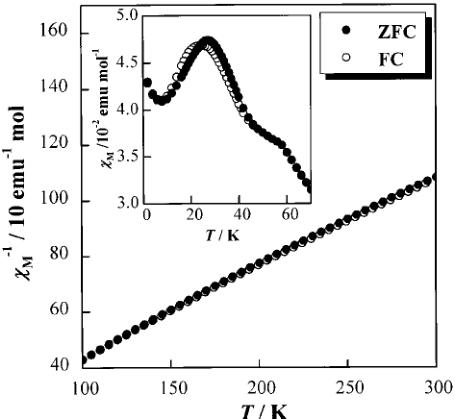
Fig. 1 Temperature dependence of the ZFC (filled symbols) and FC (open symbols) molar magnetic susceptibilities for \( Ba_{2}NdRuO_{6} \) in an applied field of 0.1 T.
3 Results and discussion
3.1 Crystal structure
The results of the powder X-ray diffraction measurements show that \( Ba_{2}NdRuO_{6} \) was formed as a single phase with a perovskite-type structure. The X-ray diffraction pattern is available as \( ESI.\dagger \) The pattern was indexed on a monoclinic unit cell, in space group \( P2_{1}/n \) , which permits an ordered arrangement of \( Nd^{3+} \) and \( Ru^{5+} \) ions over the B-sites of the \( ABO_{3} \) perovskite. The structural analysis using the Rietveld method, which was carried out with the RIETAN program, \( ^{7} \) shows that the \( Nd^{3+} \) and \( Ru^{5+} \) ions are arranged alternately and that they have a rock salt sublattice. The approximate size of the unit cell is \( \sqrt{2}a_{p}\times\sqrt{2}a_{p}\times2a_{p} \) , where \( a_{p} \) is a lattice parameter in a primitive cubic unit cell. The observed and calculated X-ray diffraction profiles, and the differences between them are available as \( ESI.\dagger \) The reliability factors are as follows: \( R_{wp}=12.07 \) , \( R_{l}=1.44 \) and \( R_{F}=3.70\% \) . The diffraction profile shows the existence of superlattice reflections [ex. (011) and (101)] which come from the ordered array between the Nd and Ru cations. The Nd and Ru cations are therefore arranged regularly over the octahedral (B) sites and

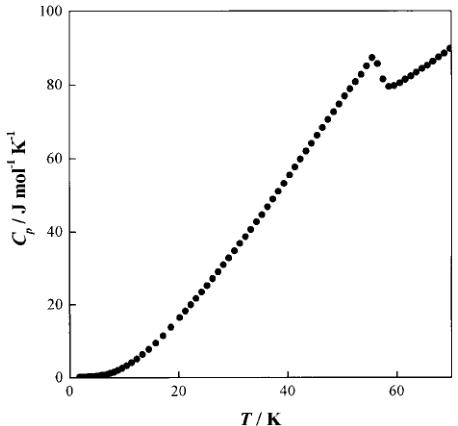
Fig. 2 Temperature dependence of the heat capacity of \( Ba_{2}NdRuO_{6} \)

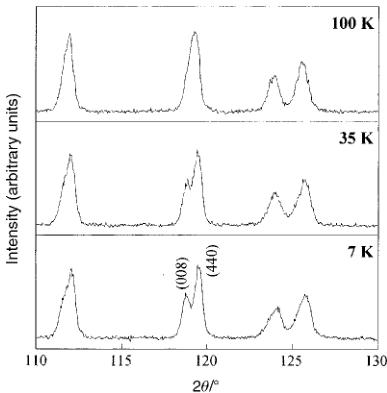
Fig. 3 Enlarged neutron diffraction profiles around \( 2\theta\approx120^{\circ} \) at each temperature.
form two interpenetrating face-centered sublattices. The crystal structure of \( Ba_{2}NdRuO_{6} \) is shown in the ESI.† The lattice parameters are \( a=5.9888(2) \) , \( b=5.9916(2) \) , \( c=8.4667(2) \) Å and \( \beta=90.026(3)^{\circ} \) . Since the angle of \( \beta \) is nearly \( 90^{\circ} \) , the monoclinic distortion of this compound is very small.
3.2 Magnetic properties
3.2.1 Magnetic susceptibility. The temperature dependence of the molar magnetic susceptibilities for \( Ba_{2}NdRuO_{6} \) is shown in Fig. 1. There is a slight divergence between the ZFC and FC susceptibilities. Two magnetic anomalies have been found in the susceptibility vs. temperature curve, i.e. a maximum in the susceptibility appears at ca. 27 K and an inflection occurs at ca. 58 K.
Table 1 Structural parameters for \( Ba_{2}NdRuO_{6} \) (space group \( P2_{1}/n^{a} \) )
| Atom | Site | x | y | z | B/Ų | μ/μB |
| At 100 K | ||||||
| Ba | 4e | -0.001(3) | -0.003(8) | 0.249(3) | 0.06(7) | |
| Nd | 2d | 1/2 | 0 | 0 | 0.09(4) | |
| Ru | 2c | 1/2 | 0 | 1/2 | 0.09(4) | |
| O(1) | 4e | 0.227(4) | 0.267(4) | 0.015(6) | 0.42(5) | |
| O(2) | 4e | 0.234(4) | -0.276(3) | -0.014(6) | 0.42(5) | |
| O(3) | 4e | -0.032(2) | 0.503(9) | 0.232(2) | 0.42(5) | |
| a=5.9920(2), | b=5.9765(2), | c=8.4480(3) Å, | β=90.02(1)°, | |||
| V=302.53(2) ų, | Rwp=8.24, | Rl=1.62, | Rf=1.53, | Rc=6.15% | ||
| At 35 K | ||||||
| Ba | 4e | 0.016(1) | 0.001(3) | 0.250(1) | 0.61 | |
| Nd | 0.29 | |||||
| Ru | 2c | 1/2 | 0 | 0 | 0.020 | 1.8(1) |
| O(1) | 4e | 0.216(6) | 0.243(3) | 0.010(2) | 0.77 | |
| O(2) | 4e | 0.214(6) | -0.251(3) | 0.007(2) | 0.62 | |
| O(3) | 4e | -0.026(2) | 0.492(2) | 0.231(1) | 0.40 | |
| a=5.9734(3), | b=5.9722(3), | c=8.4737(3) Å, | β=90.183(3)°, | |||
| V=302.29 ų, | Rwp=9.83, | Rl=2.18, | Rf=1.47, | Rc=6.41% | ||
| At 7 K | ||||||
| Ba | ||||||
| Nd | 2d | 1/2 | 0 | 1/2 | 0.29 | 2.3(1) |
| Ru | 2c | 1/2 | 0 | 2/2 | 0.61 | 2.2(1) |
| O(1) | 4e | 0.215(6) | 0.250(4) | 0.007(3) | 0.77 | |
| O(2) | 4c | 0.216(5) | -0.251(3) | 0.007(3) | 0.82(2) | |
| O(3) | 4e | -0,027(2) | 0.486(2) | 0.232(1) | 0.4(2) | |
| a=5.9715(3), | b=5.9709(3), | c=8.4761(3) Å, | β=90.178(3)°, | |||
| V=302.22 ų, | Rwp=10.88, | Rl=2.93, | Rf=1.80, | Rc=6.42% | ||
| aThe reliability factors Rsp, Rl, Rf and Rc are defined as follows: Rwp= [∑w(|F(o)|-|F(c)|)²/∑w|F(o)|²]¹/², | ||||||
| Rl= ∑l|F(o)-|F(c)|/∑lF(o), | ||||||
| Rf= ∑[|F(o)|²-|F(c)|²]²/∑lF(o)² and Rc= (∑w|F(o)|²)¹/². | ||||||
Table 2 Bond lengths ( \( \AA \) ) and angles ( \( ^{\circ} \) ) for Ba \( _{2} \) NdRuO \( _{6} \)
| At 100 K | ||||
| Nd-O(1) | 2.29(3) × 2 | Ru-O(1) | 1.95(3) × 2 | |
| Nd-O(2) | 2.30(3) × 2 | Ru-O(2) | 1.94(3) × 2 | |
| Nd-O(3) | 2.27(1) × 2 | Ru-O(3) | 1.97(1) × 2 | |
| O(1)-Nd-O(2) | 90.0(6) | O(1)-Ru-O(2) | 90.8(7) | Nd-O(1)-Ru |
| O(1)-Nd-O(3) | 90.0(14) | O(1)-Ru-O(3) | 90.6(20) | Nd-O(2)-Ru |
| O(2)-Nd-O(3) | 90.7(14) | O(2)-Ru-O(3) | 90.2(20) | Nd-O(3)-Ru |
| At 35 K | ||||
| Nd-O(1) | 2.23(3) × 2 | Ru-O(1) | 2.01(3) × 2 | |
| Nd-O(2) | ||||
| Nd-O(3) | 2.28(3) × 2 | Ru-O(2) | 1.96(3) × 2 | |
| Nd-O(3) | 1.28(1) × 2 | Ru-O(3) | 1.97(2) × 2 | |
| O(1)-Nd-O(2) (a) | 98.2(6) | O(1)-Ru-O(2) | 99.1(7) | Nd-O(1)-Ru |
| O(1)- Nd-O(3) | 91.4(14) | O(1)-Ru-O(3) | 90.5(20) | Nd-O(2)-Ru |
| O(2)- Nd-O(3) | 90.6(14) | O(2)-Ru-O(3) | 92.4(20) | Nd-O(3)-Ru |
| At 7 K | ||||
| Nd-O(1) | ||||
| Nd-O(2) | 2.24(3) × 2 | Ru-O(1) | 2.00(3) × 2 | |
| Nd-O(3) | 3.26(3) × 2 | Ru-O(2) | 1.97(3) × 2 | |
| Nd-O(3) | 4.28(1) × 2 | Ru-O(3) | 1.98(1) × 2 | |
| O(1)-Nd-O(3) | 97.9(6) | O(1)-Ru-O(2) | 98.8(7) | Nd-O(1)-Ru |
| O(2)-Nd-O(3) | 92.1(14) | O(1)-Ru-O(3) | 91.2(20) | Nd-O(2)-Ru |
| O(2)-N d-O(3) | 90.0(14) | O(2)-Ru-O(3) | 93.2(20) | Nd-O(3)-Ru |
Fitting the Curie–Weiss law to the temperature dependence of the magnetic susceptibilities in the temperature range 100 to 300 K gives an effective magnetic moment \( (\mu_{\mathrm{eff}}) \) of 4.96 \( \mu_{\mathrm{B}} \) and a Weiss constant \( (\theta) \) of -35.5 K. The predominant magnetic interaction in this compound seems to be antiferromagnetic, judging from this negative Weiss constant. This \( \mu_{eff} \) value is in reasonable agreement with the value of 5.12 \( \mu_{B} \) reported previously for \( Ca_{2}NdRuO_{6} \) .⁴ Since the theoretical moment of the \( Nd^{3+} \) ion is 3.62 \( \mu_{B} \) , the magnetic moment for the \( Ru^{3+} \) ion in \( Ba_{2}NdRuO_{6} \) is estimated to be 3.39 \( \mu_{B} \) from the relation \( \mu_{\mathrm{eff}}(\mathrm{Ba}_{2}\mathrm{NdRuO}_{6})^{2}=\mu_{\mathrm{eff}}(\mathrm{Nd}^{3+})^{2}+\mu_{\mathrm{eff}}(\mathrm{Ru}^{5+})^{2} \) . Comparable magnetic moment values have been obtained for \( Ba_{2}BrRuO_{6} \) (B=Y, La, Lu: diamagnetic)⁴,⁸ and \( Sr_{2}BrRuO_{6} \) (B=Y, Lu).²,⁸
3.2.2 Heat capacity. Fig. 2 shows the temperature dependence of the heat capacity for \( Ba_{2}NdRuO_{6} \) . A \( \lambda \) -type anomaly can be seen at 58 K, which corresponds to the antiferromagnetic transition observed in the magnetic susceptibility vs. temperature curve. No anomaly corresponding to the maximum observed at ca. 27 K in the susceptibility vs. temperature curve was detected in the heat capacity measurements.
3.2.3 Neutron diffraction. (a) Crystal structure. X-Ray diffraction data collected at room temperature indicate that \( Ba_{2}NdRuO_{6} \) has monoclinic symmetry. Powder neutron diffraction profiles for \( Ba_{2}NdRuO_{6} \) measured at 100, 35 and 7 K are available as ESI. \( ^{1} \) Refinements of the crystal structure with the neutron diffraction data measured at 100, 35 and 7 K were carried out by the Rietveld analysis technique. Fig. 3 shows enlarged neutron diffraction profiles around \( 2\theta\approx120^{\circ} \) at each temperature. At 100 K, the reflection due to the (008) and (440) planes is observed as a single peak, while at 7 and 35 K, it is separated into two peaks. These experimental results are due to the fact that the monoclinic distortion is less prominent at 100 K, and increases with decreasing temperature. Atomic positions and lattice parameters at 100, 35 and 7 K are tabulated in Table 1. At 100 K, this compound has lattice parameters of \( a=5.9920(2) \) , \( b=5.9765(2) \) , \( c=8.4480(3) \) Å and \( \beta=90.02(1)^{\circ} \) . With decreasing temperature, the lattice shrinks in the direction of the a axis, but stretches in the direction of the c axis and the angle \( \beta \) increases from \( 90^{\circ} \) . Selected bond lengths and angles for \( Ba_{2}NdRuO_{6} \) at 100, 35 and 7 K are tabulated in Table 2. At 100 K, the O–Nd–O bond angles are approximately equal and nearly \( 90^{\circ} \) . The same is true for the O–Ru–O bond angles, that is to say, both the \( Nd^{3+} \) ion and the \( Ru^{5+} \) ion are in an almost octahedral environment, surrounded by six oxygen ions. At lower temperatures (35 and 7 K), the O–Nd–O (and O–Ru–O) bond angles are no longer equal, and depart considerably from \( 90^{\circ} \) , which means that the oxygen coordination around the \( Nd^{3+} \) (and \( Ru^{5+} \) ) ions is not octahedral. The three Nd–O–Ru bond angles are approximately equal.
(b) Magnetic structure. Since the magnetic anomaly was observed at 27 and 58 K in the susceptibility vs. temperature curve, we performed neutron diffraction measurements at 100, 35 and 7 K.
In the neutron diffraction profiles collected at 35 and 7 K

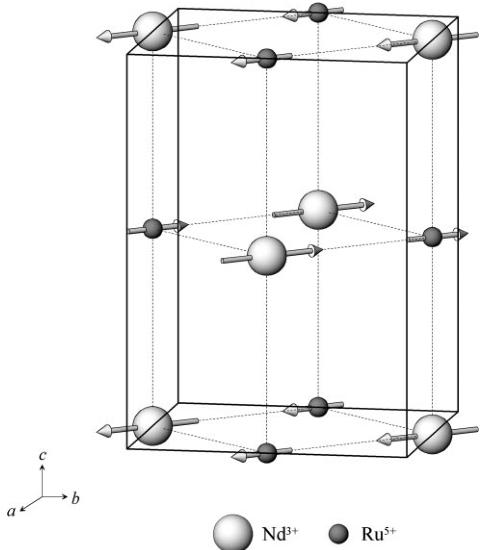
Fig. 4 The magnetic structure of \( Ba_{2}NdRuO_{6} \) . Diamagnetic ions are omitted. Larger circles \( Nd^{3+} \) ; smaller circles \( Ru^{5+} \) . The direction of the magnetic moments in the ab plane was not determined in this experiment.
(see ESI†), a number of low-angle peaks for magnetic reflections which are not observed at 100 K appear, indicating that \( Ba_{2}NdRuO_{6} \) shows the existence of antiferromagnetic ordering at these temperatures. We tried to determine the magnetic structure of \( Ba_{2}NdRuO_{6} \) from the diffraction data collected at 7 K and 35 K using the analysis program RIETAN. \( ^{7} \) There is no difference between the profiles measured between at 35 K and at 7 K, except for a variation in the intensities of the magnetic peaks, which indicates that two kinds of magnetic ions ( \( Nd^{3+} \) ion and \( Ru^{5+} \) ion) magnetically order at the same temperature, 58 K. This is consistent with the results of heat capacity measurements that a \( \lambda \) -type anomaly occurs at this temperature. The anomaly found at ca. 27 K in the susceptibility vs. temperature curve was not observed in the heat capacity measurements. The reason for this is not clear at present, but one possibility is that a reorientation of the magnetic moments may occur at this temperature. \( ^{9} \)
It has been reported that most of the magnetic structures of the antiferromagnets \( A_{2}BRuO_{6} \) (A=Sr, Ba, B=Y, Lu) are Type I (for \( Ba_{2}LaRuO_{6} \) it is Type III). \( ^{3,4} \) First of all, we carried out the determination of the magnetic structure of \( Ba_{2}NdRuO_{6} \) by considering the magnetic structural data for \( Ba_{2}BRuO_{6} \) (B=La, Y, Lu) and \( Sr_{2}BRuO_{6} \) (B=Ho, Er). The large (001) magnetic peak \( (2\theta\approx12^{\circ}) \) is observed in the profiles of \( Ba_{2}NdRuO_{6} \) at 35 and 7 K, but the (100) or (010) magnetic peak \( (2\theta\approx18^{\circ}) \) is not seen, indicating that the alignment of the magnetic moments is parallel not to the c axis, but to the a or b axes. Unfortunately, we could not definitely determine the direction of the magnetic moments from these powder neutron diffraction data. The magnetic structure determined for this compound is illustrated in Fig. 4, i.e. the magnetic type is Type I. Both \( Nd^{3+} \) and \( Ru^{5+} \) ions exist on the ab plane. The magnetic moments of both were found to be in the same direction from the analysis of the powder neutron diffraction measurements, therefore, the ab plane would seem to be a ferromagnetic plane. This result is in contrast to the cases for \( Sr_{2}HoRuO_{6} \) \( ^{10} \) and \( Sr_{2}ErRuO_{6} \) \( ^{5} \) in which the directions of the magnetic moments of \( Ho^{3+} \) and \( Ru^{5+} \) ions in the ab plane are antiparallel with each other, i.e. they order ferrimagnetically. From the Rietveld analysis, the ordered magnetic moments at 35 K are determined to be 1.9(1) for \( Nd^{3+} \) and 1.8(1) \( \mu_{B} \) for \( Ru^{5+} \) , and at 7 K they are 2.3(1) for \( Nd^{3+} \) and 2.2(1) \( \mu_{B} \) for \( Ru^{5+}\cdot \) . This is the same tendency as the results for \( Sr_{2}ErRuO_{6} \) and \( Sr_{2}HoRuO_{6} \) reported previously, i.e. the more the temperature decreases, the more the ordered magnetic moments increase, but they do not saturate, even at 4.2 K.
In order to elucidate various kinds of magnetic structures, we are studying the magnetic properties of a series of \( Ba_{2}LnRuO_{6} \) compounds through powder neutron diffraction measurements.
References
1 P. D. Battle and W. J. Macklin, J. Solid State Chem., 1984, 54, 245.
2 P. D. Battle and W. J. Macklin, J. Solid State Chem.,1984, 52, 138.
3 P. D. Battle and C. W. Jones, J. Solid State Chem., 1989, 78, 108.
4 P. D. Battle, J. B. Goodenough and R. Price, J. Solid State Chem., 1983, 46, 234.
5 P. D. Battle, C. W. Jones and F. Studer, J. Solid State Chem., 1991, 90, 302.
6 Y. Doi and Y. Hinatsu, J. Phys.: Condens. Matter, 1999, 11, 4813.
7 F. Izumi, in The Rietveld Method, ed. R. A. Young, Oxford University Press, Oxford, 1993, ch. 13.
8 R. Greatrex, N. N. Greenwood, M. Lal and I. Fernandez, J. Solid State Chem., 1979, 30, 137.
9 K. Tezka, Y. Hinatsu, K. Oikawa, Y. Shimojo and Y. Morii, J. Phys.: Condens. Matter, 2000, 12, 4151.
10 Y. Doi, Y. Hinatsu, K. Oikawa, Y. Shimojo and Y. Mori, J. Mater. Chem., 2000, 10, 797.