| Transition Temperature | 3.2 K |
|---|---|
| Experiment Temperature | 2 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | I41cd (#110) |
| Magnetic Space Group | I41'cd' (#110.248) |
| Magnetic Point Group | 4'm'm (13.3.46) |
| Lattice Parameters | 12.2448(7) 12.2448(7) 8.3592(7) 90.0000 90.0000 90.0000 |
|---|---|
| DOI | 10.1103/PhysRevB.66.014428 |
| Reference | A. Lappas, V. Alexandrakis, J. Giapintzakis, V. Pomjakushin, K. Prassides, A. Schenck, PHYSICAL REVIEW B (2002) 66 014428 |
Title
Impurity-induced antiferromagnetic order in the Haldane-gap compound \( PbNi_{2-x}Mg_{x}V_{2}O_{8} \) (x=0.24)
Authors
Alexandros Lappas, \( ^{*} \) Vassilis Alexandrakis, and John Giapintzakis Institute of Electronic Structure and Laser, Foundation for Research and Technology–Hellas, P.O. Box 1527, 711 10 Heraklion, Crete, Greece
Vladimir Pomjakushin I.M. Frank Laboratory of Neutron Physics, JINR 14980, Dubna, Russia and Laboratory for Neutron Scattering ETHZ & PSI, CH-5232 Villigen PSI, Switzerland
Kosmas Prassides School of Chemistry, Physics and Environmental Sciences, University of Sussex, Falmer, Brighton BN1 9QJ, United Kingdom
Alexander Schenck Institute for Particle Physics, Swiss Federal Institute of Technology (ETH) Zurich, CH-5232 Villigen PSI, Switzerland
Materials Studied
- \( PbNi_{2-x}Mg_{x}V_{2}O_{8} \) (specifically \( PbNi_{1.76}Mg_{0.24}V_{2}O_{8} \))
- Parent compound: \( PbNi_{2}V_{2}O_{8} \) (x=0)
Key Information
- Crystal structure / space group: Tetragonal, \( I4_{1}cd \)
- Lattice parameters: At 2 K: \( a=b=12.2448(7) \) Å, \( c=8.3592(7) \) Å
- Magnetic ordering type and temperature: Antiferromagnetic long-range order (AF LRO) below \( T_{N}=3.2 \) K.
- Propagation vector(s): \( \kappa=[000] \) (chemical and magnetic unit cells coincide).
- Magnetic moments: Refined ordered moment at \( Ni^{2+} \)-site: \( \mu=0.9(1)\mu_{B} \) at 2 K. Spins lie parallel or antiparallel to the c-axis (magnetic easy axis).
- Spin configuration: Antiferromagnetic both along the \( NiO_{6} \) chains (c-axis, intrachain) and within the ab-plane for nearest-neighbor Ni atoms (interchain).
- Other critical measured values:
- Parent compound (\( PbNi_{2}V_{2}O_{8} \)):
- Effective spin gap \( \Delta_{eff}/k=45.3(1) \) K ( \( \sim3.9 \) meV).
- Nearest-neighbor intrachain exchange energy J/k = -91.9(1) K ( \( \sim7.9 \) meV).
- Landé factor \( g\approx2.82 \).
- Easy-axis single-ion anisotropy D = -0.45 meV.
- Doped compound (\( PbNi_{1.76}Mg_{0.24}V_{2}O_{8} \)):
- High-temperature Curie constant \( C=3.41(1) \) emu K/mol.
- High-temperature Curie temperature \( \theta=-313.2(1) \) K.
- High-temperature effective magnetic moment \( \mu_{eff}\approx2.98\mu_{B}/Ni^{2+} \).
- Critical field for metamagnetic transition \( H_{c}(0)=1.7(1) \) T (extrapolated to 0 K).
- Muon precession frequencies: \( 0.5<\nu_{\mu}<3 \) MHz, corresponding to internal fields \( H_{int} \sim 36 - 192 \) G.
- Parent compound (\( PbNi_{2}V_{2}O_{8} \)):
Synthesis Method
Polycrystalline \( PbNi_{2-x}Mg_{x}V_{2}O_{8}\ (x=0\ \text{and}\ 0.24) \) powders were prepared by solid-state reaction. * Starting materials: Stoichiometric quantities of \( PbO \), \( NiC_{2}O_{4}\cdot2H_{2}O \), \( MgO \), and \( V_{2}O_{5} \) with purities \( >99.9\% \). * Conditions: 1. The mixture of reagents was first heated at \( 550\;^{\circ}C \) for 24 h to eliminate carbon-containing species. 2. Successive sintering cycles were carried out at elevated temperatures, ranging from \( 750\;^{\circ}C \) to \( 780\;^{\circ}C \), over a period of ten days. These cycles involved repeated grinding and pelletizing of the powders, with three intermediate grindings. 3. Slow cooling to room temperature followed the high-temperature reactions. * Characterization: Phase purity was established by x-ray powder diffraction using a Rigaku D/MAX-2000H diffractometer with \( Cu-K\alpha \) radiation.
Abstract
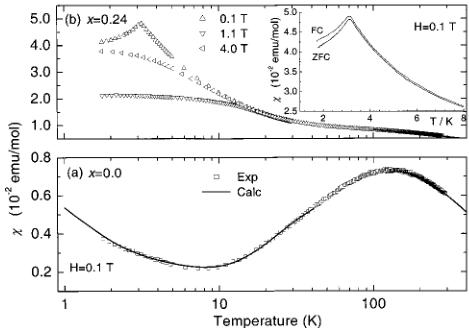
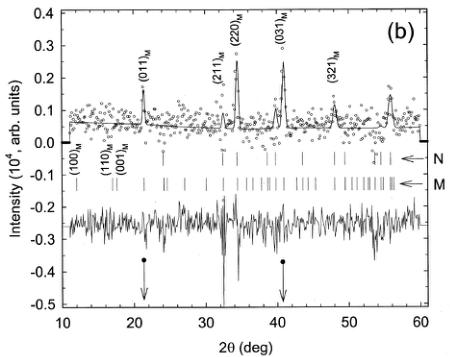
An investigation of the effect of nonmagnetic Mg doping in the Haldane gap system \( PbNi_{2}V_{2}O_{8} \) is presented. Specifically, the magnetic properties of the quasi-one-dimensional compound \( PbNi_{2-x}Mg_{x}V_{2}O_{6} \) (x=0.24), located in the heavily doped region of the \( T_{N} \), x phase diagram, have been examined using neutron powder diffraction, muon-spin relaxation ( \( \mu^{+}SR \) ) and magnetic susceptibility. Neutron-diffraction measurements show that antiferromagnetic long-range order (propagation vector \( \kappa=[000] \)) is established below \( T_{N}=3.2 \) K. The spins in the Ni sublattice lie either parallel or antiparallel to the c axis, which is the magnetic easy axis of the system. The spin configuration is antiferromagnetic both along the \( NiO_{6} \) chains, i.e., the c axis of the crystal structure, and within the ab-plane for the nearest-neighbor Ni atoms. The refined ordered moment at the \( Ni^{2+} \)-site is \( \mu=0.9(1)\mu_{B} \). To our knowledge, this is the first diffraction evidence of the antiferromagnetic ordering in this system. The static magnetic correlations of the doping-induced magnetic moments along the Ni chains were probed by zero-field \( \mu^{+}SR \) at \( T This paper investigates the impact of nonmagnetic Mg doping on the Haldane gap system \( PbNi_{2}V_{2}O_{8} \), a quasi-one-dimensional (1D) S=1 Heisenberg antiferromagnet. The introduction highlights Haldane's conjecture regarding spin-gap ground states in integer spin systems and notes that factors like single-ion anisotropy, 3D interchain coupling, or spin vacancies can suppress the Haldane gap and induce long-range magnetic order (LRO). The study focuses on the specific composition \( PbNi_{1.76}Mg_{0.24}V_{2}O_{8} \), which is in the heavily doped region of the \( T_{N} \), x phase diagram, to understand the emergence and nature of the impurity-induced LRO. Polycrystalline samples of both the parent \( PbNi_{2}V_{2}O_{8} \) and the Mg-doped \( PbNi_{1.76}Mg_{0.24}V_{2}O_{8} \) were prepared using a solid-state reaction method involving precise heating and grinding cycles. The samples were characterized using a suite of experimental techniques: X-ray powder diffraction for structural purity, dc magnetization and ac susceptibility measurements to probe macroscopic magnetic properties, neutron powder diffraction (NPD) to determine the magnetic structure and ordered moments, and zero-field muon-spin relaxation ( \( \mu^{+}SR \) ) to investigate local magnetic fields and inhomogeneities. Macroscopic magnetic measurements revealed distinct behaviors for the parent and doped compounds. The parent compound exhibited characteristic spin-gap behavior with an estimated effective spin gap of \( \Delta_{eff}/k=45.3(1) \) K and an intrachain exchange energy of J/k = -91.9(1) K. In contrast, the Mg-doped sample showed a pronounced peak in dc susceptibility at \( T_{N}=3.2 \) K, signifying a magnetic phase transition. Below \( T_{N} \), the doped compound displayed metamagnetic behavior, where an applied magnetic field induces a transition from a low to a high magnetization state. This metamagnetic transition, characterized by a critical field \( H_{c}(0)=1.7(1) \) T (extrapolated to 0 K), suggests the presence of significant magnetic anisotropy (with the c-axis as the easy axis) and competing exchange interactions. Neutron powder diffraction confirmed the establishment of antiferromagnetic LRO below \( T_{N}=3.2 \) K in \( PbNi_{1.76}Mg_{0.24}V_{2}O_{8} \). The material adopts a tetragonal crystal structure with space group \( I4_{1}cd \), and the magnetic and chemical unit cells coincide, indicating a propagation vector \( \kappa=[000] \). The spins on the \( Ni^{2+} \) sublattice are aligned parallel or antiparallel to the c-axis. The magnetic structure is antiferromagnetic both along the \( NiO_{6} \) chains (intrachain) and between nearest-neighbor Ni atoms in the ab-plane (interchain). The refined average ordered magnetic moment at 2 K was found to be \( \mu=0.9(1)\mu_{B} \) per Ni site, which is a significant reduction from the expected \( 2.0\mu_{B} \) for an \( S=1~Ni^{2+} \) ion. Complementary zero-field \( \mu^{+}SR \) measurements provided microscopic insights, revealing multiple spontaneous muon-precession frequencies ( \( 0.5<\nu_{\mu}<3 \) MHz) below \( T_{N} \). This complex internal field distribution ( \( H_{int} \sim 36 - 192 \) G) indicates a spatial inhomogeneity in the magnitude of the ordered moments along the helical \( NiO_{6} \) chains, a direct consequence of the doping-induced magnetic ordering. In the quasi-one-dimensional \( PbNi_{2}V_{2}O_{8} \) system, substitution of the magnetic \( Ni^{2+} \) (S=1) sites by nonmagnetic \( Mg^{2+} \) (S=0) cations leads to a transition from a magnetically disordered spin-gap ground state to essentially three-dimensional Néel order. We have investigated this effect for one Mg-substituted material, namely, \( PbNi_{1.76}Mg_{0.24}V_{2}Os_{8} \), located in the “heavily doped” region of the \( T_{N} \), x phase diagram. Neutron powder diffraction and muon-spin relaxation measurements were employed in the low-temperature range where the ac and dc susceptibility data illustrated that a magnetic transition takes place. Neutron powder diffraction in \( PbNi_{1.76}Mg_{0.24}V_{2}{O}_{8} \) probes an average size of the ordered moment of \( 0.9(1)\mu_{B} \) per Ni site at 2 K. The spins in the Ni sublattice lie either parallel or antiparallel to the c axis, which is the magnetic easy axis of the system. The spin-spin interaction is antiferromagnetic (below \( T_{N}=3.2 \) K) both in the \( NiO_{6} \)-chains running along the c axis (intrachain) and within the ab plane for nearest-neighbor Ni atoms (interchain). Zero-field muon-spin relaxation below \( T_{N} \) confirms the static character of the magnetic interactions arising from the doping-induced, end-of-chain local moments. Also, it provides evidence of a nonuniform moment size over the severed chain segments. It manifests as a convolution of multiple spontaneous muon-precession frequencies that give rise to an internal magnetic field distribution with spatial inhomogeneities. The magnetic susceptibility shows that the compound exhibits metamagnetic behavior at \( TMain Content Summary
Conclusion
Impurity-induced antiferromagnetic order in the Haldane-gap compound \( PbNi_{2-x}Mg_{x}V_{2}O_{8} \) (x=0.24)
Alexandros Lappas, \( ^{*} \) Vassilis Alexandrakis, and John Giapintzakis Institute of Electronic Structure and Laser, Foundation for Research and Technology–Hellas, P.O. Box 1527, 711 10 Heraklion, Crete, Greece
Vladimir Pomjakushin I.M. Frank Laboratory of Neutron Physics, JINR 14980, Dubna, Russia and Laboratory for Neutron Scattering ETHZ & PSI, CH-5232 Villigen PSI, Switzerland
Kosmas Prassides School of Chemistry, Physics and Environmental Sciences, University of Sussex, Falmer, Brighton BN1 9QJ, United Kingdom
Alexander Schenck Institute for Particle Physics, Swiss Federal Institute of Technology (ETH) Zurich, CH-5232 Villigen PSI, Switzerland (Received 5 July 2001; revised manuscript received 21 December 2001; published 16 July 2002)
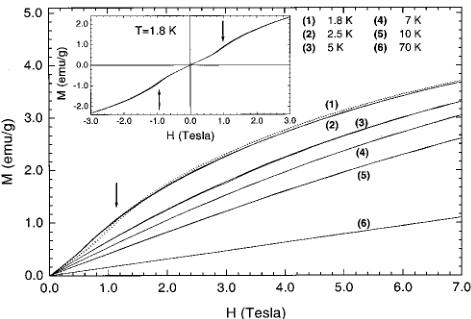
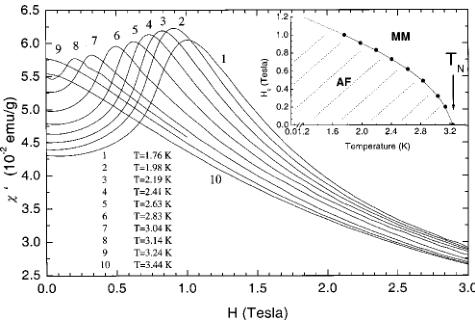
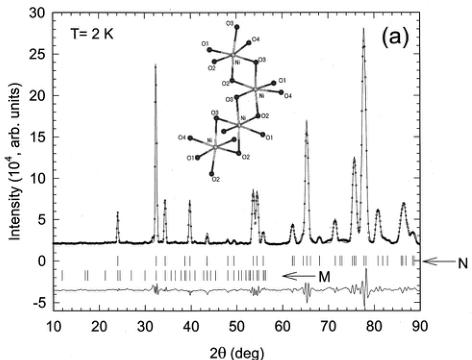
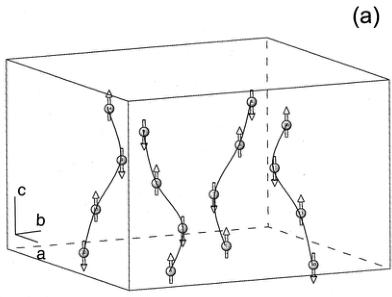
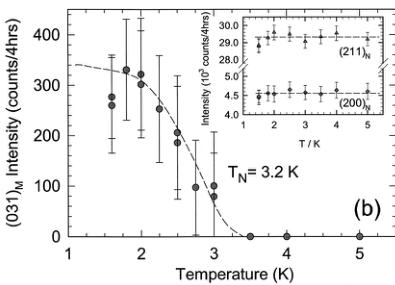
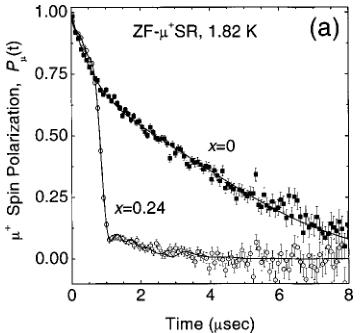
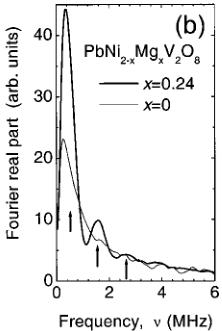
An investigation of the effect of nonmagnetic Mg doping in the Haldane gap system \( PbNi_{2}V_{2}O_{8} \) is presented. Specifically, the magnetic properties of the quasi-one-dimensional compound \( PbNi_{2-x}Mg_{x}V_{2}O_{6} \) (x=0.24), located in the heavily doped region of the \( T_{N} \) , x phase diagram, have been examined using neutron powder diffraction, muon-spin relaxation ( \( \mu^{+}SR \) ) and magnetic susceptibility. Neutron-diffraction measurements show that antiferromagnetic long-range order (propagation vector \( \kappa=[000] \) ) is established below \( T_{N}=3.2 \) K. The spins in the Ni sublattice lie either parallel or antiparallel to the c axis, which is the magnetic easy axis of the system. The spin configuration is antiferromagnetic both along the \( NiO_{6} \) chains, i.e., the c axis of the crystal structure, and within the ab-plane for the nearest-neighbor Ni atoms. The refined ordered moment at the \( Ni^{2+} \) -site is \( \mu=0.9(1)\mu_{B} \) . To our knowledge, this is the first diffraction evidence of the antiferromagnetic ordering in this system. The static magnetic correlations of the doping-induced magnetic moments along the Ni chains were probed by zero-field \( \mu^{+}SR \) at \( T DOI: 10.1103/PhysRevB.66.014428 PACS number(s): 75.25.+z, 75.50.Ee, 75.30.Gw, 75.30.Hx In recent years, the magnetic properties of low-dimensional quantum Heisenberg antiferromagnets (HAF's) have attracted a lot of interest both from theoretical and experimental points of view. \( ^{1,2} \) The knowledge acquired by studying these relatively simple systems can be implemented in understanding physical phenomena in the more complex three-dimensional solids. For instance, in the quest for unravelling the mechanism of high- \( T_{c} \) superconductivity, questions regarding the relevance of the pseudogap in two-dimensional cuprates demanded consideration. To help unravel this interrelationship, a vigorous research effort has been directed toward analogous low-dimensional spin systems, especially those with a spin-gap ground state. To this extent, various quasi-one-dimensional (1D) materials have been explored, \( ^{2} \) including the spin-Peierls \( CuGeO_{3} \) , \( ^{3} \) the Haldane compound \( Y_{2}BaNiO_{5} \) , (Ref. 4) and spin-ladder systems like the two-leg ladder \( SrCu_{2}O_{3} \) . \( ^{5} \) Such systems can also serve as a bridge between 1D and complex 2D systems. The pioneering work of Haldane \( ^{6} \) led to a breakthrough in our understanding of low-dimensional magnetism. Haldane established that the actual ground states are different for integer and half-integer Heisenberg spin systems. Thus, while half-integer systems can show quasi-long-range order, \( ^{7} \) integer spin systems have an energy gap in the spin excitation spectrum and exhibit a singlet, nonmagnetic ground state. \( ^{6} \) A rigorous description of the Haldane conjecture is presented by the valence-bond-solid (VBS) model, \( ^{8} \) which allows for a free \( S=\frac{1}{2} \) state to be associated with each end of an open chain. Electron-spin-resonance experiments on the Cu (Ref. 9) and Zn (Ref. 10) doped S=1 linear-chain Heisenberg antiferromagnet (AF) \( [\mathrm{Ni}(\mathrm{C}_{2}\mathrm{H}_{8}\mathrm{N}_{2})_{2}(\mathrm{NO}_{2})]\mathrm{ClO}_{4} \) have provided strong experimental evidence in support of the VBS ground state. Among the various factors that can suppress the Haldane gap and change the singlet ground state to a long-range-ordered (LRO) one, are single-ion anisotropy and 3D interchain coupling, which have been studied extensively. \( ^{[11]} \) Another possible factor predicted to result in the emergence of a LRO magnetic state is the creation of spin vacancies in quantum chains. \( ^{[12]} \) This largely unexplored issue of the suppression of a Haldane gap and the concurrent appearance of LRO demands new experimental investigations on appropriate model compounds. Recent experiments of this type have shown contrasting behavior, and hence are the source of motivation for further work in this direction. As such, dilution-induced free moments (on substituting Ni sites by nonmagnetic cations, e.g., \( A=Zn^{2+} \) or \( Mg^{2+} \) ) and quantum fluctuations in chain compounds with a spin-singlet ground state drive \( Y_{2}BaNiO_{5} \) to a ground state, which resembles that of the VBS, \( ^{13} \) in contrast to \( PbNi_{2}V_{2}O_{8} \) , which undergoes a transition to long-range ordering. \( ^{14} \) In the Mg-doped Haldane-gap \( PbNi_{2}V_{2}O_{8} \) compound, neutron powder diffraction data have unambiguously shown the transformation of the disordered ground state to an antiferromagnetic one. \( ^{[15]} \) In this paper, we present a detailed account of variable temperature neutron powder diffraction (NPD), zero-field muon-spin relaxation ( \( \mu^{+}SR \) ), and magnetic susceptibility results in the \( PbNi_{2-x}Mg_{x}V_{2}O_{8} \) (x=0.24) quasi-one-dimensional solid. We describe the spin configuration of the induced antiferromagnetic ground state. Zero-field \( \mu^{+}SR \) reveals that the transition to the LRO AF state is characterized by a magnetic-field distribution with large inhomogeneities. The magnitude of the staggered moment, generated by the Mg dopants, is derived by a Rietveld refinement of the neutron data. We show that the size of the moment and the presence of multiple muon-precession frequencies in the \( ZF-\mu^{+}SR \) spectra of \( PbNi_{1.76}Mg_{0.24}V_{2}O_{8} \) imply a nonuniform ordered moment size along the helical \( NiO_{6} \) -chains. We discuss microscopic features of the AF LRO state based on doping-induced ordering phenomena in quasi-1D compounds. Extended dc and ac magnetic-susceptibility measurements also show a low-temperature metamagnetic behavior for this composition. Polycrystalline \( PbNi_{2-x}Mg_{x}V_{2}O_{8}\ (x=0\ \text{and}\ 0.24) \) powders were prepared by solid-state reaction of stoichiometric quantities of \( PbO \) , \( NiC_{2}O_{4}\cdot2H_{2}O \) , \( MgO \) , and \( V_{2}O_{5} \) in air. The mixture of the starting reagents (purities \( >99.9\% \) ) was first heated at \( 550\;^{\circ}C \) for 24 h to eliminate carbon-containing species. Successive sintering cycles at elevated temperatures, ranging from \( 750\;^{\circ}C \) to \( 780\;^{\circ}C \) , were carried out after repeated grinding and pelletizing of the powders. These high-temperature reactions (followed by slow cooling to room temperature) took place over a period of ten days with three intermediate grindings. The phase purity was established by x-ray powder diffraction using a Rigaku D/MAX-2000H rotating anode (12 kW) diffractometer. Data were collected at room temperature during routine scans between \( 10\leq2\theta\leq80^{\circ} \) with a step size of \( 0.02^{\circ} \) and a count time of 3 s/step, using \( Cu-K\alpha \) radiation with a secondary graphite monochromator. For the indexing of these x-ray-diffraction patterns, longer count times of 8 s/step were used. No deviations of the crystal structure were found from that reported in the literature. \( ^{16} \) Possibly, an impurity phase limited below the 2% level of the sensitivity limit of the diffractometer is present. dc magnetization and ac susceptibility measurements were performed with an Oxford Instruments MagLab EXA system in dc magnetic fields up to 7 T, in the temperature range 1.8 to 300 K. Powder neutron diffraction profiles for \( PbNi_{1.76}Mg_{0.24}V_{2}Og_{8} \) were measured in zero applied magnetic field at temperatures between 1.5 and 5 K on the DMC high-intensity diffractometer at the Swiss Spallation Neutron Source (SINQ), using neutrons with a wavelength of 2.567 Å. The 4-g powder sample was contained in a cylindrical V can ( \( \phi5\times50\ mm^{3} \) ). An oscillating radial collimator suppressed Bragg peaks from the sample environment. For the purpose of chemical and magnetic structure determination, long-statistics scans were collected in the range \( 10\leq2\theta\leq90^{\circ} \) (in steps of \( 0.2^{\circ} \) ) over a 24-h period at 2 and 4 K. In addition, shorter scans of 4 h each were measured on warming in order to determine the temperature evolution of the magnetic state. Rietveld refinements of the powder neutron diffraction patterns were performed with the FULLPROF (Ref. 17) suite of powder diffraction software, using the internal tables of neutron scattering lengths and magnetic form factors. The \( \mu^{+}SR \) data in zero-field were collected on the GPS spectrometer of the \( \mu^{+}SR \) -dedicated \( \pi M3 \) beamline, on the 600-MeV proton accelerator at the Paul Scherrer Institute, Villigen, Switzerland. The instrument was equipped with a He-flow cryostat to access the temperature range down to 1.8 K. Pressed pellets of the powdered samples were attached with low-temperature varnish on an Ag sample-holder placed on the sample stick of the cryostat. When 100% spin-polarized positive muons are implanted in the solid sample, they come to rest at an interstitial lattice site, and then act as highly sensitive microscopic local magnetic probes. In the presence of a nonzero, static internal magnetic field the muon spin undergoes spontaneous Larmor precession with frequency \( \nu_{\mu} = (\gamma_{\mu}/2\pi)H_{\mathrm{int}} \) , where \( \gamma_{\mu}/2\pi = 13.553 \) kHz/G is the muon gyromagnetic ratio. The \( \mu SR \) technique in its variants (zero- or longitudinal-field) has proven extremely powerful in the field of small-moment magnetism, and in all cases, when magnetic order is of random, very short range, spatially inhomogeneous or incommensurate nature. \( ^{18} \) For this reason we employed it in studying the low-temperature transition in the magnetically dilute \( PbNi_{1.76}Mg_{0.24}V_{2}Os \) compound. The present oxides are isomorphous to the alkaline-earth vanadate \( SrNi_{2}V_{2}O_{8} \) \( ^{16} \) , and adopt a tetragonal crystal structure \( (a=b=12.24\ \text{\AA}, c=8.35\ \text{\AA}, \text{space group } I4_{1}cd) \) with arrays of \( NiO_{6} \) octahedra forming screw chains along the c axis. The chains are separated by \( VO_{4} \) tetrahedra and \( Pb^{2+} \) ions, resulting in an inherent quasi-1D arrangement of \( Ni^{2+} \) spins (S=1) with an average intrachain Ni-spin separation of \( \sim2.8\ \text{\AA} \) and the shortest interchain one of \( \sim5.9\ \text{\AA} \) . These compounds are good model systems to examine the effect of spin-vacancies on inducing LRO magnetism in low-dimensional solids. The temperature dependence of dc magnetic susceptibility, \( \chi_{\mathrm{dc}}(T) \) , measured at 0.1 T, for \( PbNi_{2-x}Mg_{x}V_{2}O_{8}\; (x = 0, 0.24) \) is shown in Fig. 1. It is worth noting the features in the low-temperature behavior \( (1.8 \leq T \leq 40\ K) \) of the parent compound \( (x = 0) \) . The susceptibility could be fitted well to the expression for spin-gap compounds \( ^{4,19} \) \[ \chi(T)=\chi(0)+\frac{C}{T}+\frac{a}{\sqrt{T}}\exp\Biggl(-\frac{\Delta_{\mathrm{e f f}}}{k T}\Biggr). \quad (1) \] In addition to a T-independent term, \( \chi(0)\approx1.71\times10^{-3} \) emu/mol, \( \chi_{\mathrm{dc}}(T) \) exhibits a minimum at \( \sim8 \) K, while at lower temperatures it follows a Curie law with \( C=3.66(2)\times10^{-3} \) emu K/mol. This behavior has been observed for all samples studied to date, and has been attributed to the presence of unidentified paramagnetic impurities. The Curie moment corresponds to \( \mu_{eff}\approx0.17\mu_{B} \) per formula unit. We propose that the upturn in the low-T susceptibility is due to the presence of free \( S=\frac{1}{2} \) spins at the ends of the chains terminating on the surface of the grains. Above 8 K, the susceptibility increases exponentially and exhibits a broad maximum around 120 K. The third term in Eq. (1) describes the bulk susceptibility due to the quasi-1D topology of the \( Ni^{2+} \) spins in the compound, where \( a\approx6.77\times10^{-2} \) emu \( K^{1/2}/mol \) is a constant factor and \( \Delta_{eff} \) is a finite effective spin gap. \( ^{4,19} \) A simple fitting of the susceptibility data between 1.8 and 40 K to Eq. (1) yields an estimate of the thermal activation energy \( \Delta_{eff}/k=45.3(1) \) K ( \( \sim3.9 \) meV). This is roughly consistent with the two gaps for noninteracting chains, as derived from inelastic neutron-scattering (INS) studies, \( ^{20} \) the transverse gap \( \Delta_{\perp}=\langle\Delta\rangle-0.57D=4.0(3) \) meV and the longitudinal one \( \Delta_{\parallel}=\langle\Delta\rangle+1.41D=3.1(3) \) meV, where \( \langle\Delta\rangle=0.41J \) is the Haldane gap in the isotropic chain \( ^{21} \) and D is the easy-axis (D<0) anisotropy, estimated to be -0.45 meV for \( PbNi_{2}V_{2}O_{8} \) . Furthermore, the high-temperature part ( \( 120\leq T\leq300 \) K) of the measured \( \chi_{\mathrm{dc}}(T) \) curve was fitted to a high-temperature series expansion derived for a S=1 1D HAF. \( ^{22} \) Having subtracted the Curie term from the data, the best fit was obtained for a nearest-neighbor intrachain exchange energy of J/k = -91.9(1) K ( \( \sim7.9 \) meV) and a Landé factor \( g\approx2.82 \) . The estimated in-chain coupling constant J differs by about 12% from that determined by INS measurements: \( J=9 \) meV. \( ^{20} \) From the susceptibility results on \( PbNi_{2}V_{2}O_{8} \) , we calculate a ratio \( \Delta_{eff}/|J|\sim0.5 \) , with theory predicting that for isotropic S=1 HAF chains the ratio would reach an ideal value of 0.41, \( ^{21} \) while deviations would imply important interactions between chains. The susceptibility data of the x=0.24 Mg-doped sample are in sharp contrast to those of the parent compound. Between 100 and 300 K, \( \chi_{\mathrm{dc}}(T) \) obeys the Curie-Weiss law \( \chi(T)=C/(T-\theta) \) . A linear fit to the \( \chi^{-1} \) vs T curve results in a Curie constant \( C=3.41(1) \) emu K/mol and a large Curie temperature \( \theta=-313.2(1) \) K, indicating strong antiferromagnetic spin correlations. In this high-temperature range, we estimate \( \mu_{eff}\approx2.98\mu_{B}/Ni^{2+} \) , which is close to the expected value for an S=1 paramagnetic Ni complex. At low temperatures, a pronounced “peak” in \( \chi_{\mathrm{dc}}(T) \) appears at \( \sim3.2 \) K, indicative of a magnetic phase transition. Both the peak position and the associated magnitude of the measured susceptibility, \( \chi_{\mathrm{dc}}(3.2\ \mathrm{K})\approx48.1\times10^{-3} \) emu/mol, are in FIG. 1. (a) Temperature dependence of the zero-field-cooled (ZFC) dc susceptibility \( \chi(T) \) for \( PbNi_{2}V_{2}O_{8} \) at \( H=0.1~T \) . (b) The ZFC evolution of \( \chi(T) \) for \( PbNi_{1.76}Mg_{0.24}V_{2}O_{8} \) under several magnetic fields ( \( H=0.1, 1.1, \) and 4.0 T). Inset: \( \chi_{dc} \) vs T, demonstrating marginal differences between ZFC and FC conditions. The solid lines for limited temperature ranges display the fit to the data with the functions described in Sec. III A. quantitative agreement with previous results. \( ^{14} \) Uchiyama and co-workers \( ^{14} \) reported a phase diagram for \( PbNi_{2-x}Mg_{x}V_{2}O_{8} \) in the \( T_{N} \) , x phase space, where the transition temperature rises rapidly at small x, then appears to display a maximum of \( \sim3.5 \) K at a composition around x = 0.16, while with further increase in x it decreases at a slow rate. These earlier dc susceptibility results indicate that while the “amplitude” of the peak scales with the concentration of the nonmagnetic Mg ions, its position depends on the Mg-impurity content in a nonmonotonic way. This enhancement may be attributed to the presence of free \( S=\frac{1}{2} \) spins at its ends of the chains, broken by the substitutional Mg cations. In Secs. III B and III C, we discuss the nature of this phase transition with the aid of neutron diffraction and \( \mu^{+}SR \) experiments. It is found to be a paramagnetic-to-antiferromagnetic phase transformation (vide infra). The dc susceptibility of \( PbNi_{1.76}Mg_{0.24}V_{2}Og \) exhibits a considerable field dependence, and is shown in Fig. 1(b) at representative fields. We note that very little deviation is observed at \( T FIG. 2. Magnetization M as a function of the applied magnetic field H for various temperatures above and below \( T_{N} \) (3.2 K) in \( PbNi_{1.76}Mg_{0.24}V_{2}O_{8} \) . The “arrow” marks the \( M(H) \) “inflection” point corresponding to the critical field \( [H_{c}(T)] \) for the transition to the metamagnetic phase. Inset: full hysteresis loop at \( T=1.8~K \) . actions. The result is that instead of causing the moments to flop perpendicular to the field (spin-flop phase \( ^{23} \) ), the antiferromagnet undergoes a first-order transition to a phase with a net magnetic moment. In the case of \( PbNi_{1.76}Mg_{0.24}V_{2}Os \) , this is demonstrated in Fig. 2. The magnetization M as a function of the applied field H is shown for temperatures below and above the AF ordering temperature \( T_{N}=3.2~K \) (under ZFC conditions). Well above \( T_{N} \) , the dc magnetization is linear with the applied magnetic field. For \( T Additionally, the dc applied magnetic field dependence of the real component of the ac susceptibility \( (h_{\mathrm{ac}}=1\mathrm{Oe}, f=1\mathrm{kHz}) \) for the \( PbNi_{1.76}Mg_{0.24}V_{2}Og \) compound, at \( T FIG. 3. dc magnetic field \( (H) \) dependence of the real part of the ac susceptibility \( [\chi'(H) \) , at \( h_{ac}=1 \) Oe, \( f=1 \) kHz] for \( PbNi_{1.76}Mg_{0.24}V_{2} \) O \( _{8} \) at \( T increasing temperature and disappears at \( T=T_{N} \) . The critical line defined this way (inset of Fig. 3) can be extrapolated to T=0 K, reaching an upper value of \( H_{c}=1.7(1) \) T. The latter was extracted by a phenomenological power-law fit of the type \( H_{c}(T)\sim H_{c}(0)\left[1-(T/T_{N})\right]^{n} \) , with n=0.68(5). The neutron powder diffraction pattern measured at 2 K is shown in Fig. 4(a). The chemical structure (space group \( I4_{1}cd \) ) is described well by the crystallographic model published for \( SrNi_{2}V_{2}O_{8} \) . \( ^{16} \) A few very weak extra peaks (e.g., at \( 2\theta\approx16.2^{\circ} \) , \( 36.6^{\circ} \) , and \( 51.1^{\circ} \) ), which are not indexed in the given space group, may originate from little amount of an impurity phase or/and from a small deviation from the space group. However, they are temperature independent, and thus could not be associated with the magnetic transition identified by \( \chi_{\mathrm{dc}}(T) \) . Important changes in the diffraction pattern were observed below \( T_{N}=3.2 \) K, where the magnetic susceptibility \( \chi(T) \) shows a prominent peak. The thorough investigation of the difference plot [Fig. 4(b)], between the 2- and 4-K neutron-diffraction patterns, showed marked intensity changes. All the peaks in the difference plot can be indexed on the basis of the tetragonal chemical unit cell \( [a=b=12.2448(7) \) Å and \( c=8.3592(7) \) Å at 2 K], implying that the chemical and magnetic unit cells coincide (magnetic propagation vector \( \kappa=[000] \) ). There is an increase in the intensity of reflections associated with nuclear Bragg peak positions [e.g., (220)] and the appearance of entirely new reflections, indexed as (011) and (031), which are extinct for the space group symmetry \( (I4_{1}cd) \) describing the chemical structure. Assuming that the spins are located at the 16 Ni 16b sites, we analyzed all spin configurations and their orientation with respect to the crystal axes by Rietveld refinements of the difference pattern. The absence of certain magnetic Bragg reflections, like (100)/(010), (110), and (001), produces strong constraints on the possible magnetic FIG. 4. Rietveld-refined neutron powder diffraction data ( \( \lambda = 2.567 \AA \) ) for \( PbNi_{1.76}Mg_{0.24}V_{2}O_{8} \) . Observed (points), calculated (full curve), and difference (bottom) profiles are shown. The upper (N) and lower (M) vertical lines mark the reflections due to chemical and the magnetic structures, respectively. (a) Full profile two-phase Rietveld refinement at 2 K. Inset: a schematic view of the unusual connectivity of the distorted \( NiO_{6} \) octahedral units along one quasi-1D chain of the unit cell. (b) Purely magnetic neutron diffraction pattern obtained by subtraction of the 2-K profile from that at 4 K. structures. For example, simple ferromagnetic spirals, antiferromagnetically coupled to each other would give large intensities at the \( (100) \) or \( (110) \) Bragg peak positions \( (2\theta\approx12.0^{\circ},17.0^{\circ}) \) . We have found that the spin configuration shown in Fig. 5(a) is the only one that describes the neutron data well. For this model, the calculated profile with the magnetic form factor for \( Ni^{2+} \) moment and the resulting difference curve from the observed data \( (\chi^{2}=1.55) \) are shown in Fig. 4(b). The 16 Ni atoms are arranged along four fourfold screw axes running along the c direction of the unit cell, resulting in an antiferromagnetic structure, with the spins lying only parallel or antiparallel to the c axis. That is, spins on the same chain (intrachain) and those at first nearest-neighbor chains along the a and b axes (interchain) in each \( (00z) \) -plane are coupled antiferromagnetically, whereas FIG. 5. The zero-field magnetic structure of \( PbNi_{1.76}Mg_{0.24}V_{2} O_{8} \) : (a) One chemical unit cell with the spin configuration of the \( Ni^{2+} \) ions at 2 K. (b) The temperature evolution of the antiferromagnetic \( (031)_{M} \) Bragg peak integrated intensity below \( T_{N}=3.2 \) K. The line over the data points is a guide to the eye. Inset: the temperature dependence of the integrated neutron intensity for the \( (200)_{N} \) and \( (211)_{N} \) nuclear Bragg peaks. those along the diagonal of the plane are coupled ferromagnetically. Figure 4(a) shows the results of the Rietveld refinement of the NPD profile of \( PbNi_{1.76}Mg_{0.24}V_{2}{O}_{8} \) at 2 K ( \( R_{wp} = 5.4\% \) , \( R_{exp} = 0.6\% \) ) with a two-phase model to account for both the chemical (space group: \( I4_{1}cd \) ) and magnetic (space group: P1) structures. Table I presents a compilation of the refined crystallographic parameters ( \( R_{Bragg} = 4.1\% \) ) together with selected bond distances for \( PbNi_{1.76}Mg_{0.24}V_{2}{}_{2}{O}_{8} \) . In the inset of Fig. 4(a), the deformed rhombic connectivity of apical [i.e., short Ni-O(2) and Ni-O(3)] and equatorial Ni-O bonds (Table II) is shown for the distorted \( NiO_{6} \) octahedra along the c axis of the unit cell. The medium resolution of the neutron data sets a limit for detailed refinement of the atom fractional coordinates and their site occupancies. We kept the latter constant to the values corresponding to the nominal stoichiometry of the compound. The atomic positions for Ni, Mg, and oxygen were refined, while those for V were not because of its small scattering length. Diffraction patterns with inferior experimental statistics (4 h/temperature) were measured in the range \( 1.6 \leq T \leq 5 \) K. The temperature evolution of the integrated intensity of the most intense (031) antiferromagnetic Bragg peak [Fig. 5(b)] TABLE I. Structural parameters derived from Rietveld refinements of the 2-K PbNi \( _{1.76} \) Mg \( _{0.24} \) V \( _{2} \) O \( _{8} \) neutron profile. Note: Vanadium fractional coordinates were not refined but kept constant to the position determined by earlier signal-crystal X-ray work on the isostructural SrNi \( _{2} \) V \( _{2} \) O \( _{8} \) (Ref. 16). Space group: \( I4_{1}c d \) . a=b=12.2448(7) Å and c=8.3592(7) Å. confirms that a LRO magnetic state starts to grow below a characteristic temperature \( T_{N}=3.2 \) K. In many systems, however, the large anisotropy in the interactions may promote canting, which leads to a weak ferromagnetic (FM) ground state. Therefore, we examined whether our NPD data could allow for any “rotation” of the local spin directions away from the “easy-axis” (c axis) spin configuration shown in Fig. 5(a). In the simplest case, if there is a FM component which is added to the main AF configuration, effectively leading to canting, it should give rise to some intensity contribution to the nuclear Bragg peaks. The inset of Fig. 5(b) shows the temperature dependence of the integrated neutron intensity for selected, (200) and (211), nuclear reflections. The lack of any temperature variation in their intensities, compared to that of the (031) AF reflection, and a Rietveld fit of the (2–4 K) difference pattern to the canted AF configuration, suggests that spin canting, if present, will account for less than \( \sim20\% \) of the AF moment. From the best Rietveld fit to the 2-K data \( (R_{\mathrm{Mag}}=20\%) \) , we extracted the average size of the magnetic moment per Ni ion, \( \langle\mu\rangle=0.9(1)\mu_{B} \) , in the AF spin configuration. It is worth noting that the ordered moment in \( PbNi_{1.76}Mg_{0.24}V_{2}O_{8} \) displays a marked reduction from the spin-only \( (\mu=gS) \) value of \( 2.0\mu_{B} \) expected for \( S=1~Ni^{2+} \) in antiferromagnetic or ferromagnetic substances. The unusual reduction of the experimentally deduced ordered moment poses certain questions about the microscopic mechanism responsible, which warrant further examination. Although low-dimensional “zero-point” spin fluctuations or nickel-oxygen covalency effects \( ^{25,26} \) cannot be excluded as being responsible for moment reduction in this compound, we also need to examine this effect within the framework of dilution-induced ordering phenomena in quasi-1D HAF’s. \( ^{12} \) One may wonder how the magnetic structure shown in Fig. 5(a) can represent the real physical picture when we have drawn spins at all the Ni sites, whereas for the x = 0.24 doping level we expect two out of the 16 Ni atoms in the unit cell to have been randomly replaced by Mg cations. Neither diffuse scattering nor peak broadening that would directly support spatial inhomogeneity in the moment size was evident in the neutron-diffraction experiments. The spatial inhomogeneity of ordered moments can be examined by local probe techniques such as muon-spin-relaxation ( \( \mu^{+}SR \) ) spectroscopy. \( \mu^{+}SR \) has a superb sensitivity to dilute and/or small magnetic moments, \( ^{18} \) and for this reason we employed it in its zero-field (ZF) form to study \( PbNi_{1.76}Mg_{0.24}V_{2} O_{8} \) . In Fig. 6, we present the Fourier transform of the \( ZF-\mu^{+}SR \) time spectrum at 1.82 K, and compare it with that in the parent material. The spectral distribution in the two compounds displays important differences related to the nature of their associated ground states. The presence of “peak structure” (i.e., at \( \nu_{\mu} \sim 0.5 \) , 1.5, and 2.6 MHz) in the Fourier transform of the doped compound suggests that the \( ZF-\mu^{+}SR \) signal is the result of the convolution of more than one static internal magnetic fields ( \( H_{int} \) ) at which the muon spin performs Larmor precession. No such features are evident in the Fourier spectrum of \( PbNi_{2}V_{2}O_{8} \) , in support of the disordered character of its nonmagnetic, dynamically modulated, spin-liquid ground state. Earlier \( ZF-\mu^{+}SR \) work on the doping effects on the linear-chain spin-Peierls \( (\mathrm{Cu}_{1-x}\mathrm{Zn}_{x})(\mathrm{Ge}_{1-y}\mathrm{Si}_{y})\mathrm{O}_{3} \) compound \( ^{27} \) demonstrated that induced staggered moments around the Zn or Si defects lead to antiferromagnetic order with large spatial inhomogeneity in the order moment size. In lightly doped (x or \( y \leqslant 0.02 \) ) spin-Peierls \( CuGeO_{3} \) single crystals, the field distribution and muon-spin precession TABLE II. Selected bond lengths ( \( \mathring{A} \) ) and bond angles (deg) in \( PbNi_{1.76}Mg_{0.24}V_{2}{O}_{8} \) at 2 K. The longer Ni-O(2) and Ni-O(3) bonds correspond to apical oxygen atoms along the \( NiO_{6} \) chains, and the shorter bonds together with those of Ni-O(1) and Ni-O(4) to equatorial oxygens. The subscripts in the angles are associated with lower (L) or higher (H) z-coordinate Ni atoms, respectively. in zero field arises from a single muon site, associated with a sizable internal field of \( H_{int} \sim 500 \) G. On the other hand, in the \( ZF-\mu^{+}SR \) experiments of polycrystalline \( PbNi_{1.76}Mg_{0.24}V_{2}O_{8} \) , the Fourier analysis resolves a number of intrinsically broad peaks, reflecting a nonhomogeneous internal field distribution, which is composed of a number of static local fields: \( H_{int} \sim 36 - 192 \) G. We note that the muon local field is proportional to the size of the nearby moments; \( H_{\mathrm{int}}(z) \sim \mu(z) \) . Therefore, multiple local fields in \( PbNi_{1.76}Mg_{0.24}V_{2}Og \) indicate spatial inhomogeneity in the order parameter (i.e., the staggered moment) of the antiferromagnetic ground state, that is a nonuniform ordered moment size along the \( NiO_{6} \) helical chains. Crystallographically nonequivalent muon sites, associated with the unusual topology of the \( Ni^{2+} \) ions in the 3D lattice, can give rise to such a complex internal field distribution. In the quasi-one-dimensional \( PbNi_{2}V_{2}O_{8} \) system, substitution of the magnetic \( Ni^{2+} \) (S=1) sites by nonmagnetic \( Mg^{2+} \) (S=0) cations leads to a transition from a magnetically disordered spin-gap ground state to essentially three-dimensional Néel order. We have investigated this effect for one Mg-substituted material, namely, \( PbNi_{1.76}Mg_{0.24}V_{2}Os_{8} \) , located in the “heavily doped” region of the \( T_{N} \) , x phase diagram. Neutron powder diffraction and muon-spin relaxation measurements were employed in the low-temperature range where the ac and dc susceptibility data illustrated that a magnetic transition takes place. Neutron powder diffraction in \( PbNi_{1.76}Mg_{0.24}V_{2}{O}_{8} \) probes an average size of the ordered \( ^{*} \) Corresponding author. Electronic address: lappas@iesl.forth.gr \( ^{1} \) S. Sachdev, Phys. World 12, 33 (1999). \( ^{2} \) E. Dagotto and T. M. Rice, Science 271, 618 (1996). \( ^{3} \) M. Hase, I. Terasaki, and K. Uchinokura, Phys. Rev. Lett. 70, 3651 (1993). \( ^{4} \) J. Darriet and L. P. Regnault, Solid State Commun. 86, 409 (1993). \( ^{5} \) M. Azuma, Z. Hiroi, M. Takano, K. Ishida, and Y. Kitaoka, Phys. Rev. Lett. 73, 3463 (1994). \( ^{6} \) F. D. M. Haldane, Phys. Rev. Lett. 50, 1153 (1983). FIG. 6. (a) The time evolution of the zero-field \(\mu^{+}\)-spin polarization \(P_{\mu}(t)\) for \(\mathrm{PbNi}_{2-x}\mathrm{Mg}_{x}\mathrm{V}_{2}\mathrm{O}_{8}\) (\(x=0\) and 0.24) at 1.82 K. The lines over the data points are guides to the eye. (b) The Fourier transform of the corresponding \(\mu^{+}\)SR time spectra. moment of \( 0.9(1)\mu_{B} \) per Ni site at 2 K. The spins in the Ni sublattice lie either parallel or antiparallel to the c axis, which is the magnetic easy axis of the system. The spin-spin interaction is antiferromagnetic (below \( T_{N}=3.2 \) K) both in the \( NiO_{6} \) -chains running along the c axis (intrachain) and within the ab plane for nearest-neighbor Ni atoms (interchain). Zero-field muon-spin relaxation below \( T_{N} \) confirms the static character of the magnetic interactions arising from the doping-induced, end-of-chain local moments. Also, it provides evidence of a nonuniform moment size over the severed chain segments. It manifests as a convolution of multiple spontaneous muon-precession frequencies that give rise to an internal magnetic field distribution with spatial inhomogeneities. The magnetic susceptibility shows that the compound exhibits metamagnetic behavior at \( T We thank N. Papanicolaou for discussions on the theory of quantum spin chains. It is a pleasure to acknowledge the technical assistance of A. Amato during the \( \mu^{+}SR \) experiments and L. Keller for the NPD measurements. The authors thank the Paul Scherrer Institute for the provision of neutron and muon beamtime. We also thank NATO for partial support under a “Collaborative Linkage Grant.” A.L. acknowledges additional financial support from the General Secretariat for Science & Technology (Greece) through a Greece-Slovenia “Joint Research & Technology Program.” \( ^{13} \) K. Kojima, A. Keren, L. P. Le, G. M. Luke, B. Nachumi, W. D. Wu, Y. J. Uemura, K. Kiyono, S. Miyasaka, H. Takagi, and S. Uchida, Phys. Rev. Lett. 74, 3471 (1995); C. Payen, E. Janod, K. Schoumacker, C. D. Batista, K. Hallberg, and A. A. Aligia, Phys. Rev. B 62, 2998 (2000). \( ^{14} \) Y. Uchiyama, Y. Sasago, I. Tsukada, K. Uchinokura, A. Zheludev, T. Hayashi, N. Miura, and P. Boni, Phys. Rev. Lett. 83, 632 (1999); K. Uchinokura, Y. Uchiyama, T. Masuda, Y. Sasago, I. Tsukada, A. Zheludev, T. Hayashi, N. Miura, and R. Boni, Physica B 284–288, 1641 (2000). \( ^{15} \) V. Pomjakushin, A. Lappas, V. Alexandrakis, J. Giapintzakis, K. Prassides, and A. Schenck, Paul Scherrer Institute, Scientific Report 2000, Vol. III, p. 37. \( ^{16} \) R. Wichmann and Hk. Müller-Buschbaum, Rev. Chim. Miner. 23, 1 (1986). \( ^{17} \) J. Rodriguez-Carvajal, Physica B 192, 55 (1993). \( ^{18} \) A. Schenck and F. N. Gygax, in Handbook of Magnetic Materials, edited by K. H. J. Buschow (Elsevier, Amsterdam, 1995), Vol. 9, Chap. 2, pp. 57–301. \( ^{19} \) I. Affleck, Phys. Rev. B 41, 6697 (1990); M. Troyer, H. Tsunetsugu, and D. Wurtz, ibid. 50, 13 515 (1994). \( ^{20} \) A. Zheludev, T. Masuda, I. Tsukada, Y. Uchiyama, K. Uchinokura, P. Boni, and S.-H. Lee, Phys. Rev. B 62, 8921 (2000). \( ^{21} \) M. P. Nightingale and H. W. Blöte, Phys. Rev. B 33, 659 (1986). \( ^{22} \) C. Y. Weng, Ph.D. thesis, Carnegie Mellon University, Pittsburgh, 1968; V. Gadet, M. Verdaguer, V. Briois, A. Gleizes, J. P. Renard, P. Beauvillain, C. Chappert, T. Goto, K. Le Dang, and P. Veillet, Phys. Rev. B 44, 705 (1991). \( ^{23} \) L. J. de Jongh and A. R. Miedema, Adv. Phys. 23, 1 (1974). \( ^{24} \) E. Stryjewski and N. Giordano, Adv. Phys. 26, 487 (1977). \( ^{25} \) D. E. Cox and V. J. Minkiewicz, Phys. Rev. B 4, 2209 (1971). \( ^{26} \) L. J. de Jongh, Solid State Commun. 65, 963 (1988). \( ^{27} \) K. M. Kojima, Y. Fundamoto, M. Larkin, G. M. Luke, J. Merrin, B. Nachumi, Y. J. Uemura, M. Hase, Y. Sasago, K. Uchinokura, Y. Ajiiro, A. Revcolevschi, and J.-P. Renard, Phys. Rev. Lett. 79, 503 (1997).I. INTRODUCTION
II. EXPERIMENTAL DETAILS
III. RESULTS AND DISCUSSION
A. Macroscopic magnetic properties



B. Powder neutron-diffraction measurements




Atom Wyckoff position x/a y/b z/c Occupancy Pb 8a 0 0 0 0.5 Ni 16b 0.3262(9) 0.3303(7) 0.1714(14) 0.88 Mg 16b 0.3262(9) 0.3303 (7) 0.1714(14) 0.12 V 16b 0.2596 0.0802 0.1015 1.0 O(1) 16b 0.155(1) 0.495(2) -0.097(2) 1.0 O(2) 16b 0.338(2) 0.655(1) 0.434(2) 1.0 O(3) 16b 0.161(2) 0.689(1) 0.671(2) 1.0 O(4) 16b 0.330(1) 0.499(1) 0.199(2) 1.0 C. Muon-spin relaxation measurements
d_{\mathrm{Pb-O}}/\mathring{\mathrm{A}} d_{\mathrm{Ni-O}}/\mathring{\mathrm{A}} Bond angles/deg Pb-O(1) 2.288(25)\times2 Ni-O(1) 2.081(16) Ni-O(2)-Ni 88.1(6) 3.464(19)\times2 Ni-O(2) 1.997(21) Ni-O(3)-Ni 86.5(7) Pb-O(2) 2.796(18)\times2 2.080(19) O(3)-Ni_{L}-O(2) 90.7(1.2) Pb-O(3) 3.107(18)\times2 Ni-O(3) 2.042(24) O(3)-Ni_{H}-O(2) 94.7(1.4) Pb-O(4) 2.661(14)\times2 2.096(22) 3.267(14)\times2 Ni-O(4) 2.089(21)


IV. CONCLUSIONS
ACKNOWLEDGMENTS