| Transition Temperature | 60 K |
|---|---|
| Experiment Temperature | 1.6 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | Pbnm (#62) |
| Magnetic Space Group | P21/c (#14.75) |
| Magnetic Point Group | 2/m (5.1.12) |
| Lattice Parameters | 5.26440 5.58560 7.57160 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1103/physrevb.83.064404 |
| Reference | M. Reehuis, C. Ulrich, K. Prokes, S. Mat'as, J. Fujioka, S. Miyasaka, Y. Tokura and B. Keimer, Physical Review B (2011) 83. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Er1 | Er | 0.0 | 0.0 | 8.2 | 8.20 |
| V1_1 | V | 0.0 | 0.0 | 1.47 | 1.47 |
| V1_2 | V | 0.0 | 0.0 | -1.47 | 1.47 |
Structural and magnetic phase transitions of the orthovanadates \( RVO_{3} \) (R = Dy, Ho, Er) as seen via neutron diffraction
M. Reehuis, \( ^{1} \) C. Ulrich, \( ^{2,3,4} \) K. Prokeš, \( ^{1} \) S. Mat’aš, \( ^{1} \) J. Fujioka, \( ^{5,6} \) S. Miyasaka, \( ^{7} \) Y. Tokura, \( ^{5,6,8} \) and B. Keimer \( ^{2} \)
\( ^{1} \) Helmholtz-Zentrum Berlin für Materialien und Energie, D-14109 Berlin, Germany
\( ^{2} \) Max-Planck-Institut für Festkörperforschung, D-70569 Stuttgart, Germany
\( ^{3} \) Australian Nuclear Science and Technology Organisation (ANSTO), Postal Mail Box 1 Menai, New South Wales 2234, Australia
\( ^{4} \) University of New South Wales, Sydney, New South Wales 2052, Australia
\( ^{5} \) Department of Applied Physics, University of Tokyo, 113 Tokyo, Japan
\( ^{6} \) Multiferroics Project, ERATO, Japan Science and Technology Agency, Wako 351-0198, Japan
\( ^{7} \) Department of Physics, Graduate School of Science, Osaka University, Osaka 560-0043, Japan
\( ^{8} \) Cross-Correlated Materials Research Group (CMRG) and Correlated Electron Research Group (CERG),
RIKEN Advanced Science Institute, Wako 351-0198, Japan
(Received 13 October 2010; published 10 February 2011)
The structural and magnetic phase behavior of \( RVO_{3} \) with R = Dy, Ho, and Er was studied by single-crystal neutron diffraction. Upon cooling, all three compounds show structural transitions from orthorhombic (space group \( Pbnm \) ) to monoclinic ( \( P2_{1}/b \) ) symmetry due to the onset of orbital order at \( T = 188-200 \) K, followed by Néel transitions at \( T = 110-113 \) K due to the onset of antiferromagnetic (C-type) order of the vanadium moments. Upon further cooling, additional structural phase transitions occur for \( DyVO_{3} \) and \( ErVO_{3} \) at 60 and 56 K, respectively, where the monoclinic structure changes to an orthorhombic structure with the space group \( Pbnm \) , and the magnetic order of the V sublattice changes to a G-type structure. These transition temperatures are reduced compared to the ones previously observed for nonmagnetic \( R^{3+} \) ions due to exchange interactions between the \( V^{3+} \) and \( R^{3+} \) ions. For \( ErVO_{3} \) , R-R exchange interactions drive a transition to collinear magnetic order at \( T = 2.5 \) K. For \( HoVO_{3} \) , the onset of noncollinear, weakly ferromagnetic order of the Ho moments nearly coincides with the structural phase transition from the monoclinic to the low-temperature orthorhombic structure. This transition is characterized by an extended hysteresis between 24 and 36 K. The Dy moments in \( DyVO_{3} \) also exhibit noncollinear, weakly ferromagnetic order upon cooling below 13 K. With increasing temperature, the monoclinic structure of \( DyVO_{3} \) reappears in the temperature range between 13 and 23 K. This reentrant structural transition is associated with a rearrangement of the Dy moments. A group theoretical analysis showed that the observed magnetic states of the \( R^{3+} \) ions are compatible with the lattice structure. The results are discussed in the light of recent data on the magnetic field dependence of the lattice structure and magnetization of \( DyVO_{3} \) and \( HoVO_{3} \) .
DOI: 10.1103/PhysRevB.83.064404
PACS number(s): 75.25.−j, 75.50.Ee, 61.05.fm, 61.66.Fn
I. INTRODUCTION
The interplay between spin and orbital degrees of freedom in transition metal oxides generates a multitude of collective ordering phenomena that are associated with a large variety of physical properties. Mott-insulating orthovanadates of chemical composition \( RVO_{3} \) (R = Y or trivalent rare-earth metal) are particularly interesting examples. \( ^{1-22} \) The \( V^{3+} \) ions in these compounds have a \( 3d^{2} \) -electron configuration with spin 1 and reside on a nearly cubic sublattice of the perovskite structure. Despite their seemingly simple electronic structure, one observes multiple temperature-induced structural and magnetic phase transitions, which can be attributed to the nearly degenerate vanadium \( t_{2g} \) orbitals whose occupation controls the exchange interactions between the magnetic moments on adjacent lattice sites. In the intensely investigated compound \( YVO_{3} \) , for instance, one observes three phase transitions upon cooling below room temperature. \( ^{1-9} \) At \( T_{S1} = 200 \) K, the lattice structure first changes from a high-temperature orthorhombic phase (space group \( Pbnm \) ) to a monoclinic structure with the space group \( P2_{1}/b \) . Based on the observation of a distortion of the \( VO_{6} \) octahedra through the cooperative Jahn-Teller effect and a concomitant modification of the optical absorption spectrum, this transition can be attributed to orbital ordering. \( ^{7,8} \) While the xy orbital is believed to be lowest in energy and always occupied by one of the two d electrons, the occupancy of the remaining \( t_{2g} \) orbitals, \( xz \) and \( yz \) , fluctuates at high temperatures and is locked into a G-type ordering pattern (with staggered occupation along all three spatial directions) for \( T < T_{S1} \) . The anisotropic pattern of exchange interactions generated by orbital ordering, combined with the intra-atomic spin-orbit interaction, then determines the ordering pattern of the vanadium moments below the Néel temperature \( T_{N1} = 114 \) K. The orientation of the vanadium spins below \( T_{N1} \) is noncollinear and can be described by a superposition of C-type order of the xy components (with antiferromagnetic alignment in the xy plane and ferromagnetic alignment along the z axis) and G-type order of the z components. \( ^{6,9} \) Finally, the lattice symmetry changes back to \( Pbnm \) upon cooling below \( T_{S2} = 78 \) K. This structural transition can be attributed to a rearrangement of the orbitals into a C-type ordering pattern and is accompanied by a reorientation of the magnetic moments into a collinear G-type pattern. The unusual spin dynamics of \( YVO_{3} \) in the intermediate-temperature phase ( \( T_{S2} < T < T_{N1} \) ) has
stimulated theoretical proposals according to which fluctuations of the \( xz \) and \( yz \) orbitals are not completely quenched by the crystal field. \( ^{13-17} \) The possibility of strong combined spin-orbital quantum fluctuations continues to motivate theoretical work on the pseudocubic vanadates and related compounds.
In order to obtain a realistic description of the spin-orbital phase behavior of the vanadates and other transition metal oxides with perovskite structure, one has to consider the influence of the \( GdFeO_{3} \) rotation pattern of the metal oxide octahedra that is generated by steric constraints in the crystal lattice. The strength of the \( GdFeO_{3} \) distortion is controlled by the radius \( r_{R} \) of the \( R^{3+} \) ions in \( RVO_{3} \) , which decreases continuously with increasing atomic number due to the well-known lanthanide contraction. This distortion, in turn, influences the orbital occupation via the crystal field as well as the interatomic hopping parameters via the V-O-V bond angle. Specific heat, magnetization, and Raman scattering measurements have shown that the structural and magnetic phase transitions exhibit a systematic trend as a function of \( r_{R} \) . \( ^{8} \) In particular, it was found that the second structural and magnetic phase transition at \( T_{S2} \) only appears for vanadates with ionic radii smaller than that of \( Tb^{3+} \) , while the transition temperatures \( T_{S1} \) and \( T_{N1} \) depend smoothly on \( r_{R} \) . This and other aspects of the vanadate phase diagram can be understood as a consequence of the influence of the lattice structure on the orbital occupation and the exchange interactions. \( ^{17} \)
A recent investigation of \( DyVO_{3} \) led to the discovery of a reentrant transition back to C-type magnetic and G-type orbital order at low temperatures. \( ^{[21]} \) A related transition can also be induced by an external magnetic field. In \( HoVO_{3} \) , on the other hand, application of a magnetic field favors G-type magnetic and C-type orbital order. \( ^{[22]} \) These observations highlight the influence of the localized 4f magnetic moments of the \( R^{3+} \) ions on the spin-orbital phase behavior. Neutron diffraction experiments on \( CeVO_{3} \) , \( NdVO_{3} \) , and \( TbVO_{3} \) have shown that the moments of the lanthanide ions are gradually polarized by the ordered vanadium moments for temperatures below about 60 K. \( ^{[9,11]} \) This indicates the presence of substantial R-V exchange interactions. For \( TbVO_{3} \) and \( HoVO_{3} \) , it was shown that the R-R exchange coupling then induces noncollinear order of the \( R^{3+} \) ions below \( T_{N2} = 11 \) K (Ref. 9) and 13 K (Ref. 18), respectively. However, related studies have not yet been reported for R = Dy and Er, presumably because of the large neutron absorption cross section of these ions.
The purpose of the present paper is to provide an experimental description of the magnetic order of the R and V sublattices in DyVO \( _{3} \) and ErVO \( _{3} \) . In view of the renewed interest in HoVO \( _{3} \) , we have also reinvestigated the crystal structure and magnetic ordering of this compound. While our overall picture is similar to the one of Ref. 18, some aspects of the magnetic structure are different. We discuss our results in the light of related observations on the vanadates, including in particular the magnetic-field-dependent phase behavior of DyVO \( _{3} \) and HoVO \( _{3} \) , as well as other compounds containing both 3d and 4f ions.
II. EXPERIMENTAL DETAILS
Single-crystal neutron diffraction data were collected on the four-circle diffractometer E5 and the two-axis diffractometer E4 at the BER II reactor of the Helmholtz-Zentrum Berlin. For our experiments we used cylindrical untwinned crystals of \( DyVO_{3} \) , \( HoVO_{3} \) , and \( ErVO_{3} \) with a diameter of 3 mm and a height of 5 mm. The crystals were grown by the floating-zone method as described elsewhere. \( ^{[19]} \) The seed-skewness integration method \( ^{[23]} \) as well as the method developed by Wilkinson et al. \( ^{[24]} \) were applied to determine the Bragg intensities. Due to the large absorption cross section of dysprosium all data sets (nuclear and magnetic Bragg intensities) of \( DyVO_{3} \) were collected on the instrument E5 using the shorter neutron wavelength \( \lambda = 0.89 \AA \) selected by a Cu monochromator. For the investigation of the magnetic structures of \( HoVO_{3} \) and \( ErVO_{3} \) we collected data sets using a pyrolytic-graphite (PG) monochromator selecting the longer neutron wavelength \( \lambda = 2.38 \AA \) . At 150 K, well above the Néel temperature, we collected data sets of all these vanadates in order to determine the overall scale factor from the crystal structure refinements. With the absorption- and extinction-corrected magnetic structure factors, we were able to obtain the magnetic moments of the metal ions in the magnetically ordered states. The magnetic order of the erbium moments of \( ErVO_{3} \) , which sets in at low temperature, was investigated on the instrument E4 using the neutron wavelength \( \lambda = 2.45 \AA \) selected by a PG monochromator. The refinements of the crystal structure were carried out with the program XTAL 3.4. \( ^{[25]} \) Here the nuclear scattering lengths \( b(\mathrm{O}) = 5.805 \) fm, \( b(\mathrm{V}) = -0.3824 \) fm, \( b(\mathrm{Dy}) = 16.9 \) fm, \( b(\mathrm{Ho}) = 8.08 \) fm, and \( b(\mathrm{Er}) = 8.03 \) fm were used. \( ^{[26]} \) The moments of the V and R atoms were refined with the program FULLPROF. \( ^{[27]} \) The magnetic form factors of the \( V^{3+} \) , \( Dy^{3+} \) , \( Ho^{3+} \) , and \( Er^{3+} \) ions were taken from Ref. 28.
III. RESULTS AND DISCUSSION
A. Crystal structure of HoVO_{3}
For \( HoVO_{3} \) , where the neutron absorption is much lower than that of the Dy and Er vanadates, we have investigated the crystal structure by single-crystal neutron diffraction at room temperature. The structure refinements were performed in the orthorhombic space group \( Pbnm \) (no. 62, standard setting \( Pnma \) ), using the atomic parameters of \( YVO_{3} \) as starting values. \( ^{7} \) A large number of 2184 Bragg reflections (697 unique) allowed us to accurately determine the positional parameters of the Ho, O1 (Wyckoff position 4c: \( x,y,\frac{1}{4} \) ), and O2 atoms (Wyckoff position 8d: \( x,y,z \) ) as well as the anisotropic thermal parameters. Due to the small scattering power of the vanadium atoms [in the position \( 4b(\frac{1}{2},0,0) \) ] an isotropic thermal parameter \( U_{is} = 0.0040 \, \AA^{2} \) was fixed, and it was not allowed to vary during the refinements. The refinements of a total of 23 parameters (the overall scale and extinction factor, 7 positional parameters, and 14 anisotropic thermal parameters) resulted in residuals \( R(F) = 0.018 \) and \( wR(F) = 0.017 \) . In Table I it can be seen that the obtained standard deviations are about one order of magnitude smaller than those obtained earlier by neutron powder diffraction. \( ^{12} \) On the other hand, Blake et al. \( ^{20} \) were able to reach a slightly better precision from their single-crystal neutron diffraction study. Nevertheless the values obtained in all the experiments agree very well. Only the thermal parameters \( U_{22} \) given in Ref. 20 were found to be somewhat larger than in our study. Good
TABLE I. Results of the structure refinements of the single-crystal data of \( HoVO_{3} \) collected at 295 K. The positional parameters are compared with those obtained earlier by neutron powder and single-crystal diffraction (Refs. 12 and 20). The thermal parameters \( U_{ij} \) (given in 100 Ų) are in the form \( \exp[-2\pi^{2}(U_{11}h^{2}a^{2}+\cdots+2U_{13}hla^{c}c^{c})] \) . For symmetry reasons the values \( U_{13} \) and \( U_{23} \) of the Ho and O1 atoms are equal to zero for the space group Pbnm. In Ref. 12 only the isotropic thermal parameters were given. \( a=5.2752(4) \) Å, \( b=5.6066(4) \) Å, \( c=7.5830(6) \) Å, and \( V=224.27(3) \) ų.
| Pbnm | x | y | z | U11 | U22 | U33 | U12 | U13 | U23 | Population |
| Ho | 0.980 73(4) | 0.068 71(4) | 1/4 | 0.412(9) | 0.362(7) | 0.440(8) | -0.048(6) | 0 | 0 | 1.003(2) |
| 0.980 73(2)a | 0.068 63(4)a | 1/4 | 0.514(3)a | 0.624(10)a | 0.517(3)a | -0.045(3)a | 0 | 0 | 0.993(6)b | |
| 0.9811(4)c | 0.0667(4)c | 1/4 | 0.41(5)c | 1.000c | ||||||
| V | 1/2 | 0 | 0 | 0.400 | 0.400 | 0.400 | 0 | 0 | 0 | 1.000 |
| 0.989(7)b | ||||||||||
| O1 | 0.110 34(7) | 0.461 07(5) | 1/4 | 0.611(13) | 0.671(10) | 0.474(10) | -0.089(8) | 0 | 0 | 0.997(3) |
| 0.110 56(3)a | 0.461 37(6)a | 1/4 | 0.691(4)a | 0.934(14)a | 0.486(4)a | -0.083(5)a | 0 | 0 | 1.000b | |
| 0.1108(5)c | 0.4604(6)c | 1/4 | 0.85(8)c | 1.000c | ||||||
| O2 | 0.691 40(5) | 0.303 94(4) | 0.055 96(3) | 0.578(10) | 0.609(8) | 0.760(8) | -0.111(6) | 0.089(6) | -0.120(5) | 0.998(2) |
| 0.691 48(2)a | 0.303 78(5)a | 0.056 00(2)a | 0.660(3)a | 0.858(12)a | 0.783(3)a | -0.106(4)a | 0.087(2)a | -0.126(4)a | 1.000b | |
| 0.6909(4)c | 0.3045(4)c | 0.0553(2)c | 0.82(5)c | 1.000c |
\( ^{a} \) From single-crystal neutron diffraction, Ref. 20.
\( ^{b} \) From synchrotron powder data, Ref. 20.
\( ^{c} \) From high-resolution neutron powder data, Ref. 12.
agreement is also found for the V-O bond lengths: \( d_{V1-O11} = 1.9936(2) \) Å, \( d_{V1-O21} = 2.0082(3) \) Å, \( d_{V1-O22} = 2.0241(3) \) Å (present work); \( d_{V1-O11} = 1.9979(9) \) Å, \( d_{V1-O21} = 2.011(2) \) Å, \( d_{V1-O22} = 2.024(2) \) Å (Ref. 12); \( d_{V1-O11} = 1.9944(1) \) Å, \( d_{V1-O21} = 2.0108(2) \) Å, \( d_{V1-O22} = 2.O254(3) \) Å (Ref. 20). Further, it can be seen that the structural parameters of \( HoVO_{3} \) are very similar to those of \( YVO_{3} \) \( ^{9} \) , as expected based on the similar radii of \( Y^{3+} \) (r = 1.015 Å) and \( Ho^{3+} \) (r = 1.019 Å) \( ^{29} \) .
These experiments also allowed us to assess the quality of the crystals. The absence of peaks such as (011), (013), or (203), which are forbidden in the space group \( Pbnm \) , clearly showed that the single crystal of \( HoVO_{3} \) is completely untwinned. We observed the same behavior for \( DyVO_{3} \) and \( ErVO_{3} \) . We further refined the occupancies of the Ho and the two different O sites. In Table I it can be seen that all these atoms show the full population, so that the sample is stoichiometric. Due to the fact that the single crystals of \( DyVO_{3} \) and \( ErVO_{3} \) were grown in the same way by the floating-zone method, one may assume that the crystals of these two vanadates also show the same high quality.
B. Structural and magnetic phase transitions of \( ErVO_{3} \) , \( HoVO_{3} \) , and \( DyVO_{3} \)
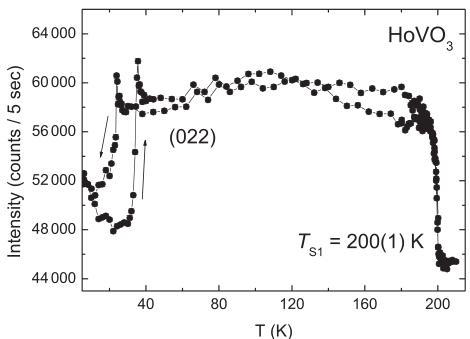
We now discuss the sequence of structural and magnetic phase transitions of \( RVO_{3} \) with R = Er, Ho, and Dy in the order of increasing radius of the \( R^{3+} \) ions. Since the \( R^{3+} \) ions in all three compounds are smaller than \( Tb^{3+} \) , they exhibit the same transition sequence \( T_{S1} \rightarrow T_{N1} \rightarrow T_{S2} \) upon cooling. Since the high-temperature structural phase transition from \( Pbnm \) to \( P2_{1}/b \) symmetry is common to all three compounds and weakly influenced by the \( R^{3+} \) ions, this transition was only studied for \( HoVO_{3} \) , for which the neutron absorption is minimal. In analogy to related observations in \( YVO_{3} \) , this transition is apparent in a pronounced intensity change of the (022) reflection at \( T_{S1} = 200(1) \) K (Fig. 1). The transition temperature extracted in this way is in good agreement with the one that was determined by thermal expansion measurements \( ^{30} \) and other thermodynamic probes. \( ^{8} \) Specific-heat measurements showed that \( T_{S1} = 188 \) and 193 K for \( DyVO_{3} \) and \( ErVO_{3} \) , respectively. \( ^{8} \) The lower-temperature transitions are influenced by the \( R^{3+} \) ions and will now be discussed separately for each compound.
1. ErVO_{3}
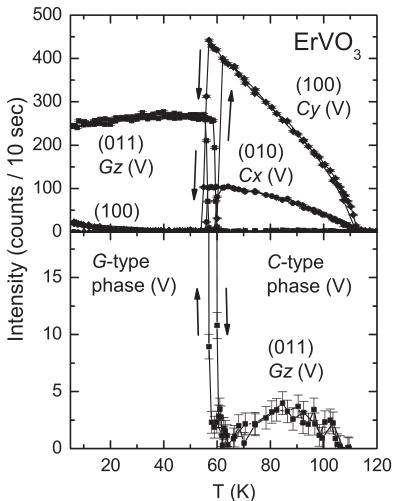
Figure 2 shows the temperature dependence of selected Bragg intensities of \( ErVO_{3} \) . The ordering of the V moments is apparent from the intensity of the (100) and (010) reflections, in analogy to observations in other vanadates. \( ^{9} \) The Néel temperature \( T_{N1} = 112(1) \) K is in good agreement with

FIG. 1. Temperature dependence of the strong nuclear reflection (022) of \( HoVO_{3} \) . At \( T_{S1} = 200 \) K a structural phase transition occurs from the high-temperature orthorhombic (Pbnm) into the monoclinic structure ( \( P2_{1}/b \) ). A strong hysteresis was found at the second phase transition in the range \( 24 < T_{S2} < 35 \) K, where the monoclinic phase changes to the low-temperature orthorhombic structure with the same space group, Pbnm, as observed above \( T_{S1} \) .
TABLE II. Magnetic moments of the V and R atoms in \( DyVO_{3} \) , \( HoVO_{3} \) , and \( ErVO_{3} \) in the magnetically ordered state. The modes \( F(++++) \) , \( C(++--) \) , and \( G(+-+-+) \) represent the spin sequences of the R and V atoms located in the Wyckoff position \( 4c(x,y,1/4; -x,-y,3/4; 1/2-x,1/2+y,1/4; 1/2+x,1/2-y,3/4) \) , and \( 4b(1/2,0,0; 1/2,0,1/2; 0,1/2,0; 0,1/2,1/2) \) , respectively.
| Basis vectors (R) | \( \mu_{x} \) ( \( \mu_{B} \) ) | \( \mu_{y} \) ( \( \mu_{B} \) ) | \( \mu_{z} \) ( \( \mu_{B} \) ) | \( \mu_{\text{expt}} \) ( \( \mu_{B} \) ) | Basis vectors (V) | \( \mu_{x} \) ( \( \mu_{B} \) | \( \mu_{y} \) ( \( \mu_{B} \) | \( \mu_{z} \) ( \( \mu_{B} \) | \( \mu_{\text{expt}} \) ( \( \mu_{B}) \) | |
| DyVO \( _{3} \) at 6 K | \( (C_{x}, F_{y}, -) \) 82% | 4.8(2) | 6.1(3) | 0 | 7.8(3) \( ^{a} \) | \( (-,-,G_{z}) \) | 1.45 \( ^{b} \) | 1.45 \( ^{b} \) | ||
| \( (F_{x}, C_{y}, -) \) 18% | 3.1(2) | 7.1(3) | 0 | 7.8(3) \( ^{a)} \) | \( (C_{x}, C_{y}, G_{z}) \) | |||||
| DyVO \( _{3} \) at 13.5 K | \( (F_{x}, C_{y}, -) \) | 2.4(2) | 5.7(3) | 0 | 6.2(3) | \( (C_{x}, C_{y}, G_{z}) \) | c | c | c | c |
| \( (F_{x}, C_{y}, G_{z}) \) | 2.3(2) | 6.1(2) | 2.1(2) | 6.9(3) | \( (-,-,G_{z}) \) | 0 | 0 | 1.42(3) | 1.42(3) | |
| HoVO \( _{3} \) at 6 K | \( (F_{x}, C_{y}, G_{z}) \) | 2 | 6.1(2) | 2.1(2) | 6 | \( (C_{x}, C_{y}, G_{z}) \) | 1.13(3) | c | c | c |
| HoVO \( _{3} \) at 25 K | \( (C_{x}, C_{y}, G_{z}) \) | 0.69(3) | 1.01(4) | 0.26(3) | 1.25(3) | |||||
| HoVO \( _{3} \) at 85 K | ||||||||||
| \( (-,-,C_{z}) \) | 0 | 0 | 8.2(2) | 8.2(2) | \( (-,-,G_{z}) \) | 0 | 0 | 1.47(3) | 1.47(3) | |
| ErVO \( _{3} \) at 1.6 K | \( (-,-,C_{z}) \) | 0 | 0 | 8 | \( (C_{x}, C_{y}, G_{z}) \) | \( (C_{x}, C_{y}, G_{z}) \) | 0.69(4) | 1.55(5) | ||
| ErVO \( _{3} \) at 57 K | \( (C_{x}, G_{y}, G_{z}) \) | 0.56(4) | 1.04(5) | |||||||
| ErVO \( _{3} \) at 85 K | 8.2(2) | 8.2(2) | \( (C_{x}, C_{y}, G_{z}) \) | 0.56(4) | ||||||
\( ^{a} \) Experimental moment \( \mu_{expt} \) was assumed to be the same for both coexisting magnetic phases.
\( ^{b} \) Fixed during the refinements.
\( ^{c} \) Not obtained from the refinement.
previous results \( [T_{N1} = 110(1) \) K (Ref. 8)] and similar to \( T_{N1} = 114 \) K observed for \( YVO_{3} \) .⁶⁻⁹ The data analysis showed that the magnetic structure is predominantly of C type, where the spin sequence is + + + - for the V atoms in the position \( 4b(\frac{1}{2},0,0; \frac{1}{2},0,\frac{1}{2},0;\frac{1}{2},0;0,\frac{1}{2},\frac{1}{2}) \) . The magnetic moments obtained from the refinement of the magnetic structure at T = 85 K are listed in Table II. For the C-type components along the a and b axes we obtained the values \( \mu_{x} = 0.56(3)\mu_{B} \) and \( \mu_{y} = 1.04(3)\mu_{B} \) . At the same temperature

FIG. 2. Temperature dependence of the magnetic reflections (100), (010), and (011) of \( ErVO_{3} \) . Below \( T_{N1} = 112 \) K the C-type ordering of the vanadium moments sets in. The strong magnetic intensities on the reflections (100) and (010) suggest the presence of the modes \( C_{y} \) and \( C_{x} \) , respectively; the weak intensity on the (011) the presence of \( G_{z} \) . Below about 60 K the magnetic structure changes to a pure G-type ordering along the c direction.
we found slightly smaller moments of \(\mu_{x}=0.49(3)\mu_{\mathrm{B}}\) and \(\mu_{y}=0.89(2)\mu_{\mathrm{B}}\) for \(\mathrm{YVO}_{3}\).⁹⁹ Since the \(\mathrm{Er}^{3+}\) ions are strongly paramagnetic, whereas \(\mathrm{Y}^{3+}\) is diamagnetic, a polarization of the erbium moments by the ordered vanadium moments may result in a weakly induced moment of the \(\mathrm{Er}^{3+}\) ions that enhances the observed magnetic moment. The presence of the (011) reflection in Fig. 2 further indicates a weak \(G_{z}\) component of the magnetic order, again in analogy to prior observations on \(\mathrm{YVO}_{3}\).⁹
With decreasing temperature we found the expected first-order transition into the phase with \( Pbnm \) lattice symmetry and G-type magnetic order at \( T_{S2} = 56(1) \) K, while with increasing temperature it was found at \( T_{S2} = 61(1) \) K (Fig. 2). The transition temperature \( T_{S2} \) is lower and the hysteresis \( \Delta T_{S2} \) larger than corresponding values for \( YVO_{3} \) [ \( T_{S2} = 76.0(5) \) K with decreasing temperature; \( \Delta T_{S2} = 2.5(3) \) K] and \( LuVO_{3} \) [ \( T_{S2} = 81.3(5) \) K; \( \Delta T_{S2} = 1.3(2) \) K], which contain nonmagnetic \( R^{3+} \) ions. \( ^{31} \) The difference reflects the influence of Er–V exchange interactions. The ordered vanadium moment in the G-type phase at 6 K, \( \mu_{z} = 1.47(3)\mu_{B} \) , is somewhat smaller than the corresponding value of \( 1.72(5)\mu_{B} \) in \( YVO_{3} \) .
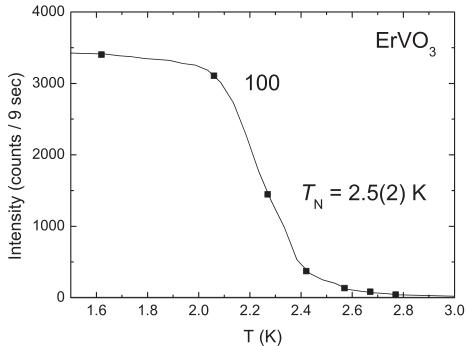
Upon further cooling below \( T_{N2} = 2.5 \) K a spontaneous increase of the reflection (100) was observed (Fig. 3). This suggests the onset of long-range magnetic ordering of the erbium sublattice driven by direct coupling between the 4f moments. In order to guide the refinement of the magnetic structure, we have determined the possible ordering patterns of the R moments in \( RVO_{3} \) compatible with the orthorhombic space group \( Pbnm \) and the propagation vector k = 0 using Bertaut's representation analysis. \( ^{32} \) Table III summarizes the transformation properties of the modes \( F(++++) \) , \( C(+-+-) \) , \( G(+-+-+) \) , and \( A(+-+-+) \) of the \( R^{3+} \) ions located in the Wyckoff position 4c: (1) \( x, y, \frac{1}{4} \) ; (2) \( -x, -y, \frac{3}{4} \) ; (3) \( \frac{1}{2} - x, \frac{1}{2} + y, \frac{1}{4} \) ; (4) \( \frac{1}{2} + x, \frac{1}{2} - y, \frac{3}{4} \) . Note that an analogous analysis for the V sublattice has been reported earlier. \( ^{9} \)
For \( ErVO_{3} \) , the absence of intensities on the (200) and (020) reflections as well as on the (001) and (021) reflections excludes the presence of any A and F modes. Further, the similar intensities on the (100) and (010) reflections and the strong intensity found for the reflection (031) are incompatible.
TABLE III. Representations of the basis vectors of \( \{R\} \) in \( RVO_{3} \) with the space groups \( Pbnm \) and \( P2_{1}/b \) and the propagation vector \( k=0 \) . The R atoms in \( Pbnm \) and \( P2_{1}/b \) are located in the Wyckoff positions \( 4c(x,y,1/4; -x,-y,3/4; 1/2-x,1/2+y,1/4; 1/2+x,1/2-y,3/4) \) and \( 4e(x,y,z; -x,-y,-z; 1/2-x,1/2+y,z; 1/2+x,1/2-y,-z) \) , respectively. The modes are \( F(++++) \) , \( C(++--) \) , \( G(+-++) \) , and \( A(+-+-) \) .
| Pbnm | x | y | z | P21/b | x | y | z |
| \( \Gamma_{1} \) | Cz | ||||||
| \( \Gamma_{2} \) | F \( _{x} \) | C \( _{y} \) | \( \Gamma_{1} \) | F \( _{x} \) | C \( _{y} \) | C \( _{z} \) | |
| \( \Gamma_{3} \) | C \( _{x} \) | F \( _{y} \) | \( \Gamma_{2} \) | C \( _{x} \) | F \( _{y} \) | ||
| \( \Gamma_{4} \) | Fz | ||||||
| \( \Gamma_{5} \) | G \( _{x} \) | A \( _{y} \) | \( \Gamma_{3} \) | G \( _{x} \) | A \( _{y} \) | A \( _{z} \) | |
| \( \Gamma_{6} \) | A \( _{z} \) | ||||||
| \( \Gamma_{7} \) | G \( _{z} \) | ||||||
| \( \Gamma_{8} \) | A \( _{x} \) | G \( _{y} \) | \( \Gamma_{4} \) | A \( _{x} \) | G \( _{y} \) | G \( _{z} \) | |
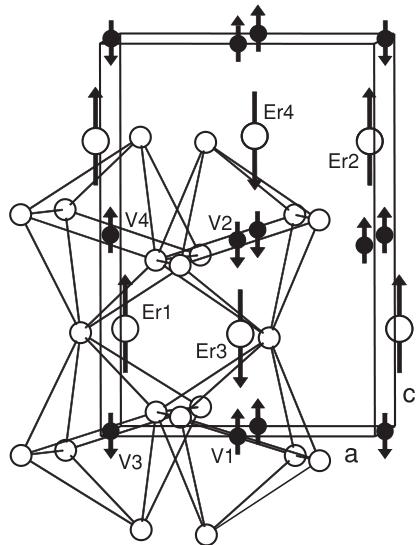
with the modes \( C_{x} \) and \( C_{y} \) . This narrows the selection of possible structures compatible with the lattice symmetry down to \( C_{z} \) (representation \( \Gamma_{1} \) in Table III) and \( G_{z} \) (representation \( \Gamma_{7} \) ). In order to deduce the C-type ordered component of the Er atoms along z we have used for the refinements ten independent \( F_{hkl}^{2} \) values (collected in the ab and bc planes). The best refinement was obtained with the former model and yielded a residual of \( R(F)=0.065 \) and a magnetic moment of the erbium atoms of \( \mu_{z}=8.2(2)\mu_{B} \) , slightly smaller than the theoretical value of the free \( Er^{3+} \) ion of \( 9.0\mu_{B} \) . The full low-temperature magnetic structure of \( ErVO_{3} \) with collinear V and Er moments is depicted in Fig. 4.
2. HoVO_{3}
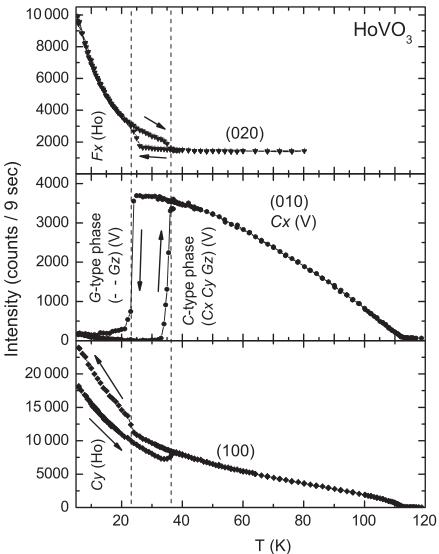
For \( HoVO_{3} \) , the onset of the C-type ordering of the V moments is observed at \( T_{N1} = 113 \) K (Fig. 5), in agreement with earlier work \( ^{30} \) and in close analogy to the behavior of \( ErVO_{3} \) described above. The V moments along x and y could be deduced from the reflections (010) and (100), respectively. The ordered moments at \( T = 85 \) K, \( \mu_{x} = 0.69(3)\mu_{B} \) and \( \mu_{y} = \)

FIG. 3. Temperature dependence of the magnetic reflection (100) of \( ErVO_{3} \) at low temperature. The reflection (100) shows spontaneous change of intensity at \( T_{N2} = 2.5(2) \) K, indicating a C-type ordering of the Er moments.

FIG. 4. Magnetic structure of \( ErVO_{3} \) at 1.6 K. Both the V and Er moments show a collinear spin arrangement along the c axis, where the magnetic structures of the V and Er sublattices are purely of G and C type, respectively. In the drawing the network of distorted corner-sharing \( VO_{6} \) octahedra is also shown.
1.01(3) \( \mu_{B} \) , are similar to those of \( ErVO_{3} \) and slightly smaller than those of \( YVO_{3} \) .⁹ A weak \( G_{z} \) component was also observed below \( T_{N1} \) , as in the other compounds. Note that the C-type ordering occurs in the monoclinic phase (space group \( P2_{1}/b \) ), where one expects a splitting of some Bragg reflections due to the monoclinic distortion. But for \( YVO_{3} \) , where the ionic radius of \( Y^{3+} \) is very similar to that of \( Ho^{3+} \) , it was found that the monoclinic angle \( \alpha \) is very close to \( 90^{\circ} \) [at 80 K \( \alpha = 89.977(3)^{\circ} \) (Ref. 7); at 85 K \( \alpha = 89.980(3)^{\circ} \) (Ref. 9)]. Since the resulting minute splitting could not be observed in the current experiment due to insufficient momentum resolution, the monoclinic reflections (hkl) and (hk-l) could not be separated. For the calculation of the weak \( G_{z} \) component we therefore only used the reflections (011) and (0-11), which are structurally forbidden in \( P2_{1}/b \) .
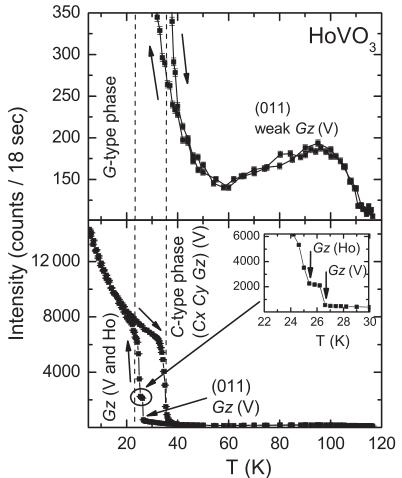
The temperature dependence of the intensities of some prominent magnetic reflections of \( HoVO_{3} \) is presented in Figs. 5 and 6. During the cooling process we found a pronounced intensity increase of the reflection (011) at 26.5(2) K, which levels off and reaches a plateau down to 25.1(2) K, where the intensity again shows a strong increase (inset of Fig. 5). The first jump can be ascribed to the change of the magnetic structure of the V sublattice from the C-type to the G-type phase, which coincides with the structural transition from monoclinic to orthorhombic symmetry (Fig. 1), as in \( ErVO_{3} \) and \( YVO_{3} \) . The second intensity increase, which is not observed in the latter two compounds, can be attributed to ordering of the Ho moments. For the reflection (010) the anomaly sets in at a slightly lower temperature of 23.5(5) K.

FIG. 5. Temperature dependence of the reflection (011) of \( HoVO_{3} \) . Magnetic intensity appears for the (011) reflection at the Néel temperature \( T_{N1} = 113 \) K due to the onset of magnetic order of the vanadium sublattice. The nonzero intensity of the (011) reflection confirms the presence of the weak \( G_{z} \) component in the C-type phase, which was also observed in \( YVO_{3} \) (Refs. 6 and 9). During the cooling process the intensity of the (011) reflection increases spontaneously at 26.6(2) K and reaches a plateau of width \( \Delta T = 1.4(2) \) K (see the inset). This indicates the onset of the G-type ordering of the V moments. At 25.2(2) K the intensity is increasing again due to an additional G-type ordering of the Ho sublattice.
With increasing temperature both the (011) and the (010) reflections show spontaneous intensity changes at 35.5(5) K. Thermal expansion measurements had uncovered a related anomaly at 38 K. \( ^{30} \) At this temperature the magnetic order of the Ho moments vanishes, while the magnetic structure of the V moments changes from the G-type to the C-type structure, which is stable up to \( T_{N1} \) . A two-step anomaly such as the one observed upon cooling is not clearly resolved in the heating cycle. Our data demonstrate that the structural transition and the rearrangement of the vanadium moments at \( T_{S2} \) are strongly coupled to the ordering of the Ho moments. This interaction is responsible for the pronounced hysteresis range of \( \Delta T_{S2} \sim 12 \) K.
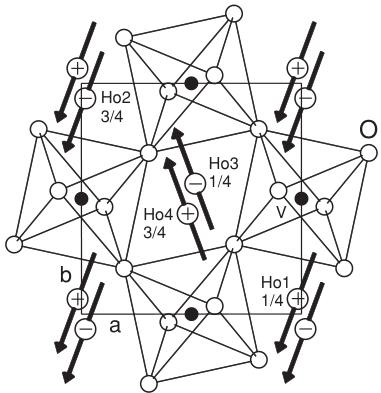
The magnetic structure of the \( Ho^{3+} \) ions in \( HoVO_{3} \) was determined from a data set collected at 6 K, where the crystal structure is orthorhombic and the vanadium sublattice is G-type ordered. Strong magnetic intensity could be observed on the reflections (100), (020), and (011) (Fig. 6), indicating the presence of C-, F-, and G-type ordering of the holmium moments. Our data analysis showed that the magnetic structure can be described with the basis vector \( (F_{x}, C_{y}, G_{z}) \) of the reducible representation \( \Gamma = \Gamma_{2} \oplus \Gamma_{7} \) (Table III). The components along x, y, and z were deduced from the intensities of the reflections (100), (020), and (011), respectively.
Earlier, an F- and C-type ordering could be found along the a and b axes, in agreement with our results, but the third

FIG. 6. Temperature dependence of the reflections (020) characteristic of a ferromagnetic (F) component of the Ho moments (upper panel) and the (010) and (100) reflections characteristic of C-type antiferromagnetic components of the V and Ho moments, respectively (lower two panels) of \( HoVO_{3} \) .
\( G_{z} \) component was not reported in Ref. 18. The moments \( \mu_{x}=3.74(12)\mu_{B} \) and \( \mu_{y}=8.65(15)\mu_{B} \) given in Ref. 18 were found to be larger than our values \( \mu_{x}=2.3(2)\mu_{B} \) and \( \mu_{y}=6.1(2)\mu_{B} \) . For the \( G_{z} \) component we found a moment amplitude of \( \mu_{y}=2.1(3)\mu_{B} \) . A picture of the magnetic structure is shown in Fig. 7. The total moment \( \mu=6.9(3)\mu_{B} \) of the holmium atoms is considerably smaller than the theoretical value of the free \( Ho^{3+} \) ion of \( 10.0\mu_{B} \) . Strongly reduced holmium moments were also observed for \( HoCrO_{3} \) and \( HoFeO_{3} \) , where the moments reach values between \( 7.5\mu_{B} \) and \( 7.75\mu_{B} \) . \( ^{33-35} \) For these compounds the magnetic order of the holmium moments sets in at 12 K ( \( HoCrO_{3} \) ) and 6.5 K ( \( HoFeO_{3} \) ), respectively. \( ^{34,36,37} \) Interestingly, for \( ErCrO_{3} \) a strongly reduced moment of \( 6.2\mu_{B} \) was found, \( ^{38} \) while the erbium moments in \( ErVO_{3} \) reach a larger value of \( \mu_{exp}=8.2\mu_{B} \) . On the other hand, the ordering temperature \( T_{N}=16.8 \) K of \( ErCrO_{3} \) (Ref. 38) is much larger than \( T_{N}=2.5 \) K observed for \( ErVO_{3} \) . The moment reduction may in part be due to crystal-field effects, but it is also possible that a fraction of the R moments (perhaps those located in domain boundaries of the complex magnetic structure) remains disordered and does not contribute to the Bragg intensity. Due to the interplay between the orbital-lattice coupling (Jahn-Teller effect) and the competing V-V, Ho-V, and Ho-Ho exchange interactions, the magnetic structure of \( HoVO_{3} \) is considerably more complex than that of \( ErVO_{3} \) , where the Jahn-Teller effect and V-V coupling dominate. The same interplay is presumably also responsible for the much lower value of the transition temperature \( T_{S2} \) in \( HoVO_{3} \) .

\[ \mathrm{H O V O}_{3}\mathrm{a t}6\mathrm{K}\rightarrow\mathrm{H o}\left(F_{x}\mathrm{C}_{y}\mathrm{G}_{z}\right),\mathrm{V}\left(-\mathrm{~-~G}_{z}\right) \]
FIG. 7. Magnetic structure of \( HoVO_{3} \) at T = 6 K shown as a projection along the c axis. The structure is comprised of the components \( (F_{x}, C_{y}, G_{z}) \) listed in Table III. The symbols + and - stand for \( G_{z} \) components of the Ho moments that point parallel and antiparallel to the c axis, respectively.
3. DyVO_{3}
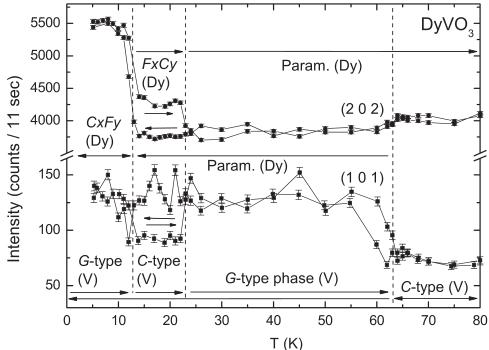
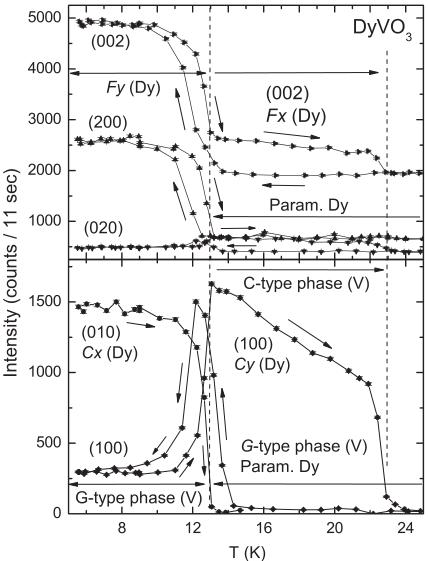
We finally address the structural and magnetic phase transitions of DyVO \( _{3} \) . The two high-temperature transitions at \( T_{S1} \) and \( T_{N1} \) in this compound are entirely in line with those of the other vanadates discussed above. Due to the strong neutron absorption cross section of dysprosium we were not able to determine the Néel temperature of DyVO \( _{3} \) with good accuracy. However, from specific-heat and magnetization measurements it was found to be \( T_{N1} = 110 \) K. \( ^{8} \) The second transition from the monoclinic lattice structure with C-type order of the V sublattice to the low-temperature orthorhombic structure with G-type order was observed by thermodynamic probes at \( T_{S2} = 57 \) and 64 K upon cooling and warming, respectively. \( ^{21} \) In line with these results, Fig. 8 shows that the intensity of the reflection (101) exhibits a spontaneous change at about 60 and 63 K with decreasing and increasing temperature, respectively. However, because of constraints imposed by strong neutron absorption, we could not study this transition in detail.
Here we focus on the low-temperature phase behavior of DyVO \( _{3} \) , which is quite unusual because this compound is located at the border of the stability range of the low-temperature orthorhombic structure. The temperature dependence of some prominent Bragg intensities is displayed in Figs. 8 and 9. With decreasing temperature, the intensity of the (101) reflection does not show any change down to 6 K, suggesting that the G-type ordering of the V moments as well as the low-temperature orthorhombic lattice structure are stable in the entire temperature range from 60 down to 6 K (Fig. 8). With increasing temperature, however, the intensity of the (101) reflection abruptly decreases at 13 K, reaching almost the same intensity as observed above 63 K. This suggests a reentrant change to the C-type ordering of the V moments combined with a transition to the monoclinic lattice structure. Finally,

FIG. 8. Temperature dependence of the reflections (101) and (202) of DyVO \( _{3} \) . Below \( T_{S2} = 63 \) K a structural phase transition occurs from the monoclinic \( (P2_{1}/b) \) into the low-temperature orthorhombic structure (Pbmm). At this temperature the reflection (101) spontaneously increases due to the onset of the G-type ordering of the vanadium moments along the c axis. During the cooling process the low-temperature orthorhombic structure as well as the G-type phase of the vanadium sublattice are stable down to 6 K. With increasing temperature the intensity of the (101) is strongly reduced in the range between 13 and 23 K. This indicates the appearance of an intermediate monoclinic phase, where the C-type ordering of the vanadium moments is stable. The additional intensity of the reflection (202) observed below 23 K indicates the presence of a ferromagnetic component of the Dy sublattice order.
at 23 K another transition sets the system back to the G-type ordering and to the low-temperature orthorhombic structure.
We now discuss the magnetic ordering of the Dy moments. In Fig. 8 the temperature dependence is shown for the reflection (202), which is characteristic of a ferromagnetic component of the Dy moments. With decreasing temperature the intensity of this reflection remains almost unchanged down to 13 K, where its intensity increases strongly. The same tendency was found for the reflections (200) and (002) (Fig. 9). With increasing temperature, a pronounced change of intensity occurs again at 13 K, where the reentrant transition of the V sublattice and the monoclinic lattice structure is observed. It reaches a plateau that is stable up to 23 K, where the intensity of these reflections decreases abruptly down to the same level as observed during the cooling process. This shows that the Dy moments are still magnetically ordered in the monoclinic phase, whereas they remain paramagnetic down to 13 K upon cooling when the lattice structure is orthorhombic. Upon further heating, the magnetic order of Dy disappears above 23 K, when the lattice structure reverts to orthorhombic symmetry.
These data demonstrate that the magnetic order of the Dy sublattice in \( DyVO_{3} \) is more stable in the monoclinic structure than in the orthorhombic one. Moreover, the magnetic structures in the two phases are different, as demonstrated by the reflections (100) and (010) in Fig. 9. In the orthorhombic phase at 6 K, strong magnetic intensity could be observed on the reflections (010) and (200), indicating the presence of C- and F-type ordering of the dysprosium moments along the a and b axes respectively. The magnetic moments of

FIG. 9. Temperature dependence of the reflections (100), (010), (200), (020), and (002) of DyVO \( _{3} \) . During the cooling process the low-temperature orthorhombic structure as well as the G-type phase of the vanadium sublattice are stable down to 6 K. Below 13 K strong magnetic intensities were observed for the reflections (010), (200), and (002), indicating the onset of antiferro- and weakly ferromagnetic ordering of the Dy atoms with the modes \( C_{x} \) and \( F_{y} \) . With increasing temperature, magnetic intensity was observable for the reflections (100), (020), and (002) between 13 and 23 K, where the intermediate monoclinic structure is again stable. This indicates a change of the magnetic structure of the Dy sublattice into a structure with the modes \( F_{x} \) and \( C_{y} \) .
the components \( C_{x} \) and \( F_{y} \) were deduced from the magnetic intensities of the reflections (010) and (200), respectively. The resulting structure of type \( (C_{x}, F_{y}, —) \) is consistent with the representation analysis of Table III.
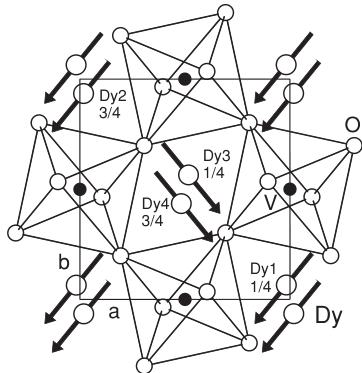
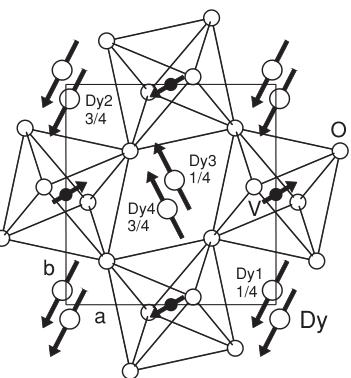
The resulting spin configuration is shown in Fig. 10. In the monoclinic phase at 13.5 K, magnetic intensity appears on the reflections (020) and (100), indicating the presence of weakly ferromagnetic order with the basis function \( (F_{x}, C_{y}, —) \) . The components along x and y were deduced from the magnetic intensities of the reflections (020) and (100), respectively. Figure 10 shows a pictorial representation of this structure. Since the lattice symmetry at this temperature is monoclinic, we also deduced the possible spin arrangements of the Dy moments for the space group \( P2_{1}/b \) . In Table III it can be seen that only four irreducible representations are generated. The spin arrangement in the ab plane is compatible with both \( Pbnm \) and \( P2_{1}/b \) , but in the monoclinic symmetry a third component along the c axis is allowed to appear in all four representations. The absence of the (010) reflection, however, shows that the \( C_{z} \) component that would be compatible with the \( F_{x} \) and \( C_{y} \) components in the ab plane is not present in \( DyVO_{3} \) . A similar situation holds in \( TbVO_{3} \) , which does

DyVO_{3} at 6 K → Dy (C_{x} F_{y}, -), ∀ (- G_{z})

DyVO_{3} at 13.5 K → Dy (F_{x} C_{y} -), ∀ (C_{x} C_{y} G_{z})
FIG. 10. Magnetic structures of DyVO_{3} at T=6 K (upper panel) and 13.5 K (lower panel) shown as projections along the c axis. In the G-type phase of the vanadium sublattice at 6 K, the magnetic order of the Dy moments can be described with the basis vector \( (C_{x}, F_{y}, —) \) . In the intermediate monoclinic phase at 13.5 K, where the V moments are C-type ordered, the Dy moments are ordered according to the basis vector \( (F_{x}, C_{y}, —) \) .
not show a second structural phase transition \( (T_{\mathrm{S2}}) \) so that the monoclinic structure with the space group \( P2_{1}/b \) remains stable down to low temperature. \( ^{9} \) The Tb moments show an analogous weakly ferromagnetic structure, \( (C_{x}, F_{y}, —) \) , below \( T_{N2} = 11 \) K, and the \( F_{z} \) component that would also be allowed in \( P2_{1}/b \) symmetry is also not observed. \( ^{9} \) As discussed earlier, the monoclinic distortions arise from the Jahn-Teller effect and thus generate a change of the point symmetry of the vanadium ions. \( ^{9} \) The influence of the superposed distortions on the R sites seems to be negligible, so that the magnetic ordering is still compatible with the symmetry of \( Pbnm \) .
The Dy sublattice magnetization in the high-temperature \( (F_{x}, C_{y}, —) \) phase at 13.5 K resulting from our analysis is \( \mu = 6.2(3)\mu_{B} \) , substantially reduced compared to the magnetic

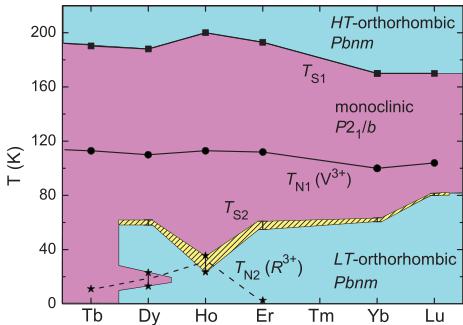
FIG. 11. (Color online) Spin-orbital phase diagram of vanadates \( RVO_{3} \) . Below \( T_{S1} \) , where the orthorhombic structure changes to the monoclinic structure, G-type order of the V orbitals is observed. In the monoclinic phase the magnetic moments of the V ions show a C-type ordering below the Néel temperature \( T_{N1} \) . With decreasing temperature a second structural phase transition ( \( T_{S2} \) ) can be observed for vanadates containing \( R^{3+} \) ions with radii smaller than \( r(Tb^{3+}) \) . Note that the monoclinic phase of DyVO \( _{3} \) between 13 and 23 K only appears during the heating process. For temperatures below \( T_{N2} \) , the magnetic moments of the \( R^{3+} \) ions show antiferromagnetic and/or weakly ferromagnetic ordering. The yellow range in the diagram represents the hysteresis observed during thermal cycling.
moment of the free \( Dy^{3+} \) ion of \( 10.0\mu_{B} \) , as in the case of Ho discussed above. The determination of the Dy moment in the low-temperature magnetic structure is more complicated due to an apparent coexistence with the high-temperature phase. In Fig. 9 it can be seen that the magnetic intensity of the (100) reflection appears in the narrow temperature range between 11 and 13 K during the cooling process, reaching a maximum that is similar to the one observed during the following heating process. This indicates that the high-temperature phase \( (F_{x}, C_{y}, —) \) briefly occurs before it changes to the low-temperature order \( (C_{x}, F_{y}, —) \) . But it can be seen that the magnetic intensity of both the (020) and the (100) reflections is still observable at 6 K, indicating a coexistence of both phases \( (C_{x}, F_{y}, —) \) and \( (F_{x}, C_{y}, —) \) . The volume fractions given in Table II were obtained under the assumption that the Dy magnetic moment is the same for both phases at 6 K. This results in a moment of \( \mu_{expt} = 7.8(3)\mu_{B} \) that is also substantially reduced compared to the magnetic moment of the free \( Dy^{3+} \) ion of \( 10.00\mu_{B} \) . A very similar moment value \( \mu_{expt} = 7.87(6)\mu_{B} \) was observed for \( DyNiO_{3} \) , where the magnetic order of the dysprosium moments sets in at \( 8.5 K \) . \( ^{39} \) In contrast, the dysprosium moment \( \mu_{expt} = 9.6(3)\mu_{B} \) of \( DyCrO_{3} \) reaches almost the moment of the free \( Dy^{3+} \) ion, while the magnetic order of the dysprosium atoms set in at the lower temperature \( T_{N} = 2.16 K \) . \( ^{40} \)
IV. CONCLUSIONS
Figure 11 summarizes the spin-orbital phase diagrams of the compounds discussed here, together with those of other rare-earth vanadates \( RVO_{3} \) . The transition temperatures \( T_{S1} \) and \( T_{N1} \) are predominantly determined by the interplay between the superexchange interactions and the orbital-lattice coupling of the vanadium ions. The \( R^{3+} \) ions influence these interactions only via their ionic radius, which determines the \( GdFeO_{3} \) -like rotation of the \( VO_{6} \) octahedra. \( ^{8,17} \) The influence of exchange interactions between the R and V atoms sets in below about 100 K. These interactions lead to a polarization of the R moments below \( T_{N1} \) and may account for a slight variation of this transition temperature among different compounds. For instance, \( T_{N1} \) is slightly higher in \( YVO_{3} \) , where the \( R^{3+} \) ions are nonmagnetic, than it is in \( DyVO_{3} \) and \( HoVO_{3} \) , where they are magnetic, despite the nearly identical \( R^{3+} \) ion radii in all three compounds.
In most vanadates with magnetic \( R^{3+} \) ions, including the \( ErVO_{3} \) compound discussed here, weak R-R exchange interactions induce magnetic order on the R sublattice at very low temperatures (i.e., \( T_{N2} = 2.5 \) K in the case of \( ErVO_{3} \) ). This is in accord with observations on other perovskites such as the orthoferrites \( RFeO_{3} \) ( \( R = Tb, Dy, Ho, Er \) ), where magnetic ordering of the R moments was observed between 3.1 and 6.5 K, while the Fe moments order at much higher Néel temperatures between 639 and 647 K. \( ^{41} \) We have seen, however, that especially in the case of \( HoVO_{3} \) and \( DyVO_{3} \) , which are located near the stability range of the low-temperature orthorhombic structure, R-V and R-R interactions can critically influence the competition between the different structural and magnetic phases. In particular, the first-order structural and magnetic transition temperature \( T_{S2} \) is substantially reduced and the corresponding hysteresis enhanced in these compounds ( \( 57 < T_{S2} < 64 \) K for \( DyVO_{3} \) ; \( ^{21} \) \( 23.5 < T_{S2} < 35 \) K for \( HoVO_{3} \) ) compared to \( YVO_{3} \) ( \( 73.5 < T_{S2} < 76.0 \) K) and \( LuVO_{3} \) ( \( 80.0 < T_{S2} < 81.3 \) K), where the \( R^{3+} \) ions are nonmagnetic. In \( HoVO_{3} \) , this transition coincides with the onset of magnetic order of the R atoms, whereas in \( DyVO_{3} \) , the complex interplay between these interactions induces an additional, reentrant structural and magnetic transition at low temperatures (Fig. 11). We have also shown that the magnetic structures of \( HoVO_{3} \) and \( DyVO_{3} \) are weakly ferromagnetic, which implies that external magnetic fields can couple efficiently to the R sublattice. In conjunction with the critical influence of the R-V exchange interactions on the spin and orbital ordering pattern of the V sublattice, this mechanism is undoubtedly responsible for the complex magnetic phase behavior of these compounds.
Finally we note that the single-ion anisotropy of the \( R^{3+} \) ions also influences the magnetic ordering pattern of the R sublattice, in addition to the R-V and R-R exchange interactions we have discussed. For R = Tb and Dy, the moment direction in the magnetically ordered (F- and C-type) phases was shown to be in the pseudotetragonal ab plane, whereas for R = Er the moments are antiferromagnetically (C-type) ordered with a moment direction parallel to the c axis. For R = Ho the F- and C-type ordering in the ab plane is still established, but it shows an additional component parallel to the pseudocubic c axis. It is interesting to see that a similar trend (albeit opposite in sign) was reported for the tetragonal intermetallic compounds \( RNi_{2}X_{2} \) (R = Tb, Dy, Ho, Er; X = Si, P, Ge). \( ^{42-46} \) In the R = Tb and R = Er members of this family, the moments were found to be aligned parallel and perpendicular to the c axis, respectively. \( ^{42,43,46} \) For the Dy and Ho compounds, different magnetic structure types can be observed. The dysprosium moments in \( DyNi_{2}Si_{2} \) and \( DyNi_{2}P_{2} \) are parallel to c, while
in \( DyNi_{2}Ge_{2} \) they form an angle to the c axis of about \( 20^{\circ} \) , and for \( HoNi_{2}P_{2} \) the moments are aligned parallel to the c axis, whereas they are aligned perpendicular to c in \( HoNi_{2}Si_{2} \) and \( HoNi_{2}Ge_{2} \) . \( ^{42-46} \) For \( RNi_{2}X_{2} \) this behavior could be attributed to the second-order term \( B_{2}^{0} \) in the crystal-field Hamiltonian, which is strongly negative for Tb and positive for \( Er. \) ^{42} For R = Dy and Ho, the magnitude of \( B_{2}^{0} \) is relatively small, and higher-order terms in the crystal-field Hamiltonian may become competitive, leading to the diversity in the observed magnetic structures. While a detailed description of the single-ion anisotropy of the \( R^{3+} \) ions in
\( ^{1} \) A. S. Borukhovich, G. V. Bazuev, and G. P. Shveikin, Sov. Phys. Solid State 16, 286 (1974).
\( ^{2} \) V. G. Zubkov, A. S. Borukhovich, G. V. Bazuev, I. I. Matveenko, and G. P. Shveikin, Sov. Phys. JETP 39, 896 (1974).
\( ^{3} \) H. C. Nguyen and J. B. Goodenough, Phys. Rev. B 52, 324 (1995).
\( ^{4} \) V. G. Zubkov, G. V. Bazuev, and G. P. Shveikin, Sov Phys. Solid State 18, 1165 (1976).
\( ^{5} \) H. Kawano, H. Yoshizawa, and Y. Ueda, J. Phys. Soc. Jpn. 63, 2857 (1994).
\( ^{6} \) C. Ulrich, G. Khaliullin, J. Sirker, M. Reehuis, M. Ohl, S. Miyasaka, Y. Tokura, and B. Keimer, Phys. Rev. Lett. 91, 257202 (2003).
\( ^{7} \) G. R. Blake, T. T. M. Palstra, Y. Ren, A. A. Nugroho, and A. A. Menovsky, Phys. Rev. Lett. 87, 245501 (2001); Phys. Rev. B 65, 174112 (2002).
\( ^{8} \) S. Miyasaka, Y. Okimoto, M. Iwama, and Y. Tokura, Phys. Rev. B 68, 100406(R) (2003).
\( ^{9} \) M. Reehuis, C. Ulrich, P. Pattison, B. Ouladdiaf, M. C. Rheinstädter, M. Ohl, L. P. Regnault, M. Miyasaka, Y. Tokura, and B. Keimer, Phys. Rev B 73, 094440 (2006).
\( ^{10} \) P. Bordet, C. Chaillout, M. Marezio, Q. Huang, A. Santoro, S.-W. Cheong, H. Takagi, C. S. Oglesby, and B. Batlogg, J. Solid State Chem. 106, 253 (1993).
\( ^{11} \) M. Reehuis, C. Ulrich, P. Pattison, M. Miyasaka, Y. Tokura, and B. Keimer, Eur. Phys. J. B 64, 27 (2008).
\( ^{12} \) M. J. Martínez-Lopez, J. A. Alonso, M. Retuerto, and M. T. Fernández-Díaz, Inorg. Chem. 47, 2634 (2008).
\( ^{13} \) G. Khaliullin, P. Horsch, and A. M. Oleś, Phys. Rev. Lett. 86, 3879 (2001).
\( ^{14} \) Y. Motome, H. Seo, Z. Fang, and N. Nagaosa, Phys. Rev. Lett. 90, 146602 (2003).
\( ^{15} \) I. V. Solovyev, Phys. Rev. B 74, 054412 (2006).
\( ^{16} \) A. M. Oleś, P. Horsch, and G. Khaliullin, Phys. Rev. B 75, 184434 (2007).
\( ^{17} \) P. Horsch, A. M. Oleś, L. F. Feiner, and G. Khaliullin, Phys. Rev. Lett. 100, 167205 (2008).
\( ^{18} \) A. Bombik, B. Leśniewska, and A. Oleś, Phys. Status Solidi A 50, K17 (1978).
\( ^{19} \) S. Miyasaka, T. Okuda, and Y. Tokura, Phys. Rev. Lett. 85, 5388 (2000).
\( ^{20} \) G. R. Blake, A. A. Nugroho, M. J. Gutmann, and T. T. M. Palstra, Phys. Rev. B 79, 045101 (2009).
\( ^{21} \) S. Miyasaka, T. Yasue, J. Fujioka, Y. Yamasaki, Y. Okimoto, R. Kumai, T. Arima, and Y. Tokura, Phys. Rev. Lett. 99, 217201 (2007).
RVO \( _{3} \) has not been provided, it seems plausible that the relative weakness of the single-ion anisotropy for R = Dy and Ho enhances the polarizability of the R sublattice and thus contributes to the complex phase behavior of these compounds.
ACKNOWLEDGMENT
We acknowledge the financial support of the Deutsche Forschungsgemeinschaft under Grant No. UL 164/4.
\( ^{22} \) J. Fujioka, T. Yasue, S. Miyasaka, Y. Yamasaki, T. Arima, H. Sagayama, T. Inami, K. Ishii, and Y. Tokura, Phys. Rev. B 82, 144425 (2010).
\( ^{23} \) J. Peters, J. Appl. Crystallogr. 36, 1475 (2003).
\( ^{24} \) C. Wilkinson, H. W. Khamis, R. F. D. Stansfield, and G. J. McIntyre, J. Appl. Crystallogr. 21, 471 (1988).
\( ^{25} \) XTAL.3.4 User's Manual, edited by S. R. Hall, G. S. D. King, and J. M. Stewart (University of Australia Press, Lamb, Perth, 1995).
\( ^{26} \) V. F. Sears, in International Tables of Crystallography, edited by A. J. C. Wilson (Kluwer, Dordrecht, 1992), Vol. C, p. 383.
\( ^{27} \) J. Rodriguez-Carvajal, Physica B 192, 55 (1993).
\( ^{28} \) P. J. Brown, in International Tables of Crystallography (Ref. 26), Vol. C, p. 391.
\( ^{29} \) R. D. Shannon, Acta Crystallogr. A 32, 751 (1976).
\( ^{30} \) M. Sikora, C. Marquina, M. R. Ibarra, A. A. Nugroho, and T. T. M. Palstra, J. Magn. Magn. Mater. 316, e692 (2007).
\( ^{31} \) M. Reehuis, C. Ulrich, J. Fujioka, S. Miyasaka, Y. Tokura, and B. Keimer (unpublished).
\( ^{32} \) E. F. Bertaut, Acta Crystallogr. A 24, 217 (1968); see also J. Phys. (Paris) Colloque 32, C3-462 (1971); J. Magn. Magn. Mater. 24, 267 (1981).
\( ^{33} \) N. Shamir, H. Shaked, and S. Shtrikman, Physica B 90, 211 (1977).
\( ^{34} \) N. Koehler, E. O. Wollan, and M. K. Wilkinson, Phys. Rev. 118, 58 (1960).
\( ^{35} \) H. Schuchert, S. Hüfner, and R. Faulhaber, Z. Phys. 220, 280 (1969).
\( ^{36} \) E. F. Bertaut, G. Bassi, G. Buisson, P. Burlet, J. Chappert, A. Delapalme, J. Mareschal, G. Roult, R. Aleonard, R. Pauthenet, and J. P. Rebouillat, J. Appl. Phys. 37, 1038 (1966).
\( ^{37} \) J. Mareschal and J. Sivardière, J. Phys. (Paris) 30, 967 (1969).
\( ^{38} \) M. Eibschütz, R. L. Cohen, and K. W. West, Phys. Rev. 178, 572 (1969).
\( ^{39} \) A. Muñoz, J. A. Alonso, M. J. Martínez-Lope, and M. T. Fernández-Díaz, J. Solid State Chem. 182, 1982 (2009).
\( ^{40} \) E. F. Bertaut and J. Mareschal, J. Phys. (Paris) 29, 67 (1968).
\( ^{41} \) S. C. Parida, S. K. Rakshit, and Z. Singh, J. Solid State Chem. 181, 101 (2008).
\( ^{42} \) A. Szytuła, Phys. Scr., T 49, 284 (1993).
\( ^{43} \) G. André, P. Bonville, F. Bourée, A. Bombik, M. Kolenda, A. Oleś, A. Pacyna, W. Sikora, and A. Szytuła, J. Alloys Compd. 224, 253 (1995).
\( ^{44} \) Y. Hashimoto, T. Shigeoka, N. Iwata, H. Yoshizawa, Y. Oohara, and M. Nishi, J. Magn. Magn. Mater. 903, 140 (1995).
\( ^{45} \) Z. Islam, C. Detlefs, A. I. Goldman, S. L. Bud'ko, P. C. Canfield, and A. Zheludev, Solid State Commun. 108, 371 (1998).
\( ^{46} \) M. Reehuis, W. Jeitschko, Th. Ebel, and N. Stüsser, J. Alloys Compd. 287, 32 (1999).