| Transition Temperature | 453 K |
|---|---|
| Experiment Temperature | 295 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | Pna21 (#33) |
| Magnetic Space Group | Pn'a21' (#33.146) |
| Magnetic Point Group | m'm2' (7.3.22) |
| Lattice Parameters | 5.24800 6.51100 5.07000 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1016/0038-1098(77)91139-5 |
| Reference | M. Wintenberger, R. Marchand, M. Maunaye, Solid State Communications (1977) 21 733 - 735 |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Mn1 | Mn | 0.0 | 0.0 | 3.8 | 3.80 |
ETUDE CRISTALLOGRAPHIQUE ET MAGNETIQUE DE MnSiN₂ PAR DIFFRACTION DES NEUTRONS
M. Wintenberger
Centre d'Etudes Nucléaires de Grenoble, Département de Recherche Fondamentale, Laboratoire de Diffraction Neutronique, 85X, 38041 Grenoble Cedex, France
et
R. Marchand et M. Maunaye
Laboratoire de Chimie Minérale C, UER Structure et Propriétés de la Matière, Université de Rennes, Avenue du Général Leclerc, 35031 Rennes Cedex, France
(Req u le 26 octobre 1976 par E.F. Bertaut)
Par diffraction neutronique on a déterminé la température de Néel (180°C) et la structure magnétique de MnSiN₂, et on a amélioré les coordonnées cristallographiques obtenues antérieurement par rayons X seuls.
1. INTRODUCTION
CETTE étude fait suite à celle de deux autres nirures ternaires, MnGeN_{2}^{1} et ZnGeN_{2}^{2} pour lesquels les neutrons ont permis de préciser la structure cristallographique grâce à la longueur de Fermi élevée de l'azote, et de déterminer la structure magnétique du composé contenant du manganèse. Les trois nirures sont des composés tétraédriques normaux à structure dérivée de celle de la wurtzite et du type de \( \beta \) FeNaO_{2}, avec pour groupe spatial Pna2_{1} et Z = 4.
Lors de l'étude aux rayons X de la structure de MnSiN_{2} à partir de diagrammes de poudre, Maunaye et al. \( ^{3} \) ont obtenu les coordonnées réduites suivantes:
| x | y | z | |
| Mn | 0,074 | 0,625 | -0,005 |
| Si | 0,074 | 0,124 | -0,013 |
| N1 | 0,068 | 0,112 | 0,352 |
| N11 | 0,086 | 0,639 | 0,388 |
avec un facteur
\[ R=\frac{\Sigma\neg\neg I_{obs}-I_{calc}}{\Sigma\neg I_{obs}}=0,092. \]
Ceci conduit à des distances moyennes:
\[ \mathrm{Si}-\mathrm{N}=1,845\mathrm{\AA}\quad\mathrm{Mn}-\mathrm{N}=2,002\mathrm{\AA}. \]
Pour étudier la susceptibilité magnétique de MnSiN_{2}, on est gêné par l'existence d'un faible ferromagnétisme superposé, mais on peut prévoir que ce composé doit être antiferromagnétique avec un point de Néel supérieur à la température ambiante, comme MnGeN_{2}.
2. EXPERIENCES
Nous avons enregistré les diagrammes de diffraction neutronique sur poudre à température ambiante et à des températures variables jusqu'à 290°C, avec \( \lambda = 1,146 \) Å. A 290°C n'apparaissent que des raies d'origine nucléaire. A température ambiante on observe des raies magnétiques semblables à celles de MnGeN \( _{2} \) . De même que pour ce dernier composé, il n'y a pas de dilatation sensible et anisotrope de la maille au-dessus de la transition magnétique, contrairement à ce qui se passe dans FeNaO \( _{2} \) .
3. STRUCTURE CRISTALLINE
Les intensités observées pour les raies nucléaires donnent un accord médiocre avec les intensités neutroniques calculées à partir des coordonnées indiquées plus haut (R = 0,27). Pour améliorer ce résultat nous avons utilisé un programme d'affinement par moindres carrés qui traite simultanément les données des rayons X et celles des neutrons. \( ^{5} \) Nous avons repris les données de rayons X de \( ^{8} \) et affecté à tous les atomes un facteur d'agitation thermique B = 0,5. Ceci a permis de fixer la plupart des coordonnées. Celles qui restaient définies avec une faible précision ont été ajustées en imposant la condition suivante: que les quatre distances Mn–N diffèrent assez peu les unes des autres, et qu'il en soit de même pour les quatre distances Si–N. nous avons alors obtenu les valeurs ci-dessous:
| x | y | z | |
| Mn | 0,072 | 0,628 | -0,005 |
| 0,071 | 0,130 | 0 | |
| Ni | 0,055 | 0,082 | 0,351 |
| N1 | 0,102 | 0,655 | 0,410 |
Tableau 1. Intensités nucléaires observées et calculées à 290°C
| h k l | I_{calc} | I_{obs} normalisé |
| 1 1 0 | 103,5 | 103,3 |
| 0 1 1 | ||
| 0 2 0 | 15,3 | 20,3 |
| 1 1 1 | ||
| 1 2 0 | 40 | 38,4 |
| 2 0 0 | 31,7 | 31,5 |
| 0 0 2 | 92,5 | 81,7 |
| 2 1 0 | ||
| 1 2 1 | 250 | 234 |
| 2 0 1 | 132 | 130 |
| 2 1 1 | 17,2 | 22,5 |
| 1 1 2 | 17 | 26 |
| 2 2 0 | 4,3 | 6,7 |
| 2 0 2 | 51 | 38 |
| 2 1 2 | 17,6 | 21,7 |
| 3 1 0 | ||
| 2 3 0 | 68,5 | 79,8 |
| 1 3 0 | ||
| 0 2 2 | 35,2 | 44,2 |
| 0 3 1 | ||
| 2 2 1 | ||
| 1 2 2 | 142,2 | 143 |
| 1 3 1 |
avec R = 0,065 pour les rayons X et R = 0,09 pour les neutrons.
Les intensités nucléaires observées et calculées sont portées dans le Tableau 1.
Les distances interatomiques ont pour valeurs
\[ \mathrm{Mn-N}\quad2,13-2,12-2,11-2,10\mathrm{soit~en~moyenne~}2,11_{5} \]
\[ \mathrm{Si-N}\quad1,81-1,78-1,73-1,71\mathrm{soit~en~moyenne~}1,75, \]
La distance Si–N se rapproche alors de la plupart de celles qui ont été observées jusqu'ici et qui sont rassemblées dans. \( ^{6} \)
\[ \begin{aligned}&LiSi_{2}N_{3}\quad&1,75\ \textup{\AA}\\&\alpha-Si_{3}N_{4}\quad&1,738\ \textup{\AA}\\&\beta-Si_{3}N_{4}\quad&1,737\ \textup{\AA}\\&Si_{2}N_{2}O\quad&1,72\ \textup{\AA}\\&N(SiH_{3})_{3}\quad&1,738\ \textup{\AA}.\\ \end{aligned} \]
Toutes ces valeurs sont bien inférieures aux valeurs calculées en utilisant les rayons tétraédriques donnés dans la littérature; on trouve 1,87 Å d'après Parthé \( ^{7} \) ou 1,85 Å d'après Van Vechten et Phillips. \( ^{8} \) En fait dans les

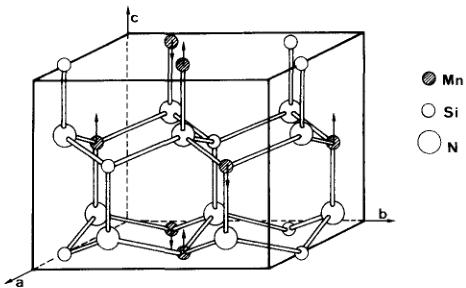
Fig. 1. Structure cristallographique (idéalisée) et structure magnétique de MnSiN₂.
Tableau 2. Intensité magnétiques observées et calculées à température ambiante
| h k l | I_{calc} | I_{\text{obs}} normalisé |
| 1 0 0 | 4,8 | 4,2 |
| 1 1 0 | 26 | 25,2 |
| 0 1 1 | ||
| 1 0 1 | 15,2 | 16,7 |
| 1 1 1 | ||
| 0 2 0 | 25,2 | 24,9 |
| 1 2 0 | 0 | 1,2 |
composés mentionnés ci-dessus l'azote forme toujours moins de quatre liaisons covalentes. Ainsi dans la molécule plane N(SiH_{3}){4} l'azote forme trois liaisons à 120° l'une de l'autre avec ses trois voisins Si et devrait posséder une paire libre. D'après Hedberg \( ^{9} \) et Gillespie \( ^{10} \) cette paire libre se trouverait délocalisée sur les trois liaisons N-Si en leur donnant partiellement un caractère de double liaison, ce qui expliquerait le raccourcissement de la distance interatomique. Les mêmes observations sont valables pour les autres composés, et peuvent s'étendre à MnSiN{2} en le considérant comme constitué d'un charpente (SiN_{2}){n}^{2n-} dans laquelle s'insèrent des ions Mn^{2+}, qui forment avec cette charpente des liaisons très peu covalentes. Les angles Si-N-Si sont d'ailleurs égaux à 120° et 126° dans MnSiN{2}. A l'appui d'un tel modèle on peut encore remarquer que dans LiSi_{2}N_{3}, \( ^{6} \) où existent deux types d'atomes d'azote, l'un ayant deux voisins Si et l'autre trois, la distance Si-N vaut 1,70 Å pour le premier, qui aurait deux paires libres, et 1,76 Å pour le second, qui aurait une seule paire libre.
En ce qui concerne les distances Ge–N les données expérimentales sont moins nombreuses. Dans MnGeN₂ on trouve 1,90 Å, très voisin de la somme des rayons (1,92 Å), avec des angles Ge–N–Ge de 115 et 120°.
Dans CaGeN₂¹¹ Ge–N = 1,85 Å, et dans N(GeH₃)₃¹² Ge–N = 1,83 Å. D'après¹³ la délocalisation de paires libres serait peu prononcée pour Ge–N parce qu'elle impliquerait un empiètement 2p–4d, moins probable que l'empiètement 2p–3d de la liaison Si–N.
4. STRUCTURE MAGNETIQUE
Comme pour MnGeN₂ la maille Magnétique est identique à la maille chimique et les intensités magnétiques observées indiquent un mode \( Gz(+ - + -) \) : moments de même signe pour les spins 1 et 3 en x, y, z et 1/2 - x, 1/2 + y, 1/2 + z opposés à ceux (2 et 4) situés en -x, -y, 1/2 + z et 1/2 + x, 1/2 - y, z (Fig. 1). Le groupe magnétique est \( Pr^{l}a^{2}l \) . Les intensités magnétiques calculées et observées à température ambiante, avec un moment de \( 3,8 \mu_{B}/Mn \) , sont portées dans le Tableau 2. De la variation thermique des intensités magnétiques on peut déduire que la température de Néel est voisine de 180°C. MnGeN₂, pour lequel le moment de Mn à l'ambiance est de 3,5 μB, a probablement une température de Néel un peu plus basse.
Pour \( MnSiN_{2} \) on calcule alors, dans l'approximation du champ moléculaire, une valeur moyenne de l'integrale d'échange Mn-N-Mn, J = 19 K. A titre de comparaison, l'intégrale d'échange Fe-O-Fe dans β-FeNaO₂ vaut 31 K, et l'intégrale Mn-O-Mn à 90° dans MnO vaut 7 K.¹⁴ La liaison Mn-N apparaît ainsi plus covalente que la liaison Mn-O, mais moins que la liaison Fe-O, est il n'est pas injustifié de faire intervenir son caractère ionique dans la discussion des longueurs et des angles des liaisons de \( MnSiN_{2} \) .
REFERENCES
-
WINTENBERGER M., GUYADER J. & MAUNAYE M., Solid State Commun. 11, 1458 (1972).
-
WINTENBERGER M., MAUNAYE M. & LAURENT Y., Mat. Res. Bull. 8, 1049 (1973).
-
MAUNAYE M., MARCHAND R., GUYADER J., LAURENT Y. & LANG J., Bull. Soc. Fr. Minéral. Cristallogr. 94, 561 (1971).
-
BERTAUT E.F., DELAPALME A. & BASSI G., J. Phys. 25, 545 (1964).
-
World List of Computer Programs No. 216. J. Appl. Crystallogr., 6, 309 (1973).
-
DAVID J., LAURENT Y., CHARLOT J.P. & LANG J., Bull. Soc. Fr. Mineral. Cristallogr 96, 21 (1973).
-
PARTHE E., Crystal Chemistry of Tetrahedral Structures. Gordon and Breach, New York (1964).
-
VAN VECHTEN J.A. & PHILLIPS J.C., Phys. Rev. B2, 2160 (1970).
-
HEDBERG K., J. Amer. Chem. Soc. 77, 6491 (1955).
-
GILLESPIE R.J., Molecular Geometry Van Nostrand, New York (1972).
-
MAUNAYE M., GUYADER J., LAURENT Y. & LANG J., Bull. Soci. Fr. Minéral. Cristallogr. 94, 347 (1971).
-
GLIDEWELL C., RANKIN D.W.H. & ROBIETTE A.G., J. Chem. Soc., A2935 (1970).
-
BEAGLEY B. & CONRAD A.R., Trans. Faraday Soc. 66, 2740 (1970).
-
SMART J.S., Effective Field Theories of Magnetism. Saunders (1966).
The Neel temperature (180°C) and magnetic structure of \( MnSiN_{2} \) have been obtained by neutron diffraction as well as better atomic coordinates than those deduced previously from X-ray data only.