| Transition Temperature | 30 K |
|---|---|
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | P-3c1 (#165) |
| Magnetic Space Group | P-3'c'1 (#165.94) |
| Magnetic Point Group | -3'm' (20.4.74) |
| Lattice Parameters | 5.17360 5.17360 14.14570 90.00 90.00 120.00 |
|---|---|
| DOI | 10.1016/0022-3697(61)90103-2 |
| Reference | E. Bertaut, L. Corliss, F. Forrat, R. Aleonard and R. Pauthenet, Journal of Physics and Chemistry of Solids (1961) 21 234-251. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Nb1 | Nb | 0.0 | 0.0 | 0.0 | 0.00 |
| Co1 | Co | 0.0 | 0.0 | 3. | 3.00 |
| Co2 | Co | 0.0 | 0.0 | 3. | 3.00 |
Title
ETUDE DE NIOBATES ET TANTALATES DE METAUX DE TRANSITION BIVALENTS
Authors
E. F. BERTAUT, L. CORLISS*, et F. FORRAT Centre d'Etudes Nucléaires de Grenoble
R. ALEONARD et R. PAUTHENET Laboratoire d'Electrostatique et de Physique du Métal, Grenoble
*Adresse actuelle : Brookhaven National Laboratories Upton, Long Island, N.Y. (USA).
Materials Studied
- \( A_{2}M_{4}O_{9} \) (general formula, where A = Nb, Ta; M = Mn, Fe, Co, Mg, Ni)
- \( Nb_{2}Mn_{4}O_{9} \)
- \( Nb_{2}Co_{4}O_{9} \)
- \( Nb_{2}Fe_{4}O_{9} \)
- \( Nb_{2}Mg_{4}O_{9} \)
- \( Ta_{2}Co_{4}O_{9} \)
- \( Ta_{2}Mn_{4}O_{9} \)
- \( Ta_{2}Mg_{4}O_{9} \)
- \( Nb_{2}Ni_{4}O_{9} \)
Key Information
- Crystal structure / space group:
- Hexagonal for \( A_{2}M_{4}O_{9} \) (A = Nb, Ta; M = Mn, Fe, Co, Mg)
- Orthorhombic for \( Nb_{2}Ni_{4}O_{9} \)
- Most probable space group: \( P\bar{3}c1 \)
- Magnetic ordering type and temperature:
- \( Nb_{2}Mn_{4}O_{9} \): Antiferromagnetic, \( T_N = 125^\circ K \), \( \Theta_P = -250^\circ K \)
- \( Nb_{2}Co_{4}O_{9} \): Antiferromagnetic (revealed by neutron diffraction at 4.2K), \( \Theta_P = -10^\circ K \) (from Curie-Weiss fit above 30K), \( T_N \approx 30^\circ K \) (inferred from susceptibility behavior)
- Propagation vector(s): Not explicitly stated as a vector, but the magnetic order conserves the crystallographic cell, implying k=0 for the magnetic structure.
- Magnetic moments:
- \( Mn^{2+} \): \( S = 5/2 \) (spin-only value, \( C = 4.31 \) per ion, calculated \( 4.39 \))
- \( Co^{2+} \):
- Paramagnetic region (\( T > 40^\circ K \)): \( S = 4/2 \) (indicating orbital contribution, \( C = 3.0 \) per ion, calculated between \( 1.88 \) for \( S=3/2 \) and \( 5.61 \) for \( J=L+S=9/2 \))
- Antiferromagnetic region (\( T = 4.2^\circ K \)): \( S = 3/2 \) (spin-only value, suggesting orbital moment is blocked)
- Lattice parameters (Hexagonal):
- \( Nb_{2}Co_{4}O_{9} \): a = 5.177 Å, c = 14.168 Å
- \( Nb_{2}Fe_{4}O_{9} \): a = 5.233 Å, c = 14.236 Å
- \( Nb_{2}Mn_{4}O_{9} \): a = 5.335 Å, c = 14.320 Å
- \( Nb_{2}Mg_{4}O_{9} \): a = 5.171 Å, c = 14.173 Å
- \( Ta_{2}Co_{4}O_{9} \): a = 5.181 Å, c = 14.174 Å
- \( Ta_{2}Mn_{4}O_{9} \): a = 5.337 Å, c = 14.333 Å
- \( Ta_{2}Mg_{4}O_{9} \): a = 5.170 Å, c = 14.143 Å
- Lattice parameters (Orthorhombic):
- \( Nb_{2}Ni_{4}O_{9} \): a = 10.144 Å, c = 14.318 Å (b-parameter not given)
- Other critical measured values:
- Densities (g/cm³):
- \( Nb_{2}Co_{4}O_{9} \): 5.72
- \( Nb_{2}Fe_{4}O_{9} \): 5.44
- \( Nb_{2}Mn_{4}O_{9} \): 5.19
- \( Nb_{2}Mg_{4}O_{9} \): 4.32
- \( Ta_{2}Co_{4}O_{9} \): 7.47
- \( Ta_{2}Mn_{4}O_{9} \): 6.81
- \( Ta_{2}Mg_{4}O_{9} \): 6.12
- Exchange coefficients for \( Nb_{2}Mn_{4}O_{9} \): \( n = -21.6 \), \( n' = -7.3 \) (where \( n \) is interaction between different sublattices, \( n' \) within the same sublattice).
- Exchange coefficients for \( Nb_{2}Co_{4}O_{9} \): \( n = -3.34 \), \( n' = +1.67 \) (assuming \( T_N = 30^\circ K \)).
- Anisotropy constant for \( Nb_{2}Co_{4}O_{9} \): \( K_1 \approx 1.3 \cdot 10^6 \) ergs/cm³ at 4.2K.
- Spin direction: Along the c-axis for both \( Nb_{2}Mn_{4}O_{9} \) and \( Nb_{2}Co_{4}O_{9} \).
- Atomic positions (z-coordinates for cations, x,y,z for oxygen):
- \( Nb_{2}Mn_{4}O_{9} \): Nb (4c) z = 0.3575; M1 (4d) z = 0.0181; M11 (4d) z = 0.297; O1 (6f) x = 0.300; O11 (12g) x = 0.334, y = 0.295, z = 0.0884
- \( Nb_{2}Co_{4}O_{9} \): Nb (4c) z = 0.360; M1 (4d) z = 0.027; M11 (4d) z = 0.307; O1 (6f) x = 0.305; O11 (12g) x = 0.333, y = 0.295, z = 0.0833
- Densities (g/cm³):
Synthesis Method
The niobates and tantalates were prepared by mixing constituent oxides. The mixtures were heated for 10 hours, then homogenized by grinding, and finally re-annealed under the same conditions. Specific temperature and atmosphere conditions varied depending on the M ion: * Mn: 1250°C under H² * Mg: 1400°C in air * Ni and Co: 1300°C in air * Fe: 1200°C under argon
Abstract
The structure of \( A_{2}M_{4}O_{9} \) (A = Nb, Ta; M = Mn, Fe, Co, Mg) has been studied by X-rays. It derives from the corundum type structure \( (\alpha - \mathrm{Al}_{2}\mathrm{O}_{3}) \) by an ordering of the cations A and M. The most probable space group is \( P\bar{3}c1 \). Magnetic measurements and neutron diffraction show up the antiferromagnetic nature of \( Nb_{2}Mn_{4}O_{9} \) and \( Nb_{2}Co_{4}O_{9} \). The spins form chains along the lines \( \frac{1}{3}\frac{2}{3}\alpha \) (+spins) and \( \frac{2}{3}\frac{1}{3}\alpha \) (-spins).
Main Content Summary
This research investigates the structural and magnetic properties of niobates and tantalates with the general formula \( A_{2}M_{4}O_{9} \), where A is Nb or Ta, and M is a bivalent transition metal (Mn, Fe, Co, Ni) or Mg. The study aims to understand how these compounds, which are structural derivatives of corundum (\( \alpha-Al_{2}O_{3} \)) and hematite (\( \alpha-Fe_{2}O_{3} \)) through cation ordering, exhibit varying spin configurations. The work is divided into four parts: crystallographic study by X-rays, neutron diffraction of \( Nb_{2}Mn_{4}O_{9} \) and \( Nb_{2}Co_{4}O_{9} \), magnetic measurements, and a theoretical analysis of magnetic configurations.
The crystallographic study, primarily using X-ray powder diffraction, revealed that the \( A_{2}M_{4}O_{9} \) compounds (except \( Nb_{2}Ni_{4}O_{9} \), which is orthorhombic) crystallize in a hexagonal system, deriving from the rhombohedral corundum structure. The presence of superlattice reflections indicates ordering of \( A^{5+} \) and \( M^{2+} \) ions, leading to a lowering of symmetry. Based on extinction rules and the absence of piezoelectric effects, the most probable space group is determined to be \( P\bar{3}c1 \). A surprising finding is that the \( A^{5+} \) ions (Nb, Ta) occupy positions where their coordination octahedra share a face, causing significant displacement of the Nb atoms from the octahedron centers due to strong Coulombic repulsion.
Neutron diffraction experiments on \( Nb_{2}Mn_{4}O_{9} \) and \( Nb_{2}Co_{4}O_{9} \) were conducted at room, liquid nitrogen, and liquid helium temperatures. At room temperature, the atomic positions and oxygen parameters were refined using a least-squares method, yielding good agreement between observed and calculated intensities. At low temperatures, significant changes in diffraction patterns confirmed the onset of antiferromagnetic order in both compounds, with the magnetic unit cell coinciding with the crystallographic one. For both \( Nb_{2}Mn_{4}O_{9} \) and \( Nb_{2}Co_{4}O_{9} \), the magnetic structure corresponds to a "mode 3" configuration, characterized by two antiparallel spin chains along the c-axis, specifically along the lines \( \frac{1}{3}\frac{2}{3}z \) and \( \frac{2}{3}\frac{1}{3}z \). The spins are aligned along the c-axis.
Magnetic susceptibility measurements confirmed the antiferromagnetic nature. For \( Nb_{2}Mn_{4}O_{9} \), a Néel temperature of \( T_N = 125^\circ K \) and a Curie-Weiss temperature of \( \Theta_P = -250^\circ K \) were found, with a Curie constant consistent with \( Mn^{2+} \) in a \( ^6S \) state (\( S=5/2 \)). For \( Nb_{2}Co_{4}O_{9} \), the susceptibility curve was more complex, but indicated antiferromagnetism below approximately \( 30^\circ K \). The Curie constant for \( Co^{2+} \) in the paramagnetic region suggested an orbital contribution (\( S=4/2 \)), while neutron diffraction data at 4.2K were best fitted with a spin-only value (\( S=3/2 \)), implying that the orbital moment of \( Co^{2+} \) is largely quenched at very low temperatures. A theoretical analysis using a matrix method explored possible magnetic configurations and stability conditions, confirming the observed magnetic structure and providing insights into the nature of exchange interactions.
Conclusion
The structure of \( A_{2}M_{4}O_{9} \) (\( \mathrm{A} = \mathrm{Nb}, \mathrm{Ta}; \mathrm{M} = \mathrm{Mn}, \mathrm{Fe}, \mathrm{Co}, \mathrm{Mg} \)) constitutes a new type of corundum superstructure, similar to ilmenites, but with a cation ratio of 1:2 instead of 1:1. The most probable space group is \( P \bar{3} c 1 \). Quite surprisingly, the coordination octahedra of pentavalent niobium share a common face. Consequently, Coulombic repulsion significantly displaces the neighboring Nb atoms from the centers of the octahedra.
The substances \( \mathrm{Nb}_2\mathrm{Co}_4\mathrm{O}_9 \) and \( \mathrm{Nb}_2\mathrm{Mn}_4\mathrm{O}_9 \) exhibit an antiferromagnetic chain structure. The line \( \frac{1}{3} \frac{2}{3} \) carries spins oriented along \( c \), while the line \( \frac{2}{3} \frac{1}{3} \) carries spins oriented in the opposite direction.
\( \mathrm{Mn}^{2+} \) is in a \( ^6S \) state. The situation in \( \mathrm{Co}^{2+} \) is more delicate. Susceptibility measurements in the paramagnetic region (\( T > 40^\circ K \)) indicate a moment of \( S = \frac{4}{2} \), i.e., an orbital contribution, whereas neutron diffraction measurements in the antiferromagnetic region (\( T = 4.2^\circ K \)) indicate a moment of \( S = \frac{3}{2} \), i.e., the spin-only value. It is therefore probable that at very low temperatures, the orbital moment of \( \mathrm{Co} \) is completely blocked.
ETUDE DE NIOBATES ET TANTALATES DE METAUX DE TRANSITION BIVALENTS
E. F. BERTAUT, L. CORLISS* et F. FORRAT
Centre d'Etudes Nucléaires de Grenoble
et
R. ALEONARD et R. PAUTHENET
Laboratoire d'Electrostatique et de Physique du Métal, Grenoble
(Received 10 April 1961)
Résumé—La structure de \( A_{2}M_{4}O_{9} \) (A = Nb, Ta ; M = Mn, Fe, Co, Mg) a été étudiée aux rayons X. Elle dérive de la structure du corindon \( Al_{2}O_{3}-\alpha \) par un ordre des cations A et M. Le groupe d'espace le plus probable est \( P\bar{3}c1 \) . Les mesures magnétiques et la diffraction neutronique montrent la nature antiferromagnétique de \( Nb_{2}Mn_{4}O_{9} \) et de \( Nb_{2}Co_{4}O_{9} \) . Les spins forment des chaînes selon les droites \( \frac{1}{3}\frac{1}{2}\alpha \) (spins+) et \( \frac{1}{3}\frac{1}{2}\alpha \) ((spins−).
Abstract—The structure of \( A_{2}M_{4}O_{9} \) (A = \( Nb, Ta; M = Mn, Fe, Co, Mg \) ) has been studied by X-rays. It derives from the corundum type structure \( (\alpha - \mathrm{Al}_{2}\mathrm{O}_{9}) \) by an ordering of the cations A and M. The most probable space group is \( P\bar{3}c1 \) . Magnetic measurements and neutron diffraction show up the antiferromagnetic nature of \( Nb_{2}Mn_{4}O_{9} \) and \( Nb_{2}Co_{4}O_{9} \) . The spins form chains along the lines \( \frac{1}{3}\frac{1}{2}\alpha \) (+spins) and \( \frac{1}{3}\frac{1}{2}\alpha \) (-spins).
INTRODUCTION
Les combinaisons du type niobate et tantalate \( ^{(1)} \) \( A_{2}MO_{6} \) où A = Nb, Ta ; M = métal de transition bivalent et Mg sont bien connues. Nous les complétons par l'étude des composés \( A_{2}M_{4}O_{9} \) où M = Mn, Fe, Co, Ni, Mg.
Le présent travail rentre dans le cadre d'un programme d'études plus général, celui de la "substitution isomorphé", c'est-à-dire de la substitution des ions présents dans une structure ionique connue par d'autres ions, de rayons comparables et de valences en général différentes, tout en conservant le type de structure. Citons comme exemple la substitution
\[ \mathrm{Ca^{2+}+Si^{4+}\rightarrow T^{3+}+Fe^{3+}\ (T=terre\ rare)} \]
qui a abouti à la découverte des grenats ferrima-
- Adresse actuelle : Brookhaven National Laboratories Upton, Long Island, N.Y. (USA).
† Nous n'avons pas encore réussi à préparer les composés avec M = Cu. gnétiques. \( ^{(2)} \) Dans le cas actuel, la substitution
\[ \mathrm{A^{5+}+2M^{2+}\rightarrow3Fe^{3+}ouAl^{3+}} \]
relie directement les structures \( A_{2}M_{4}O_{9} \) au type corindon \( Al_{2}O_{3} \) et à l'hématite \( Fe_{2}O_{3} \) comme nous allons le montrer dans l'étude cristallographique de la première partie.
En dehors de l'intérêt purement cristallographique de la structure et des paramètres qui la définissent, on peut se demander comment la configuration des spins varie dans les composés dérivant du type corindon tels que \( Cr_{2}O_{3} \) ; \( Fe_{2}O_{3}-\alpha \) ; les ilminétes \( TiMO_{3} \) et enfin les niobates (et tantalates) \( A_{2}M_{4}O_{9} \) . C'est pourquoi nous avons entrepris au Centre d'Etudes Nucléaires de Grenoble, une étude par diffraction neutronique des composés \( Nb_{2}Mn_{4}O_{9} \) et \( Nb_{2}Co_{4}O_{9} \) . Cette étude fait l'objet de la deuxième partie.
La troisième partie est consacrée aux mesures magnétiques et à leur discussion. Les mesures de
susceptibilité en fonction de la température permettent de déterminer des températures antiferromagnétique et de Curie-Néel, ainsi que des valeurs des moments magnétiques et de certaines intégrales d'échange. L'interprétation de la structure magnétique, trouvée par diffraction neutronique s'en trouve grandement facilitée.
Dans une quatrième partie, nous examinons, par un calcul matriciel toutes les structures magnétiques qui conservent la maille cristallographique et nous établissons les critères de stabilité de la structure observée.
Enfin, nous résumons dans les conclusions, les principaux résultats obtenus.
PREMIERE PARTIE
Préparation
Les niobates et tantalates ont été préparés à partir du mélange des oxydes constituants dans des conditions de température et d'atmosphère variant selon l'ion M comme il suit :
Mn (1.250°C sous H²) ; Mg (1.400°C à l'air) ; Ni et Co (1.300°C à l'air) Fe (1.200°C sous argon). Après un chauffage de 10 heures, les produits sont homogénéisés par broyage et finalement recuits dans les mêmes conditions.
Etude cristallographique aux rayons X
La méthode des poudres a été employée en
Tableau 1. Comparaison d'un diffractogramme de \( Nb_{9}Co_{4}O_{9} \) et de \( Fe_{2}O_{3}-\alpha \) sous radiation \( K\alpha \) du cobalt
| Indice h k l | Nb_{2}Co_{4}O_{9} | Fe_{2}O_{3}-\alpha | ||
| d | I_{obs} | d | I_{obs} | |
| 0 0 2 | 7,07 | 1 | — | — |
| 1 0 0 | 4,48 | 17 | — | — |
| 1 0 2 | 3,78 | 23 | 3,68 | 18 |
| 0 0 4 | 3,54 | 4 | — | — |
| 1 0 4 | 2,77 | 100 | 2,69 | 100 |
| 1 1 0 | 2,58 | 57 | 2,51 | 75 |
| 0 0 6 | 2,36 | 5 | — | — |
| 1 1 3 | 2,27 | 20 | 2,20 | 18 |
| 2 0 0 | 2,24 | 3 | — | — |
| 2 0 2 | 2,13 | 2 | — | — |
| 1 0 6,1 1 4 | 2,09 | 5 | — | — |
| 2 0 4 | 1,891 | 28 | 1,84 | 63 |
| 0 0 8 | 1,768 | 5 | — | — |
| 1 1 6 | 1,741 | 43 | 1,69 | 63 |
| 2 1 0 | 1,692 | 3 | — | — |
| 1 0 8,2 1 2 | 1,645 | 15 | 1,60 | 13 |
| 2 0 6 | 1,623 | 1 | — | — |
| 2 1 4 | 1,526 | 38 | 1,485 | 50 |
| 3 0 0 | 1,492 | 28 | 1,452 | 50 |
| 3 0 2,1 1 8 | 1,459 | 4 | — | — |
| 2 0 8 | 1,387 | 7 | 1,351 | 3 |
| 3 0 4,2 1 6 | 1,374 | 3 | — | — |
| 1,0,10 | 1,348 | 13 | 1,308 | 18 |
| 2 2 0 | 1,292 | 7 | 1,259 | 13 |
| 3 0 6 | 1,261 | 3 | 1,230 | 3 |
| 1,1,10;3,1,0 | 1,241 | 2 | — | — |
| 3,1,2;2,1,8 | 1,222 | 19 | 1,190 | 8 |
| 2,0,10 | 1,195 | 15 | 1,195 | 5 |
| 3 1 4 | 1,171 | 17 | 1,140 | 13 |
| 3 0 8 | 1,140 | 2 | — | — |
| 2 2 6 | 1,133 | 15 | 1,104 | 10 |
| 2,1,11 | 1,085 | 21 | 1,056 | 8 |
utilisant, soit une chambre Debye–Scherrer et la radiation filtrée \(K\alpha\) du fer, soit un diffractographe enregistreur et la radiation \(K\alpha_{1}\) du cobalt, monochromatisée par la technique de Guinier.
L'analogie des diagrammes avec ceux de \( Fe_{2}O_{3}-\alpha \) est frappante comme le montre le Tableau 1. Nous y avons représenté les données de diffraction (indices h k l, distances réticulaires d et intensités observées) de \( Nb_{2}Co_{4}O_{9} \) et à titre de comparaison celles de \( Fe_{2}O_{3}-\alpha \) en notation hexagonale. Toutes les positions de raies fortes et moyennes dont les indices obéissent à la règle -h +k+l = 3n coïncident pratiquement. charges élevées se trouvent aussi loin que possible les uns des autres. Remarquons cependant que la structure de \( Al_{2}O_{3}-\alpha \) (et de \( Fe_{2}O_{3}-\alpha \) ) élucidée par PAULING et HENDRICKS \( ^{(3)} \) constitue une exception à une des règles de Pauling. En effet, dans le type corindon, les octaèdres d'oxygène de coordination sont groupés par paires ayant une face en commun.
La structure la plus simple que l'on puisse concevoir placerait une seule sorte d'ions \( A^{5+} \) ou \( M^{2+} \) sur chacun des trois sous-réseaux rhomboédriques du corindon qui correspondent aux translations 0 0 0 ; \( \frac{2}{3} \) \( \frac{1}{3} \) ; \( \frac{1}{3} \) \( \frac{2}{3} \) . Dans le groupe
Tableau 2. Paramètres cristallins
| Formule | Systeme | Maille (Å) | DX (g/cm³) | |
| a | c | |||
| Nb₂Co₄O₉ | Hexagonal | 5,177 | 14,168 | 5,72 |
| Nb₂Fe₄O₉ | ,, | 5,233 | 14,236 | 5,44 |
| Nb₂Mn₄O₉ | ,, | 5,335 | 14,320 | 5,19 |
| Nb₂Mg₄O₉ | ,, | 5,171 | 14,173 | 4,32 |
| Ta₂Co₄O₉ | ,, | 5,181 | 14,174 | 7,47 |
| Ta₂Mn₄O₉ | ,, | 5,337 | 14,333 | 6,81 |
| Ta₂Mg₄O₉ | ,, | 5,170 | 14,143 | 6,12 |
| Nb₂Ni₄O₉ | Orthorhombique | a = 10,144 | c = 14,318 | |
Le Tableau 2 résume les paramètres en Å et les densités en g/cm³ des mailles hexagonales. Nous y avons également inclus les paramètres de \( Nb_{2}Ni_{4}O_{9} \) , composé orthorhombique, dont nous nous réservons l'étude.
De nombreuses raies de surstructure indiquent clairement que les ions \( A^{5+} \) et \( M^{2+} \) s'ordonnent, abaissant la symétrie rhomboédrique à celle hexagonale. Les règles d'extinction h k l existe à tous les ordres, h o h l n'existe qu'avec l = 2n, ainsi que l'absence de tout effet piézoélectrique que nous avons cherché selon la méthode de GIEBE et SCHEIBE font apparaître le groupe d'espace \( P \bar{3} c \) 1 comme étant le plus probable.
Selon les règles de Pauling, basées sur des raisonnements d'énergie électrostatique, il semble naturel de constituer un modèle où les ions \( A^{5+} \) de \( P\bar{3}c1 \) on a sa disposition un site \( (4c):\pm00z \) ; 00, \( \frac{1}{2}+\bar{z} \) et deux sites \( (4d):\pm(\frac{3}{2},\frac{3}{2},\frac{3}{2},\frac{1}{2}+\bar{z}) \) pour placer les cations tandis que le paquetage compact des atomes d'oxygène peut être réalisé dans les positions
(12g) ± (x y z ; \( \bar{y} \) , x-y, z ; y-x, \( \bar{x} \) , z ; \( \bar{y} \) , \( \bar{x} \) , \( \frac{1}{2} \) +z ; x, x-y, \( \frac{1}{2} \) +z ; y-x, y, \( \frac{1}{2} \) +z) et (6f) ± (x, 0, \( \frac{1}{4} \) ; 0, x, \( \frac{1}{4} \) ; \( \bar{x} \) , \( \bar{x} \) , \( \frac{1}{4} \) )
Selon notre première hypothèse, les ions \( A^{5+} \) seraient les plus éloignés les uns des autres dans une position (4d) tandis que dans une position (4c), deuxième hypothèse à envisager, ils seraient couplés par paires dont les octaèdres d'oxygène de coordination auraient une face en commun. Fait inattendu, c'est la deuxième hypothèse qui se trouve réalisée. Ceci est clairement démontré par
Tableau 3. Correspondance entre les positions atomiques dans \( Fe_{2}O_{3}-\alpha \) et dans \( Nb_{2}Co_{4}O_{9} \)
| Fe_{2}O_{3}-\alphaDescription hexagonale | 'Translations rhomboédriques | Nb_{2}Co_{4}O_{9} |
| R \overline{3}c1 | P \overline{3}c1Nb en [4(c)] \pm (00z ; 00 \frac{1}{2}+z) | |
| Fe en [12(c)] \pm (00z ; 00 \frac{1}{2}+z) + | \begin{pmatrix}0 & 0 \\ \frac{2}{3} & \frac{1}{3} \\ \frac{1}{3} & \frac{2}{3}\end{pmatrix} | Co_{1} en [4(d)] \pm (\frac{1}{3} \frac{2}{3}z ; \frac{1}{3} \frac{1}{3}+z)Co_{11} en [4(d)] |
| O en [18(e)] \pm (xO \frac{1}{4}; Ox \frac{1}{4}; \overline{x}\overline{x}\overline{x}) | \begin{pmatrix}0 & 0 \\ \frac{2}{3} \frac{1}{3} \\ \frac{1}{3} \frac{2}{3}\end{pmatrix} | O_{11} en (12g) position générale |
La description hexagonale de \( Fe_{2}O_{3}-\alpha \) , conformément aux Tables Internationales \( ^{(4)} \) est rapportée au centre de symétrie à l'origine \( (z=0,105+0,250=0,355; x=0,292) \) . Elle diffère de la description de PAULING \( ^{(3)} \) par une translation de \( \frac{1}{2} \) selon Oz.
la mesure de l'intensité de la raie (100) qui dans la première hypothèse est observée quatre fois trop forte, alors que l'accord avec la deuxième hypothèse est bon.
La correspondance entre les positions atomiques dans \( Fe_{2}O_{3}-\alpha \) et \( Nb_{2}Mn_{4}O_{9} \) est illustrée par le Tableau 3. Remarquons que dans la description de PAULING, les centres de symétrie sont en \( \pm(00z) \) avec \( z=\pm\frac{1}{4} \) tandis que dans notre description, en conformité avec les Nouvelles Tables Internationales, \( ^{(4)} \) les centres de symétrie se trouvent à l'origine et en \( (00\frac{1}{2}) \) .
Alors que les rayons X permettent de fixer les positions des atomes avec une assez bonne précision, nous remettons la détermination des paramètres d'oxygène et la description de la structure au chapitre suivant, car la section efficace relativement élevée de l'oxygène en diffraction neutronique permet d'obtenir une précision meilleure qu'aux rayons X.
DEUXIEME PARTIE
Etude de \( Nb_{2}Co_{4}O_{9} \) et \( Nb_{2}Mn_{4}O_{9} \) par diffraction neutronique
Des diagrammes de diffraction ont été réalisés à la température ordinaire et à celles de l'azote et de l'hélium liquide au diffractomètre à neutrons du Centre d'Etudes Nucléaires de Grenoble. Un système à moniteur automatisé assure une indépendance complète des fluctuations de la pile et une bonne reproductibilité des mesures d'intensité. Les intensités de diffraction sont enregistrées "point par point" avec des intervalles angulaires de \( \Delta\Theta=3' \) . Un monocristal de cuivre produit un faisceau monocinétique de longueur d'onde \( \lambda=1.198\ \AA \) . La composante \( \lambda/2 \) est de 2,5 pour cent. On en corrige les intensités observées de la manière habituelle.
Etude à température ordinaire
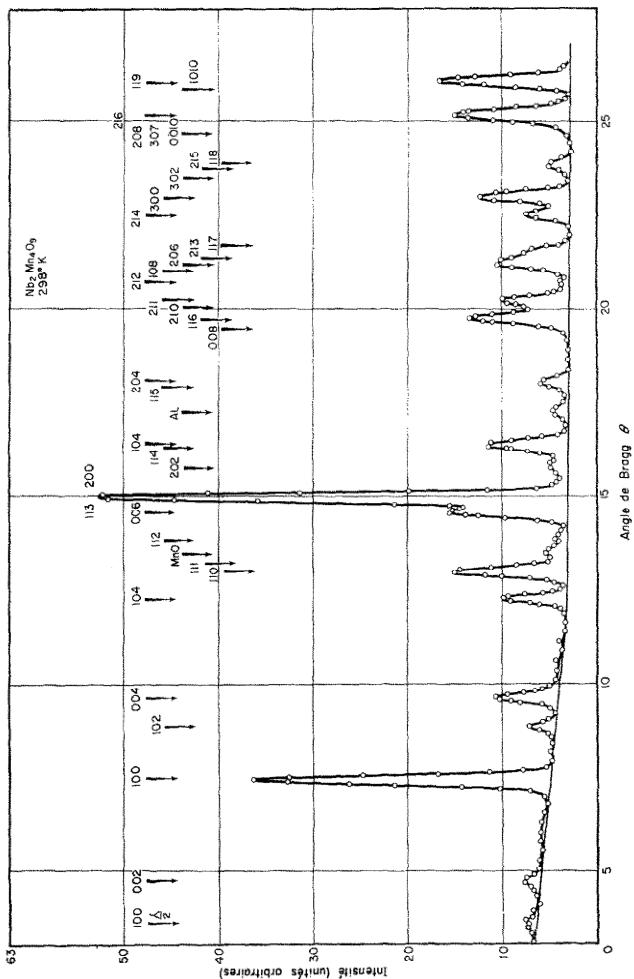
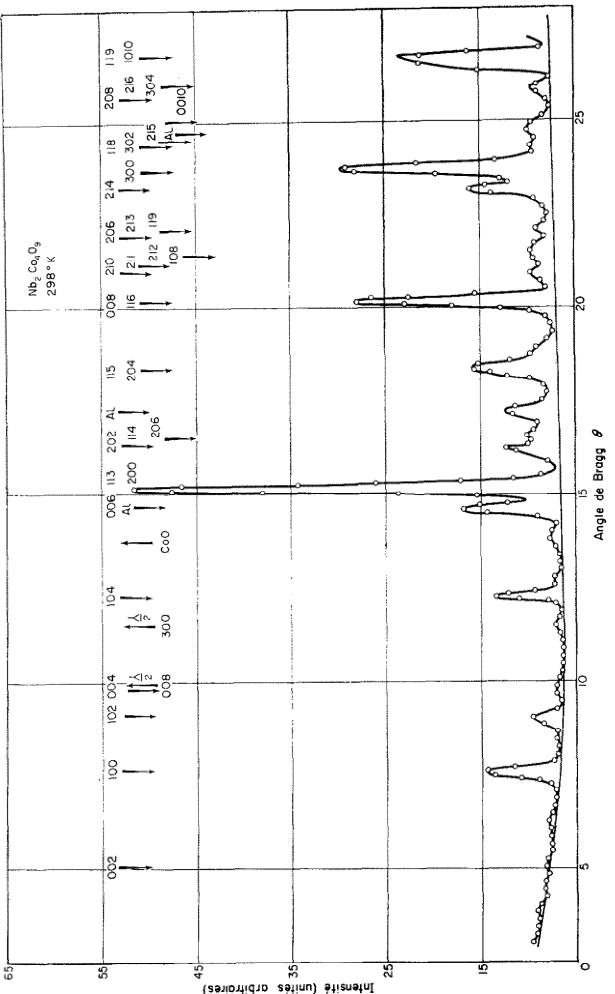
La Fig. 1 représente les enregistrements à température ordinaire. Les raies dues au portéchantillon en aluminium sont marquées Al. A cause de nombreuses superpositions de raies, la méthode des moindres carrés a été appliquée, non pas aux facteurs de structure, mais aux intensités.
Comme valeurs de départ des paramètres de positions, on a utilisé les valeurs de x des atomes lourds, connus approximativement par l'étude aux rayons X et les paramètres des atomes d'oxygène dans \( Fe_{2}O_{3}-\alpha \) . Légèrement corrigés par des considérations stériques. Les intensités ont été calculées comme
\[ I_{c}=p F^{2}/(\sin\Theta\sin2\Theta) \]
où F est le facteur de structure ordinaire, p la multiplicité des plans de réflexion. Dans le calcul d'intensité, on doit tenir compte du fait qu'à toute raie "rhomboédrique" h k i l se trouve superposée une raie de structure k h i l pour l ≠ 3n. [Exemple :

Fig. 1(a). Diagramme à température ordinaire de Nb-Mn-0.6

Fig. 1(b). Diagramme à température ordinaire de NbCoCr.
Tableau 4. Paramètres de position, groupe P 3 c 1
| Nb2Mn4O9 | Nb2Co4O9 | ||
| Nb | 4c | z = 0,3575 | z = 0,360 |
| M1 | 4d | z = 0,0181 | z = 0,027 |
| M11 | 4d | z = 0,297 | z = 0,307 |
| O1 | 6f | x = 0,300 | x = 0,305 |
| O11 | 12g | x = 0,334 | x = 0,333 |
| y = 0,295 | y = 0,295 | ||
| z = 0,0884 | z = 0,0833 |
Tableau 5. Intensités observées et calculées (Température ordinaire)
| h k l | Nb2Mn4O9 | Nb2Co4O9 | ||
| Ic | I0 | Ic | I0 | |
| 002 | 20 | 21 | 0 | 2 |
| 100 | 472 | 443 | 127 | 128 |
| 102 | 16 | 26 | 49 | 40 |
| 004 | 93 | 106 | 6 | 10 |
| 104 | 102 | 88 | 101 | 131 |
| 110, 111 | 162 | 179 | 0 | 0 |
| 112 | 4 | 3 | 0 | 1 |
| 006, 113, 200 | 877 | 875 | 738 | 751 |
| 202 | 38 | 35 | 34 | 32 |
| 114, 106 | 162 | 141 | ||
| 204, 115 | 22 | 42 | 140 | 132 |
| 008, 116 | 159 | 156 | 357 | 343 |
| 210, 211 | 114 | 127 | ||
| 212, | 2 | 9 | 104 | 104 |
| 108, 206 | 162 | 185 | ||
| 213, 117 | 27 | 43 | ||
| 214 | 59 | 68 | 31 | 23 |
| 300 | 159 | 143 | 453 | 426 |
| 302, 118 | 26 | 36 | ||
| 215 | 39 | 32 | ||
| 0010, 208 | 198 | 201 | 47 | 43 |
| 304, 216 | ||||
| 1010 119 | 248 | 223 | 284 | 299 |
| R = 0,07 | R = 0,065 | |||
(0 1 2) raie “rhomboédrique” et (1 0 2) raie de surstructure sont superposées.]
Les longueurs de FERMI × 10^{12} suivantes ont été utilisées : \( b(\mathrm{Mn}) = -0,37 \) ; \( b(\mathrm{Co}) = 0,25 \) ; \( b(\mathrm{Nb}) = 0,69 \) ; \( b(\mathrm{O}) = 0,58 \) .
Par deux itérations de la méthode de moindres carrés, nous avons déduit les sept paramètres de position de \( Nb_{2}Mn_{4}O_{9} \) et \( Nb_{2}Co_{4}O_{9} \) figurant dans le Tableau 4. L'accord entre intensités observées et calculées, résumées dans le Tableau 5 est satisfaisant, les facteurs
\[ \mathcal{A}=\sum|I_{\mathrm{o b s}}-I_{\mathrm{c a^{\prime}c}}|/\sum I_{\mathrm{c a l c}} \]
étant voisins de 0,07 pour les deux composés. Des corrections de vibrations thermiques n'ont pas été appliquées. des atomes de Nb est commun à deux octaèdres. La répulsion coulombienne déplace les atomes Nb vers les plus grands triangles, de sorte que Nb se trouve bien écarté du centre de l'octaèdre. La différence entre les deux distances Nb-OI = 2,23 Å et Nb-OII = 1,85 Å est exceptionnellement large (0,38 Å) comparée aux différences correspondantes dans Al₂O₃-α (0,145 Å) et dans Fe₂O₃-α (0,075 Å). (3) Les octaèdres autour des M ont un grand triangle en commun, fourni par les OII. Alors que les distances MnI-OII (3 OII à 2,27 Å, 3 OII à 2,22 Å) oscillent peu autour de la valeur normale de 2,23 Å, les distances MnII-OII (2,35 Å) et MnII-OI (1,99 Å) sont bien différentes, la dernière étant anormalement courte. Il se peut que les atomes OI ne soient pas tout à fait dans
Tableau 6. Distances interatomiques
| Nb_{2}Co_{4}O_{9} | Nb_{2}Mn_{4}O_{9} | |
| Nb-Nb | 3,12 | 3,08 |
| M_{I}-M_{I} | 3,09 | 3,12 |
| M_{I}-M_{II} | 3,12 | 3,17 |
| Nb-O_{I} | 2,21 | 2,22 |
| Nb-O_{II} | 1,82 | 1,85 |
| M_{II}-O_{I} | 1,98 | 1,99 |
| M_{II}-O_{II} | 2,25 | 2,35 |
| M_{I}-O_{II} | 2,26 | 2,27 |
| M_{I}-O'_{II} | 2,08 | 2,22 |
| O_{I}-O_{I} | 2,73 | 2,77 |
| O_{II}-O_{II} | 2,93 | 2,92 |
| O_{I}-O_{II} | 2,90 | 2,91 |
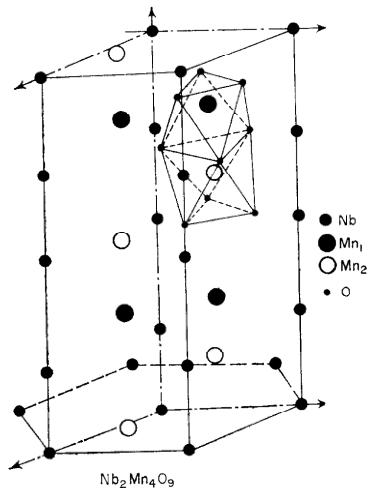
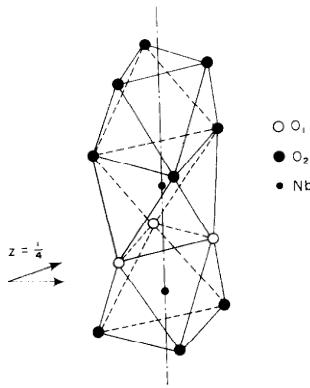
Description de la structure. La Fig. 2 représente la structure des niobates et tantalates de formule \( A_{2}M_{4}O_{9} \) . La structure peut être décrite par des chaînes d'octaèdres selon c ne contenant qu'une sorte de cations; A selon 00x, M selon \( \frac{1}{3} \) \( \frac{2}{3} \) x et \( \frac{2}{3} \) \( \frac{1}{3} \) x. Sur trois octaèdres d'une chaîne, deux sont occupés par les cations. Le Tableau 6 résume les principales distances interatomiques dans \( Nb_{2}Mn_{4}O_{9} \) . On remarque la grande déformation des octaèdres d'oxygène autour des atomes de Nb (Fig.3). Chaque octaèdre est formé par deux triangles équilatéraux dont le plan est perpendiculaire à l'axe ternaire. Les côtés des triangles sont respectivement 2,77 Å ( \( O_{I}-O_{I} \) ) et 2,92 Å ( \( O_{I}-O_{II} \) ). Le plus petit triangle qui écrante l'action répulsive le plan z = \( \frac{1}{4} \) imposé par le choix du groupe \( P\overline{3}c1 \) . Dans le groupe non centrosymétrique \( P3c1 \) le paramètre z est à nouveau libre. Mais comme alors le nombre de paramètres devient prohibitif, nous n'avons pas approfondi ce point pour l'instant, quitte à le reprendre plus tard.
Les différences entre les distances interatomiques dans les niobates de Co et de Mn (Tableau 6) s'expliquent principalement par la différence entre les rayons ioniques de ces cations.
Etude aux basses températures
\( Nb_{2}Mn_{4}O_{9} \) . Déjà, à la température de l'azote liquide, on observe une variation très notable des intensités, encore accentuée à celle de l'hélium

FIG. 2. Structure cristallographique des niobates et tantalates \( AgM_{4}O_{9} \) (A = Nb, Ta; M = Mn, Fe, Co, Mg).
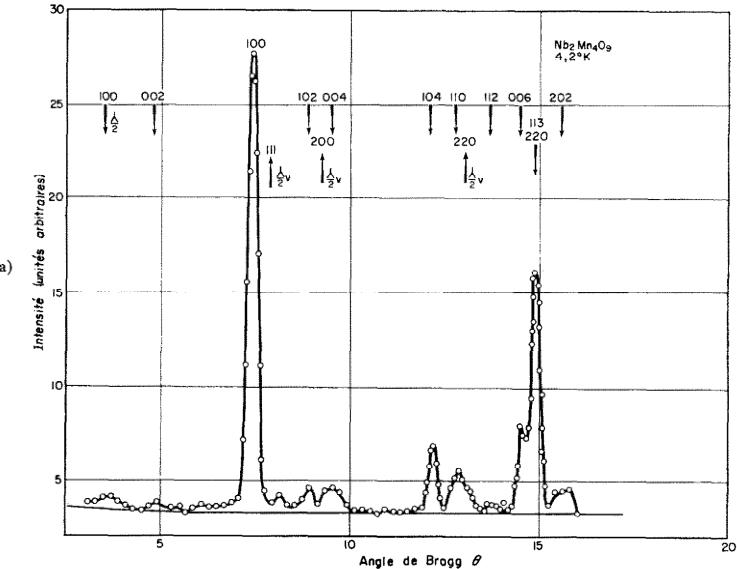
liquide. On remarque notamment sur la Fig. 4 que le rapport des intensités \( I(1\ 1\ 3)/I(1\ 0\ 0) \) est inversé. Comme le cryostat utilisé possède un porte-échantillon en laiton, deux diagrammes,

Fig. 3. Coordinations de Nb.
l'un avec, l'autre sans la substance, ont été enregistrés. Ce dernier montre la présence de raies faibles dues au laiton et produites par la composante \( \lambda/2 \) de raies fortes du laiton. Elles sont repérées par les flèches \( \uparrow \) sur la figure. Les intensités totales sont calculées à partir du diagramme différence des deux diagrammes précédents. La raie (1 1 3) étant une raie d'oxygène, sert d'étalon interne, compte tenu des composantes non résolues (mais considérablement plus faibles) de (2 0 0) et (1 1 2). En admettant que les paramètres atomiques soient aux basses températures les mêmes que ceux déterminés à l'ambiance, on remarque que les raies (0 0 2) n'ont pas de composante magnétique, tandis que la variation d'intensité est maximum pour la raie (1 0 0). On en déduit que la direction des spins est selon l'axe c.
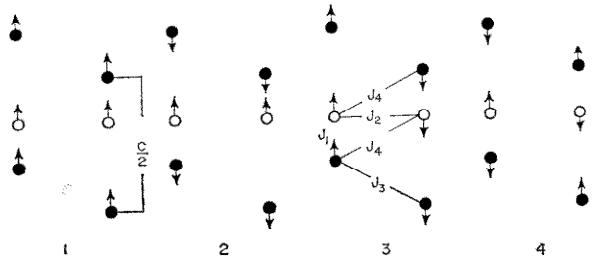
Comme il n'y a pas apparation de raies nouvelles, nous pouvons conclure que l'ordre antiferromagnétique s'installant aux basses températures, conserve la maille cristallographique. Dans ces conditions, il est alors relativement simple d'énumérer les configurations différentes possibles dont le nombre maximum est égal au nombre de réseaux de Bravais occupés par des ions magnétiques, soit à huit dans le cas présent. La Fig. 5 illustre les huit configurations possibles. Le calcul permettant de les établir selon la méthode exposée par l'un de nous \( ^{5,6} \) est donnée dans la quatrième partie.
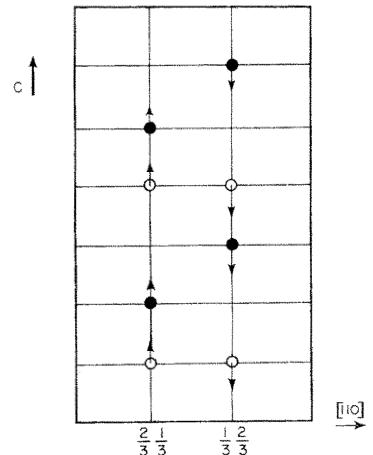
Parmi les modèles possibles, c'est le mode 3 (Fig. 5) qui fournit le meilleur accord avec les intensités observées. La configuration magnétique est décrite par deux chaînes de spins, l'une, le long de la droite \( \frac{1}{3} \) z constitue le sous-réseau magnétique \( M_{1} \) , l'autre, le long de la droite \( \frac{2}{3} \) z antiparallèle à la précédente constitue le sous-réseau \( M_{2} \) . Le groupe magnétique de SHUBNIKOV est \( P\overline{3}^{\prime}c^{\prime}1 \) . La Fig. 6 distingue les positions cristallographiques ( \( Mn_{1}O \) et \( Mn_{11}O \) ) et montre en même temps la direction des spins.
Le Tableau 7 résume les indices de h k l, les intensités nucléaires déjà calculées (cf. Tableau 5), les intensités magnétiques calculées dans l'hypothèse de spins \( S = \frac{5}{2} \) alignés selon c et totalement saturés (3ème colonne) en utilisant le facteur de forme de \( Mn^{2+}(7) \) , la somme \( I_{tot} \) dcs intensités calculées (4ème colonne) et enfin à titre de comparaison (5ème colonne) l'intensité observée corrigée de la contribution du cryostat. L'accord


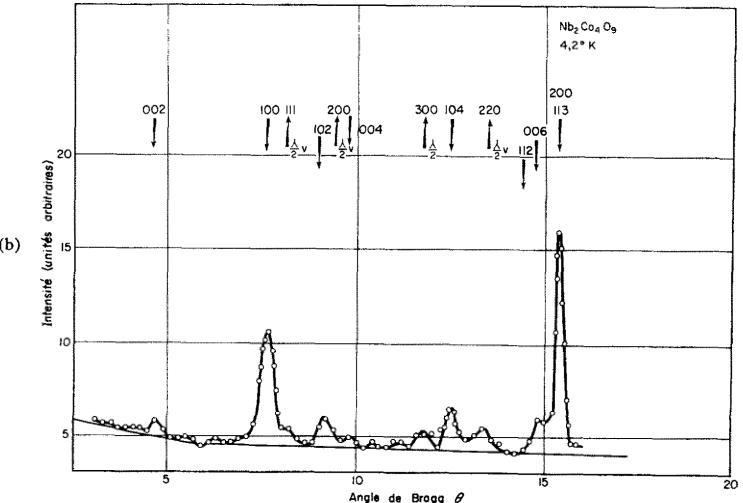
FIG. 4. Diagrammes à 4,2°K de \( Nb_{2}Mn_{4}O_{9} \) (a) et de \( Nb_{8}Co_{4}O_{9} \) (b).

FIG. 5. Modèles magnétiques. Quatre autres motifs se déduisent de ceux dessinés en conservant le motif central (constitué par 4 atomes) et en renversant l'orientation des spins après une translation c/2.

FIG. 6. Structure magnétique de \( Nb_{9}Co_{4}O_{9} \) et \( Nb_{9}Mn_{4}O_{9} \)
est jugé satisfaisant, compte tenu de la précision plus faible de nos mesures d'intensités aux basses températures.
Signe des interactions. Les voisins \( Mn^{2+} \) les plus proches \( (d=3,166\ \text{\AA}) \) ayant leurs octaèdres de coordination accolés par une face, ont leurs spins parallèles, ce qui suggère la présence d'interactions directes positives. Cependant, les mesures magnétiques (3ème partie) montrent d'une manière convaincante que toutes les interactions aussi bien dans une chaîne, qu'entre les chaînes, sont négatives (cf. 4ème partie) en confirmation de la prédiction théorique de GOODENOUGH \( ^{(8)} \) selon laquelle les interactions directes \( Mn^{2+}-Mn^{2+} \) sont négatives.
\( Nb_{2}Co_{4}O_{9} \) . Nous n'avons pas noté de variation sensible des intensités dans les diagrammes à la température ordinaire et à celle de l'azote liquide. A la température de l'hélium liquide, la contribution magnétique est nette et qualitative-ment analogue à celle dans \( Nb_{2}Mn_{4}O_{9} \) quoique moins spectaculaire, comme le montre l'accroissement notable du rapport \( I(100)/I(113) \) .
Alors que l'existence d'un ordre antiferromagnétique est clairement révélée aux neutrons, il serait difficile d'inférer ce résultat sur la seule base de la mesure de susceptibilité magnétique. En effet, \( 1/\chi \) ne montre pas de minimum net comme dans \( Nb_{2}Mn_{4}O_{9} \) (cf. Fig. 8).
Le seul modèle compatible avec les intensités observées (et corrigées comme plus haut) est le modèle 3 (Figs. 5 et 6). Pour ajuster les intensités magnétiques, on dispose de deux paramètres, la direction et la valeur des moments magnétiques, la contribution du moment orbital dans \( Co^{2+} \) étant en général non négligeable.
Comme les intensités des raies (004) et (006) n'ont pas varié, nous supposons les moments parallèles à l'axe c. On obtient alors un bon accord entre raies fortes (100) et moyennes (104) observées et calculées en prenant \( S\sigma/\sigma_{0}=\frac{3}{8} \) . Ici \( \sigma/\sigma_{0} \) est le rapport des saturations à 4,2 K \( ^{0} \) et au zéro absolu. Dans le calcul de l'intensité magnétique, on a
Tableau 7. Intensités aux basses températures (4,2°K)
| Nb2Mn4O9 | ||||
| h k l | Icalc | Iobs | ||
| Inec | Imag | I tot | ||
| 0 0 2 | 20 | 0 | 20 | 17 |
| 1 0 0 | 472 | 1132 | 1604 | 1550 |
| 1 0 2 | 16 | 15 | 31 | 49 |
| 0 0 4 | 93 | 0 | 93 | 78 |
| 1 0 4 | 102 | 122 | 224 | 209 |
| 110, 111 | 162 | 0 | 162 | 178 |
| 006, 113, 200 | 877 | 137 | 1014 | 1014 |
| h k l | Icalc | Iobs | ||
| Inec | Imag | I tot | ||
| 0 0 2 | 2 | 0 | 2 | 15 |
| 1 0 0 | 128 | 422 | 550 | 542 |
| 1 0 2 | 40 | 7 | 47 | 62 |
| 0 0 4 | 10 | 0 | 10 | 26 |
| 1 0 4 | 131 | 34 | 165 | 156 |
| 112, 006 | 862 | 51 | 913 | 913 |
| 113, 200 | ||||
encore utilisé le facteur de forme de \( Mn^{2+}(7) \) . Dans l'hypothèse d'une saturation pratiquement totale* \( (\sigma/\sigma_{0} \sim 1) \) , la valeur du moment correspondrait au spin seul de \( Co^{2+} \) , c'est-à-dire à un moment orbital complètement bloqué à \( 4,2^{\circ}K \) .
Nous avons repris les calculs, tenant compte d'une contribution orbitale en supposant que \( S\sigma/\sigma_{0}=\frac{4}{2} \) . Pour accorder les intensités observées et calculées de la raie (1 0 0), il est alors nécessaire de supposer les spins parallèles au plan (0 0 2). Mais alors, l'intensité calculée de la raie (1 0 4) est deux fois plus grande que celle observée, ce qui est certainement en dehors de l'erreur de mesure possible.
En résumé, les intensités des raies fortes (1 0 0) et moyennes (1 0 4) sont en accord, avec une valeur de spin seul ( \( S = \frac{3}{2} \) ) les spins étant parallèles à l'axe c. Elles sont en désaccord avec une valeur \( S = \frac{4}{2} \) .
TROISIEME PARTIE
Propriétés magnétiques du niobate de manganèse et du niobate de cobalt
L'étude des propriétés magnétiques du niobate de cobalt \( Nb_{2}O_{5} \cdot 4CoO \) et du niobate de manganèse \( Nb_{2}O_{5} \cdot 4MnO \) à été faite sur des échantillons polycristallins. A une température donnée T comprise entre 2,5°K et l'ambiance, on a mesuré, par la méthode d'extraction axiale la variation de l'aimantation spécifique \( \sigma \) en fonction du champ magnétique interne \( H_{t} \) ; au-dessus de la température ambiante, on a déterminé directement la susceptibilité au moyen d'une balance de translation. Les résultats se résument ainsi :
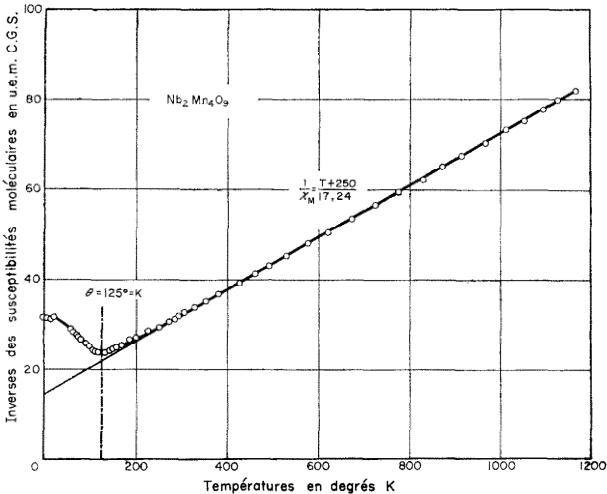
\( Nb_{2}O_{5} \cdot 4MnO \) est antiferromagnétique (Fig. 7) avec une température de Neél \( \Theta_{N} \) à 125°K et une

FIG. 7. \( 1/x_{m}(T) \) pour \( Nb_{9}O_{5} \cdot 4MnO \)

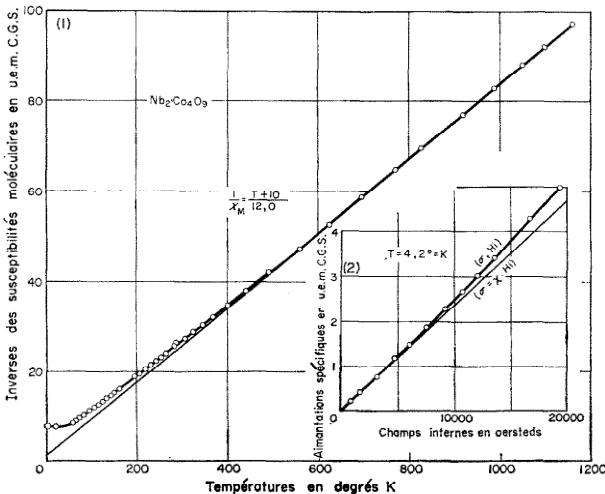
FIG. 8. (a) \( 1/x_{m}(T) \) pour \( Nb_{9}Os \cdot 4CoO \) (b) \( \sigma(H) \) à \( T = 4,2^{\circ}K \) .
température de Curie \(\Theta_P\) à \(-250^{\circ}\mathrm{K}\). Les isothermes \((\sigma_t, H_t)\) tracées jusqu'à environ 20.000 Oe sont linéaires, même aux très basses températures ; le coefficient angulaire des droites correspondantes définit la valeur de la susceptibilité. Aux températures supérieures à \(\Theta_N\) la courbe \((1/\chi_m, T)\) définit une constante de Curie \(C\) égale à 17,24 soit 4,31 par ion \(\mathrm{Mn}^{2+}\) en bon accord avec la valeur 4,39 calculée par cation considéré dans l'état \(^6S\). Si l'on désigne par \(n\) et \(n'\) les coefficients de champ moléculaire représentant respectivement les interactions entre ions sur deux sous-réseaux différents et celles entre ions sur un même sous-réseau, on peut, à partir des valeurs numériques de \(\Theta_N\) et \(\Theta_P\) et de leurs expressions\(^{(9)}\)
\[ \Theta_{N}=C/2(n^{\prime}-n)\mathrm{e t}\Theta_{P}=C/2(n^{\prime}+n) \]
en fonction de n et n', calculer n = -21,6 et n' = -7,3. On remarque que n = +3n' et que la susceptibilité au zéro absolu est de l'ordre de 2/3 de la susceptibilité à la température de transition \( \Theta_{N} \) .
Des résultats sur \( Nb_{9}O_{5} \cdot 4CoO \) (Fig. 8), il est plus difficile de déduire l'existence de l'antiferromagnétisme. Aux températures supérieures à \( 30^{\circ}K \) ( \( 1/X_{m}, T \) ) suit une loi de Curie Weiss avec \( \Theta_{P} = -10^{\circ} \) et C = 12,0, soit 3,0 par ion \( Co^{2+} \) . Cette constante de Curie est comprise entre les valeurs 1,88 et 5,61 calculées pour cet ion respectivement avec S = 3/2 et \( J = L + S = 9/2 \) ; elle est en accord avec la plupart des constantes de Curie expérimentales relatives à cet ion (10, 11, 12) et plus particulièrement avec les valeurs 3,07 dans \( CoO(13) \) et 3,02 dans \( Fe_{2}O_{3} \cdot CoO(14) \) . Il semble que, dans ces deux dernières substances et dans le niobate de cobalt, l'amplitude du blocage du moment, sous l'effet du champ cristallin, soit du même ordre de grandeur ; on fera remarquer que dans ces composés, chaque ion \( Co^{2+} \) est entouré d'un octaèdre d'ions oxygène. Aux températures inférieures à \( 30^{\circ}K \) , les courbes \( (\sigma, H_{t}) \) présentent une courbure dont la concavité est tournée vers l'axe des \( \sigma \) (Fig. 8), la susceptibilité représentée par le rapport \( \sigma/H_{t} \) croît avec le champ ; pour tracer la courbe \( (1/X_{m}, T) \) on a convenu de prendre pour la valeur de la susceptibilité celle qui correspond au coefficient angulaire de la tangente à l'origine de la courbe. Un résultat semblable a déjà été observé sur MnO et \( MnF_{2}(12) \) ; il peut être expliqué par l'augmentation de susceptibilité due au fait que, sous l'action du champ magnétique, la direction d'antiferromagnétisme tend à se rapprocher du plan perpendiculaire à ce champ. (15, 10) Dans le cas d'un cristal uniax, si l'on représente l'énergie de couplage de la direction d'antiferromagnétisme avec cet axe par une expression de la forme \( K_{1} \) sin \( ^{2} \) dans laquelle \( \Theta \) représente l'angle de cette direction avec l'axe du cristal, la susceptibilité d'une poudre dans un champ H s'exprime par la relation
\[ \chi=\frac{1}{3}\chi_{1}+\frac{2}{3}\chi_{1}+\frac{2}{15}.\left(\frac{\chi_{1}-\chi_{1}}{K_{1}}\right)^{2}.H^{2} \]
où \( \chi_{1} \) et \( \chi_{2} \) représentent respectivement les susceptibilités suivant les directions d'antiferromagnétisme et une direction perpendiculaire. A 4,2°K, \( \chi_{1} \) est très faible ; on le suppose nul ; on déduit \( K_{1} \) de l'ordre de 1,3·10⁶ ergs/cm³, ce qui est grand, mais d'un ordre de grandeur admissible. En prenant \( \Theta_{N} = 30°K \) , on trouve n = -3,34 et \( n' = +1,67 \) .
Pour ces deux niobates, dans un intervalle de température de l'ordre de 300° au-dessus de \( \Theta_{N} \) , on a remarqué qu'aux erreurs d'expérience près, la susceptibilité est indépendante du champ appliqué (jusqu'à 20.000 Oe) et que la courbe (1/Xm, T) est au-dessus et s'écarte d'autant plus de la droite de paramagnétisme à haute température que l'on s'approche de \( \Theta_{N} \) . Cette allure de courbe, observée sur d'autres antiferromagnétiques \( ^{(21,13)} \) est à rapprocher de celle mesurée sur les ferromagnétiques dans la zone paramagnétique; comme pour ces derniers, elle est peut être due aux fluctuations du champ moléculaire. \( ^{(17)} \)
QUATRIEME PARTIE
Configurations magnétiques
Les configurations d'équilibre des spins sont solution d'une équation matricielle \( ^{(5, 6)} \) de la forme
\[ (\zeta-\lambda)T(\pmb{k})=0 \quad (1) \]
La dimension de la matrice (ζ) est égale au nombre n de réseaux de Bravais, occupés par des atomes magnétiques. (λ) est une matrice diagonale d'éléments λtδt(j = 1, ..., n). Les paramètres λt sont égaux pour des sous-réseaux équivalents (c'est-à-dire reliés par des opérations de symétrie du groupe). Leur connaissance permet d'évaluer l'énergie d'échange (2). Les vecteurs T(k) à n
composantes \(T_{j}(\boldsymbol{k})\) (\(j=1,\ldots,n\)) sont liés aux vecteurs spins par (3).
\[ H=-2\sum\lambda_{t t} \quad (2) \]
\[ \boldsymbol{\sigma}_{j}(\boldsymbol{R})=\sum_{k}T_{j}(\boldsymbol{k})\mathrm{i x p}-(\boldsymbol{k}\cdot\boldsymbol{R})^{*} \quad (3) \]
Ici \(\sigma_{j}\) est un vecteur unitaire de même direction que le spin \(S_{j}\) (\(\sigma_{j}=S_{j}/S_{j}\)). Les éléments de la matrice (\(\zeta\)) sont
\[ \zeta_{t j}=\sum_{j}C_{t j}\mathrm{i x p}\boldsymbol{k}.\left(\boldsymbol{R}_{t}-\boldsymbol{R}_{j}\right) \quad (4) \]
\[ \mathbf{o}\dot{\mathbf{u}}\quad C_{t j}=S_{t}J_{t j}S_{j} \quad (5) \]
\( J_{ij} \) est l'intégrale d'échange. Lorsque les mailles cristallographiques et magnétiques coïncident, on trouve toutes les configurations fondamentales possibles en posant \( k = 0 \) . \( \sigma_{j}(R) \) et \( T_{j}(0) \) s'identifient alors.
La méthode générale \( (k \neq 0) \) reste cependant valable. On peut montrer qu'il suffit d'étudier une seule solution exprimée en fonction de k pour trouver tous les modes possibles. \( ^{19} \)
Dans les niobates de Co et Mn, les mailles cristallographiques et magnétiques coïncident, de sorte qu'en posant k = 0, on aura à résoudre un système de dimension 8 (car il y a 4 atomes \( M_{I} \) et 4 atomes \( M_{II} \) ). De même, il y aura dans la matrice ( \( \lambda \) ) 8 termes diagonaux, dont 4 égaux à \( \lambda_{I} \) et 4 à \( \lambda_{II} \) . Profitant de la remarque faite plus haut, nous allons étudier le système (1) non pas pour k = 0, mais pour k = (00l). Cela nous permet de ramener la dimension de la matrice à 4. Posant successivement l = 0 et l = 1, nous trouverons en tout 8 modes (Fig. 5).
Mise en équation :
Nous considérons les cations magnétiques
\[ \mathbf{I}(\frac{1}{3}\frac{2}{3}\bar{z}\mathbf{I}),\mathbf{I I}(\frac{1}{3}\frac{2}{3}\bar{z}\mathbf{I I}), \]
\[ \mathbf{I}-(\frac{2}{3}\frac{1}{3},-z_{\mathrm{I}})\mathrm{e t}\mathbf{I I}-(\frac{2}{3}\frac{1}{6},-z_{\mathrm{I I}}). \]
Nous tabulons en partie la mise en équation du problème. Du Tableau 8 et à l'aide de (1) et (4), on déduit :
\[ \begin{aligned}\lambda_{\mathrm{I}}T_{\mathrm{I}}(\boldsymbol{k})&=A J_{2}\mathrm{i x p}2l z_{\mathrm{I}}T_{\mathrm{I}-}(\boldsymbol{k})\\&\quad+J_{1}\mathrm{i x p}l(z_{\mathrm{I}-}z_{\mathrm{II}})T_{\mathrm{II}}(\boldsymbol{k})\\&\quad+A J_{4}\mathrm{i x p}l(z_{\mathrm{I}}+z_{\mathrm{II}})T_{\mathrm{II}-}(\boldsymbol{k})\end{aligned} \quad (6) \]
\[ \begin{aligned}\lambda_{\mathrm{II}}T_{\mathrm{II}}(\boldsymbol{k})&=A J_{3}\mathrm{i x p}l z_{\mathrm{II}}\mathrm{i x p}l/2T_{\mathrm{II}-}(\boldsymbol{k})\\&\quad+J_{1}\mathrm{i x p}l(\bar{z}_{\mathrm{II}}-z_{\mathrm{I}})T_{\mathrm{I}}(\boldsymbol{k})\\&\quad+A J_{4}\mathrm{i x p}l(z_{I}+z_{\mathrm{II}})T_{\mathrm{I}-}(\boldsymbol{k})\end{aligned} \quad (7) \]
Ici, on a abrégé
\[ \begin{aligned}A&=\mathrm{i x p}(-h+k)/3+\mathrm{i x p}(2h+k)/3\\&\quad+\mathrm{i x p}-(h+2k)/3\end{aligned} \quad (8) \]
La signification des intégrales d'échange est illustrée par le Tableau 8 et la Fig. 5. Complétant les équations écrites par celles relatives
Tableau 8. Voisinages et intégrales d'échange (Nb_{2}Mn_{0}O_{9})
| Atome | Voisins | Distance (Å) | Intégrale d'échange |
| I( \( \frac{1}{3} \) \( \frac{1}{2} \) I) | 1 voisin II en ( \( \frac{1}{3} \) \( \frac{1}{2} \) I) | 3,17 | y1 |
| 3 voisins I-en ( \( \frac{1}{3} \) \( \frac{1}{2}I \) ; \( \frac{1}{3} \) \( \frac{1}{2}I; \) \( \frac{1}{3} \) \( \frac{1}{2}I) | 3,12 | y2 | |
| 3 voisins II-en ( \( \frac{1}{3} \) \( \frac{1}{2}\)II; etc.) | 4,06 | y4 | |
| II( \( \frac{1}{3} \) \( \frac{1}{2}I\)I) | 1 voisin I en ( \( \frac{1}{3} \) \( \frac{1}{2}\)I) | 3,17 | y1 |
| 3 voisins II-en ( \( \frac{1}{3} \) \( \frac{1}{2}\)II- \( \frac{1}{2} \) ; etc.) | 3,36 | y3 | |
| 3 voisins I-en ( \( \frac{1}{3} \) \( \frac{1}{2}I; \) etc. . .) | 4,06 | y4 |
- Les valeurs \( x_{I} = 0,0181 \) ; \( x_{II} = -0,203 \) ont été utilisées.
aux atomes I— et II— et posant
\( Q_{j}(k)=T_{j}(k)\mathrm{i}\mathrm{x}\mathrm{p}-l z_{j}\mathrm{p}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{j}=\mathrm{I},\mathrm{II},\mathrm{I}-,\mathrm{II}- \) (9) le système (I) prend la forme (10) où \( M(k) \) est la matrice (11) dont les lignes se rapportent respectivement aux sous-réseaux I, I-, II, II-
\[ M(k)Q(k)=0 \quad (10) \]
\[ M(k)=\begin{pmatrix}-\lambda_{\mathrm{I}}&AJ_{2}&J_{1}&AJ_{4}\\A^{*}J_{2}&-\lambda_{\mathrm{I}}&A^{*}J_{4}&J_{1}\\J_{1}&AJ_{4}&-\lambda_{\mathrm{II}}&AJ_{3}\exp\frac{1}{2}l\\A^{*}J_{4}&J_{1}&A^{*}J_{3}\exp-\frac{1}{2}l&-\lambda_{\mathrm{II}}\end{pmatrix} \quad (11) \]
Lorsque \(k = (00l)\), \(A = 3\). Faisons d'abord \(h = k = l = 0\). Transformant \(M(0)\) par la matrice \(U(12)\), on obtient une diagonalisation partielle de \(M(0)\) en deux sous-matrices \(M_{1}'\) et \(M_{2}'\) (15)
\[ U=\begin{pmatrix}{{{1}}}&{{{\cdot}}}&{{{-1}}}&{{{\cdot}}} \\{{{1}}}&{{{\cdot}}}&{{{1}}}&{{{\cdot}}} \\{{{\cdot}}}&{{{1}}}&{{{\cdot}}}&{{{-1}}} \\{{{\cdot}}}&{{{1}}}&{{{\cdot}}}&{{{1}}}\end{pmatrix}\Bigg/\sqrt{2} \quad (12) \]
On a
\[ Q=U Q^{\prime};M^{\prime}Q^{\prime}=0\mathrm{a v e c} \quad (13) \]
\[ M^{\prime}=U^{-1}M U=\begin{pmatrix}M_{1}^{\prime}&\cdot\\ \cdot&M_{2}^{\prime}\end{pmatrix} \quad (14) \]
\[ M_{1}^{\prime}=\begin{pmatrix}-\lambda_{\mathrm{I}}+3J_{2}&J_{1}+3J_{4}\\J_{1}+3J_{4}&-\lambda_{\mathrm{I I}}+3J_{3}\end{pmatrix}; \]
\[ M_{2}^{\prime}=\begin{pmatrix}-\lambda_{\mathrm{I}}-3J_{2}&J_{1}-3J_{4}\\J_{1}-3J_{4}&-\lambda_{\mathrm{I I}}-3J_{3}\end{pmatrix} \quad (15) \]
Posons
\[ Q_{1}^{\prime}=1;Q_{2}^{\prime}=\exp i\phi \quad (16) \]
On obtient
\[ \begin{aligned}\lambda_{\mathrm{I}}&=3J_{2}+(J_{1}+3J_{4})\exp i\phi\\\lambda_{\mathrm{II}}&=3J_{3}+(J_{1}+3J_{4})\exp-i\phi\end{aligned} \quad (17) \]
D'ou
\[ \lambda_{\mathrm{I}}+\lambda_{\mathrm{I I}}=3(J_{2}+J_{3})+2(J_{1}+3J_{4})\cos\phi \quad (18) \]
\(\lambda_{\mathrm{I}}+\lambda_{\mathrm{II}}\) doit être maximum. On doit distinguer deux cas
\[ \begin{array}{l}(1)J_{1}+3J_{4}>0.Alsors\phi=0;Q_{1}^{\prime}=Q_{2}^{\prime}=1\end{array} \quad (19) \]
(2) \(J_{1}+3J_{4}<0\). Alors \(\phi=\pi\); \(Q_{1}^{\prime}=-\mathcal{Q}_{2}^{\prime}\) (20) Discutant de la même manière la sous-matrice \(M_{2}^{\prime}\) (15), on a
\[ (3)J_{1}-3J_{4}>0a v e c Q_{3}^{\prime}=Q_{4}^{\prime}=1 \quad (21) \]
\[ (4)J_{1}-3J_{4}<0a v e c Q_{3}^{\prime}=-Q_{4}^{\prime} \quad (22) \]
On a alors
\[ \lambda_{\mathrm{I}}+\lambda_{\mathrm{I I}}=-3(J_{2}+J_{3})\pm(J_{1}-3J_{4}) \quad (23) \]
où le signe+correspond au cas (3), - au cas (4).
Les modes des atomes I, I-, II, II- sont représentés grâce à (12)-(21) par les colonnes de la matrice (Q) (24)
Faisant \(h = k = 0\) et \(l = 1\) dans (11) on trouve quatre modes supplémentaires qui se déduisent des quatre modes précédents par un changement de signe de l'ir.teraction \(J_{3}\). Nous ne les discuterons pas davantage. C'est le cas (3) (21) qui est observé
\[ (Q)=\begin{pmatrix}1&1&-1&-1\\1&-1&1&-1\\1&-1&-1&1\\1&1&1&1\end{pmatrix} \quad (24) \]
Conditions de stabilité. Ecrivons que la matrice \( [\lambda_{0}-\zeta(k_{0}+dk)] \) a des racines positives pour dk petit, \( k_{0} \) (= 0) étant le vecteur k d'équilibre, \( (\lambda_{0}) \) étant la matrice dont les éléments diagonaux sont
\[ \lambda_{I}=-3J_{2}+J_{1}-3J_{4};\lambda_{I I}=-3J_{3}+J_{1}-3J_{4} \quad (25) \]
En dehors de \( \lambda_{I}>0 \) et \( \lambda_{II}>0 \) et de la condition (21) on trouve les conditions de stabilité suivantes
\[ \begin{aligned}J_{3}<0&;J_{2}+J_{3}+2J_{4}<0;2(3J_{2}J_{3}-J_{1}J_{4})\\-&(J_{2}+J_{3})(J_{1}-3J_{4})>0\end{aligned} \]
\[ [6J_{2}-(J_{1}+3J_{4})<0;6J_{3}-(J_{1}+3J_{4})<0] \quad (26) \]
(Les conditions les moins restrictives sont écrites entre crochets.) Avec les notations de la troisième partie, on a, à une constante de proportionnalité près :
\[ n=3(J_{2}+J_{3}+2J_{4});n^{\prime}=J_{1} \quad (27) \]
Le mode (3) (Fig. 5) et (25) est favorisé par des interactions \(J_2, J_3, J_4\) négatives et \(J_1\) positive. Dans le cas de \(\mathrm{Nb}_2\mathrm{Co}_4\mathrm{O}_9\), on a \(n\) négatif et \(n'\) positif. Par contre, dans \(\mathrm{Nb}_2\mathrm{Mn}_4\mathrm{O}_9\), \(n'\) (donc \(J_1\)) coefficient d'interaction dans un même sous-réseau de Néel est négatif, contrairement à ce que suggérerait la structure.

\[x = J_2/J_4 \quad y = J_3/J_4\]
Cas de \(\mathrm{Nb}_2\mathrm{Mn}_4\mathrm{O}_9\). De la relation trouvée expérimentalement \(n = 3n'\), on déduit que
\[J_1 = J_2 + J_3 + 2J_4 \quad (28)\]
\(J_1\) étant négatif, \(J_4\) doit être différent de zéro et certainement négatif d'après (21). Posant
\[x = J_2/J_4 ; \quad y = J_3/J_4 \quad (29)\]
les inégalités significatives deviennent après substitution de (28) et (29)
\[y > 0 \text{ (a); } -2x + y - 1 < 0 \text{ (b); } x - 2y - 1 < 0 \text{ (c);}\]
\[x^2 + y^2 - 4xy + 4 + x + y < 0 \text{ (d)} \quad (30)\]
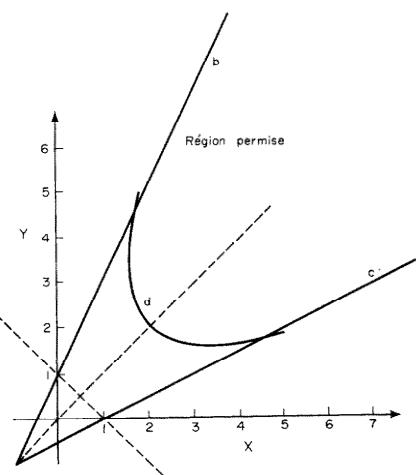
Elles délimitent le domaine de stabilité compris entre les droites (b) et (c) et la branche positive
de l'hyperbole (d) (Fig. 9). On en déduit que \(x\) et \(y\) ne peuvent tomber au-dessous d'une valeur minimum de \(\frac{1}{2}(1 + \sqrt{6}) = 1,73\). En admettant \(J_2 \sim J_3\), \(x\) et \(y\) seraient au moins supérieures à \(+2\).
En résumé, dans \(\mathrm{Nb}_2\mathrm{Mn}_4\mathrm{O}_9\) toutes les interactions \(J_j\) (\(j = 1, 2, 3, 4\)) sont négatives et non nulles, et en admettant \(J_2 \sim J_3\) les interactions \(J_2\) et \(J_3\) seraient au moins deux fois plus intenses que \(J_4\), tandis que \(J_1\) serait, selon (28) au moins six fois plus fort que \(J_4\).
Enfin, on peut montrer, soit par la méthode de Dzyaloshinskyi, (20) soit par une méthode matricielle (21) que lorsque les spins sont dirigés selon l'axe \(c\), les composés hexagonaux étudiés doivent être des antiferromagnétiques sans ferromagnétisme faible "parasitique". Celui-ci, effective-ment, n'est pas observé.
CONCLUSIONS
La structure de \(\mathrm{A}_2 \mathrm{M}_4 \mathrm{O}_9\) (\(\mathrm{A} = \mathrm{Nb}, \mathrm{Ta}; \mathrm{M} = \mathrm{Mn}, \mathrm{Fe}, \mathrm{Co}, \mathrm{Mg}\)) constitue un nouveau type de surstructure du corindon au même titre que les ilminités. Mais alors que dans les ilminités le rapport des cations est \(1:1\), il est ici \(1:2\). Le groupe d'espace le plus probable est \(P \bar{3} c 1\). Fait assez surprenant, les octaèdres de coordination du niobium pentavalent ont une face commune. En conséquence, la répulsion coulombienne déplace les atomes Nb voisins proches très notablement des centres de l'octaèdre.
Les substance \(\mathrm{Nb}_2\mathrm{Co}_4\mathrm{O}_9\) et \(\mathrm{Nb}_2\mathrm{Mn}_4\mathrm{O}_9\) ont une structure antiferromagnétique en chaînes. La droite \(\frac{1}{2} \frac{3}{2}\) porte des spins orientés selon \(c\), la droite \(\frac{3}{2} \frac{1}{2}\) porte des spins orientés en sens inverse.
\(\mathrm{Mn}^{2+}\) est dans un état \(^6S\). La situation dans \(\mathrm{Co}^{2+}\) est plus délicate. Les mesures de susceptibilité dans la région paramagnétique (\(T > 40^\circ K\)) indiquent un moment de \(S = \frac{4}{2}\), c'est-à-dire une contribution orbitale tandis que les mesures par diffraction neutronique dans la région antiferromagnétique (\(T = 4,2^\circ K\)) indiquent un moment de \(S = \frac{3}{2}\), c'est-à-dire de la valeur de spin seul. Il est donc probable qu'aux très basses températures, le moment orbital de \(\mathrm{Co}\) soit complètement bloqué.
REFERENCES
- Strukturbericht, Vol. II, p. 55. (1928-1932). Akad. Verlagsges.
-
BERTAUT E. F. et FORRAT F., C.R. Acad. Sci., Paris 242, 382 (1956).
-
PAULING L. et HENDRICKS S. B., J. Amer. Chem. Soc. 47, 781 (1925).
-
International Tables for X-ray Crystallography. The Kynoch Press, Birmingham (1952).
-
BERTAUT E. F., C.R. Acad. Sci., Paris 250, 85 (1960).
-
BERTAUT E. F., C.R. Acad. Sci., Paris 252, 76 (1961).
-
HASTINGS J. M., ELLIOT N. et CORLISS L. M., Phys. Rev. 115, 13 (1959).
-
GOODENOUGH J. B., Phys. Rev. 117, 1442 (1960).
-
NEEL L., Ann. Phys., Paris 3, 137 (1948).
-
BENOIT R., C.R. Acad. Sci., Paris 231, 1216 (1950).
-
SERRES A., Ann. Phys. Paris 17, 5 (1932).
-
BIZETTE H., Ann. Phys., Paris 1, 233 (1946).
-
TROMBE F., J. Phys. Radium 12, 171 (1951).
-
FALLOT M. et MARONI P., J. Phys. Radium 12, 257 (1951).
-
NEEL L., Proc. Intern. Conf. Théor. Phys. Kyoto. (1953).
-
NAGAMIYA T., Proc. Theor. Phys. 4, 342 (1951).
-
NEEL L., Ann. Phys. Paris, 17, 5 (1932).
-
WANNIER G. H., Elements of Solid State Theory, University Press, Cambridge (1959).
-
BERTAUT E. F., C.R. Acad. Sci., Paris 252. 252 (1961).
-
DZYALOSHINSKI I., J. Phys. Chem. Solids 4, 241 (1958).
-
BERTAUT E. F., C.R. Acad. Sci., Paris 252; 2078 (1961).