| Transition Temperature | 348 K |
|---|---|
| Experiment Temperature | 77 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | R-3c (#167) |
| Magnetic Space Group | C2'/c' (#15.89) |
| Magnetic Point Group | 2'/m' (5.5.16) |
| Lattice Parameters | 4.62600 4.62600 14.49300 90.00 90.00 120.00 |
|---|---|
| DOI | 10.1016/0038-1098(70)90469-2 |
| Reference | M. Pernet, D. Elmale and J.-C. Joubert, Solid State Communications (1970) 8 1583-1587. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Fe1 | Fe | 4.7 | 0.0 | 0.0 | 4.70 |
STRUCTURE MAGNETIQUE DU METABORATE DE FER FeBO \( _{3} \)
Michel Pernet, David Elmaleh et Jean-Claude Joubert
Laboratoire d'Electrostatique et de Physique du Métal Cedex No. 166, 38 – Grenoble-Gare, France
(Reçu le 21 juillet 1970 par E.F.Bertaut)
Le borate de fer \( FeBO_{3} \) à structure calcite s'ordonne antiferromagnétiquement avec une température de Néel de \( 348^{\circ}K \) . Au dessous de cette température, il possède une faible composante ferromagnétique.
L'étude par diffraction neutrinoque révèle l'existence d'un mode antiferromagnétique prépondérant A situé dans le plan perpendiculaire à l'axe rhomboédrique, en bon accord avec les études par effet Mössbauer et avec la théorie macroscopique. Le moment observé pour le fer est de \( 4,70 \mu_{B} \) . L'étude de l'intensité de la raie magnétique (100) entre la température de l'azote liquide et \( 120^{\circ}C \) permet de déterminer la variation de l'aimantation sur les sous-réseaux antiferromagnétiques.
1. INTRODUCTION
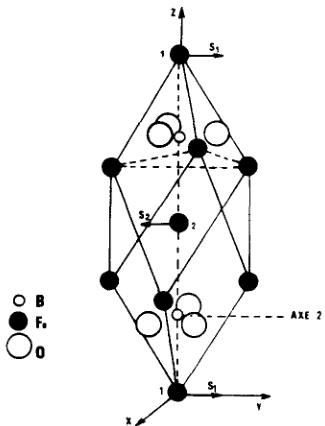
LE BORATE de fer \( FeBO_{3} \) possédant la structure calcite, \( ^{1} \) cristallise dans le groupe d'espace \( R3c(D_{3d}^{6}) \) , avec deux molécules par maille (Fig.1). Dans la maille rhomboédrique ( \( a = 5,512 \AA \) , \( \alpha = 49^{\circ}40' \) ), les positions atomiques sont les suivantes:
2 Fe en (b) : 0, 0, 0 ; 1/2, 1/2, 1/2
2B en (a) : 1/4, 1/4, 1/4 ; 3/4, 3/4, 3/4
6O en (e) avec \( u \approx 0.54 \) .
Ce composé antiferromagnétique présente au des- sous de la température de Néel, une faible com- posante ferromagnétique. Une étude par diffraction neutronique a permis d'en déterminer la structure magnétique.
II. PARTIE EXPÉRIMENTALE
Cette étude a été effectuée sur un échantillon polycristallin préparé selon la méthode exposée par J.C. Joubert et al. \( ^{2} \) La préparation a nécessité l'emploi d'acide orthoborique enrichi à 98,5% en isotope \( {}^{11} \) B du bore, puisque l'isotope \( {}^{10} \) B absorbe très fortement les neutrons. Des diagrammes

FIG. 1. Structure de \( FeBO_{3} \)
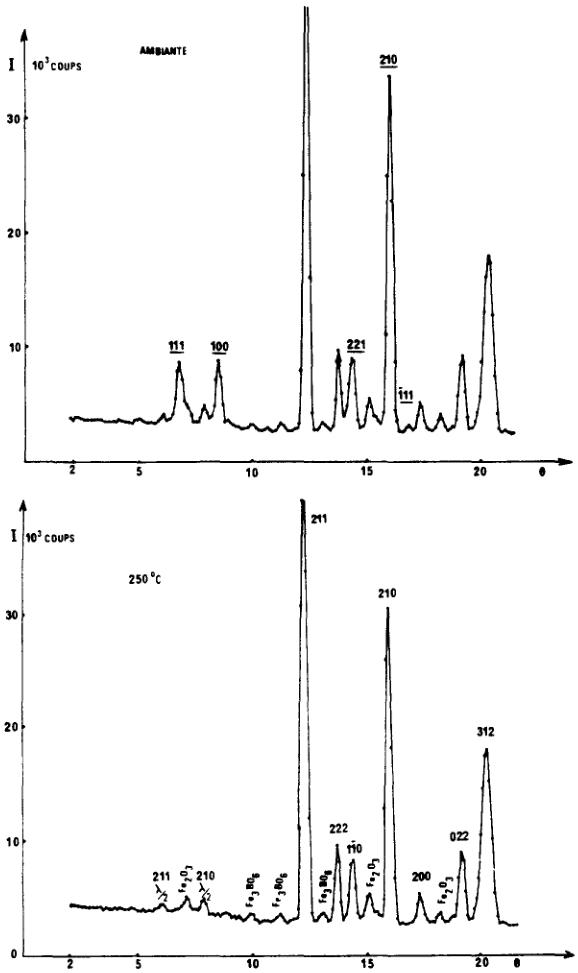
de diffraction neutrinoque ont été enregistrés aux températures suivantes: \( 250^{\circ} \) C, ambiante (Fig. 2) azote liquide.
Toutes les raies magnétiques qui apparaissent

FIG. 2. Diagrammes de diffraction neutronique de FeBO₃ à température ambiante et à 250°C (λ = 1,15 Å). Les indices des raies magnétiques sont soulignés.
à la température ambiante et à celle de l'azote liquide s'indexent dans une maille indigentique à la maille chimique. La présence des raies (111) et (100) révèle l'existence d'un mode antiferromagnétique prépondérant. La température de Neel est de 348°K et il n'y a pas de réorientation des moments de spin entre 4,2°K et \( T_{C}^{3} \) contrairement à ce qui se produit pour \( Fe_{2}O_{3}\alpha \) .
III. STRUCTURE MAGNETIQUE
Elle a été déterminée par utilisation de la théorie "macroscopique" développée par
E.F. Bertaut.⁵ Comme les mailles chimique et magnetique sont identiques, le vecteur de propagation est nul : \(\vec{k} = 0\). Dans la maille élémentaire contenant deux ions magnétiques 1 et 2 (Fig.1), on numérote les spins correspondants \(\vec{S}_1\) et \(\vec{S}_2\). On introduit les combinaisons linéaires:
\[ \vec{F}=\vec{S}_{1}+\vec{S}_{2}\quad;\quad\vec{A}=\vec{S}_{1}-\vec{S}_{2} \]
On utilise un système de coordonnées dans lequel l'axe z est confondu avec l'axe 3, l'axe y aligné avec un des axes binaires, et l'axe x est contenu dans le plan de symétrie. On construit les matrices de transformation des vecteurs spins sous les opérations du groupe ponctuel \(G = D_{3d}\). Leurs transposées forment une représentation \(\Gamma\) du groupe. La méthode macroscopique permet de déterminer les vecteurs de base, c'est-à-dire les combinaisons linéaires de spins se transformant selon une représentation irréductible et décrivant la structure magnétique. La technique de l'opéra- teur de projection a permis de trouver ces vecteurs de base (Tableau 1).
Tableau 1. Représentations irréductibles et fonctions de base du groupe \( D_{3d} \) .
| Représentations | Operateurs | Fonctions de base | |||
| E 2C3 | 3C2 i | 2S3 3d | |||
| A1g | 1 | 1 | 1 | 1 | 1 |
| A2g | 1 | 1 | -1 | 1 | -1 |
| Eg | 2 | -1 | 0 | 2 | -1 |
Les composantes \(A_{z}\) et \(F_{z}\) se transforment respectivement selon \(A_{1g}\) et \(A_{2g}\), celles suivant \(x\) et \(y\), se transforment selon \(E_{g}\) et permettent la construction de l'invariant
\[ F_{x}A_{y}-F_{y}A_{x}. \]
Dans l'hypothèse d'un hamiltonien d'ordre deux, de la forme
\[ H=a F^{2}+b A^{2}+d(F_{x}A_{y}-F_{y}A_{x})+c F_{z}^{2}+e A_{z}^{2} \]
il n'y a pas de termes de couplage entre les composantes xy et celles selon Oz. Les spins sont soit dans le plan Oxy, soit selon Oz.
Etude des diagrammes de diffraction neutronique L'intensité d'une raie magnétique s'écrit:
\[ I_{M_{\mathrm{c a l}}}=N\Big(\frac{e^{2}\gamma}{m c^{2}}\Big)^{2}p^{2}f^{2}q^{2}\mathcal{F}_{N}^{2} \]
N: facteur de normalisation entre les intesités théoriques et observées, a été calculé à partir de l'intensité nucléaire de la raie (211) à la température ambiante (facteur de diffusion utilisé pour le bore: 0,63)⁶ p: multiplicité
\(f\) : facteur de forme magnétique de Fe\(^{3+}\) 7 \(q\) : \((\sin^{2}\alpha)\) où \(\alpha\), angle entre le vecteur diffusion et la direction des spins, a été calculé d'après la formule donnée par Shirane\(^{8}\) \(\mathcal{F}_{M}\) : facteur de structure magnétique : \(\vec{S}_{1} \pm \vec{S}_{2} \exp \pi i (h + k + l)\) selon qu'il s'agit d'un mode \(F\) ou d'un mode \(A\). Les réflexions observées du type \(h + k + l\) impair indiquent la présence dominante du mode \(A\), et la raie (111) exclut l'orientation selon l'axe Oz. Le faible ferromagnétisme dû au mode \(F\) apparaît nettement dans les mesures magnétiques. \(^{2}\) Par diffraction neutrrique, il ne pourrait être détecté que sur des monocristaux, en utilisant la technique des neutrons polarisés.
Le diagramme de poudre ne permet pas non plus de préciser la direction antiferromagnétique dans le plan Oxy. Les intensités des raies purement magnétiques (111), (100), (111) donnent un moment observé pour le fer à 77K égal à 4,7μB, valeur compatible avec l'existence d'ions Fe3+.
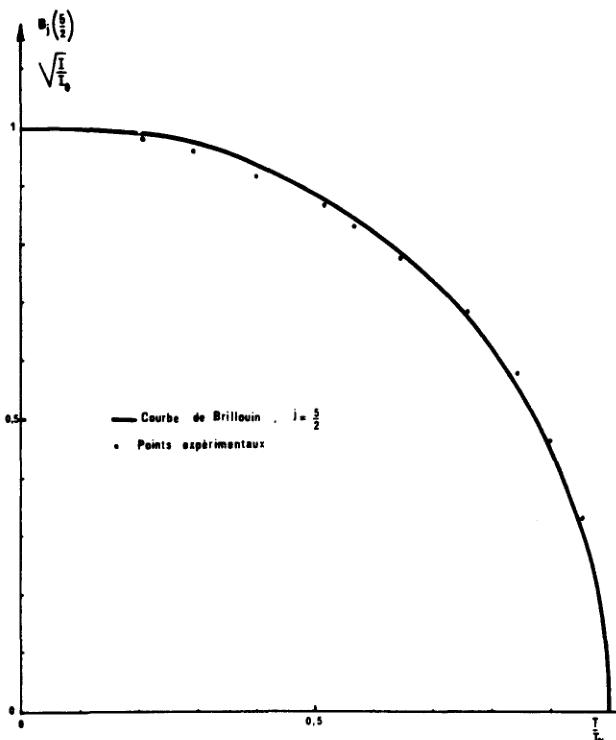
L'étude de l'intensité de la raie (100) en fonction de la température, entre 80K et 400K, permet de déterminer la variation de l'aimantation sur le sous-réseau antiferromagnétique. La courbe d'aimantation correspondante, est pratiquement superposée à la courbe de Brillouin tracée pour J = 5/2 (Fig. 3), sauf au voisinage immédiate de \( T_{N} \) où la variation de l'aimantation est en \( (T - T_{N}) \) avec \( \beta = 0,354 \pm 0,005 \) .
IV. CONCLUSION
L'étude du borate de fer FeBO_{3} par diffraction neutronique a montré l'existence d'un mode antiferromagnétique prépondérant, perpendiculaire à l'axe rhomboédrique, et compatible avec l'existence d'un faible ferromagnétisme, ceci en accord avec l'étude par effet Mössbauer^{3} et l'étude théorique de Dzyaloshinsky.^{9}

FIG. 3. Variation de l'intensité de la raie (100) en fonction de la température.
REFERENCES
-
BERNAL I., STRUCK C.W., WHITE J.G. Acta Crystallogr. 16, 849 (1963).
-
JOUBERT J.C., SHIRK T., WHITE W.B. et ROY R., Mater. Res. Bull. 3, 671 (1968).
-
KURTZIG A.J., WOLFE R., LECRAW R.C. et NIELSEN J.W., Appl. Phys. Lett. 14, 850 (1969).
-
SHULL C.G., STRAUSER W.A. et WOLLAN E.O., Phys. Rev. 83, 333 (1951).
-
BERTAUT E.F., Magnetism, Vol. III, Chap. 4 (Edited by RADO et SUHL), Academic Press (1963).
-
ETOURNEAU J., Thèse de Doctorat ès Sciences, Bordeaux (1970).
-
BROCKHOUSE B.N., CORLISS L.M. et HASTINGS J.M., Phys. Rev., 98, 1721 (1955).
-
SHIRANE G., Acta Crystallogr. 12, 282 (1959).
-
DZYALOSHINSKY I., J. Phys. Chem. Solids 4, 241 (1958).
-
EIBSCHUTZ M., PFEIFFER L. et NIELSEN J.W., J. appl. Phys. 41, 1276 (1970).
Iron borate \( FeBO_{3} \) with calcite like structure undergoes antiferromagnetic order at 348K. Below this temperature it behaves as a weak ferromagnet.
Neutron diffraction shows the spins to be perpendicular to the rhombohedral axis, in good agreement with Mössbauer study and group theory. Iron magnetic momentum is \( 4.70\mu_{B} \) . Temperature dependence of magnetization on the two antiferromagnetic sublattices was investigated by following the 100 magnetic reflection between 4.2K and 120°C.