| Transition Temperature | 91 K |
|---|---|
| Experiment Temperature | 4.2 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | Pnma (#62) |
| Magnetic Space Group | Pnm'a (#62.444) |
| Magnetic Point Group | m'mm (8.3.26) |
| Lattice Parameters | 7.581 14.565 7.645 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1016/0022-3697(78)90043-4 |
| Reference | P. Schobinger-Papamantellos, Journal of Physics and Chemistry of Solids (1978) 39 197-205. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Tb1 | Tb | 1.2 | 1.1 | 6.9 | 7.09 |
| Tb2 | Tb | -4.3 | 2.6 | 6.7 | 8.37 |
| Tb3 | Tb | 0.03 | 0.0 | 7.70 | 7.70 |
ON THE MAGNETIC STRUCTURE AND MAGNETIC PHASE TRANSITIONS OF \( Tb_{5}Ge_{4} \) . A NEUTRON DIFFRACTION STUDY
PENELOPE SCHOBINGER-PAPAMANTELLOS Institut für Kristallographie und Petrographie der ETH Zürich, Switzerland†
(Received 25 June 1976; accepted in revised form 28 February 1977)
Abstract— \( Tb_{5}Ge_{4} \) crystallizes in the orthorhombic space group \( Pnma \) , and orders antiferromagnetically below \( T_{N}=91K \) . Neutron diffraction powder data at 4.2K reveal a ten-sublattice canted antiferromagnetic arrangement. The structure, which is described by the magnetic space group \( Pnma' \) ( \( \Gamma_{8u} \) ) with propagation vector k=0, has three-dimensional components for the atoms in the \( 8(d) \) positions, and is almost colinear for the atoms in the \( 4(c) \) positions. The magnetic interaction in the layers formed by the Tb atoms in the \( (010) \) plane is mainly ferromagnetic, in agreement with the high paramagnetic Curie temperature of 85K. The structure is antiferromagnetically compensated through an antisymmetry center. The main axis of antiferromagnetism is parallel to z. Magnetic phase transitions have been observed by applying a magnetic field in the \( (010) \) plane. The structure is stabilized through exchange interactions via conduction electrons. Because of the low symmetry, the Hamiltonian may contain anisotropic terms that result in a canted arrangement.
INTRODUCTION
The structures and magnetic properties of rare earth germanium intermetallic compounds have been extensively studied \( ^{[1,2]} \) . In particular the compounds \( Re_{5}Ge_{4} \) (Re = rare earth) constitute a group of isostructural compounds with interesting magnetic properties \( ^{[3-5]} \) . All are antiferromagnetic below their ordering temperature and possess a high, positive paramagnetic Curie temperature \( \theta \) (indicating strong ferromagnetic interactions), which varies linearly with the de Gennes factor \( (g - 1)^{2}J(J + 1) \) . For some of these compounds (e.g. \( Gd_{5}Ge_{4} \) ), two antiferromagnetic transitions were reported \( ^{[3]} \) . Since the \( \theta/T_{N} \) ratio is positive and greater than one, antiferro- to ferro-magnetic ["metamagnetic"] transitions may occur below \( T_{N} \) (as has been observed in many layered structures where the anisotropy forces are opposed to the exchange forces \( ^{[5-7]} \) ).
We report here a model for the magnetic structure of \( Tb_{5}Ge_{4} \) , derived from neutron diffraction powder data taken at 4,2K. In addition we describe the dependence of the magnetic intensity on magnetic field and on temperature.
EXPERIMENTAL
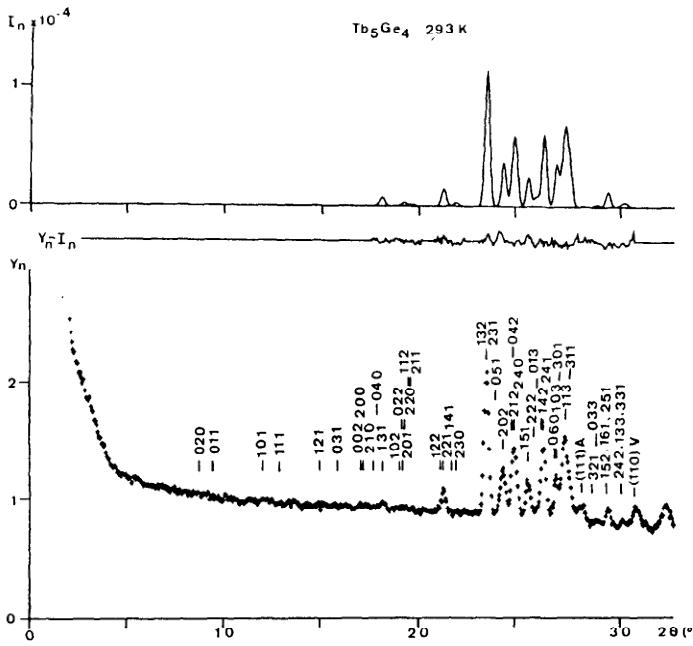
A powder sample was prepared by arc melting of the elements (Johnson and Matthey; Tb, 99.99%, Ge 99.999%) in an argon atmosphere, remelting several times, and finally annealed at \( 1580^{\circ} \) C in a Ta crucible under vacuum for 24 hr. Small single crystals were produced and analyzed to be \( Tb_{5}Ge_{4} \) . X-Ray powder data collected with a Guinier focusing camera ( \( CuK_{\alpha} \) ) showed no other phases. Neutron diffraction data ( \( \lambda \) 1.14 Å) were collected with a powder diffractometer at the EL-3 reactor in Saclay. The sample was contained in a vanadium cylinder 8 mm in diameter. Three sets of intensity data were measured, one at room temperature and the other two at 4.2 K with and without a magnetic field of 15 kOe, applied along the scattering vector. The data were corrected for absorption. The measured \( \mu R = 0.99(1) \) factor was surprisingly high, indicating the presence of a high absorbing rare earth impurity. Figures 1 and 2 display the data after absorption corrections were applied.
Line profile analysis \( ^{[8,9]} \) was used to refine the structure.
The observed broadening of the \( (010) \) peak at \( \lambda1.15\AA \) (insert to Fig. 2) is due to vertical divergence effects only \( ^{[10]} \) , since other possible explanations such as additional reflections or short range order could be excluded from consideration of the peak shape at \( \lambda2.3\AA \) .
Since the assymmetry correction in the line profile analysis considers only peak broadening up to a maximum of 3 times the halfwidth, the shape of this peak was altered to a Gaussian having the same integrated intensity in order to carry out the calculation of the profile and the related R factors.
The nuclear structure
The calculation of the nuclear intensities at 293 K was based on the space group Pnma, positional parameters (Table 1), and overall temperature factor \( B = 0.76 \AA^{2} \) of the isomorphic compound \( Sm_{5}Ge_{4} \) [4]. (No attempt was made to calculate intensities based on the alternative space group \( Pn2_{1}a \) of \( Sm_{5}Ge_{4} \) , since there would be more parameters.) These parameters could not be refined because the \( \sin \theta/\lambda \) range over which the line profile analysis could be extended (less than 10 overlapping reflections) was too small. The profile parameters used for the calculation of the halfwidth, were obtained by using refined powder data for other materials, having no overlapping reflections.

Fig. 1. Neutron diffraction pattern from paramagnetic (293 K) \( Tb_{5}Ge_{4} \) . The full curve is the calculated profile. \( Y_{n}-I_{n} \) is the difference diagram. The curve with crosses shows the measured intensities corrected for absorption.
Table 1. Structure parameters assumed for \( Tb_{5}Ge_{4} \) at 293 K (from \( Sm_{6}Ge_{4} \) [4]) and refined lattice parameters. Refined parameters from the neutron intensities of \( Tb_{5}Ge_{4} \) at 4.2 K. The estimated standard deviations are given in parentheses and correspond to the last digit. \( \mu \) is the ordered magnetic moment of \( Tb_{5} \) , \( \mu_{x} \) , \( \mu_{y} \) , \( \mu_{z} \) the x, y, z, components of \( \mu \) and \( \theta_{x} \) , \( \theta_{y} \) , \( \theta_{z} \) the angles between \( \mu \) and x, y, z; a, b, c the lattice parameters, \( R_{n} \) , \( R_{m} \) , \( R_{w} \) , the agreement values for nuclear, magnetic and weighted profile intensities (Rietveld[8])
| R_{n} | T | |||||||
| R_{m} | [K] | Tb | Tb' | Tb'' | Ge | Ge' | Ge'' | a |
| R_{w_{p}} | at 8(d) | at 8(d) | at 4(c) | at 8(d) | at 4(c) | at 4(c) | b | |
| 0.09 | x | 0.1205(5) | 0.9747(5) | 0.2880(8) | 0.2206(11) | 0.9132(16) | 0.1761(15) | 7.613(3) |
| 293 | y | 0.1157(3) | 0.1004(3) | 0.25 | 0.9551(6) | 0.25 | 0.25 | 14.633(5) |
| 0.13 | z | 0.3888(5) | 0.8219(5) | 0.00248(8) | 0.5312(11) | 0.1115(15) | 0.6333(15) | 7.691(3) |
| 0.08 | x | 0.1358(25) | 0.9795(25) | 0.3162(36) | 0.2206(11) | 0.9132(16) (0.1761(15) | 0.6333(15) | 7.581(3) |
| 0.039 4.2 | y | 0.1216(9) | 0.0889(9) | 0.25 | 0.9551(6) | 0.30 | 0.25 | 14.565(5) |
| 0.066 | z | 0.3438(32) | 0.8072(33) | -0.06510(35) | 0.5312(11) | 0.1115(15) (0.6333(15) | 0.6333(15) | 7.645(3) |
| \( \mu[\mu_{B}] \) | 7.1(2) | 8.4(2) | 7.7(1) | Overall temp. factor = 0.76 ( \( \AA^{2} \) ) | ||||
| \( \mu_{x}[\mu_{B}] \) | \( \theta_{x} \) [deg.] | 1.2(2) | 80 - 4.3(2) - 59 | 0.03(3) | 88 | Scale factor = 0.220(3) | ||
| \( \mu_{y}[\mu_{B}] \) | \( \theta_{y} \) [deg.] | 1.1(2) | 81 | 2.6(2) | 72 | 90 | ||
| \( \mu_{z}[\mu_{D}] \) | \( \theta_{z} \) [deg.] | 6.9(1) | 13 | 6.7(2) | 37 | 7.70(15) | 2 | |
Profile parameters PH = 28 × 10⁴, QH = -12.9 × 10⁴, RH = 2 × 10⁴.
The scattering lengths \( b_{Tb} = 0.76 \) . \( b_{Ge} = 0.819 \times 10^{-12} \) cm were used. In a first approximation the resulting scale factor \( c = 0.28(1) \) ( \( I_{calc} = c I_{obs} \) ) was used to derive the absolute measured magnetic intensities. The refined lattice parameter values given in Table 1 are in good agreement with those published in [3]. The reliability factor \( R_{n} = \Sigma |I_{obs} - I_{calc}| / \Sigma I_{obs} \) is 0.09. The magnetic structure of \( Tb_{5}Ge_{4} \)
The 20 Tb atoms in \( Tb_{5}Ge_{4} \) are distributed in two general \( 8(d) \) and one special \( 4(c) \) sets of positions in the Pnma space group. In the present study these atoms are numbered in the sequence of the International Tables and will be referred as follows: \( Tb(1-8) \) , \( Tb'(1'-8') \) at \( 8(d) \) and \( Tb''(1''-4'') \) at \( 4(c) \) (see Tables 1 and 3).

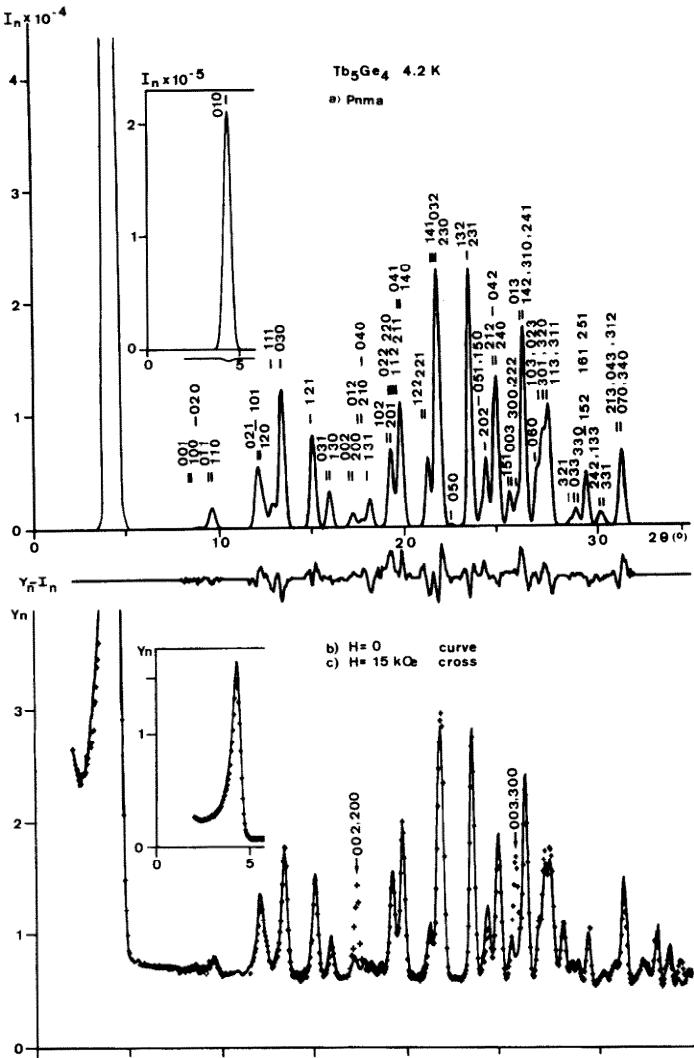
Fig. 2. Neutron diffraction patterns from antiferromagnetic \( Tb_{5}Ge_{4} \) at 4.2 K. (a) the calculated profile in the space group \( Pnm'a \) and the difference diagram. (b) and (c) the absorption corrected/observed intensities with (crosses) and without (solid line) a magnetic field (15 kOe) applied in the direction of the scattering vector.
In the powder diagram recorded at 4.2 K additional magnetic superstructure lines are present, which do not correspond to the extinction rules of the Pnma group. However, the additional lines could be indexed in the same orthorhombic cell, the magnetic propagation vector being k = 0.
The very strong intensities of the superstructure lines (010), (030) and (070) allow preliminary statements to be made concerning the magnetic structure. The magnetic structure is most probably two-dimensional, with the moments of the magnetic atoms almost confined to the (010) plane. Since there is no ferromagnetism, each one of the three non-equivalent positions might have an antiferromagnetic arrangement. In addition the crystallographic mirror plane m becomes an antisymmetry mirror plane \( m' \) for the 4(c) atoms having their moments in
Table 2. The irreducible representations \(\Gamma_{ik}\) of Pnma[12] and the corresponding magnetic modes along \(x\), \(y\), \(z\) for the symmetry positions \(4(c)\) and \(8(d)\)
| x | y | z | x | y | z | group | |
| \( \Gamma_{1}=\Gamma_{1k} \) | C_{v} | C_{H_{v}} | G_{Bv} | A_{B2} | Pnma | ||
| \( \Gamma_{2}=\Gamma_{2k} \) | C_{x} | F_{2} | G_{Bx} | C_{Bv} | F_{B2} | Pn'm'a | |
| \( \Gamma_{3}=\Gamma_{3k} \) | F_{x} | C_{z} | F_{Bx} | A_{Bv} | G_{B2} | Pn'm'a' | |
| \( \Gamma_{4}=\Gamma_{4k} \) | F_{x} | A_{Hx} | F_{Bv} | C_{Bz} | Pn'm'a' | ||
| \( \Gamma_{5}=\Gamma_{5u} \) | A_{x} | G_{z} | R_{v} | Q_{v} | L_{z} | Pn'm'a' |
the plane. Provided that the chemical space group at 4.2 K remains Pnma, the number of independent magnetic moment components is eight. For the 8(d) position the reflection operation through the antimirror plane \( m' \) , perpendicular to b, relates atoms 1 to 7, 2 to 8, 3 to 5 and 4 to 6, leaving the sign of \( \mu_{x} \) and \( \mu_{z} \) , for these atoms, unchanged while changing the sign of their transverse component \( \mu_{y} \) . The large absolute (0k0) intensities indicate that the contributions of the 20 Tb atoms to the (0k0) structure factors are in phase. The (0k0) phase factors for each set of 8(d) atoms:
\[ \begin{array}{r}{\cos2\pi k y(1-1-1+1+1-1-1+1)}\\ {-i\sin2\pi k y(1+1-1-1-1+1+1)}\end{array} \]
show that the cosine term makes an intensity contribution only if the relative signs of the magnetic moments are \( (+-+-\cdots+-) \) . Because of the antimirror plane, these signs might be attributable to the \( \mu_{y} \) components alone; but \( \mu_{x} \) cannot contribute to (0k0) intensities \( (q=0) \) .
The sine term on the other hand, contributes only if the relative signs are \( (++-\cdots-++ \) , agreeing with the antimirror operation, requiring an antisymmetry center, and suggesting only one magnetic mode contributing to \( (0k0) \) intensities. The configurations for the \( 8(d) \) site \( (++-\cdots-++ \) and for the \( 4(c) \) one \( (+-+-) \) (derived by similar arguments) are called R and A [11]. Moreover since the two \( 8(d) \) positions have the same y value [3], they ought to have the same sign for \( \mu_{x} \) and \( \mu_{z} \) in the R mode; otherwise (010), (030) and (070) would have a very small intensity resulting from the \( 4(c) \) atoms alone.
Using three observed magnetic \( (0k0) \) absolute intensities scaled by the nuclear scale factor (assuming no essential parameter shifts), we can derive the absolute magnetic structure factors. These are linear functions of the three \( \mu_{x} \) and \( \mu_{z} \) magnetic moment components. If \( \mu_{z} \) , \( \mu_{z}^{\prime} \) and \( \mu_{z}^{\prime\prime} \) are the z-components of magnetic moment for Tb, Tb' and Tb", then the absolute measured structure amplitude in \( [\mu_{B}] \) expressed as \( P = \Sigma \mu_{i} e^{i k r_{i}} = A + i B \) , will depend only on the imaginary part of this expression for the R and A configurations. The equations for the \( (0k0) \) reflections are:
\[ (010)\qquad5.32\mu_{z}+4.72\mu_{z}^{\prime}+4\mu_{z}^{\prime\prime}=105.8[\mu_{B}] \]
\[ (030)\qquad6.56\mu_{z}+7.592\mu_{z}^{\prime}-4\mu_{z}^{\prime\prime}=69.5[\mu_{B}] \]
\[ (050)\quad-3.78\mu_{z}-0.104\mu_{z}^{\prime}+4\mu_{z}^{\prime\prime}=0. \]
| Pnm'u' | ||||||||||||||||||||
| h | k | l | I_{nuc} | I_{mag} | I_{tot} | I_{obs} | h | k | l | I_{nuc} | I_{maga} | I_{tot} | I_{obs} | |||||||
| 0 | 1 | 0 | — | 200736 | 200736 | 199967 | 0 | 5 | 1 | 583 | 0 | 583 | 732 | |||||||
| 0 | 0 | 1 | — | 0 | 0 | 0 | 1 | 5 | 0 | — | 197 | 197 | 250 | |||||||
| 1 | 0 | 0 | — | -0 | -0 | 0 | 2 | 0 | 2 | 2244 | 1192 | 3436 | 3776 | |||||||
| 0 | 2 | 0 | 94 | — | 94 | 27 | 2 | 1 | 2 | 568 | 1702 | 2271 | 2209 | |||||||
| 0 | 1 | 1 | 64 | 735 | 799 | 760 | 0 | 4 | 2 | 1883 | 28 | 1911 | 1844 | |||||||
| 1 | 1 | 0 | — | 658 | 658 | 631 | 2 | 4 | 0 | 1171 | 4287 | 5459 | 5363 | |||||||
| 1 | 0 | 1 | 125 | 3731 | 3856 | 3990 | 1 | 5 | 1 | 1753 | 6 | 1760 | 2113 | |||||||
| 0 | 2 | 1 | — | 238 | 238 | 269 | 0 | 0 | 3 | — | 0 | 0 | 0 | |||||||
| 1 | 2 | 0 | — | 1371 | 1371 | 1521 | 3 | 0 | 0 | — | 0 | 0 | 0 | |||||||
| 1 | 1 | 1 | 104 | 1515 | 1620 | 1194 | 2 | 2 | 2 | 1145 | 89 | 1234 | 1595 | |||||||
| 0 | 3 | 0 | — | 8929 | 8929 | 8062 | 0 | 1 | 3 | 32 | 427 | 460 | 632 | |||||||
| 1 | 2 | 1 | 4 | 5714 | 5719 | 6412 | 1 | 4 | 2 | 576 | 4824 | 5401 | 5956 | |||||||
| 0 | 3 | 1 | 18 | 849 | 867 | 842 | 3 | 1 | 0 | — | 0 | 0 | 0 | |||||||
| 1 | 3 | 0 | — | 1329 | 1329 | 1194 | 2 | 4 | 1 | 2695 | 2498 | 5193 | ||||||||
| 0 | 0 | 2 | 41 | 186 | 228 | 192 | 0 | 6 | 0 | 2326 | — | 2326 | 2269 | |||||||
| 2 | 0 | 0 | 248 | 403 | 652 | 860 | 1 | 0 | 3 | 144 | 708 | 852 | 831 | |||||||
| 0 | 1 | 2 | — | 398 | 398 | 673 | 0 | 2 | 3 | — | 310 | 310 | 322 | |||||||
| 2 | 1 | 0 | 0 | 6 | 7 | 12 | 3 | 0 | 1 | 2548 | 1030 | 3578 | 3840 | |||||||
| 0 | 4 | 0 | 122 | — | 122 | 136 | 3 | 2 | 0 | — | 39 | 39 | 42 | |||||||
| 1 | 3 | 1 | 757 | 793 | 1551 | 1187 | 1 | 1 | 3 | 2530 | 134 | 2665 | 2786 | |||||||
| 1 | 0 | 2 | 136 | 876 | 1012 | 1816 | 3 | 1 | 1 | 1169 | 4114 | 5283 | 4679 | |||||||
| 2 | 0 | 1 | 298 | 2910 | 3208 | 4416 | 3 | 2 | 1 | 17 | 262 | 280 | 223 | |||||||
| 0 | 2 | 2 | 17 | 188 | 206 | 267 | 0 | 3 | 3 | — | 808 | 808 | 883 | |||||||
| 2 | 2 | 0 | 0 | 632 | 633 | 754 | 3 | 3 | 0 | — | 145 | 145 | 160 | |||||||
| 1 | 1 | 2 | 6 | 704 | 710 | 795 | 1 | 5 | 2 | 834 | 140 | 974 | 824 | |||||||
| 2 | 1 | 1 | 12 | 5251 | 5264 | 5966 | 1 | 6 | 1 | 73 | 1545 | 1618 | 1276 | |||||||
| 0 | 4 | 1 | — | 1178 | 1178 | 1357 | 2 | 5 | 1 | 10 | 285 | 295 | 216 | |||||||
| 1 | 4 | 0 | — | 400 | 400 | 463 | 2 | 4 | 2 | 21 | 113 | 135 | 83 | |||||||
| 1 | 2 | 2 | 447 | 321 | 768 | 971 | 1 | 3 | 3 | 386 | 35 | 421 | 266 | |||||||
| 2 | 2 | 1 | 591 | 2471 | 3062 | 2658 | 3 | 3 | 1 | 267 | 48 | 316 | 234 | |||||||
| 1 | 4 | 1 | — | 8127 | 8127 | 7783 | 2 | 1 | 3 | 540 | 787 | 1327 | 1205 | |||||||
| 0 | 3 | 2 | — | 3660 | 3660 | 3707 | 0 | 4 | 3 | — | 196 | 196 | 206 | |||||||
| • | 2 | 3 | 0 | 342 | 5715 | 6057 | 6931 | 3 | 1 | 2 | 350 | 18 | 369 | |||||||
| 0 | 5 | 0 | — | 122 | 122 | 0 | 0 | 7 | 0 | — | 2970 | 2970 | 3567 | |||||||
| 1 | 3 | 2 | 6299 | 920 | 7220 | 7249 | 3 | 4 | 0 | — | 186 | 186 | 243 | |||||||
| 2 | 3 | 1 | 4321 | 2494 | 6815 | 6915 | ||||||||||||||

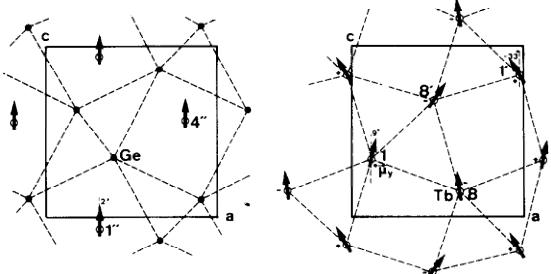
C LAYER Y=0.25
S LAYER Y=0.11, ATOM Nr 1.8,1.8
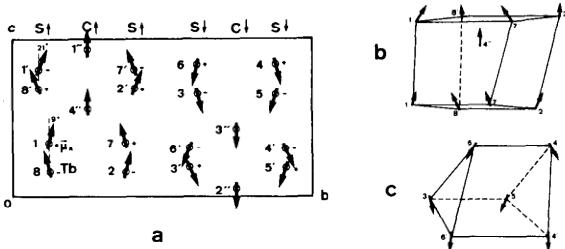
Fig. 3. Magnetic moment arrangement of two of the characteristic layers C and S extending perpendicular to the b axis \( (y = 0.25 \) and \( y \approx 0.11) \) in the structure of \( Tb_{5}Ge_{4} \) . The two \( Tb^{*} \) atoms in the C layer have their moments essentially parallel to z (the angle is \( 2^{\circ} \) ). The moment projections of the 2 Tb and 2 \( Tb^{*} \) atoms on the S layer make angles \( 9^{\circ} \) and \( 33^{\circ} \) with z. The moment component \( \mu_{v} \) is given by a + or - sign.
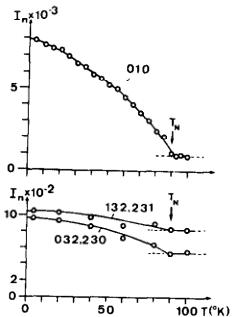
\( Er_{5}Ge_{4} \) are 30, 21 and 7 K, respectively. The temperature variation of the three strongest magnetic reflections of \( Tb_{5}Ge_{4} \) : (010), (132) + (231) and (141) + (032) + (230) is illustrated in Fig. 5. This shows that their magnetic contribution vanishes at a much higher Néel temperature \( T_{N}=91 \) K. In a neutron pattern at 40 K all magnetic reflections are still present but they have a much lower intensity than at 4.2 K. Therefore the reported [3] Néel temperature for \( Tb_{5}Ge_{4} \) does not correspond to a magnetic phase transition. This discrepancy in the \( T_{N} \) values

Fig. 4(a). A two dimensional projection of the magnetic structure of \( Tb_{5}Ge_{4} \) in the \( (0yz) \) plane. The moment component \( \mu_{z} \) is given by \( a + or - sign \) . The angle of the moment projection \( (0yz) \) with z is \( 9^{\circ} \) . For Tb and \( 21^{\circ} \) , for Tb'. For Tb" it is parallel to z. \( S \uparrow \) and \( C \uparrow \) symbolize the ferri- and ferro-magnetic layers extending perpendicular to y and the moment direction (b) and (c) show the characteristic polyhedra: deformed cubes and trigonal prisms formed by the Tb atoms.

Fig. 5. The temperature dependence measurements of the strongest magnetic intensities of \( Tb_{5}Ge_{4} \) .
might perhaps result from the difficulty in finding the minimum on the very flat reciprocal susceptibility curve characteristic of an antiferromagnetic and strongly anisotropic compound \( ^{[5]} \) .
The (010) intensity depends only upon the \( \mu_{z} \) component of the magnetic modes, while the other reflections depend upon all components. Within the limits of statistical errors it seems from the temperature dependence of (010) that the moments of the three non-equivalent Tb positions behave in much the same way. In addition we can conclude that no second magnetic phase contributes to those intensities except in the unlikely event that its transition temperature is identical. In the case of \( Ho_{5}Ge_{4} \) , for example, it was found that there were two transition temperatures, 18 and 21 K. They were attributed to two different magnetic structures, although in the nuclear pattern the compound appeared to be single phase.
One of these magnetic structures is similar to that of \( Tb_{5}Ge_{4} \) , but with another direction for the main axis of antiferromagnetism. The second structure is associated with a propagation vector \( (k = 1/2, 0, 0) \) . Reference will be made to these experimental results at a later stage.
Field dependence measurements
In Figs. 2(b) and 2(c) the 4.2 K neutron pattern is plotted for a magnetic field \(H=0\) (full curve) and \(H=\)


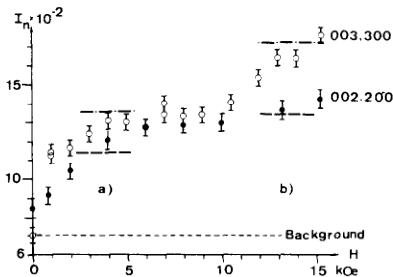
Fig. 6. The field dependence of the magnetic intensities (002) + (200) and (003) + (300) (open circles). The dotted lines --- correspond to calculated values of (002) + (200), while the broken lines --- correspond to those of (003) + (300) for the mechanisms shown in the upper part of the figure (a), (b). In the upper part of the figure the field influence on the x and z directions are shown separately. The magnetic moment projections are drawn with a common origin in the \( (x0z) \) plane.
15 kOe (cross curve) applied along the scattering vector. Two cases may be immediately recognized: (a) the field perpendicular to the (010) plane and (b) the field in the plane (010). From the (0k0) reflections it is evident that at most a very small \( F_{y} \) component appears. The structure remains unchanged ( \( L_{x}P_{y}R_{z} \) , \( G_{x}A_{z} \) ) when the field is perpendicular to (010).
This behaviour is in accord with the preliminary assumption made that the transverse magnetic components are very small and that \( [010] \) is the hard direction of magnetization.
On the other hand, a field acting in the (010) plane gives rise to magnetic phase transitions that can be assumed from the increase in the (002) + (200) and
(004) + (400) reflections and the appearance of the (003) + (300) reflection even for fields below 1 kOe. The intensities of the three lines did not change on turning or shaking the sample. On reversing the field some hysteresis was observed. Other effects such as movement of Bloch walls [18], or preferred orientation of the crystallites, giving rise to nuclear contributions, can be excluded from the fact that the (003) + (300) line has zero nuclear and magnetic intensity. The strong influence of the magnetic field in the directions (00l) and (h00) is in good agreement with the conclusion that the magnetic structure has its main axis of antiferromagnetism parallel to z. In Fig. 6 (lower part) the observed intensities of the two reflections (002) + (200) and (003) + (300) are plotted vs the applied field.
Since the magnetic cell is pseudotetragonal ( \( a \cong c \) ), it was not possible to follow separately the field influence along the x and z directions. Therefore the critical fields (at least 6) could not be derived from the transitions associated with the 10 sublattice cross structure of \( Tb_{5}Ge_{4} \) . Figure 6 shows that the observed neutron intensities of the (002) + (200) and (003) + (300) lines both increase with the field but each with a different slope for very low field values. They achieve saturation at 5 kOe. At about 10 kOe (region b) a second transition with a less steep slope is visible but not saturation is achieved up to 15 kOe. In fact from pulsed field measurements† the ferromagnetic transition is found to occur in fields much higher than 15 kOe.
In order to make some quantitative estimates of those effects, all possible spin flip transitions as described by other authors \( ^{[15,17]} \) , have been tried for canted spin systems along the x and z directions.
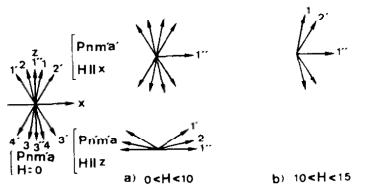
In Fig. 6 (upper part) the projections of the 10 magnetic sublattices onto the plane \( (x0z) \) are shown with a common origin. They are denoted in the same way as the correpsponding atoms (Tables 1 and 3), which implies that the sublattices of Tb and Tb' and Tb" each contain 2 atoms. The mechanisms we have found to explain the distinct regions \( (a, b) \) of the experimental data are shown separately for the x and z directions.
The effect of a field along x
When the field is applied parallel to the x axis, a structure with \( F_{x} \) components will be favored (Table 3). This transition can be described as
\[ P n m^{\prime}a\xrightarrow[H\|x]{}\quad P n m^{\prime}a^{\prime}. \]
By making the hypothesis that the interaction between the Tb" sublattices (having the largest distances (Fig. 3)) is the weakest one, then the ferromagnetic transition will take place first for Tb". The two Tb" sublattices (1", 3") will be confined towards the x direction (region a). The sublattices 2 and 3 containing Tb (2, 3, 6, 8), and 1' and 4' containing Tb' (1', 4', 6', 7') having an x component opposed to the field are shown to flip in region (b) for a field \( 10 < H < 15 \) kOe.
These transitions only influence the intensities of the (200) and (300) reflections (Table 5) and it is expected that they will fall to zero at higher field values.
The effect of a field along z
The effect of a magnetic field applied along the z direction favors a transition to a space group with a ferromagnetic z component such as
\[ P n m^{\prime}a\xrightarrow[H\|z]{}\quad P n^{\prime}m^{\prime}a. \]
This transition implies a rotation of the main axis of antiferromagnetism from z to x that in turn leads to a rearrangement of the magnetic moments along this direction.
The signs of the Tb (1, 2) moments along the main axis of antiferromagnetism are opposite for \( Pn'm'a \) (along x) and the same for \( Pnm'a \) (along z). For the rest of the signs see Table 3. In Fig. 6 this transition is shown to occur in region (a) for very low fields. This mechanism was the only one that could explain the strong intensity of (003) in Table 5; we expect that the (003) intensity will fall to zero for higher fields.
CONCLUSIONS
The refinement of this magnetic structure was accomplished by an iterative parameter least-square method using the line profile analysis procedure [8]. 17 parameters were refined from 71 observations. The resulting R-factor values indicate that the chosen structure model is probably correct. The refined positional parameters of Tb at 4.2 K show that the polyhedra (Figs. 4(b), 4(c)) formed by those atoms are less symmetrical.
Table 5. Calculated and scaled (to the (200) + (002) measured peak intensity for H = 0 kOe) magnetic and nuclear intensities \( I_{mag} \) and \( I_{nuc} \) for the transitions illustrated in Fig. 6, under the influence of a magnetic field along the x and z directions (separately) in the regions (a), (b). In the last two columns is given the total resulting intensity from the \( (h00) + (00l) \) reflections occurring at the same 2 \( \theta \) angle
| I_{mag} (200) | I_{mag} (300) | I_{mag} (002) | I_{mag} (003) | I_{mag} + I_{nuc} (200) + (002) | I_{mag} (300) + (003) | |
| H kOe | H \| x | H \| z | H \| x and H \| z | |||
| 0 | 54 | 0 | 24 | 0 | 110 | 0 |
| (a) 0-10 | 290 | 53 | 96 | 628 | 420 | 681 |
| (b) 10-15 | 490 | 387 | 96 | 628 | 610 | 1015 |
than at 293 K. Low temperature X-ray diffraction data is required for a more detailed discussion of the structure. Our effort to obtain such data, however, has been unsuccessful because of serious extinction problems and high absorption.
The magnetic structure of \( Tb_{5}Ge_{4} \) described in the Shubnikov group \( Pnm'a \) belongs to the single irreducible representation \( \Gamma_{8u} \) of the space group \( Pnma \) , which is associated with the propagation vector k=0.
The occurrence of ferromagnetically coupled ferrimagnetic layers parallel to the (010) plane agrees with the high value of the paramagnetic Curie temperature \( \theta \) . The three-dimensional structure is also in agreement with the high anisotropy of the compound, showing a characteristic metamagnetic behaviour in the pulsed field measurements, and with the occurrence of magnetic phase transitions observed by neutron diffraction when the magnetic field is acting in the (010) plane. The flopping of the main axis of antiferromagnetism when the field is acting parallel to it, indicates that the anisotropy in the plane (010) should not be very high \( ^{[6]} \) .
The structure is antiferromagnetically compensated through a sign change over the antisymmetry center. The magnetic moment values (7.1, 8.4, 7.7[ \( \mu_{B} \) ]) of the 3 Tb non-equivalent positions are near the saturation value of the free ion and indicates that it is not reduced by crystalline field effects, as might have been assumed from the \( T_{N} \) and the low symmetry. The different magnetic moment directions and the canted spin arrangement of this structure is most likely resulting from (a) the different influence of the crystalline field on the three equivalent positions and (b) the possibility of an antisymmetric exchange term of the Dzialoshinski–Moriya kind in the Hamiltonian that can be expected in the case of such a low crystal symmetry \( ^{[19]} \) . The exchange interactions here, as for most rare earth alloys, are expected to take place via the conduction electrons.
Acknowledgements—I would like to express my gratitude to Dr. P. Meriel for his encouragement and stimulating discussions on this study. I also wish to thank Dr. M. Sougi for his interest, and for carrying out the temperature dependence measurements, Dr. R. Plumier and Mr. A. Meidan-Gross for their help and for obtaining pulsed field and susceptibility measurements, Prof. E. F. Bertaut for his encouragement, Mr. Haefeli for his kind cooperation in the sample preparation, the ETH institute für Reaktortechnik, and in particular Dr. P. Fischer, for their support.
The main experimental part of this study was carried out during a research leave from the Institute of Crystallography of the ETH in Zürich. I wish to thank Prof. A. Niggli for making this leave possible as well as Dr. P. Meriel and the Saclay authorities for their kind hospitality in accepting me as a guest scientist at the "Service de Physique du Solide et de Résonance Magnétique".
REFERENCES
-
Wallace W. E., Progress in Solid State Chemistry (Edited by H. Reiss and J. D. McCaldin), Vol. 6, p. 155. Pergamon Press, Oxford (1971).
-
Wallace W. E., Rare Earth Intermetallics. Academic Press, New York/London (1973).
-
Holtzberg F., Gambino R. J. and McGuire T. R., J. Phys. Chem. Solids 28, 2283 (1967).
-
Smith G. S., Johnson Q. and Tharp A. G., Acta Cryst. 22, 269 (1967).
-
Herpin A., Théorie du Magnétisme, p. 477. Presses Universitaires de France (1968); Herpin A. and Meriel P., J. Phys. Rad. 22, 337 (1961).
-
Néel Louis, Compte Rendu 242, 1549 (1956).
-
Jacobs I. S. and Lawrence P. E., Phys. Rev. 164, 866 (1967).
-
Rietveld H. M., RCN Rep. 104, Petten, The Netherlands (1969).
-
von Wartburg W., AF-SSP-46, Würenlingen (1970).
-
Klug H. P. and Alexander L. E., X-Ray Diffraction Procedures, 2nd Edn, p. 251. Wiley, New York (1959).
-
E. F. Bertaut, In Treatise of Magnetism (Edited by H. Suhl and G. Rado), Vol. III, p. 186. Academic Press, New York (1963).
-
Bertaut E. F., Acta Cryst. A24, 217 (1968).
-
Opechowski W. and Guccione R., In Treatise of Magnetism (Edited by H. Suhl and G. Rado), Vol, IIA, pp. 105–165. Academic Press, New York (1965).
-
Koptsik B. A., Shubnikov groups, Moscow University (1966).
-
Bertaut E. F., Ann. Phys. 7, 203 (1972).
-
Steinsvoll O., Shirane C., Nathans R., Blume M., Alperin H. A., and Pickart S. J., Phys. Rev. 161, 499 (1967).
-
Holmes L. M. and Van Uitert L. G., Phys. Rev. B5, 138, 147 (1972).
-
Plumier R., J. de Phys. 27, 213 (1966); C.R. Acad. Sci. 267, 1057 (1968).
-
Moriya T., Phys. Rev. 120, 91 (1961).