| Transition Temperature | 7 K |
|---|---|
| Experiment Temperature | 2 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | P63/mmc (#194) |
| Magnetic Space Group | C2'/c' (#15.89) |
| Magnetic Point Group | 2'/m' (5.5.16) |
| Lattice Parameters | 8.8587(6) 8.8587(9) 9.6244(5) 90 90 120.000(9) |
|---|---|
| DOI | 10.1103/physrevb.97.014431 |
| Reference | M.S. Henriques, D.I. Gorbunov, A.V. Andreev, X. Fabreges, A. Gukasov, M. Uhlarz, V. Petricek, B. Ouladdiaf and J. Wosnitza, Physical Review B (2018) 97 014431. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Pr1 | Pr | 0.0 | 0.0 | 3.2 | 3.20 |
| Pr2 | Pr | 0.5 | 0.5 | 1.3 | 1.39 |
Complex magnetic order in the kagome ferromagnet Pr₃Ru₄Al₁₂
M. S. Henriques, \( ^{1,2} \) D. I. Gorbunov, \( ^{3} \) A. V. Andreev, \( ^{2} \) X. Fabrèges, \( ^{4} \) A. Gukasov, \( ^{4} \) M. Uhlarz, \( ^{3} \) V. Petříček, \( ^{2} \) B. Ouladdiaf, \( ^{1} \) and J. Wosnitza \( ^{3,5} \)
\( ^{1} \) Institut Laue Langevin, 71 Avenue des Martyrs, F-38042 Grenoble, France
\( ^{2} \) Institute of Physics, Academy of Sciences, Na Slovance 2, 182 21 Prague, Czech Republic
\( ^{3} \) Hochfeld-Magnetlabor Dresden (HLD-EMFL), Helmholtz-Zentrum Dresden-Rossendorf, 01328 Dresden, Germany
\( ^{4} \) Laboratoire Léon Brillouin, CE de Saclay, DSM/IRAMIS, F-91191 Gif-sur-Yvette, France
\( ^{5} \) Institut für Festkörper- und Materialphysik, TU Dresden, 01062 Dresden, Germany
(Received 25 July 2017; revised manuscript received 21 November 2017; published 24 January 2018)
In the hexagonal crystal structure of \( Pr_{3}Ru_{4}Al_{12} \) , the Pr atoms form a distorted kagome lattice, and their magnetic moments, are subject to competing exchange and anisotropy interactions. We performed magnetization, magnetic-susceptibility, specific-heat, electrical-resistivity, and neutron-scattering measurements. \( Pr_{3}Ru_{4}Al_{12} \) is a uniaxial ferromagnet with \( T_{C} = 39 \) K that displays a collinear magnetic structure (in the high-temperature range of the magnetically ordered state) for which the only crystallographic position of Pr is split into two sites carrying different magnetic moments. A spin-reorientation phase transition is found at 7 K. Below this temperature, part of the Pr moments rotate towards the basal plane, resulting in a noncollinear magnetic state with a lower magnetic symmetry. We argue that unequal RKKY exchange interactions competing with the crystal electric field lead to a moment instability and qualitatively explain the observed magnetic phases in \( Pr_{3}Ru_{4}Al_{12} \) .
DOI: 10.1103/PhysRevB.97.014431
I. INTRODUCTION
Praseodymium is unique among the rare-earth elements. In the solid state, it usually exists in a singlet ground state with weak exchange interactions. The magnetic moments in both symmetry positions, hexagonal and cubic, of the double hcp allotrope are totally quenched by the crystal-field effect \( [1-5] \) . Although the exchange interactions are not strong enough to induce ordered magnetic moments on the \( 4f \) electrons, Pr is close to magnetic ordering. An external perturbation, such as application of pressure or magnetic field, induces ordered magnetic moments \( [1,6,7] \) . At sufficiently low temperatures (several tens of millikelvins), Pr displays a cooperative phase that, however, originates from ordered nuclear, not electronic, spins \( [8-12] \) .
Since Pr is a light rare-earth element, crystal-field splittings are comparable with exchange energies (for heavy rare-earth elements, the crystal field acts as a source of magnetic anisotropy that is small compared to the exchange). Given a nonmagnetic lowest-energy level, a transition to a state with a long-range magnetic order can occur only if the exchange energy exceeds a threshold value determined by the next higher-energy level. When \( Pr^{3+} \) (electronic configuration \( 4f^{2} \) ) ions are placed in a crystal-field environment of a given compound, different ground states may result. Prominent examples are the binary systems \( PrX_{2} \) and \( PrX_{5} \) , for which the magnetic ground state depends on the element X through the corresponding crystal-field scheme [13–20]. The compounds with X = Co are ferromagnetic, whereas those with X = Ni and Cu are paramagnetic. In general, paramagnetic Pr-based intermetallic compounds host either a singlet or a nonmagnetic doublet and display Van Vleck paramagnetism. In the absence of long-range magnetic ordering, the orbitals are the only active degrees of freedom, and multipolar moments come into play. Quadrupolar interactions were found to play an important role in the magnetic and elastic properties of the Van Vleck paramagnet \( PrNi_{5} \) [18,21], and ordered quadrupolar moments were observed for some nonmagnetic heavy-fermion superconductors, e.g., \( PrV_{2}Al_{20} \) and \( PrIr_{2}Zn_{20} \) [22–24].
These examples reflect that Pr-based intermetallic compounds often display intriguing electronic properties driven primarily by the crystal electric fields and exchange interactions. New ground states are expected to arise when \( Pr^{3+} \) ions reside on a geometrically frustrated lattice where these interactions can compete with each other.
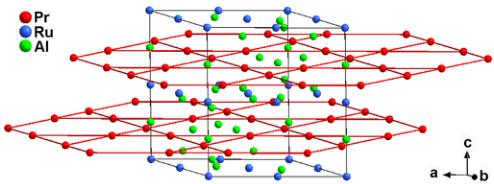
Recently, \( R_{3}Ru_{4}Al_{12} \) (R is a rare-earth element or uranium) compounds came into the focus of research interest due to their unusual electronic properties. They crystallize in the hexagonal crystal structure of \( Gd_{3}Ru_{4}Al_{12} \) type (space group \( P6_{3}/mmc \) ) [25–27]. In this structure, the R atoms occupy one crystallographic position and form two layers of a distorted kagome network parallel to the basal plane (Fig. 1). Geometrical frustration is evident for compounds with antiferromagnetically coupled R elements.
The type of magnetic order of \( R_{3}Ru_{4}Al_{12} \) depends on the R element. For the light rare-earth elements Pr and Nd, the compounds are ferromagnetic [28–30], whereas for the heavy rare-earth elements Gd, Tb, Dy, and Yb antiferromagnetic ground states were reported [31–38]. The compounds with La, Ce, and Y do not display a magnetic order [28,29,31]. The geometrical frustration is manifested by multiple field-induced phase transitions in applied magnetic field and complex magnetic structures in zero field. In particular, \( U_{3}Ru_{4}Al_{12} \) displays a noncollinear triangular network of magnetic moments confined to the basal plane. \( Dy_{3}Ru_{4}Al_{12} \) also exhibits a noncollinear arrangement of magnetic moments with the main

FIG. 1. Hexagonal crystal structure of \( Pr_{3}Ru_{4}Al_{12} \) (space group \( P6_{3}/mmc \) ). The red network represents the kagome lattice formed by the Pr atoms.
component along the c axis. \( Nd_{3}Ru_{4}Al_{12} \) is a collinear uniaxial ferromagnet for which the only crystallographic position of the Nd atoms is split into two magnetically inequivalent sites (orbits) with different Nd magnetic moments.
Motivated by these unusual results, in the present work we study the electronic properties of the Pr-based member of the \( R_{3}Ru_{4}Al_{12} \) family (so far, relatively scarce information on \( Pr_{3}Ru_{4}Al_{12} \) is available from a study of polycrystals in Refs. [28,29]). We find \( Pr_{3}Ru_{4}Al_{12} \) to be a strongly anisotropic ferromagnet with unexpected magnetic structures. In the high-temperature range of the magnetically ordered state, the only crystallographic position of Pr is split into two sites carrying different magnetic moments which are collinear parallel to the hexagonal sixfold axis. With decreasing temperature, a spin-reorientation transition occurs, at which some of the Pr magnetic moments tilt towards the basal plane, making the resulting magnetic structure noncollinear. We argue that the distorted kagome lattice leads to unequal exchange interactions competing with the crystalline electric field and resulting in the observed arrangements of the magnetic moments.
II. EXPERIMENTAL DETAILS
A single crystal of \( Pr_{3}Ru_{4}Al_{12} \) was grown by a modified Czochralski method in a tri-arc furnace from a quasi-stoichiometric mixture of the pure elements (99.9% Pr, 99.99% Ru, and 99.999% Al) with an Al mass excess of 1%. Backscattered Laue patterns were used to check the single crystallinity and to orient the crystal for magnetization, magnetic-susceptibility, specific-heat, electrical-resistivity, and neutron-scattering measurements.
The crystal structure of \( Pr_{3}Ru_{4}Al_{12} \) was checked by single-crystal x-ray diffraction. The diffracted intensities were collected at ambient temperature using a four-circle diffractometer (Gemini of Agilent) equipped with a Mo x-ray tube \( [\lambda(\mathrm{Mo}K\alpha)=0.71073\ \text{\AA}] \) , Mo-enhanced collimator, graphite monochromator, and an Atlas CCD detector. The CRYSALIS PRO [39] program was used to index the lattice, refine the unit cell, reduce the data, and perform the absorption correction (face-indexing and Gaussian spherical-harmonics algorithms). Superflip [40] was employed to solve the structure, whereas the refinements were carried out by use of the numerical program JANA2006 [41] taking into account all reflections. The final R factor for the crystal structure solved in the space group \( P6_{3}/mmc \) (type \( Gd_{3}Ru_{4}Al_{12} \) ) converged to 2.6%. The lattice parameters of \( Pr_{3}Ru_{4}Al_{12} \) , \( a=8.858(7)\ \text{\AA} \) , and \( c=9.624(4)\ \text{\AA} \) , are in good
TABLE I. Refined relative atomic coordinates \( (x, y, z) \) , equivalent isotropic displacement parameters \( U_{eq} \) , and their estimated standard deviations for \( Pr_{3}Ru_{4}Al_{12} \) .
| Atom | Wyckoff position | x | y | z | U_{eq} |
| Pr | 6h | 0.19165(3) | 0.38329(6) | 1/4 | 0.0039(2) |
| Ru1 | 2a | 0 | 0 | 0 | 0.0030(3) |
| Ru2 | 6g | 0.5 | 0.5 | 0 | 0.0040(3) |
| Al1 | 6h | 0.56176(9) | 0.43824(9) | 1/4 | 0.0040(8) |
| Al2 | 12k | 0.32460(3) | 0.16231(9) | 0.07558(9) | 0.0044(6) |
| Al3 | 4f | 1/3 | 2/3 | 0.00781(3) | 0.0048(8) |
| Al4 | 2b | 0 | 0 | 1/4 | 0.0055(9) |
agreement with those reported by Niermann and Jeitschko for polycrystals of the same composition prepared by arc melting [26]. The refined atomic positions and equivalent isotropic displacement parameters are given in Table I. The occupancies for all the atomic sites do not deviate from 1.
The temperature and field dependences of the magnetization and ac magnetic susceptibility (excitation amplitude of 10 mT, frequency of 97 Hz) were measured along the principal crystallographic directions, \( a\left(\left[100\right]\right) \) , \( b\left(\left[120\right]\right) \) , and \( c\left(\left[001\right]\right) \) , between 2 and 300 K using a physical property measurement system (PPMS) in static fields up to 14 T. All field-dependent magnetization curves have been corrected for demagnetization effects and are presented as a function of internal magnetic field \( \mu_{0}H_{i} \) . The PPMS served also for specific-heat measurements utilizing the relaxation method and for electrical-resistivity measurements using the four-point method (excitation current I = 5 mA).
Magnetization in pulsed magnetic fields up to 58 T was measured at the Dresden High Magnetic Field Laboratory. The high-field magnetometer is described in Ref. [42]. Absolute values of the magnetization were calibrated using static-field measurements.
A single crystal of \( Pr_{3}Ru_{4}Al_{1}2 \) was investigated using the neutron Laue diffractometer CYCLOPS at the Institut Lau-Langevin [43]. The crystal was cooled from 300 down to 2 K at 1 K/min, and Laue patterns were recorded every minute. Then the temperature was stabilized at 2 and 10 K. A set of 20 images was recorded at each temperature. These images were corrected and averaged. The neutron Laue patterns allow fast inspection of a large part of the reciprocal space of the crystal across the magnetic phase transitions. In addition, they are particularly useful for finding and verifying the propagation vector(s) of each phase.
Further neutron-diffraction experiments were performed on a single crystal of \( Pr_{3}Ru_{4}Al_{12} \) using the two-axis diffractometer 6T2 at the Laboratoire Léon Brillouin, Saclay, France [44]. The single crystal was wrapped in Al foil and inserted in the cryostat. A set of strong and well-centered nuclear reflections was used to orient the single crystal. Data sets were collected at 50, 10, and 2 K for incident-neutron wavelengths of \( \lambda = 0.902 \) Å and \( \lambda = 2.40 \) Å. For each wavelength and temperature, the data, collected by a position-sensitive detector (PSD), were used to obtain neutron-scattering intensity frames, giving an image of the reciprocal space. Larger reflection sets were

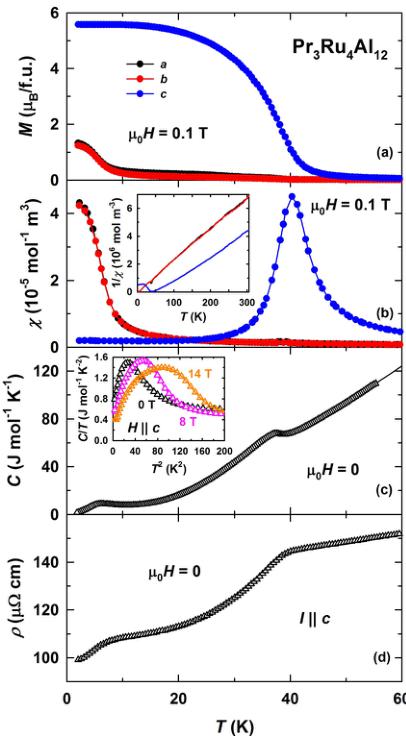
FIG. 2. Temperature dependence of (a) the magnetization M and (b) the magnetic susceptibility \( \chi \) , both for a field of 0.1 T applied along the principal crystallographic directions, (c) the specific heat C, and (d) the electrical resistivity \( \rho \) of \( Pr_{3}Ru_{4}Al_{12} \) . The insets in (b) and (c) show \( 1/\chi \) vs T and C/T vs \( T^{2} \) , respectively.
recorded after substituting the PSD by a single-lifting counter. The program JANA2006 [41] was employed to solve the nuclear and the magnetic structures of \( Pr_{3}Ru_{4}Al_{12} \) . The Pr magnetic moment was refined from integrated intensities assuming that the magnetic form factor is in accordance with the dipolar approximation, having the form \( \langle j_{0}\rangle + c_{2}\langle j_{2}\rangle \) , where \( \langle j_{0}\rangle \) and \( \langle j_{2}\rangle \) are the radial integrals calculated for the \( Pr^{3+} \) ion and the constant \( c_{2} \) is the ratio between the orbital and the total magnetic moment of \( Pr^{3+} \) .
III. RESULTS
Figure 2(a) shows the temperature-dependent magnetization M for fields applied along the principal crystallographic directions of a \( Pr_{3}Ru_{4}Al_{12} \) single crystal in 0.1 T. A pronounced anisotropy is evident between the basal plane and the c axis. The increase of the magnetization at about 40 K is related to the onset of magnetic order. Overall, the \( M(T) \) dependence for field applied along the c axis is of the ferromagnetic type. Although no additional anomalies are observed for the c direction below the ordering temperature, the magnetization
TABLE II. Effective magnetic moments \(\mu_{\mathrm{eff}}\) per Pr atom and paramagnetic Curie temperatures \(\theta\) for fields applied along the principal crystallographic directions of \(\mathrm{Pr}_{3}\mathrm{Ru}_{4}\mathrm{Al}_{12}\) obtained from fits in the listed temperature ranges.
| H||a | H||b | H||c | |
| \( \mu_{\text{eff}} \) (units of \( \mu_{\text{B}}/\text{Pr} \) ) | 3.0(1) | 3.0(1) | 3.5(2) |
| \( \theta \) (K) | 3(2) | 3(2) | 61(2) |
| Temperature range (K) | 50-300 | 50-300 | 150-300 |
displays an additional increase below 10 K when the field is applied along the basal plane. For the same field orientation, the temperature-dependent magnetic susceptibility \( \chi \) also grows in the low-temperature region [Fig. 2(b)]. Additionally, a sharp maximum is observed at 40 K for field applied along the c axis. The inverse magnetic susceptibility \( 1/\chi \) measured up to 300 K is shown in the inset in Fig. 2(b). Above 150 K, \( 1/\chi \) can be described using the Curie-Weiss law, \( \chi = C/(T - \theta) \) , where C is the Curie constant proportional to the square of the effective magnetic moment \( \mu_{eff} \) and \( \theta \) is the paramagnetic Curie temperature. The obtained \( \mu_{eff} \) and \( \theta \) values are listed in Table II. \( \mu_{eff} \) per Pr atom is somewhat lower than the \( 3.58\mu_{B} \) expected for a free \( Pr^{3+} \) ion for the a and b axes and close to it for the c axis. The positive \( \theta \) values reflect the dominance of ferromagnetic exchange interactions in \( Pr_{3}Ru_{4}Al_{12} \) . The pronounced difference between the \( \theta \) values for the basal-plane directions and for the c axis is related to the large magnetic anisotropy of \( Pr_{3}Ru_{4}Al_{12} \) .
The specific heat C indicates the presence of two phase transitions as a function of temperature [Fig. 2(c)]. The magnetically ordered state sets in at the Curie temperature, \( T_{C} = 39 \) K. This value is in agreement with 40 K found in Refs. [28,29] for polycrystals. At \( T_{sr} = 7 \) K, another phase transition occurs. The low-temperature C/T vs \( T^{2} \) data do not allow us to determine the Sommerfeld coefficient \( \gamma \) owing to their nonlinear character [inset in Fig. 2(c)]. Application of magnetic fields shifts the phase transition at \( T_{sr} \) to higher temperatures. However, using the data obtained in the highest field of 14 T, one still cannot determine \( \gamma \) and the Debye temperature reliably.
The electrical resistivity \( \rho \) exhibits a pronounced decrease just below \( T_{C} \) and \( T_{sr} \) [Fig. 2(d)]. Anomalies in M, C, and \( \rho \) around 7 K were also reported in Ref. [29], where a polycrystalline \( Pr_{3}Ru_{4}Al_{12} \) sample was studied.
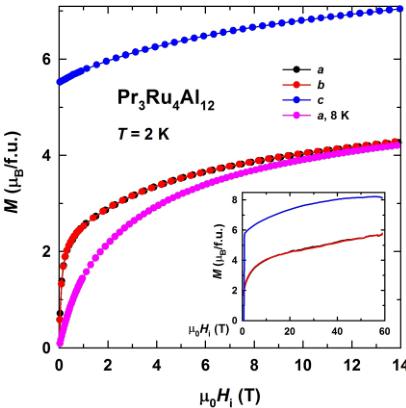
Additional information on the type of magnetic order was obtained from field-dependent magnetization data (Fig. 3). At 2 K, the easy-magnetization direction is the c axis with a spontaneous magnetic moment \( M_{s}^{c} = 5.5 \mu_{B}/f.u. \) (the magnetization is shown only for the descending field; the hysteresis will be discussed below). Taking into account also the \( M(T) \) dependence for field applied along the c axis [see Fig. 2(a)], it can be concluded that \( Pr_{3}Ru_{4}Al_{12} \) is a ferromagnet. An increase in the magnetization beyond \( M_{s}^{c} \) in larger fields is most likely due to crossing of crystal-field levels [1]. The hard-magnetization direction lies in the basal plane of the hexagonal lattice. No magnetic anisotropy is observed within this plane since the magnetization displays identical behavior for fields applied along the a and b axes. No hysteresis was found for field applied along the basal-plane directions.

FIG. 3. Magnetization as a function of fields applied along the principal crystallographic directions of \( Pr_{3}Ru_{4}Al_{12} \) at 2 and 8 K. The inset shows the magnetization in fields up to 58 T at 2 K.
Although the basal plane is hard, there is a nonzero projection of the spontaneous magnetic moment, \( M_{s}^{ab} \approx 1 \mu_{B}/f.u. \) , onto the a and b directions at 2 K. With increasing temperature, \( M_{s}^{ab} \) decreases and is zero at 8 K. In pulsed magnetic fields up to 58 T, the magnetization increases continuously for all field orientations (inset in Fig. 3). The large magnetic anisotropy between the c axis and the basal plane persists up to the highest applied field.
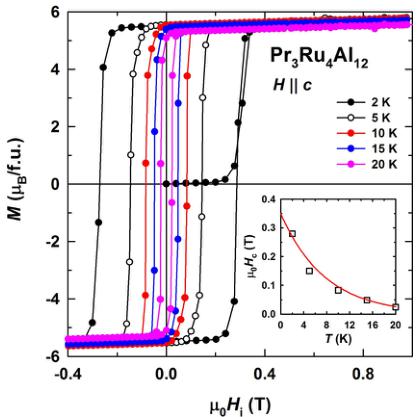
Since \( Pr_{3}Ru_{4}Al_{12} \) is a strongly anisotropic ferromagnet, it exhibits a pronounced magnetic hysteresis (Fig. 4). The hysteresis loops at low temperatures have a shape close to rectangular. At 2 K, when the field is applied to a demagnetized (zero-field cooled) sample, the initial susceptibility is low as the

FIG. 4. Hysteresis loops for field applied along the c axis of \( Pr_{3}Ru_{4}Al_{12} \) between 2 and 20 K. The inset shows the temperature dependence of the coercivity, where the solid line is a fit explained in the text.
domain walls are frozen. They begin to move at the activation field equal to the sample's coercivity \( H_{c} \) . At 2 K, \( \mu_{0}H_{c} \approx 0.3 \) T. Above the activation field, the sample is in a single-domain state. As the crystal is remagnetized over a complete hysteresis cycle, the activation field stays equal to that of the demagnetized sample. This behavior reflects that the main mechanism of the magnetic hysteresis is domain-wall motion. The coercive field decreases with temperature exponentially, \( \mu_{0}H_{c}(T) = A \exp(-BT) \) , where A = 0.35 T and \( B = 0.13 K^{-1} \) (inset in Fig. 4). The steep temperature dependence of the coercive field suggests that the hysteresis is due to the large coercivity of narrow domain walls, which is appropriate for ferromagnets with large magnetic anisotropy [45,46].
It follows from our data that the ferromagnetic order of \( Pr_{3}Ru_{4}Al_{12} \) displays pronounced changes with temperature. Between \( T_{C} \) and \( T_{sr} \) , the magnetic moments are aligned along the c axis. Below \( T_{sr} \) , a nonzero projection of \( M_{s} \) onto the basal plane points to a deviation of the magnetic moments from the c axis. In order to determine the magnetic structures of both phases and obtain information on the origin of the phase transition at \( T_{sr} \) , we performed a single-crystal neutron-diffraction study.
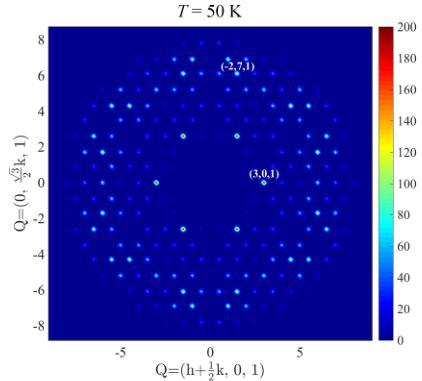
Figure 5 shows neutron-scattering intensity maps for the \( (hk1) \) planes of the \( Pr_{3}Ru_{4}Al_{12} \) single crystal as measured at 50, 10, and 2 K. A refinement of the neutron-diffraction intensities recorded at 50 K (Fig. 5, top panel) revealed that the structure at this temperature is consistent with the \( P6_{3}/mmc \) space group and with our single-crystal x-ray data. Missing reflections are caused by weak nuclear structure factors, and this is mostly due to the small size of the single crystal available for the neutron-diffraction experiments. The final refinement factors for the nuclear structure are R = 5.5% and wR = 7% (Table III).
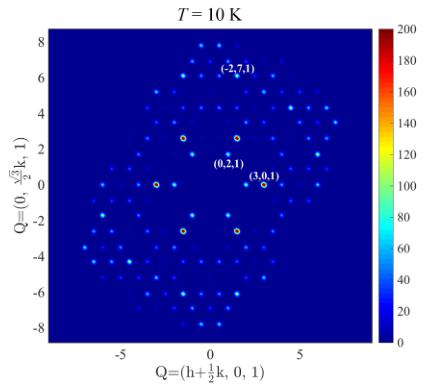
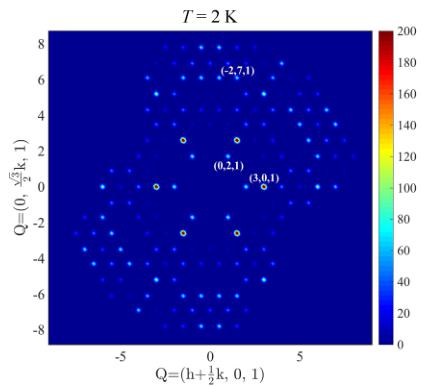
When cooling the crystal to 10 K (i.e., below \( T_{C} \) ), magnetic scattering intensity is observed at lattice positions corresponding to the primitive hexagonal \( P6_{3}/mmc \) lattice (Fig. 5, middle panel). Therefore, the magnetic structure at this temperature is described by a magnetic propagation vector k = 0. The same conclusion applies to the data collected at 2 K (Fig. 5, bottom panel); that is, the magnetic and crystallographic unit cells coincide, as expected for the magnetic phase transitions at 39 and 7 K and in agreement with the macroscopic data presented above. The absence of extra magnetic reflections was also confirmed by the mentioned Laue patterns taken at 2 and 10 K.
To describe a magnetic structure, one has to consider the differential cross section for elastic magnetic scattering (unpolarized beam), which can be written as
\[ \frac{d\sigma}{d\Omega}=N\frac{(2\pi)^{3}}{V}\left(\frac{\gamma r_{0}g}{2}\right)^{2}S(\underline{Q}) \quad (1) \]
and
\[ S(\underline{Q})=\left|\sum_{j}f(\underline{Q})|\hat{\underline{Q}}\times\underline{\mu}_{j}\times\hat{\underline{Q}}|e^{-W_{j}}e^{i\underline{Q}\underline{R}_{j}}\right|^{2}, \quad (2) \]
where N and V are the number and volume of the magnetic unit cells, respectively, \( \gamma \) is the gyromagnetic ratio, \( r_{0} \) is the classical radius of the electron, and g is the g factor of the electron. The structure factor \( S(\underline{Q}) \) depends on the



FIG. 5. Integrated intensities in the \( (hk1) \) planes of a \( Pr_{3}Ru_{4}Al_{12} \) single crystal from neutron diffraction taken at 50, 10, and 2 K (represented in orthogonal axes).
magnetic form factor \( f(\mathbf{Q}) \) , and the sum runs over all j magnetic atoms in the magnetic unit cell, located at the position \( R_{j} \) , having a Debye-Waller factor \( W_{j} \) and ordered moment \( \mu_{j} \) . More precisely, the term \( [\hat{Q} \times \mu_{j} \times \hat{Q}]e^{iQ R_{j}} \) in Eq. (2) expresses that only the component perpendicular to the scattering vector Q (as \( \hat{Q} = Q/|Q| \) ) contributes to the magnetic Bragg intensity. This helps to define the direction of the magnetic moments in certain magnetic systems. A full characterization of \( S(\mathbf{Q}) \) is needed for a complete solution of a magnetic structure and takes into account twinning and formation of magnetic domains.
The search for possible magnetic structures of \( Pr_{3}Ru_{4}Al_{12} \) was carried out for the data sets collected at 10 and 2 K using a symmetry approach and supported by the macroscopic data. As a starting point, it was assumed that only the Pr atoms carry a magnetic moment ordered at least for some of the possible sites. Under these conditions, there are eight maximal subgroups of \( P6_{3}/mmc1' \) which are compatible with the propagation vector k = 0. From these Shubnikov groups, six are hexagonal, and two are orthorhombic. A reasonable solution for the magnetic structure of \( Pr_{3}Ru_{4}Al_{12} \) at 10 K within these maximal magnetic space groups could not be found. For the hexagonal groups, the symmetry conditions allow only one position for the Pr atoms in the unit cell in which the magnetic moments are oriented along c. This leads to a total magnetic moment of around \( 7\mu_{B}/f.u. \) , which is not in accordance with the magnetization measurements [see Fig. 2(a)]. For both orthorhombic space groups, the Pr position is split into two distinct ones. However, the problem of nonphysical magnetic moments persists, as it is symmetry forbidden that both atoms carry ordered magnetic moments. Thus, the spin configuration of \( Pr_{3}Ru_{4}Al_{12} \) breaks the maximal symmetry and has to be found in the subgroups with lower magnetic symmetry.
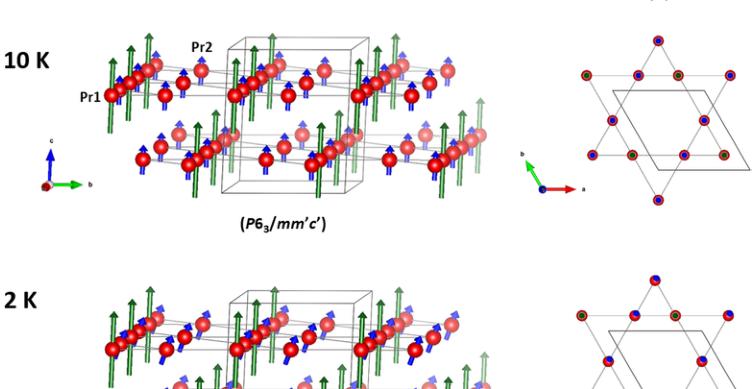
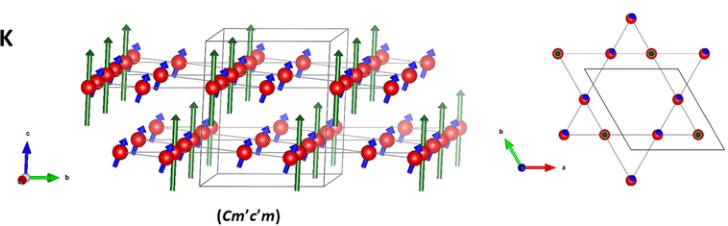
A search for a magnetic model of \( Pr_{3}Ru_{4}Al_{12} \) at \( 10~K \) started by considering the orthorhombic Shubnikov subgroups. The best solution was indeed found in the subgroup \( Cm^{\prime}c^{\prime}m \) for which the two Pr positions (4c for Pr1 and 8g for Pr2) carry magnetic moments oriented along c [i.e., having the form \( (0,0,m_{c}) \) , where \( m_{c} \) is the moment component along c] in a collinear configuration (Fig. 6 and Table III). Nevertheless, the moments are not of equal magnitude: the magnetic moments were refined as \( m_{c}(\mathrm{Pr1}) = 3.1(3)\mu_{\mathrm{B}} \) and \( m_{c}(\mathrm{Pr2}) = 1.4(2)\mu_{\mathrm{B}} \) . Consequently, the total magnetization is about \( 5.9~\mu_{B}/f.u. \) , in good agreement with the bulk-magnetization measurements (Fig. 2). The details of the symmetry constraints considered and the final refinement factors are given in Table III.
An unequal arrangement of moments was found previously in the magnetic structure of \( Nd_{3}Ru_{4}Al_{12} \) at 2 K [30]. Yet the atom at the position 8g has a larger spin component than the atom at the position 4c in the case of Pr, and the opposite was found for Nd. Furthermore, all the reasoning concerning the reflection intensities and the absence of ordering within the Ru sublattice that was employed previously for the determination of the magnetic structure of \( Nd_{3}Ru_{4}Al_{12} \) at 2 K is valid here as well for \( Pr_{3}Ru_{4}Al_{12} \) at 10K. That is, (i) the reflections (hkl) with \( l = 2n + 1 \) (n is an integer) show increased scattering intensity when compared to 50 K, for which possible Ru moments oriented along c (Ru1) or perpendicular to c (Ru2) do not contribute; (ii) a different spin amplitude is needed to explain the differences between the observed and calculated structure factors for the reflections of the types \( (h - 2h l) \) , \( (hhl) \) , and \( (-2kkl) \) , in addition to the macroscopic magnetization results; and (iii) the absence of all magnetic reflections of the type (00l).
TABLE III. Results from the refinement of the single-crystal neutron-diffraction data of \( Pr_{3}Ru_{4}Al_{12} \) collected at 50, 10, and 2 K. For each Shubnikov group, the transformation to the standard setting is indicated in the parent set basis \( (a_{\mathrm{H}}, b_{\mathrm{H}}, \mathrm{and} c_{\mathrm{H}} \) are the lattice parameters of the hexagonal unit cell). The component of the magnetic moment along the lattice direction i is \( m_{i} \) ; the total magnetic moments in the basal plane and along the c axis are \( M_{ab} \) and \( M_{c} \) , respectively; and refinement factors are R and wR. Errors refer to estimated standard deviations.
| Temperature (K) | |||
| 50 | 10 | 2 | |
| Space group | \( P6_{3}/mmc \) | \( Cm'c'm \) | \( C2'/c' \) |
| Transformation to the standard setting | \( (a_{\mathrm{H}}, a_{\mathrm{H}} + 2b_{\mathrm{H}}, c_{\mathrm{H}}; 0, 0, 0) \) | \( (a_{\mathrm{H}} + b_{\mathrm{H}}, -a_{\mathrm{H}} + b_{\mathrm{H}}, c_{\mathrm{H}}; 0, 0, 0) \)$ | |
| Label | Pr1 | Pr1 / Pr2 | Pr1 / Pr2 |
| Multiplicity | 6 | 2 / 4 | 2 / 4 |
| Constraints on \( m_{i} \) | |||
| Symmetry | 0, 0, \( m_{c} \) / 0, 0, \( m_{c} \) | \( m_{a}, m_{a}, m_{c} / m_{a}, m_{b}, m_{c} \) | |
| Other | \( m_{a} = m_{b} \) | ||
| \( m_{a} \) ( \( \mu_{\mathrm{B}} \) ) | 0 / 0.5(2) | ||
| \( m_{c} \) ( \( \mu_{\mathrm{B}} \) ) | 3.1(3) / 1.4(2) | 3.2(3) / 1.3(2) | |
| \( M_{ab} \) ( \( \mu_{\mathrm{B}} \) /f.u.) | 1.0(4) | ||
| \( M_{c} \) ( \( \mu_{\mathrm{B}} \) /f.u.) | 5.9(7) | 5.8(7) | |
| Refinement factors: \( R \) , \( wR \) (%) | 5.5, 7.0 | ||
(Fig. 5) indicates that the main spin component of the Pr atoms is indeed oriented along the c axis.
As the temperature is lowered to 2 K, there are no new reflections in our neutron data or any relevant change in the intensity maps when compared to 10 K (Fig. 5, middle and bottom panels). This is not particularly surprising taking into account that the transition at 7 K is not a change in the type of magnetic order, but rather a tilting of the magnetic moments without a change in the k = 0 propagation vector. Furthermore, the component of the magnetic moment projecting into the basal plane is very small [estimated as \( \approx 1 \mu_{B}/f.u. \) in a field of 0.1 T; see Fig. 2(a)], while its main projection remains along c and seems not to change much between 2 and 10 K. To better resolve the differences between the two configurations one has to rather use other techniques such as polarized neutron diffraction and x-ray magnetic scattering. However, as the moment configuration at 10 K is known and using group-subgroup relations and symmetry reasoning, a possible solution for the magnetic structure of \( Pr_{3}Ru_{4}Al_{12} \) at 2 K is presented here.
As described above, the magnetic model of \( Pr_{3}Ru_{4}Al_{12} \) at 10 K could not be found within the spin configurations allowed by the maximal space groups of the parent space group for
(a)

(b)

FIG. 6. Magnetic structures of \( Pr_{3}Ru_{4}Al_{12} \) at 1 and 2 K represented in the parent hexagonal unit cell (dark gray lines). Only the Pr atoms are represented (red spheres). (a) At 10 K the magnetic structure is collinear, with Pr1 having a larger moment (green vector), whereas Pr2 develops a smaller moment (blue vector), which is tilted towards the basal plane at 2 K. (b) Projection of the magnetic moments in one kagome unit onto the basal plane. (The corresponding transformation from the hexagonal basis to the standard setting is given in Table III.)

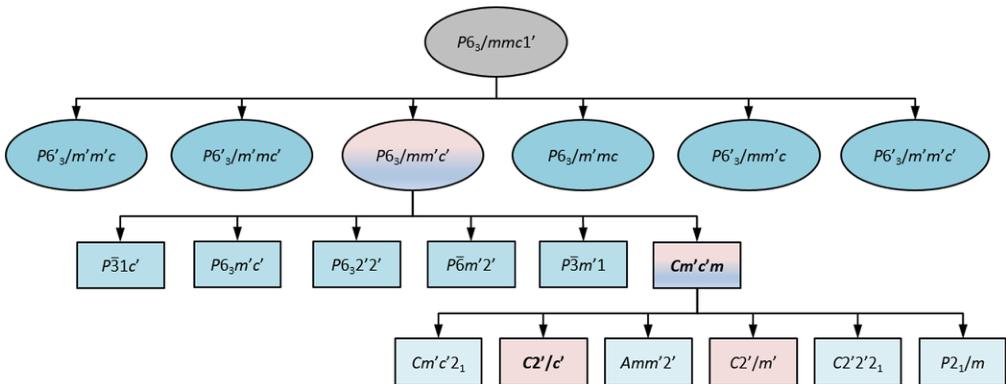
FIG. 7. Hierarchy of the group-subgroup relations descending from the paramagnetic phase with space group \( P6_{3}/mmc1' \) for a magnetic ordering with the propagation vector k=0. The elliptical frames indicate the k-maximal magnetic space groups. Only subgroups of the \( P6_{3}/mmc' \) and of \( Cm'c'm \) magnetic space groups are shown in the third and fourth rows, respectively. The groups tested at 2 and 10 K are indicated with a different color (bicolor if tested at both temperatures and pink if tested only at 2 K). The groups that best describe the magnetic configuration at each temperature are emphasized in bold.
k = 0. The ferromagnetic order breaks the hexagonal paramagnetic symmetry of \( Pr_{3}Ru_{4}Al_{12} \) , lowering it to orthorhombic by imposing three equivalent, nontrivial, twinned magnetic configurations. In general, the symmetry reduction caused by magnetic ordering tends to be minimal. Furthermore, as the group-subgroup relations are kept and the k-maximal magnetic groups do not fit the experimental data at 10 K, to derive the magnetic structure of \( Pr_{3}Ru_{4}Al_{12} \) at 2 K we first examined the branch with hexagonal and trigonal subgroups of \( P6_{3}/mmc' \) (that is, the magnetic space groups at the same level as \( Cm'c'm \) ; Fig. 7) that allow tilting of the Pr magnetic moments towards the basal plane. None of the moment configurations given by the symmetry operations of any of these space groups satisfies the macroscopic data at this temperature. Thus, in the following step we restricted the search to subgroups of the \( Cm'c'm \) magnetic space group.
Possible symmetries of the magnetic ordering of \( Pr_{3}Ru_{4}Al_{12} \) descending from the \( Cm'c'm \) Shubnikov group consistent with the propagation vector were first computed by the tool K-SUGROUPSMAG [47], and the resulting spin models were then inspected using MVISUALIZE [47], both tools from the Bilbao Crystallographic Server. Within the set of subgroups of \( Cm'c'm \) shown in Fig. 7, only the magnetic groups \( C2'/m' \) and \( C2'/c' \) allow spin tilting projecting ferromagnetic components in the basal plane. Furthermore, only the symmetry operations of the latter subgroup are compatible with the absence of magnetic anisotropy in the basal plane. Thus, the magnetic structure of \( Pr_{3}Ru_{4}Al_{12} \) 2 K was refined in the Shubnikov space group \( C2'/c' \) (Fig. 6). In this model, Pr at the 6h position (in the parent setting) is split in two independent magnetic sites, Pr1 (4e) and Pr2 (8f), due to the symmetry reduction from hexagonal to monoclinic. For Pr1 the spin configuration assumes the form \( (m_{a}, m_{a}, m_{c}) \) , whereas the spin components of Pr2 have the general form \( (m_{a}, m_{b}, m_{c}) \) , where \( m_{i} \) is the component of the moment along the lattice direction i. In a first refinement attempt all parameters were kept free, but this led to unphysical magnetic moments and very large errors in the spin components lying in the basal plane. Then, as it is known that there is a small component in the (ab) plane and that there is no magnetic anisotropy in this plane, the in-plane spin components of Pr2 were forced to be equal, that is \( m_{a}(\mathrm{Pr2}) = m_{b}(\mathrm{Pr2}) \) . Furthermore, the unphysical moments and very large errors found in the refinement of \( m_{a}(\mathrm{Pr1}) \) indicate that this component is very small at 2 K and probably does not contribute to the magnetic component found in the basal plane in the bulk magnetization measurements. Consequently, the resulting magnetic structure is noncollinear. The Pr1 magnetic moment is fully developed to the value \( gJ\mu_{B} = 3.2 \mu_{B} \) oriented along c, whereas the Pr2 magnetic moment is tilted towards the basal plane, making an angle of \( 22^{\circ} \) with the c axis. Thus, each Pr2 moment makes a projection of \( \approx 0.5 \mu_{B} \) onto the basal plane, which leads to a spontaneous magnetic moment of about \( 1 \mu_{B}/f.u. \) in the (ab) plane. This in good agreement with our magnetization data. Further details of the refinement are listed in Table III. A comparison with other models considered can be found in the Supplemental Material [48].
For the subgroup \( C2^{\prime}/c^{\prime} \) there are no extra systematic magnetic extinctions. Nevertheless, the prevailing direction of the magnetic moments dictates additional forms for the magnetic structure factors, particularly for atoms located at special positions. In this case, the tilting of the magnetic moments towards the basal plane can add magnetic scattering intensity to reflections of the type \( (hh\ell) \) with h = 1, 2 and l = 2. In fact, for the reflection (222) the calculated and observed (integrated) magnetic scattering intensities (in arbitrary units) are 410(80) and 620(145), respectively, in good agreement with the existence of a magnetic component in the basal plane at 2 K. Nevertheless, one has to keep in mind that there are six nontrivial twinned configurations (as the group-subgroup index is 12) which superimpose in the diffraction pattern, hampering the observation of these rules.
In \( Pr_{3}Ru_{4}Al_{12} \) , the onset of ferromagnetic order and the tilting of the magnetic moments towards the basal plane introduce two successive symmetry reductions compatible with a first orthorhombic distortion and a second monoclinic distortion of the lattice (compared to the hexagonal paramagnetic lattice). These distortions could, in principle, be experimentally observed if the magnetostructural coupling is strong enough. In the present work, the lattice distortions were not carefully explored, but the diffraction patterns and the final refinement factors obtained (Table III) are a good indication that, if such a coupling exists in the single crystal, its effect is rather weak or below the detection limits of the current techniques.
In an earlier work it was suggested that the Ru atoms in \( Dy_{3}Ru_{4}Al_{12} \) participate in exchange interactions and might even carry ordered magnetic moments [31]. Additionally, even the \( La_{3}Ru_{4}Al_{12} \) compound with nonmagnetic La shows anomalies in the magnetization and electrical resistivity at 6 K [29], which might point to a magnetic ordering of the Ru moments. In our analysis of the neutron data, we tried to refine the Ru magnetic moments. This led to substantially worse refinement factors (see Table II of the Supplemental Material [48]). We may conclude that the Ru magnetic moments in \( Pr_{3}Ru_{4}Al_{12} \) , if any, are below the detection limit of our neutron-diffraction study.
IV. DISCUSSION AND CONCLUSION
Next, we discuss the possible origin of the observed magnetic structures. The magnetism of rare-earth-based intermetallic compounds can be described in terms of exchange interactions and magnetocrystalline anisotropy. The topology of the crystal structure of \( Pr_{3}Ru_{4}Al_{12} \) might lead to unequal exchange and crystal-electric-field (CEF) interactions for different \( Pr^{3+} \) ions.
It is useful to compare \( Pr_{3}Ru_{4}Al_{12} \) with its closest analog, \( Nd_{3}Ru_{4}Al_{12} \) [30]. Although \( Pr^{3+} \) and \( Nd^{3+} \) ions are different in terms of the spin and the shape of the aspherical 4f charge clouds [49], two similarities are obvious: (i) both compounds are ferromagnets with \( T_{C} = 39 \) K, and (ii) their magnetic moments are partly quenched and aligned along the c axis, at least in the high-temperature range of the magnetic ordering. The main difference is the presence of an additional phase transition in \( Pr_{3}Ru_{4}Al_{12} \) at \( T_{sf} \) .
A CEF might quench the orbital magnetic moment and, due to the strong spin-orbit interaction, also the spin magnetic moment of Pr. As the splitting of the Pr positions occurs on a kagome lattice, we ascribe the inequivalence of the Pr1 and Pr2 sites to a moment instability due to unequal exchange interactions in the presence of the CEF. Since the exchange field of Ruderman-Kittel-Kasuya-Yosida (RKKY) type acting on the Pr ions is modulated, some sites are subject to a large exchange field leading to the full development of the Pr magnetic moments, and some are subject to a weak exchange field, keeping the moments low.
The non-Kramers character of the \( Pr^{3+} \) ion implies a splitting of the J = 4 ground-state multiplet into a singlet and four doublets by an axial CEF. For both Pr sites in \( Pr_{3}Ru_{4}Al_{12} \) , the exchange interactions are strong enough to induce magnetic order in the system. The energy scale of the exchange is given by \( T_{C} = 39 \) K. For the Pr1 atoms, all CEF levels are expected to be populated appreciably as these atoms carry a fully developed magnetic moment. Therefore, the overall CEF splitting is less than \( T_{C} \) . The Pr2 magnetic moments are situated in a weaker exchange field due to the competing exchange interactions. This leads to a more preferential population of the lower CEF levels; thus, the Pr2 magnetic moment is partly quenched to \( 1.4 \mu_{B} \) .
For comparison, geometric frustration affects the magnetic structure of the antiferromagnet \( TbNiAl \) ( \( T_{N} = 47 \) K) in a similar way [50,51]. In the high-temperature range of the magnetically ordered state, \( 23\ K < T < T_{N} \) , one crystallographic position of Tb is split into three magnetic sites. At 28 K, the atoms at two sites carry the same magnetic moment, \( 7.9\ \mu_{B} \) , while the moment at the third site is strongly reduced to \( 1.2\ \mu_{B} \) . A similar situation is observed for the isostructural antiferromagnet CePdAl, for which one third of the Ce magnetic moments are reduced to zero below \( T_{N} = 2.9\ K \) [51,52]. Finally, another intermetallic compound, \( TbRu_{2}Ge_{2} \) , also displays magnetic structures characterized by one or several Tb sites with zero magnetic moment, even in applied magnetic field [53,54].
For \( Pr_{3}Ru_{4}Al_{12} \) , we observe different orientations of the Pr1 and Pr2 magnetic moments. This can be explained by considering different local magnetic anisotropies of these atoms. As the magnetocrystalline anisotropy arises due to the electrostatic interaction between the 4f charge cloud and the CEF, the CEF should be different for the two magnetic sites, e.g., due to a local distortion. Probably, there is no such distortion in \( Nd_{3}Ru_{4}Al_{12} \) , resulting in the absence of a spin-reorientation transition [30].
For \( Pr_{3}Ru_{4}Al_{12} \) ,the anisotropy of the Pr1 site is uniaxial. For Pr2, there are competing contributions to the magnetic anisotropy, most likely due to the presence of higher-order terms in the anisotropy energy. With increasing temperature from the ground state, their contribution usually falls off more rapidly than the lower-order contribution [55,56]. We expect that the higher-order terms tend to zero around \( T_{sf} \) and the uniaxial term will become the dominant contribution to the anisotropy above \( T_{sf} \) , where the magnetic anisotropy of the Pr2 site is uniaxial, similar to Pr1.
To conclude, in the present work we have shown that \( Pr_{3}Ru_{4}Al_{12} \) is a strongly anisotropic ferromagnet with unusual magnetic structures. At elevated temperatures, the crystallographic position of the Pr atoms splits in two, carrying different magnetic moments aligned along the c axis. A spin-reorientation phase transition is observed at 7 K to a noncollinear low-temperature magnetic structure. The smaller moments rotate towards the basal plane, whereas the larger moments remain aligned along the c axis. We argue that this unusual behavior is due to an instability of the magnetic moments affected by unequal exchange interactions in the presence of the crystalline electric field.
ACKNOWLEDGMENTS
The crystallographic part was supported by Project No. 15-12653S of the Czech Science Foundation using instruments of the ASTRA laboratory established within the Operation program Prague Competitiveness, Project No. CZ.2.16/3.1.00/24510. The work was supported within the
program of Large Infrastructures for Research, Experimental Development and Innovation (Project No. LM2015050) and Project No. LTT17019 financed by the Ministry of Education, Youth and Sports, Czech Republic. Further support to this
[1] T. Johansson, B. Lebech, M. Nielsen, H. B. Møller, and A. R. Mackintosh, Phys. Rev. Lett. 25, 524 (1970).
[2] B. D. Rainford and J. G. Houmann, Phys. Rev. Lett. 26, 1254 (1971).
[3] J. G. Houmann, M. Chapellier, A. R. Mackintosh, P. Bak, Q. D. McMasters, and K. A. Gschneidner, Jr., Phys. Rev. Lett. 34, 587 (1975).
[4] J. G. Houmann, B. Lebech, A. R. Mackintosh, W. J. L. Buyers, O. D. McMasters, and K. A. Gschneider, Jr., Phys. B (Amsterdam, Neth.) 86–88, 1156 (1977).
[5] J. G. Houmann, B. D. Rainford, J. Jensen, and A. R. Mackintosh, Phys. Rev. B 20, 1105 (1979).
[6] K. A. McEwen, G. J. Cock, L. W. Hoeland, and A. R. Mackintosh, Phys. Rev. Lett. 30, 287 (1973).
[7] K. A. McEwen, W. G. Stirling, and C. Vettier, Phys. Rev. Lett. 41, 343 (1978).
[8] P. E. Gregers-Hansen, M. Krusius, and G. R. Pickett, Phys. Rev. Lett. 29, 420 (1972).
[9] P. E. Lindelof, I. E. Miller, and G. R. Pickett, Phys. Rev. Lett. 35, 1297 (1975).
[10] M. Eriksen, C. M. Muirhead, and R. C. Young, Phys. B (Amsterdam, Neth.) 107, 67 (1981).
[11] H. B. Møller, J. Z. Jensen, M. Wulff, A. R. Mackintosh, O. D. McMasters, and K. A. Gschneidner, Jr. Phys. Rev. Lett. 49, 482 (1982).
[12] M. Eriksen, E. M. Forgan, C. M. Muirhead, and R. C. Young, J. Phys. F 13, 929 (1983).
[13] R. S. Craig, S. G. Sankar, N. Marzouk, V. U. S. Rao, W. E. Wallace, and E. Segal, J. Phys. Chem. Solids 33, 2267 (1972).
[14] K. Andres, E. Bucher, J. P. Maita, and A. S. Cooper, Phys. Rev. Lett. 28, 1652 (1972).
[15] K. Andres, E. Bucher, P. H. Schmidt, J. P. Maita, and S. Darack, Phys. Rev. B 11, 4364 (1975).
[16] E. W. Lee and F. Pouranian, Phys. Status Solidi A 33, 483 (1976).
[17] F. J. A. M. Greidanus, L. J. de Jongh, W. J. Huiskamp, A. Furrer, and K. H. J. Buschow, Phys. B (Amsterdam, Neth.) 115, 137 (1983).
[18] V. M. T. S. Barthem, D. Gignoux, A. Naït-Saada, D. Schmitt, and G. Creuzet, Phys. Rev. B 37, 1733 (1988).
[19] Z. Tie-song, J. Han-min, G. Guang-hua, H. Xiu-feng, and C. Hong, Phys. Rev. B 43, 8593 (1991).
[20] P. Javorsky, G. Schaudy, T. Holubar, and G. Hilscher, Solid State Commun. 91, 259 (1994).
[21] S. Kato, H. Kitazawa, H. Suzuki, and G. Kido, J. Phys. Soc. Jpn. 67, 2501 (1998).
[22] T. Onimaru, K. T. Matsumoto, Y. F. Inoue, K. Umeo, T. Sakakibara, Y. Karaki, M. Kubota, and T. Takabatake, Phys. Rev. Lett. 106, 177001 (2011).
[23] M. Tsujimoto, Y. Matsumoto, T. Tomita, A. Sakai, and S. Nakatsuji, Phys. Rev. Lett. 113, 267001 (2014).
research was given by the Materials Growth and Measurement Laboratory and Grant No. 16-03593S of the Czech Science Foundation. We acknowledge the support of HLD at HZDR, a member of the European Magnetic Field Laboratory (EMFL).
[24] Y. Shimura, M. Tsujimoto, B. Zeng, L. Balicas, A. Sakai, and S. Nakatsuji, Phys. Rev. B 91, 241102(R) (2015).
[25] R. E. Gladyshevskii, O. R. Strusievicz, K. Cenzual, and E. Parthé, Acta Crystallogr., Sect. B 49, 474 (1993).
[26] J. Niermann and W. Jeitschko, Z. Anorg. Allg. Chem. 628, 2549 (2002).
[27] N. G. Bukhan'ko, A. I. Tursina, S. V. Malyshev, A. V. Gribanov, Y. D. Seropegin, and O. I. Bodak, J. Alloys Compd. 367, 149 (2004).
[28] W. Ge, H. Ohta, C. Michioka, and K. Yoshimura, J. Phys. Conf. Ser. 344, 012023 (2012).
[29] W. Ge, C. Michioka, H. Ohta, and K. Yoshimura, Solid State Commun. 195, 1 (2014).
[30] D. I. Gorbunov, M. S. Henriques, A. V. Andreev, V. Eigner, A. Gukasov, X. Fabrèges, Y. Skourski, V. Petříček, and J. Wosnitza, Phys. Rev. B 93, 024407 (2016).
[31] D. I. Gorbunov, M. S. Henriques, A. Vandreev, A. Gukasov, V. Petříček, N. V. Baranov, Y. Skourski, V. Eigner, M. Paukov, J. Prokleška, and A. P. Gonçalves, Phys. Rev. B 90, 094405 (2014).
[32] S. Nakamura, S. Toyoshima, N. Kabeya, K. Katoh, T. Nojima, and A. Ochiai, JPS Conf. Proc. 3, 014004 (2014).
[33] S. Nakamura, S. Toyoshima, N. Kabeya, K. Katohn, T. Nojima, and A. Ochiai, Phys. Rev. B 91, 214426 (2015).
[34] D. I. Gorbunov, M. S. Henriques, A. Y. Andreev, Y. Skourski, and M. Dušek, J. Alloys Compd. 634, 115 (2015).
[35] M. S. Henriques, D. I. Gorbunov, D. Kriegner, M. Valiska, A. V. Andreev, and Z. Matěj, J. Magn. Magn. Mater. 400, 125 (2016).
[36] V. Chandragiri, K. K. Iyer, and E. V. Sampathkumaran, Intermetallics 76, 26 (2016).
[37] V. Chandragiri, K. K. Iyer, and E. V. Sampathkumaran, J. Phys. Condens. Matter 28, 286002 (2016).
[38] I. Ishii, K. Takezawa, H. Goto, S. Kamikawa, A. V. Andreev, D. I. Gorbunov, M. S. Henriques, and T. Suzuki, J. Phys. Conf. Ser. 807, 012002 (2017).
[39] Agilent Technologies, CRYSALIS PRO, version 1.171.37.31, Yarnton, UK.
[40] L. Palatinus and G. Chapuis, J. Appl. Crystallogr. 40, 786 (2007).
[41] V. Petříček, M. Dušek, and L. Palatinus, Z. Kristallogr. 229, 345 (2014).
[42] Y. Skourski, M. D. Kuz'min, K. P. Skokov, A. V. Andreev, and J. Wosnitza, Phys. Rev. B 83, 214420 (2011).
[43] B. Ouladdiaf, J. Archer, J. R. Allibon, P. Decapentrie, M.-H. Leme-Cailleau, J. Rodriguez-Carvajal, A. W. Hewat, S. York, D. Brau, and G. J. McIntyre, J. Appl. Crystallogr. 44, 392 (2011).
[44] A. Gukasov, A. Goujon, J.-L. Meuriot, Ch. Person, G. Exil, and G. Koskas, Phys. B (Amsterdam, Neth.) 397, 131 (2007).
[45] H. R. Hilzinger and H. Kronmüller, Phys. Status Solidi B 54, 593 (1972).
[46] B. Barbara, G. Fillion, D. Gignoux, and R. Lemaire, Solid State Commun. 10, 1149 (1972).
[47] J. M. Perez-Mato, S. V. Gallego, E. S. Tasci, L. Elcoro, G. de la Flor, and M. I. Aroyo, Annu. Rev. Mater. Res. 45, 1 (2015).
[48] See Supplemental Material at http://link.aps.org/supplemental/10.1103/PhysRevB.97.014431 for comparison of the different models considered to solve the magnetic structure of \( Pr_{3}Ru_{4}Al_{12} \) at 2 K.
[49] M. D. Kuz'min and A. M. Tishin, in Handbook of Magnetic Materials, edited by K. H. J. Buschow (Elsevier, Amsterdam, 2008), Vol. 17, p. 149.
[50] G. Ehlers and H. Maletta, Z. Phys. B 99, 145 (1996).
[51] A. Dönni, G. Ehlers, H. Maletta, P. Fischer, H. Kitazawa, and M. Zolliker, J. Phys. Condens. Matter 8, 11213 (1996).
[52] A. Oyamada, S. Maegawa, M. Nishiyama, H. Kitazawa, and Y. Isikawa, Phys. Rev. B 77, 064432 (2008).
[53] D. Gignoux and D. Schmitt, J. Alloys Compd. 326, 143 (2001).
[54] A. Garnier, D. Gignoux, D. Schmitt, and T. Shigeoka, Phys. Rev. B 57, 5235 (1998).
[55] C. Zener, Phys. Rev. 96, 1335 (1954).
[56] H. B. Callen and E. Callen, J. Phys. Chem. Solids. 27, 1271 (1966).