| Transition Temperature | 74 K |
|---|---|
| Experiment Temperature | 4.2 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | R-3 (#148) |
| Magnetic Space Group | P-1' (#2.6) |
| Magnetic Point Group | -1' (2.3.5) |
| Lattice Parameters | 6.38700 6.38700 19.99600 90.00 90.00 120.00 |
|---|---|
| DOI | 10.1016/0038-1098(81)90253-2 |
| Reference | A. Wiedenmann, J. Rossat-Mignod, A. Louisy, R. Brec and J. Rouxel, Solid State Communications (1981) 40 1067-1072. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Mn1 | Mn | 4.74 | 0.0 | 0.0 | 4.74 |
NEUTRON DIFFRACTION STUDY OF THE LAYERED COMPOUNDS MnPSe_{3} AND FePSe_{3}
A. Wiedenmann and J. Rossat-Mignod
Laboratoire de Diffraction Neutronique, Département de Recherche Fondamentale, Centre d'Etudes Nucléaires de Grenoble, 85 X, F-38041 Grenoble Cedex, France
and
A. Louisy, R. Brec and J. Rouxel
Laboratoire de Chimie des Solides, U.E.R. de Chimie, Université de Nantes, 44072 Nantes Cedex, France
(Received 11 August 1981 by E.F. Bertaut)
In the insulating compounds \( MnPSe_{3} \) (1) and \( FePSe_{3} \) (2) the divalent transition metal ions form planar honeycomb lattices. A neutron diffraction study revealed a collinear antiferromagnetic order below \( T_{N} = 74 \pm 2 \) K (1) and \( T_{N} = 119 \pm 1 \) K (2) with the corresponding wavevectors \( k = [0 \ 0 \ 0] \) (1) and \( k = [1/2 \ 0 \ 1/2] \) (2). In \( MnPSe_{3} \) the magnetic moments \( (m_{0} = 4.74 \mu_{B}) \) lie within the basal plane and in \( FePSe_{3} \) ( \( m_{0} = 4.9 \mu_{B} \) ) they are pointing along the c-axis. The collinear structures are determined by the dominating intralayer interactions between first ( \( J_{1} \) ), second ( \( J_{2} \) ) and third neighbours ( \( J_{3} \) ) which in \( MnPSe_{3} \) are all antiferromagnetic whereas in \( FePSe_{3} \) \( J_{1} \) is ferromagnetic and \( J_{2} \) and \( J_{3} \) are antiferromagnetic.
1. INTRODUCTION
THE INSULATING COMPOUNDS \( MnPSe_{3} \) and \( FePSe_{3} \) belong to the layered \( MPX_{3} \) family (M = first row transition metal, X = S, Se). The manganese and iron selenophosphates can be considered as two-dimensional \( MSe_{2} \) layers of the \( CdJ_{2} \) type in which one third of the cations have been substituted by \( (P_{2}) \) pairs. The stacking of the \( SeM_{2/3}(P_{2})_{1/3}Se \) slabs give rise to Van der Waals' gaps, and it has been shown [1-5] that ions or molecules can easily be intercalated in the voids of the gap.
We report, in this article, on a neutron diffraction study of the magnetic structure and of the magnetic phase transition of \( MnPSe_{3} \) and \( FePSe_{3} \).
2. EXPERIMENTAL
Polycrystalline samples of \( MPSe_{3} \) compounds were obtained from the elements using previously described methods [6, 7]. X-ray powder spectra which were recorded in order to check the crystallographic purity, have shown that the samples are in a single phase.
The neutron diffraction experiments were carried out with powdered samples on the 800-cell multidetector diffractometer, installed at the SILOE-reactor of the Nuclear Research Center at Grenoble. Neutron diffraction pattern were recorded using monochromatic neutrons at 2.475 Å wavelength, at various temperatures between 4.2 and 170 K in a range of Bragg-angles \( 3^{\circ} < \theta < 43^{\circ} \) (resolution \( \Delta\theta = 0.05^{\circ} \) ).
3. CRYSTALLOGRAPHIC STRUCTURES
The observed reflections in the neutron diffraction pattern of both compounds in the paramagnetic region were indexed in the rhombohedral system respecting the extinction condition of the space group R3. The lattice parameters a and c of the hexagonal cell and the reduced atomic positions were refined by least-squares routines leading to satisfactory agreement between observed and calculated values of the peak positions and the integrated intensities (Tables 1 and 2) respectively. In the measured temperature range and in particular at the magnetic ordering temperature no change in the nuclear structure was observed but a thermal expansion of the lattice parameters (Table 3).
The position parameters of \( FePSe_{3} \) are in good agreement with X-ray data [8] and very similar values were found for \( MnPSe_{3} \) (Table 4). Structure calculations in a non-centrosymmetric space group R3, as it was proposed in [10], did not improve the refinements.
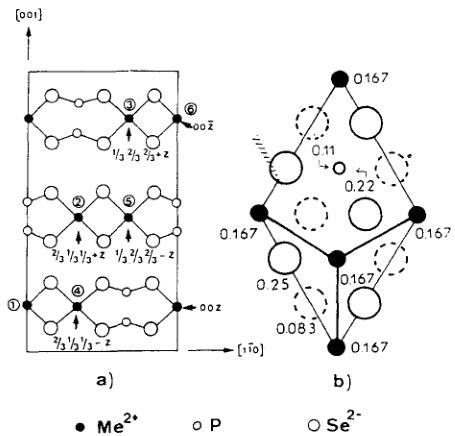
In the crystallographic structures (Fig. 1), hexagonal layers of selenium atoms are stacked along the c-axis in an AB-sequence. In every other slab of Se-atoms one third of the octahedral sites are occupied by \( P_{2} \) pairs and two thirds by the divalent 3d ions. Due to the special value of their position parameter z = 1/6, the metallic ions form a honeycomb lattice in the \( (001) \) planes, where the distances between the three first nearest
Table 1. Observed and calculated intensities of neutron diffraction powder spectra for MnPSe₃ (T = 100 K, centrosymmetric model R3: R = 2%)
| hkl | Intensity | [barn/cell] |
| Observed | Calculated | |
| 101 | 118.9 | 110.2 |
| 012 | 99.0 | 89.0 |
| 006 | ||
| 015 | 1066.5 | 1059.3 |
| 110 | ||
| 113 | 2331.5 | 2297.5 |
| 113 | ||
| 021 | 114.2 | 119.6 |
| 202 | 63.1 | 71.3 |
| 024 | 27.6 | 22.6 |
| 116 | ||
| 116 | 191.6 | 240.9 |
| 025 | ||
| 018 | ||
| 009 | 26.6 | 35.6 |
| 122 | 191.8 | 158.9 |
| 212 | ||
| 214 | 41.3 | 36.7 |
| 124 | ||
| 300 | ||
| 119 | 4534.6 | 4521.7 |
| 119 |
neighbours (n.n.) are about 3.6 Å the six second n.n. of the order of 6.3 Å and the three third n.n. about 7.3 Å. The symmetry of the \( Me^{2+} \) ion site in reality is trigonal due to a slight distortion of the selenium octahedra along the c-axis. Neighbouring \( Me^{2+} \) -layers are stacked in an ABC-sequence and separated by \( r' = 6.7 \) Å.
From this structure the intralayer exchange interactions are expected to be stronger than the inter-layer coupling, which should lead to a quasi-bidimensional behaviour.
4. MAGNETIC STRUCTURE
For \( MnPSe_{3} \) the neutron diffraction pattern shows an increase of the intensities of some reflections below \( T_{N} = 74 \pm 2 \) K but no additional peaks. The wavevector of the magnetic order is thus \( k = [0\ 0\ 0] \) . Thus the magnetic cell is the same as the crystallographic one and the group symmetry remains unchanged at this transition.
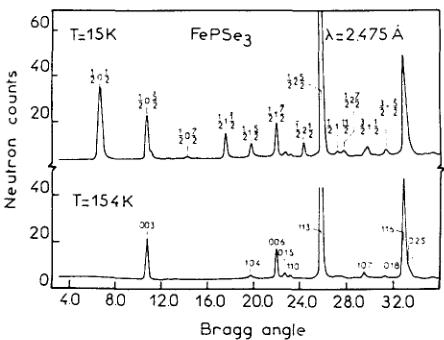
In the case of \( FePSe_{3} \) many superlattice peaks appear below \( T_{N}=119\pm1K \) (Fig. 2). They are indexed with a vector \( k=[1/2\ 0\ 1/2] \) which is a symmetry point
Table 2. Observed and calculated intensities of neutron diffraction powder spectra for FePSe₃ (T = 154 K, centrosymmetric model R³: R = 11%)
| hkl | Intensity | [barn/cell |
| Observed | Calculated | |
| 003 | 94.0 | 90.5 |
| 104 | 21.8 | 22.6 |
| 101 | 0 | 0 |
| 012 | 0 | 0 |
| 006 | ||
| 015 | 276.4 | 298.1 |
| 110 | ||
| 113 | 3194.7 | 3073.0 |
| 113 | 100.0 | 124.0 |
| 107 | 1789.6 | 1869.5 |
| 116 | ||
| 116 | ||
| 025 | 350.0 | 309.0 |
| 018 | ||
| 009 | ~40 | 55.8 |
| 122 | ~10 | 31.3 |
| 212 | ||
| 214 | ~60 | 73.6 |
| 124 |

Fig. 1. Rhombohedral structure of the \( MnPSe_{3} \) phases. (a) in the (110) plane; (b) in the (001) plane: numbers represent the position along the c-direction in reduced unit.
Table 3. Hexagonal cell parameters of \( MnPSe_{3} \) and \( FePSe_{3} \) determined from neutron diffraction data at different temperatures
| MnPSe3 | FePSe3 | |||
| T | 100 K | 4.2 K | 154 K | 15 K |
| a [Å] | 6.394 (2) | 6.387 (2) | 6.273 (3) | 6.262 (3) |
| c [Å] | 20.019 (6) | 19.996 (6) | 19.812 (6) | 19.805 (5) |
Table 4. Atomic positions in MnPSe_{3} and FePSe_{3} (R\bar{3}) (between brackets values obtained from X-ray analysis)
| Atom | Site | x | y | z |
| Mn | 6c | 0.0 | 0.0 | 0.1661 |
| P | 6c | 0.0 | 0.0 | 0.4443 |
| Se | 18f | 0.3305 | -0.0016 | 0.0818 |
| Fe | 6c | 0.0 | 0.0 | 0.1665 (0.1671) |
| P | 6c | 0.0 | 0.0. | 0.4486 (0.4455) |
| Se | 18f | 0.3282 (0.3314) | 0.0073 (0.0059) | 0.0801 (0.0828) |

Fig. 2. Neutron diffraction pattern of FePSe₃ in the paramagnetic and in the ordered phase. Magnetic reflections are indexed by k = [1/2 0 1/2].
of the Brillouin zone. The magnetic cell is doubled along the a- and c-directions as compared to the crystallographic cell and the symmetry is then lowered from rhombohedral to triclinic. The transition temperatures \( T_{N} \) deduced from the thermal variation of the magnetic intensities (Fig. 4) are in good agreement with the results of \( {}^{31}P-NMR \) measurements \( [T_{N}(\mathrm{MnPSe}_{3}) \) : 74 K; \( T(\mathrm{FePSe}_{3}) \) : 112 K] [9] and with previous susceptibility measurements.
The wavevectors \( k = [0\ 0\ 0] \) and \( k = [1/2\ 0\ 1/2] \) lead to collinear magnetic structures, where \( m_{0} \) is the common moment direction. The intensity of a magnetic reflection defined by the scattering vector \( h = H + k \) , where H is a Brillouin zone, is the given by: \( I(\mathbf{h}) = (0.27)^{2}f_{m}^{2}(\mathbf{h})\sum\sin^{2}\alpha(\mathbf{h})|\mathbf{F}_{m}^{\prime}(\mathbf{h})|^{2}. \)
\(f_{m}\) is the magnetic form factor, \(\alpha\) the angle between the scattering vector \(\mathbf{h}\) and the magnetic moment direction. \(F_{m}\) is the geometrical structure factor
\[ \mathbf{F}_{m}^{\prime}(\mathbf{h})=\sum\mathbf{m}_{j}\exp\left\{2\pi i(\mathbf{h}\mathbf{R}_{j})\right\}. \quad (2) \]
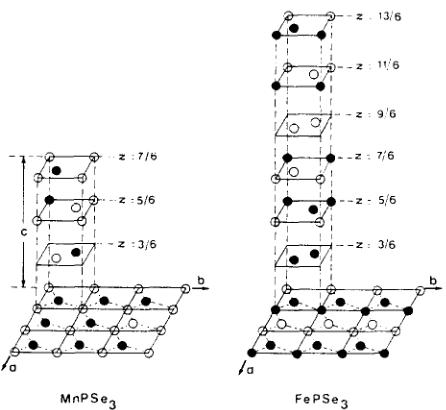
In both compounds the planar honeycomb metal–ion lattice can be generated by two hexagonal Bravais lattices: the first one contains the atoms in (0 0 z), (2/3 1/3 1/3 + z) and (1/3 2/3 2/3 + z), the second one contains the atoms in (0 0 z), (2/3 1/3 1/3 − z) and (1/3 2/3 2/3 − z). The magnetic structure factors have been calculated for the two Bravais lattices in (0 0 z) and (2/3 1/3 1/3 − z) (numbers 1 and 4 in Fig. 1) which belong to the same (0 0 1) plane.
The corresponding expressions for ferro- and antiferromagnetic coupling of the two lattices are reported in Table 5. \( F_{m}^{\prime} \) depends only on the Miller indice l of the Brillouin zones and it shows systematic extinctions only in the case of an antiferromagnetic coupling between these two lattices.
For \( MnPSe_{3} \) all reflections with l = 3n (006, 110, 113, 116, 009, 300, 119) have no magnetic contribution so that ferromagnetic coupling must be excluded. For \( FePSe_{3} \) the systematic extinction of the reflections \( h = [hkl] + k \) with l = 3n + 1 implies in the same way an antiferromagnetic coupling of the considered Bravais lattices.
The array of the magnetic moments \( \mathbf{m}^{(1)}(\mathbf{R}_{\mathbf{n}}) \) and \( \mathbf{m}^{(2)}(\mathbf{R}_{\mathbf{n}}) \) can be deduced from the knowledge of the
Table 5. Magnetic structure factor calculated for MnPSe₃ and FePSe₃ for ferro- and antiferromagnetic coupling of the two Bravais lattices (0 0 z) and (2/3 1/3 1/3 - z) located at the same plane with z = 1/6
| Couplage | MnPSe3k = [000] | FePSe3k = [1/201/2] |
| m2 = m1 | F'm = 2m0cos2πlzfor l = 3n: F'm2 = 4m02l ≠ 3n: F'm2 = m02 | F'm = 2m0i sin 2π(l + 1/2)zfor l = 3n + 1: F'm2 = 4m02l ≠ 3n + 1: F'm2 = m02 |
| m2 = -m1 | F'm = 2m0i sin 2πlzfor l = 3n: F'm2 =0l ≠ 3n: F'm2 = 3m02 | F'm = 2m0 cos 2π(l + 1/2)zfor l = 3n + 0: F'm2 = 0l ≠ 3n + 1: F'm2 = 3m02 |
Table 6. Observed and calculated values of magnetic reflection intensities of MnPSe_{3} (T = 4.2 K; \( \phi \) is the angle between the moment direction and the c-axis)
| hkl | Intensities [bam/cell] | ||
| Observed | Calculated \( \phi = 70^{\circ} \) | \( \phi = 90^{\circ} \) | |
| 1 0 1 | 125.08 | 125.12 | 116.9 |
| 0 1 2 | 129.49 | 131.23 | 129.5 |
| 1 0 4 | 130.33 | 128.52 | 137.21 |
| 1 1 3 | 0 | 0 | 0 |
| 0 2 1 | 73.66 | 71.19 | 65.17 |
| 2 0 2 | 69.02 | 70.18 | 65.54 |
| 1 0 7 | 89.29 | 92.69 | 99.19 |
| 0 2 4 | 63.13 | 63.13 | 62.42 |
| 1 1 6 | 0 | 0 | 0 |
| 0 0 9 | 0 | 0 | 0 |
| 1 2 2 | 79.79 | 85.73 | 79.21 |
| 2 0 7 | 52.38 | 51.72 | 54.43 |
| 2 1 4 | 82.55 | 80.49 | 77.29 |
| 1 0 5 | 119.43 | 119.43 | 130.10 |
| 0 0 6 | 0 | 0 | 0 |
| 1 1 0 | 0 | 0 | 0 |
| m ⊥ c | R | 0.02 | 0.06 |
| |m0| |μB| | 4.70 | 4.74 | |
coupling between the two Bravais lattices and the rhombohedral translations \( R_{n} \) by:
\[ \begin{aligned}&\mathbf{m}^{(1,2)}(\mathbf{R}_{n})\;=\;\mathbf{m}_{0}^{(1,2)}\exp\left\{2\pi i\mathbf{k}\mathbf{R}_{n}\right\}\\&\mathbf{w i t h}\mathbf{m}_{0}^{(2)}=-\mathbf{m}_{0}^{(1)}.\\ \end{aligned} \quad (3) \]
For both compounds, the magnetic structure is represented in Fig. 3.
4.1. Direction of magnetic moments
The common direction of the magnetic moments can be obtained from the intensities of the magnetic reflections, which depend on the angle \( \alpha \) between h and \( m_{0} \) [see equation (1)].
In the case of MnPSe_{3} with k = [0 0 0] the value

Fig. 3. Magnetic structures of: MnPSe_{3}(k = [0 0 0], m ⊥ c) and FePSe_{3}(k = [1/2 0 1/2], m ⊥ c).
sin²α(h) can be replaced by the average ⟨sin²α⟩ over the equivalent ⟨hkl⟩ reflections of the R³ group:
\[ \langle\sin^{2}\alpha\rangle=1-\frac{\frac{1}{2}(h^{2}+k^{2}+hk)a^{*}\sin^{2}\phi+l^{2}c^{2*}\cos\phi}{|h^{2}|} \quad (4) \]
It depends on the angle \(\phi\) between the magnetic moment direction and the hexagonal \(c\)-axis. However from powder spectra it is impossible to determine the moment direction within the basal plane.
The magnetic reflection intensities calculated for a moment direction perpendicular to the c-axis (\(\phi = 90^{\circ}\)) lead to reliability factor \(R = 0.06\) and a moment value of \(4.74 \mu_{B}\) and 4 K. This result can be improved (\(R = 0.02\)) by a refinement of the angle \(\phi\), which leads to values of \(\phi = 70^{\circ}\) and of \(m_{0} = 4.70 \mu_{B}\). In Table 6 the observed intensities are compared with the calculated ones for both values of \(\phi\).
However, it should be noted that an angle \( \phi \) different from \( 90^{\circ} \) would result from a competition between a single ion anisotropy and a dipolar anisotropy.
Table 7. Observed and calculated positions and intensities of magnetic reflections of FePSe_{3} at 15 K
| \( h_{m} \) \( k_{m} \) \( l_{m} \) | Bragg angle | Intensities [barn/cell] | ||
| Observed | Calculated | Observed | Calculated | |
| 1/2 0 1/2 | 6.724 | 6.782 | 89.6 | 85.5 |
| 1/2 0 5/2 | 11.210 | 11.144 | 13.7 | 29.4 |
| 1/2 1 3/2 | — | 12.615 | 0.0 | 0.0 |
| 1/2 0 7/2 | 14.286 | 14.270 | 7.9 | 16.9 |
| 1/2 1 1/2 | 17.635 | 16.635 | 142.1 | 141.5 |
| 1/2 1 5/2 | 19.855 | 19.840 | 103.0 | 104.8 |
| 1/2 1 9/2 | — | 20.084 | 0.0 | 0.0 |
| 3/2 0 3/2 | — | 20.75 | 0.0 | 0.0 |
| 1/2 1 7/2 | 21.9a | 21.857 | 53.3 | 80.25 |
| 1/2 1 11/2 | 21.2 | 21.218 | ~0 | 3.5 |
| 1/2 2 1/2 | 24.38 | 24.321 | 111.5 | 110.9 |
| 1/2 0 13/2 | — | 24.94 | 0 | 3.5 |
| 1/2 2 5/2 | 26.0a | 26.062 | 95.0 | 103.6 |
| 3/2 0 9/2 | — | 26.26 | 0.0 | 0.0 |
| 1/2 1 11/2 | 27.2a | 27.192 | ||
| 1/2 2 7/2 | 27.73 | 27.725 | 200 | 118.7 |
| 1/2 1 13/2 | 30.4 | 30.372 | ~50 | |
| 3/2 1 5/2 | 31.37 | 31.363 | 96.7 | 75.6 |
| R | 0.08 | |||
| \( |m_{0}|\mu_{B} \) | 4.9 | |||
\( ^{a} \) Nuclear reflections superposed.

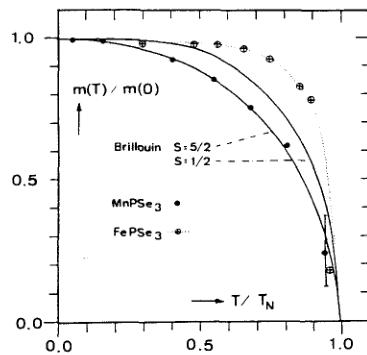
Fig. 4. Thermal variation of the reduced magnetic moments in \( MnPSe_{3} \) and \( FePSe_{3} \) determined from magnetic intensities. Full lines represent Brillouin functions for S = 5/2 and 1/2.
Furthermore \( \phi \) should vary with temperature. As no temperature dependent change in the intensity ratio of different reflections was experimentally observed, it seems reasonable to assume that the antiferromagnetic direction lies within the basal plane.
In the case of \( FePSe_{3} \) , where the symmetry of the ordered phase is lowered, the values of \( \sin^{2}\alpha(\mathbf{h}) \) must be calculated for each reflection. A satisfactory agreement of calculated and observed magnetic intensities is only achieved if moments are taken parallel to the c-axis. At 15 K, the refinement leads to a reliability factor of R = 0.08 (Table 7) with a magnetic moment value of \( 4.9 \mu_{B} \) . The high value of m might be due to spin-orbit coupling; the moment direction deduced from the neutron diffraction data is in agreement with a Mössbauer effect study [7].
In Fig. 4, we have reported the thermal variation of the reduced moment value \( m(T)/m(0) \) , measured from magnetic reflexion intensity changes, vs reduced temperature \( T/T_{N} \) , where \( m(0) \) is the value extrapolated at T = 0, and \( T_{N} \) is the Néel temperature.
It can be seen that the experimental data in the case of \( MnPSe_{3} \) is rather close to a Brillouin curve for S = 5/2. For \( FePSe_{3} \) , the observed variation has a more complex shape which departs from a Brillouin function calculated with S = 1/2. This behaviour may be due to a fairly strong Ising character of this phase and to important two-dimensional correlations.
5. DISCUSSION
The comparison between \( MnPSe_{3} \) and \( FePSe_{3} \( shows that, whereas all the \) Mn^{2+} \( ions are surrounded, in --- the basal plane by three neighbours in an antiferromagnetic configuration, in \( FePSe_{3} \) , there exists in the same plane lines of ferromagnetically linked neighbour iron atoms (Fig. 3). These lines are antiferromagnetically coupled to each other.
The difference between both magnetic structures must be due to a change in the intralayer interactions in both compounds. The stability conditions of a Heisenberg or XY system in a 2D-honeycomb lattice have been studied in a mean field approximation [11, 12] taking into account first n.n., second n.n. and third n.n. interactions of the spins within the basal plane, and neglecting the weak interlayer coupling. The magnetic phases are then characterized by \( (k_{x} k_{y} \Psi) \) where \( k_{x} \) and \( k_{y} \) are the wavevector components in the basal plane, and \( \Psi \) is the angle between the moment direction of the two Bravais lattices. Beside of three helical structures, the phase diagram contains four collinear magnetic structures: (a) a ferromagnetic phase (0 0, 0), (b) an antiferromagnetic phase (0 0, \( \pi \) ) like MnPSe \( _{3} \) where all three first n.n. are antiparallel, (c) an antiferromagnetic phase (1/2, 0, 0) where two first n.n. are antiparallel and one is parallel, and (d) an antiferromagnetic structure (1/2 0, \( \pi \) ) with two first n.n. parallel and one antiparallel. The last case (d) is realised by FePSe \( _{3} \) .
The exchange integrals of both compounds may be estimated from the paramagnetic Curie temperatures \(\theta_{p}\) and the Néel temperatures:
\[ k_{B}\theta_{p}=\frac{3}{2}S(S+1)(3J_{1}+6J_{2}+3J_{3}), \quad (5) \]
\[ k_{B}T_{N}=\frac{3}{2}S(S+1)\lambda, \quad (6) \]
where
\[ \lambda\left(\mathrm{MnPSe}_{3}\right)=-3J_{1}+6J_{2}-3J_{3}, \quad (7) \]
\[ \lambda\left(\mathrm{FePSe}_{3}\right)=J_{1}-2J_{2}-3J_{3}. \quad (7) \]
In the case of MnPSe_{3} with \(\theta_{p} = -200\) K and \(T_{N} = 74\) K equations (5) and (6) lead to \(J_{2}/k_{B} = -1.8\) K and \((J_{1} + J_{3})/k_{B} = -7.8\) K. The stability conditions for the different magnetic phases are now used. As the phase \((0, \pi)\) is only stable if \(J_{2} \geqslant 1/2J_{1}\), \(J_{1}\) must be necessarily antiferromagnetic. A second condition requires \(4J_{3} \leqslant 6J_{2} - J_{1}\) which indicates that the \((0, \pi)\) phase is more stable than the helical one. Thus we found for the MnPSe_{3}:
\[ J_{2}/k_{B}=-1.8\mathrm{K}, \]
\[ -6.8\mathrm{K}\leqslant J_{1}/k_{B}\leqslant-3.6\mathrm{K}, \]
\[ -4.2\mathrm{K}\leqslant J_{3}/k_{B}\leqslant-1.0\mathrm{K}, \]
\[ \mathrm{with}\left(J_{1}+J_{3}\right)/k_{B}=-7.8\mathrm{K}. \]
All three intralayer interactions are antiferromagnetic. It is remarkable that the third n.n. coupling \( J_{3} \) via the P–P pairs are of the same order of magnitude than the second neighbour coupling \( J_{2} \) (super–super exchange via two Se-atoms). Furthermore the first n.n. coupling \( J_{1} \) is only about two times stronger than \( J_{2} \) and \( J_{3} \) . In \( FePSe_{3} \) with \( \theta_{p}=0 \) and \( \hat{T}_{N}=119 \) K one gets the relations:
\[ J_{2}=5.19-J_{1}, \]
\[ J_{3}=-10.4+J_{1}\quad\mathrm{a n d}\quad(J_{1}+2J_{2}+J_{3})=0. \]
The stability conditions for the \( (1/2,0,\pi) \) phase requires \( J_{2}\leqslant1/2J_{1} \) which is satisfied only for a ferromagnetic n.n. coupling \( (J_{1}>0) \) . Then the range of possible values for \( J_{1},J_{2} \) and \( J_{3} \) is restricted by the stability condition to:
\[ 3.47\mathrm{K}\leqslant J_{1}/k_{B}\leqslant10.4\mathrm{K}, \]
\[ -5.2\mathrm{K}\leqslant J_{2}/k_{B}\leqslant1.73, \]
\[ -2\mathrm{K}\leqslant J_{3}/k_{B}\leqslant0. \]
So the exchange interactions in FePSe_{3} are of the same order of magnitude as in MnPSe_{3}, only the first n.n. has an opposite sign in FePSe_{3} (J_{1}>0).
The fact that the magnetic cell of FePSe_{3} is doubled along the c-direction but not that of MnPSe_{3} may not result from a change of the interplanar interactions J'; rather it may be due to the change of the sign of J_{1}, leading to a different value of the wavevector k_{x} within the plane, which for a collinear 3-dimensional structure requires k_{x}=1/2 (note that [1/2 0 0] is not a wavevector of a collinear magnetic structure).
The strong intralayer exchange interactions in both compounds lead to a bidimensional magnetic short-range order observed far above \( T_{N} \) by a modulation of the diffuse neutron scattering intensity at low angles. Detailed investigations are going on and shall be presented elsewhere.
REFERENCES
-
A. Le Mehaute, G. Ouvrard, R. Brec & J. Rouxel, Mat. Res. Bull. 12, 1191 (1977).
-
R. Brec, D.M. Schleich, G. Ouvrard, A. Louisy & J. Rouxel, Inorg. Chem. 18, 7, 1814 (1979).
-
A.H. Thomson & M.S. Whittingham, Mat. Res. Bull. 12, 741 (1977).
-
R. Clement & M.L.H. Green, J. Chem. Soc. Dalton, 1566 (1978).
-
S. Otami, M. Shimada, F. Kanamaru & M. Koizumi, Inorg. Chem. 19, 5, 1249 (1980).
-
V.W. Klingen, R. Ott & H. Hahn, Z. Anorg. Allg. Chem. 396, 271 (1973).
-
B. Taylor, J. Steger, A. Wold & E. Kostiner, Inorg. Chem. 13, 11, 2719 (1974).
-
R. Brec, G. Ouvrard, A. Louisy & J. Rouxel, Ann. Chim. FR. 5, 499 (1980).
-
Y. Chabre, P. Segransan, C. Berthier & G. Ouvrard, Fast Ions Transport in Solids (Edited by P. Vashista, J.N. Mundy & G.K. Shenov), 221 (1979).
-
W. Klingen, Thesis, Hohenheim, West Germany (1969).
-
E. Rastelli, A. Tassi & L. Reatto, Physica 97, 1 (1979).
-
L.P. Regnault (to be published).