| Transition Temperature | 4 K |
|---|---|
| Experiment Temperature | 1.5 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | Pnma (#62) |
| Magnetic Space Group | Pn'ma (#62.443) |
| Magnetic Point Group | m'mm (8.3.26) |
| Lattice Parameters | 15.76000 7.43000 18.38000 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1016/0304-8853(87)90294-0 |
| Reference | P. Lacorre, M. Leblanc, J. Pannetier and G. Ferey, Journal of Magnetism and Magnetic Materials (1987) 66 219-224. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Cr1 | Cr | -1.49 | 0.0 | 1.49 | 2.11 |
| Cr2 | Cr | -1.69 | 0.0 | -0.88 | 1.91 |
| Cr3 | Cr | 2.18 | 0.0 | -0.17 | 2.19 |
ORDERED MAGNETIC FRUSTRATION: X. MAGNETIC STRUCTURE OF α-KCrF₄ AT 1.5 K
P. LACORRE \( ^{1,2} \) , M. LEBLANC \( ^{1} \) , J. PANNETIER \( ^{2} \) and G. FEREY \( ^{1,a} \)
\( ^{1} \) Laboratoire des Fluorures, UA449, Faculté des Sciences, Université du Maine, Route de Laval, 72017 Le Mans Cedex, France
\( ^{2} \) Institut Laue-Langevin, 156X, 38042 Grenoble Cedex, France
Received 30 October 1986
The magnetic structure of orthorhombic \( \alpha \) -KCrF \( _{4} \) at 1.5 K (S.G. Pnma, \( a=15.76\ \AA \) , \( b=7.43\ \AA \) , \( c=18.38\ \AA \) , Z=24) was solved from powder neutron diffraction data. Magnetic constraints, due to antiferromagnetic coupling inside the triangular cycles of \( Cr^{3+}F_{6} \) corner sharing octahedra, lead approximately to a star configuration of moments in the (010) plane \( (\mu_{\mathrm{Cr1}}=2.11(11)\mu_{\mathrm{B}},\mu_{\mathrm{Cr2}}=1.91(12)\mu_{\mathrm{B}},\mu_{\mathrm{Cr3}}=2.19(6)\mu_{\mathrm{B}}) \) . The magnetic coupling between \( Cr^{3+} \) along [010], which corresponds to the direction of infinite columns, is strictly antiferromagnetic.
1. Introduction
Experimental examples of magnetic frustration [1] are still rather scarce [2–11]. Among them, the most common case is provided by the triangular plane lattice with antiferromagnetic interactions, which has also been extensively studied, from a theoretical point of view (see for example refs. [12–15] and references therein). This geometry leads to three antiferromagnetic sublattices oriented at \( 120^{\circ} \) to each other.
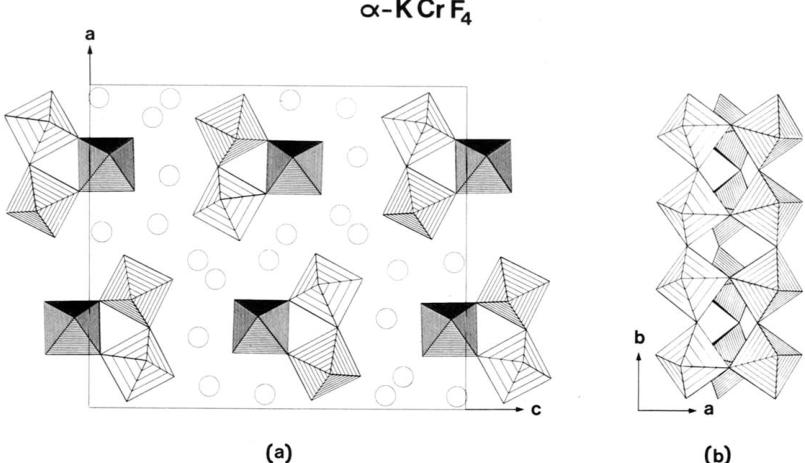
α-KCrF₄, first isolated by de Kozak [16], provides an interesting example for the study of frustration. Dewan and Edwards solved its crystal structure [17,18] using an orthorhombic unit cell (S.G. Pnma, a = 15.76 Å, b = 7.43 Å, c = 18.38 Å, Z = 24). It is built up from isolated infinite triangular columns of corner sharing CrF₆ octahedra (fig. 1) between which K⁺ ions are inserted.
Within the isolated columns, the \( Cr^{3+} \) sublattice, submitted to \( d^{3}-d^{3}180^{\circ} \) antiferromagnetic superexchange interactions, is trigonal prismatic. Therefore it involves both frustrating triangular (within the (010) plane) and non-frustrating square platelets of nearest neighbours. This must lead to a quasi-1D frustrated magnetic behaviour below the Néel temperature \( T_{N}=4(1) \) K [19,20]. In this paper, we present the magnetic structure of \( \alpha-KCrF_{4} \) and compare the results with those obtained on HTB-FeF \( _{3} \) [3] in which the trigonal prisms share edges and form a 3D magnetic sublattice.
2. Experimental
The powdered sample was obtained from a stoichiometric mixture of elementary fluorides, heated at \( 700^{\circ} \) C for 24 h in gold tubes sealed under argon. The neutron diffraction patterns at 5 and 1.5 K were collected on the high-flux powder diffractometer D1B of the Institut Laue–Langevin at Grenoble, using a wavelength of 2.518 Å. The powdered sample was contained in a vanadium can ( \( \phi = 10 \) mm, h = 50 mm) held in a standard helium cryostat. Two patterns were recorded below and above the Néel temperature, at 1.5 and 5 K, respectively. All refinements were performed with the Rietveld program [21,22]. The scattering lengths and magnetic form factors were taken from refs. [23] and [24], respectively.

Fig. 1. Crystal structure of \( \alpha \) -KCrF \( _{4} \) drawn with the program STRUPLO84 (29). (a) (010) projection; (b) view of one triangular column of corner sharing CrF \( _{6} \) octahedra. The density of hatching increases from CrI to Cr3. Circles = K \( ^{+} \) .

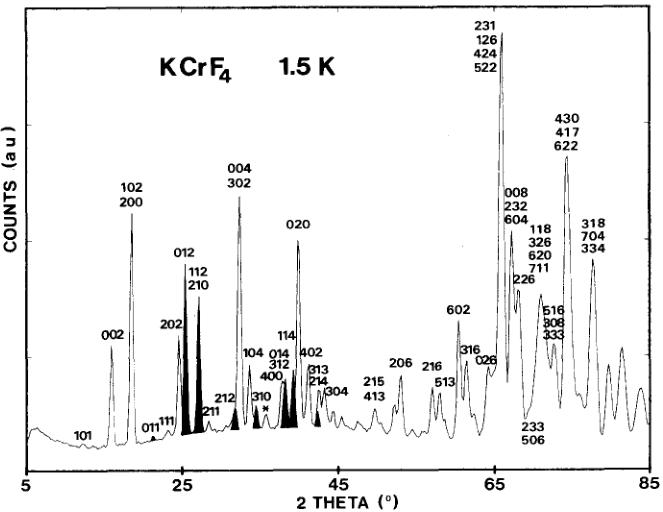
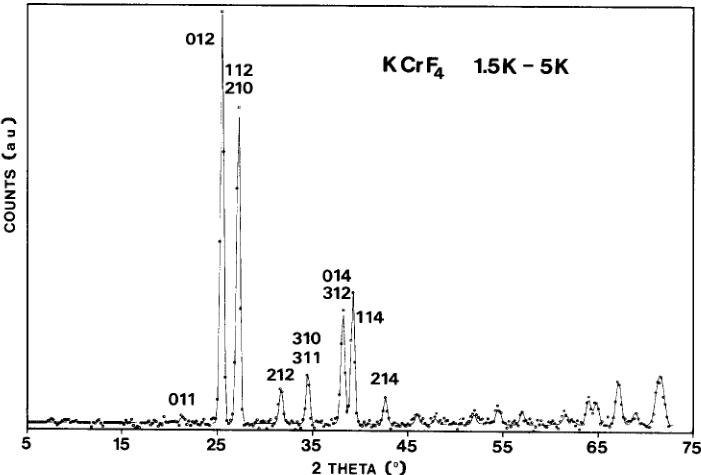
Fig. 2. Neutron diffraction pattern of \( \alpha \) -KCrF \( _{4} \) at 1.5 K. Purely magnetic peaks are shaded. \( \bullet \) = impurity (CrF \( _{3} \) ).
3. Magnetic structure – results and discussion
At 5 K, the compound is not yet magnetically ordered. At 1.5 K, we note an increase in some nuclear reflections and the onset of additional magnetic peaks (fig. 2). All new reflections can be indexed in the nuclear cell.
The coupling modes of \( KCrF_{4} \) were determined by using Bertaut's macroscopic theory [25].
Let for example, \( \tilde{2}_{x} \) , \( \tilde{2}_{z} \) and i be the three independent symmetry elements of space group Pnma. In \( \alpha \) -KCrF \( _{4} \) Cr \( ^{3+} \) ions occupy three crystallographically different sites on the 8d general position of the space group Pnma.
Let \( S_{i} \) (i=1,8) be the magnetic moments of 8 \( Cr^{3+} \) on equivalent positions (table 1). We can define, on each of the three sublattices, eight base vectors, built from linear combinations of the moments, which represent the possible magnetic modes of coupling:
\[ \begin{array}{l}F=S_{1}+S_{2}+S_{3}+S_{4}+S_{5}+S_{6}+S_{7}+S_{8},\\ \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(ferromagnetic mode)\\ G=S_{1}-S_{2}+S_{3}-S_{4}+S_{5}-S_{6}+S_{7}-S_{8},\\ C=S_{1}+S_{2}-S_{3}-S_{4}+S_{5}+S_{6}-S_{7}-S_{8},\\ A=S_{1}-S_{2}-S_{3}+S_{4}+S_{5}-S_{6}-S_{7}+S_{8},\\ P=S_{1}+S_{2}+S_{3}+S_{4}-S_{5}-S_{6}-S_{7}-S_{8},\\ Q=S_{1}-S_{2}+S_{3}-S_{4}-S_{5}+S_{6}-S_{7}+S_{8},\\ R=S_{1}+S_{2}-S_{3}-S_{4}-S_{5}-S_{6}+S_{7}+S_{8},\\ L=S_{1}-S_{2}-S_{3}+S_{4}-S_{5}+S_{6}+S_{7}-S_{8}.\end{array} \]
These base vectors lead to the eight irreducible representations, given in table 2.
According to Knocke [19,20], \( \alpha \) -KCrF \( _{4} \) orders antiferromagnetically. All of the eight modes are compatible with this experimental result (if we reduce to zero the ferromagnetic component of the
Table 1
Coordinates of magnetic ions \( Cr^{3+} \) (general position 8d) of space group Pnma
| S1 | x | y | z |
| S2 | \( \bar{x} \) | 1/2 + y | \( \bar{z} \) |
| S3 | 1/2 + x | 1/2 - y | 1/2 - z |
| S4 | 1/2 - x | \( \bar{y} \) | 1/2 + z |
| S5 | \( \bar{x} \) | \( \bar{y} \) | \( \bar{z} \) |
| S6 | x | 1/2 - y | z |
| S7 | 1/2 - x | 1/2 + y | 1/2 + z |
| S8 | 1/2 + x | y | 1/2 - z |
Table 2
Irreducible representations of \( Cr^{3+} \) in space group Pnma
| Mode | x | y | z |
| Γ1(+++) | Gx | Cy | Az |
| Γ2(+-+) | Fx | Ay | Cz |
| Γ3(-++) | Cx | Gy | Fz |
| Γ4(--+) | Ax | Fy | Gz |
| Γ5(++-) | Qx | Ry | Lz |
| Γ6(+--) | Px | Ly | Rz |
| Γ7(-+-) | Rx | Qy | Pz |
| Γ8(---) | Lx | Py | Qz |
\(\Gamma_{2}\), \(\Gamma_{3}\) and \(\Gamma_{4}\) modes). The calculations were carried out using the atomic positions of Dewan and Edwards [26,18]. Owing to the large number of atomic position parameters in the cell compared with the limited number of reflections available from the neutron diffraction data, we decided to refine the magnetic structure from the difference pattern 1.5–5 K. Thus, only the magnetic contribution of \(\mathrm{Cr}^{3+}\) ions is considered. This method is a reasonable approximation owing to the small change of temperature (1.5–5 K) which does not produce any appreciable variation of the positional, thermal and cell parameters. The positional parameters of \(\mathrm{Cr}^{3+}\) were held fixed at the (room temperature) values given by Edwards and we only refined magnetic moments on these sites. The eight possible modes were tested.
The value of the magnetic moments was obtained by scaling the experimental nuclear diffraction profile (5 K pattern) to that calculated with the structural parameters determined by Edwards. In addition, this allowed us to verify that there was no significant variation of the structure between room temperature and 1.5 K. The best fit between observed and calculated magnetic intensities was obtained for the \(\Gamma_{6}\) mode \(P_{x}L_{y}R_{z}\) giving \(R_{\Gamma}=0.037\), \(R_{\mathrm{wp}}=0.119\) for \(2\theta<45^{\circ}\) (\(R_{\Gamma}=0.083\), \(R_{\mathrm{wp}}=0.145\) for the whole pattern). Fig. 3 shows the observed and calculated profiles.
The components of magnetic moments on the cell axis are reported in table 3. The moments lie in the xOz plane. It was not possible to refine their y-component. Therefore, this component, if it exists, must be very close to zero.
The relatively low value of the moments \( \approx2\mu_{B} \) is not unexpected, owing to the low magnetic

Fig. 3. Observed ( \( \cdot \) ) and calculated (-) magnetic intensities (difference pattern 1.5–5 K). \( 2\theta < 45^{\circ} \) , after refinement: \( R_{1} = 0.035 \) , \( R_{wp} = 0.119 \) ; whole pattern: \( R_{1} = 0.083 \) , \( R_{wp} = 0.145 \) .
ordering temperature. At 1.5 K, the magnetic saturation is not yet reached.
Magnetic dipolar energy and field calculations show that, on every \( Cr^{3+} \) site, magnetic dipolar energy is negative and that the magnetic dipolar field has roughly the same orientation as the magnetic moments (table 4).
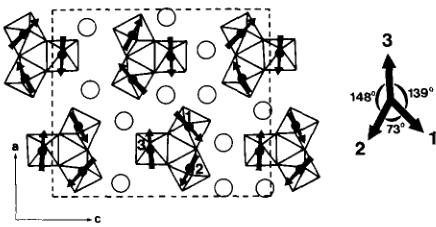
The spin arrangement of \( \alpha \) -KCrF \( _{4} \) has a plane star configuration, but rather distorted from the ideal star arrangement ( \( 3 \times 120^{\circ} \) ) with one small ( \( 73^{\circ} \) ) and two large angles ( \( 139^{\circ} \) and \( 148^{\circ} \) ) (fig. 4). Between two consecutive planes along z, the spin coupling is strictly antiferromagnetic within each infinite column of octahedra. An analogy of spin configuration in a basic triangular arrangement can be made with other compounds such as HTB-FeF \( _{3} \) (3D-antiferromagnet below \( T_{N} = 110 \) K) [3], CsVCl \( _{3} \) [27] or CsVI \( _{3} \) [28] (1D antiferromagnets with \( T_{N} = 13.3 \) and 32 K, respectively). They all crystallise in the hexagonal symmetry and present magnetic sublattices oriented at \( 120^{\circ} \) from each other in the triangular planes. The coupling between the planes is strictly antiferromagnetic, as in \( \alpha \) -KCrF \( _{4} \) , but in the latter the angle between the spins differs significantly from \( 120^{\circ} \) . This deviation results from the difference in the crystal symmetry of these compounds. Indeed, the hexagonal symmetry of the columns in HTB-FeF \( _{3} \) and CsVX \( _{3} \) implies identical \( \theta \) (M-X-M) super-exchange angles in the triangular plane and there-
Refined magnetic moments ( \( \mu_{B} \) ) in \( \alpha \) -KCrF \( _{4} \) at 1.5 K. Atomic positions are held fixed at their RT values [26]
| Cr3+ | Atomic positions | Magnetic moments | |||||
| x | y | z | Mx | My | Mz | M | |
| 1 | 0.3685 | -0.0006 | 0.6310 | -1.49 [10] | 0 | 1.49 [5] | 2.11 [11] |
| 2 | 0.1357 | -0.0019 | 0.6264 | -1.69 [11] | 0 | -0.88 [5] | 1.91 [12] |
| 3 | 0.2529 | -0.0009 | 0.4530 | 2.18 [5] | 0 | -0.17 [10] | 2.19 [6] |
Table 4
Magnetic dipolar energy \(E\) (j mol\(^{-1}\)) and field \(H(T)\) on Cr sites in \(\alpha\)-KCrF\(_{4}\).
| Atom | E | Hx | Hy | Hz |
| Cr1 | -0.788 | -0.1102 | 0 | 0.0552 |
| Cr2 | -0.658 | -0.1085 | 0 | -0.0462 |
| Cr3 | -0.676 | 0.0797 | 0 | 0.0053 |

Fig. 4. Magnetic structure of \( \alpha \) -KCrF \( _{4} \) . Moments lie in the (010) plane.
fore equal exchange integrals J between M ions thereby leading to three \( 120^{\circ} \) AF sublattices. The orthorhombic symmetry of \( \alpha \) -KCrF \( _{4} \) provides additional degrees of freedom in the triangle and allows different M-X-M angles (fig. 5). As \( J_{ex} \) varies linearly with \( \cos^{2}\theta \) [30], the inequality of \( \theta \) implies different \( J_{ex} \) which could explain both the slightly different values of the magnetic moments of the three crystallographically different \( Cr^{3+} \) and the deviation from the ideal star configuration. The latter point was actually confirmed by a Monte Carlo simulation [31] of the ground state configuration of spins in an isolated column: using a linear \( J_{ex} \) vs. \( \cos^{2}\theta \) relationship, the calculated spin arrangement deviates from the \( 120^{\circ} \) configuration and shows one smaller and two larger angles; although the deviations from the ideal star model are smaller than observed experimentally, the trend is clearly reproduced and indicates that the departure from the ideal spin configuration originates essentially in the structural distortion of the columns.
Acknowledgements
The authors gratefully acknowledge Dr. A.J. Edwards (University of Birmingham) for providing them with the atomic coordinates of \( \alpha \) -KCrF \( _{4} \) prior to publication, and Professor D. Babel (University of Marburg) for helpful discussions.
References
[1] G. Toulouse, Commun. Phys. 2 (1977) 115.
[2] G. Ferey, M. Leblanc, R. de Pape and J. Pannetier, Inorganic Solid Fluorides, ed. P. Hagenmüller (Academic Press, New York, London, 1985) p. 395.
[3] M. Leblanc, G. Ferey, R. de Pape and J. Pannetier, Solid State Commun. 58 (1986) 171.
[4] M. Leblanc, G. Ferey, Y. Calage and R. de Pape, J. Solid State Chem. 53 (1984) 360.

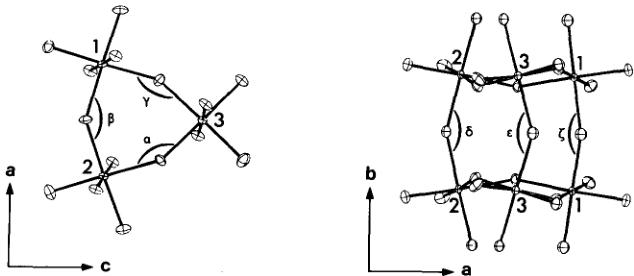
Fig. 5. Super-exchange angles \(\theta(\mathrm{Cr}-\mathrm{F}-\mathrm{Cr})\) inside the column [26]. \(\alpha=144.6^{\circ}\), \(\beta=140.2^{\circ}\), \(\gamma=149.0^{\circ}\), \(\delta=149.9^{\circ}\), \(\epsilon=148.5^{\circ}\), \(\zeta=149.9^{\circ}\).
[5] Y. Laligant, M. Leblanc, J. Pannetier and G. Ferey, J. Phys. C 19 (1986) 1081.
[6] Y. Laligant, J. Pannetier and G. Ferey, J. Solid State Chem. (submitted).
[7] Y. Laligant, J. Pannetier, Y. Calage, G. Heger and G. Ferey, J. Solid State Chem. (to be submitted).
[8] G. Ferey, R. de Pape and B. Boucher, Acta Cryst. B34 (1978) 1084.
[9] G. Ferey, M. Leblanc, R. de Pape and J. Pannetier, Solid State Commun. 53 (1985) 559.
[10] G. Ferey, R. de Pape, M. Leblanc and J. Pannetier, Rev. Chim. Min. 23 (1986) 294.
[11] P. Lacorre, J. Pannetier and G. Ferey, J. Magn. Magn. Mat. 66 (1987) 213.
[12] H. Kawamura and S. Miyashita, J. Phys. Soc. Japan 53 (1984) 9.
[13] D.H. Lee, J.D. Joannopoulos and J.W. Negele, Phys. Rev. B 33 (1986) 450.
[14] S. Katsura, T. Ide and T. Morita, J. Stat. Phys. 42 (1986) 381.
[15] S.E. Korshunov and G.V. Uimin, J. Stat. Phys. 43 (1986) 1.
[16] A. de Kozak, Rev. Chim. Min. 8 (1971) 301.
[17] J.C. Dewan and A.J. Edwards, J. Chem. Soc. Chem. Comm. (1977) 533.
[18] A.J. Edwards, Inorg. Chem. (in press).
[19] G. Knocke, Dissertation, Marburg (1976).
[20] G. Knocke and D. Babel, Z. Naturforsch. 30b (1975) 454.
[21] H.M. Rietveld, J. Appl. Cryst. 2 (1969) 65.
[22] A.W. Hewat, Harwell Report AERE-R 7350 (1973).
[23] L. Koester and H. Rauch, Summary of Neutron Scattering Lengths, IAEA Contract 2517/RB (1981).
[24] R.E. Watson and A.J. Freeman, Acta Cryst. 14 (1961) 27.
[25] E.F. Bertaut, Magnetism III, eds. G.T. Rado and H. Suhl (Academic Press, New York, 1963) p. 149.
[26] A.J. Edwards, private communication.
[27] K. Hirakawa, H. Ikeda, H. Kadowaki and K. Ubukoshi, J. Phys. Soc. Japan 52 (1983) 2882.
[28] H.W. Zandbergen, J. Solid State Chem. 37 (1981) 308.
[29] R.X. Fischer, J. Appl. Cryst. 18 (1985) 258.
[30] G.A. Sawatzky and F. van der Woude, J. de Phys. Colloq. 12 (1974) 1027.
[31] P. Lacorre and J. Pannetier, in preparation.