| Transition Temperature | 51 K |
|---|---|
| Experiment Temperature | 11 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | Pnma (#62) |
| Magnetic Space Group | Pnm'a' (#62.447) |
| Magnetic Point Group | m'm'm (8.4.27) |
| Lattice Parameters | 7.86840 15.12070 7.96280 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1088/0953-8984/14/30/309 |
| Reference | J.M. Cadogan, D.H. Ryan, Z. Altounian, H.B. Wang and I.P. Swainson, Journal of Physics: Condensed Matter (2002) 14 7191-7200. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Nd1 | Nd | 1.84 | 0.0 | 0.16 | 1.85 |
| Nd2 | Nd | 2.79 | 1.01 | 1.12 | 3.17 |
| Nd3 | Nd | 2.47 | 0.14 | 1.20 | 2.75 |
The magnetic structures of \( Nd_{5}Si_{4} \) and \( Nd_{5}Ge_{4} \)
This content has been downloaded from IOPscience. Please scroll down to see the full text.
2002 J. Phys.: Condens. Matter 14 7191
(http://iopscience.iop.org/0953-8984/14/30/309)
View the table of contents for this issue, or go to the journal homepage for more
Download details:
IP Address: 128.119.168.112
This content was downloaded on 09/09/2015 at 19:42
Please note that terms and conditions apply.
The magnetic structures of \( Nd_{5}Si_{4} \) and \( Nd_{5}Ge_{4} \)
J M Cadogan \( ^{1,4} \) , D H Ryan \( ^{2} \) , Z Altounian \( ^{2} \) , H B Wang \( ^{2} \) and I P Swainson \( ^{3} \)
\( ^{1} \) School of Physics, The University of New South Wales, Sydney, NSW 2052, Australia
\( ^{2} \) Department of Physics and Centre for the Physics of Materials, McGill University, Montreal, Quebec, Canada H3A 2T8
\( ^{3} \) Neutron Programme for Materials Research, Steacie Institute for Molecular Sciences, National Research Council, Chalk River Laboratories, Ontario, Canada K0J 1J0
E-mail: j.cadogan@unsw.edu.au
Received 5 June 2002
Published 17 July 2002
Online at stacks.iop.org/JPhysCM/14/7191
Abstract
We have determined the magnetic structures of \( Nd_{5}Si_{4} \) and \( Nd_5Ge_4 \) by means of high-resolution neutron powder diffraction. The crystal space groups of these compounds are tetragonal \( P4_{1}2_{1}2 \) and orthorhombic Pnma, respectively. Their magnetic ordering temperatures are 66(2) and 51(2) K, respectively, and both magnetic structures can be described as canted structures, with net antiferromagnetism in one plane with ferromagnetism perpendicular to that plane. The magnetic space groups are \( P4_{1}2_{1}^{\prime}2^{\prime} \) and \( Pnm^{\prime}a^{\prime} \) and their ferromagnetic ordering directions are [001] and [100], respectively.
1. Introduction
The \( R_{5}Si_{4} \) and \( R_{5}Ge_{4} \) compounds (R = rare earth) were first studied by Smith et al [1, 2] 35 years ago and much work on the crystallography of these compounds has been done with sometimes conflicting structures being reported for some compounds, suggesting that these compounds may, in fact, be polymorphic. However, much less is known about their physical properties, including their magnetic behaviour. Concentrating on the 5:4 compounds, Holzberg et al [3] reported the magnetic properties of the \( R_{5}Ge_{4} \) series of compounds and Schobinger-Papamantellos reported the magnetic properties of \( Tb_{5}Ge_{4} \) [4], \( Ho_{5}Ge_{4} \) [5] and \( Nd_{5}Ge_{4} \) [6].
The \( R_{5}Si_{4} \) and \( RsGe_{4} \) compounds are the subjects of renewed interest in the magnetism community due to the observation of a giant magnetocaloric effect in the \( \mathrm{Gd}_{5}(\mathrm{Si}, \mathrm{Ge})_{4} \) compounds by Gschneidner and Pecharsky [7, 8]. Recently, Ritter et al [9] reported the magnetic structures of the \( \mathrm{Tb}_{5}(\mathrm{Si}, \mathrm{Ge})_{4} \) compounds and showed that there is a strong coupling between the crystallography and magnetism in these compounds. Such a coupling is believed to play an important role in determining the extent of the magnetocaloric effect in such compounds [10]. In particular, Ritter et al [9] observed magnetic reorientations below the
magnetic ordering temperatures right across the \( \mathrm{Tb}_{5}(\mathrm{Si}_{x}\mathrm{Ge}_{1-x})_{4} \) system, including the end-members \( Tb_{5}Si_{4} \) and \( Tb_{5}Ge_{4} \) . In the intermediate composition range from \( x \sim 0.35 \) to 0.65 they also observed a change in crystal structure from monoclinic in the paramagnetic regime to orthorhombic below. Such a change in crystal structure accompanying the magnetic ordering was also observed by Gschneidner and Pecharsky [7, 8] in the \( \mathrm{Gd}_{5}(\mathrm{Si}_{x}\mathrm{Ge}_{1-x})_{4} \) , system in the range \( x \sim 0.24-0.50 \) . A magnetic reorientation was observed in the \( Gd_{5}Ge_{4} \) end-member but not in \( Gd_{5}Si_{4} \) .
Recently, Boulet et al [11] reported a study of the magnetic and electrical properties of various Nd–Si binary phases, including \( Nd_{5}Si_{4} \) . They measured a magnetic ordering temperature of 67 K in \( Nd_{5}Si_{4} \) and concluded that the magnetic ordering direction of \( Nd_{5}Si_{4} \) is the crystallographic c-axis but they did not derive the details of the magnetic structure. Gschneidner et al [12] reported that the ordering temperatures of \( Nd_{5}Si_{4} \) and \( Nd_{5}Ge_{4} \) are 71 and 55 K, respectively.
In this paper we present the first determination of the magnetic structure of \( Nd_{5}Si_{4} \) by means of high-resolution neutron diffraction. We have also determined the magnetic structure of \( Nd_{5}Ge_{4} \) , which we will present here, but we will concentrate on \( Nd_{5}Si_{4} \) since the magnetic structure of \( Nd_{5}Ge_{4} \) has already been reported by Schobinger-Papamantellos and Niggli [6].
2. Experimental methods
The \( Nd_{5}Si_{4} \) and \( Nd_{5}Se_{4} \) samples were prepared in a tri-arc furnace with a base pressure less than \( 6 \times 10^{-7} \) mbar. Stoichiometric amounts of the pure elements were melted several times under Ti-gettered argon to ensure homogeneity. Powder x-ray diffraction patterns were obtained using Cu Kα radiation on an automated Nicolet-Stoe diffractometer. Ac susceptibility was measured on a Quantum Design PPMS at a frequency of 377 Hz and an ac magnetic field amplitude of \( 398 \, A m^{-1} \) . No dc bias fields were applied during the susceptibility experiments.
Neutron powder diffraction experiments were carried out on \( \sim \) 4 g samples on the DUALSPEC C2 high-resolution powder diffractometer located at the NRU reactor, Chalk River Laboratories, Ontario, operated by Atomic Energy Canada Ltd. The neutron wavelength was 2.3685(1) Å. A review of the neutron scattering facilities at Chalk River, including a description of C2, can be found in [13]. Patterns were obtained for each compound over the temperature range 11–295 K and all diffraction patterns were analysed by the Rietveld method using the FullProf [14] program.
3. Results and discussion
3.1. \( Nd_{5}Si_{4} \)
The \( Nd_{5}Si_{4} \) sample was two-phase, with \( \sim5 \) wt% of hexagonal \( Nd_{5}Si_{3} \) (space group \( P6_{3}/mcm \) ) as an impurity which was included in all pattern refinements reported here.
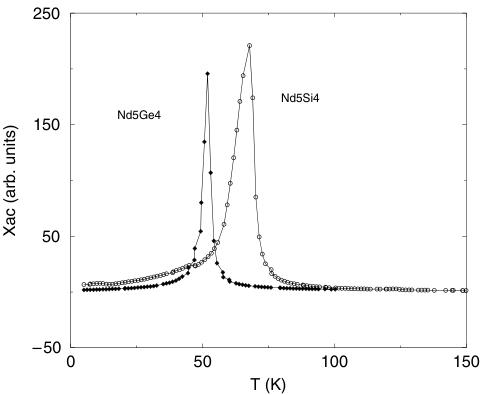
In figure 1 we show the ac susceptibility traces of \( Nd_{5}Si_{4} \) and \( Nd_{5}{Ge}_{4} \) . The magnetic ordering temperatures deduced from standard Curie–Weiss fits to the high-temperature regions of these data yield magnetic ordering temperatures of 66(2) and 51(2) K for \( Nd_{5}Si_{4} \) and \( Nd_{5}{G}e_{4} \) , respectively. Both magnetic ordering peaks in the susceptibility traces are sharp, albeit slightly asymmetric, and we see no evidence of further magnetic reorientation events in the magnetically ordered regimes, in contrast to the Tb- and Gd-based systems discussed earlier.
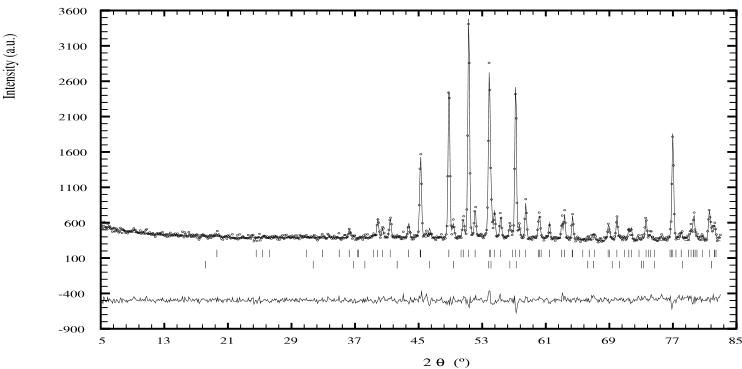
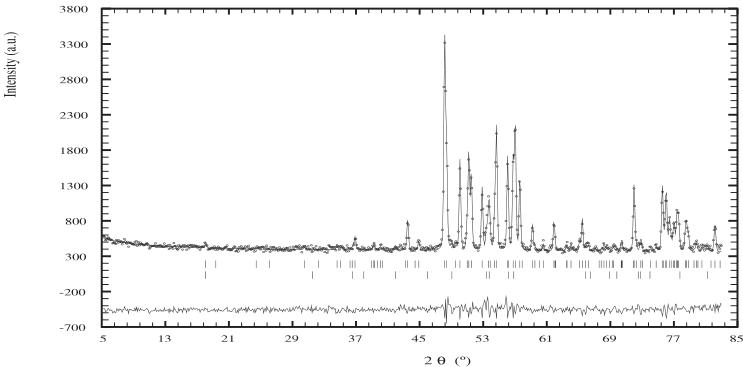
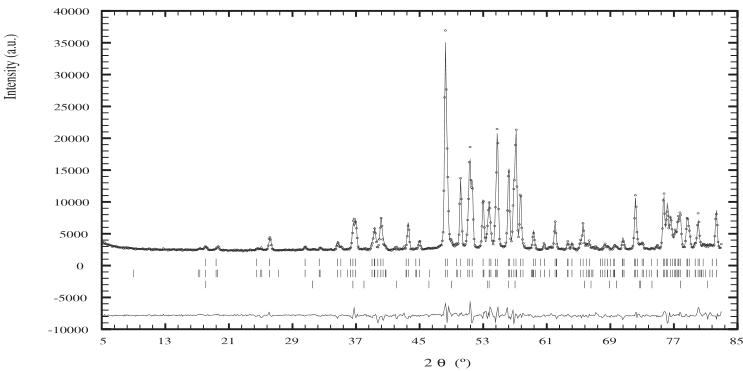
In figure 2 we show the neutron diffraction patterns of \( Nd_{5}Si_{4} \) obtained at 295 and 12 K. In table 1 we give the atomic position parameters of \( Nd_{5}Si_{4} \) derived from the refinement of the neutron diffraction pattern obtained at 295 K, which comprises only nuclear scattering.

Figure 1. Ac susceptibility traces of \( Nd_{5}Si_{4} \) (open circles) and \( Nd_{5}Ge_{4} \) (filled diamonds).
Table 1. Refined atomic positions in \( Nd_{5}Si_{4} \) at 295 K (obtained with an overall isotropic thermal parameter \( (B_{iso}) \) of \( 0.84\ \AA^{2} \) ).
| Atom | Site | x | y | z |
| Nd | 4a | 0.1901(21) | 0.1901(21) | 0 |
| Nd | 8b | 0.0142(14) | 0.1326(17) | 0.6192(12) |
| Nd | 8b | 0.9861(17) | 0.3667(17) | 0.2025(6) |
| Si | 8b | 0.0529(30) | 0.2810(28) | 0.8070(12) |
| Si | 8b | 0.2826(31) | 0.3270(34) | 0.6926(12) |
The crystal structure of \( Nd_{5}Si_{4} \) is tetragonal with the space group \( P4_{1}2_{1}2 \) (No 92). The structure type is that of \( Zr_{5}Si_{4} \) and there are three Nd sites and two Si sites. The lattice parameters (at 295 K) determined by neutron diffraction are \( a = 7.8760(8) \) Å and \( c = 14.8010(18) \) Å. The standard refinement 'R-factors (%)' are: \( R(\text{Bragg}) = 6.2 \) and \( R(\text{weighted profile}) = 8.4 \) .
Comparison of the neutron patterns taken at 295 K (above the ordering temperature) and 12 K (below the ordering temperature) shows magnetic contributions to nuclear scattering peaks in addition to the appearance of additional peaks not allowed by the crystal space group. This is most clearly illustrated by the appearance of a strong magnetic (001) peak at \( 2\theta = 9^{\circ} \) . Thus, we may conclude that the magnetic structure of \( Nd_{5}Si_{4} \) is neither a simple ferromagnet nor an antiferromagnet, but is most probably a combination of the two, i.e. a canted ferromagnet (vide infra).
To determine the magnetic structure of \( Nd_{5}Si_{4} \) we carried out a group theory analysis of the possible magnetic space groups and magnetic ordering modes derived from the \( P4_{1}2_{1}2 \) space group. There are seven magnetic space groups associated with the \( P4_{1}2_{1}2 \) crystal space group [15], namely \( P4_{1}2_{1}2 \) , \( P4_{1}^{\prime}2_{1}2^{\prime} \) , \( P4_{1}^{\prime}2_{1}^{\prime}2 \) , \( P4_{1}^{\prime}2_{1}^{\prime}2 \) and \( P_{c}4_{1}2_{1}2 \) , \( P_{c}4_{1}2_{1}2 \) and \( P_{f}4_{1}2_{1}2 \) . We omit the 'grey' group \( P4_{1}2_{1}2_{1}^{\prime} \) since it does not correspond to an ordered magnetic structure. We can rule out the last three of these seven groups due to the fact that we do not observe any additional magnetic peaks involving half-integer Miller indices. The behaviour of the magnetic moments within the remaining four magnetic space groups can then be deduced by


Figure 2. Neutron powder diffraction patterns of \( Nd_{5}Si_{4} \) at 295 K (top) and 12 K (bottom). The Bragg markers (top to bottom) are \( Nd_{5}Si_{4} \) and \( Nd_{5}Si_{3} \) in the 295 K pattern, and \( Nd_{5}Si_{4} \) (nuclear), \( Nd_{5}Si_{4} \) (magnetic) and \( Nd_{5}Si_{3} \) in the 12 K pattern.
Table 2. Character table of the 422 group (using the notation of Joshua [16]).
| Representation | E | C4z± | C2z | C2xy | C2ab | Magnetic space group |
| Γ1 | +1 | +1 | +1 | +1 | +1 | P4 1 2 1 2 |
| Γ2 | +1 | +1 | +1 | −1 | −1 | P4 1 2 1 2 |
| Γ3 | +1 | −1 | +1 | +1 | −1 | P4 1 2 1 2 |
considering the character table of the 422 group which underpins these magnetic space groups, shown in table 2.
Table 3. Atomic positions and generating operations of the Nd 4a sites in \( Nd_{5}Si_{4} \)
| Atom number | X | Y | Z | Generating operation | Moment |
| 1 | x | x | 0 | Identity | \( (\mu_{x}, \mu_{y}, \mu_{z}) \) |
| 2 | -x | -x | \( \frac{1}{2} \) | \( 2(0 \frac{1}{2})[0 \ 0 \ z] \) | \( (-\mu_{x}, -\mu_{y}, \mu_{z}) \) |
| 3 | -x + \( \frac{1}{2} \) | x + \( \frac{1}{2} \) | \( \frac{1}{4} \) | \( 4^{*}(0 \ 0 \ \frac{1}{4})[0 \ \frac{1}{2} \ z] \) | \( (-\mu_{y}, \mu_{x}, \mu_{z}) \) |
| 4 | x + \( \frac{1}{2} \) | -x + \( \frac{1}{2} \) | \( \frac{3}{4} \) | \( 4^{-}(0 \ 0 \ \frac{3}{4})[\frac{1}{2} \ 0 \ z] \) | \( (\mu_{y}, -\mu_{x}, \mu_{z}) \) |
The point group of the Nd 8b sites is I which leads to a completely arbitrary magnetic moment direction with no restrictions dictated by symmetry. The Nd 4a site has the point group \( \cdot\cdot2 \) indicating a twofold rotation axis along the planar diagonal directions \( \langle110\rangle \) , corresponding to \( C_{2ab} \) in the character table. The admissible magnetic point groups of the Nd 4a site are:
• \( \cdot\cdot2 \) with the Nd magnetic moment parallel to the twofold axis (from the \( \Gamma_{1} \) and \( \Gamma_{4} \) representations); and
• \( \cdot\cdot2' \) with the Nd magnetic moment perpendicular to the twofold axis (from the \( \Gamma_{2} \) and \( \Gamma_{3} \) representations).
The four Nd 4a sites are related to each other by the generating operations given in table 3, using the standard notation employed in the International X-ray Crystallography Tables to describe crystallographic operations \( [17] \) . Now, if we denote the magnetic moment components of atom 1 by \( \mu_{x} \) , \( \mu_{y} \) and \( \mu_{z} \) , we deduce the moments of the remaining three 4a atoms as shown in table 3, ignoring any time-reversal operations at this stage.
The final magnetic structures can then be derived from the character table for each possible magnetic space group by incorporating the characters of the generating operations, which takes into account the effects of time reversal.
We note here that:
• \( \Gamma_{1} \) and \( \Gamma_{4} \) yield a \( \cdot\cdot2 \) magnetic point group for the 4a sites so the magnetic moment must be parallel to the twofold axis; i.e. the moment must lie in the tetragonal a-b plane and hence \( \mu_{z}=0 \) ;
• \( \Gamma_{2} \) and \( \Gamma_{3} \) yield a \( \cdot\cdot2' \) magnetic point group for the 4a sites so the magnetic moment must be perpendicular to the twofold axis; i.e. the moment may have components in the plane and also along the tetragonal c-axis;
- the magnitudes \( \mu_{x} \) and \( \mu_{y} \) must be equal to ensure that the planar component lies along a \( \langle110\rangle \) diagonal direction.
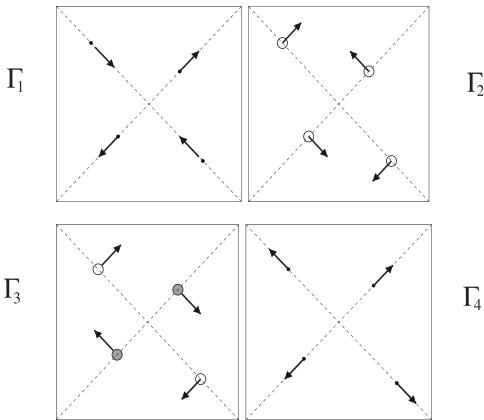
These magnetic modes are shown schematically in figure 3, projected onto the tetragonal a–b basal plane.
As stated earlier, the magnetic moment orientations at the Nd 8b sites are not subject to any symmetry-related restrictions. In table 4 we show the atomic positions of the eight Nd 8b sites and their generating operations.
Thus, we have four possible magnetic structures for \( Nd_{5}Si_{4} \) which we write in table 5 using the standard notation for the magnetic modes, namely \( F = \{++++\} \) , \( G = \{+-+-\} \) , \( C = \{++--\} \) and \( A = \{+-+-\} \) . We use the superscript notation \( (+ \) or \( - \) ) to represent the moment orientations of the eight Nd 8b atoms as two symmetry-related groups of four. For example, \( G_{x}^{+} \) represents \( \{+-+-+--\} \) and \( G_{z}^{-} \) represents \( \{+-+-+--\} \) .
The best fit to the 12 K neutron diffraction pattern of \( Nd_{5}Si_{4} \) was obtained with the \( \Gamma_{2} \) representation, corresponding to the magnetic space group \( P4_{1}2_{1}^{\prime}2^{\prime} \) . The refinement R-factors (%) for the best fit are: \( R(\mathrm{Bragg}) = 5.1 \) , \( R(F) = 4.0 \) and \( R(\mathrm{mag}) = 7.7 \) . For comparison,

Figure 3. Possible magnetic structures of the Nd 4a site in \( Nd_{5}Si_{4} \) projected onto the tetragonal a–b plane. \( \Gamma_{1} \) and \( \Gamma_{4} \) are planar whereas \( \Gamma_{2} \) and \( \Gamma_{3} \) have components along the c-axis, as denoted by the filled or unfilled circles which represent components either into the plane or out of the plane.
Table 4. Atomic positions and generating operations of the Nd 8b sites in \( Nd_{5}Si_{4} \)
| Atom number | X | Y | Z | Generating operation | Moment |
| 1 | x | y | z | Identity | \( (\mu_{x}, \mu_{y}, \mu_{z}) \) |
| 2 | -x | -y | z + \( \frac{1}{2} \) | 2(0 0 \( \frac{1}{2} \) )[0 0 z] | \( (-\mu_{x}, -\mu_{y}, \mu_{z}) \) |
| 3 | -y + \( \frac{1}{2} \) | x + \( \frac{1}{2} \) | z + \( \frac{1}{4} \) | 4^{+}(0 0 \( \frac{1}{4} \) )[0 \( \frac{1}{2} \) z] | \( (-\mu_{y}, \mu_{x}, \mu_{z}) \) |
| 4 | y + \( \frac{1}{2} \) | -x + \( \frac{1}{2} \) | z + \( \frac{\pi}{4} \) | 4^{-}(0 0 \( \frac{3}{4} \) )[ \( \frac{1}{2} \) 0 z] | \( (\mu_{y}, -\mu_{x}, \mu_{z}) \) |
| 5 | -x + \( \frac{1}{2} \) | y + \( \frac{1}{2} \) | -z + \( \frac{1}{4} \) | 2(0 \( \frac{1}{2} \) 0)[ \( \frac{1}{4} \) y \( \frac{8}{8} \) ] | \( (-\mu_{x}, \mu_{y}, -\mu_{z}) \) |
| 6 | x + \( \frac{1}{2} \) | -y + \( \frac{1}{2} \) | -z + \( \frac{\pi}{4} \) | 2( \( \frac{1}{2} \) 0 0)[x \( \frac{1}{4} \) \( \frac{8}{8} \) ] | \( (\mu_{x}, -\mu_{y}, -\mu_{z}) \) |
| 7 | y | x | -z | 2[x x 0] | \( (\mu_{y}, \mu_{x}, -\mu_{z}) \) |
| 8 | -y | -x | -z + \( \frac{1}{2} \) | 2[x - x \( \frac{1}{4} \) ] | \( (-\mu_{y}, -\mu_{x}, -\mu_{z}) \) |
Table 5. Nd 4a and 8b site magnetic modes in \( Nd_{5}Si_{4} \)
| Representation | 4a mode | 8b mode | Magnetic space group |
| \( \Gamma_{1} \) | A_{x}G_{y} | A_{x}^{-}G_{y}^{+}F_{z}^{-} | P4_{1}2_{1}2 |
| \( \Gamma_{2} \) | A_{x}G_{y}F_{z} | A_{x}^{+}G_{y}^{-}F_{z}^{+} | P4_{1}2_{1}^{\prime}2^{\prime} |
| \( \Gamma_{3} \) | G_{x}A_{y}C_{z} | G_{x}^{-}A_{y}^{+}C_{z}^{-} | P4_{1}^{\prime}2_{1}2^{\prime} |
| \( \Gamma_{4} \) | G_{x}A_{y} | G_{x}^{+}A_{y}^{-}C_{z}^{+} | P4_{1}^{\prime}2_{1}^{\prime}2^{\prime} |
the corresponding R-factors for the second-best fit are 10.8, 8.2 and 27.1, respectively, for the \( \Gamma_{4} \) representation. The refined Nd magnetic moment components are given in table 6.
The net magnetization of \( Nd_{5}Si_{4} \) is zero along the directions a (or b) whereas there is a significant magnetization along the tetragonal c-axis, corresponding to an average Nd magnetic moment of \( 2.58(7)\mu_{B} \) . The Nd moments shown in table 6 are less than the ‘free-ion’ moment of \( Nd^{3+} \) ion of \( 3.27\mu_{B} \) , most probably due to the fact that the measurement
Table 6. Nd magnetic moment components in \( Nd_{5}Si_{4} \) at 12 K.
| Site | \( \mu_{x} \) ( \( \mu_{B} \) ) | \( \mu_{y} \) ( \( \mu_{B} \) ) | \( \mu_{z} \) ( \( \mu_{B} \) ) | Total moment ( \( \mu_{B} \) ) |
| 4a | 0.36(4) | 0.36(4) | 2.34(6) | 2.39(6) |
| 8b | 0.33(4) | 0.43(4) | 2.41(6) | 2.47(6) |
| 8b | 1.38(4) | 0.58(4) | 2.35(6) | 2.79(6) |
Table 7. Refined atomic positions in \( Nd_{5}Ge_{4} \) at 295 K (obtained with an overall isotropic thermal parameter \( (B_{iso}) \) of \( 0.52\ \mathring{A}^{2} \) ).
| Atom | Site | x | y | z |
| Nd | 4c | 0.2888(23) | \( \frac{1}{4} \) | 0.0020(20) |
| Nd | 8d | 0.1197(12) | 0.1161(7) | 0.3429(13) |
| Nd | 8d | 0.9757(13) | 0.0991(10) | 0.8176(15) |
| Ge | 4c | 0.9159(20) | \( \frac{1}{4} \) | 0.1032(18) |
| Ge | 4c | 0.1801(17) | \( \frac{1}{4} \) | 0.6373(19) |
| Ge | 8d | 0.2197(14) | 0.9567(7) | 0.5305(14) |
was made at \( T/T_{C} = 0.16 \) . Crystal-field quenching may also be a factor. Our observation of ferromagnetism along the tetragonal c-axis of \( Nd_{5}Si_{4} \) is in agreement with the magnetization measurements of Boulet et al [11].
3.2. \( Nd_{5}Ge_{4} \)
Schobinger-Papamantellos and Niggli [6] have previously reported neutron diffraction measurements on \( Nd_{5}Ge_{4} \) and they determined the magnetic space group to be \( Pnm'a' \) . We have also studied \( Nd_{5}Ge_{4} \) and here we will present a very brief summary of our structure determination, which is in full agreement with that of Schobinger-Papamantellos and Niggli [6].
The \( Nd_{5}Ge_{4} \) sample was two-phase, with \( \sim10 \) wt% of hexagonal \( Nd_{5}Ge_{3} \) as an impurity. This impurity phase was included in all pattern refinements reported here.
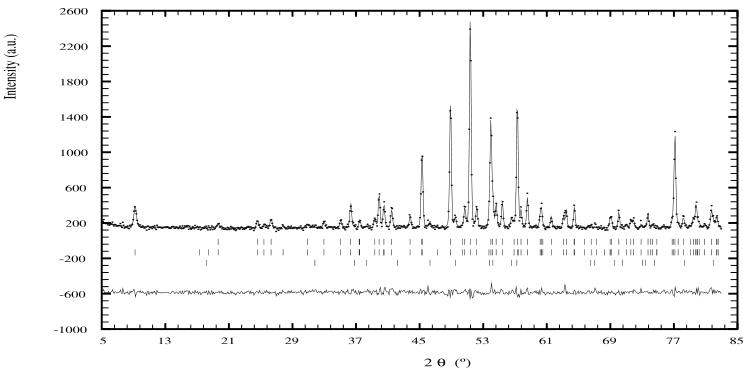
In figure 4 we show the neutron diffraction patterns of \( Nd_{5}Ge_{4} \) obtained at 295 and 11 K. Our ac susceptibility work shows that \( Nd_{5}Ge_{4} \) orders magnetically at 51(2) K, compared with the values of 52 K determined by Schobinger-Papamantellos and Niggli [6] and 54 K determined by Gschneidner et al [12]. In table 7 we give the atomic parameters of \( Nd_{5}Ge_{4} \) derived from the refinement of the neutron diffraction pattern obtained at 295 K, which comprises only nuclear scattering. The crystal structure of \( Nd_{5}Ge_{4} \) is orthorhombic with the space group \( P_{nma} \) (No 62). There are three Nd sites and three Ge sites and the structure type is that of \( Sm_{5}Ge_{4} \) . The lattice parameters (at 295 K) determined by neutron diffraction are \( a = 7.8684(9) \) Å, \( b = 15.1207(16) \) Å and \( c = 7.9628(9) \) Å. The refinement 'R-factors (%)' are: R(Bragg) = 5.3, R(weighted profile) = 8.4.
As was the case with \( Nd_{5}Si_{4} \) , there are magnetic contributions to nuclear scattering peaks in addition to the appearance of additional peaks not allowed by the crystal space group. This is most clearly illustrated by the appearance of a strong magnetic (111) peak at \( 2\theta = 26^{\circ} \) .
There are eight possible magnetic space groups associated with the Pnma crystal space group \( [15] \) , as shown in table 8. The point group of the Nd 8d sites is 1 which leads to a completely arbitrary magnetic moment direction. The 4c site has the point group \( \cdot m\cdot \) , i.e. with a mirror plane whose normal is along the crystal b-axis and the possible admissible magnetic point groups of the 4c site are:


Figure 4. Neutron powder diffraction patterns of \( Nd_{5}Ge_{4} \) obtained at 295 K (top) and 11 K (bottom). The Bragg markers (top to bottom) are \( Nd_{5}Ge_{4} \) and \( Nd_{5}Ge_{3} \) in the 295 K pattern, and \( Nd_{5}Ge_{4} \) (nuclear), \( Nd_{5}Ge_{4} \) (magnetic) and \( Nd_{5}Ge_{3} \) in the 11 K pattern.
• \( \cdot m\cdot \) with the Nd magnetic moment perpendicular to the mirror plane (from the \( \Gamma_{1}^{+} \) , \( \Gamma_{2}^{+} \) , \( \Gamma_{3}^{+} \) or \( \Gamma_{4}^{-} \) representations). Thus, the moment must lie along [010] and hence \( \mu_{x} \) and \( \mu_{z}=0 \) ;
• \( \cdot m^{\prime} \) with the Nd magnetic moment lying in the mirror plane (from the \( \Gamma_{3}^{+} \) , \( \Gamma_{4}^{+} \) , \( \Gamma_{1}^{-} \) or \( \Gamma_{2}^{-} \) representations), so \( \mu_{y}=0 \) .
The possible magnetic modes for the Nd 4c and 8d sites in \( Nd_{5}Ge_{4} \) are shown in table 8.
The best fit to the 11 K neutron diffraction pattern of \( Nd_{5}Ge_{4} \) is obtained with the \( \Gamma_{3}^{+} \) structure, corresponding to the magnetic space group \( Pnm^{\prime}a^{\prime} \) . The refinement R-factors (%) for the best fit are: \( R(\text{Bragg}) = 6.7 \) , \( R(F) = 4.8 \) and \( R(\text{mag}) = 11.7 \) . For comparison, the corresponding R-factors for the second-best fit are 10.1, 7.2 and 20.9, respectively, for the \( \Gamma_{4}^{+} \) representation. The refined Nd magnetic moment components are given in table 9.
Table 8. Nd 4c and 8d site magnetic modes in \( Nd_{5}Ge_{4} \)
| Representation | 4c mode | 8d mode | Magnetic space group |
| \( \Gamma_{1}^{+} \) | \( G_{y} \) | \( A_{x}^{+}G_{y}^{+}C_{z}^{+} \) | Pnma |
| \( \Gamma_{2}^{+} \) | \( F_{y} \) | \( C_{x}^{+}F_{y}^{+}A_{z}^{+} \) | \( Pn^{\prime}ma^{\prime} \) |
| \( \Gamma_{3}^{+} \) | \( F_{x}G_{z} \) | \( F_{x}^{+}C_{y}^{+}G_{z}^{+} \) | \( Pnm^{\prime}a^{\prime} \) |
| \( \Gamma_{4}^{+} \) | \( G_{x}F_{z} \) | \( G_{x}^{+}A_{y}^{+}F_{z}^{+} \) | \( Pn^{\prime}m^{\prime}a \) |
| \( \Gamma_{1}^{-} \) | \( A_{x}C_{z} \) | \( A_{x}^{-}G_{y}^{-}C_{z}^{-} \) | \( Pn^{\prime}m^{\prime}a^{\prime} \) |
| \( \Gamma_{2}^{-} \) | \( C_{x}A_{z} \) | \( C_{x}^{-}F_{y}^{-}A_{z}^{-} \) | \( Pnm^{\prime}a \) |
| \( \Gamma_{3}^{-} \) | \( C_{y} \) | \( F_{x}^{-}C_{y}^{-}G_{z}^{-} \) | \( Pn^{\prime}ma \) |
| \( \Gamma_{4}^{-} \) | \( A_{y} \) | \( G_{x}^{-}A_{y}^{-}F_{z}^{-} \) | \( Pnma^{\prime} \) |
Table 9. Nd magnetic moment components in \( Nd_{5}Ge_{4} \) at 11 K.
| Site | \( \mu_{x} \) ( \( \mu_{B} \) ) | \( \mu_{y} \) ( \( \mu_{B} \) ) | \( \mu_{z} \) ( \( \mu_{B} \) ) | Total moment ( \( \mu_{B} \) ) |
| 4c | 1.84(4) | 0 | 0.16(6) | 1.85(6) |
| 8d | 2.79(4) | 1.01(4) | 1.12(6) | 3.17(6) |
| 8d | 2.47(4) | 0.14(4) | 1.20(6) | 2.75(6) |
The net magnetization of \( Nd_{5}Ge_{4} \) is zero along the b- and c-directions whereas there is a significant magnetization along the orthorhombic a-axis [100]. The average Nd magnetic moment at 11 K in \( Nd_{5}Ge_{4} \) is \( 2.74(7)\mu_{B} \) .
4. Conclusions
We have determined the magnetic structures of \( Nd_{5}Si_{4} \) and \( Nd_{5}Ge_{4} \) by means of high-resolution neutron powder diffraction. The magnetic space group of \( Nd_{5}Si_{4} \) is \( P4_{1}2_{1}^{\prime}2^{\prime} \) which corresponds to the \( \Gamma_{2} \) representation of the underlying 422 group. \( Nd_{5}Si_{4} \) is antiferromagnetic in the tetragonal basal plane and ferromagnetic along the c-axis. At 12 K, the ferromagnetic order gives an average Nd moment along the c-axis of \( 2.37(7)\mu_{B} \) and an average total Nd moment of \( 2.58(7)\mu_{B} \) .
The magnetic space group of \( Nd_{5}Ge_{4} \) is \( Pnm'a' \) which corresponds to the \( \Gamma_{3}^{+} \) representation of the underlying mmm group. \( Nd_{5}Ge_{4} \) is antiferromagnetic along the orthorhombic b- and c-axes and ferromagnetic along the a-axis. At 11 K, the ferromagnetic order gives an average Nd moment along the a-axis of \( 2.47(7)\mu_{B} \) and an average total Nd moment of \( \( 2.74(7)\mu_{B} \) .
Acknowledgments
This work was supported by grants from the University Research Support Programme (UNSW), the Natural Sciences and Engineering Research Council of Canada and ‘Fonds pour la formation de chercheurs et l’aide à la recherche’, Québec.
References
[1] Smith G S, Tharp A G and Johnson Q 1966 Nature 210 1148–9
[2] Smith G S, Tharp A G and Johnson Q 1967 Acta Crystallogr. 22 940–3
[3] Holzberg F, Gambino R J and McGuire T R 1967 J. Phys. Chem. Solids 28 2283–9
[4] Schobinger-Papamantellos P 1978 J. Phys. Chem. Solids 39 197–205
[5] Schobinger-Papamantellos P 1979 J. Physique Coll. Suppl. 40 C5 156–8
[6] Schobinger-Papamantellos P and Niggli A 1981 J. Phys. Chem. Solids 42 583–6
[7] Gschneidner K A Jr and Pecharsky V K 2000 Annu. Rev. Mater. Sci. 30 387–429
[8] Pecharsky V K and Gschneidner K A Jr 2001 Adv. Mater. 13 683–6
[9] Ritter C, Morellon L, Algarabel P A, Magen C and Ibarra M R 2002 Phys. Rev. B 65 094405
[10] Rao G H 2000 J. Phys.: Condens. Matter 12 L93–9
[11] Boulet P, Weitzer F, Hiebl K and Noël H 2001 J. Alloys Compounds 315 75–81
[12] Gschneidner K A Jr, Pecharsky V K, Pecharsky A O, Ivchenko V V and Levin E M 2000 J. Alloys Compounds 303–4 214–22
[13] Powell B M 1990 Neutron News 1 16–20
[14] Rodríguez-Carvajal J 1993 Physica B 192 55–69
[15] Opechowski W and Guccione R 1965 Magnetism vol IIA, ed G T Rado and H Suhl (New York: Academic) ch 3, pp 105–65
[16] Joshua S J 1991 Symmetry Principles and Magnetic Symmetry in Solid State Physics (Bristol: Hilger)
[17] Hahn T (ed) 1996 International Tables for Crystallography vol A, 4th edn (Dordrecht: Kluwer Academic)