| Transition Temperature | 7 K |
|---|---|
| Experiment Temperature | 2 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | P4/nmm (#129) |
| Magnetic Space Group | P2'/c (#13.67) |
| Magnetic Point Group | 2'/m (5.3.14) |
| Lattice Parameters | 4.08370 4.08370 8.95670 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1103/physrevb.91.064418 |
| Reference | Q. Zhang, W. Tian, S.G. Peterson, K.W. Dennis and D. Vaknin, Physical Review B (2015) 91 064418. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Ce1 | Ce | 0.7 | 0.3 | 0.0 | 0.76 |
| Mn1 | Mn | -3.32 | 0.0 | 0.0 | 3.32 |
Spin reorientation and Ce-Mn coupling in antiferromagnetic oxypnictide CeMnAsO
Qiang Zhang, \( ^{1,2,*} \) Wei Tian, \( ^{3} \) Spencer G. Peterson, \( ^{1,2} \) Kevin W. Dennis, \( ^{1} \) and David Vaknin \( ^{1,2,\dagger} \)
\( ^{1} \) Ames Laboratory, Ames, Iowa, 50011, USA
\( ^{2} \) Department of Physics and Astronomy, Iowa State University, Ames, Iowa, 50011, USA
\( ^{3} \) Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA
(Received 12 November 2014; revised manuscript received 18 December 2014; published 18 February 2015)
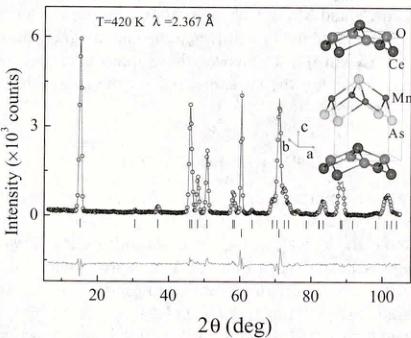
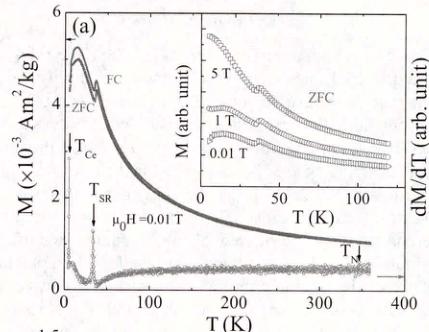
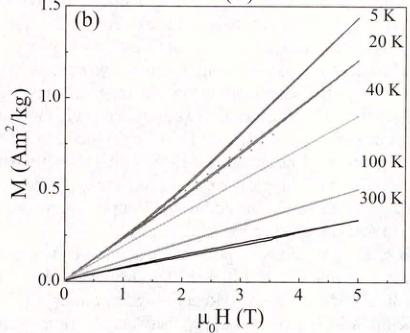
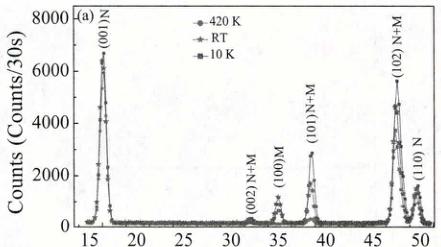
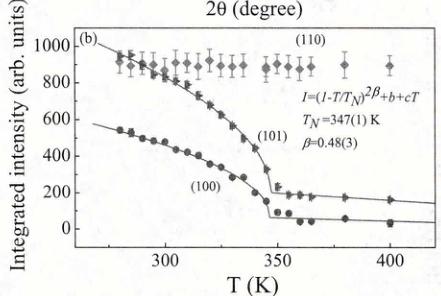
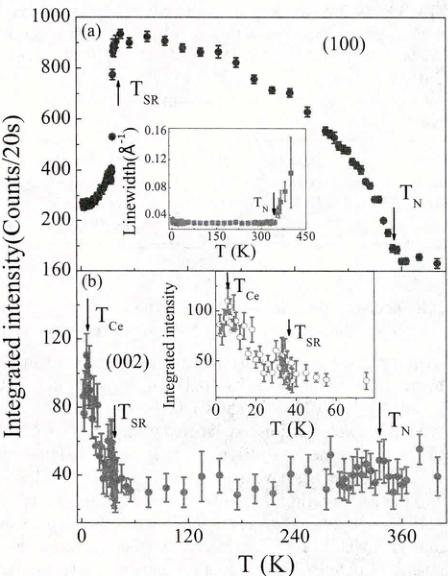
Structure and magnetic properties of high-quality polycrystalline CeMnAsO, a parent compound of the "1111"-type oxypnictides, have been investigated using neutron powder diffraction and magnetization measurements. We find that CeMnAsO undergoes a C-type antiferromagnetic order with \( Mn^{2+}(S=5/2) \) moments pointing along the c axis below a relatively high Néel temperature of \( T_{N}=347(1) \) K. Below \( T_{SR}=35 \) K, two simultaneous transitions occur where the Mn moments reorient from the c axis to the ab plane preserving the C-type magnetic order, and Ce moments undergo long-range AFM ordering with antiparallel moments pointing in the ab plane. Another transition to a noncollinear magnetic structure occurs below 7 K. The ordered moments of Mn and Ce at 2 K are \( 3.32(4)\mu_{B} \) and \( 0.81(4)\mu_{B} \) , respectively. We find that CeMnAsO primarily falls into the category of a local-moment antiferromagnetic insulator in which the nearest-neighbor interaction ( \( J_{1} \) ) is dominant with \( J_{2} DOI: 10.1103/PhysRevB.91.064418 PACS number(s): 74.25.Ha, 74.70.Xa, 75.50.Ee The discovery of superconductivity (SC) in LaFeAsO_{1-x}F_{x} [1] has triggered renewed interest in superconductivity and also in itinerant magnetism in general. In the Fe-based "1111" and "122" pnictides, the emergence of superconductivity is accompanied by the suppression of the stripe-like antiferromagnetic (AFM) ordering of Fe^{2+} and a tetragonal (T)-orthorhombic (O) structural transition [2]. It has also been suggested that AFM/structural fluctuations may be the driving forces for superconductivity [3]. In view of the prominent role of magnetism in driving superconductivity in the Fe-based pnictides, in particular by doping with transition-metal ions, systematic investigations of the magnetic and structural properties of the isostructural "1111" and "122" parent pnictides involving the square lattice of other transition metals are called for [4]. In fact, the various transition metals influence subtle and specific structural, magnetic, and electronic properties, which provides insight to understanding how the magnetism is related to the SC state [5]. Furthermore, compared with the parent "122" compounds, the parent "1111" oxypnictides RTAsO (R = magnetic and nonmagnetic rare earths, T = transition metals Fe, Co, Ni, Mn, etc.) are more intriguing as they offer the possibility to tweak an additional coupling between the rare-earth R and the transition-metal ions. CeFeAsO is an itinerant poor metal with a T-O structural transition at \( T_{S} \approx 150 \) K followed by stripe-like AFM order of Fe at \( T_{N} \approx 145 \) K [6]. Recent \( \mu \) SR studies [7] have indicated relatively strong coupling between the rare-earth Ce and Fe, and further neutron and x-ray scattering studies have shown the coupling leads to a gradual Fe spin-reorientation at low temperatures [8]. By contrast, in the heavy-fermion metal CeNiAsO [9], Ni does not order magnetically but two successive AFM transitions associated with Ce ions are observed [10]. In CeCoAsO, a ferromagnetic ordering is found below \( \sim75 \) K with no indication for Ce ordering at lower temperatures [11]. To date, little attention has been paid to CeMnAsO for which magnetization and heat capacity measurements indicate that Mn moments order above room temperature and a first-order magnetic transition emerges at \( \sim35 \) K, possibly related to a Mn spin reorientation [12]. It has also been proposed that the Ce spins do not undergo long range order but are parasitically induced to order below \( \sim35 \) K [12]. However, the AFM Néel temperature \( T_{N} \) , actual magnetic structures, the values of the ordered moments, and the interplay between Ce and Mn in CeMnAsO have not been determined. Here, we report neutron diffraction, and magnetization results on CeMnAsO to answer these questions, and also to critically compare the structure and magnetism with related pnictides. Previous reports on the synthesis of CeMnAsO used CeAs and \( Mn_{2}O_{3} \) [12] and added excess Ti as an oxygen getter which resulted in the formation of CeMnAsO with a secondary phase. In the present study, MnO and CeAs as starting materials were mixed thoroughly in stoichiometric proportions. (CeAs was prepared firstly by reacting Ce and As powder at \( 600\ ^{\circ}C \) for 35 h and then at \( 950\ ^{\circ}C \) for 8 h.) The mixed powder was sealed in an evacuated tantalum tube and sintered at \( 1150\ ^{\circ}C \) for 40 h. A single-phase polycrystalline CeMnAsO powder was then obtained and characterized by x-ray and neutron diffraction methods. Neutron powder diffraction (NPD) measurements on \( \approx \) 4-g CeMnAsO sample were conducted on the HB1A triple-axis spectrometer with a fixed-incident-energy 14.6 meV (located at the high flux isotope reactor, HFIR, at the Oak Ridge National Laboratory, USA). The measurements on HB1A were performed with an HOPG analyzer to lower background scattering (providing approximately 1-meV energy resolution). A thick block of HOPG was used to filter out the \( \lambda/2 \) component from the incident beam. The data between 2 < T < 300 K were collected using an orange cryostat and a high-temperature furnace was used for the measurements between 300 < T < 420 K. All the neutron diffraction data were analyzed using Rietveld refinement program Fullprof suite [13]. The temperature and magnetic field dependence of the magnetization were carried out in a superconducting quantum interference device (Quantum Design MPMS-75, SQUID) magnetometer. Neutron powder diffraction pattern at 420 K is shown in Fig. 1 indicating the purity of the material with no indication of a secondary phase in CeMnAsO, consistent with our x-ray diffraction measurement at room temperature (not shown here). Rietveld analysis confirms the tetragonal \( ZrCuSiAs-Te \) structure with space group P4/nmm, as illustrated in the inset of Fig. 1. Similar to the tetragonal structure in \( RFeAsO \) (R is a rare-earth element) [8] or LaMnAsO [14], the structure of CeMnAsO consists of MnAs and CeO layers where the \( Mn^{2+} \) ions form a square lattice. Our neutron diffraction results show no change in the crystal structure of this compound down to 2 K. The refined atomic positions, lattice constants, and volume of CeMnAsO at 420 K and the lowest measured temperature of 2 K are summarized in Table I. FIG. 1. (Color online) Rietveld refinement fit to neutron diffraction pattern at 420 K and a graphic representation of the crystal structure for CeMnAsO using the best fit parameters listed in Table I. The observed data and the fit are indicated by the open circles and solid lines, respectively. The difference curve is shown at the bottom. The vertical bars mark the positions of Bragg reflections for the phases of CeMnAsO (up) and Al sample holder (below). TABLE I. Refined atomic positions, lattice constants, lattice volume V at \(T = 420\) and 2 K for CeMnAsO space group \(P4/nmm\). Ce: \(2c\left(\frac{1}{4},\frac{1}{4},z\right)\); Mn: \(2b\left(\frac{3}{4},\frac{1}{4},\frac{1}{2}\right)\); As: \(2c\left(\frac{1}{4},\frac{1}{4},z\)); O: \(2a\left(\frac{3}{4},\frac{1}{4},0\right)\). The temperature dependence of the zero-field-cooled (ZFC) and field-cooled (FC) magnetization in Fig. 2(a) shows a clear magnetic transition at 35 K emphasized by a single peak in the first derivative of magnetization with no indication of additional anomaly up to 370 K. The anomaly at 35 K has been previously attributed to a spin reorientation (SR) transition of Mn [12]. Our susceptibility measurements show that this FIG. 2. (Color online) (a) Temperature dependence of the zero-field-cooling (ZFC) and FC magnetization in a low field of 0.01 T for CeMnAsO. The curve at the bottom shows the first derivative of FC curve with no indication of \( T_{N} \approx 347 \) K. The inset shows the temperature dependence of the ZFC magnetization at 0.01, 1, and 5 T. (b) Field dependence of magnetization at different temperatures in CeMnAsO. FIG. 3. (Color online) (a) Comparison of the neutron diffraction patterns at 420 K, RT, and 10 K. (b) Integrated intensity of (110), (100), and (101) reflections as a function of temperature with a fit to a power law with relevant parameters as shown in the figure. magnetic transition is not shifted by external magnetic fields up to 5 T in accordance with typical behavior of a spin reorientation transition (the transition temperature at 35 K is labeled \( T_{SR} \) hereafter). The thermal hysteresis of the magnetization below \( T_{SR} \) is indicative of the first-order nature of the transition. Below 7 K, both ZFC and FC magnetization decrease implying the emergence of another magnetic transition. We point out that such anomalous decrease below 7 K was not observed by Tsukamoto et al. presumably because of the influence of a secondary phase as mentioned in Ref. [12]. Interestingly, we do not observe a clear anomaly in the magnetization in the temperature range 35–370 K potentially identifying \( T_{N} \) . However, the neutron measurements of the (100) and (101) magnetic Bragg peaks shown in Fig. 3(b) exhibit a sharp increase in the integrated intensity below \( \approx347 \) K, which we identify as the AFM transition temperature \( T_{N} \) of the Mn sublattice. We note that a weak and broader (100) Bragg peak persists above \( T_{N} \) with a linewidth that increases with temperature indicating the presence of short-range ordered Mn spins above \( T_{N} \) , as shown in the inset of Fig. 4(a). This suggests the existence of strong spin fluctuations above \( T_{N} \) that tend to wash out any anomaly in the susceptibility at \( T_{N} \) even in its first derivative with respect to temperature. The absence or weak peak in the derivative of the susceptibility is characteristic of the two-dimensional nature of the Mn magnetic system with a strong inplane coupling that gives rise to short range fluctuating magnetic order, as has been found in other systems [15,16]. This is consistent with the overall behavior of the order parameters as a function of temperature as expressed in the (100) and the (101) magnetic reflections shown in FIG. 4. (Color online) (a) Temperature dependence of the integrated intensity of (100) peak. The inset shows the temperature dependence of the linewidth of (100) peak. (b) Temperature dependence of the integrated intensity of (002) peak. The inset shows a zoomed-in view at low temperatures below 80 K with a peak at T = 7 K that we attribute to additional magnetic transition in the Ce sublattice. Fig. 3(b). The intensity of both peaks is modeled by a power law: \[ I(T)=a(1-T/T_{N})^{2\beta}+b+c T, \quad (1) \] where a is an intensity scale factor (at T=0) and b and c account for background and signal temperature dependent above \( T_{N} \) . Our fit to both peaks yields \( T_{N}=347\pm1 \) K and \( \beta=0.47\pm0.03 \) . The overall temperature dependence with a relatively large \( \beta \) (compared to \( \beta=0.125 \) for the 2D Ising model or \( \beta\approx0.36 \) for the 3D Heisenberg model) has been explained for similar 2D system with inplane exchange coupling \( J_{1} \) that is much larger than interlayer one \( J_{c} \) , \( J_{c}/J_{1}<<1 \) [17]. Figure 2(b) shows magnetic field dependence of the magnetization at different temperatures. Whereas the magnetization at room temperature (RT) shows a very weak hysteresis, typical of AFM behavior, i.e., linear M versus H curve is observed in \( T_{SR} < T < T_{N} \) . Below \( T_{SR} \) , the magnetization first rises linearly at low fields indicative of an AFM behavior, with a weak jump in the slope at approximately 1.5 T, indicating a possible field-induced metamagnetic transition. However, the magnetization is far from saturation even at 5 T, indicating that the magnetic structure under magnetic field is mostly preserved, and that the external magnetic field induces a transformation to weakly canted AFM structures below \( T_{SR} \) . TABLE II. The symmetry-allowed basis vectors \( [m_{x}, m_{y}, m_{z}] \) for the space group P4/nmm with \( \mathbf{k} = (0,0,0) \) in CeMnAsO. Mn1: \( (0.75, 0.25, 0.5) \) , Mn2: \( (0.25, 0.75, 0.5) \) , Ce1: \( (0.25, 0.25, 0.126) \) , and Ce2: \( (0.75, 0.75, 0.874) \) . A comparison of the neutron diffraction patterns at different temperature windows \( T > T_{N} \) (420 K), \( T_{SR} < T < T_{N} \) (RT), \( 7 K < T < T_{SR} \) (10 K) is shown in Fig. 3(a) (nuclear and magnetic Bragg reflections are labeled N and M, respectively). At RT, whereas the (100) Bragg peak is purely magnetic, the (101) and (102) peaks have nuclear and magnetic contributions due to the Mn ordering. At 10 K (below \( T_{SR} \) ), the intensity of the (100) peak decreases dramatically whereas the intensities of the (101) and (102) increase, evidence for a change in magnetic structure. The magnetic contribution to the (002) nuclear peak below \( T_{N} \) is negligible, however it increases below \( T_{SR} \) and peaks at \( \approx7 \) K [see Fig. 4(b)]. As discussed below, the intensities of the (100) and (002) peaks reflect the order parameters of Mn and Ce moments, respectively. All the magnetic reflections can be indexed on the high-temperature nuclear (chemical) unit cell with a magnetic propagation vector \( k = (0,0,0) \) . SARAH representational analysis program [18] is used to derive the symmetry allowed magnetic structures. The decomposition of the magnetic representation ( \( \Gamma_{Mag} \) ) into the irreducible representations is \( \Gamma_{3}^{1} + \Gamma_{6}^{1} + \Gamma_{9}^{2} + \Gamma_{10}^{2} \) and \( \Gamma_{2}^{1} + \Gamma_{3}^{1} + \Gamma_{9}^{2} + \Gamma_{10}^{2} = \Gamma_{2}^{1} + \Gamma_{3}^{1} + \Gamma_{6}^{1} + \Gamma_{10}^{2} \) for Mn sites and Ce sites, respectively. The symmetry allowed basis vectors are summarized in Table II. There are two FM ( \( \Gamma_{3}^{1} \) and \( \Gamma_{9}^{2} \) ) and three AFM ( \( \Gamma_{1}^{1} \) , \( \Gamma_{6}^{1} \) , and \( \Gamma_{10}^{2} \) ) solutions. However, the two FM solutions can be discarded at all temperatures as there is no FM contribution to the nuclear Bragg reflections in our neutron diffraction patterns consistent with the magnetization measurements below \( T_{N} \) . Thus only the three AFM solutions are considered for the data refinement to obtain the magnetic structures at different temperature windows. Rietveld refinement fits to neutron diffraction patterns and the graphic representation of the determined magnetic structures of CeMnAsO at different temperatures are shown in Fig. 5. In \( T_{SR} < T < T_{N} \) , there is no evidence for Ce moment ordering and the neutron diffraction pattern is best fitted using \( \Gamma_{6}^{1} \) model, i.e., the Mn spins are antiparallel at Mn1 and Mn2 sites, forming a nearest-neighbor antiferromagnetic alignment in ab plane and the planes are stacked ferromagnetically along c axis, i.e., C-type AFM order with the Mn moments along c axis, as shown in Fig. 5(a) at 45 K. As the temperature decreases to \( T_{SR} \) , the magnetic structure is preserved and the Mn magnetic moment gradually increases with an average moment \( 2.29(3)\mu_{B} \) at RT and \( 2.78(2)\mu_{B} \) at 45 K. In the temperature range \( 7 K < T < T_{SR} \) , the refinement of the neutron diffraction patterns are not satisfactory with (a) FIG. 5. (Color online) Rietveld refinement fits to neutron diffraction patterns and the graphic representations of the determined magnetic structures of CeMnAsO at (a) 45, (b) 10, and (c) 2 K. The observed data and the fit are indicated by the open circles and solid lines, respectively. The difference curve is shown at the bottom. The vertical bars mark the positions of Bragg reflections for the nuclear phase (up) and magnetic phase (down) in CeMnAsO. The middle vertical bars in (c) mark the positions of the phase of Al sample holder. The inset of (b) shows the temperature dependence of the linewidth of (002) peak. the assumption of Mn ordering only and the ordering of Ce magnetic moments is required to obtain good agreement with the data. Trial refinements assuming a linear combination of the \( \Gamma_{6}^{1} \) of Mn sites and \( \Gamma_{2}^{1} \) of Ce sites, \( \Gamma_{10}^{2} \) of Mn sites and \( \Gamma_{2}^{1} \) of C sites, or \( \Gamma_{6}^{1} \) of Mn sites and \( \Gamma^{2}_{10} \) of C sites do not fit the data well. A satisfactory fit to the diffraction patterns below \( T_{SR} \) is obtained by using \( \Gamma_{10}^{2} \) , i.e., antiparallel Ce spins at Ce1 and Ce2 sites and antiparallel Mn spins at Mn1 and Mn2 sites with ordered Mn and Ce moments in the ab plane. Thus, Mn maintains the C-type magnetic structure but the ordered Mn magnetic moments reorient to the ab plane, and simultaneously the Ce spins align antiferromagnetically along c, similar to the magnetic structure in PrMnSbO [19] and NdMnAsO [20] below their SR transitions. It is impossible to determine the absolute angle between Mn (or Ce) moments with respect to a axis in ab plane due to the tetragonal nature. FIG. 6. (Color online) Schematic illustration of the proposed magnetic structures for Ce and Mn sublattices in the CeMnAsO. Note that different ac and ab planes are used to illustrate the magnetic structures above and below \( T_{SR} \) , respectively. of the system, nevertheless we show both Mn and Ce moments along a axis in Fig. 5(b). Note that there is no significant broadening of the (002) peak below/above \( T_{SR} \) , as shown in the temperature dependence of its linewidth [see the inset of Fig. 5(b)] indicating long-range ordered Ce below \( T < T_{SR} \) . Below \( T_{SR} \) , whereas there is no anomaly at 7 K in the intensity of the (100) reflection [see Fig. 4(a)], the intensity of the (002) reflection increases slightly peaking at \( \sim7 \) K [see Fig. 4(b)], consistent with the peak in the magnetization shown in Fig. 2(a), which confirms there is another magnetic transition in the Ce sublattice. Furthermore, the good refinement of the neutron diffraction pattern at 2 K is still obtained by using \( \Gamma_{10}^{2} \) model within uncertainties. Since the refinement using \( \Gamma_{10}^{2} \) model of Ce1 and Ce2 spins requires antiparallel and confined spins to the ab plane, it is very likely that the transition observed at 7 K is due to a finite angle between Ce and Mn spins, forming a noncollinear magnetic structure between Ce and Mn moments as theoretically predicted [21]. However, we emphasize that our powder data is not sufficiently sensitive to determine the accurate relative angle between Ce and Mn moments. The quality of the refinement to the 2 K data has a tendency to be slightly improved when this angle is increased from \( 0^{\circ} \) to \( \sim20^{\circ} \) . The best refinement results using a \( 20^{\circ} \) angle are shown in Fig. 5(c). At 2 K, the average ordered Mn moment is \( 3.32(4)\mu_{B} \) whereas the average ordered Ce moment is in the range of \( 0.75(3)-0.81(4)\mu_{B} \) (depending on the relative angle between Ce and Mn moments). The reduced Mn ordered moment (from that of S=5/2; \( \sim5\mu_{B} \) for an ideal localized moment) in CeMnAsO is likely due to the spin-dependent hybridization between the Mn 3d and As 4p orbitals as in BaMnAsF [22] and BaMn \( _{2} \) As \( _{2} \) [23] that all share similar MnAs layer. Such hybridization was also noted for iron based pnictides such as SrFe \( _{2} \) As \( _{2} \) [24]. It is worthwhile noting that the (002) peak intensity and the peak in the susceptibility at 7 K in CeMnAsO are different from the observations in the isostructural NdMnAsO in which both the intensity of the magnetic peak and the susceptibility saturate below 4 K with no indication of a magnetic transition in the Nd sublattice [20]. Our proposed schematic illustration of the magnetic transitions in CeMnAsO is summarized in Fig. 6. The ordered Mn moments 3.32(4) \(\mu_{B}\) at 2 K compared to the 5 \(\mu_{B}\) expected from a localized moment indicate that in the spectrum of itinerant versus local-moment AFM, CeMnAsO tends to be the latter [12]. This is different from the itinerant CeFeAsO with a much lower ordered Fe moment of \(\sim0.9\mu_{B}\) compared to the 4\(\mu_{B}\) expected from a localized moment [8]. The inplane checker-board-like AFM structure of the C-type order in CeMnAsO in \(T Another significant difference between CeMnAsO and CeFeAsO is that the T-O structural transition observed above \( T_{N} \) in CeFeAsO is absent in CeMnAsO. It is generally accepted that the T-O structural transition in CeFeAsO and other “1111” Fe-based pnictides has a magnetic origin [27] and is induced by magnetic fluctuations [28,29]. The stripelike AFM structure in “1111” Fe-based pnictides can be separated into two Néel sublattices each defined by NNN Fe spins in the basal plane [30]. Due to \( J_{2} > J_{1}/2 \) , there is a strong frustration between the two sublattices and the orthorhombic distortion reduces the frustration and lowers the total energy (magnetic and elastic energy) [27,28,30]. The absence of such magnetic frustration may explain the absence of a T-O structural transition in CeMnAsO. This is further consistent with the absence of the T-O transition in the isostructural BaMnAsF [22], and in the Mn-based “122” systems \( BaMn_{2}As_{2} \) [27]. The AFM structure in both systems is G type with the NN Mn spins antiparallel along all the directions and moments along the c axis. We note that the T-O transition at \( \approx35 \) K found in PrMnSbO below its \( T_{N}=230 \) K is likely driven by local f electrons in \( Pr^{3+} \) , unlike the T-O transition in the “1111” Fe-based pnictides driven by the transition metal magnetism. Different from PrMnSbO, no structural transition below \( T_{N} \) is observed in CeMnAsO, the mechanism of which deserves further investigations. As compared to \( BaMn_{2}As_{2} \) with antiparallel Mn spins along c axis, the parallel Mn spins along c axis in \( CeMnAsO \) suggests that the interlayered magnetic interaction \( J_{c} > 0 \) in \( BaMn_{2}As_{2} \) but \( J_{c} < 0 \) in \( CeMnAsO \) . The Néel temperature of 625 K in \( BaMn_{2}As_{2} \) with three-dimensional magnetism is much higher than 347 K in \( CeMnAsO \) . Assuming the inplane exchange coupling \( J_{1} \) is of the same order of magnitude this implies a much weaker magnetic interlayer interaction \( J_{c} \) in \( CeMnAsO \) , however, with strong 2D correlations (fluctuated) as discussed above. The much weaker interlayer magnetic interaction due to the longer distance between adjacent MnAs layers leads to a quasi-two-dimensional AFM character in \( CeMnAsO \) similar to other “1111” systems [31]. For the doped Fe-based superconductors, it is commonly observed that the emergence of the SC is accompanied with the suppression of both the structural and magnetic transitions with \( J_{2} > J_{1}/2 \) . However, for CeMnAsO, there is no evidence for T-O structural transition and \( J_{2} < J_{1}/2 \) . Further, CeMnAsO is a local moment antiferromagnet in contrast to the itinerant antiferromagnetism in Fe-based superconductors. Both indicate that Mn at the transition-metal site may prevent the emergence of superconductivity in Mn-doped “1111” and “122” Fe-based pnictides, which is supported by experimental evidence that the substitution of Mn for Fe in \( \mathrm{Ba(Fe_{1-x}Mn_{x})_{2}Mn_{2}} \) does not induce SC [33]. The Mn SR transition is not observed in \( LaMnAsO \) [20], \( BaMnAsF \) [22], or \( BaMn_{2}As_{2} \) [27] where there is no magnetic rare-earth ion, but is found in \( CeMnAsO \) and \( NdMnAsO \) [20], which indicates the SR transition in \( CeMnAsO \) is driven by the coupling between rare-earth Ce and Mn. The \( Mn^{2+} \) moment, commonly displays very weak single-ion anisotropy as expected for the \( L=0 \) of \( Mn^{2+} \) [32], favors orientation along the c axis. As soon as \( Ce^{3+} \) spins ( \( S=1/2 \) and \( L=3 \) ) order below 35 K, the Ce-Mn coupling exerts an effective field that induces a flop of \( Mn^{2+} \) spins to the basal plane. We point out that there is also a spin reorientation in \( CeFeAsO \) [8] and \( CeCrAsO \) [12] but not in \( CeCoAsO \) [11] or \( CeNiAsO \) [10]. In \( CeFeAsO \) , the stripelike \( Fe^{2+} \) spins rotate uniformly and gradually in the ab plane below \( \approx14 \) K and the SR of Cr occurs at \( \approx36 \) K. Recently, we performed neutron diffraction measurements on \( CeCoAsO \) and confirmed the FM behavior of Co without evidence for a Co SR transition or Ce ordering in agreement with previously reported studies [11]. SR of transition-metal ions Mn, Fe, Cr, has also been observed in other systems due to the coupling between magnetic rare-earth f and transition-metal d moments, such as in \( RFeO_{3} \) (R = Ce and Nd) [34], \( RFe_{2} \) (R = Ce and Nd) [35], \( R_{2}Fe_{14}B \) (R = Nd and Er) [36], hexagonal \( HoMnO_{3} \) [37], and \( RCrO_{3} \) (R = Ce, Nd, and Sm) [38]. In summary, we report on the structure and magnetic properties in CeMnAsO. Whereas no structural transition is observed above and below the Néel temperature in tetragonal CeMnAsO, it exhibits a set of complex magnetic transitions. We find two-dimensional short-range ordered Mn (most likely dynamic in nature, i.e., spin fluctuations) above \( T_{N} = 347(1) \) K. Below \( T_{N} \) , the Mn spins order in a C-type AFM structure with moments pointing along the c axis. A spin reorientation of the Mn moments from the c axis to the ab plane, while keeping the C-type order occurs below \( T_{SR} = 35 \) K, is induced by long-range ordering of the Ce via Ce-Mn coupling. Below 7 K, the collinear magnetic structure transforms to a noncollinear one with an angle between the Ce and Mn moments. A possible field-induced metamagnetic transition is observed below \( T_{SR} \) in magnetization measurements. The local-moment antiferromagnetism with dominant NN interaction and negligible NNN interaction with \( J_{2} < J_{1}/2 \) in CeMnAsO contrasts with the itinerant antiferromagnetism in CeFeAsO with \( J_{2} > J_{1}/2 \) . We also point out that the spin reorientation transition is common not only to Mn, but also to Fe or Cr ions in the oxypnictides and other oxides or intermetallics induced by strong coupling between rare-earth R and the transition-metal ions. Research at Ames Laboratory is supported by the U.S. Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering under Contract No. DE-AC02-07CH11358. Use of the high flux isotope reactor at the Oak Ridge National Laboratory, was supported by the U.S. Department of Energy, Office of Basic Energy Sciences, Scientific User Facilities Division. [1] Y. Kamihara, T. Watanabe, M. Hirano, and H. Hosono, J. Am. Chem. Soc. 130, 3296 (2008). [2] P. C. Canfield and S. L. Bud'ko, Annu. Rev. Cond. Mat. Phys. 1, 27 (2010). [3] P. J. Hirschfeld, M. M. Korshunov, and I. I. Mazin, Rep. Prog. Phys. 74, 124508 (2011); A. V. Chubukov, Annu. Rev. Cond. Mat. Phys. 3, 57 (2012). [4] J. Zhao, D. T. Adroja, D. Yao, R. Bewley, S. Li, X. F. Wang, G. Wu, X. H. Chen, J. Hu, and P. Dai, Nat. Phys. 5, 555 (2009). [5] H. Ohta, Phys. Rev. B 79, 184407 (2009). [6] J. Zhao, Q. Huang, Clarina de la. Cruz1, S. Li, J. W. Lynn, Y. Chen, M. A. Green, G. F. Chen, G. Li, Z. Li, J. L. Luo, N. L. Wang, and P. Dai, Nat. Mater. 7, 953 (2008). [7] H. Maeter, H. Luetkens, Yu. G. Pashkevich, A. Kwadrin, R. Khasanov, A. Amato, A. A. Gusev, K. V. Lamonova, D. A. Chervinskii, R. Klingeler, C. Hess, G. Behr, B. Büchner, and H.-H. Klauss, Phys. Rev. B 80, 094524 (2009). [8] Q. Zhang, W. Tian, H. Li, J.-W. Kim, J. Yan, R. W. McCallum, T. A. Lograsso, J. L. Zarestky, S. L. Bud'ko, R. J. McQueeney, and D. Vaknin, Phys. Rev. B 88, 174517 (2013). [9] Y. K. Luo, L. Pourovskii, S. E. Rowley, Y. Li, C. Feng, A. Georges, J. Dai, G. Cao, Z. Xu, Q. Si, and N. P. Ong, Nat. Mater. 13, 777 (2004). [10] Y. K. Luo, H. Han, H. Tan, X. Lin, Y. Li, S. Jiang, C. Feng, J. Dai, G. Cao, Z. Xu, and S. Li, J. Phys.: Condens. Matter 23, 175701 (2001). [11] R. Sarkar, A. Jesche, C. Krellner, M. Baenitz, C. Geibel, C. Mazumdar, and A. Poddar, Phys. Rev. B 82, 054423 (2010). [12] Y. Tsukamoto, Y. Okamoto, K. Matsuhira, M. Whangbo, and Z. Hiroi, J. Phys. Soc. Jpn. 80, 094708 (2011). [13] J. Rodriguez-Carvajal, Physica B 192, 55 (1993). [14] T. Hanna, S. Matsuishi, K. Kodama, T. Otomo, S.-I. Shamoto, and H. Hosono, Phys. Rev. B 87, 020401(R) (2013). [15] D. Vaknin, E. Caignol, P. K. Davies, J. E. Fischer, D. C. Johnston, and D. P. Goshorn, Phys. Rev. B 39, 9122 (1989). [16] D. Vaknin, S. K. Sinha, C. Stassis, L. L. Miller, and D. C. Johnston, Phys. Rev. B 41, 1926 (1990). [17] A. Singh, Z. Tešanović, H. Tang, G. Xiao, C. L. Chien, and J. C. Walker, Phys. Rev. Lett. 64, 2571 (1990). [18] A. S. Wills, Physica B 276-278, 680 (2000). [19] S. A. J. Kimber, A. H. Hill, Y.-Z. Zhang, H. O. Jeschke, R. Valenti, C. Ritter, I. Schellenberg, W. Hermes, R. Pöttgen, and D. N. Argyriou, Phys. Rev. B 82, 100412(R) (2010). [20] N. Emery, E. J. Wildman, J. M. S. Skakle, A. C. Mclaughlin, R. I. Smith, and A. N. Fitch, Phys. Rev. B 83, 144429 (2011). [21] C. Lee, E. Kan, H. Xiang, R. K. Kremer, S. Lee, Z. Hiroi, and Z. Whangbo, Inorg. Chem. 51, 6890 (2012). [22] B. Saparov, D. J. Singh, V. O. Garlea, and A. S. Sefat, Sci Rep. 3, 2154 (2013). [23] J. An, A. S. Sefat, D. J. Singh, and M.-H. Du, Phys. Rev. B 79, 075120 (2009). [24] Y. Lee, D. Vaknin, H. Li, W. Tian, J. L. Zarestky, N. Ni, S. L. Bud'ko, P. C. Canfield, R. J. McQueeney, and B. N. Harmon, Phys. Rev. B 81, 060406(R) (2010); A. Marcinkova, T. C. Hansen, C. Curfs, S. Margadonna, and J. W. G. Bos, ibid. 82, 174438 (2010). [25] D. C. Johnston, R. J. McQueeney, B. Lake, A. Honecker, M. E. Zhitomirsky, R. Nath, Y. Furukawa, V. P. Antropov, and Y. Singh, Phys. Rev. B 84, 094445 (2011). [26] M. J. Calderón, G. León, B. Valenzuela, and E. Bascones, Phys. Rev. B 86, 104514 (2012). [27] Y. Singh, M. A. Green, Q. Huang, A. Kreyssig, R. J. McQueeney, D. C. Johnston, and A. I. Goldman, Phys. Rev. B 80, 100403 (2009). [28] R. M. Fernandes, A. V. Chubukov, and J. Schmalian, Nat. Phys. 10, 97 (2014). [29] Q. Zhang, R. M. Fernandes, J. Lamsal, J. Yan, S. Chi, G. S. Tucker, D. K. Pratt, J. W. Lynn, R. W. McCallum, P. C. Canfield, T. A. Lograsso, A. I. Goldman, D. Vaknin, and R. J. McQueeney, Phys. Rev. Lett. 114, 057001 (2015). [30] R. M. Fernandes, L. H. VanBebber, S. Bhattacharya, P. Chandra, V. Keppens, D. Mandrus, M. A. McGuire, B. C. Sales, A. S. Sefat, and J. Schmalian, Phys. Rev. Lett. 105, 157003 (2010). [31] M. Ramazanoglu, J. Lamsal, G. S. Tucker, J.-Q. Yan, S. Calder, T. Guidi, T. Perring, R. W. McCallum, T. A. Lograsso, A. Kreyssig, A. I. Goldman, and R. J. McQueeney, Phys. Rev. B 87, 140509(R) (2013). [32] R. Toft-Petersen, N. H. Andersen, H.-F. Li, J. Li, W. Tian, S. L. Bud'ko, T. B. S. Jensen, C. Niedermayer, M. Laver, O. Zaharko, J. W. Lynn, and D. Vaknin, Phys. Rev. B 85, 224415 (2012). [33] A. Thaler, H. Hodovanets, M. S. Torikachvili, S. Ran, A. Kracher, W. Straszheim, J. Q. Yan, E. Mun, and P. C. Canfield, Phys. Rev. B 84, 144528 (2011). [34] S. J. Yuan, L. Li, T. F. Qi, S. X. Cao, J. C. Zhang, L. E. DeLong, and G. Cao, J. Appl. Phys. 114, 113909 (2013); J. Bartolomé, E. Palacios, M. D. Kuz'min, F. Bartolomé, I. Sosnowska, R. Przeniosło, R. Sonntag, and M. M. Lukina, Phys. Rev. B 55, 11432 (1997). [35] K. P. Belov, A. K. Zvezdin, A. M. Kadomtseva, and R. Z. Levitin, Usp. Fiz. Nauk 119, 447 (1976). [36] K. Y. Guslienko, X. C. Kou, and R. Grössinger, J. Magn. Magn. Mater. 150, 383 (1995). [37] O. P. Vajk, M. Kenzelmann, J. W. Lynn, S. B. Kim, and S.-W. Cheong, Phys. Rev. Lett. 94, 087601 (2005). [38] Y. Cao, W. Ren, Z. Feng, S. Yuan, B. Kang, B. Lu, and J. Zhang, Appl. Phys. Lett. 104, 232405 (2014), and references therein. Copyright of Physical Review B: Condensed Matter & Materials Physics is the property of American Physical Society and its content may not be copied or emailed to multiple sites or posted to a listserv without the copyright holder's express written permission. However, users may print, download, or email articles for individual use.I. INTRODUCTION
II. EXPERIMENTAL DETAILS
III. RESULTS AND DISCUSSION
A. Crystalline structure

T Atom Atomic position a ( \( \textup{\AA} \) ) c ( \( \textup{\AA} \) ) V ( \( \textup{\AA}^{3} \) ) 420 K Ce z = 0.1263(6) 4.1032(2) 9.0038(3) 151.594(8) As z = 0.6696(4) 2 K Ce z = 0.1287(4) 4.0837(3) 8.9567(4) 149.370(6) As z = 0.6720(5) B. Multiple magnetic transitions and field-induced metamagnetic transition revealed in magnetization measurements





Atom \( \Gamma_{2}^{1} \) \( \Gamma_{3}^{1} \) \( \Gamma_{6}^{1} \) \( \Gamma_{9}^{2} \) \( \Gamma_{10}^{2} \) Mn1 [0 0 m_{z}] [0 0 m_{z}] [m_{x} m_{y} 0] [m_{x} m_{y} 0] Mn2 [0 0 m_{z}] [0 0 -m_{z}] [m_{x} m_{y} 0] [-m_{x} -m_{y} 0] Ce1 [0 0 m_{z}] [0 0 m_{x}] [m_{x} m_{y} 0] [m_{x}, m_{y} 0] Ce2 [0 0 -m_{z}] [0 0 m_{z}] [m_{x} x y 0] [-m_{x} -m_{y} 0] C. Evidence of Mn spin reorientation and long-range Ce spin orderings determined by NPD measurements


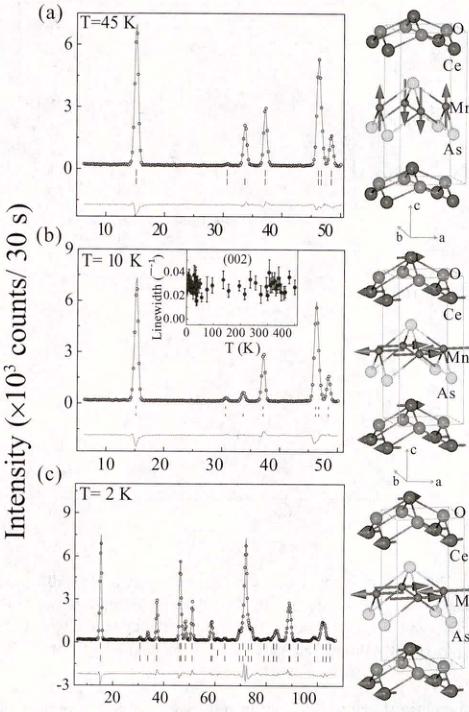
D. Magnetic interactions and absence of T-O structural transitions above and below \( T_{N} \)
E. Ce-Mn coupling
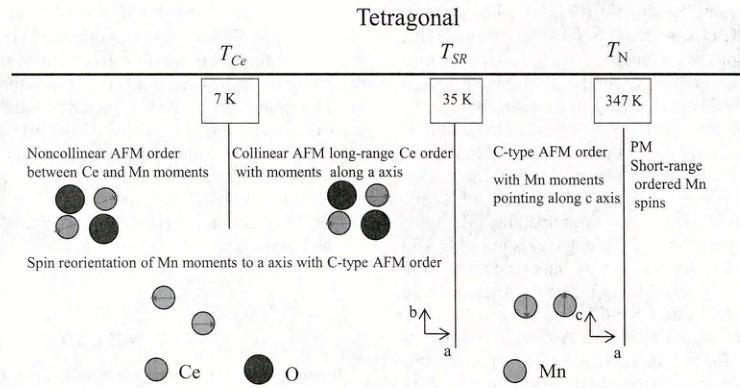
IV. CONCLUSION
ACKNOWLEDGMENTS