| Transition Temperature | 120 K |
|---|---|
| Experiment Temperature | 8 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | P21/c (#14) |
| Magnetic Space Group | P21'/c' (#14.79) |
| Magnetic Point Group | 2'/m' (5.5.16) |
| Lattice Parameters | 5.65140 5.63780 7.97310 90.00 90.20 90.00 |
|---|---|
| DOI | 10.1088/0953-8984/16/1/013 |
| Reference | G. Popov, M.V. Lobanov, E.V. Tsiper, M. Greenblatt, E. ad N Caspi, A. Borissov, V. Kiryukhin and J.W. Lynn, Journal of Physics: Condensed Matter (2003) 16 135-145. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Mn1 | Mn | 4.16 | 1.27 | 1.1 | 4.48 |
| Re1 | Re | 0.2 | -0.07 | -0.9 | 0.93 |
Crystallographic and magnetic structure of the \( Sr_{2}MnReO_{6} \) double perovskite
This content has been downloaded from IOPscience. Please scroll down to see the full text.
2004 J. Phys.: Condens. Matter 16 135
(http://iopscience.iop.org/0953-8984/16/1/013)
View the table of contents for this issue, or go to the journal homepage for more
Download details:
IP Address: 130.127.238.233
This content was downloaded on 14/01/2015 at 11:48
Please note that terms and conditions apply.
Crystallographic and magnetic structure of the \( Sr_{2}MnReO_{6} \) double perovskite
Guerman Popov \( ^{1,5} \) , Maxim V Lobanov \( ^{1} \) , Eugene V Tsiper \( ^{1,6} \) , Martha Greenblatt \( ^{1,7} \) , El'ad N Caspi \( ^{2} \) , Alexandre Borissov \( ^{3} \) , Valery Kiryukhin \( ^{3} \) and Jeffrey W Lynn \( ^{4} \)
\( ^{1} \) Department of Chemistry and Chemical Biology, Rutgers University, 610 Taylor Road, Piscataway, NJ 08854, USA
\( ^{2} \) Materials Science Division, Argonne National Laboratory, Argonne, IL 60439, USA
\( ^{3} \) Department of Physics and Astronomy, Rutgers University, 136 Frelinghuysen Road, Piscataway, NJ 08854, USA
\( ^{4} \) NIST Center for Neutron Research, National Institute of Standards and Technology, 100 Bureau Drive, Stop 8562, Gaithersburg, MD 20899, USA
E-mail: greenblatt@rutchem.rutgers.edu
Received 6 August 2003
Published 15 December 2003
Online at stacks.iop.org/JPhysCM/16/135 (DOI: 10.1088/0953-8984/16/1/013)
Abstract
The crystal and magnetic structure of the ordered double perovskite \( Sr_{2}MnReO_{6} \) was investigated by neutron diffraction. Monoclinic (space group \( P2_{1}/n \) ) distortion of the parent cubic double perovskite structure was revealed, and the refined Mn–O–Re bond angles deviate significantly from \( 180^{\circ} \) . The monoclinic distortion produces antisymmetric exchange interactions, leading to a canted magnetic structure, for which a possible model is proposed and refined. No structural transitions were observed upon cooling or in an external magnetic field. Complementary x-ray synchrotron diffraction data support the neutron diffraction findings.
1. Introduction
The discovery of high tunnelling magnetoresistance \( [1] \) in the \( Sr_{2}FeMoO_{6} \) double perovskite (DP) stimulated the search for similar effects in related double perovskites. Recently a series of isoelectronic \( (\mathrm{d}^{5}-\mathrm{d}^{1}) \) Mn–Re DPs, \( Ba_{2-x}Sr_{x}MnReO_{6} \) , have been synthesized and investigated by laboratory powder x-ray diffraction (PXD) and dc magnetization \( [2] \) . In particular, \( Sr_{2}MnReO_{6} \) showed anomalous field-dependent magnetization isotherms with a
significant difference between field-cooled (FC) and zero-field-cooled (ZFC) regimes, as well as unusual discontinuities in the magnetization isotherms at \( H \sim 3 \) T.
In this work we present the results of high-resolution neutron powder diffraction (ND) studies of the structural and magnetic properties of \( Sr_{2}MnReO_{6} \) . In order to investigate the effect of magnetic field on the magnetic structure, experiments in external magnetic fields of up to 5 T were performed under both FC and ZFC conditions. Complementary x-ray synchrotron diffraction measurements were also performed, and the results support the ND findings concerning the crystallographic structure.
2. Experimental details
Single-phase \( Sr_{2}MnReO_{6} \) was synthesized by heating a stoichiometric mixture of SrO, MnO and \( ReO_{3} \) in evacuated silica tubes at \( 1000^{\circ}C \) for a total time of 170 h with two intermediate grindings. Details of the procedure are given in [2].
Neutron powder diffraction data were collected using the high-resolution BT-1 32 detector neutron powder diffractometer at the NIST Center for Neutron Research. The sample was sealed in a vanadium container inside a dry He-filled glove-box. A closed-cycle He refrigerator was used for temperature control. A \( \mathrm{Cu(311)} \) monochromator with a \( 90^{\circ} \) take-off angle, \( \lambda = 1.5402(1) \) Å, and in-pile collimation of 15 min of arc were used. Data were collected over the range of \( 3^{\circ}-168^{\circ} \) \( 2\theta \) with a step size of \( 0.05^{\circ} \) . The instrument is described in the NCNR Website (http://www.ncnr.nist.gov/). An external magnetic field was produced by a CT-MAG bottom-loading vertical field magnet. The GSAS program [3] with the EXPGUI interface [4] was used for the Rietveld analysis.
High-resolution synchrotron x-ray diffraction (SXD) data were collected on the X22C beamline at the National Synchrotron Light Source, Brookhaven National Laboratory. Data were collected at \( T = 8 \, K \) . Bragg–Brentano geometry was used with the direct synchrotron beam monochromated by a double Ge(111) crystal monochromator ( \( \lambda = 1.48788 \, \AA \) ). Data were collected using the Ge(111) crystal analyser.
3. Results and discussion
3.1. Crystallographic structure
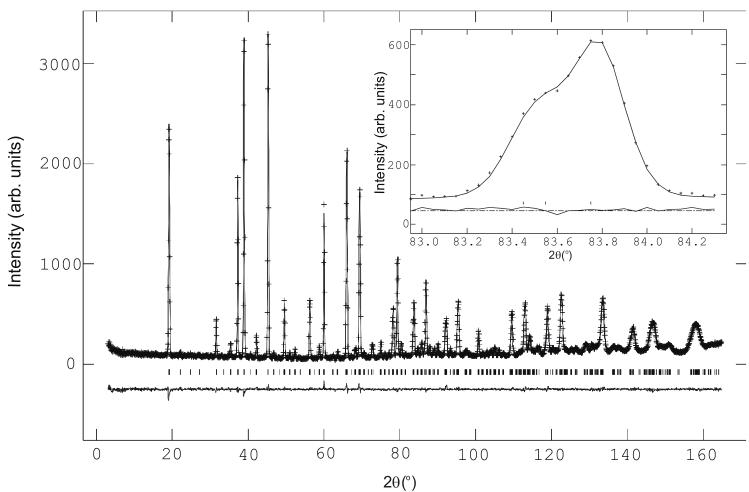
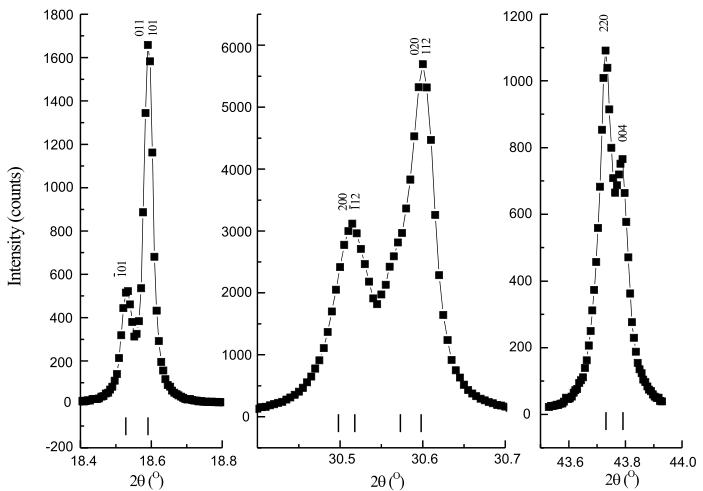
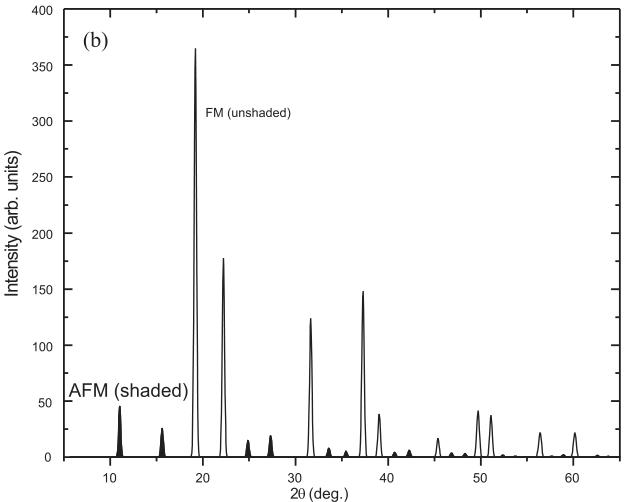
\( Sr_{2}MnReO_{6} \) was previously reported as an undistorted double perovskite structure (space group \( Fm\overline{3}m \) ) based on laboratory PXD data [2]. However, the room temperature (RT) ND spectrum showed split reflections and superlattice peaks, consistent with a primitive monoclinic lattice (figure 1(a)). The same splitting pattern is observed in the 8 K SXD data (figure 1(b)), and a Rietveld refinement of the crystallographic model described below is in good agreement with both RT ND data and 8 K SXD data.
The monoclinic distortion is described in the \( P2_{1}/n \) space group (Glazer tilt system \( a^{+}b^{-}b^{-} \) ), corresponding to a 'classic' Pnma structure of simple perovskites, which is commonly observed in double perovskite compounds [5]. Attempts to refine thermal factors (TFs) anisotropically led to some negative eigenvalues of thermal tensors, hence the final refinements were performed with isotropic TFs. Unconstrained refinement of Mn and Re occupation numbers resulted in zero antisite Mn/Re mixing. The Rietveld fit of the RT spectrum is shown in figure 1(a). Atomic parameters and reliability factors are summarized in table 1 and selected interatomic distances and bond angles are shown in table 2. The Mn–O interatomic distances are consistent with the \( Mn^{2+} \) oxidation state. The calculated bond valence sum at RT for the Mn ion, s = 2.23, and the three Mn–O distances are nearly identical (table 2), which rules out the presence of a Jahn–Teller active \( Mn^{3+} \) ion. Oxygen occupancy
(a)

(b)

Figure 1. (a) Observed, calculated and difference powder neutron diffraction profiles of \( Sr_{2}MnReO_{6} \) at room temperature, with reflection positions marked. Inset: \( (440)_{\mathrm{c}} \) peak showing splitting into \( (404)_{\mathrm{m}} \) , \( (404)_{\mathrm{m}} \) , \( (044)_{\mathrm{m}} \) due to monoclinic distortion. (b) Selected peaks from the SXD pattern (T = 8 K), showing monoclinic splitting. Miller indices are shown.
Table 1. Refined structural parameters of \( Sr_{2}MnReO_{6} \) at 300 and 8 K. Rietveld analyses of powder neutron diffraction data were done in the \( P2_{1}/n \) space group with the following atomic positions: Sr at 4e (x, y, z), Mn at 2c (0, 1/2, 0), Re at 2d (1/2, 0, 0), O1, O2 and O3 at 4e (x, y, z). \( B_{iso} \) is the isotropic thermal (atomic displacement) parameter. Occupancies (frac) of all oxygen sites were constrained to the same value due to correlation with thermal parameters. At 8 K the occupancies were fixed at the RT values. 8 K data correspond to the unconstrained \( P2_{1}^{\prime}/n^{\prime} \) model for the magnetic structure. Numbers in parentheses represent standard deviation of the last significant digits.
| 300 K | 8 K | ||
| a ( \( \textup{\AA} \) ) | 5.667 98(8) | 5.651 39(9) | |
| b ( \( \textup{\AA} \) ) | 5.645 06(8) | 5.637 80(9) | |
| c ( \( \textup{\AA} \) ) | 7.9900(1) | 7.9731(1) | |
| \( \beta \) (deg) | 90.063(2) | 90.202(1) | |
| V ( \( \textup{\AA}^{3} \) ) | 255.647(6) | 254.034(7) | |
| Sr | x | 0.5024(5) | 0.5044(4) |
| y | 0.5169(3) | 0.5239(2) | |
| z | 0.2501(4) | 0.2502(4) | |
| \( B_{\textup{iso}} \) ( \( \textup{\AA}^{2} \) ) | 1.14(2) | 0.54(2) | |
| Mn | \( B_{\textup{iso}} \) ( \( \textup{\AA}^{3} \) ) | 0.82(5) | 0.40(5) |
| Re | \( B_{\textup{iso}} \) ( \( \textup{\AA} \) ) | 0.43(2) | 0.18(2) |
| O1 | frac | 0.967(3) | 0.967 |
| x | 0.2374(4) | 0.2370(4) | |
| y | 0.2092(4) | 0.2057(4) | |
| z | -0.0268(3) | -0.0275(3) | |
| \( B_{\textup{iso}} \) ( \( \text up{\AA}^{2} \) ) | 0.88(4) | 0.33(4) | |
| O2 | frac | 0.967(3) | 0.967 |
| x | 0.2900(4) | 0.2925(4) | |
| y | 0.7367(4) | ||
| z | -0.0299(3) | -0.0324(3) | |
| \( B_{\textup{iso}} \) ( \( \textup{\AA}^{2} \) ) | 0.92(4) | 0.51(4) | |
| O3 | frac | 0.967(3) | 0.967 |
| x | 0.4443(4) | 0.4404(4) | |
| y | -0.0059(5) | -0.0094(4) | |
| z | 0.2363(3) | 0.2368(3) | |
| \( B_{\textup{iso}} \) ( \( \textup{\AA}^{2} \) ) | 0.76(4) | 0.26(3) | |
| \( \chi^{2} \) | 1.621 | 1.195 | |
| \( R_{\textup{p}} \) , \( R_{\textup{wp}} \) (%) | 4.52, 5.58 | 5.26, 6.70 |
factors were constrained to be equal for the three oxygen sites during the refinements because of high correlation with TFs; the refined value was 0.967(3), corresponding to the chemical formula of \( Sr_{2}MnReO_{5.80(2)} \) (henceforth \( Sr_{2}MnReO_{6} \) ). A similar oxygen deficiency has been reported by powder neutron diffraction for the \( Ba_{2}MnReO_{5.89(4)} \) [6].
In spite of the pseudocubic lattice, the bond angles show significant deviations from ideal \( 180^{\circ} \) geometry (the average Mn–O–Re angle is \( 162.2^{\circ} \) ), which is typical for perovskite-like compounds. A remarkable example is BaLaMnMoO \( _{6} \) , where no reflection splitting can be observed even from high-resolution synchrotron diffraction data; however, refinement of neutron diffraction data showed a triclinic \( (I\bar{1}) \) structure with an average Mn–O–Mo angle of \( 165^{\circ} \) [7].
The observed monoclinic distortion in \( Sr_{2}MnReO_{6} \) is already prominent at RT, i.e. well above the magnetic transition temperature ( \( T_{c} = 120 K \) [2]). This is in contrast with the
Table 2. Selected interatomic distances ( \( \AA \) ) and bond angles (deg) in \( Sr_{2}MnReO_{6} \) at 300 and 8 K.
| 300 K | 8 K | |
| Mn-O1 | 2.133(2) [ \( \times \) 2] | 2.144(2) [ \( \times \) 2] |
| Mn-O2 | 2.132(2) [ \( \times \) 2] | 2.120(2) [ \( \times \) 2] |
| Mn-O3 | 2.130(3) [ \( \times \) 2] | 2.125(2) [ \( \times \) 2] |
| Re-O1 | 1.912(2) [ \( \times \) 2] | 1.897(2) [ \( \times \) 2] |
| Re-O2 | 1.919(2) [ \( \times \) 2] | 1.935(2) [ \( \times \) 2] |
| Re-O3 | 1.915(3) [ \( \times \) 2] | 1.920(2) [ \( \times \) 2] |
| Mn-O1-Re | 162.8(1) | 161.9(1) |
| Mn-O2-Re | 161.8(1) | 159.6(1) |
| Mn-O3-Re | 161.9(1) | 160.5(1) |
case of \( Sr_{2}FeMoO_{6} \) , where a tetragonal \( (I4/m) \) distortion appears simultaneously with the onset of magnetic order [8]. At low temperature, the magnitude of the tilting distortion in \( Sr_{2}MnReO_{6} \) is slightly increased, as reflected in the increased deviation of the Mn–O–Re bond angles from the ideal \( 180^{\circ} \) (the average value at 8 K is \( 160.7^{\circ} \) ). The Re–O distance variance is also increased, probably as a result of orbital ordering of the Jahn–Teller active \( \mathrm{Re}^{6+}(\mathrm{d}^{1}) \) ions.
The monoclinic distortion allows Dzyaloshinskii–Moriya (DM) antisymmetric exchange interaction \( [9, 10] \) that leads to a canting of the Mn moments. Usually these effects are discussed in the context of 'weak ferromagnetism', where the ferromagnetic (FM) component is produced by a slight canting of the antiferromagnetic (AF) sublattices, as occurs for example in \( La_{2}CuO_{4} \) and related high-temperature superconducting cuprates [11]. In the case of \( Sr_{2}MnReO_{6} \) the opposite situation is encountered, i.e. the structural distortion produces an AF component as a result of the FM structure canting.
3.2. \( Re^{6+} \) magnetic form factor calculation
Magnetic form factors for the \( Re^{6+} \) ion were obtained from spin density computed with the nonrelativistic Hartree–Fock (HF) method using the Gaussian 98 program [12]. The LANL2DZ basis set with an effective core potential (ECP) [13], which is suitable for heavy atoms, was employed. The form factors \( \langle j0(k)\rangle \) and \( \langle j2(k)\rangle \) were obtained by numerical integration with a step size of 0.001 Å. An MP4 Moller–Plesset perturbation theory resulted in no visible improvements in the form factors.
The atomic form factor for the \( Re^{6+} \) ion was obtained using the same LANL2DZ basis set and a known analytical approximation for the neutral Re atom ( \( Re^{0} \) ). Since ECP basis sets do not contain information about core electrons an assumption was made that the core electron contribution is the same in \( Re^{0} \) and \( Re^{6+} \) . Therefore the \( Re^{6+} \) form factor was calculated as
\[ f(\mathbf{R}\mathbf{e}^{\mathrm{o t}})=f_{\mathrm{E C P}}(\mathbf{R}\mathbf{e}^{\mathrm{o t}})-f_{\mathrm{E C P}}(\mathbf{R}\mathbf{e}^{\mathrm{o t}})+f(\mathbf{R}\mathbf{e}^{\mathrm{o t}}) \quad (1) \]
where \( f_{ECP} \) are computed separately with the ECP basis set and \( f(\mathrm{Re}^{0}) \) is tabulated in the International Tables for Crystallography.
Analytical approximations for both the magnetic and atomic form factors were found by a least-squares fit to an empirical expression
\[ f(k)=\sum_{i=1}^{N}a_{i}\exp(-b_{i}k^{2})+c \quad (2) \]
with the weighing scheme \( w = \exp\{-(k - k_{0})^{2}\} \) ; the parameters are listed in table 3.
Table 3. Parameters of the analytical approximation (equation (2)) to the atomic form factor \( (N = 4, k_{0} = 0.5) \) and \( \langle j_{0} \rangle \) and \( \langle j_{2} \rangle \) magnetic form factors \( (N = 3, k_{0} = 0.25) \) for \( Re^{6+} \) .
| \( \langle j_{0}\rangle \) | \( \langle j_{2}\rangle \) | Atomic | |
| \( a_{1} \) | 5.501 | 5.222 | 28.752 1 |
| \( b_{1} \) | 12.361 | 10.441 | 1.632 17 |
| \( a_{2} \) | -4.500 | 2.870 | 14.883 7 |
| \( b_{2} \) | 10.754 | 16.017 | 8.011 88 |
| \( a_{3} \) | 2.002 | 1.996 | 14.203 1 |
| \( b_{3} \) | -0.002 | -0.004 | 0.337 1 |
| \( a_{4} \) | — | — | 0.785 47 |
| \( b_{4} \) | — | — | 66.110 0 |
| c | -2.006 | -2.011 | 10.376 |
3.3. Magnetic structure
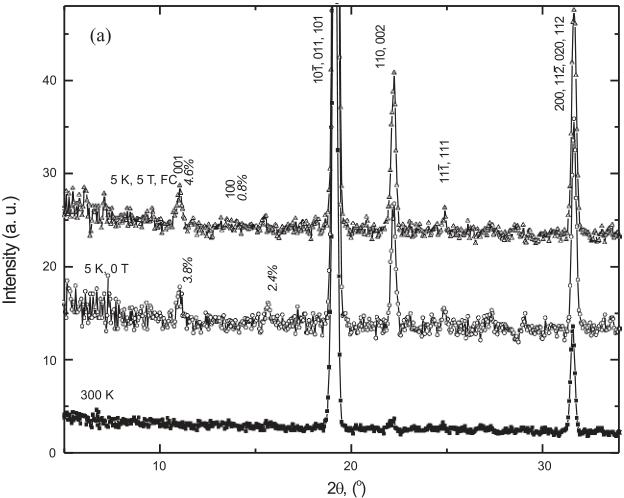
Additional reflections as well as an increase in intensity in the nuclear reflections are clearly seen in the low-temperature ND data (figure 2(a)). The extra reflections can be indexed on the basis of a magnetic unit cell with dimensions equal to the crystallographic ones. AF ordering of the Mn moments violates F-centring of the parent cubic \( Fm\overline{3}m \) cell—therefore we will refer subsequently to the reflections with an odd sum of Miller indices in the \( Fm\overline{3}m \) setting as AF, and the rest as FM. These reflections do not originate from a crystallographic phase transition since they are not observed in the 8 K SXD spectrum, and we consequently consider their intensity as entirely magnetic.
The most significant magnetic intensity is in the \( (110/002)_{\mathrm{m}} = (200)_{\mathrm{c}} \) reflections (subscripts m and c refer to the 'true' monoclinic and parent cubic structures, respectively). This shows unambiguously that the dominant contribution is FM (figure 2(b)), and the intensity is consistent with the Mn sublattice as a primary origin.
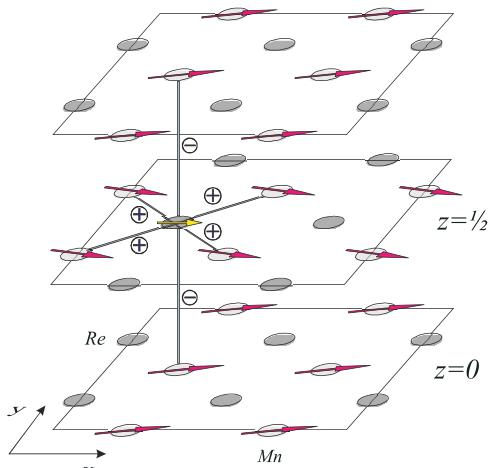
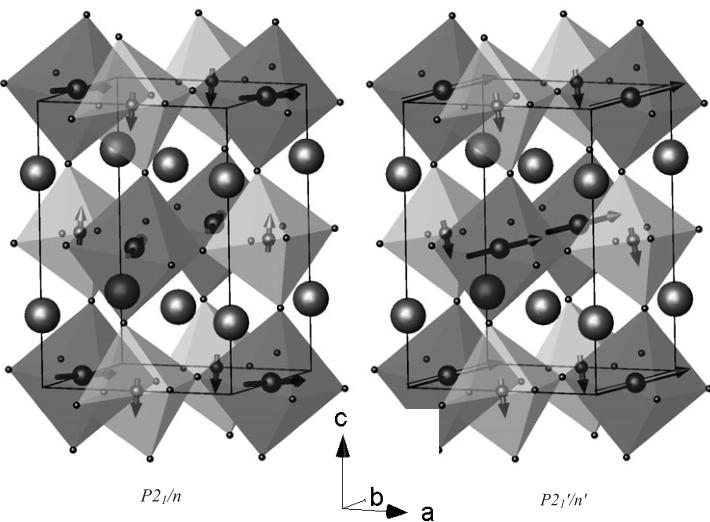
The high level of pseudosymmetry due to the small magnitude of the monoclinic distortion prevents an unambiguous determination of the magnetic structure, both in the choice of the magnetic symmetry and, especially, in the relative orientation of magnetic moments with respect to the crystallographic axes. The magnetic intensities can be adequately fitted by two different models for the magnetic structure. They are nearly indistinguishable on the basis of the present experimental data due to the low intensity of AF reflections. The two models correspond to magnetic (Shubnikov) groups \( P2_{1}/n \) and \( P2_{1}^{\prime}/n^{\prime} \) (figure 3, table 4). There are symmetry restrictions on the allowed directions of magnetic moment components, i.e. the FM components of the Mn and Re magnetic moment are directed along the \( b_{m} \) axis in the \( P2_{1}/n \) model or lie within the \( (ac)_{\mathrm{m}} \) plane in the \( P2_{1}^{\prime}/n^{\prime} \) one.
Attempts to distinguish the two models were made by comparing FWHMs \( (\omega) \) of low-angle magnetic reflections. The presence of a primed screw axis \( 2_{1}^{\prime} \) in the \( P2_{1}^{\prime}/n^{\prime} \) group imposes the extinction condition \( 0k0, k = 2n \) , and hence the AF peak at \( 2\theta \sim 15.5^{\circ} \) is a single \( (100)_{\mathrm{m}} \) peak in this model, while in the \( P2_{1}/n \) group there are two reflections, \( (100)_{\mathrm{m}} \) and \( (010)_{\mathrm{m}} \) , which, however, cannot be resolved with the present data, and their presence can be inferred only from extra broadening. A fit of the peaks with a simple Gaussian peak shape (characteristic of the BT-1 diffractometer) yielded \( \omega_{001} = 0.33(5)^{\circ} \) and \( \omega_{100} = 0.29(7)^{\circ} \) , i.e. no additional broadening was detected and thus the \( P2_{1}^{\prime}/n^{\prime} \) model appears to be more favourable; however, insufficient intensity prevents us from making a definite conclusion. The unconstrained Rietveld refinement also yielded a slight preference towards the \( P2_{1}^{\prime}/n^{\prime} \) model (table 4).


Figure 2. (a) Low-angle region of powder neutron diffraction profiles of \( Sr_{2}MnReO_{6} \) at 300 and 5 K, without field and field-cooled in 5 T with reflection indices in the monoclinic setting. The intensities were normalized to that of \( (440)_{\mathrm{c}} \) peak at \( \sim66^{\circ} \) with a predominantly nuclear contribution. Relative intensities of the two low-angle peaks are shown. (b) Neutron diffraction difference pattern showing the contribution from the magnetic scattering.

Figure 3. Spin arrangements of \( Mn^{2+} \) and \( Re^{6+} \) in \( Sr_{2}MnReO_{6} \) according to the two models proposed. Darker octahedra contain \( Mn^{2+} \) which has a larger moment.
Table 4. Refined magnetic parameters of \( Sr_{2}MnReO_{6} \) at 8 K in three models: one with \( P2_{1}/n \) symmetry and two with \( P2_{1}^{\prime}/n^{\prime} \) symmetry—with and without an ordered Re moment.
| P21/n' | P21/n' | ||
| Unconstrained | No Re moment | ||
| Mn | \( \mu_{x} \) | 1.24(7) | 4.16(8) |
| \( \mu_{y} \) | 4.34(5) | 1.27(5) | |
| \( \mu_{z} \) | 0.3(3) | -1.1(3) | |
| \( |\mu| \) | 4.53(6) | 4.49(8) | |
| Re | \( \mu_{x} \) | -0.1(1) | -0.2(1) |
| \( \mu_{y} \) | -0.02(7) | -0.07(6) | |
| \( \mu_{z} \) | 0.1(4) | -0.9(4) | |
| \( |\mu| \) | 0.1(4) | 0.9(4) | |
| \( \chi^{2} \) | 1.179 | 1.164 | |
| \( R_{p}, R_{wp} \) (%) | 5.23, 6.65 | 5.18, 6.60 |
The refinement is insensitive to the presence of an ordered Re moment yielding identical R-factors for models without any moment at the Re site or for an unconstrained refinement with all six components of the moments allowed to refine (table 4). This is reminiscent of a similar ambiguity in the isoelectronic \( Sr_{2}FeMoO_{6} \) , where contradictory data for the magnitude and even the presence of an ordered Mo moment exist. Chmaissem et al [8] reported ferrimagnetic alignment of the \( Fe^{3+} \) and \( Mo^{5+} \) moments. However, they claimed that unconstrained refinements were too poorly determined to give a unique result for the \( Mo^{5+} \) moment. Moritomo et al [14] also reported ferrimagnetic alignment with \( \mu_{Mo} = -0.9(2) \) \( \mu_{B} \) .
at 15 K. On the other hand, Garcia-Landa et al [15] claimed no moment on \( Mo^{5+} \) . Khattak et al [6] claimed no moment on \( Re^{6+} \) in \( Ba_{2}MnReO_{6} \) , yet their model is equivalent to one of our 'constrained' models which indeed produced an inferior refinement (see below). Our diffraction data in an external field seem to favour the existence of an ordered Re moment (see section 4)—hence in our final refinements we allowed the Re moment to refine, and the refined total Re magnetic moment is in agreement with the spin-only \( d^{1} \) configuration for the \( P2_{1}^{\prime}/n^{\prime} \) refinement (table 4).
The presence of the AF component of the Mn moment, and (possible) nonzero moment on the Re site do not appear to originate from B-site mixing: the refined value of mixing is zero within the experimental error, consistent with the synchrotron x-ray diffraction results. An unusual feature is that, assuming a Re moment is present and allowed to refine, the Mn and Re moments are oriented approximately perpendicular to each other: \( \mu_{Mn} \) nearly parallel to the x-axis, and \( \mu_{Re} \) nearly parallel to z; the angle between refined Mn and Re moments is \( 89^{\circ} \) . Attempts to artificially force the antiparallel alignment of FM (x and z) components with zero or a freely refineable AF (y) component led to a significant deterioration of the fit ('constrained models').
There is a possibility that the complex magnetic structure observed actually represents a phase-separated state. There are neutron diffraction reports for the phase separation in the similar \( Ca_{2}FeReO_{6} \) DP, where an ordered Re moment was also observed [16, 17]. However, we found no evidence for reflection splitting or anomalous broadening, even with high-resolution synchrotron data, and therefore prefer a single-phase description. The perpendicular arrangement is surprising considering that the dominant interaction is supposed to be \( 180^{\circ} \) superexchange (SE), which would favour collinear alignment of the Mn and Re moments either in a FM structure, according to the Goodenough–Kanamori–Anderson Mn–Re \( (d^{5}-d^{1}) \) coupling or in a ferrimagnetic arrangement as is commonly observed in similar double perovskites [8, 14, 18]. However, the Mn–O–Re \( 180^{\circ} \) SE interaction is substantially weakened here because of the structure distortion (relevant Mn–O–Re bond angle averages to \( 160.7^{\circ} \) at 8 K) and significant energy mismatch between Mn and Re orbitals [18]. Therefore, a DM interaction, which is described by the term \( H_{DM} = -D_{ij}(S_{i} \times S_{j}) \) and is normally weak ( \( \sim1 \) K) [19] may be sufficient to produce the observed magnetic structure. The relatively high value of \( T_{c} \) originates from the \( 90^{\circ} \) Mn–O–O–Mn interactions, which are nearly insensitive to this distortion [20].
We note that as far as the y component is concerned, the interactions are competing: for each Re atom there are four Mn neighbours favouring a ‘positive’ y component and two favouring a ‘negative’ one (figure 4). The frustration and resultant ‘glassy’ component in the Re moment can explain the previously published time relaxation of magnetization [2], which can be fitted by an expression for logarithmic relaxation \( \chi(t) = \chi_{0} + S \ln(t) \) , typical for a spin glass [21].
The pseudocubic lattice precludes an unambiguous determination of the direction of moments with respect to crystallographic axes. The choice of \( P2_{1}^{\prime}/n^{\prime} \) magnetic symmetry decouples the y-component of the magnetic moment from the others, and therefore its magnitude is determined with relatively good accuracy. On the other hand, the relative magnitudes of x and z components are determined with large uncertainty. Completely unconstrained refinement yields the main component directed along the x-axis, which is the 'long' axis when normalized to the aristotype. Such behaviour has recently been observed in the similar BaLaMnMoO \( _{6} \) double perovskite [7], and is consistent with an empirical rule known for orthorhombic (Pnma) CMR manganites. According to this rule [22], the easy magnetization axis is predicted to coincide with the direction of maximum orthorhombic strain \( \varepsilon_{i}=a_{i}-\langle a\rangle \) , where \( a_{i} \) is normalized to the aristotype cell parameter and \( \langle a\rangle \) is their

Figure 4. Schematic illustration of the origin of frustration for the y component of the Re moment. For clarity only x (FM) and y (AFM) components of the magnetic moments are shown.
(This figure is in colour only in the electronic version)
arithmetic average. The observed monoclinic \( P2_{1}/n \) structure is ‘pseudo-orthorhombic’ ( \( \beta \) is close to \( 90^{\circ} \) ), and a simple calculation of the \( \varepsilon_{i} \) values (using lattice parameters at T = 8 K) yields \( \varepsilon_{x} = 0.0016 \) , \( \varepsilon_{y} \sim \varepsilon_{z} = -0.0008 \) , supporting the proposed moment orientation along the x axis \( ^{8} \) .
3.4. Experiments in an external field
There is no detectable change in the position or intensity of the non-magnetic reflections upon the application of a magnetic field, ruling out the possibility of a field-induced structural transition.
The ferromagnetic reflections undergo an expected intensity increase when the magnetic field is applied. Substantial hysteresis is observed, i.e. intensities of the FM reflections obtained in the experiment without an external field, but after cooling the sample in a 5 T field (FC), are substantially different from those obtained on a zero-field cooled sample (ZFC).
Moreover, the low-angle AF reflections undergo a redistribution of intensity with the applied field: the intensity of the \( (001)_{\mathrm{m}} \) reflection slightly increases with the field, while the intensity of the \( (100)_{\mathrm{m}} \) reflection decreases and nearly vanishes in the pattern collected under FC. Such behaviour is difficult to explain assuming a single sublattice AF component and can therefore serve as further evidence for the existence of an ordered Re moment. Assuming the \( P2_{1}^{\prime}/n^{\prime} \) model with both Mn and Re moments present, the expressions for the magnetic structure factors are \( (\mu_{\mathrm{y}}^{\mathrm{Mn}} \) is the y component of Mn at \( (0, 1/2, 0) \) and \( \mu_{\mathrm{y}}^{\mathrm{Re}} \) is the y component
of Re at \( (1/2, 0, 0) \) :
\[ |F_{001}|\sim\mu_{y}^{\mathrm{Mn}}\times f_{\mathrm{Mn}}+\mu_{y}^{\mathrm{Re}}\times f_{\mathrm{Re}};\quad|F_{100}|\sim\mu_{y}^{\mathrm{Mn}}\times f_{\mathrm{Mn}}-\mu_{y}^{\mathrm{Re}}\times f_{\mathrm{Re}}. \quad (3) \]
An applied magnetic field tends to align the Mn and Re moments ferromagnetically, leading to the observed intensity redistribution.
4. Conclusions
The present neutron and synchrotron x-ray diffraction study of \( Sr_{2}MnReO_{6} \) revealed a monoclinic (SG \( P2_{1}/n \) ) distortion of the parent cubic double perovskite structure. This distortion is characterized primarily by a significant deviation of the Mn–O–Re bond angles from \( 180^{\circ} \) geometry, as shown by Rietveld refinements. The observed monoclinic distortion produces antisymmetric exchange interactions, leading to a canted magnetic structure, for which a possible model (with \( P2_{1}^{\prime}/n^{\prime} \) Shubnikov symmetry) is proposed and refined. Field-dependent neutron diffraction measurements support the existence of a magnetic moment on the Re ion.
Acknowledgments
The authors are grateful to B Toby and Q Huang for the help with the experiments at NIST and discussions, and to S Nagler, G Feltcher, A Mamchik and V Pomjakushin for helpful discussions. This work was supported by the National Science Foundation grant DMR-0233697.
References
[1] Kobayashi K-I, Kimura T, Sawada H, Terakura K and Tokura Y 1998 Nature 395 677
[2] Popov G, Greenblatt M and Croft M 2003 Phys. Rev. B 67 024406
[3] Larson C and Von Dreele R B 1994 Los Alamos Natl Lab. LAUR 86-748
[4] Toby B H 2001 J. Appl. Crystallogr. 34 210
[5] Woodward P M 1997 Acta Crystallogr. B 53 32
[6] Khattak C P, Cox D E and Wang F F Y 1975 J. Solid State Chem. 13 77
[7] Caspi E N, Jorgensen J D, Lobanov M V and Greenblatt M 2003 Phys. Rev. B 67 134431
[8] Chmaissem O, Kruk R, Dabrowski B, Brown D E, Xiong X, Kolesnik S, Jorgensen J D and Kimball C W 2000 Phys. Rev. B 62 14197
[9] Dzyaloshinskii I 1958 J. Phys. Chem. Solids 4 241
[10] Moriya T 1961 Phys. Rev. 120 91
[11] See for example Stein J, Entin-Wohlman O and Aharony A 1996 Phys. Rev. B 53 775
[12] Frisch M J et al 1995 GAUSSIAN 98 Rev. A 10 (Pittsburgh, PA: Gaussian)
[13] Hay P J and Wadt W R 1985 J. Chem. Phys. 299 270
[14] Moritomo Y, Xu S, Machida A, Akimoto T, Nishibori E, Takata M, Sakata M and Ohoyama K 2000 J. Phys. Soc. Japan 69 1723
[15] Garcia-Landa B, Ritter C, Ibarra M R, Blasco J, Algarabel P A, Mahendiran R and Garcia J 1999 Solid State Commun. 110 435
[16] Westerburg W, Lang O, Ritter C, Felser C, Tremel W and Jacob G 2002 Solid State Commun. 122 201
[17] Granado E, Huang Q, Lynn J W, Gopalakrishnan J, Greene R L and Ramesha K 2002 Phys. Rev. B 66 064409
[18] Sleight A W and Weiher J F 1972 J. Phys. Chem. Solids 33 679
[19] Deisenhofer J, Eremin M V, Zakharov D V, Ivanshin V A, Eremina R M, Krug von Nidda H-A, Mukhin A A, Balbashov A M and Loidl A 2002 Phys. Rev. B 65 104440
[20] Blasse G 1965 Phillips Res. Rep. 20 327
[21] Ginzburg S L 1989 Irreversible Phenomena in Spin Glasses (Moscow: Nauka) chapter 1 (in Russian)
[22] Terakura K, Solovyev I V and Sawada H 2000 Colossal Magnetoresistive Oxides ed Y Tokura (London: Gordon and Breach)