| Transition Temperature | 110 K |
|---|---|
| Experiment Temperature | 1.5 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | I41/acd (#142) |
| Magnetic Space Group | I41'/a'cd' (#142.568) |
| Magnetic Point Group | 4'/m'm'm (15.5.57) |
| Lattice Parameters | 5.18680 5.18680 24.12280 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1016/j.jssc.2004.02.012 |
| Reference | C. Autret, C. Martin, M. Hervieu, R. Retoux, B. Raveau, G. Andre and F. Bouree, Journal of Solid State Chemistry (2004) 177 2044-2052. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Mn1 | Mn | 0.0 | 0.0 | 2.4 | 2.40 |
Structural investigation of \( Ca_{2}MnO_{4} \) by neutron powder diffraction and electron microscopy
C. Autret, \( ^{a} \) C. Martin, \( ^{a,*} \) M. Hervieu, \( ^{a} \) R. Retoux, \( ^{a} \) B. Raveau, \( ^{a} \) G. André, \( ^{b} \) and F. Bourée \( ^{b} \)
\( ^{a} \) Laboratoire CRISMAT, UMR 6508 CNRS ISMR4, 6 bd Maréchal Juin, 14050 Caen Cedex 4, France
\( ^{b} \) Laboratoire Léon Brillouin, CEA-CNRS Saclay, 91191 Gif-sur-Yvette Cedex, France
Received 24 October 2003; received in revised form 19 January 2004; accepted 1 February 2004
Abstract
The first member of the Ruddlesden–Popper family, \( Ca_{2}MnO_{4} \) , has been revisited. Coexistence of two structures has been shown from electron microscopy at room temperature and neutron diffraction data have evidenced two antiferromagnetic structures at low temperature. Two forms, with an orthorhombic \( Aba2\ (a \approx b \approx a_{p}\sqrt{2} \) and \( c \approx 12\ \AA) \) and a tetragonal \( I4_{1}/cad\ (a \approx a_{p}\sqrt{2} \) and \( c \approx 24\ \AA) \) symmetries, were found to coexist coherently within the same matrix.
© 2004 Elsevier Inc. All rights reserved.
Keywords: Ruddlesden–Popper phases; Neutron diffraction; Electron microscopy
1. Introduction
The numerous studies of the perovskite manganites \( Ln_{1-x}AE_{x}MnO_{3} \) (Ln is a trivalent rare-earth and AE a divalent alkaline-earth) carried out these last years have shown fascinating properties. Besides their colossal magnetoresistance (CMR) effect [1,2], phenomena such as charge and orbital ordering [3–8] and phase separation [9–16] were evidenced. Besides this large family, the Ruddlesden–Popper manganites \( (Ln,AE)_{n+1}Mn_{n}O_{3n+1} \) [17], which consist of a regular intergrowth of single rock-salt with multiple perovskite layers, are of great interest. CMR properties were indeed observed for the n=2 member, \( La_{1.2}Sr_{1.8}Mn_{2}O_{7} \) [18,19] and for the n=1 phases \( Ln_{2-x}Ca_{x}MnO_{4} \) [20]. Also, charge-orbital ordering was discovered in \( Ln_{0.5}Ca_{1.5}MnO_{4} \) [21,22] and \( Ln_{0.5}Sr_{1.5}MnO_{4} \) [23–25]. In fact, the crystal chemistry of these oxides, as well as their magnetic properties, are rather complex and subject to controversy. This is in particular the case of the parent manganite \( Ca_{2}MnO_{4} \) which was first reported, similarly to \( K_{2}NiF_{4} \) to be tetragonal, \( I4/mmm \) [17], with \( a\approx a_{p}\approx3.67\mathring{A} \) ( \( a_{p} \) being the parameter of the perovskite unit cell) and \( c\approx12.08\mathring{A} \) , but was later on shown to exhibit a doubling of the c parameter ( \( \approx24\mathring{A} \) ), due to a disorder of oxygen positions in the basal plane of the perovskite layer, corresponding to the space group \( I4_{1}/acd \) [26–28]. The rotation of the octahedra in opposite directions around the c-axis, between two successive perovskite layers, is at the origin of the doubling of the c parameter. The antiferromagnetic structure was described in an \( a\approx a_{p}\sqrt{2} \) , \( c\approx24\mathring{A} \) cell [29,30], different from that observed for \( K_{2}NiF_{4} \) [31]. More recently, a different crystalline cell, from orthorhombic symmetry, with \( a\approx b\approx a_{p}\sqrt{2} \) and \( c\approx12\mathring{A} \) , and possible space groups \( Aba2 \) or \( Abma \) was observed by electron diffraction for \( Ca_{2}MnO_{4} \) [20]. But, due to the existence of numerous pancake-like defects, it appeared impossible to obtain accurate description of the structure by using X-ray or neutron diffraction data. In order to understand the structural behavior of \( Ca_{2}MnO_{4} \) , we have revisited its synthesis and structure using electron microscopy and neutron diffraction. We report herein on the coherent coexistence of two crystalline phases \( (I4_{1}/acd \) and \( Aba2) \) in \( Ca_{2}MnO_{4} \) .
2. Experimental section
\( Ca_{2}MnO_{4} \) was prepared by standard high temperature solid-state reaction starting from a stoichiometric mixture of \( MnO_{2} \) and CaO. The reagents were first
mixed in an agate mortar and heated in air at \( 900^{\circ} \) C for 12 h. After grinding, the powder was pressed in the form of bars under \( 1 \, ton/cm^{2} \) and finally sintered in air at \( 1350^{\circ} \) C for 48 h with slow heating and cooling rates. Note that this synthesis temperature is intermediate between those previously used by Leonowicz et al. ( \( 900^{\circ} \) C) for single crystal preparation [26] and by Maignan et al. ( \( 1500^{\circ} \) C) for ceramics, which exhibited numerous defects [20]. In fact, in this paper, it was soon reported that the synthesis conditions have an influence on the microstructure of the samples. The phase purity of this new sample was checked by X-ray and electron diffraction (ED). The cationic composition was obtained by energy dispersive spectroscopy (EDS) analyses which showed an homogeneous composition corresponding to the nominal one. The oxygen ratio was determined, by redox titration and neutron powder diffraction (NPD), to 4 in the limit of accuracy of the techniques.
Electron microscopy samples were prepared by crushing the bars in n-butanol and the small crystallites in suspension were deposited on a holey carbon film, supported by a nickel grid. The electron diffraction was performed with a JEOL 200CX electron microscope equipped with a tilting and rotating goniometer and the high-resolution electron microscopy (HREM) with a TOPCON 002B microscope (200 kV and point resolution of 1.8 Å). Theoretical images were calculated using Mac Tempas program [33].
NPD experiments were performed at the Orphée reactor (CEA/Saclay, France), on the two-axis diffractometers 3T2 ( \( \lambda = 1.225 \AA \) ) and G4.1 ( \( \lambda = 2.426 \AA \) ). The temperature dependence of the magnetic and crystalline structure was studied by recording data from 1.4 K to 300 K by 5 K steps on G4.1 (in the angular range \( 11^{\circ} < 2\theta < 91^{\circ} \) by step of \( 0.1^{\circ} \) ). A measurement ( \( 6^{\circ} < 2\theta < 125.7^{\circ} \) by step of \( 0.05^{\circ} \) ) has been done on 3T2 at 300 K. All these data were refined with the Fullprof program [32].
Magnetization measurements were carried out using a Superconducting Quantum Interference Device (SQUID) in the temperature range 5–400 K during warming after a magnetic field of 1.45 T was applied at low temperature (zero field cooling process).
3. Results and discussion
3.1. Room temperature study
3.1.1. Electron diffraction and high-resolution electron microscopy
The reciprocal space was reconstructed by tilting around the crystallographic axes. As previously reported for calcium based Ruddlesden–Popper phases [20], the ED investigation reveals a highly complex microstructural state. Consequently, numerous crystallites have been characterized by ED, EDS and HREM. In contrast to the previous studies of \( Ca_{2}MnO_{4} \) [20], this investigation shows two phases, which correspond to the same cationic composition. One indeed observes two sets of reflections corresponding to both forms, previously identified [20,26–28], which coexist in the form of more or less extended domains, coherently intergrown within the same crystal.
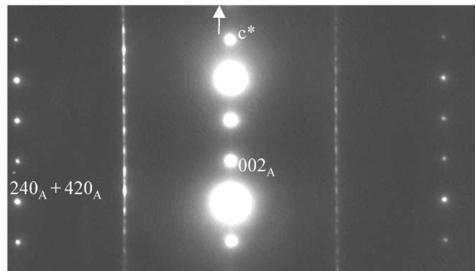
The first set of reflections, correspond to the A-type orthorhombic cell, \( a_{A} \approx a_{p} \sqrt{2} \) , \( b_{A} \approx a_{p} \sqrt{2} \) and \( c_{A} \approx 12.08 \, \AA \) , previously reported for \( Ca_{2}MnO_{4} \) [20], compatible with the space groups \( Aba2 \) (No. 41) and \( Abma \) (No. 64). In the following, the suffix “A” refers to these A-type lattices. Two typical ED patterns given in Fig. 1 illustrate the micro-twinning phenomena generated by the orthorhombic distortion of the cell. In the [001] pattern (Fig. 1a), the \( h \, k \, 0 \) , \( h = 2n + 1 \) , reflections are pointed by white arrows but weaker reflections are also observed along the horizontal axis (apparently \( b^{*} \) ), as a result of \( 90^{\circ} \) oriented domains, the \( b^{*} \) and \( a_{\perp} \) vectors of the two variants being parallel. The formation of twinning domains is also clearly illustrated in Fig. 1b, by the systematic superimposition of the [120] and [210] variants. Along that direction, diffuse streaks appear parallel to \( c^{*} \) , which have been interpreted as the signature of “nano-twinning” [20], the bright field imaging revealing domains of a few nanometers thickness along c.
The second set of reflections evidences the I-type tetragonal cell, with \( a_{I} \approx a_{A} \approx a_{p} \sqrt{2} \) and \( \varepsilon_{I} \approx 2c_{A} \approx 24.16 \AA \) , consistent with the space group \( I4_{1}/acd \) (No. 142), first observed by Leonowicz et al. [26] and the label “I” will be used to refer to this structure. The doubling of the c-axis is clearly observed from the [120] ED pattern (Fig. 1c).
The description of the three \( I4_{1}/acd-Abma \) - and \( Aba2 \) -frameworks remains an intergrowth of one single perovskite layer and one rock-salt type layer. These structures are close and the main difference concerns the positions of the oxygen located in the \( [MnO_{2}] \) planes. They involve the presence or the absence of rotation of the octahedra in the (001) plane. In the case of orthorhombic \( Abma \) -type structure, there is no rotation of the octahedra in the plane but the oxygen atoms move along z (positions \( 8e:\frac{1}{4}\frac{1}{4}z \) ). In the case of orthorhombic \( Aba2 \) -type structure, the octahedra rotate in the plane and can be tilted along z, the \( c_{A} \) parameter being close to \( 12\AA \) (positions \( 8b:xy \) ). In the case of the tetragonal \( I4_{1}/acd \) -type structure, the octahedra rotate in the (001) plane, without tilting along z, and the doubling of the c parameter results from an opposite rotation of octahedra along the \( c_{I} \) -axis (due to the \( 4_{1} \) axis) implying a stacking parameter of \( 24\AA \) .
ED patterns and HREM images were simulated for the three space groups, considering the positional

(a)

(b)

(c)
Fig. 1. \( Ca_{2}MnO_{4} \) ED patterns: (a) 4-type structure, [001] ED pattern: white arrows point the extra reflections associated to the orthorhombic distortion, the weaker ones resulting from a twinning phenomenon. (b) Systematic superimposition of the [120] and [210] variants: the diffuse streaks parallel to \( c^{*} \) are the signature of “nano-twining” (c) [120] ED pattern of a crystal zone exhibiting the \( I4_{1}/acd \) structure.
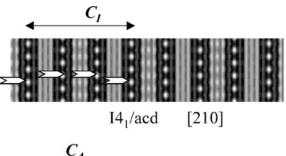
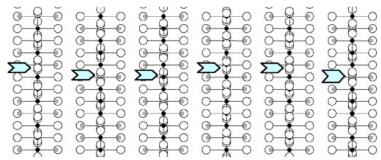
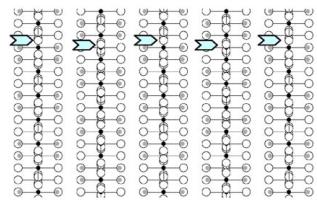
parameters obtained from NPD calculations (next section). The [100] and [010] patterns and HREM images do not provide significant difference of contrast. Conversely, viewing the crystals along the \( \{210\}_{I} \) direction of the \( I4_{1}/acd \) -phase or along the \( [210]_{A} \) and \( [120]_{A} \) directions of the \( Aba2 \) -phase allows to clearly observe a variation of the contrast at the level of the \( [MnO_{2}] \) planes. This is illustrated in Fig. 2a, using the refined atomic positions (Table 1) and keeping a similar oxygen displacement for the orthorhombic phase; the images are calculated for a focus value close to -550 Å (Scherzer value), a crystal thickness of 48 Å and an objective aperture of 0.9 Å \( ^{-1} \) . The displacement of the oxygen atoms of the basal plane of the octahedra induces alternately shorter and longer projected spacing, resulting in the sequence of bright and less bright dots along a row perpendicular to \( \vec{c} \) . Adjacent rows are shifted by \( d_{210} \) or not shifted, so that three possible arrangements are theoretically observed along \( \vec{c} \) ; they are schematically drawn in Fig. 2b. In the \( \{210\}_{I} \) images, the sequence along \( \vec{c} \) is white–dark–dark–white, due to the \( 4_{1} \) axis, whereas there is no shift in the \( [210]_{A} \) images and white and dark spots alternate in the \( [120]_{A} \) images. Note that for this focus value, the Abma calculated images do not exhibit this typical alternation of bright and less bright dots, in agreement with the special positions of the oxygen atoms, but a different grey and uniform contrast at this level. Thus, taking into consideration the experimental observations, the A-type domains can be described in the Aba2 space group only. HREM images display another interesting information on the origin of the streaks observed in the ED patterns along \( c^{*} \) . One example is shown in Fig. 2c, where the bright dots positions are marked by white circles. They first confirm the perfect Ruddlesden–Popper type structure, without intergrowth defects. Second, the sequence of shifting of the rows along \( \vec{c} \) delimits four domains, which are only a few nanometers thick. The streaks can be correlated to two types of distortion of the octahedral layers and to their more or less ordered stacking mode, leading to the formation of nano-twinning domains.
3.1.2. Neutron powder diffraction (3T2 data)
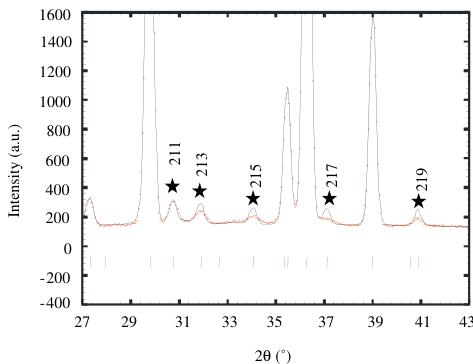
The main peaks of this room temperature pattern correspond to an \( I4/mmm\ K_{2}NiF_{4} \) structure ( \( a \approx a_{p} \) and \( c \approx 12\ \AA \) ) but weak reflections, notified by stars in Fig. 3, indicate that the structure has to be described in the \( I4_{1}/acd \) , in agreement with the electron microscopy study, with \( a \approx a_{p}\sqrt{2} \) and \( c \approx 24\ \AA \) . No orthorhombic distortion could be detected from NPD data, due to the coexistence of quadratic and orthorhombic phases and to the too small distortion of the orthorhombic form. The refinement performed in \( I4_{1}/acd \) allowed all the peaks to be indexed, with the following reliability factors \( R_{p} = 10.7\% \) , \( R_{wp} = 12\% \) and \( R_{Bragg} = 6.18\% \) and \( \chi^{2} \) close to 18.4. However, a close inspection of the patterns revealed an anomalous width for the reflections that differentiate \( I4_{1}/acd \) from \( I4/mmm \) with the rule: \( hk\ l \) , \( l = 2n + 3 \) , indicating a shorter coherence length along the c-axis. Two profiles were thus used to refine these data, one for the intense reflections and the other for the peaks belonging to the rule \( hk\ l \) , \( l = 2n + 3 \) . This refinement improved significantly the results with \( R_{p} = 5.5\% \) , \( R_{wp} = 5.89\% \) , \( R_{Bragg} = 2.32\% \) and \( \chi^{2} \) close to 4.61 [34]. Let us note that the O(2) B factor, that was refined to a slightly high value ( \( >1\ \AA^{2} \) ) in the





I4/ \( \alpha \) d [210]

Aba2 [120]

(b) Aba2 [210]
Fig. 2. Characterization of the I-type structure in \( Ca_{2}MnO_{4} \) : (a) Calculated images (focus value close to \( -550\AA \) , crystal thickness of \( 48\AA \) , objective aperture of \( 0.9\AA^{-1} \) ) of the different structures. (b) Drawing of the three possible arrangements corresponding to the images given in (a): along \( \{210\}_{I} \) , \( [210]_{A} \) and \( [120]_{A} \) . The shifting, or not, of the dots along c in the adjacent layers is outlined by open arrows. Grey circles are for Ca, black for Mn and white for O. (c) Typical experimental HREM of a crystallite exhibiting streaks along \( c^{*} \) : the bright dots positions are marked by white circles.
Table 1
\( Ca_{2}MnO_{4} \) refined crystallographic parameters, inter-atomic distances and angles, from NPD at 300 K
| Atoms | Site | x | y | z | B ( \( \textup{\AA}^{2} \) ) |
| Ca | 16d | 0 | 0.25 | 0.55107(3) | 0.51(1) |
| Mn | 8a | 0 | 0.25 | 0.375 | 0.21(1) |
| O \( _{\text{apical}} \) | 16d | 0 | 0.25 | 0.45562(2) | 0.59(1) |
| O \( _{\text{equatorial}} \) | 16f | 0.21004(6) | 0.46004(6) | 0.125 | 0.71(1) |
| Mn-O \( _{\text{ap}} \) | 1.9947(6) \( \textup{\AA} \) | Mn-O \( _{\text{eq}} \) | 1.8571(4) \( \textup{\AA} \) | Mn-O \( _{\text{eq}} \) -Mn | 161.84(2) \( ^{\circ} \) |
Space group \( I4_{1}/acd \) ; \( a=5.1868(1)\mathring{A} \) ; \( c=24.1228(2)\mathring{A} \) ; \( V=648.984\mathring{A}^{3} \)
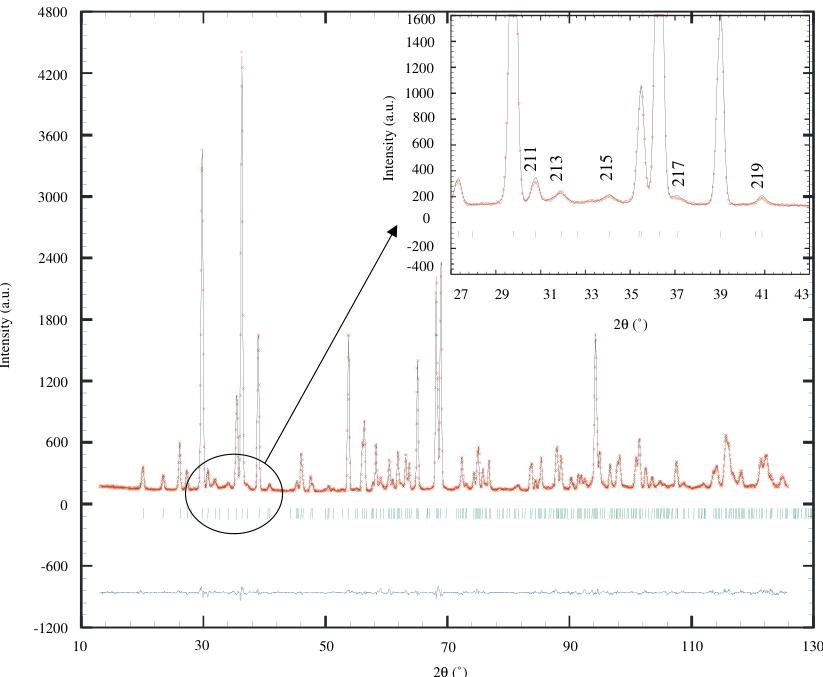
first case, takes now a small value \( (0.71\mathring{\mathrm{A}}^{2}) \) . The final observed and calculated patterns are shown in Fig. 4 and the refined lattice parameters, atomic positions and selected inter-atomic distances and angles are summarized in Table 1. The \( MnO_{6} \) octahedra are elongated along the c-axis: \( d(\mathrm{Mn}-\mathrm{O}_{\mathrm{ap}})=1.9447\mathring{\mathrm{A}} \) ( \( \times2 \) ) and \( d(\mathrm{Mn}-\mathrm{O}_{\mathrm{eq}})=1.8571\mathring{\mathrm{A}} \) ( \( \times4 \) ). The \( MnO_{6} \) octahedra rotation is very strong, involving \( Mn-O_{eq}-Mn \) angles of \( \approx161^{\circ} \) .
Thus, the room temperature NPD pattern of this \( Ca_{2}MnO_{4} \) can be refined as a single phase with the \( I4_{1}/acd \) symmetry, but using two sorts of profiles, indicating a disorder along z. This is in agreement with the electron microscopy study which shows the
coexistence of two phases, that can both be described by using different rotations of the \( MnO_{6} \) octahedra along this direction, and evidences nano-twinning domains along that direction.

Fig. 3. Enlargement of the \( Ca_{2}MnO_{4} \) diffraction pattern (300 K) at low angles, showing the anomalous width of reflections indexed with stars.
3.2. Temperature dependence: NPD G4.1 data and magnetic properties
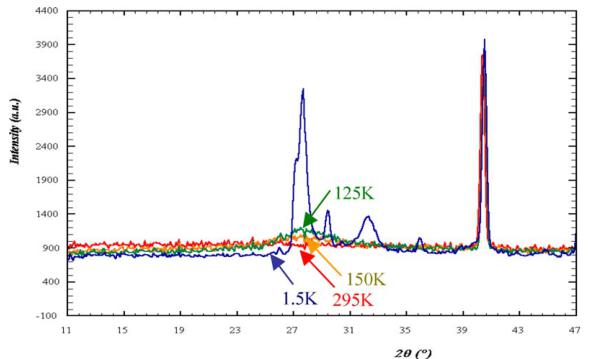
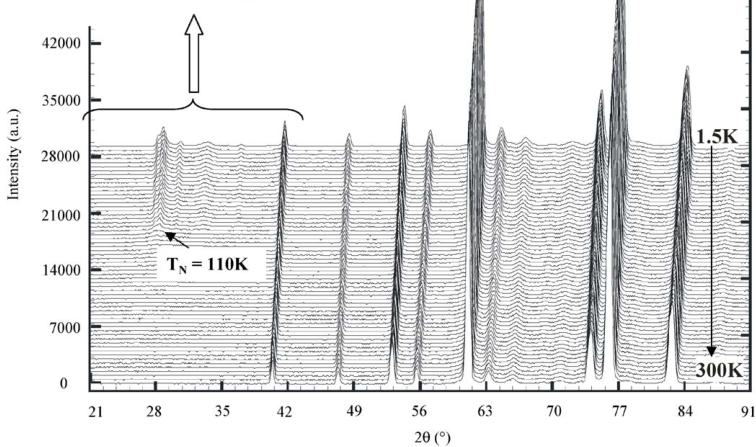
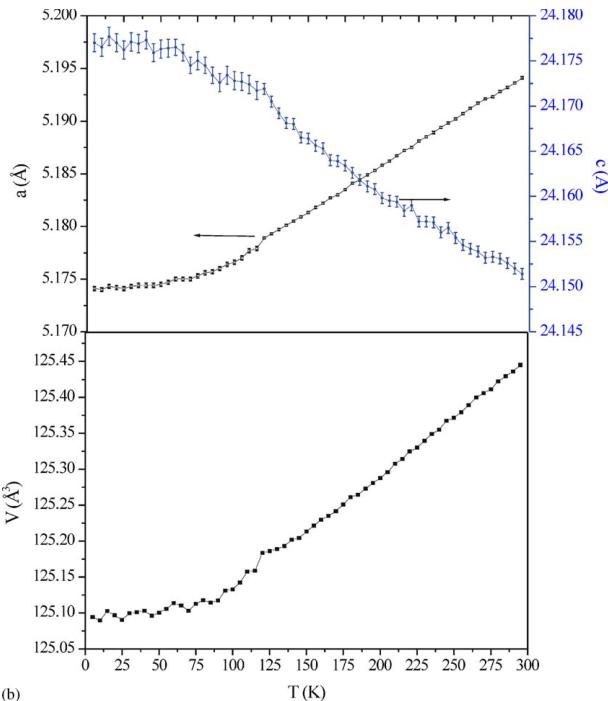
The NPD patterns recorded using G4.1 from 1.5 to 300 K do not show any structural transition (Fig. 5a). The structure remains \( I4_{1}/acd \) and the broadening of the \( h\,k\,l \) , \( l = 2n + 3 \) reflections, previously discussed for 300 K, is preserved. Decreasing the temperature, the c parameter increases but the a one decreases, these evolutions are more pronounced for the higher temperatures ( \( T > 110\,K \) ) than the lower ones ( \( T < 110\,K \) ). It corresponds to a kink in the cell volume vs. temperature curve (Fig. 5b) at this temperature which corresponds to \( T_{N} \) (see below), showing the influence of the spin order on the MnO lattice. The elongation of the \( MnO_{6} \) octahedra, previously reported at 300 K ( \( d_{eq}/d_{ap} = 0.955 \) ), is also observed at low temperature and is even more pronounced ( \( d_{eq}/d_{ap} = 0.950 \) ). Moreover, new peaks, with low intensity but well defined, characteristic of antiferromagnetism (and whose indexation is discussed in the next section) appear at low angle in the NPD patterns, clearly below \( T_{N} \approx 110\,K \) (Fig. 5a). Nevertheless, a careful inspection of the background of the patterns (inset of Fig. 5a) shows an increase of the

Fig. 4. Final refinement, with experimental (+), calculated (−) and difference NPD patterns of \( Ca_{2}MnO_{4} \) , in insert enlargement showing the good peak shape for all the reflections.
signal for temperature higher than \( T_{N} \) (as shown with the 125 and 150 K patterns), with a typical Warren profile characteristic of 2D compounds [35], in the \( 2\theta \) range where the AFM peaks are well defined at lower temperature.
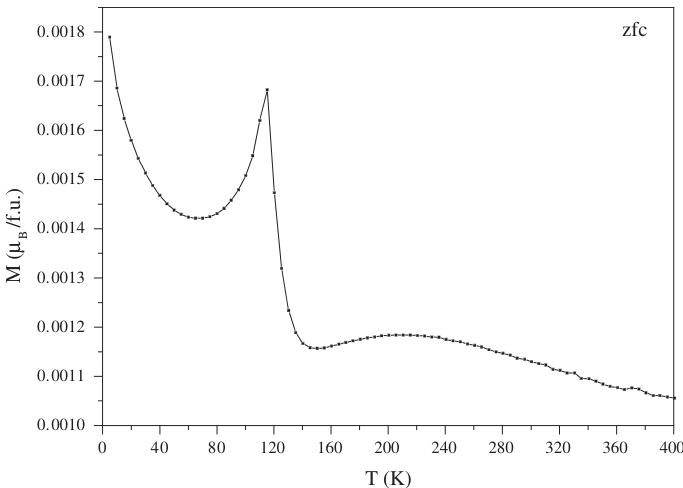
The behavior versus temperature has also been studied by magnetization \( (M) \) measurements, as shown in Fig. 6. Whatever the temperature, no ferromagnetism is evidenced and the \( T_{N} \) value, determined by the peak on the \( M(T) \) curve at \( \approx115 \) K, is in agreement with the one obtained by NPD. The bump observed at higher temperature ( \( \approx230 \) K) is characteristic of layered compounds [36], it corresponds to magnetic interactions in the planes that are not coherent along the stacking axis.
3.3. Low temperature structure: 1.5K-NPD G4.1 data
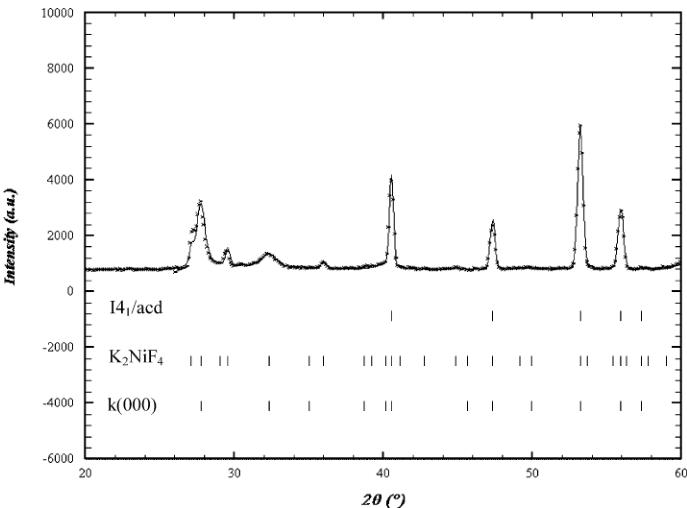
The analysis of the 1.5K data shows two sets of magnetic Bragg peaks implying that two propagation vectors are necessary to describe the magnetic structure (Fig. 7). As explained in the 1.2 section and due to the fact that only G4.1 data are available, the pattern has been refined by using one crystallographic phase \( (I4_{1}/acd) \) and two magnetic structures, the results have thus to be taken with caution.
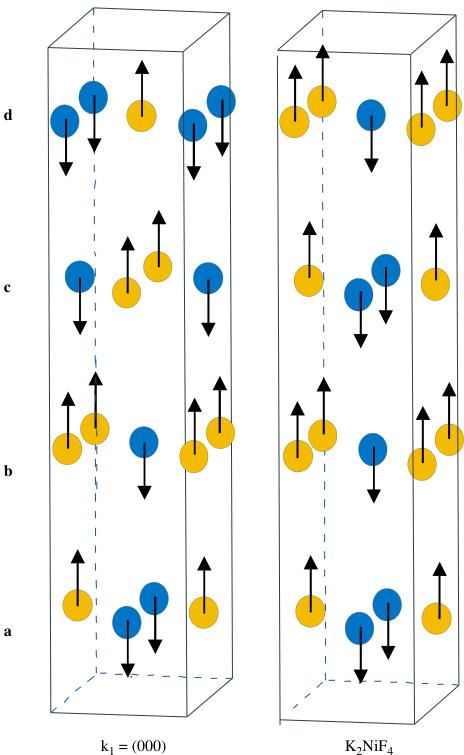
The first set of peaks, corresponding to the propagation vector \( k_{1}=(000) \) , obeys the selection rule \( h+k+l=2n \) and thus the Mn moments related by the I-translation \( \left[\frac{1}{2}\frac{1}{2}\frac{1}{2}\right] \) are parallel, the magnetic cell is identical to the chemical one \( (a_{\mathrm{p}}\sqrt{2}, 24\mathrm{\AA}) \) and the Mn magnetic moments are parallel to the c-axis, with \( M_{z}=2.4(1)\mu_{\mathrm{B}} \) . This model is identical to the one previously observed [29,30] for \( Ca_{2}MnO_{4} \) . It can be described (Fig. 8) as the antiferromagnetic stacking of AFM planes \( (a, c \) and \( b, d) \) .
The identification of the second magnetic structure is not so simple due to the low intensity of the peaks and their overlapping with those of the first one. This second


Fig. 5. Temperature dependence of the NPD patterns registered on the G4.1 diffractometer from 1.5 to 300K for \( Ca_{2}MnO_{4} \) with an enlargement of the small angles part for selected temperatures (a) and corresponding temperature dependence of the lattice parameters (b).

Fig. 5 (continued).

Fig. 6. Magnetization versus temperature curve in an external field of 1.45 T.

Fig. 7. Observed and calculated profiles in low angles region for NPD pattern at 1.5 K.

Fig. 8. Magnetic models.
set of peaks could probably be associated with \( K_{2}NiF_{4} \) whose structure consists of a ferromagnetic coupling of antiferromagnetic planes \( (a, c \) and \( b, d \) , respectively—Fig. 8), with \( M_{z} = 0.9(1) \mu_{B} \) . Even if it is difficult to give a ratio between both magnetic phases, it is clear that the one corresponding to \( K_{2}NiF_{4} \) is in minority.
For both structures, the \( (a,b) \) planes are AFM but they differ by the staking mode along c. This leads to an average Mn moment of \( 2.6\mu_{B} \) in \( Ca_{2}MnO_{4} \) , that is a value smaller than the one expected for \( Mn^{4+} \) ( \( 3\mu_{B} \) ).
Finally it is worth pointing out that a mixture of magnetic structures \( k(000) \) and \( K_{2}NiF_{4} \) were also previously observed for \( Rb_{2}MnF_{4} \) by Birgeneau et al. [37].
4. Conclusion
In conclusion, this study shows the existence, for \( Ca_{2}MnO_{4} \) , of two structural distortions with the \( I4_{1}/cad \) and \( Aba2 \) symmetries, which coexist in a coherent manner within the same matrix. It also shows that below \( T_{N} \) , two antiferromagnetic structures are generated. Thus, this complex crystalline and magnetic state observed in \( Ca_{2}MnO_{4} \) should be taken into consideration for the understanding of the properties of closely related Ruddlesden–Popper phases.
Acknowledgments
The authors are grateful to J. Rodriguez-Carvajal, Z. Jirak, N. Guiblin and A. Maignan for many fruitful discussions.
References
[1] C.N.R. Rao, B. Raveau (Eds.), Colossal Magnetoresistance, Charge Ordering and Related Properties of Manganese Oxides, World Scientific, Singapore, 1998.
[2] Y. Tokura (Eds.), Colossal Magnetoresistive Oxides, Gordon and Breach Science Publishers, New York, 1999.
[3] P.M. Woodward, D.E. Cox, T. Vogt, C.N.R. Rao, A.K. Cheetham, Chem. Mater. 11 (1999) 3528.
[4] P. Radaelli, D.E. Cox, M. Marezio, S.W. Cheong, Phys. Rev. B 55 (1997) 3015.
[5] F. Damay, Z. Jirak, M. Hervieu, C. Martin, A. Maignan, B. Raveau, G. André, F. Bourée, J. Magn. Magn. Mater. 190 (1998) 221.
[6] M. Hervieu, A. Barnabé, C. Martin, A. Maignan, F. Damay, B. Raveau, Eur. Phys. J. B 8 (1999) 31.
[7] Z. Jirak, S. Krupicka, Z. Simsa, M. Dlouha, S. Vratislav, J. Magn. Magn. Mater. 53 (1985) 153.
[8] C.H. Chen, S.W. Cheong, H.Y. Hwang, J. Appl. Phys. 81 (1997) 4326.
[9] S. Yunoki, J. Hu, A. Malvezzi, A. Moreo, N. Furukawa, E. Dagotto, Phys. Rev. Lett. 80 (1998) 845.
[10] E. Dagotto, S. Yunoki, A. Malvezzi, A. Mareo, J. Hu, S. Capponi, D. Poilblanc, F. Furukawa, Phys. Rev. B 58 (1998) 6414.
[11] S. Yunoki, A. Moreo, Phys. Rev. B 58 (1998) 6403.
[12] P. Schiffer, A.P. Ramirez, W. Bao, S.W. Cheong, Phys. Rev. Lett. 75 (1995) 3336.
[13] P.G. Radaelli, D.E. Cox, M. Marezio, S.W. Cheeng, P. Schiffer, A.P. Ramirez, Phys. Rev. Lett. 75 (1995) 4448.
[14] G. Allodi, R. De Renzi, G. Guidi, F. Licci, M.W. Piepper, Phys. Rev. B 56 (1997) 6036.
[15] G. Allodi, R. De Renzi, F. Licci, M.W. Piepper, Phys. Rev. Lett. 81 (1998) 4736.
[16] N. Fukumoto, S. Mori, N. Yamamoto, Y. Moritomo, T. Katsufuji, C.H. Chen, S.W. Cheong, Phys. Rev. B 60 (1999) 12963.
[17] S.N. Ruddlesden, P. Popper, Acta Crystallogr. 10 (1957) 538.
[18] Y. Moritomo, Y. Tomioka, A. Asamitsu, Y. Tokura, Nature (London) 380 (1996) 141.
[19] R. Mahesh, R. Mahendiran, A.K. Raychaudhuri, C.N.R. Rao, J. Solid State Chem. 122 (1996) 448.
[20] A. Maignan, C. Martin, G. Van Tendeloo, M. Hervieu, B. Raveau, J. Mater. Chem. 8 (1998) 2411.
[21] M. Ibarra, R. Retoux, M. Hervieu, C. Autret, A. Maignan, C. Martin, B. Raveau, J. Solid State Chem. 170 (2003) 361.
[22] C. Autret, R. Retoux, M. Hervieu, B. Raveau, Chem. Mater. 13 (2001) 4745.
[23] B.J. Sternlieb, J.P. Hill, U.C. Wildbruger, G.M. Luke, B. Nachumi, Y. Moritomo, Y. Tokura, Phys. Rev. Lett. 76 (1996) 2169.
[24] Y. Murakami, H. Kawada, H. Kawata, M. Tanaka, T. Arima, Y. Moritomo, Y. Tokura, Phys. Rev. Lett. 80 (1998) 1932.
[25] T. Kimura, K. Hatsuda, Y. Ueno, R. Kajimoto, H. Mochizuki, H. Yoshizawa, T. Nagai, Y. Matsuhi, A. Yamazaki, Y. Tokura, Phys. Rev. B 65 (2001) 020407.
[26] M.E. Leonowicz, K.R. Poeppelmeier, J.M. Longo, J. Solid State Chem. 59 (1985) 71.
[27] J. Takahashi, N. Kamegashira, Mater. Res. Bull. 28 (1993) 565.
[28] I.D. Fawcett, J.E. Sunstrom, M. Greenblatt, M. Craft, K.V. Ramanujachary, Chem. Mater. 10 (1998) 3643.
[29] D.E. Cox, G. Shirane, Phys. Rev. 188 (1969) 188.
[30] K. Tezuka, M. Inamura, Y. Hinatsu, Y. Shimojo, Y. Morii, J. Solid State Chem. 145 (1999) 705.
[31] E. Legrand, R. Plumier, Phys. Stat. Sol. 2 (1962) 317.
[32] J. Rodriguez-Carvajal, Physica B 192 (1993) 55.
[33] R. Kilaas, Mac Tempas Program, N. Schryvers, EMAT, Anvers University.
[34] J. Rodríguez-Carvajal Recent developments of the program FULLPROF, Commission On Powder Diffraction International Union of Crystallography Newsletter No. 26, December 2001, pp. 12–19.
[35] B.E. Warren, X-ray Diffraction, Addison-Wesley Publishing Company, London, 1969.
[36] G. Leffem, Ph. Courbin, C. Delmas, J.L. Soubeyroux, Z. Anorg. Allg. Chem 476 (1981) 69.
[37] R.J. Birgeneau, J. Guggenheim, G. Shirane, Phys. Rev. B 1 (1970) 2211.