| Transition Temperature | 4.8 K |
|---|---|
| Experiment Temperature | 1.7 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | P21/c (#14) |
| Magnetic Space Group | P21'/c (#14.77) |
| Magnetic Point Group | 2'/m (5.3.14) |
| Lattice Parameters | 9.79040 8.71590 5.33640 90.00 108.93 90.00 |
|---|---|
| DOI | 10.1103/physrevb.82.024429 |
| Reference | G. Nenert, M. Isobe, I. Kim, C. Ritter, C.V. Colin, A.N. Vasiliev, K.H. Kim and Y. Ueda, Physical Review B (2010) 82 024429. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Cr1 | Cr | 2.41 | 0.0 | 1.24 | 2.33 |
Interplay between low dimensionality and magnetic frustration in the magnetoelectric pyroxenes \( LiCrX_{2}O_{6} \) (X=Ge, Si)
Gwilherm Nénert, \( ^{1,*} \) Masahiko Isobe, \( ^{2} \) Ingyu Kim, \( ^{3} \) Clemens Ritter, \( ^{1} \) Claire V. Colin, \( ^{4} \) Alexander N. Vasiliev, \( ^{5} \)
Kee Hoon Kim, \( ^{3} \) and Yutaka Ueda \( ^{2} \)
\( ^{1} \) Institut Laue-Langevin, Boîte Postale 156, 38042 Grenoble Cedex 9, France
\( ^{2} \) Institute for Solid State Physics, University of Tokyo, 5-1-5 Kashiwa, Chiba 277-8581, Japan
\( ^{3} \) CeNSCMR, Department of Physics and Astronomy, Seoul National University, Seoul 151-747, Korea
\( ^{4} \) Institut Néel, CNRS/Université Joseph Fourier, BP 166, 38042 Grenoble, France
\( ^{5} \) Low Temperature Physics Department, Moscow State University, Moscow 119991, Russia
(Received 9 April 2010; revised manuscript received 2 July 2010; published 28 July 2010)
We have investigated the magnetic and magnetoelectric properties of \( LiCrGe_{2}O_{6} \) and reinvestigated the magnetic properties of \( LiCrSi_{2}O_{6} \) . Using superconducting quantum interference device magnetometry, electrical polarization, and neutron diffraction, we give evidence for the presence of magnetic frustration in the magnetoelectric pyroxenes \( LiCrX_{2}O_{5} \) (X=Si, Ge). While pyroxene materials have been widely investigated for their low dimensional properties, we suggest that the magnetic frustration is likely to play a more important role into the nature of the magnetic ground state. The existence and possible interplay of low dimensionality and magnetic frustration resulting in multiferroic and/or magnetoelectric properties in the pyroxenes will probably open new avenues to tune and investigate the richness of the physic in this family.
DOI: 10.1103/PhysRevB.82.024429
PACS number(s): 75.85.+t, 75.25.−j, 75.47.Lx, 75.50.Ee
I. INTRODUCTION
In recent years, the coupling between magnetic and dielectric properties in transition metal oxides gave rise to a significant research effort. \( ^{1-3} \) This effort is governed by the emergence of new fundamental physics and potential technological applications. \( ^{2-4} \) Multiferroic materials exhibit simultaneously (ferro)magnetic, ferroelectric and ferroelastic properties. Contrary to multiferroic materials, magnetoelectric materials show an induced electrical polarization by a magnetic field. A proper understanding of the interplay between the various physical properties of these two types of materials relies heavily on the knowledge of the detailed crystal and magnetic structures.
One class of compounds which have been investigated in this context is the class of pyroxene materials. They have the general formula \( AMX_{2}O_{6} \) where A is an alcali (+I) or alkali-earth ion (+II), M is a transition metal ion (+II or +III) while X=Si, Ge. These materials have been extensively investigated due to their importance in mineralogy \( ^{5-9} \) and their low dimensional magnetic properties. \( ^{10-15} \) The recent work by Jodlauk et al. shed some different light on these materials motivated by the idea that this family could be a good representative of a magnetically frustrated lattice. \( ^{16,17} \) The existence and possible interplay of low dimensionality and magnetic frustration resulting in multiferroic and/or magneto-electric properties in the pyroxenes will probably open new avenues to tune and investigate the richness of the physico in this family. We aim here to present the first evidence for the interplay between low dimensionality and magnetic frustration in magnetoelectric pyroxenes.
Lately, we have started to investigate the structural, magnetic, and dielectric properties of various \( ACrX_{2}O_{6} \) materials as a function of temperature and magnetic field. \( ^{[12-14]} \) In this contribution, we report on the effect of replacing silicon by germanium in \( LiCrX_{2}O_{6} \) . We have investigated magnetic properties of \( LiCrX_{2}O_{6} \) (X=Si, Ge) powder samples using superconducting quantum interference device (SQUID) magnetometry. Furthermore, in order to allow a comparison with our previous work on \( LiCrSi_{2}O_{6} \) , \( ^{[13]} \) we have investigated the magnetic, magnetoelectric and crystal structures of the pyroxene \( LiCrGe_{2}O_{6} \) by electrical polarization measurement and powder neutron diffraction. Magnetic exchange couplings in \( LiCrGe_{2}O_{6} \) extracted from magnetization measurements suggest a magnetic ground state similar to the one reported in \( LiCrSi_{2}O_{6} \) , however with a less pronounced one-dimensional (1D) character. This is in perfect agreement with the antiferromagnetic order determined below \( T_{N}=4.8(2) \) K by neutron diffraction. Corroborating the determined magnetic structure (magnetic symmetry \( P2_{1}^{\prime}/c \) ), the magnetic field dependence of the electrical polarization evidences a clear linear magnetoelectric effect below \( T_{N} \) . The unexpected lower 1D character in \( LiCrGe_{2}O_{6} \) is discussed in light of the interplay between low dimensionality of the crystal structure and the magnetic frustration in \( LiCrX_{2}O_{6} \) .
II. EXPERIMENT
Polycrystalline samples of \( LiCrGe_{2}O_{6} \) and \( LiCrSi_{2}O_{6} \) were prepared by a solid-state reaction with an appropriate molar ratio of \( Li_{2}CO_{3} \) , \( Cr_{2}O_{3} \) , and \( GeO_{2}/SiO_{2} \) . The weighted mixtures were pressed into pellets and heated at 1273 K in air for several days with one intermediate grinding.
Polycrystalline \( LiCrGe_{2}O_{6} \) and \( LiCrS_{2}O_{6} \) magnetization measurements were carried out by a SQUID magnetometer in the temperature range of 2–350 K and external magnetic fields of 1000 Oe. Neutron diffraction measurements were carried out on a \( LiCrGe_{2}O_{6} \) powder. The precise crystal and magnetic structures were investigated using high resolution powder data at 1.7 and 10 K using the D2B diffractometer at the ILL. The measurements were carried out at a wavelength of 1.594 Å corresponding to the (335) Bragg reflexion of a


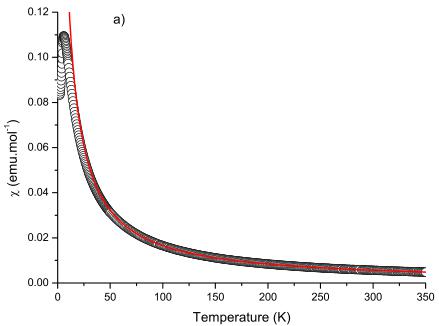
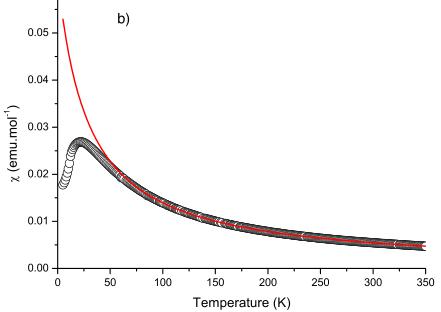
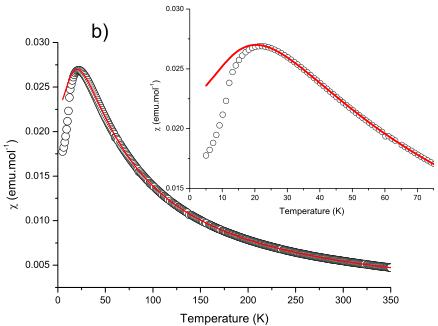
FIG. 1. (Color online) Zero field cooled magnetic susceptibility of (a) \( LiCrGe_{2}O_{6} \) and of (b) \( LiCrSi_{2}O_{6} \) . The lines represent a Curie-Weiss temperature dependence fit defined by \( \chi=\frac{C}{T-\theta} \) .
germanium monochromator. The neutron detection is performed with \( {}^{3} \) He counting tubes spaced at \( 1.25^{\circ} \) intervals for D2B. A complete diffraction pattern is obtained after 25 steps of \( 0.05^{\circ} \) in \( 2\theta \) . Diffraction data analysis was done using the FullProf refinement package. \( ^{18} \)
To investigate the magnetoelectric properties of \( LiCrGe_{2}O_{6} \) , we measured the variation of the electric polarization P as a function of the magnetic field and temperature. A polycrystalline pellet was thinned down to 0.48 mm in thickness and silver epoxy was used to make electrodes on both sides. For magnetoelectric cooling, we applied an electric field \( E = \pm 208 \) kV/m with H = 9 T at 10 K and cooled down to 2 K. Then, we measured the isothermal current variation under the same applied E while sweeping H at a rate of 200 Oe/s from 9 to -9 T by using a Keithely 617 electrometer. We integrated the current to obtain the magnetic field dependence of the electrical polarization. Similarly, we measured the current variation under E = 208 kV/m and at a fixed H while increasing temperature at a rate of 5 K/min and obtained the P versus T curve from integration of the current.
III. RESULTS AND DISCUSSION
A. Magnetic properties
The measured temperature dependence of the magnetic susceptibilities in an external magnetic field of 1000 Oe of

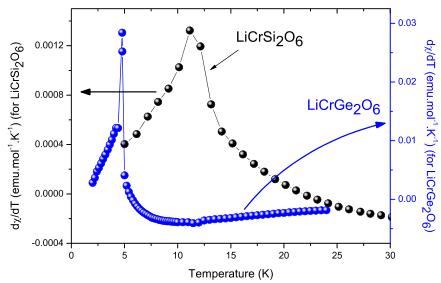
FIG. 2. (Color online) Derivative of the magnetic susceptibility emphasizing the long range magnetic order below \( T_{N}=11.1(5) \) K for \( LiCrSi_{2}O_{6} \) and \( T_{N}=4.8(2) \) K for \( LiCrGe_{2}O_{6} \)
LiCrGe_{2}O_{6} and LiCrSi_{2}O_{6} is shown in Fig. 1. We fitted the magnetic susceptibility with a Curie-Weiss temperature dependence defined by \( \chi=\frac{C}{T-\theta} \) . The fit was made in the range 100 to 350 K. Below around 75 K, the magnetic susceptibilities depart from the Curie-Weiss model for both compounds. The determined effective moment is \( \mu_{eff}=3.6998(5)\mu_{B} \) and


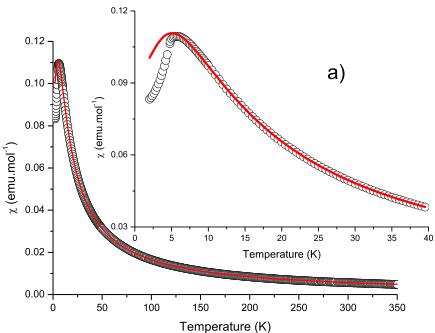
FIG. 3. (Color online) Temperature dependence of the magnetic susceptibility \( \chi \) for a) \( LiCrGe_{2}O_{6} \) and for b) \( LiCrSi_{2}O_{6} \) . The solid line represents the best fit of the experimental data to Eq. (2) for (a) T>15 K ( \( LiCrGe_{2}O_{6} \) ) and for (b) T>22 K ( \( LiCrSi_{2}O_{6} \) ).

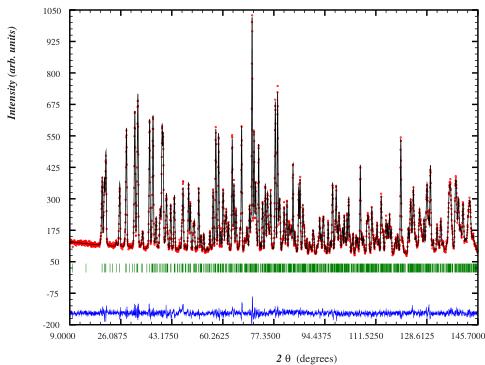
FIG. 4. (Color online) Neutron powder pattern ( \( \lambda=1.594 \) Å) of \( LiCrGe_{2}O_{6} \) sample collected at 10 K using the D2B diffractometer. The refinement has been done in the \( P2_{1}/c \) space group with the following statistics: \( R_{p}=3.33\% \) and \( R_{wp}=4.28\% \) .
\( \theta=-3.19(3) \) K for \( LiCrGe_{2}O_{6} \) and \( \mu_{eff}=3.7905(6)\mu_{B} \) and \( \theta=-28.88(5) \) K for \( LiCrSi_{2}O_{6} \) . This is in agreement with a previous report. \( ^{15} \)
One characteristic of these pyroxene materials is that they are good representative of low dimensional magnetism with linear chains running along the c axis. \( ^{10-15} \) Magnetic response shows for both compounds a broad maximum characteristic of low dimensional magnetism (see Figs. 1 and 3). Evidence for long range order is given by the derivative \( d\chi/dT \) as illustrated in Fig. 2. In the following, we will therefore treat the magnetic susceptibility data using the formalism developed for low dimensional magnetism. \( ^{19} \)
For a uniform chain of classical spins based on the Hamiltonian \( \mathcal{H}=-2J\Sigma_{s}\mathbf{S}_{i+1}\mathbf{g}\mu_{B}[S(S+1)]^{1/2}-\Sigma_{i}\mathbf{H}\cdot S_{i} \) , the magnetic susceptibility can be expressed as \( ^{19} \)
\[ \chi_{chain}=\frac{Ng^{2}\beta^{2}S(S+1)}{3k_{b}T}\times\frac{1+u}{1-u}, \quad (1) \]
where u is the well-known Langevin function defined as \( u=\coth[2JS(S+1)/k_{b}T]-k_{b}T/[2JS(S+1)] \) with S=3/2. Considering the existence of a long range order at low temperature, we assumed an interchain interaction \( J' \) between the chains. Applying the mean-field approximation, the susceptibility of \( LiCrX_{2}O_{6} \) can be expressed as
\[ \chi=\frac{\chi_{chain}}{1-\left(\frac{zJ'}{Ng^{2}\beta^{2}}\right)\chi_{chain}}, \quad (2) \]
where z is the number of nearest-neighbor chains, N Avogadro's number, g the gyromagnetic factor of a free electron spin, and \( \beta \) the Bohr magneton. With g fixed at 2.00, the least-squares fit of the experimental data above 15 K for \( LiCrGe_{2}O_{6} \) to the above expression led to \( J/k_{b} = -1.41(1) \) K, a Curie constant \( C = 1.7395(9) \) emu mol \( ^{-1} \) K \( ^{-1} \) corresponding to \( \mu_{eff} = 3.730(1) \) \( \mu_{B} \) and an interchain exchange coupling \( J'/k_{b} = 0.64(3) \) K taking into account z = 4. The resulting fit is shown together with the experimental data in Fig. 3(a). For \( LiCrSi_{2}O_{6} \) , the fit of the data using Eq. (2) gives \( J/k_{b} = -5.688(8) \) K, \( J'/k_{b} = 1.89(3) \) K and \( C = 1.7689(7) \) corresponding to \( \mu_{eff} = 3.7618(7) \) \( \mu_{B} \) [see Fig. 3(b)].
These estimations of the intrachain and interchain magnetic exchange couplings in \( LiCrX_{2}O_{6} \) are in good agreement with their respective magnetic structures (see Sec. III C and Ref. 13). Moreover, these results suggest that \( LiCrGe_{2}O_{6} \) has a less 1D character than \( LiCrSi_{2}O_{6} \) since the ratio \( \left|J/J'\right| \) is smaller [2.1(1) versus 3.01(5)]. This is really counterintuitive as the magnetic \( CrO_{6} \) chains are further apart in \( LiCrGe_{2}O_{6} \) predisposing it to a more marked 1D character compared to \( LiCrSi_{2}O_{6} \) .²⁰⁻²³ We discuss this point in more details in Sec. III C.
B. Structural investigation
The refined lattice parameters at 10 K are \( a = 9.79037(12) \) Å, \( b = 8.71595(12) \) Å, \( c = 5.33641(7) \) Å, and \( \beta = 108.9300(7)^{\circ} \) . The pattern was refined in the space group \( P2_{1}/c \) , taking as starting structural model the one reported
TABLE I. Crystallographic coordinates extracted from the Rietveld refinement carried out on powder neutron diffraction (D2B) using the space group \( P12_{1}/c1 \) at 10 K with cell parameters \( a=9.79037(12) \) Å, \( b=8.71595(12) \) Å, \( c=5.33641(7) \) Å, and \( \beta=108.9300(7)^{\circ} \) .
| Atom | Wyckoff | x | y | z | U_{iso} |
| Li | 4e | 0.2577(8) | 0.0133(7) | 0.2192(14) | 0.0048(13) |
| Cr | 4e | 0.2513(4) | 0.6591(4) | 0.2121(7) | 0.0036(6) |
| Ge_{1} | 4e | 0.04743(17) | 0.3438(2) | 0.2756(3) | 0.0035(2) |
| Ge_{2} | 4e | 0.55471(16) | 0.8418(2) | 0.2290(3) | 0.0035(2) |
| O_{1a} | 4e | 0.8574(2) | 0.3327(3) | 0.1732(4) | 0.00509(18) |
| O_{1b} | 4e | 0.3641(2) | 0.8311(3) | 0.1041(5) | 0.00509(18) |
| O_{2a} | 4e | 0.1146(2) | 0.5262(3) | 0.2839(4) | 0.00509(18) |
| O_{2b} | 4e | 0.6312(3) | 0.0065(3) | 0.3872(5) | 0.00509(18) |
| O_{3a} | 4e | 0.1175(2) | 0.2911(2) | 0.6097(5) | 0.00509(18) |
| O_{3b} | 4e | 0.6139(2) | 0.6880(3) | 0.4547(4) | 0.00509(18) |

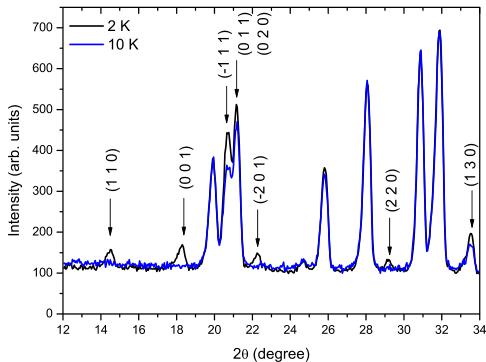
FIG. 5. (Color online) Fragment of the D2B neutron diffraction pattern of \( LiCrGe_{2}O_{6} \) at 2 and 10 K. New reflections appear and/or increase in intensity which can be described with a magnetic propagation vector k=0.
previously for \( LiCrSi_{2}O_{6} \) (see Ref. 13) The good agreement between the calculated and observed patterns is presented in Fig. 4. Structural parameters obtained from the refinement are listed in Table I. Between 1.7 and 10 K, the crystal structure does not change noticeably. Consequently we report here only the results at 10 K.
C. Determination of the magnetic structure
High resolution neutron powder data have been collected at 10 and 1.7 K on the D2B diffractometer. In the 1.7 K pattern, new reflections appear and/or increase in intensity as shown in Fig. 5. These magnetic reflections like in \( LiCrSi_{2}O_{6} \) can be indexed with a magnetic propagation vector \( k=0 \) .¹³ Additionally, the magnetic reflections appearing are identical to those appearing in \( LiCrSi_{2}O_{6} \) suggesting that the magnetic structure of \( LiCrGe_{2}O_{6} \) is similar to the one of \( LiCrSi_{2}O_{6} \) .
The possible magnetic structures compatible with the symmetry of \( LiCrGe_{2}O_{6} \) and a magnetic propagation vector k=0 have been discussed previously. \( ^{13} \) Keeping the same notations, we recall here the results of the derivations of the possible magnetic structures in Table II.
Since \( LiCrGe_{2}O_{6} \) has the same crystal structure as \( LiCrSi_{2}O_{6} \) and since the magnetic reflections are similar, we perform the refinement of the 1.7 K data using as starting magnetic model the one reported for \( LiCrSi_{2}O_{6} \) . \( ^{13} \) This magnetic model is described by the irreducible representation \( \Gamma_{4} \)
TABLE II. Basis vectors for the atoms of the 4e site.
| Basis vectors | x | y | z |
| \( \Gamma_{1} \) | \( L_{1x} \) | \( M_{y} \) | \( L_{1z} \) |
| \( \Gamma_{2} \) | \( L_{3x} \) | \( L_{2y} \) | \( L_{3z} \) |
| \( \Gamma_{3} \) | \( M_{x} \) | \( L_{1y} \) | \( M_{z} \) |
| \( \Gamma_{4} \) | \( L_{2x} \) | \( L_{3y} \) | \( L_{2z} \) |

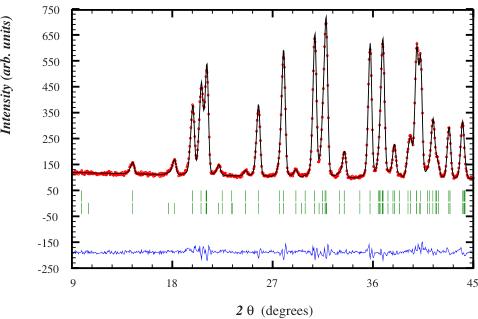
FIG. 6. (Color online) Fragment of the D2B neutron diffraction pattern of \( LiCr Ge_{2} O_{6} \) at 1.7 K and refined by using the \( \Gamma_{3}4 \) model ( \( Cr^{3+} \) spins along the c axis, \( P2_{1}^{\prime}/c \) symmetry).
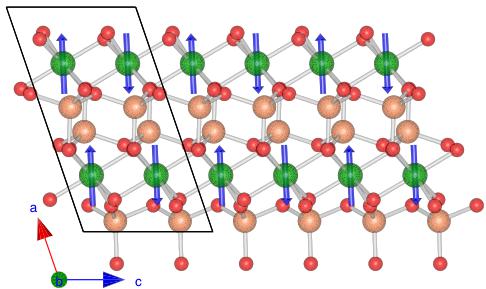
resulting in an antiferromagnetic coupling within the chains and a ferromagnetic coupling between the chains. We obtain a good description using the magnetic model of \( LiCrSi_{2}O_{6} \) , however a better fit could be obtained by setting \( L_{3y} \) to zero, lowering the \( R_{mag} \) factor from 6.88 to 5.02%. This better fit is shown in Fig. 6. Within the experimental resolution, we find that \( L_{2x}=2.41(3)\mu_{B} \) ; \( L_{3y}=0 \) and \( L_{2z}=1.24(7)\mu_{B} \) at 1.7 K. This corresponds to a magnetic structure with ferromagnetically coupled chains of \( CrO_{6} \) octahedra as shown in Fig. 7.
The magnetic moment at \( T=1.7\ K \) is \( \|\mu(\mathrm{Cr}^{3+})\|=2.33(3)\mu_{B} \) . This is a significantly higher magnetic moment than the one reported for \( LiCrSi_{2}O_{6} \) [2.33(3) versus \( 2.06(4)\mu_{B} \) ]. \( ^{13} \) This magnetic moment is reduced only by about \( 7(1)\% \) compared to the saturation of the magnetic form factor of \( Cr^{3+} \) determined experimentally which is \( 2.5\mu_{B} \) . \( ^{25} \) In \( LiCrGe_{2}O_{6} \) , the interchain distance Cr-Cr at 1.7 K is \( 5.5809(40)\mathring{A} \) which is significantly higher than \( 5.3352(55)\mathring{A} \) found in \( LiCrSi_{2}O_{6} \) . At a first guess, one would expect that the low dimensional character of this compound should be more pronounced than in \( LiCrSi_{2}O_{6} \) and thus reduce further the magnetic moment. However, this is in disagreement with the extracted value of the magnetic ex-

FIG. 7. (Color online) Magnetic structure of \( LiCrGe_{2}O_{6} \) . The magnetic coupling between the \( CrO_{6} \) chains is ferromagnetic while the magnetic coupling within the chains is antiferromagnetic. The magnetic structure representation has been made using VESTA (Ref. 24).

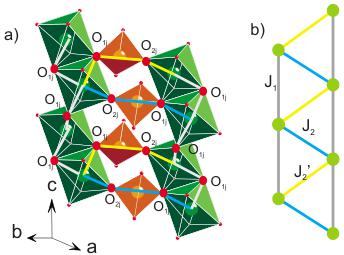
FIG. 8. (Color online) (a) The \( CrO_{6} \) zigzag chains separated by \( GeO_{4} \) tetrahedra. We indicated in gray, blue and yellow the main magnetic exchange interactions. We emphasize the oxygens \( O_{1j} \) and \( O_{2j} \) which are involved in the magnetic exchange paths (b) We show the equivalent magnetic lattice keeping the same color code. \( J_{1} \) is of magnetic superexchange type, while \( J_{2} \) and \( J_{2}^{\prime} \) are of super-super-exchange type. \( J_{1} \) magnetic exchange path goes via \( Cr-O_{1j}-Cr \) , while \( J_{2} \) and \( J_{2}^{\prime} \) , go via \( Cr-O_{1j}-O_{2j}-Cr \) .
change coupling constant and the neutron data. Indeed the ratio \( |J/J'| \) for \( LiCrGe_{2}O_{6} \) is lower than for \( LiCrSi_{2}O_{6} \) suggesting that the magnetic order in \( LiCrGe_{2}O_{6} \) has a more 3D character than in \( LiCrSi_{2}O_{6} \) . This is supported by the fact that the broad maximum and the Néel temperature of \( LiCrGe_{2}O_{6} \) are closer than in \( LiCrSi_{2}O_{6} \) (see Fig. 3) and by the less reduced magnetic moment determined from neutron data.
Consequently, we need to take into account other parameters responsible for a reduction of the magnetic moment in this system. One possibility is to consider the magnetic frustration as suggested by Jodlauk. \( ^{16} \) Indeed, three different magnetic exchange are possible between the transition metal ions in these pyroxenes: one along the \( CrO_{6} \) chain \( \mathrm{Cr-O_{1j}-Cr} \) ( \( J_{1} \) in Fig. 8), and two between the chains going trough \( \mathrm{Cr-O_{1j}-O_{2j}-Cr} \) ( \( J_{2} \) and \( J_{2}^{\prime} \) in Fig. 8) (j=a or b, see Table I). We remind that there are 2 types of \( X_{7}O_{4} \) and consequently \( 2O_{1j} \) and \( 2O_{2j} \) . If all three magnetic exchanges are antiferromagnetic, we have to deal with a magnetically frustrated system. While the resulting magnetic coupling between the chains is ferromagnetic as determined from the SQUID and neutron data, this does not exclude a competition between these three interactions. Taking further apart the chains would then lead to a decrease of the magnetic frustration. This is exactly what we observe in \( LiCrX_{2}O_{6} \) where the magnetic moment increases as the distance between the chains increases. The ratio \( \left|\theta/T_{N}\right| \) which is a measure of the magnetic frustration \( ^{26} \) decreases from 2.61(1) to 0.66(4) when going from Si to Ge. We note that while the \( \left|\theta/T_{N}\right| \) ratios that we are dealing with are not high, there is a clear indication that the magnetic frustration decreases. This gives further support to our interpretation.
Consequently, we interpret the low magnetic moment in \( LiCrSi_{2}O_{6} \) as the main result of the magnetic frustration. While the magnetic properties of \( AMX_{2}O_{6} \) pyroxenes have been extensively investigated due to their pseudo-1D character, the magnetic frustration is likely to play the most important role in determining the nature of the magnetic ground


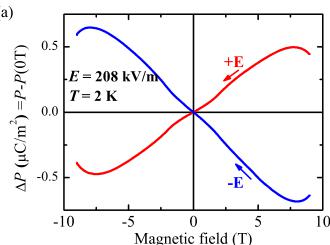
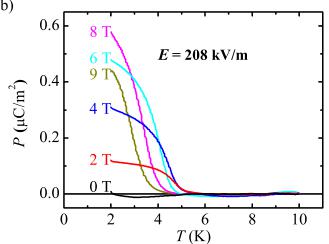
FIG. 9. (Color online) (a) The \( \Delta P[=P(H)-P(0)] \) versus H curve between -9 and 9 T, and (b) P versus T curves from 2 to 10 K at various fixed H, obtained from integration of magnetoelectric and pyroelectric currents, respectively. A constant E=208 kV/m perpendicular to H was applied during the measurements.
state. Our results shade some light on this key parameter driving the magnetic ground state in the AMX_{2}O_{6} pyroxenes.
D. Magnetoelectric properties
The magnetic structure determined from neutron diffraction allows for the presence of a linear magnetoelectric effect. \( ^{13,27} \) The magnetic space group \( (P2_{1}^{\prime}/c) \) is identical to the one of \( LiCrSi_{2}O_{6} \) where a linear magnetoelectric effect has been already reported. \( ^{13,16} \) Revealing the actual presence of this possible linear magnetoelectric effect in \( LiCrGe_{2}O_{6} \) would further confirm the interest that presents the pyroxene family to find new magnetoelectric and/or multiferroic materials.
In Fig. 9, we present our results on the variation of the polarization as a function of magnetic field and temperature. In the P versus H curves, an almost linear variation of P with H is observed below \( |H|=7 \) T. Small wiggles around \( H=\pm2 \) T are likely to arise from the angular averaging effects of the magnetoelectric responses in different crystallographic orientations. Above \( |H|=8 \) T, P begins to decrease, indicating that the spin configuration changes in this field region. In the P versus T curves in Fig. 9(b), the P values at H=9 T are indeed smaller than those at H=8 T, confirming the decrease of P above 8 T. We interpret this effect as a likely spin-flip transition around H=8 T. Moreover, the temperature where a net P develops in the P versus T curves seems to systematically decrease with the increase of the magnetic field. This is usually what is observed for classical Heisenberg systems.
Despite of the averaging due to the polycrystalline nature of our sample, we notice that the value of the induced electrical polarization is similar in magnitude to the one reported for a single crystal of \( LiCrSi_{2}O_{6} \) . \( ^{16} \) As the magnetoelectric tensor components depend on the values of the magnetic components; one could expect that the magnetoelectric effect in \( LiCrGe_{2}O_{6} \) is larger than in \( LiCrSi_{2}O_{6} \) . \( ^{13} \) This seems to be effectively the case.
IV. CONCLUSION
We have investigated the magnetic and crystal structures of \( LiCrGe_{2}O_{6} \) as a function of temperature using powder neutron diffraction. Below \( T_{N}=4.8(2) \) K, \( LiCrGe_{2}O_{6} \) exhibits a long range antiferromagnetic order commensurate with the lattice with \( k=0 \) . It is characterized by ferromagnetic layers alternating along the c axis giving rise to an overall antiferromagnetic ground state. Using mean-field approximation, we estimated the magnetic exchange interaction parameters
\( ^{*} \) Corresponding author; nenert@ill.eu
\( ^{1} \) M. Fiebig, J. Phys. D 38, R123 (2005).
\( ^{2} \) W. Eerenstein, N. D. Mathur, and J. F. Scott, Nature (London) 442, 759 (2006).
\( ^{3} \) S.-W. Cheong and M. Mostovoy, Nature Mater. 6, 13 (2007).
\( ^{4} \) A. Pimenov, A. A. Mukhin, V. Yu. Ivanov, V. D. Travkin, A. M. Balbashov, and A. Loidl, Nat. Phys. 2, 97 (2006); A. B. Sushkov, R. V. Aguilar, S. Park, S.-W. Cheong, and H. D. Drew, Phys. Rev. Lett. 98, 027202 (2007).
\( ^{5} \) J. B. Thompson, Am. Mineral. 55, 292 (1970); G. J. Redhammer, H. Ohashi, and G. Roth, Acta Crystallogr., Sect. B: Struct. Sci. 59, 730 (2003); C. Satto, P. Millet, and J. Galy, Acta Crystallogr., Sect. C: Cryst. Struct. Commun. 53, 1727 (1997); E. Baum, W. Treutmann, M. Behruzi, W. Lottermoser, and G. Amthauer, Z. Kristallogr. 183, 273 (1988); M. J. Origlieri, R. T. Downs, R. M. Thompson, C. J. S. Pommier, M. Bonner Denton, and G. E. Harlow, Am. Mineral. 88, 1025 (2003); R. M. Thompson and R. T. Downs, ibid. 89, 614 (2004); Li Zhang, Hans Ahsbahs, Stefan S. Hafner, and Ali Kutoglu, ibid. 82, 245 (1997); T. alrt, R. J. Angel, R. Miletich, T. Armbruster, and T. Peters, ibid. 83, 1176 (1998).
\( ^{6} \) G. J. Redhammer and G. Roth, Z. Kristallogr. 219, 585 (2004). Please note that the coordinates given in the paper contain an error. The x coordinate of \( Si_{1} \) is 0.0487 and not 0.487.
\( ^{7} \) G. J. Redhammer and G. Roth, Z. Kristallogr. 219, 278 (2004).
\( ^{8} \) G. J. Redhammer, G. Roth, W. Paulus, G. André, W. Lottermoser, G. Amthauer, W. Treutmann, and B. Koppelhuber-Bitschnau, Phys. Chem. Miner. 28, 337 (2001).
\( ^{9} \) W. Lottermoser, G. J. Redhammer, K. Forcher, G. Amthauer, W. Paulus, G. André, and W. Treutmann, Z. Kristallogr. 213, 101 (1998).
\( ^{10} \) S. J. Blundell, C. A. Steer, F. L. Pratt, I. M. Marshall, W. Hayes, and R. C. C. Ward, Phys. Rev. B 67, 224411 (2003); J. L. Gavalino, S. Mushkolaj, H. R. Ott, P. Millet, and F. Mila, Phys. Rev. Lett. 85, 409 (2000); J. van Wezel and J. van den Brink, EPL 75, 957 (2006); Liu Yichang, Sun Liqun, H. Inoue, and S.
both between and within the chains. We found that \( J_{intra}/k_{b} = -5.688(8) \) K and \( J_{inter}/k_{b} = 1.89(3) \) K in good agreement with the magnetic structure determined from neutron diffraction. The associated magnetic symmetry is \( P2_{1}^{\prime}/c \) . This symmetry allows a linear magnetoelectric effect, which is confirmed experimentally. We argue that the higher magnetic moment determined from neutron compared to \( LiCrSi_{2}O_{6} \) arises from a release of the magnetic frustration while taking away the \( CrO_{6} \) chains. Our work suggests that the magnetic ground state in the \( AMX_{2}O_{6} \) pyroxene is significantly affected by the magnetic frustration rather than only by the low dimensionality of the structure.
ACKNOWLEDGMENTS
Work at SNU is supported by the National Creative Research Initiative and KRF (KRF-2008-314-c00101) programs.
Qin, Phys. Rev. B 63, 134428 (2001); J. Lou, T. Xiang, and Z. Su, Phys. Rev. Lett. 85, 2380 (2000); B. Pedrini, S. Wessel, J. L. Gavilano, H. R. Ott, S. M. Kazakov, and J. Karpinski, Eur. Phys. J. B 55, 219 (2007); B. Pedrini, J. L. Gavilano, D. Rau, H. R. Ott, S. M. Kazakov, J. Karpinski, and S. Wessel, Phys. Rev. B 70, 024421 (2004); M. Isobe, E. Ninomiya, A. N. Vasiliev, and Y. Ueda, J. Phys. Soc. Jpn. 71, 1423 (2002); S. V. Streltsov, O. A. Popova, and D. I. Khomskii, Phys. Rev. Lett. 96, 249701 (2006); S. V. Streltsov and D. I. Khomskii, Phys. Rev. B 77, 064405 (2008); P. Millet, F. Mila, F. C. Zhang, M. Mambrini, A. B. Van Oosten, V. A. Pashchenko, A. Sulpice, and A. Stepanov, Phys. Rev. Lett. 83, 4176 (1999); M. Isobe and Y. Ueda, J. Magn. Magn. Mater. 272-276, 948 (2004); M. Isobe, Y. Ueda, A. N. Vasiliev, T. N. Voloshok, and O. L. Ignatchik, ibid. 258-259, 125 (2003); A. N. Vasiliev, O. L. Ignatchik, A. N. Sokolov, Z. Hiroi, M. Isobe, and Y. Ueda, JETP Lett. 78, 551 (2003).
\( ^{11} \) M. D. Lumsden, G. E. Granroth, D. Mandrus, S. E. Nagler, J. R. Thompson, J. P. Castellan, and B. D. Gaulin, Phys. Rev. B 62, R9244 (2000).
\( ^{12} \) G. Néner, C. Ritter, M. Isobe, O. Isnard, A. N. Vasiliev, and Y. Ueda, Phys. Rev. B 80, 024402 (2009).
\( ^{13} \) G. Néner, M. Isobe, C. Ritter, O. Isnard, A. N. Vasiliev, and Y. Ueda. Phys. Rev. B 79, 064416 (2009).
\( ^{14} \) G. Néner, I. Kim, M. Isobe, C. Ritter, A. N. Vasiliev, K. H. Kim, and Y. Ueda, Phys. Rev. B 81, 184408 (2010).
\( ^{15} \) A. N. Vasiliev, O. L. Ignatchik, A. N, Sokolov, Z. Hiroi, M. Isobe, and Y. Ueda. Phys. Rev. B 72, 012412 (2005).
\( ^{16} \) S. Jodlauk, P. Becker, J. A. Mydosh, D. I. Khomskii, T. Lorenz, S. V. Streltsov, D. C. Hezel, and L. Bohatý, J. Phys.: Condens. Matter 19, 432201 (2007).
\( ^{17} \) W.-M. Zhang, W. M. Saslow, and M. Gabay, Phys. Rev. B 44, 5129 (1991).
\( ^{18} \) J. Rodriguez-Carvajal, Physica B 192, 55 (1993).
\( ^{19} \) J. C. Bonner and M. E. Fisher, Phys. Rev. 135, A640 (1964); T. Smith and S. A. Friedberg, ibid. 176, 660 (1968).
\( ^{20} \) G. J. Redhammer, G. Roth, and G. Amthauer, Acta Crystallogr., Sect. C: Cryst. Struct. Commun. 64, i97 (2008).
\( ^{21} \) E. F. Bertaut, in Magnetism, edited by G. T. Rado and H. Shul (Academic, New York, 1963), Vol. III, Chap. 4.
\( ^{22} \) O. V. Kovalev, in Representations of the Crystallographic Space Groups: Irreducible Representations, Induced Representations and Corepresentations, edited by H. T. Stokes and D. M. Hatch (Gordon and Breach, Amsterdam, 1993).
\( ^{23} \) J. Rodríguez-Carvajal, BasIreps: A program for calculating irreducible representations of space groups and basis functions for
axial and polar vector properties (see http://wwwold.ill.fr/dif/Soft/fp/php/downloads.html)
\( ^{24} \) K. Momma and F. Izumi, J. Appl. Crystallogr. 41, 653 (2008).
\( ^{25} \) P. J. Brown, J. B. Forsyth, and F. Tasset, Solid State Sci. 7, 682 (2005).
\( ^{26} \) A. P. Ramirez, Annu. Rev. Mater. Sci. 24, 453 (1994).
\( ^{27} \) International Tables for Crystallography, in Physical Properties of crystals, edited by A. Authier (Kluwer Academic Publishers, Dordrecht, 2003), Vol. D.