| Transition Temperature | 0.1 K |
|---|---|
| Experiment Temperature | 0.068 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | Fd-3m (#227) |
| Magnetic Space Group | I41'/amd' (#141.555) |
| Magnetic Point Group | 4'/mm'm (15.4.56) |
| Lattice Parameters | 10.35040 10.35040 10.35040 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1103/physrevlett.119.187202 |
| Reference | S. Petit, E. Lhotel, F. Damay, P. Boutrouille, A. Forget and D. Colson, Physical Review Letters (2017) 119 187202. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Er1 | Er | -3.1 | 3.1 | 0.0 | 4.38 |
Long-Range Order in the Dipolar XY Antiferromagnet \( Er_{2}Sn_{2}O_{7} \)
S. Petit, \( ^{1,*} \) E. Lhotel, \( ^{2,\dagger} \) F. Damay, \( ^{1} \) P. Boutrouille, \( ^{1} \) A. Forget, \( ^{3} \) and D. Colson \( ^{3} \)
\( ^{1} \) Laboratoire Léon Brillouin, CEA, CNRS, Université Paris-Saclay, CE-Saclay, 91191 Gif-sur-Yvette, France
\( ^{2} \) Institut Néel, CNRS and Université Grenoble Alpes, 38042 Grenoble, France
\( ^{3} \) Service de Physique de l'Etat Condensé, CEA, CNRS, Université Paris-Saclay, CE-Saclay, 9191 Gif-sur-Yvette, France (Received 4 May 2017; published 30 October 2017)
\( Er_{2}Sn_{2}O_{7} \) remains a puzzling case among the extensively studied frustrated compounds of the rare-earth pyrochlore family. Indeed, while a first-order transition towards a long-range antiferromagnetic state with the so-called Palmer-Chalker structure is theoretically predicted, it has not yet been observed, leaving the issue as to whether it is a spin-liquid candidate open. We report on neutron scattering and magnetization measurements which evidence a second-order transition towards this Palmer-Chalker ordered state around 108 mK. Extreme care was taken to ensure a proper thermalization of the sample, which has proved to be crucial to successfully observe the magnetic Bragg peaks. At the transition, a gap opens in the excitations, superimposed on a strong quasielastic signal. The exchange parameters, refined from a spin-wave analysis in applied magnetic field, confirm that \( Er_{2}Sn_{2}O_{7} \) is a realization of the dipolar XY pyrochlore antiferromagnet. The proximity of competing phases and the strong XY anisotropy of the \( Er^{3+} \) magnetic moment might be at the origin of enhanced fluctuations, leading to the unexpected nature of the transition, the low ordering temperature, and the observed multiscale dynamics.
DOI: 10.1103/PhysRevLett.119.187202
Frustration in magnetism is usually characterized by the inability of a system to condense into an ordered state, even well below the temperature range of the magnetic interactions \( [1] \) . This reflects the presence, at the classical level, of a large ground-state degeneracy, which prevents the system from choosing a unique ground state. Nevertheless, the system may eventually order owing to the presence of additional terms in the Hamiltonian, like second-neighbor or Dzyaloshinski-Moriya interactions, or owing to “order by disorder” phenomena \( [2,3] \) , which lift the degeneracy and stabilize a unique ordered state. Conversely, fluctuations, originating for example from the proximity of competing phases, can hinder magnetic ordering, resulting in an unconventional correlated state with exotic excitations.
The pyrochlore oxide \( Er_{2}Sn_{2}O_{7} \) appears to belong to this category. In this compound, the \( Er^{3+} \) magnetic moments reside on the vertices of a lattice made of corner sharing tetrahedra, and are confined by a strong XY anisotropy within local planes, perpendicular to the \( \langle111\rangle \) axes. The magnetic interactions are found to be governed by dipolar interactions, in addition to a quasi-isotropic antiferromagnetic exchange tensor [4]. Mean field calculations show that, in the T=0 phase diagram, this interaction tensor locates \( Er_{2}Sn_{2}O_{7} \) in an antiferromagnetic phase, called the "Palmer-Chalker" phase [5] (see Fig. 1), close to the boundary with another ordered phase, the so-called \( \psi_{2} \) phase, which is realized in the related compound \( Er_{2}Ti_{2}O_{7} \) [6]. The predicted Néel temperature is about \( T_{N}^{MF}\approx1.3 \) K. Monte Carlo simulations [7] have pointed out that fluctuations tend to lower the ordering temperature, with \( T_{N}^{MC}\approx200 \) mK.
Experimentally, no phase transition has been detected in \( Er_{2}Sn_{2}O_{7} \) down to 20 mK in muon spin relaxation measurements [8] and down to about 100 mK in magnetization [4,9] and neutron scattering experiments [10] (note, however, that the existence of magnetic ordering below 100 mK was mentioned in [11]). Yet Palmer-Chalker-like short-range correlations have been reported below 5 K, taking the form of a broad diffuse quasielastic signal in neutron scattering measurements [4,10]. In this Letter, using neutron diffraction and magnetization measurements, we show that \( Er_{2}Sn_{2}O_{7} \) does order in the Palmer-Chalker state at a Néel temperature \( T_{N} \approx 108 \) mK. This long-range ordering is characterized by magnetic Bragg peaks which develop on top of the broad diffuse scattering. The latter disappears progressively as the ordered magnetic moment increases, indicating a second-order transition. Concomitantly, the slow dynamics previously observed in ac susceptibility above the magnetic transition persist at low temperature and coexist with the Palmer-Chalker ordering. In addition,

FIG. 1. Sketch (on a single tetrahedron) of three Palmer-Chalker configurations forming distinct magnetic domains below \( T_{N} \) (three others are obtained by reversing all spins). The local XY planes perpendicular to the \( \langle111\rangle \) axes are indicated by colored disks. Spins are pairwise antiparallel, and collinear with an edge of the tetrahedron. These configurations can be described as chiral spin crosses.
on entering the ordered phase, inelastic neutron scattering (INS) experiments reveal new features in the spin excitation spectrum stemming from the magnetic Bragg peaks. Using INS measurements performed in applied magnetic field, we determine the exchange parameters of a model Hamiltonian, confirming previous estimations.
Magnetization and ac susceptibility measurements were performed on a superconducting quantum interference device (SQUID) magnetometer equipped with a dilution refrigerator developed at the Institut Néel [12]. Neutron diffraction experiments were performed on the G4.1 diffractometer (LLB-Orphée facility) with \( \lambda=2.426\mathring{A} \) . INS measurements were carried out on the triple-axis spectrometer 4F2 using a final wave vector \( k_{f}=1.15\mathring{A}^{-1} \) . The energy resolution was about 70 \( \mu \) eV. The sample was a pure polycrystalline \( Er_{2}Sn_{2}O_{7} \) compound, synthesized by a solid-state reaction from a stoichiometric mixture of \( Er_{2}O_{3} \) (99.9%) and \( SnO_{2} \) (99.996%). The powder was ground and heated for 6–8 h four times from 1400°C to 1450°C in air, cooled down to room temperature, and reground after each calcination.
An important issue regarding the measurements at very low temperature concerns the thermalization of the powder sample. For magnetization measurements, a few milligrams of \( Er_{2}Sn_{2}O_{7} \) were mixed with Apiezon N grease in a copper pouch, to improve the thermal contact and reduce the thermalization time. For neutron-scattering experiments, a dedicated vanadium cell was used in the dilution fridge. The cell was filled with He gas up to 40 bars. During the experiments, it became obvious that a non-negligible heating was induced by the sample's activation in the neutron beam. This effect was all the more important when the incident flux was large. Special care was then taken to minimize this effect for a better temperature control. For INS measurements, the neutron flux was reduced with a lead attenuator. For diffraction measurements, short counting times (of about 30 min) were programmed, alternating with deactivation (hence cooling) periods of 1 h. This thermalization issue probably explains why the transition had not been reported in previous neutron-scattering measurements.
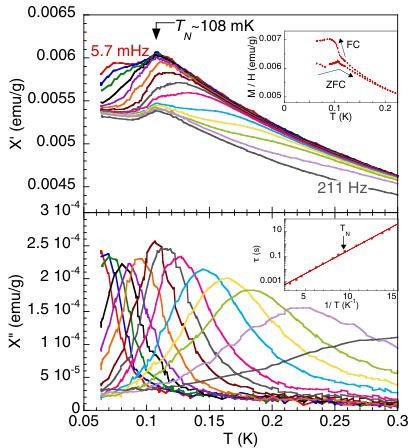
Zero field cooled–field cooled (ZFC-FC) magnetization measurements show an antiferromagnetic transition at \( T_{N} = 108 \pm 5 \) mK (see inset of Fig. 2). It manifests as a peak in the ZFC curve, while the FC magnetization sharply increases at the transition. This effect, although less pronounced, is similar to what is observed in \( Er_{2}Ti_{2}O_{7} \) [13] and could be due to the polarization of uncompensated magnetic moments at domain boundaries. This magnetic transition is also evidenced by a peak at \( T_{N} \) in the real part of the ac susceptibility (see top of Fig. 2). A frequency-dependent signal, a signature of slow dynamics, comes on top of this peak, as a bump which moves towards high temperature when the frequency increases. It is associated with a peak in the imaginary part of the ac susceptibility, which follows the same thermal-activated law above and below the Néel temperature (see bottom inset of Fig. 2).

FIG. 2. The ac susceptibility \( \chi^{\prime} \) (top) and \( \chi^{\prime\prime} \) (bottom) vs temperature T measured for several frequencies f between 5.7 mHz and 211 Hz, with \( \mu_{0}H_{ac} = 0.1 \) mT. Top inset: Magnetization M/H vs T measured in a ZFC-FC procedure with \( \mu_{0}H = 1 \) mT. Bottom inset: Relaxation time \( \tau = 1/2\pi f \) vs 1/T extracted from the maxima of \( \chi^{\prime\prime} \) . The line is a fit with the Arrhenius law: \( \tau = \tau_{0}\exp(E/T) \) with \( \tau_{0} \approx 6 \times 10^{-5} \) s and \( E \approx 0.9 \) K.
showing that the slow dynamics is not affected by the transition.
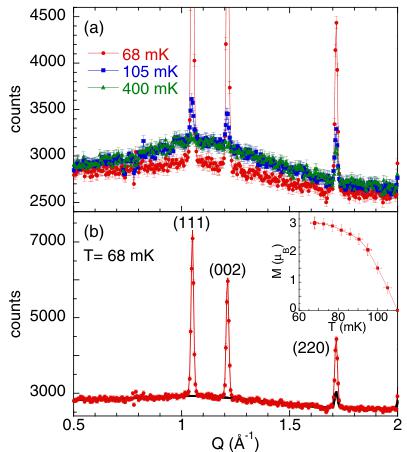
Neutron diffraction confirms the presence of antiferromagnetic ordering at very low temperature, as shown in Fig. 3. Intensity increases on existing crystalline Bragg peak positions, indicating a \( k = 0 \) propagation vector. The main magnetic peaks appear at 1.07 and 1.22 Å \( ^{-1} \) , corresponding to the \( Q = (111) \) and (002) wave vectors, and emerge from the diffuse scattering signal characteristic of short-range Palmer-Chalker correlations [4,10]. The latter has almost disappeared at the lowest temperature ( \( T = 68 \) mK), indicating that most of the magnetic moment is ordered [see Fig. 3(a)]. Rietveld refinements show that, among the possible irreducible representations authorized by the \( k = 0 \) propagation vector [6,14], neutron intensities can only be properly modeled by the \( \Gamma_{7} \) -Palmer-Chalker representation [15]. At the lowest temperature, the ordered moment is 3.1 \( \mu_{B} \) , i.e., about 80% of the magnetic moment of the \( Er^{3+} \) ground-state doublet, estimated at 3.8 \( \mu_{B} \) [4] [see Fig. 3(b)]. The remaining \( Er^{3+} \) moments are embedded in short-range-only Palmer-Chalker correlations, as reflected by the persistence of a weak diffuse signal. This ordered moment value is consistent with what is expected in a conventional second-order phase transition at the corresponding \( T/T_{N} \) ratio. The second-order nature is further confirmed by the gradual increase of the ordered moment below \( T_{N} \) [see inset of Fig. 3(b)].

FIG. 3. (a) Diffractograms at 68 mK (red), 105 mK (blue) and 400 mK (green). (b) Diffractogram at 68 mK. The black line is the fit corresponding to the nuclear contribution plus the diffuse Palmer-Chalker scattering. The red line shows the fit of the whole signal, including the magnetic long-range Palmer-Chalker contribution. Inset: Temperature dependence of the ordered magnetic moment deduced from the refinements.
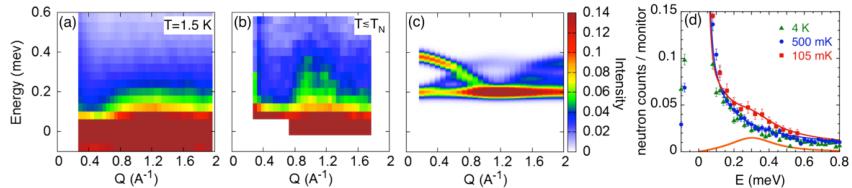
We now focus on the excitation spectrum associated with this magnetic ordering. As previously reported, at temperatures as high as 10 K, the INS spectrum includes a strong quasielastic signal [10]. Its intensity is stronger around \( Q_{o} = 1.1 \, \AA^{-1} \) , which corresponds to the position of the maximum intensity of the Palmer-Chalker diffuse scattering [see Fig. 4(a)]. On cooling, the intensity increases, while the width decreases, corresponding to a slowing down of the fluctuations, reaching a characteristic time of about \( 10^{-11} \) s close to \( T_{N} \) . This quasielastic signal persists down to temperatures below \( T_{N} \) [see Fig. 4(b)]. Nevertheless, because of self-heating in the neutron beam, the effective temperature actually reached by the sample at the lowest temperature of the dilution fridge ( \( T_{min} = 70 \, mK \) ) is estimated to be 105 mK from the intensity of the magnetic Bragg peaks, thus just below \( T_{N} \) (corresponding to an ordered moment of \( 0.8 \, \mu_{B} \) ). Additional features, stemming from the Bragg peaks at \( Q \approx 1 \) and \( 1.2 \, \AA^{-1} \) , also arise in the ordered regime [see Fig. 4(b)]. In the cut shown in Fig. 4(d), this additional signal manifests as a broad band in the \( 0.2 \leq \omega \leq 0.5 \, meV \) range, superimposed on the quasielastic response.
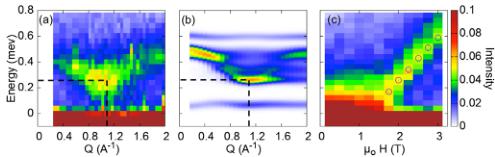
To further analyze these results, we have refined the exchange parameters previously estimated from magnetization measurements [4]. We have used a well-documented procedure [19,20], which consists in applying a magnetic field to drive the ground state towards a field-polarized state and analyzing the spin excitations in terms of conventional spin waves. Owing to the polycrystalline nature of the \( Er_{2}Sn_{2}O_{7} \) sample, the magnetic field is applied simultaneously in all crystallographic directions, leading to an average excitation spectrum. INS measurements were performed as a function of magnetic field at 1.5 K. Above about \( \mu_{o}H = 1.5 \) T, the response is no longer quasielastic-like, and a dispersive spectrum is observed with the opening of a gap [see Fig. 5(a)]. Its value is \( \Delta = 0.26 \pm 0.04 \) meV at \( Q_{o} = 1.1 \) Å \( ^{-1} \) for a field of \( \mu_{o}H = 2 \) T. \( \Delta \) increases roughly linearly further increasing the field, as illustrated in Fig. 5(c).
To determine the exchange parameters, we consider the following Hamiltonian: \( \mathcal{H} = \mathcal{H}_{\mathrm{CEF}} + \frac{1}{2} \sum_{\langle i,j\rangle} \mathbf{J}_{i} \widetilde{\mathcal{J}} \mathbf{J}_{j} + g_{1} \mu_{B} \mathbf{H} \cdot \mathbf{J}_{i} \) , where J is the \( Er^{3+} \) magnetic moment, \( H_{CEF} \) is the crystal electric field (CEF) Hamiltonian, H denotes the magnetic field, \( g_{1} \) is the effective g factor, and \( \widetilde{J} \) is the anisotropic exchange tensor, which incorporates the dipolar interaction truncated to its nearest neighbors. It is written in the \( (\mathbf{a}_{ij}, \mathbf{b}_{ij}, \mathbf{c}_{ij}) \) frame linked with \( Er^{3+} - Er^{3+} \langle ij \rangle \) nearest-neighbor bonds [21],

FIG. 4. Inelastic neutron scattering in zero field: powder-averaged spectrum \( S(Q,\omega) \) measured (a) at 1.5 K and (b) below \( T_{N} \) , at about 105 mK. The neutron intensity is normalized to the monitor. Constant energy scans were carried out to minimize self-heating effects. (c) Excitation spectrum in the Palmer-Chalker phase obtained from random phase approximation (RPA) calculations with the exchange parameters \( J_{a}=J_{b}=0.03 \) K, \( J_{c}=0.05 \) K, and \( J_{4}=0 \) at T=0. (d) Energy cuts averaged for \( 1\leq Q\leq1.2 \) Å \( ^{-1} \) at several temperatures: 4 K (green triangles), 500 mK (blue dots), 105 mK (red squares). The blue line is a fit involving a Gaussian profile, centered at zero energy to model the elastic response, and a quasielastic contribution \( [1+n(\omega)]\times A\omega\Gamma/(\omega^{2}+\Gamma^{2}) \) . \( 1+n(\omega) \) is the detailed balance factor, A=0.2, and \( \Gamma=0.046 \) meV. The red line contains an additional inelastic contribution, shown separately by the orange line and described by a Lorentzian profile \( [1+n(\omega)]\times B\gamma\{1/[(\omega-\omega_{o})^{2}+\gamma^{2}]-1/[(\omega+\omega_{o})^{2}+\gamma^{2}]\} \) with B=0.016, \( \omega_{o}=0.3 \) meV, and \( \gamma=0.016 \) meV.

FIG. 5. Inelastic neutron scattering in the field polarized phase. (a) Powder-average spectrum \( S(Q,\omega) \) measured at T=1.5 K with \( \mu_{0}H=2 \) T. (b) Calculated powder-average spectrum \( S(Q,\omega) \) at 2 T and T=0 with \( J_{a}=J_{b}=0.03 \) K, \( J_{c}=0.05 \) K, and \( J_{4}=0 \) . (c) Powder average spectrum at \( Q_{o}=1.1 \) Å \( ^{-1} \) and at T=1.5 K as a function of field H. The empty blue circles are the values of the gap obtained from the calculations with the above parameters. The neutron intensity is normalized to the monitor.
\[ \begin{aligned}\mathbf{J}_{i}\widetilde{\mathcal{J}}\mathbf{J}_{j}=&\sum_{\mu,\nu=x,y,z}J_{i}^{\mu}D_{\mathrm{nn}}(a_{i j}^{\mu}a_{i j}^{\nu}+b_{i j}^{\mu}b_{i j}^{\nu}-2c_{i j}^{\mu}c_{i j}^{\nu})J_{j}^{\nu}\\&+\sum_{\mu,\nu=x,y,z}J_{i}^{\mu}(\mathcal{J}_{a}a_{i j}^{\mu}a_{i j}^{\nu}+\mathcal{J}_{b}b_{i j}^{\mu}b_{i j}^{\nu}+\mathcal{J}_{c}c_{i j}^{\mu}c_{i j}^{\nu})J_{j}^{\nu}\\&+{\mathcal{J}_{4}}\sqrt{2}\mathbf{b}_{i j}\cdot(\mathbf{J}_{i}\times\mathbf{J}_{j}),\end{aligned} \]
where \( D_{\mathrm{nn}} = (\mu_{o}/4\pi)[(g_{\mathrm{j}}\mu_{\mathrm{B}})^{2}/r_{\mathrm{nn}}^{2}] = 0.022 \) K is the pseudodipolar contribution (with \( r_{nn} \) the nearest-neighbor distance in the pyrochlore lattice), \( J_{a} \) , \( J_{b} \) , \( J_{c} \) are effective exchange parameters, and \( J_{4} \) corresponds to the antisymmetric Dzyaloshinski-Moriya interaction. This model takes into account the specific CEF scheme which strongly confines the spins within the local XY planes [4]. The powder average of the spin excitation spectrum \( S(Q, \omega)_{H} \) is then calculated for a given field H using the RPA.
To compare with the polycrystalline experimental data shown in Fig. 5(a), the average over all field directions has to be performed. As a first approximation, we consider that the powder spectrum can be described by averaging over the high symmetry directions of the system, \( \langle001\rangle \) , \( \langle110\rangle \) , and \( \langle111\rangle \) , taking into account their multiplicity: \( S(Q,\omega)=\frac{1}{13}\left[3S(Q,\omega)_{HH}\right]+6S(Q,\omega)_{HH}\left[\left\langle110\right\rangle+4S(Q,\omega)_{HH}\left[\left\langle111\right\rangle\right]\right] \) . Assuming \( J_{4}=0 \) , since the Dzyaloshinski-Moriya interaction is expected to be small compared to symmetric exchange, the best agreement is obtained with \( J_{a}=J_{b}=0.03\pm0.003 \) K, \( J_{c}=0.05\pm0.01 \) K, thus consistent with the uncertainty range given in Ref. [4]. Calculations reproduce the strong intensity close to \( Q_{o} \) and the presence of a gap of about 0.25 meV [see Fig. 5(b)]. They also account for the field dependence of the gap at \( Q_{o} \) above 1.5 T, as shown in Fig. 5(c) by the blue open circles. RPA calculations performed with these exchange parameters at T=0 in zero field, predict a gapped flat mode at 0.2 meV, together with excitations dispersing up to 0.4 meV [see Fig. 4(c)]. While the value of the gap is consistent with the measured inelastic contribution, the predicted dispersion is hardly distinguishable in the data of Fig. 4(b). It is instructive to compare the \( Er_{2}Sn_{2}O_{7} \) behavior with results obtained on \( Gd_{2}Sn_{2}O_{7} \) . The latter, in which the \( Gd^{3+} \) magnetic moment is almost isotropic, is known as the archetype of the dipolar Heisenberg pyrochlore antiferromagnet. In spite of very different anisotropies in both compounds, calculations predict identical behaviors for thermodynamic and dynamical properties: the transition towards the Palmer-Chalker phase is expected to be first order [7,22], while a spin-wave spectrum, similar to Fig. 4(c), should develop at low temperature, consisting of dispersive branches on top of a gapped flat mode [23–25]. \( Gd_{2}Sn_{2}O_{7} \) indeed follows these predictions [26,27], and the opening of the gap occurs well above \( T_{N} \) [28]. In \( Er_{2}Sn_{2}O_{7} \) , the scenario appears more complex: the temperature dependence of the ordered magnetic moment points out a second-order transition. The lack of clear dispersion in the experimental INS spectrum can be attributed to the proximity of \( T_{N} \) , so that conventional spin waves are expected to develop at lower temperature. However, the strong XY character of the system, which can lead to unconventional excitations as lines of vortices [29], insufficiently captured by the RPA, might induce a peculiar Q dependence of the spectrum.
The strong ratio between dipolar and exchange interactions in \( Er_{2}Sn_{2}O_{7} \) , which is about 0.5–0.7 (against 0.15 in \( Gd_{2}Sn_{2}O_{7} \) [24]) also appears crucial. Preliminary calculations with \( Er_{2}Sn_{2}O_{7} \) parameters at T = 0 and Q = (1, 1, 1) show that accounting for the long-range part of the dipolar interaction beyond the truncation considered above and in Refs. [4,7], slightly reduces the gap value, but does not affect the ground state. It was, however, established in Heisenberg systems that, at finite temperature, long-range dipolar interactions tend to weaken the Palmer-Chalker state stability, due to the proximity of an unconventional state with a k = (1/2, 1/2, 1/2) propagation vector [30,31] (proposed to be the magnetic state stabilized in \( Gd_{2}Ti_{2}O_{7} \) [32]). The proximity of \( Er_{2}Sn_{2}O_{7} \) with such a state, in addition to the proximity with the \( \psi_{2} \) state evoked above, might reinforce the fluctuations in the Palmer-Chalker state at finite temperature and explain the low ordering temperature, the unexpected second order of the transition, as well as the structure of the spectrum close to the transition. Note that the very low temperature considered here could suggest a role of quantum fluctuations, but they have been shown to not destabilize the Palmer-Chalker state much [7,23].
Finally, as reported in numerous frustrated magnets [33], \( Er_{2}Sn_{2}O_{7} \) hosts a complex spin dynamics where several time scales coexist, even in the long-range order regime. In addition to the fast fluctuations observed by inelastic neutron scattering, slow dynamics are observed in ac susceptibility above \( T_{N} \) . They persist below \( T_{N} \) , coexisting both with the magnetic ordering along with magnetic moments fluctuating at the muon time scale [8]. The characteristic energy barrier of this slow dynamics, \( E = 0.9 \, \text{K} (= 0.078 \, \text{meV}) \) , is smaller than the gap of the Palmer-Chalker state. It might be
associated with the spins at the boundary between the six existing domains, as previously reported in kagome and pyrochlore systems [34,35].
We have shown that the pyrochlore \( Er_{2}Sn_{2}O_{7} \) orders in the Palmer-Chalker state at about 100 mK. As confirmed by the analysis of the exchange couplings, it is the realization of the dipolar XY pyrochlore antiferromagnet. The absence of a first-order transition along with multiscale dynamics are signatures of an unconventional magnetic state. Further calculations accounting for the XY character and for the long-range dipolar interactions at finite temperature are needed to understand the role of fluctuations and may enlighten the existence of exotic excitations. The proximity of \( Er_{2}Sn_{2}O_{7} \) with competing phases might also enhance fluctuations, as recently proposed in the context of another pyrochlore compound \( Yb_{2}Ti_{2}O_{7} \) [36,37]. In that perspective, our study points out the importance of multiphase competitions in the novel magnetic states emerging in frustrated systems.
We thank C. Paulsen for allowing us to use his SQUID dilution magnetometers. This work was partly funded by public grants from the French National Research Agency (Dymage project, Grant No. 13-BS04-0013) and by the Laboratoire d'Excellence Physics Atom Light Mater (LabEx PALM) overseen by the French National Research Agency (ANR) (1Dmag project).
Note added in proof.—Recently, we became aware of a manuscript on another Erbium XY pyrochlore \( Er_{2}Pt_{2}O_{7} \) which orders in a Palmer-Chalker ground state below 0.38 K [38].
\( ^{*} \) sylvain.petit@cea.fr \( ^{*} \) elsa.lhotel@neel.cnrs.fr
[1] Introduction to Frustrated Magnetism, edited by C. Lacroix, P. Mendels, and F. Mila (Springer-Verlag, Berlin, 2011).
[2] J. Villain, R. Bidaux, J.-P. Carton, and R. Conte, J. Phys. (Paris) 41, 1263 (1980).
[3] E. F. Shender, Zh. Eksp. Teor. Fiz. 83, 326 (1982) [Sov. Phys. JETP 56, 178 (1982)].
[4] S. Guitteny, S. Petit, E. Lhotel, J. Robert, P. Bonville, A. Forget, and I. Mirebeau, Phys. Rev. B 88, 134408 (2013).
[5] S. E. Palmer and J. T. Chalker, Phys. Rev. B 62, 488 (2000).
[6] A. Poole, A. S. Wills, and E. Lelièvre-Berna, J. Phys. Condens. Matter 19, 452201 (2007).
[7] H. Yan, O. Benton, L. D. C. Jaubert, and N. Shannon, Phys. Rev. B 95, 094422 (2017); arXiv:1311.3501.
[8] J. Lago, T. Lancaster, S. J. Blundell, S. T. Bramwell, F. L. Pratt, M. Shirai, and C. Baines, J. Phys. Condens. Matter 17, 979 (2005).
[9] K. Matsuhira, Y. Hinatsu, K. Tenya, H. Amitsuka, and T. Sakakibara, J. Phys. Soc. Jpn. 71, 1576 (2002).
[10] P. M. Sarte, H. J. Silverstein, B. T. K. Van Wyk, J. S. Gardner, Y. Qiu, H. D. Zhou, and C. R. Wiebe, J. Phys. Condens. Matter 23, 382201 (2011).
[11] S. T. Bramwell, M. Shirai, and C. Ritter, Institut Laue-Langevin Experimental Report No. 5-31-1496, 2004.
[12] C. Paulsen, in Introduction to Physical Techniques in Molecular Magnetism: Structural and Macroscopic Techniques—Yesa 1999, edited by F. Palacio, E. Ressouche, and J. Schweizer (Servicio de Publicaciones de la Universidad de Zaragoza, Zaragoza, 2001), p. 1.
[13] O. A. Petrenko, M. R. Lees, and G. Balakrishnan, J. Phys. Condens. Matter 23, 164218 (2011).
[14] A. S. Wills, M. E. Zhitomirsky, B. Canals, J. P. Sanchez, P. Bonville, P. Dalmas de Réotier, and A. Yaouanc, J. Phys. Condens. Matter 18, L37 (2006).
[15] See Supplemental Material at http://link.aps.org/supplemental/10.1103/PhysRevLett.119.187202 for more details about the possible magnetic structures, which includes Refs. [6,14,16–18].
[16] G. Ferey, R. de Pape, M. Leblanc, and J. Pannetier, Rev. Chim. Miner. 23, 474 (1986).
[17] E. Lhotel, S. Petit, S. Guitteny, O. Florea, M. Ciomaga Hatnean, C. Colin, E. Ressouche, M. R. Lees, and G. Balakrishnan, Phys. Rev. Lett. 115, 197202 (2015).
[18] A. Yaouanc, P. Dalmas de Réotier, P. Bonville, J. A. Hodges, V. Glazkov, L. Keller, V. Sikolenko, M. Bartkowiak, A. Amato, C. Baines, P. J. C. King, P. C. M. Gubbens, and A. Forget, Phys. Rev. Lett. 110, 127207 (2013).
[19] L. Savary, K. A. Ross, B. D. Gaulin, J. P. C. Ruff, and L. Balents, Phys. Rev. Lett. 109, 167201 (2012).
[20] K. A. Ross, L. Savary, B. D. Gaulin, and L. Balents, Phys. Rev. X 1, 021002 (2011).
[21] B. Z. Malkin, T. T. A. Lummen, P. H. M. van Loosdrecht, G. Dhalenne, and A. R. Zakirov, J. Phys. Condens. Matter 22, 276003 (2010).
[22] O. Cepas, A. P. Young, and B. S. Shastry, Phys. Rev. B 72, 184408 (2005).
[23] A. G. Del Maestro and M. J. P. Gingras, J. Phys. Condens. Matter 16, 3339 (2004).
[24] A. Del Maestro and M. J. P. Gingras, Phys. Rev. B 76, 064418 (2007).
[25] S. S. Sosin, L. A. Prozorova, P. Bonville, and M. E. Zhitomirsky, Phys. Rev. B 79, 014419 (2009).
[26] P. Bonville, J. A. Hodges, M. Ocio, J. P. Sanchez, P. Vulliet, S. Sosin, and D. Braithwaite, J. Phys. Condens. Matter 15, 7777 (2003).
[27] J. R. Stewart, J. S. Gardner, Y. Qiu, and G. Ehlers, Phys. Rev. B 78, 132410 (2008).
[28] S. S. Sosin, L. A. Prozorova, A. I. Smirnov, P. Bonville, G. Jasmin-LeBras, and O. A. Petrenko, Phys. Rev. B 77, 104424 (2008).
[29] R. Savit, Phys. Rev. B 17, 1340 (1978).
[30] M. Enjalran, and M. J. P. Gingras, arXiv:0307152.
[31] O. Cepas and B. S. Shastry, Phys. Rev. B 69, 184402 (2004).
[32] J. D. M. Champion, A. S. Wills, T. Fennell, S. T. Bramwell, J. S. Gardner, and M. A. Green, Phys. Rev. B 64, 140407(R) (2001).
[33] J. S. Gardner, M. J. P. Gingras, and J. E. Greedan, Rev. Mod. Phys. 82, 53 (2010).
[34] E. Lhotel, V. Simonet, J. Ortloff, B. Canals, C. Paulsen, E. Suard, T. Hansen, D. J. Price, P. T. Wood, A. K. Powell, and R. Ballou, Phys. Rev. Lett. 107, 257205 (2011).
[35] S. Tardif, S. Takeshita, H. Ohsumi, J. I. Yamaura, D. Okuyama, Z. Hiroi, M. Takata, and T. H. Arima, Phys. Rev. Lett. 114, 147205 (2015).
[36] J. Robert, E. Lhotel, G. Remenyi, S. Sahling, I. Mirebeau, C. Decorse, B. Canals, and S. Petit, Phys. Rev. B 92, 064425 (2015).
[37] L. D. C. Jaubert, O. Benton, J. G. Rau, J. Oitmaa, R. R. P. Singh, N. Shannon, and M. J. P. Gingras, Phys. Rev. Lett. 115, 267208 (2015).
[38] A. M. Hallas et al., arXiv:1705.06680.