| Transition Temperature | 35 K |
|---|---|
| Experiment Temperature | 2 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | Pbca (#61) |
| Magnetic Space Group | P21'/c (#14.77) |
| Magnetic Point Group | 2'/m (5.3.14) |
| Lattice Parameters | 9.180564 9.048310 13.580979 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1021/acs.inorgchem.6b01844 |
| Reference | L. Lander, M. Reynaud, J. Rodriguez-Carvajal, J.-M. Tarascon and G. Rousse, Inorganic Chemistry (2016) 55 11760-11769. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Fe_1 | Fe | 3.49 | 3.32 | 0.0 | 4.82 |
| Fe_2 | Fe | -3.49 | -3.32 | 0.0 | 4.82 |
Title
Magnetic Structures of Orthorhombic \( Li_{2}M(SO_{4})_{2} \) (M = Co, Fe) and \( Li_{x}Fe(SO_{4})_{2} \) (x = 1, 1.5) Phases
Authors
Laura Lander, \( ^{\dagger,\ddagger,\S} \) Marine Reynaud, \( ^{\parallel} \) Juan Rodriguez-Carvajal, \( ^{\perp} \) Jean-Marie Tarascon, \( ^{\dagger,\ddagger,\S} \) and Gwenaëlle Rousse \( ^{*,\dagger,\ddagger,\S} \)
\( ^{\dagger} \) UMR8260 “Chimie du Solide et Energie”, Collège de France, 11 place Marcelin Berthelot, 75231 Paris Cedex 05, France \( ^{\ddagger} \) Réseau sur le Stockage Electrochimique de l'Energie (RS2E), FR CNRS 3459, 33 rue Saint Leu, 80039 Amiens Cedex, France \( ^{\S} \) Sorbonne Universités–UPMC University Paris 06, 4 Place Jussieu, 75005 Paris, France \( ^{\parallel} \) CIC Energique, Albert Einstein 48, 01510 Miñano Vitoria, Álava, Spain \( ^{\perp} \) Institut Laue-Langevin (ILL), BP 156, 6 rue Jules Horowitz, 38042 Grenoble Cedex 9, France \( ^{*} \) E-mail: gwenaelle.rousse@college-de-france.fr.
Materials Studied
The specific materials studied are: * Orthorhombic \( \mathrm{Li}_{2}\mathrm{Co}(\mathrm{SO}_{4})_{2} \) * Orthorhombic \( \mathrm{Li}_{2}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \) * Orthorhombic \( \mathrm{Li}_{1.5}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \) * Orthorhombic \( \mathrm{Li}_{1}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \)
Other materials mentioned for comparison or as impurities: * Orthorhombic \( \mathrm{Li}_{2}\mathrm{Ni}(\mathrm{SO}_{4})_{2} \) (isostructural counterpart) * Monoclinic \( \mathrm{Li}_{2}\mathrm{M}(\mathrm{SO}_{4})_{3} \) (M = Fe, Co) (polymorphic counterparts) * \( \mathrm{FeSO}_{4}\cdot\mathrm{H}_{2}\mathrm{O} \) (impurity in \( \mathrm{Li}_{1}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \))
Key Information
- Crystal structure / space group: Orthorhombic, space group \( Pbca \) for all studied compounds.
- Magnetic ordering type: Antiferromagnetic long-range ordering. All compounds exhibit collinear magnetic structures with a spin sequence of \( (++---+-+) \).
- Magnetic ordering temperature (Néel temperature, \( T_{N} \)):
- \( \mathrm{Li}_{2}\mathrm{Co}(\mathrm{SO}_{4})_{2} \): 15(1) K (from SQUID), 15(3) K (from NPD)
- \( \mathrm{Li}_{2}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \): 13(1) K (from SQUID), 12(2) K (from NPD)
- \( \mathrm{Li}_{1.5}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \): 35(2) K (from SQUID), 35(2) K (from NPD)
- \( \mathrm{Li}_{1}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \): 42(2) K (from SQUID), 42(1) K (from NPD)
- Propagation vector(s): \( \mathbf{k} = (0, 0, 0) \) for all compounds, meaning the magnetic unit cell coincides with the nuclear unit cell.
- Magnetic moments (at 2 K):
- \( \mathrm{Li}_{2}\mathrm{Co}(\mathrm{SO}_{4})_{2} \): 3.11(5) \( \mu_{B} \) (moments along c-axis)
- \( \mathrm{Li}_{2}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \): 2.98(4) \( \mu_{B} \) (moments in ab-plane, \( M_{x} = +2.70(5) \, \mu_{B} \), \( M_{y} = +1.27(8) \, \mu_{B} \), \( M_{z} = 0 \))
- \( \mathrm{Li}_{1.5}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \): 4.82(10) \( \mu_{B} \) (moments in ab-plane, \( M_{x} = +3.49(12) \, \mu_{B} \), \( M_{y} = +3.32(9) \, \mu_{B} \), \( M_{z} = 0 \))
- \( \mathrm{Li}_{1}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \): 4.12(9) \( \mu_{B} \) (moments along c-axis)
- Lattice parameters (at 2 K):
- \( \mathrm{Li}_{2}\mathrm{Co}(\mathrm{SO}_{4})_{2} \): \( a = 9.189(2) \) Å, \( b = 9.087(2) \) Å, \( c = 13.662(1) \) Å
- \( \mathrm{Li}_{2}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \): \( a = 9.269(2) \) Å, \( b = 9.201(3) \) Å, \( c = 13.669(2) \) Å
- \( \mathrm{Li}_{1.5}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \): \( a = 9.181(6) \) Å, \( b = 9.048(3) \) Å, \( c = 13.581(5) \) Å
- \( \mathrm{Li}_{1}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \): \( a = 9.159(4) \) Å, \( b = 8.918(6) \) Å, \( c = 13.396(3) \) Å
- Other critical measured values:
- Curie constant C (emu·K·mol\(^{-1}\)):
- \( \mathrm{Li}_{2}\mathrm{Co}(\mathrm{SO}_{4})_{2} \): 5.5(2)
- \( \mathrm{Li}_{2}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \): 3.7(1)
- \( \mathrm{Li}_{1.5}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \): 3.7(1)
- \( \mathrm{Li}_{1}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \): 4.4(1)
- Curie-Weiss temperature \( \theta_{CW} \) (K):
- \( \mathrm{Li}_{2}\mathrm{Co}(\mathrm{SO}_{4})_{2} \): -89(2)
- \( \mathrm{Li}_{2}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \): -22(1)
- \( \mathrm{Li}_{1.5}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \): -55(1)
- \( \mathrm{Li}_{1}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \): -101(2)
- Effective moment \( \mu_{eff} \) ( \( \mu_{B} \)):
- \( \mathrm{Li}_{2}\mathrm{Co}(\mathrm{SO}_{4})_{2} \): 6.6(3)
- \( \mathrm{Li}_{2}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \): 5.4(1)
- \( \mathrm{Li}_{1.5}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \): 5.4(2)
- \( \mathrm{Li}_{1}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \): 5.9(1)
- Frustration parameter \( |\theta_{CW}/T_{N}| \):
- \( \mathrm{Li}_{2}\mathrm{Co}(\mathrm{SO}_{4})_{2} \): 5.9(4)
- \( \mathrm{Li}_{2}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \): 1.6(2)
- \( \mathrm{Li}_{1.5}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \): 1.6(1)
- \( \mathrm{Li}_{1}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \): 2.5(2)
- Magnetic space groups:
- \( \mathrm{Li}_{2}\mathrm{Co}(\mathrm{SO}_{4})_{2} \): \( Pb^{\prime}c^{\prime}a^{\prime} \) (based on \( \Gamma_{2} \))
- \( \mathrm{Li}_{2}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \): \( P112_{1}^{\prime}/a \) (based on \( \Gamma_{6} \oplus \Gamma_{8} \))
- \( \mathrm{Li}_{1.5}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \): \( P112_{1}^{\prime}/a \) (based on \( \Gamma_{6} \oplus \Gamma_{8} \))
- \( \mathrm{Li}_{1}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \): \( Pb^{\prime}c^{\prime}a^{\prime} \) (based on \( \Gamma_{2} \))
- Magneto-electric effect: All compounds potentially exhibit a linear magneto-electric effect below \( T_{N} \) due to their magnetic space groups having a negative character for the inversion center (spatial inversion associated with time reversal).
- Curie constant C (emu·K·mol\(^{-1}\)):
Synthesis Method
The samples were prepared as follows: * Orthorhombic \( \mathrm{Li}_{2}\mathrm{M}(\mathrm{SO}_{4})_{2} \) (M = Co, Fe): Prepared by mechanical milling following a previously reported procedure. * \( \mathrm{Li}_{2}\mathrm{Co}(\mathrm{SO}_{4})_{2} \): Obtained by ball-milling stoichiometric amounts of anhydrous \( \mathrm{CoSO}_{4} \) and \( \mathrm{Li}_{2}\mathrm{SO}_{4} \) for 10 hours under air using a Retsch PM100 planetary mill. * \( \mathrm{Li}_{2}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \): Obtained from a mixture of anhydrous \( \mathrm{FeSO}_{4} \) and \( \mathrm{Li}_{2}\mathrm{SO}_{4} \) ground for 10 hours under an argon atmosphere to prevent oxidation of \( \mathrm{Fe}^{II} \) to \( \mathrm{Fe}^{III} \). * Delithiated phases \( \mathrm{Li}_{1.5}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \) and \( \mathrm{Li}_{1}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \): While these phases can be obtained by electrochemical extraction, for neutron diffraction, they were prepared through chemical oxidation of \( \mathrm{Li}_{2}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \) using stoichiometric amounts of \( \mathrm{NO}_{2}\mathrm{BF}_{4} \) as an oxidation agent (0.5 and 1 equivalent, respectively) in acetonitrile.
Abstract
We report herein on the magnetic properties and structures of orthorhombic \( \mathrm{Li}_{2}\mathrm{M}(\mathrm{SO}_{4})_{2} \) (M = Co, Fe) and their oxidized phases \( \mathrm{Li}_{x}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \) (x = 1, 1.5), which were previously studied as potential cathode materials for Li-ion batteries. The particular structure of these orthorhombic compounds (space group \( Pbca \)) consists of a three-dimensional network of isolated \( MO_{6} \) octahedra enabling solely super-super-exchange interactions between transition metals. We studied the magnetic properties of these phases via temperature-dependent susceptibility measurements and applied neutron powder diffraction experiments to solve their magnetic structures. All compounds present an antiferromagnetic long-range ordering of the magnetic spins below their Néel temperature. Their magnetic structures are collinear and follow a spin sequence (+ + - - + - + -) where the orientation of the magnetic moments varies with the nature of M. While \( \mathrm{Li}_{2}\mathrm{Co}(\mathrm{SO}_{4})_{2} \) and \( \mathrm{Li}_{1}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \) adopt the magnetic space group \( Pb^{\prime}c^{\prime}a^{\prime} \), the magnetic space group for \( \mathrm{Li}_{2}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \) and \( \mathrm{Li}_{1.5}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \) is ( P112_{1}^{\prime}/a
Magnetic Structures of Orthorhombic \( Li_{2}M(SO_{4})_{2} \) (M = Co, Fe) and \( Li_{x}Fe(SO_{4})_{2} \) (x = 1, 1.5) Phases
Laura Lander, \( ^{\dagger,\ddagger,\S} \) Marine Reynaud, \( ^{\parallel} \) Juan Rodriguez-Carvajal, \( ^{\perp} \) Jean-Marie Tarascon, \( ^{\dagger,\ddagger,\S} \) and Gwenaëlle Rousse \( ^{*,\dagger,\ddagger,\S} \)
\( ^{\dagger} \) UMR8260 “Chimie du Solide et Energie”, Collège de France, 11 place Marcelin Berthelot, 75231 Paris Cedex 05, France \( ^{\ddagger} \) Réseau sur le Stockage Electrochimique de l'Energie (RS2E), FR CNRS 3459, 33 rue Saint Leu, 80039 Amiens Cedex, France \( ^{\S} \) Sorbonne Universités–UPMC University Paris 06, 4 Place Jussieu, 75005 Paris, France
\( ^{1} \) CIC Energique, Albert Einstein 48, 01510 Miñano Vitoria, Álava, Spain
\( ^{\perp} \) Institut Laue-Langevin (ILL), BP 156, 6 rue Jules Horowitz, 38042 Grenoble Cedex 9, France
☑ Supporting Information
ABSTRACT: We report herein on the magnetic properties and structures of orthorhombic \( \mathrm{Li}_{2}\mathrm{M}(\mathrm{SO}_{4})_{2} \) (M = Co, Fe) and their oxidized phases \( \mathrm{Li}_{x}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \) (x = 1, 1.5), which were previously studied as potential cathode materials for Li-ion batteries. The particular structure of these orthorhombic compounds (space group \( Pbca \) ) consists of a three-dimensional network of isolated \( MO_{6} \) octahedra enabling solely super-super-exchange interactions between transition metals. We studied the magnetic properties of these phases via temperature-dependent susceptibility measurements and applied neutron powder diffraction experiments to solve their magnetic structures. All compounds present an antiferromagnetic long-range ordering of the magnetic spins below their Néel temperature. Their magnetic structures are collinear and follow a spin sequence (+ + - -

effect. We found that the orientation of the magnetic moments varies with the nature of M. While \( \mathrm{Li}_{2}\mathrm{Co}(\mathrm{SO}_{4})_{2} \) and \( \mathrm{Li}_{1}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \) adopt the magnetic space group \( Pb^{\prime}c^{\prime}a^{\prime} \) , the magnetic space group for \( \mathrm{Li}_{2}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \) and \( \mathrm{Li}_{3.5}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \) is \( P112_{1}^{\prime}/a \) , which might hint for a possible monoclinic distortion of their nuclear structure. Moreover we compared the orthorhombic phases to their monoclinic counterparts as well as to the isostructural orthorhombic \( \mathrm{Li}_{2}\mathrm{Ni}(\mathrm{SO}_{4})_{2} \) compound. Finally, we show that this possible magneto-electric feature is driven by the topology of the magnetic interactions.
INTRODUCTION
Through the years, research on Li-ion batteries has produced a multitude of novel materials, which perform poorly as electrode materials but show a panoply of exciting physical properties such as superconductivity in \( Na_{3}CoO_{2}\cdot nH_{2}O^{1/2} \) (derived from the profoundly studied \( LiCoO_{2} \) ) or multiferroic properties in \( LiCoPO_{4} \) and \( LiNiPO_{4} \) . \( ^{3} \) Similarly, \( LiFeAs_{2}O_{7} \) , which was initially studied for its Li extraction capability \( ^{4} \) but soon disregarded because of the presence of As, presents an incommensurate cycloidal structure below 35 K. \( ^{5} \) The reverse is also true as witnessed by the recently attractive electrochemical properties of \( Li_{2}MO_{3} \) (M = Ru, Ir) phases, which have been long explored for their thermoelectric and magnetic properties. \( ^{6,7} \)
Such an apparent link between magnetic and electrochemical properties in a defined compound is not fortuitous but simply rooted in the fact that both the electrochemical potential of the redox couple as well as the magnetic interactions are governed by the iono-covalency of the metal–oxygen bond. Along that line our group had previously tried to establish a correlation between \( T_{N} \) and the \( Fe^{3+}/Fe^{2+} \) redox potential in Fe-based polyanionic compounds \( ^{8} \) such as borates, phosphates and fluorosulfates. \( ^{9-15} \) Expanding the knowledge of the magnetism–electrochemistry interplay might help to develop technologically interesting devices not only for the battery community but also for other research fields such as multiferroics.
We recently described a new family of bisulfates \( \mathrm{Li}_{2}\mathrm{M}(\mathrm{SO}_{4})_{2}(\mathrm{M}=\mathrm{Mn},\mathrm{Fe},\mathrm{Co},\mathrm{Ni},\mathrm{Zn},\mathrm{Mg}) \) , which crystallize in two polymorphic configurations—monoclinic and orthorhombic. \( ^{[16,17]} \) Thanks to the inductive effect, the two \( \mathrm{Li}_{2}\mathrm{Fe}(\mathrm{SO}_{4})_{3} \) polymorphs exhibit redox potentials above \( 3.8\ V \) vs \( \mathrm{Li}^{+}/\mathrm{Li}^{0} \) upon electrochemical cycling. \( ^{[8]} \) The isolated \( MO_{6} \) octahedra in the structural framework of both polymorphs solely allow M—O—O—M super-super-exchange interactions between the metal centers, which turns them into interesting model compounds for magnetic studies. Indeed, monoclinic \( \mathrm{Li}_{2}\mathrm{M}(\mathrm{SO}_{4})_{3} \) (M = Fe, Co) and orthorhombic \( \mathrm{Li}_{2}\mathrm{Ni}(\mathrm{SiO}_{4})_{2} \) present a long-range

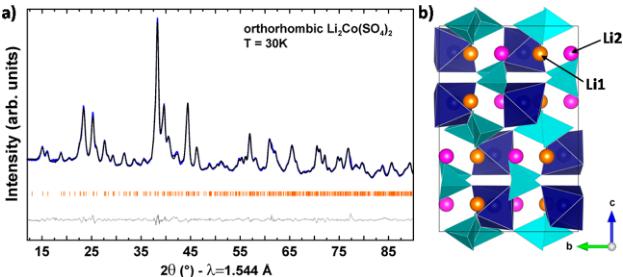
Figure 1. (a) Rietveld refinement of the neutron powder pattern of orthorhombic \( Li_{2}Co(SO_{4})_{2} \) recorded at 30 K. The blue, black, and gray lines represent the observed, calculated, and difference patterns, respectively. The Bragg positions are illustrated as orange bars. (b) Structure of \( Li_{2}Co(SO_{4})_{2} \) . \( CoO_{6} \) and \( SO_{4} \) polyhedra are shown in blue and light blue, respectively. Li1 and Li2 sites are represented as orange (Li1 site) and pink spheres (Li2 site).
antiferromagnetic ordering with a possible magneto-electric effect for the latter. \( ^{18,19} \)
The particular magnetic properties of orthorhombic \( Li_{2}Ni(SO_{4})_{2} \) , where time reversal is associated with the inversion center, motivated us to examine also the isostructural orthorhombic phases \( Li_{2}Fe(SO_{4})_{2} \) and \( Li_{2}Co(SO_{4})_{2} \) and to expand the magnetic studies to other 3d transition metals in these orthorhombic bisulfates. In particular, we aim to know if the time reversal in \( Li_{2}Ni(SO_{4})_{2} \) is specific to \( Ni^{2+} \) or rather to the orthorhombic structure and the topology of super-super-exchange pathways. In other words, the purpose of this study is to examine if any other transition metal, besides \( Ni^{2+} \) , pertaining to the orthorhombic \( Li_{2}M(SO_{4})_{2} \) structure would also order magnetically with time reversal associated with inversion. To answer this question we herein report a detailed study of the temperature-dependent magnetic susceptibility of orthorhombic \( Li_{2}Co(SO_{4})_{2} \( and \) Li_{x}Fe(SO_{4})_{2} \( (x = 1, 1.5, 2). We further use neutron powder diffraction to determine their ground-state magnetic structures, and we show that the whole series of compounds would potentially present a magnetoelectric effect. ## ■ EXPERIMENTAL SECTION Sample Preparation. The samples of orthorhombic \( \mathrm{Li_{2}M(SO_{4})_{2}} \) (M = Co, Fe) were prepared by mechanical milling following a previously reported procedure. \( ^{[17]} \) \( \mathrm{Li_{2}Co(SO_{4})_{2}} \) was obtained after ball-milling stoichiometric amounts of anhydrous \( CoSO_{4} \) and \( Li_{2}SO_{4} \) for 10 h under air using a Retsch PM100 planetary mill, whereas \( \mathrm{Li_{2}Fe(SO_{4})_{2}} \) was obtained from a mixture of anhydrous \( FeSO_{4} \) and \( Li_{2}SO_{4} \) ground for 10 h under argon atmosphere in order to avoid the oxidation of \( Fe^{III} \) into \( Fe^{III} \) .
In contrast to the Fe phase, the cobalt compound is electrochemically inactive. Thus, only the Fe phases were oxidized. The delithiated phases \( \mathrm{Li_{1.5}Fe(SO_{4})_{2}} \) and \( \mathrm{Li_{1}Fe(SO_{4})_{2}} \) can be obtained by electrochemical extraction as previously demonstrated. \( ^{[17,20]} \) However, in order to prepare them in quantity sufficient for neutron diffraction, they were obtained through chemical oxidation of \( \mathrm{Li_{3}Fe(SO_{4})_{2}} \) using stoichiometric amounts of \( NO_{2}BF_{4} \) as oxidation agent (0.5 and 1 equiv, respectively) in acetonitrile. These chemically delithiated samples present X-ray diffraction patterns similar to the electrochemically prepared samples.
Structural Characterization. Laboratory X-ray powder diffraction (XRD) patterns were recorded with a Bruker D8 Advance diffractometer equipped with a Cu Kα radiation ( \( \lambda_{1} = 1.54056 \) Å, \( \lambda_{2} = 1.54439 \) Å) and a LynxEye detector.
Neutron powder diffraction (NPD) was performed on the high-intensity D20 diffractometer at the Institut Laue Langevin (ILL, Grenoble, France) to determine the magnetic structures of the title compounds. NPD patterns on D20 were recorded in high-resolution conditions (take-off angle \( 90^{\circ} \) ) with two different wavelengths: \( \lambda = 1.544 \) and 2.419 Å obtained with a Ge monochromator.
Nuclear and magnetic structures were refined using the Rietveld method as implemented in the FullProf suite of program. \( ^{[21,22]} \) For the magnetic structure determination, Bertaut's symmetry analyses \( ^{[23]} \) were carried out with the BasIReps program of FullProf suite.
Magnetic Measurements. Susceptibility measurements were carried out using a SQUID XL magnetometer (Quantum design), in zero field cooled (ZFC) and field cooled (FC) modes, under applied magnetic fields of 10 kOe between 350 and 10 K. Isothermal magnetization curves \( M = f(H) \) were recorded at 2 K for each sample. For the measurements, powder samples of roughly 20-30 mg were placed into gel caps in such a way as to avoid any motion of the sample.
■ RESULTS
Crystal Structures. The crystalline quality of the four samples \( \mathrm{Li_{2}Co(SO_{4})_{2}} \) , \( \mathrm{Li_{2}Fe(SO_{4})_{2}} \) , \( \mathrm{Li_{1.5}Fe(SO_{4})_{2}}' \) , and \( \mathrm{Li_{1}Fe(SO_{4})_{2}} \) , was checked via XRD measurements. \( \mathrm{Li_{2}Co(SO_{4})_{2}} \) and \( \mathrm{Li_{2}Fe(SO_{4})_{2}} \) were obtained as pure samples, while \( \mathrm{Li_{1.5}Fe(SO_{4})_{2}}^{-} \) and \( \mathrm{Li_{1}Fe(SO_{4})_{2}}^{-} \) , which were prepared via chemical oxidation by \( NO_{2}BF_{4} \) , showed tiny contaminations of pristine \( \mathrm{Li_{2}Fe(SO_{4})_{2}}^{-} \) and \( \mathrm{Li}_{2}\mathrm{SO}_{4} \) for the former and \( FeSO_{4}\cdot H_{2}O \) for the latter. Indeed, direct synthesis for these oxidized \( \mathrm{Li_{1.5}Fe(SO_{4})_{2}} \cdot \mathrm{Li_{1}Fe(SO_{4})_{2}}^{-} \) phases is not possible. As a result, obtaining phase-pure compounds in a sufficient quantity to perform neutron diffraction is rather challenging. However, these contaminations were below 5%. To further check the nuclear structures, we performed Rietveld refinements of the high-resolution neutron powder diffraction patterns recorded at 30 K for the pristine phases \( \mathrm{Li_{2}Co(SO_{4})_{2}} \) и \( \mathrm{Li_{2}Fe(SO_{4})_{2}}^{-} \cdot \mathrm{Li_{1.5}Fe(SO_{4})_{2}}^{-} \cdot \mathrm{Li_{1}Fe(SO_{4})_{2}}^{-} \cdot \mathrm{Li_{1}F e(SO_{4})_{2}}^{-} \cdot \mathrm{Li_{1}F e(S O_{4})_{2}}^{-} \cdot \mathrm{Li_{1}F e(S O)_{4}}^{-} \cdot \mathrm{Li_{1}F e(S O)_{4}}^{-}} \) . These temperatures were chosen because they are above the Néel temperatures, as will be explained later. The NPD patterns were refined against the orthorhombic structure (space group \( Pbca \) ) initially proposed by Isasi et al. for the nickel analogue \( \mathrm{Li_{2}Ni(SO_{4})_{2}}^{-} \) and as previously reported by our group. \( ^{[17,20,24]} \) The results of these refinements as well as their structures are summarized in Figure S11-2 and Table S11-3 (Supporting Information). The structural models derived from XRD were here fully confirmed by NPD measurements indicating that the structures were preserved between room temperature and the above-mentioned temperatures. The so far unreported Rietveld refinement of \( \mathrm{Li_{2}Co(SO_{4})_{2}}^{-} \) is shown in Figure 1a with the
Table 1. Structural Data and Bond Valence Sum Analysis (BVS) from the Rietveld Refinement of the Neutron Powder Diffraction Pattern of Orthorhombic \( Li_{2}Co(SO_{4})_{2} \) Recorded at 30 K \( ^{a} \)
| Orthorhombic Li2Co(SO4)2 | ||||||
| space group Pbca | RBrarg = 2.14% | χ2 = 12.7 | ||||
| a = 9.1957(3) Å | b = 9.0949(3) Å | c = 13.6783(5) Å | V = 1143.9(8) Å3 | |||
| atom | Wyckoff position | x/a | y/b | z/c | Biso (Å2) | BVS |
| Li1 | 8c | 0.475(2) | 0.7259(18) | 0.3660(18) | 2.4(2) | 0.97(23) |
| Li2 | 8c | 0.702(2) | 0.551(2) | 0.6331(16) | 2.4(2) | 1.10(31) |
| Co | 8c | 0.8683(14) | 0.6052(15) | 0.3733(10) | 0.6(2) | 2.05(33) |
| S1 | 8c | 0.6590(5) | 0.8130(4) | 0.5101(3) | 0.9(3) | 5.86(47) |
| S2 | 8c | 0.5739(5) | 0.4307(5) | 0.2737(3) | 0.9(3) | 5.81(49) |
| O1 | 8c | 0.5017(4) | 0.7983(6) | 0.5239(4) | 1.36(7) | 2.02(29) |
| O2 | 8c | 0.7073(5) | 0.9679(4) | 0.4945(4) | 1.36(7) | 1.82(24) |
| O3 | 8c | 0.6934(7) | 0.7310(6) | 0.4186(3) | 1.36(7) | 1.96(29) |
| O4 | 8c | 0.7442(6) | 0.7542(7) | 0.5936(3) | 1.36(7) | 1.86(30) |
| O5 | 8c | 0.4788(5) | 0.4993(6) | 0.3488(3) | 1.36(7) | 2.12(36) |
| O6 | 8c | 0.5228(7) | 0.4623(5) | 0.1725(3) | 1.36(7) | 2.02(29) |
\( ^{a} \) Isotropic temperature factors \( B_{iso} \) were constrained identical for a same chemical species.



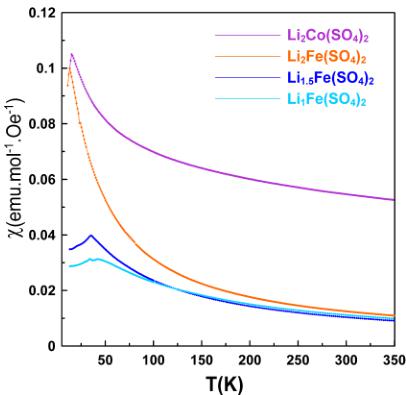
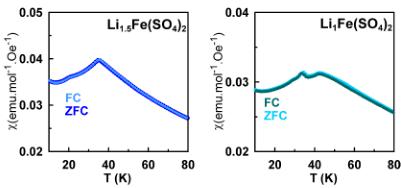
Figure 2. Temperature dependence of the molar magnetic susceptibility of orthorhombic \( \mathrm{Li}_{2}\mathrm{Co}(\mathrm{SO}_{4})_{2} \) (pink), \( \mathrm{Li}_{2}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \) (orange), \( \mathrm{Li}_{1.5}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \) (blue), and \( \mathrm{Li}_{1}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \) (light blue) recorded at 10 kOe in ZFC mode. Comparison of ZFC and FC curves recorded at 10 kOe for all four compounds is shown in the right panels.
structural data summarized in Table 1. The lattice parameters are \( a = 9.1957(3) \) Å, \( b = 9.0949(3) \) Å, and \( c = 13.6783(5) \) Å.
All atoms are located on the Wyckoff position 8c with two distinct crystallographic Li sites and one single crystallographic site for the transition metal. Orthorhombic \( \mathrm{Li}_{2}\mathrm{M}(\mathrm{SO}_{4})_{2} \) consists of isolated \( MO_{6} \) octahedra (blue) that are connected to \( SO_{4} \) tetrahedra (light blue) via their oxygen vertices (Figure 1b). The so formed 3D network hosts Li atoms (orange and pink for the Li1 and Li2 crystallographic sites, respectively) in its voids. The super-super-exchange pathways between the metal centers via two oxygen atoms (M–O–O–M) might lead to magnetic interactions as previously observed in monoclinic \( \mathrm{Li}_{2}\mathrm{M}(\mathrm{SO}_{4})_{3} \) . This was an impetus to measure the magnetic properties of the orthorhombic phases.
Magnetic Properties. The temperature dependence of the molar magnetic susceptibilities of the four title compounds was probed with a SQUID magnetometer in both zero-field cooled (ZFC) and field cooled (FC) conditions. The \( \chi = f(T) \) susceptibility curves present a typical Curie–Weiss antiferromagnetic behavior above 100 K, as shown in Figure 2. At lower temperatures, the susceptibility curves display a cusp indicating a long-range antiferromagnetic ordering as discussed in detail later.
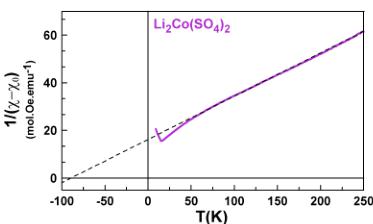
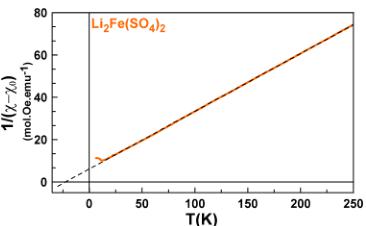
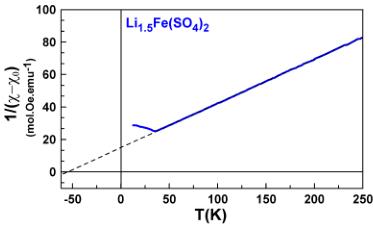
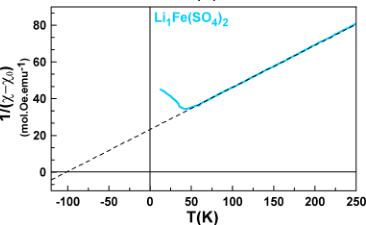
To obtain more information about the spin state of the transition metal centers and the strength of the interactions, we fitted the high temperature region (above 100 K) of the susceptibility curves to the modified Curie–Weiss equation \( \chi = \chi_{0} + \frac{C}{(\chi_{0} - \chi_{0})} \) with \( \chi_{0} \) as a temperature-independent component arising from the sample holder and core diamagnetism of the compound, C is the Curie constant, and \( \theta_{CW} \) is the Curie–Weiss temperature.
The final fits are shown in Figure 3. The magnetic constants (Curie–Weiss temperature \( \theta_{CW} \) , frustration parameter f, Curie constant C, and effective moment \( \mu_{eff} \) ) and the diamagnetic contributions \( \chi_{0} \) deduced from the fits are gathered in Table 2. The Curie–Weiss temperatures \( \theta_{CW} \) show negative values




Figure 3. Inverse susceptibility fitted with the modified Curie–Weiss law for \( \mathrm{Li}_{2}\mathrm{Co}(\mathrm{SO}_{4})_{2} \) (pink), \( \mathrm{Li}_{2}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \) (orange), \( \mathrm{Li}_{1.5}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \) (blue), and \( \mathrm{Li}_{1}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \) (light blue).
Table 2. Magnetic Parameters of the Orthorhombic \( Li_{x}M(SO_{4})_{2} \) Phases Deduced from Magnetic Measurements and Neutron Diffraction and Compared to the Expected Theoretical Values
| electronic configuration | Li2CoII(SO4)2 | Li2FeII(SO4)2 | Li1.5FeIII/III(SO4)2 | Li1FeIII(SO4)2 |
| d7: t2g5e2 | d6: t2g4e2 | d5: t2g3e2 | d5: t2g3e2 | |
| S = 3/2, L = 3 | S = 2, L = 2 | S = 5/2, L = 0 | S = 5/2, L = 0 | |
| Experimental Values Deduced from Magnetic Measurements (H = 10 kOe) | ||||
| Néel temperature TN (K) | 15(1) | 13(1) | 35(2) | 42(2) |
| Curie constant C (emu·K·mol−1) | 5.5(2) | 3.7(1) | 3.7(1) | 4.4(1) |
| Curie-Weiss temperature θCW (K) | -89(2) | -22(1) | -55(1) | -101(2) |
| χ0 (emu·mol−1·Oe−1) | 0.039(4) | 0.001(1) | 0 | 0 |
| effective moment μeff (μB) | 6.6(3) | 5.4(1) | 5.4(2) | 5.9(1) |
| frustration parameter |θCW/TN| | 5.9(4) | 1.6(2) | 1.6(1) | 2.5(2) |
| Experimental Values Deduced from Neutron Diffraction | ||||
| Néel temperature TN (K) | 15(3) | 12(2) | 35(2) | 42(1) |
| magnetic moment at 2 K (μB) | 3.11(5) | 2.98(4) | 4.82(10) | 4.12(9) |
| Expected Theoretical Values | ||||
| effective moment μeff (μB) | ||||
| μeff = g·(J(J + 1))1/2 | 6.6 | 6.7 | 5.9 | |
| μeff = (4S(S + 1) + L(L + 1))1/2 | 5.2 | 5.5 | 5.9 | |
| μeff = 2(S(S + 1))1/2 | 3.9 | 4.9 | 5.9 | |
| magnetic moment m = g·S (μB) | 3 | 4 | 5 | |
pointing out an antiferromagnetic coupling between the magnetic spins of the transition metal centers. Note that \( \theta_{CW} \) presents larger absolute values with increasing oxidation state of the Fe atom.
To calculate the effective magnetic moment \( \mu_{eff} \) of a cation, various approaches can be applied. For a free ion the formula \( \mu_{\mathrm{eff}}(J) = \mathrm{g}\cdot[J(J + 1)]^{1/2} \) is used with g being the Landé gyromagnetic factor and J being the total angular momentum \( (S + L) \) . However, due to the crystal field splitting of the d-orbitals in a coordinated cation, the effective moment is calculated either with the formula \( \mu_{S+L} = [4S(S + 1) + L(L + 1)]^{1/2} \) or \( \mu_{S} = 2[S(S + 1)]^{1/2} \) . The former is valid if the orbital angular momentum L is decoupled from the spin angular momentum S, while the latter is used for a quenched orbital moment L with a spin-only effective moment. The experimental \( \mu_{eff} \) values obtained for \( \mathrm{Li}_{2}\mathrm{Fe}(\mathrm{SO}_{4})_{3} \) and \( \mathrm{Li}_{1}\mathrm{Fe}(\mathrm{SO}_{4}) \) (5.4(1) and 5.9(1) \( \mu_{B} \) per Fe atom, respectively) correspond well to what we expect for \( Fe^{II+} \) and \( Fe^{III+} \) in an octahedral environment with an orbital angular momentum uncoupled from the spin contribution \( (\mu_{\mathrm{S+L}}) \) . For \( \mathrm{Li}_{1.5}\mathrm{Fe}(\mathrm{SO}_{3})_{2} \) we obtain an effective magnetic moment of 5.4(2) \( \mu_{B} \) . The large effective moment \( \mu_{eff} \) for \( \mathrm{Li}_{2}\mathrm{Co}(\mathrm{SO}_{4}) \) (6.6(3) \( \mu_{B} \) ) can be explained by the strong spin–orbit coupling (L·S) often observed for high-spin \( Co^{2+} \) and a strong magnetic anisotropy related to the triplet ground state. \( ^{10,25,26} \)
Taking a closer look at the low-temperature part of the susceptibility curves (Figure 2), we can see that all four compounds show characteristic cusps of an antiferromagnetic ordering occurring at Néel temperatures of \( \sim \) 15 and \( \sim \) 13 K for \( \mathrm{Li}_{2}\mathrm{Co}(\mathrm{SO}_{4}\mathrm{})_{2} \) and \( \mathrm{Li}_{2}\mathrm{Fe}(\mathrm{SO}_{4})_{1} \) , respectively. In the case of the oxidized phase \( \mathrm{Li}_{1}\mathrm{Fe}(\mathrm{SO}_{4})_{1} \) , the curve shows two cusps at \( \sim \) 35 and \( \sim \) 42 K; the first ordering temperature (35 K) likely
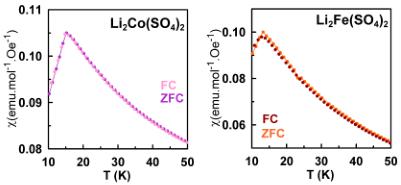
corresponds to the Néel temperature of \( FeSO_{4}\cdotH_{2}O \) , which was present as a minor impurity, as detected by XRD and NPD. The partially oxidized phase \( \mathrm{Li}_{1.5}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \) also displays two features in the susceptibility curve, at \( \sim20 \) and \( \sim35 \) K; the latter temperature corresponds to \( T_{\mathrm{N}} \) of \( \mathrm{Li}_{1.5}\mathrm{Fe}(\mathrm{SO}_{5})_{2} \) as will be further demonstrated by NPD patterns, while the former one (smaller feature) remains still unknown. However, no magnetic ordering of a secondary phase was observed in the NPD patterns of \( \mathrm{Li}_{1.5}\mathrm{Fe}(\mathrm{SO}_4)_{2} \) recorded below the Néel temperature. Comparing the recorded ZFC and FC curves we can state that for \( \mathrm{Li}_{2}\mathrm{Co}(\mathrm{SO}_{4})_{2} \) as well as for the Fe-based samples, both curves are superimposable over the whole range of temperature.
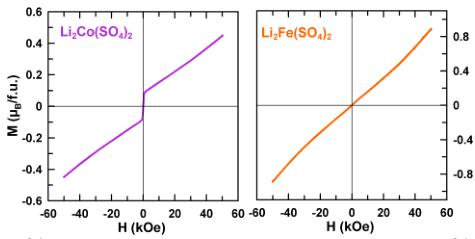
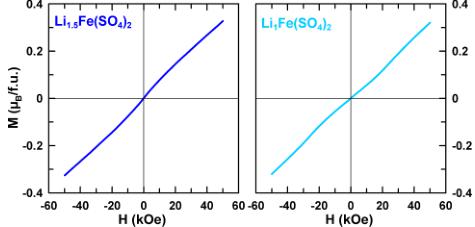
These observations prompted us to check the field dependence of the magnetization at 2 K of the orthorhombic phases \( \mathrm{Li}_{2}\mathrm{Co}(\mathrm{SO}_{4})_{1} \) and \( \mathrm{Li}_{x}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \) (x = 2, 1.5, 1) (Figure 4).


Figure 4. Isothermal magnetization curves of \( Li_{2}Co(SO_{4})_{2} \) (purple), \( Li_{2}Fe(SO_{4})_{2} \) (orange), \( Li_{1.5}Fe(SO_{4})_{2} \) (blue), and \( Li_{1}Fe(SO_{4})_{2} \) (light blue) recorded at 2 K.
The magnetization curves of the iron-based samples show a linear response as expected for a collinear antiferromagnetic ground state. \( \mathrm{Li}_{2}\mathrm{Co}(\mathrm{SO}_{4})_{3} \) shows a magnetization curve typical for an antiferromagnet, but with a contribution likely related to a small ferromagnetic impurity in the sample that was not detected by XRD. This contribution may also be at the origin of the large \( \chi_{0} \) obtained for \( \mathrm{Li}_{2}\mathrm{Co}(\mathrm{SO}_{4})_{\mathrm{2}} \) . Lastly, all the \( \mathrm{Li}_{x}\mathrm{M}(\mathrm{SO}_{4})_{2} \) phases exhibit a rather low frustration parameter \( |\theta_{\mathrm{CW}}/T_{\mathrm{N}}| \) indicating that a long-range magnetic order should establish below \( T_{\mathrm{N}} \) (Table 2).
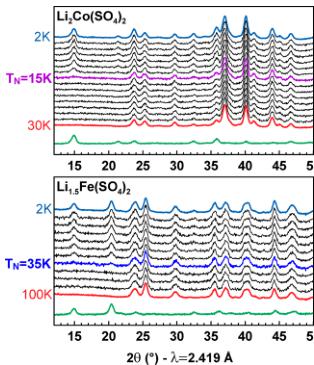
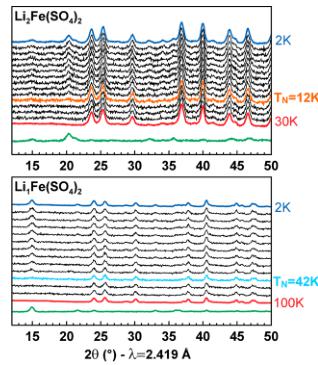
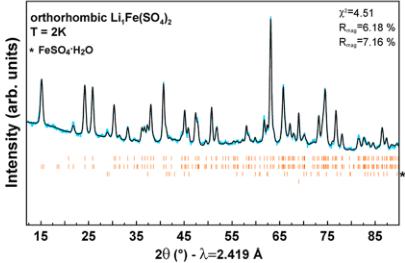
In a next step, to gain a better understanding of the antiferromagnetic ground states of the orthorhombic phases, we conducted NPD experiments. Upon cooling the four title compounds at the wavelength \( \lambda = 2.419 \, \AA \) (Figure 5), we clearly observe a gradual growing of additional peaks assigned to the long-range antiferromagnetic ordering of the magnetic moments as illustrated in the difference pattern (green) between 30 or 100 K (red) and 2 K (blue). At the same time, the Bragg peaks of the nuclear structure do not change suggesting that the structure remains intact over the whole temperature range. The transition temperatures observed by NPD experiments are in good agreement with the Néel temperatures deduced from SQUID measurements (Table 2).
Magnetic structure refinements were performed on NPD patterns recorded below the Néel temperature at 2 K with a wavelength of \( \lambda = 2.419 \, \AA \) . For all compounds, all magnetic peaks can be indexed with a propagation vector \( \mathbf{k} = (0, 0, 0) \) , which means that the magnetic unit cell coincides with the nuclear unit cell. However, because the relative intensities of the magnetic peaks differ from one sample to another, one should expect differences in their magnetic structures. To solve the magnetic structures, we performed a symmetry analysis using Bertaut's method as implemented in the BasIReps program of the FullProf suite. \( ^{[21,23]} \) This procedure was explained in details in one of our previous papers \( ^{[19]} \) so that it is just shortly recalled here. The eight irreducible representations associated with the 8c Wyckoff site occupied by the transition metals are
\[ \Gamma_{\mathrm{m a g}}(8c)=3\Gamma_{1}\oplus3\Gamma_{2}\oplus3\Gamma_{3}\oplus3\Gamma_{4}\oplus3\Gamma_{5}\oplus3\Gamma_{6}\oplus3\Gamma_{7}\oplus3\Gamma_{8} \]


Figure 5. Evolution of the neutron powder diffraction patterns of orthorhombic \( \mathrm{Li}_{2}\mathrm{Co}(\mathrm{SO}_{4})_{x} \) , \( \mathrm{Li}_{2}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \) , \( \mathrm{Li}_{3}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \) , and \( \mathrm{Li}_{1}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \) while cooling the sample to 2 K. Blue patterns are measured at 2 K, while red ones are measured at 30 K for \( \mathrm{Li}_{2}\mathrm{Co}(\mathrm{SO}_{4}_{2}) \) and \( \mathrm{Li}_{3}\mathrm{Fe}(\mathrm{SO}_{4})_{3} \) and at 100 K for \( \mathrm{Li}_{1.5}\mathrm{Fe}(\mathrm{SO}_{3})_{2} \) and \( \mathrm{Li}_{1}\mathrm{Fe}(\mathrm{SO}_{4}) \) . Green patterns correspond to the difference between the blue and the red patterns, i.e., solely the magnetic contribution. The patterns were recorded with a wavelength of \( \lambda = 2.419 \, \AA \) . The respective Néel temperatures \( T_{N} \) are indicated.




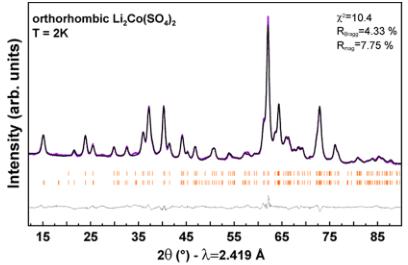
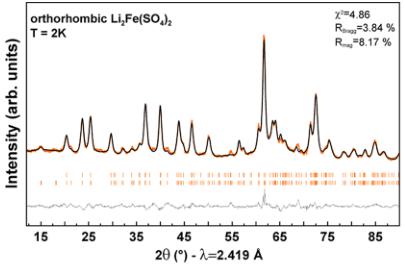
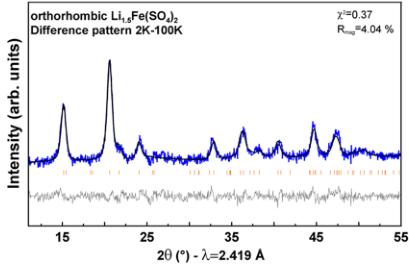
Figure 6. Rietveld refinements of the nuclear and magnetic structures of orthorhombic \( Li_{3}Co(SO_{4})_{2} \) , \( Li_{2}Fe(SO_{4})_{2} \) , \( Li_{1.5}Fe(SO_{4})_{2} \) , and \( Li_{1}Fe(SO_{4})_{2} \) phases. The colored symbols correspond to the recorded patterns. The black and gray lines represent the calculated and difference pattern, respectively. The Bragg positions are shown as orange bars, where the upper phase corresponds to the nuclear structure and the bottom one to the magnetic structure. The phase marked with a star in \( Li_{1}Fe(SO_{4})_{2} \) is attributed to \( FeSO_{4}\cdot H_{2}O \) . Further, the vanadium peak of the sample container was included in this refinement. For \( Li_{1.5}Fe(SO_{4})_{2} \) the refinement was done on the difference pattern 2–100 K that contains only the magnetic contribution.
Table 3. Lattice Parameters and Magnetic Structures of Orthorhombic \( Li_{x}M(SO_{4})_{2} \) Deduced from Rietveld Refinements of NPD Pattern Recorded at 2 K \( ^{a} \)
| Orthorhombic Li2M(SO4)2 M = Co, Fe and Li2Fe(SO4)2 with x = 1.5 and 1 | ||||
| magnetic structures | k = (0, 0, 0) | |||
| compound | Li2Co(SO4)2 | Li2Fe(SO4)2 | Li1.5Fe(SO4)2 | Li1Fe(SO4)2 |
| a (Å) | 9.189(2) | 9.269(2) | 9.181(6) | 9.159(4) |
| b (Å) | 9.087(2) | 9.201(3) | 9.048(3) | 8.918(6) |
| c (Å) | 13.662(1) | 13.669(2) | 13.581(5) | 13.396(3) |
| irreducible representation | Γ2 | Γ6 ⊕ Γ8 | Γ6 ⊕ Γ8 | Γ2 |
| Shubnikov space group | Pb′c′a′ | P1121′/a | P1121′/a | Pb′c′a′ |
| Mx(μB) | 0 | +2.70(5) | +3.49(12) | 0 |
| My(μB) | 0 | +1.27(8) | +3.32(9) | 0 |
| Mz(μB) | +3.11(5) | 0 | 0 | +4.12(9) |
| M(μB) | 3.11(5) | 2.98(4) | 4.82(10) | 4.12(9) |
\( ^{a} \) Components of the magnetic moments are shown along x, y, and z, and the resulting magnitude of the magnetic moments (M) are given for each compound. The eight magnetic atoms in the unit cell obtained by the symmetry operators \( (x, y, z) \) , \( (-x + 1/2, -y, z + 1/2) \) , \( (-x, y + 1/2, -z + 1/2) \) , \( (x + 1/2, -y + 1/2, -z) \) , \( (-x, -y, -z) \) , \( (x + 1/2, y, -z + 1/2) \) , \( (x, -y + 1/2, z + 1/2) \) , and \( (-x + 1/2, y + 1/2, z) \) have their magnetic moments following the sequence \( (++---+ \) .
Each of these representations is composed of three basis vectors \( \Psi_{i} \) (i = 1, 2, 3) corresponding to the moments oriented along the a, b, and c axes. The possible spin configurations and the corresponding Shubnikov space groups are given in Table S14. We tested all possibilities obtained by the symmetry analysis against the NPD patterns recorded at 2 K and compared the goodness of the fit for each representation. For \( \mathrm{Li}_{2}\mathrm{Co}(\mathrm{SO}_{4})_{2} \) and \( \mathrm{Li}_{1}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \) , the best fit was obtained with the irreducible representation \( \Gamma_{2} \) , with moments mainly along [001] ( \( \Psi_{3} \) basis vector). The refinement of the other components gives negligible values with standard deviations bigger than the refined values; so we have fixed arbitrarily to zero the ab-components. These two compounds therefore exhibit the exact same magnetic structure as the previously reported Ni counterpart (recalled in Figure S14 (Supporting Information)) \( ^{19} \) and the same Shubnikov space group \( Pb^{\prime}c^{\prime}a^{\prime} \) . The Rietveld refinements (nuclear and magnetic contributions) at 2 K for \( \mathrm{Li}_{2}\mathrm{Co}(\mathrm{SO}_{4})_{3} \) and \( \mathrm{Li}_{1}\mathrm{Fe}(\mathrm{PO}_{4})_{2} \) are shown in Figure 6. Regarding \( \mathrm{Li}_{2}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \) the magnetic structure resolution was not so straightforward. Testing the possibilities from symmetry analysis on the 2 K pattern did not lead to any satisfactory fit. None of the eight representations could provide an accurate

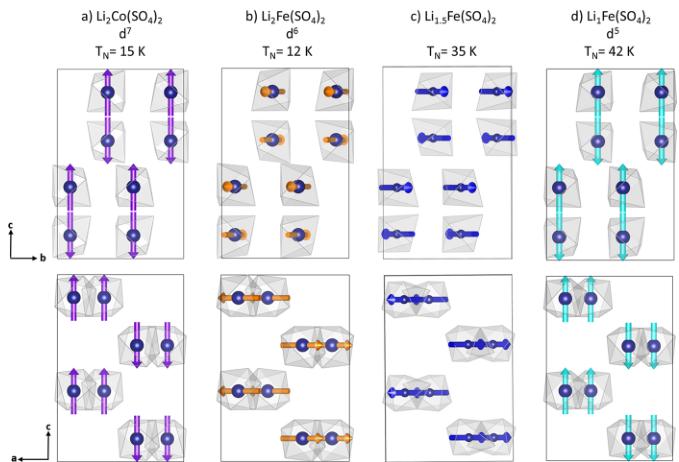
Figure 7. Magnetic structures of (a) \( \mathrm{Li_{2}Co(SO_{4})_{2}} \) , (b) \( \mathrm{Li_{3}Fe(SO_{4})_{2}} \) , (c) \( \mathrm{Li_{1.5}Fe(SO_{4})_{2}} \) and (d) \( \mathrm{Li_{1}Fe(SO_{4})_{2}} \) . Magnetic moments are represented as arrows through the transition metal center shown as blue spheres. For the sake of clarity, Li, S, and O atoms are omitted.
description of the intensities of the magnetic peaks. A moderate agreement was found with \( \Gamma_{6} \) (Shubnikov group \( Pb c^{\prime}a \) ) with moments along \( a\left(\Psi_{1}\right) \) or \( \Gamma_{8} \) (Shubnikov group \( Pb^{\prime}c a \) ) with moments along \( b\left(\Psi_{2}\right) \) . The resulting patterns are compared to the experimental contribution (difference pattern 2–30 K) in Figure SI5 (Supporting Information). Adding components along b and \( c\left(\Psi_{2}\right. \) and \( \Psi_{3} \) ) for \( \Gamma_{6} \) or along a and \( c\left(\Psi_{1}\right. \) and \( \Psi_{3} \) ) for \( \gamma_{8} \) did not improve the quality of the fit. However, we obtain a very good agreement by mixing \( \Gamma_{6} \) and \( \Gamma_{8} \) representations, i.e. putting the magnetic moment as a linear combination of \( \Psi_{1}\left(\Gamma_{6}\right) \) and \( \Psi_{2}\left(\Gamma_{8}\right) \) . The exact same situation (mixture of \( \Psi_{1}\left(\Gamma_{6}\right) \) and \( \Psi_{2}\left(\Gamma_{8}\right) \) ) was found for \( \mathrm{Li_{1.5}Fe(SO_{4})_{2}} \), for which we directly worked on the difference pattern 2–100 K to circumvent the problem of impurities arising from the difficult preparation of that intermediate oxidized structure (Figure SI5 (Supporting Information)). The Shubnikov group corresponding to the mixing \( \Gamma_{6} \oplus \Gamma_{8} \) is \( P112_{1}^{\prime}/a \) , so the set of eight Fe atoms splits into two sets of four atoms, so we have two independent sites in the unit cell. However as we cannot see any structural distortion from our powder diffraction patterns, we have constrained to have the two sites the same magnitude of their magnetic moments. The general operators of \( P112_{1}^{\prime}/a \) are \( 1 = (x, y, z) \) , \( 2_{1}^{\prime} = (-x + 1/2, -y, z + 1/2)^{\prime} \) , \( -1^{\prime} = (-x, -y, -z)^{\prime} \) , \( a = (x + 1/2, y, -z + 1/2) \) and the representative atoms of the two Fe sites are \( \mathrm{Fe}(1) \approx (0.85, 0.61, 0.37) \) and \( \mathrm{Fe}(2) \approx (0.15, 0.11, 0.13) \) . The second site representative is generated by the operator \( (-x, y + 1/2, -z + 1/2) + [1, -1, 0] \) of the \( Pbca \) space group that is no more a symmetry operator in \( P112_{1}^{\prime}/a \) . The magnetic moments of the atoms in the general position generated by the above operators are \( (u, v, w) \) , \( (u, v, -w) \) , \( (-u, -v, -w) \) , \( (-u, -v, w) \) . The constraint we have applied is that w = 0 (collinear structure) for all cases and the magnetic moment of \( \mathrm{Fe}(2) \) is opposite to the magnetic moment of \( \mathrm{Fe}(1) \) . The final Rietveld refinements of the magnetic structures of the four title compounds are gathered in Figure 6 with the respective magnetic moments summarized in Table 3. The magnetic structures deduced from the Rietveld refinements are shown in Figure 7. We found a long-range antiferromagnetic alignment of the magnetic spins carried by the transition metal centers of the four compounds in agreement with the results of the susceptibility measurements. For all magnetic structures— \( Li_{2}Co(SO_{4})_{2} \) and \( Li_{1}Fe(SO_{4})_{2} \) that adopt \( \Psi_{3}\left(\Gamma_{2}\right) \) as well as \( Li_{3}Fe(SO_{4})_{2} \) and \( Li_{1.5}Fe(SO_{4})_{2} \) for which we obtained \( \Psi_{1}\left(\Gamma_{6}\right) \) and $ \Psi_{2}\left(\Gamma_{8}\right) ) —the eight magnetic moments in the cell present the sign sequence \( \left(++--+-\right) \) where + and - signs represent the spin direction of the eight magnetic atoms taken in the same order as in the International Tables for Crystallography for position 8c in the \( Pbca \) space group. The four compounds present therefore collinear magnetic structures, which can be also described as a ferromagnetic arrangement in the [110] direction with an antiferromagnetic stacking along [001]. However, as initially guessed from the relative intensities of the magnetic reflections, the orientation of the magnetic moments differs from one compound to the other. While for \( Li_{2}Co(SO_{4})_{2} \) and \( Li_1Fe(SO_{4})_{2} \) the magnetic moments are found collinear to the c-axis, they are orientated in the ab-plane with zero contribution of the z-component for \( Li_{2}Fe(SO_{4})_{2} \) and \( Li_{1.5}F_{e}(SO_{4})_{2} \) . Lastly, the values of the magnetic moments obtained at 2 K are in agreement with what is commonly observed: slightly lower than expected for the iron based compounds (unsaturated moments); and slightly higher for \( Co^{2+} \) as a result of the strong anisotropy.
■ DISCUSSION
For all four title compounds, susceptibility measurements as well as NPD experiments revealed a long-range antiferromagnetic arrangement of the magnetic spins. \( \mathrm{Li_{2}Co(SO_{4})_{2}} \) and \( \mathrm{Li_{1}Fe(SO_{4})_{2}} \) are described in the Shubnikov space group \( Pb^{\prime}c^{\prime}a^{\prime} \) with the sign sequence \( \left(++--+-\right) \) , i.e. the same Shubnikov space group as in the previously reported orthorhombic \( \mathrm{Li_{2}Ni(SO_{4})_{2}} \) phase. \( ^{19} \) Regarding \( \mathrm{Li_{2}Fe(SO_{4})_{2}} \) and \( \mathrm{Li_{1.5}Fe(SO_{4})_{2}} \) , the magnetic structure is found to be a mixture of representations \( \Gamma_{6} \) and \( \Gamma_{8} \) with the magnetic space
group \( P112_{1}^{\prime}/a \) , in which we have applied constraints to the magnetic moments of the two independent sites (see above). The magnetic moments have been constrained to be within the \( (a,b) \) -plane and we obtain the same spin sequence \( (++---+-+ \) ). First of all, we should note that having a mixture of representations is pretty uncommon and only about 10% of the magnetic structures show such a situation. \( ^{27} \) This case has been reported for compounds such as \( RbMnF_{4} \) and orthoferrites. \( ^{27,28} \) Moreover, having a monoclinic symmetry for the magnetic space group indicates that the nuclear structure should also be of monoclinic symmetry. \( ^{29} \) However, in the present case, we could not identify any monoclinic distortion based on the Rietveld refinements of the XRD patterns of \( Li_{2}Fe(SO_{4})_{2} \) and \( Li_{1.5}Fe(SO_{4})_{2} \) . \( ^{17} \) Indeed, the Bragg peaks present an intrinsic broadening caused by the mechanochemical synthesis approach, and refining the structural model in a monoclinic symmetry is almost impossible as the number of parameters increases a lot and they may be highly correlated.
The magnetic structures of \( \mathrm{Li_{2}M(SO_{4})_{2}} \) show an identical spin sequence for all compounds (M = Fe with x = 2, 1.5, and 1 and M = Co) and correspond to that of \( \mathrm{Li_{2}Ni(SO_{4})_{2}} \) . The exchange pathways between the metal centers are therefore expected to be similar to the ones deduced for \( \mathrm{Li_{2}Ni(SO_{4})_{2}} \) below \( T_{N} = 28 \) K (Figure SI6 (Supporting Information)), \( ^{19} \) with three super-super-exchange pathways ( \( J_{1} \) and \( J_{3} \) negative, \( J_{2} \) positive) to get the observed magnetic structures as ground states.
Looking at the Néel temperatures, it appears that \( T_{N} \) increases from 12 to 16 and 28 K when going from \( \mathrm{Fe}^{2+} \) ( \( d^{6} \) ) to \( \mathrm{Co}^{2+} \) ( \( d^{7} \) ) and \( \mathrm{Ni}^{2+} \) ( \( d^{8} \) ), respectively. Such a trend has been similarly observed for malonate-based \( \mathrm{Na}_{2}\mathrm{M}(\mathrm{H}_{2}\mathrm{C}_{3}\mathrm{O}_{4})_{2}\cdot2\mathrm{H}_{2}\mathrm{O} \) phases \( ^{30} \) but is exactly the opposite to what was observed for \( AMSO_{4}F \) for instance. \( ^{10,11} \) Therefore, caution should be exercised as there is no evident trend regarding the evolution of \( T_{N} \) with the population of antibonding orbitals when comparing chemically different atoms. When looking at the iron series, we observe increasing ordering temperatures from orthorhombic \( \mathrm{Li}_{2}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \) ( \( \mathrm{Fe}^{2+} \) ; \( d^{6} \) system) to \( \mathrm{Li}_{1.5}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \) and \( \mathrm{Li}_{1}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \) ( \( \mathrm{Fe}^{3+} \) ; \( d^{5} \) system) that are in good agreement with stronger orbital interactions due to the depopulation of the \( t_{2g} \) orbitals of the transition metal upon oxidation. The influence of the oxidation state of iron on magnetism has been also observed for \( \mathrm{LiFeSO}_{4}F \) and monoclinic \( \mathrm{Li}_{2}\mathrm{Fe}(\mathrm{SO}_{4}) \) \( ^{2,11,18} \) with a stronger antiferromagnetic behavior (higher \( T_{N} \) , larger absolute \( \theta_{CW} \) ) for the isotropic \( \mathrm{Fe}^{3+} \) ( \( d^{5} \) ) ion as compared to \( \mathrm{Fe}^{2+} \) ( \( d^{6} \) ). Further comparing the orthorhombic \( \mathrm{Li}_{2}\mathrm{M}(\mathrm{SO}_{4})_{2} \) compounds to their monoclinic counterparts (Table SI5 (Supporting Information)), we can state that the orthorhombic phases systematically show higher \( T_{N} \) and larger absolute \( \theta_{CW} \) values suggesting stronger antiferromagnetic interactions. This does not come as a surprise given the structural differences of the two polymorphs, where the orthorhombic phases present shorter M–M distances and a higher density enhancing the super-super-exchange interactions.
Lastly, the magnetic structures of the herein presented orthorhombic \( \mathrm{Li_{2}M(SO_{4})_{2}} \) phases with the spin sequence \( (++---+-+ \) present a reverted magnetic moment \( (+M\rightarrow-M) \) by the spatial inversion \( (x,y,z\rightarrow-x,-y,-z) \) . The \( Pb^{\prime}c^{\prime}a^{\prime} \) and \( P112_{1}^{\prime}/a \) magnetic space groups involved here present a negative character for the inversion center, thus the spatial inversion is associated with time reversal. This characteristic enables the linear magneto-electric effect to be active below \( T_{N} \) , which means that a magnetic field can induce an electrical polarization and vice versa. Intense research in the mid-1960s focused on controlling the cross-coupling of magnetic and electric properties for technical applications. \( ^{31} \) Especially in the data storage sector the magneto-electric effect attracted a lot of attention for the development of multiferroics. \( ^{32} \) However, only few materials present this quality, such as \( Cr_{2}O_{3} \) and the yttrium iron garnet (YIG). \( ^{33-35} \)
In the present study, we show that all the reported orthorhombic \( \mathrm{Li_{2}M(SO_{4})_{_{2}}} \) phases present the same spin sequence as orthorhombic \( \mathrm{Li_{2}Ni(SO_{4})_{_{2}}} \) . \( ^{19} \) Therefore, we can conclude that this possible magneto-electric effect is not linked to the \( Ni^{2+} \) transition metal center, but indeed more generally to the orthorhombic structural framework of these materials and the topology of the super-super-exchange interactions between transition metals inherent to this structure type. We believe that this new insight into the relation between structure and magnetic properties should help to widen the rather small family of magneto-electric compounds in the future.
■ CONCLUSION
Temperature-dependent molar susceptibility measurements as well as neutron powder diffraction measurements revealed a long-range antiferromagnetic interaction between the transition metal centers of orthorhombic \( \mathrm{Li_{2}Co(SO_{4})_{2}} \) , \( \mathrm{Li_{2}Fe(SO_{4})_{2}} \) , and its oxidized phases \( \mathrm{Li_{1.5}Fe(SO_{4})_{2}} \) and \( \mathrm{Li_{1}Fe(SO_{4})_{2}} \) . For all four phases, the effective magnetic moments deduced from the inverse susceptibility fitted with the modified Curie–Weiss correspond to the theoretical values obtained for an unquenched orbital contribution. The magnetic structures of the four title compounds were described in the Shubnikov groups \( Pb^{\prime}c^{\prime}a^{\prime} \) (irreducible representation \( \Gamma_{2} \) ) ( \( \mathrm{Li_{2}Co(SO_{4})_{2}} \) and \( \mathrm{Li_{1}Se(SO_{4})_{2}} \) ) and \( P112_{1}^{\prime}/a \) ( \( \Gamma_{6}\oplus\Gamma_{8} \) ) ( \( \mathrm{Li_{1.5}Fe(SO_{4})_{2}} \) , \( \mathrm{Li_{2}Fe(SO_{4})_{2}} \) ); all of them enabling the linear magneto-electric effect to be active below the Néel temperature. Thus, in this study, we were able to expand this unusual feature initially observed in \( \mathrm{Li_{2}Ni(SO_{4})_{2}} \) to the other transition metal centers ( \( Co^{II+} \) , \( Fe^{II+} \) , \( Fe^{III+} \) ) and we could show that this feature is not related to the 3d metal but is inherent to the orthorhombic structure of these phases.
■ ASSOCIATED CONTENT
Supporting Information
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.inorg-chem.6b01844.
Rietveld refinements, structural data and structures of \( \mathrm{Li_{4}Fe(SO_{4})_{2}} \) (x = 2, 1.5, 1); results of symmetry analysis for the Pbca space group; neutron difference patterns for \( \mathrm{Li_{2}Fe(SO_{4})_{2}} \) and \( \mathrm{Li_{3.5}Fe(SO_{4})_{2}} \) ; magnetic structure and exchange pathways for \( \mathrm{Li_{2}Ni(SO_{4})_{2}} \) ; magnetic information on monoclinic \( \mathrm{Li_{2}M(SO_{4})_{2}} \) \( \left(\mathrm{M}=\mathrm{Co}, \mathrm{Mn}, \mathrm{Fe}(\mathrm{II}), \mathrm{Fe}(\mathrm{III})\right) \) (PDF)
Magnetic crystallographic information for \( \mathrm{Li_{2}Co(SO_{4})_{2}} \) (MCIF)
Magnetic crystallographic information for \( \mathrm{Li_{2}Fe(SO_{4})_{2}} \) (MCIF)
Magnetic crystallographic information for \( \mathrm{Li_{1.5}Fe(SO_{4})_{2}} \) (MCIF)
Magnetic crystallographic information for \( \mathrm{Li_{1}Fe(SO_{4})_{2}} \) (MCIF)
AUTHOR INFORMATION
Corresponding Author
\( ^{*} \) E-mail: gwenaelle.rousse@college-de-france.fr.
Notes
The authors declare no competing financial interest.
ACKNOWLEDGMENTS
The authors would like to thank Thomas Hansen for his precious help in collecting neutron powder diffraction data on the diffractometer D20 at the Institut Laue Langevin (ILL, Grenoble, France). ILL is acknowledged for allocating beamtime (Proposal 5-31-2328). L.L. acknowledges the French Agence Nationale de la Recherche (ANR) via the research project "Hipolite" for her Ph.D. grant. M.R. acknowledges the Spanish Ministerio de Economía y Competitividad (MINECO) for her postdoctoral fellowship "Ayudas Juan de la Cierva-Formación 2014", reference number FJCI-2014-19990, as well as the support of MINECO through the project reference number ENE2013-44330-R (Proyectos I + D, Retos 2013).
REFERENCES
(1) Schaak, R. E.; Klimczuk, T.; Foo, M. L.; Cava, R. J. Superconductivity Phase Diagram of \( NaXCoO2.1.3H2O \) . Nature 2003, 424, 527–529.
(2) Takada, K.; Sakurai, H.; Takayama-Muromachi, E.; Izumi, F.; Dilanian, R. A.; Sasaki, T. Superconductivity in Two-Dimensional CoO \( _{2} \) Layers. Nature 2003, 422, 53–55.
(3) Kornev, I.; Bichurin, M.; Rivera, J.-P.; Gentil, S.; Schmid, H.; Jansen, A. G. M.; Wyder, P. Magnetoelectric Properties of LiCoPO \( _{4} \) and LiNiPO \( _{4} \) . Phys. Rev. B: Condens. Matter Mater. Phys. 2000, 62(18), 12247–12253.
(4) Wurm, C.; Morcrette, M.; Rousse, G.; Dupont, L.; Masquelier, C. Lithium Insertion/Extraction Into/From LiMX2O7 Compositions (M = Fe, V; X = P, As) Prepared via a Solution Method. Chem. Mater. 2002, 14, 2701–2710.
(5) Rousse, G.; Rodriguez-Carvajal, J.; Wurm, C.; Masquelier, C. Spiral Magnetic Structure in the Iron Disarotene LiFeAs2O7: A Neutron Diffraction Study. Phys. Rev. B: Condens. Matter Mater. Phys. 2013, 88 (21), 214433.
(6) Terasaki, I.; Abe, S.; Yasui, Y.; Okazaki, R.; Taniguchi, H. Ruthenium Oxide as a Thermoelectric Material: Unconventional Thermoelectric Properties in Li \( _{2} \) RuO \( _{3} \) . J. Mater. Chem. C 2015, 3 (40), 10430–10435.
(7) Modic, K. A.; Smidt, T. E.; Kimchi, I.; Breznay, N. P.; Biffin, A.; Choi, S.; Johnson, R. D.; Coldea, R.; Watkins-Curry, P.; McCandless, G. T.; Chan, J. Y.; Gandara, F.; Islam, Z.; Vishwanath, A.; Shekhter, A.; McDonald, R. D.; Analytis, J. G. Realization of a Three-Dimensional Spin–anisotropic Harmonic Honeycomb Iridate. Nat. Commun. 2014, 5, 4203.
(8) Rousse, G.; Tarascon, J.-M. Sulfate-Based Polyanionic Compounds for Li-Ion Batteries: Synthesis, Crystal Chemistry and Electrochemistry Aspects. Chem. Mater. 2014, 26 (1), 394–406.
(9) Tao, L.; Neilson, J. R.; Melot, B. C.; McQueen, T. M.; Masquelier, C.; Rousse, G. Magnetic Structures of LiMBO \( _{3} \) (M = Mn, Fe, Co) Lithiated Transition Metal Borates. Inorg. Chem. 2013, 52(20), 11966–11974.
(10) Melot, B. C.; Rousse, G.; Chotard, J.-N.; Kemei, M. C.; Rodriguez-Carvajal, J.; Tarascon, J.-M. Magnetic Structure and Properties of NaFeSO_{4}F and NaCoSO_{4}F. Phys. Rev. B: Condens. Matter Mater. Phys. 2012, 85 (9), 94415.
(11) Melot, B. C.; Rousse, G.; Chotard, J.- N.; Ati, M.; Rodriguez-Carvajal, J.; Kemei, M. C.; Tarascon, J.-M. Magnetic Structure and Properties of the Li-Ion Battery Materials FeSO_{4} F and LiFeSO_{4} F. Chem. Mater. 2011, 23 (11), 2922–2930.
(12) Rousse, G.; Rodriguez-Carvajal, J.; Patoux, S.; Masquelier, C. Magnetic Structures of the Triphylite LiFePO \( _{4} \) and of Its Delithiated Form FePO \( _{4} \) . Chem. Mater. 2003, 15 (21), 4082–4090.
(13) Rousse, G.; Rodriguez-Carvajal, J.; Wurm, C.;Masquelier, C. Magnetic Structure of Two Lithium Iron Phosphates: A- and B-Li_{3}Fe_{2}(PO_{4})_{3}. Appl. Phys. A: Mater. Sci. Process. 2002, 74 (1), s704–s706.
(14) Rousse, G.; Rodriguez-Carvajal, J.; Wurm, C.; Massquelier, C. A Neutron Diffraction Study of the Antiferromagnetic Diphosphate LiFeP_{2}O_{7}. Solid State Sci. 2002, 4 (7), 973–978.
(15) Rousse, G.; Rodriguez-Carvajal, J.; Wurm, C.; Maskquelier, C. Magnetic Structural Studies of the Two Polymorphs of Li3Fe2 (PO4) 3: Analysis of the Magnetic Ground State from Super-Super Exchange Interactions. Chem. Mater. 2001, 13 (12), 4527–4536.
(16) Reynaud, M.; Ati, M.; Melot, B. C.; Sougrati, M. T.; Rousse, G.; Chotard, J.-N.; Tarascon, J.-M. Li_{2}Fe(SO_{4})_{2} as a 3.83 V Positive Electrode Material. Electrochem. Commun. 2012, 21, 77–80.
(17) Lander, L.; Reynaud, M.; Rousse, G.; Sougrati, M. T.; Laberty-Robert, C.; Messinger, R. J.; Deschamps, M.; Tarascon, J.-M. Synthesis and Electrochemical Performance of the Orthorhombic Li_{2}Fe(SO_{4})_{2} Polymorph for Li-Ion Batteries. Chem. Mater. 2014, 26 (14), 4178–4189.
(18) Reynaud, M.; Rousse, G.; Chotard, J.-N.; Rodriguez-Carvajal, J.; Tarascon, J.-M. Maritime Li_{2}(SO_{4}){2} (M = Co, Fe, Mn) and Li{1}Fe(SO_{4})_{2}: Model Compounds for Super–super Exchange Magnetic Interactions. Inorg. Chem. 2013, 52, 10456–10466.
(19) Reynaud, M.; Rodriguez-Carvajal, J.; Chotard, J.-N.; Tarascon, J.-M.; Rousse, G. Magnetic Structure and Properties of Orthorhombic Li_{2}Ni(SO_{4})_{2}: A Possible Magnetoelectric Material. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 89 (10), 104419.
(20) Lander, L.; Reynaud, M.; Carrasco, J.; Katcho, N. A.; Bellin, C.; Polian, A.; Baptiste, B.; Rousse, G.; Tarascon, J.-M. Unveiling the Electrochemical Mechanisms of Li \( _{2} \) Fe(SO \( _{4} \) ) \( _{2} \) Polymorphs by Neutron Diffraction and Density Functional Theory Calculations. Phys. Chem. Chem. Phys. 2016, 18 (21), 14509–14519.
(21) Rodriguez-Carvajal, J. FullProf Suite. https://www.ill.eu/sites/fullprof/index.html.
(22) Rietveld, H. M. A Profile Refinement Method for Nuclear and Magnetic Structures. J. Appl. Crystallogr. 1969, 2 (2), 65–71.
(23) Bertaut, E. F. Magnetic Structure Analysis and Group Theory. J. Phys. Colloques 1971, 32 (C1), 463–470.
(24) Isasi, J.; Jaulmes, S.; Elfakir, A.; Quarton, M. Crystal Structure of Dilithium Nickel Disulfate, \( Li_{2}Ni(SO_{4})_{2} \) . Z. Kristallogr. - New Cryst. Struct. 2001, 216 (3), 331–332.
(25) Melot, B. C.; Chotard, J.-N.; Rousse, G.; Ati, M.; Reynaud, M.; Tarascon, J.-M. Synthesis, Structure, and Magnetic Properties of the \( NaCoXO_{4}F\cdot2H_{2}O \) Phases Where X = S and Se. Inorg. Chem. 2011, 50 (16), 7662–7668.
(26) Borovik-Romanov, A. S.; Karasik, V. R.; Kreines, N. M. The Antiferromagnetism of Anhydrous Sulfates of \( Ni^{2+} \) , \( Fe^{2+} \) , \( Co^{2+} \) and \( Cu^{2+} \) . J. Exptl. Theoret. Phys. 1957, 4 (31), 18–24.
(27) Moron, M. C.; Palacio, F.; Rodriguez-Carvajal, J. Crystal and Magnetic Structures of \( RbMnF_{4} \) and \( KMnF_{4} \) Investigated by Neutron Powder Diffraction: The Relationship between Structure and Magnetic Properties in the \( Mn^{3+} \) Layered Perovskites \( AMnF_{4} \) (A= Na, K, Rb, Cs). J. Phys.: Condens. Matter 1993, 5 (28), 4909.
(28) Izyumov, Y. A.; Naiash, V. E.; Petrov, S. B. Symmetry Analysis in Neutron Diffraction Studies of Magnetic Structures: 4. Theoretical Group Analysis of Exchange Hamiltonian. J. Magn. Magn. Mater. 1979, 13 (3), 275–282.
(29) Curie, P. Sur La Symétrie Dans Les Phénomènes Physiques, Symétrie D'un Champ Électrique et D'un Champ Magnétique. J. Phys. Theor. Appl. 1894, 3 (1), 393–416.
(30) Rousse, G.; Radtke, G.; Klein, Y.; Ahouari, H. Long-Range Antiferromagnetic Order in Malonate-Based Compounds Na \( _{2} \) M(H \( _{3} \) C \( _{3} \) O \( _{4} \) ) \( _{2} \) \( \cdot \) 2H \( _{2} \) O (M = Mn, Fe, Co, Ni). Dalton Trans. 2016, 45 (6), 2536–2548.
(31) O'Dell, T. H. Magnetoelectrics—a New Class of Materials. Electron. Power 1965, 11 (8), 266.
(32) Fiebig, M. Revival of the Magnetoelectric Effect. J. Phys. D: Appl. Phys. 2005, 38 (8), R123–R152.
(33) Folen, V. J.; Rado, G. T.; Stalder, E. W. Anisotropy of the Magnetoelectric Effect in \( Cr_{2}O_{3} \) . Phys. Rev. Lett. 1961, 6 (11), 607.
(34) Shtrikman, S.; Treves, D. Observation of the Magnetoelectric Effect in \( Cr_{2}O_{3} \) Powders. Phys. Rev. 1963, 130 (3), 986–988.
(35) Krichevtsov, B. B.; Pavlov, V. V.; Pisarev, R. V. Giant Linear Magnetoelectric Effect in Garnet Ferrite Films. JETP Lett. 1989, 49(8), 535.