| Transition Temperature | 272 K |
|---|---|
| Experiment Temperature | 77 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | Pm-3m (#221) |
| Magnetic Space Group | Cmm'm' (#65.486) |
| Magnetic Point Group | m'm'm (8.4.27) |
| Lattice Parameters | 3.869 3.869 3.869 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1103/physrev.125.1893 |
| Reference | W.J. Takei, R.R. Heikes and G. Shirane, Physical Review (1962) 125 1893-1897. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Mn1_1 | Mn | 0.64 | 0.64 | 0.0 | 0.91 |
| Mn1_2 | Mn | 1.34 | 1.34 | 0.0 | 1.90 |
Magnetic Structure of Mn_{4}N-Type Compounds
W. J. Takei, R. R. Heikes, and G. Shirane Westinghouse Research Laboratories, Pittsburgh, Pennsylvania (Received November 1, 1961)
A series of \( Mn_{4}N \) -type compounds has been investigated by means of magnetic saturation measurements and neutron diffraction experiments. Reinvestigation of \( Mn_{4}N \) has given revised moments with \( 3.85\mu_{B} \) at the corner of the cubic unit cell antiparallel to the three face-centered moments of \( 0.90\mu_{B} \) at \( 77^{\circ}K \) . Replacement of the nitrogen, located at the body-centered position, by carbon lowers the saturation moment by increasing the moment of the face-centered Mn while leaving the corner atom unchanged. Partial replacement of the nitrogen by vacancies also decreases the saturation moment. Small vacancy concentrations increase the face-centered moments while leaving the corner moment essentially unchanged. At larger vacancy concentrations, both the corner and face-centered moments decrease. These results are explicable in terms of a model in which nitrogen acts as an electron donor and the various local environments cause differing energy level splittings of the Mn atoms.
I. INTRODUCTION
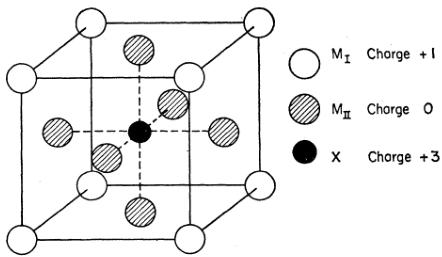
MANGANESE nitride is a representative of a series of transition metal carbides and nitrides which have the simple structure shown in Fig. 1. From a structural viewpoint, the chemical formula can be written as \( (M_{\mathrm{II}})_{3}M_{\mathrm{I}}X \) , where \( M_{I} \) is the corner atom, \( M_{II} \) , the three face-centered atoms, and X, the carbon or nitrogen which is at the body-centered position. Examples of other compounds belonging to this series are \( Fe_{4}N_{1} \) , \( Fe_{3}NiN_{1} \) , and \( Mn_{3}AlC \) . It is known that the carbon or nitrogen can deviate from unity, the nitrogen in \( Mn_{4}N \) having a range of 0.7 to 1.2.
Several magnetic and neutron diffraction investigations of the magnetic ordering in these compounds have been made in order to study the electronic distributions in the metal atoms and the role of nitrogen and carbon. In a study of several iron containing nitrides of this series, Wiener and Berger \( ^{1} \) assumed that nitrogen donated one electron to each of the three face-centered atoms. In the case of \( Fe_{4}N \) , they proposed the magnetic structure shown in Table I. A corner iron moment of \( 3\mu_{B} \) was parallel to the three face-centered moments of \( 2\mu_{B} \) to give the total moment of \( 9\mu_{B} \) . This structure was in agreement with the results of a subsequent neutron diffraction investigation of Frazer. \( ^{4} \)
The saturation moment of \( Mn_{4}N \) , \( 1.2\mu_{B} \) , is too small to be the resultant of a ferromagnetic arrangement of Mn moments of reasonable magnitude. For this reason, among others, various ferrimagnetic structures were proposed \( ^{1,3,6} \) as listed in Table I. Nitrogen was assumed to be an electron donor in each case but by assuming differing assignments of electrons to the s and d shells, different moment magnitudes were obtained. A neutron diffraction investigation of \( Mn_{4}N \) , although it confirmed the fact that the spin arrangement was ferrimagnetic, resulted in a structure, listed in Table I, which had not been proposed previously. The spin arrangement had a corner moment of \( 3.5\mu_{B} \) antiparallel to the three face-centered moments of \( 0.8\mu_{B} \) . This large difference in the magnitude of the moments of the corner and face-centered Mn makes it evident that nitrogen not only donates electrons to the face-centered atoms, but has also split their energy levels.
Juza and Puff \( ^{1} \) showed that partial replacement of the nitrogen in \( Mn_{4}N \) by carbon or vacancies decreased the saturation moment. Their model for \( Mn_{4}N \) was used as an explanation for this decrease. This model had a corner moment of \( 3.2\mu_{B} \) and a face-centered moment of \( 2.0\mu_{B} \) antiparallel to the other two face-centered moments of \( 2.0\mu_{B} \) to give the net moment of \( 3.2+2.0-2(2.0) \) equal to \( 1.2\mu_{B} \) . It was assumed that only the antiparallel face-centered moments of \( -2.0\mu_{B} \) were affected by the substitutions, changing to the corner type with a moment of \( -3.2\mu_{B} \) . Thus, a greater fraction of the positive moments were cancelled and the net moment reduced by \( 3.2-2.0 \) or \( 1.2\mu_{B} \) for each change. Three face-centered Mn were changed by each nitrogen vacancy and one by each carbon substitution.
The type of mechanism assumed by Juza and Puff for the reduction of saturation moment cannot be occurring in the structure as determined by the neutron diffraction study. The \( 2.7\mu_{B} \) difference in moment magnitude between a corner and face-centered type Mn

FIG. 1. Crystal structure of \( (M_{II})_{3}M_{I}X \) -type compounds. Charges refer to model as described in Sec. IV of text.
TABLE I. Magnetic structures of \( Mn_{4}N \) -type compounds. Asterisks indicated neutron diffraction studies.
| M1(0,0,0) | M2(3,3,0) | M3(3,0,3) | M4(0,3,3) | |
| Fe,N | ||||
| Wiener and Berger \( ^{*} \) | +3 | +2 | +2 | +2 |
| *Frazer \( ^{b} \) | ||||
| Mn,N | ||||
| Wiener and Berger \( ^{a} \) | +4 | +3 | -3 | -3 |
| Guillaume \( ^{b} \) | -5 | +2 | +2 | +2 |
| Juza and Puff \( ^{d} \) | +3.2 | +2 | -2 | -2 |
| *Takei et al. \( ^{e} \) | +3.5 | -0.8 | -0.8 | -0.8 |
| *This investigation | +3.9 | -0.9 | -0.9 | -0.9 |
| Mn \( _{3} \) AlC | ||||
| *Model 1 | 0(Al) | +1.2 | +1.2 | +1.2 |
| *Model 2 | +1.9 | +0.9 | +0.9 |
would result in moment changes with composition which would be too large. The decrease would be explained, however, if the corner moment remained constant and removal of an electron from the face-centered atom increased its moment by \( 1\mu_{B} \) . Each nitrogen vacancy would remove a total of three electrons from the face-centered atoms resulting in a total increase of \( 3\mu_{B} \) at these sites. Correspondingly, for the carbon substitution case, by the donation of two electrons instead of the three by nitrogen, there would be a total increase of \( 1\mu_{B} \) at the face-centered sites for each replacement. These assumptions were tested by an investigation to determine the atomic moment values in several of these substitutional compounds, listed in Table II.
II. EXPERIMENTAL
A. Sample Preparation
The samples prepared for this investigation are shown in Table II. All were in the form of powders. The starting material for all N-containing samples was \( Mn_{4}N \) or \( Mn_{5}N_{2} \) , prepared following the procedure of Mah, \( ^{7} \)

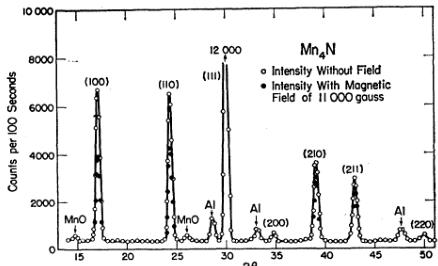
FIG. 2. Neutron diffraction pattern of \( Mn_{4}N \) at 77°K. Cylindrical powder sample \( \frac{3}{2} \) -in. diam×1 in. \( \lambda=1.15 \) A. Monitor period 104 sec.
\( ^{7} \) A. D. Mah, J. Amer. Chem. Soc. 80, 2954 (1958).
by passing purified nitrogen over Mn powder. The desired sample was then prepared by mixing stoichiometric amounts of the components into a Norton RA84 alundum extraction thimble, sealing in an evacuated silica tube, and heating at \( 1000^{\circ} \) C for periods up to one week for homogenization. The \( Mn_{3}AlC \) was prepared by placing the components in a recrystallized alumina combustion boat, melting at \( 1300^{\circ} \) C in an argon atmosphere, cooling and powdering the produce, reheating to 1300 for approximately one hour and then annealing at \( 1000^{\circ} \) C for three days.
B. Measurements
The results of x-ray and magnetic saturation measurements are shown in Table II. The magnetic measurements were made on a balance designed by R. C. Miller and D. E. Cox of these Laboratories, based on the Faraday method. Measurements were made in fields up to 10 000 gauss and at temperatures from 77°K up to the Néel temperature, the results quoted being obtained from extrapolations of moment versus 1/H.
The neutron diffraction experiments were conducted at the Westinghouse Testing Reactor utilizing a wavelength of 1.15 A. Samples were placed in thin walled (0.010 in.) Al sample holders and mounted in a magnet-cryostat system. A magnetic field up to 11 000 gauss could be applied parallel to the scattering vector of the reflection to eliminate the magnetic scattering and thereby determine the nuclear scattering directly. Wide angle room temperature runs were also made using thin walled (approximately 0.010 in.) silica tubes. The sample shapes in all cases were \( \frac{3}{8} \) -in. or \( \frac{1}{4} \) -in. diameter cylinders, 1 in. to \( 1\frac{1}{2} \) in. high, requiring about 10 g of sample.
II. RESULTS
A. Mn_{4}N
In the previous neutron diffraction study of \( Mn_{4}N \) , the available neutron flux required a relatively large amount of sample, approximately 75 g. In order to obtain this quantity of material, it was necessary to combine the products of several preparative runs. Due to the variation in composition, this procedure introduced an inhomogeneity of the diffraction sample. It contained an excess of nitrogen, partially due to the presence of \( Mn_{2}N \) , and had a smaller average saturation
TABLE II. Mn_{4}N-type compounds.
| a0(A) | σπ²κ(μB) | Néel temperature(°K) | |
| Mn4N | 3.865 | 1.14 | 745 |
| Mn4N0.92 | 3.855 | 0.84 | 750 |
| Mn4N0.8 | 3.836 | 0.45 | 778 |
| Mn4N0.76C0.25 | 3.865 | 0.88 | 850 |
| Mn3AlC | 3.869 | 3.63 | 272 |
TABLE III. Intensity data for Mn₄N at room temperature. λ=1.15 Å. Observed intensities adjusted by scale factor and appropriate Lorentz factors. Calculated intensities modified by temperature factor of 0.50×10⁻¹⁸ ų for nitrogen.
| Reflection | I_{total} observed | I_{mag} observed | I_{mag} calc. | I_{total} calc. |
| (100) | 8.6 | 3.5 | 3.6 | 8.8 |
| (110) | 14.7 | 5.3 | 5.0 | 15.2 |
| (111) | 45.3 | 0.1 | 45.2 | |
| (200) | 1.7 | 2.2 | ||
| (210) | 22.0 | 3.6 | 3.4 | 22.9 |
| (211) | 19.9 | 2.6 | 2.4 | 21.6 |
| (220) | 2.8 | 5.2 | ||
| (300) | 22.6 | 22.9 | ||
| (221) | ||||
| (310) | 17.9 | 18.0 | ||
| (311) | 122.7 | 123.0 | ||
| (320) | 18.3 | 17.1 | ||
| (321) | 33.2 | 33.6 | ||
| (322) | 31.8 | 32.0 | ||
| (410) | ||||
| (330) | 24.0 | 23.6 | ||
| (411) | ||||
| (331) | 112.1 | 112.6 |
moment of \( 0.98\mu_{B} \) at \( 77^{\circ}K \) . The much smaller samples that can be studied at the reactor presently available to us has permitted the re-examination of \( Mn_{4}N \) utilizing the product of one particular preparative run. This sample did not have a nitrogen excess and had a saturation moment of \( 1.14\mu_{B} \) at \( 77^{\circ}K \) . The diffraction pattern, taken at \( 77^{\circ}K \) , is shown in Fig. 2. Small traces of MnO are present in the sample. The greater resolution and smaller background available at this diffraction facility has improved the data despite the use of less sample and shorter stepping times. Room temperature scans were made to an angle, \( 2\theta \) , of \( 90^{\circ} \) . As shown in Table III, this allowed an accurate determination of the scale and temperature factors as a check on the nuclear intensities as determined by diffraction experiments with a magnetic field.
The new study did not change any of the previous results basically, but did give slightly larger individual atomic moments. Since the calculations involved are typical of those for the entire series, the various steps will be discussed. The large magnetic scattering present in the (100) and (110) reflections is due to the presence of ferrimagnetic ordering. Various types of arrangements can give this result but the polarized neutron experiments described in the previous paper \( ^{6} \) showed that the correct model was one in which the three face-centered moments were antiparallel to the corner moment, the resultant moment being in the same direction as that at the corner. Therefore, the magnetic scattering in reflections with mixed indices is proportional to \( (\mu_{\mathrm{I}} - \mu_{\mathrm{II}}) \) , and since the two moments differ in sign, is proportional to the sum of their absolute values.
\[ I_{\mathrm{m a g}}=j\langle q^{2}\rangle(0.269)^{2}f^{2}(\mu_{\mathrm{I}}-\mu_{\mathrm{I I}})^{2}, \]
where j is the multiplicity; \( \langle q^{2}\rangle \) , the average value of \( \sin^{2}\alpha \) where \( \alpha \) is the angle between the scattering and magnetic vectors and is equal to \( \frac{2}{3} \) in this case; 0.269 results from a combination of fundamental atomic constants; and f is the magnetic form factor. By use of the \( Mn^{2+} \) form factor, an average value of \( 4.75\mu_{B} \) is obtained for \( \mu_{I}-\mu_{II} \) at liquid nitrogen temperature. This value can then be combined with that of the net moment, \( \mu_{I}+3\mu_{II}=1.14\mu_{B} \) , obtained from the magnetic saturation measurements to give the individual atomic moments, \( 3.85\mu_{B} \) at the corner and \( -0.90\mu_{B} \) at the face-centered sites. Because of the symmetry, the spin direction with respect to the cell edges cannot be determined.
B. Carbon Containing Compounds
The data for the carbon-substituted compound, \( Mn_{4}N_{0.75}C_{0.25} \) has the same general appearance as that for \( Mn_{4}N \) and its analysis proceeds in exactly the same manner. \( (\mu_{\mathrm{I}}-\mu_{\mathrm{II}}) \) is \( 4.5\mu_{B} \) at room temperature which, when combined with the saturation moment of \( 0.58\mu_{B} \) gives \( \mu_{I} \) and \( \mu_{II} \) equal to \( 3.52\mu_{B} \) and \( -0.98\mu_{B} \) , respectively. Thus the corner moment has essentially the same value as in \( Mn_{4}N \) , \( 3.53\mu_{B} \) at room temperature, while the face-centered moment has increased in magnitude. At \( 77^{\circ}K \) , replacement of 0.25 nitrogen by carbon results in a decrease of 0.26 in the saturation moment, or one electron per replacement, corresponding to the donation of two electrons by carbon instead of the three by nitrogen. Complete replacement of all the nitrogen by carbon should then result in a face-centered moment of \( 0.90+\frac{1}{3} \) or \( 1.23\mu_{B} \) . A report has been made of the preparation of \( Mn_{4}C \) (mixed with \( 30\%_{0} \) non-magnetic \( Mn_{25}C_{6} \) ) by extremely rapid quenching from \( 1050^{\circ}C \) .⁸ It was reported as weakly magnetic with a moment approximately one-tenth that of nickel which has a moment of \( 0.6\mu_{B}/atom \) . If the same type of magnetic structure was maintained in this compound, a corner moment of \( 3.85\mu_{B} \) antiparallel to three face-centered moments of \( 1.23\mu_{B} \) would be expected. The net moment of \( 0.16\mu_{B} \) would yield an algebraic average of \( 0.04\mu_{B}/Mn \) .
The nuclear structure for \( Mn_{3}AlC \) with Al at the
TABLE IV. Intensity data for \( Mn_{3}AlC \) at 77°K. \( \lambda=1.15 \) A. Observed intensities adjusted by scale factor and appropriate Lorentz factors.
| Reflection | I_{total} observed | I_{\text{mag}} (I_{\text{tot}} - I_{\text{me}}) | I_{\text{mag}} calc. Model 1 | I_{\text{mag}} calc. Model 2 | I_{\text{me}} calc. |
| (100) | 0.37 | 0.32 | 0.40 | 0.33 | 0.02 |
| (110) | 24.5 | 2.5 | 0.56 | 0.69 | 22.8 |
| (111) | 19.8 | 2.9 | 2.3 | 2.3 | 16.4 |
| (200) | 1.5 | 1.2 | 1.3 | 1.3 | 0.06 |
| (210) | 0.6 | 0.3 | 0.4 | 0.3 | 0.09 |
| (211) | 44.1 | 0.2 | 0.3 | 0.2 | 44.5 |
\( ^{8} \) E. R. Morgan, J. Metals 6, 983 (1954).
TABLE V. Atomic moments in Bohr magnetons for Mn₄N-type compounds. Numbering as shown in Fig. 1.
| 300°K | 77°K | |||
| μI | μII | μI | μII | |
| Mn4N | 3.53 | -0.89 | 3.85 | -0.90 |
| Mn4N0.92 | 3.54 | -0.96 | 3.79 | -0.99 |
| Mn4N0.8 | 2.93 | -0.86 | 3.30 | -0.95 |
| Mn4N0.75C0.25 | 3.52 | -0.98 | ||
| Mn3AIC | 1.21 | |||
corner sites, \( ^{2} \) was confirmed by the room temperature diffraction pattern. This contained nuclear scattering only since it was above the Curie temperature of \( 27^{2}K \) . \( Mn_{4}AlC \) has been reported as “probably a normal ferromagnetic” \( ^{9} \) and diffraction patterns taken at \( 77^{\circ}K \) are in agreement with this type of structure. However, two ferromagnetic models, given in Table I, can satisfy the data as shown in Table IV. Model 1 is an equal moment structure with the saturation moment of \( 3.63\mu_{B} \) a result of three face-centered moments of \( 1.21\mu_{B} \) each. This moment is in agreement with the \( 1.23\mu_{B} \) predicted above for the face-centered atoms in \( Mn_{4}C \) . Model 2 can be discussed by referring to the vertical axis in Figure 1 as the c axis. The face-centered atoms in the basal plane would then have a moment of \( 1.9\mu_{B} \) while the other Mn, in the plane at \( \frac{1}{2}c \) , would have a moment of \( 0.9\mu_{B} \) each. The calculated intensity in this type of structure is a function of the angle \( \Phi \) between the c axis and the spin direction. In order to fit the diffraction data, the spin direction must be approximately perpendicular to the c axis, i.e., in or near the planes described. The intensities for Model 2, given in Table IV are calculated for \( \Phi \) equal to \( 90^{\circ} \) . Both models have the (110) magnetic reflection smaller than the observed value but the latter is obtained as the difference between two large numbers and can be considerably in error. Although the moment magnitudes for Model 2 are different from the \( 1.21\mu_{B} \) in Model 1, the average value is the same. Therefore, the value of \( 1.21\mu_{B} \) is listed for the face-centered moment in Table V for the comparison with the other results.
C. Nitrogen Deficient Compounds
The data analysis for the compounds with vacancies partially substituted for nitrogen proceeds in the same manner as for \( Mn_{4}N \) . At \( 77^{\circ}K \) , a value of \( 4.78\mu_{B} \) is obtained for \( (\mu_{I}-\mu_{II}) \) of \( Mn_{4}N_{0.92} \) . When combined with the saturation moment of \( 0.84\mu_{B} \) , this yields average atomic moments of 3.54 and \( -0.99\mu_{B} \) for \( \mu_{I} \) and \( \mu_{II} \) , respectively. Again the corner moment has stayed essentially constant while the face-centered moment has increased in magnitude with a total change of about \( 3\mu_{B} \) for each nitrogen vacancy in agreement with the idea that nitrogen has donated three electrons. The compound \( Mn_{4}N_{0.8} \) which has 20% of the nitrogen replaced by vacancies presents different results. If the simple rules followed in the previous compounds were maintained, it would be expected that the average face-centered moment at \( 77^{\circ}K \) would be equal to \( 0.90 + 0.2(3)(\frac{1}{3}) \) or \( 1.10\mu_{B} \) . The saturation moment then would be \( 3.85 - 3(1.10) \) or \( 0.55\mu_{B} \) and the value of \( (\mu_{I} - \mu_{II}) \) obtained from the diffraction experiments would be \( 3.85 - (-1.10) \) or \( 4.95\mu_{B} \) . However, the measured saturation moment is \( 0.45\mu_{B} \) , and the value of \( (\mu_{I} - \mu_{II}) \) is only \( 4.25\mu_{B} \) , a considerable decrease from the \( Mn_{4}N \) value rather the expected increase. As a consequence, the average corner moment derived from the data has decreased from \( 3.85\mu_{B} \) to \( 3.30\mu_{B} \) and a value of \( 0.95\mu_{B} \) is obtained for the face-centered moment. These values are explicable as a result of the model for \( Mn_{4}N \) discussed below.
IV. DISCUSSION
An attempt will now be made to show that the experimental results on the systems discussed above can be interpreted in terms of the splitting of the d levels of the Mn atom. First, let us consider the role of the nitrogen atom. It is commonly accepted \( ^{1} \) that its role is as a donor of electrons. Magnetic considerations in \( Fe_{4}N \) make this hypothesis reasonable; furthermore, size considerations in this type of structure tend to force one to the same conclusion. In this discussion, we will assume that the nitrogen donates three electrons to the face-centered atoms.
Let us now examine the energy level schemes of the Mn atoms. To do this, consider Fig. 1. The charges of the M atoms (Mn in this case) are based on the assumption that each atom gives up one electron to a conduction band and, in addition, each face-centered atom receives an electron from the nitrogen. Let us first treat the corner atoms. Consider the d-wave functions xy, yz, xz, \( x^{2}-y^{2} \) , \( 3z^{2}-r^{2} \) , the first three forming a triplet while the remaining two form a doublet. We might expect, from a study of the figure, that the doublet will lie a bit lower than the triplet in \( Mn_{4}N \) . However, as nitrogen atoms are removed, the face-centered atoms become positively charged, a circumstance which tends to lower the triplet level. It will be assumed that if three or more nitrogen neighboring to a corner Mn are removed, the triplet level becomes sufficiently low so that Hund's rule is violated. The six d electrons of the corner Mn are just sufficient to fill the lower triplet level, giving a net spin of zero. This assumption is, of course, arbitrary and the necessary number of vacancies, z, was chosen to fit the experimental data. Consider now the face-centered atoms. Experimentally, we know that \( \mu_{II} \sim 1\mu_{B} \) . Furthermore, it appears that the removal of a nitrogen causes \( \mu_{II} \) to increase to \( 2\mu_{B} \) by the removal of an electron. This requires that the energy level scheme be such that one of the five 3d levels is raised sufficiently so that Hund's rule is not obeyed. A study of Fig. 1 easily reveals that the d levels will be split into a doublet and
3 singlet levels. Furthermore, it is rather clear that the singlet \( 3s^{2}-r^{2} \) level will be the highest. It must, of course, be regarded as an assumption that the splitting is large enough so that all 7 electrons are confined to the lower four levels, giving a net spin of \( \sim1\mu_{B} \) . Removal of an electron from this set of levels (by the removal of nitrogen) will cause the moment to increase to \( \sim2\mu_{B} \) .
In order to understand these systems, it is necessary to make one further assertion. It is clear from the magnetic structure as determined by neutron diffraction that the dominant magnetic interaction is between a corner atom and a face-centered atom. This interaction is antiferromagnetic. It will now be necessary to assert that a face-centered Mn having two neighboring nitrogen vacancies turns its spin parallel to the corner Mn. This assumption can be made plausible on the following basis. As the substances are essentially metallic in nature, the indirect ferromagnetic coupling via the conduction electrons must be present. Removing electrons from the face-centered atoms is equivalent to diminishing the radius of the Mn and consequently to a lessening of the antiferromagnetic direct interaction.
Having attempted to rationalize our assumptions, let us see how the data are treated.
A. \( Mn_{4}N \) . The present model would give rise to moments of \( 4\mu_{B} \) and \( 1\mu_{B} \) on the corner and face-centered atoms, respectively.
B. Carbon containing compounds. As discussed in the previous section, carbon is treated as giving one less electron than the nitrogen. This is equivalent to forming one face-centered moment of \( \sim2\mu_{B} \) for each carbon added. On the suggested level scheme, this is acceptable.
C. Nitrogen-deficient compounds. Expressions for \( \mu_{T} \) and \( \mu_{TT} \) may be written down from the suggested model. Using the formula \( Mn_{4}N_{1-x} \)
\[ \begin{aligned}\mu_{\mathrm{I}}=&3.85\{1-\left[1-28x^{2}(1-x)^{6}\right.\\&\left.-8x(1-x)^{7}-(1-x)^{8}]\right\},\end{aligned} \quad (1) \]
\[ \mu_{\mathrm{TT}}=x^{2}(-1.9)+2x(1-x)(1.4)+(1-x)^{2}(0.9), \quad (2) \]
where in Eq. (1) the subtractive term in square brackets represents the number of corner Mn having three or more neighboring nitrogen vacancies. In Eq. (2) the first term represents the corner Mn having two neighboring vacancies; the second term represents those with

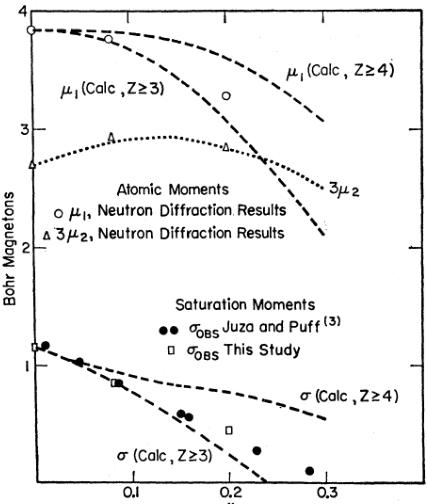
FIG. 3. Experimental and calculated atomic moments of \( Mn_{4}N_{1-x} \) as a function of x. Z is the number of nitrogen vacancies about a corner atom assumed as sufficient to result in zero moment.
one, and the third with none. It should also be remarked that the experimentally observed moments of \( 3.85\mu_{B} \) and \( 0.9\mu_{B} \) are being used for the corner and face-centered atoms, respectively, rather than the theoretical values of \( 4\mu_{B} \) and \( 1\mu_{B.} \)
The results of Equations (1) and (2) and the calculated saturation moments are compared with experiment in Fig. 3. The curves for \( z \geqslant 4 \) , as a criterion for zero corner moment, are also shown. It can be seen that the model reproduces the experimental variation of moments with change in nitrogen content. However, the choice of \( z \geqslant 3 \) results in a more rapid decrease in the corner and saturation moments than is observed and a better fit could be obtained by a number fractionally greater than three. This may be due to the fact that certain geometrical configurations of three nitrogen vacancies do not split the energy levels sufficiently for Hund's rule to be violated.