TmAgGe (3.1)
Three+ propagation vectors| Transition Temperature | 4.2 K |
|---|---|
| Experiment Temperature | 1.5 K |
| Parent Space Group | P-62m (#189) |
| Magnetic Space Group | P-6'2m' (#189.224) |
| Magnetic Point Group | -6'm'2 (26.3.97) |
| Lattice Parameters | 14.0520 14.0520 4.1430 90.0000 90.0000 120.0000 |
|---|---|
| DOI | 10.1016/j.jmmm.2009.05.064 |
| Reference | S. Baran, D. Kaczorowski, A. Arulraj, B. Penc and A. Szytula, Journal of Magnetism and Magnetic Materials (2009) 321 3256-3261. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Tm1_1 | Tm | -6.44 | 0.0 | 0.0 | 6.44 |
| Tm1_2 | Tm | -6.44 | 0.0 | 0.0 | 6.44 |
| Tm1_3 | Tm | -6.44 | -6.44 | 0.0 | 6.44 |
Title
Frustrated magnetic structure of TmAgGe
Authors
S. Baran \( ^{a,*} \) , D. Kaczorowski \( ^{b} \) , A. Arulraj \( ^{c} \) , B. Penc \( ^{a} \) , A. Szytula \( ^{a} \) a M. Smoluchowski Institute of Physics, Jagiellonian University, Reymonta 4, PL-30 059 Kraków, Poland b Institute of Low Temperature and Structure Research, Polish Academy of Sciences, P. O. Box 1410, PL-50 950 Wrocław, Poland c Helmholtz-Zentrum Berlin, Glienicker Str. 100, D-14 109 Berlin, Germany
Materials Studied
TmAgGe
Key Information
- Crystal structure / space group: Hexagonal ZrNiAl-type, space group P6\( \overline{2} \)m.
- Magnetic ordering type and temperature: Antiferromagnetic ordering below T\(_{N}\) = 4.2(1) K.
- Propagation vector(s): Three different propagation vectors are required: \( \vec{k}=[\frac{1}{2},0,0] \), \( \vec{k}^{\prime}=[-\frac{1}{2},\frac{1}{2},0] \) and \( \vec{k}^{\prime\prime}=[0,\frac{1}{2},0] \).
- Magnetic moments:
- Tm magnetic moments at 1.5 K (zero field): 6.44(10)\(\mu_{B}\)
- Effective magnetic moment (\(\mu_{eff}\)) in paramagnetic region: 7.37(4)\(\mu_{B}\)
- Saturation magnetic moment in field-induced ferromagnetic state (1.72 K, 5 T): 3.9(3)\(\mu_{B}\)
- Average Tm magnetic moment in canted ferromagnetic structure: 4.29\(\mu_{B}\)
- Lattice parameters:
- a = 7.026(2) Å
- c = 4.143(2) Å
- c/a = 0.5897(4)
- V = 177.1(2) Å\(^{3}\)
- x\(_{Tm}\) = 0.576(2)
- x\(_{Ag}\) = 0.250(2)
- Other critical measured values:
- Paramagnetic Curie temperature (\(\theta_{p}\)): 12.1(1) K
- Metamagnetic transition field: B = 0.3 T
- Energy gap (\(\varDelta\)) from magnetic susceptibility fit: 13.2(3) K
- Energy gap (\(\varDelta\)) from specific heat fit: 15.7(9) K
- Debye temperature (\(\Theta_{D}\)) from resistivity fit: 257.7 K
- Specific heat jump (\(\Delta C_{p}\)) at T\(_{N}\): approximately 14 J/molK
Synthesis Method
Polycrystalline samples of TmAgGe were synthesized by arc melting high-purity elements (Tm: 3N; Ag: 4N; Ge: 5N) under a titanium-gettered argon atmosphere. To ensure homogeneity, the resulting ingot was turned over and remelted several times. Afterwards, the sample was annealed in an evacuated quartz ampoule at 600\(^{\circ}\)C for one week. The product quality was examined by X-ray powder diffraction at room temperature, confirming the hexagonal ZrNiAl-type crystal structure and an almost single-phase character.
Abstract
The RAgGe (R = rare earth) ternary intermetallics crystallize in the hexagonal crystal structure of the ZrNiAl-type \( [1,2] \). In this type of structure the rare earth ions occupy equivalent 3g positions with an orthorhombic point symmetry. The results of magnetic measurements, performed on polycrystalline and single-crystalline samples of these compounds, revealed in several of them antiferromagnetic ordering in the ground state and strong influence of the crystalline electric field (CEF) effect in both the ordered and paramagnetic regions \( [3-7] \). In particular, TmAgGe was characterized as an antiferromagnet with the Néel temperature \( 4.2(1) \) K \( [5] \), easy-plane magnetic anisotropy and distinct metamagnetic features observed for magnetic field applied perpendicular to the c-axis \( [6] \).
In the present work the magnetic ordering in TmAgGe has been probed by neutron powder diffraction, and the physical properties of the compound have been investigated within wide temperature range by magnetization, electrical resistivity and heat capacity measurements.
Main Content Summary
This study investigates the physical and magnetic properties of the ternary intermetallic compound TmAgGe through a combination of magnetometric, transport, calorimetric, and neutron diffraction measurements. The compound crystallizes in the hexagonal ZrNiAl-type structure (space group P6\( \overline{2} \)m), with lattice parameters a = 7.026(2) Å and c = 4.143(2) Å at 6.1 K. The Tm atoms occupy 3g sites with orthorhombic point symmetry.
Magnetic measurements confirm antiferromagnetic ordering below a Néel temperature of T\(_{N}\) = 4.2 K. In the paramagnetic region, the compound exhibits a paramagnetic Curie temperature of \( \theta_{p}=12.1(1) \) K and an effective magnetic moment of \( \mu_{eff}=7.37(4) \mu_{B} \), close to the free Tm\(^{3+}\) ion value. A metamagnetic transition is observed at 0.3 T at 1.72 K, with a saturation magnetic moment of 3.9(3) \(\mu_{B}\) at 5 T, significantly smaller than the free ion value, suggesting a strong crystalline electric field (CEF) effect. Electrical resistivity measurements show metal-like conductivity with an anomaly at T\(_{N}\), and the data above T\(_{N}\) can be described by the Bloch–Grüneisen–Mott formula, yielding a Debye temperature of \( \Theta_{D} = 257.7 \) K.
Specific heat measurements reveal a sharp lambda-shaped anomaly at T\(_{N}\), with a jump of approximately 14 J/molK. The magnetic entropy reaches Rln2 at the transition, indicating a doublet or closely separated singlets as the ground state, consistent with CEF splitting. Furthermore, the low-temperature behavior of both magnetic susceptibility and specific heat is well described by the spin-wave theory for antiferromagnets with a linear dispersion relation and an energy gap (\(\varDelta\)). The derived energy gap values are in reasonable agreement: \( \varDelta = 13.2(3) \) K from susceptibility and \( \varDelta = 15.7(9) \) K from specific heat.
Neutron powder diffraction was crucial for determining the magnetic structure. The magnetic reflections observed below T\(_{N}\) indicate a complex, non-collinear "triangular" magnetic structure confined within the basal plane. This structure requires three distinct propagation vectors: \( \vec{k}=[\frac{1}{2},0,0] \), \( \vec{k}^{\prime}=[-\frac{1}{2},\frac{1}{2},0] \), and \( \vec{k}^{\prime\prime}=[0,\frac{1}{2},0] \). The Tm magnetic moments are determined to be 6.44(10)\(\mu_{B}\) at 1.5 K. This magnetic structure is consistent with previous single-crystal magnetization studies and helps explain the observed average magnetic moment in a field-induced canted ferromagnetic state.
Conclusion
The ternary compound TmAgGe crystallizes in the hexagonal ZrNiAl-type crystal structure. It exhibits an antiferromagnetic ordering below 4.2 K, as derived from the magnetic susceptibility, the electrical resistivity and the specific heat data. The value of Néel temperature is in good agreement with the previously reported result. The neutron diffraction data indicate that this compound exhibits a magnetic structure with "triangular" arrangement of the Tm magnetic moments confined within the basal plane. Three different propagation vectors: \( \vec{k} = [\frac{1}{2}, 0, 0] \), \( \vec{k}' = [-\frac{1}{2}, \frac{1}{2}, 0] \), and \( \vec{k}'' = [0, \frac{1}{2}, 0] \) are necessary to describe the magnetic order. This result follows the group theory predictions and is in good agreement with the single-crystal magnetization data. The low-temperature dependencies of the magnetic susceptibility and the specific heat reveal the presence of antiferromagnetic magnons. The value of magnetic moment derived from the neutron diffraction data is smaller than the free Tm\(^{3+}\) ion value, but well accounts for the value of the average magnetic moment in canted ferromagnetic structure, expected to form in TmAgGe in the presence of strong external magnetic field.
Frustrated magnetic structure of TmAgGe
S. Baran \( ^{a,*} \) , D. Kaczorowski \( ^{b} \) , A. Arulraj \( ^{c} \) , B. Penc \( ^{a} \) , A. Szytula \( ^{a} \)
a M. Smoluchowski Institute of Physics, Jagiellonian University, Reymonta 4, PL-30 059 Kraków, Poland
b Institute of Low Temperature and Structure Research, Polish Academy of Sciences, P. O. Box 1410, PL-50 950 Wrocław, Poland
c Helmholtz-Zentrum Berlin, Glienicker Str. 100, D-14 109 Berlin, Germany
ARTICLE INFO
Article history: Received 11 May 2009 Available online 6 June 2009
PACS: 65.40.-b 75.25.+z 75.30.Cr 75.50.Ee
Keywords: Rare earth intermetallics Frustrated antiferromagnet AF magnons Neutron scattering
A B S T R A C T
The RAgGe (R = rare earth) ternary intermetallics crystallize in the hexagonal crystal structure of the ZrNiAl-type \( [1,2] \) . In this type of structure the rare earth ions occupy equivalent 3g positions with an orthorhombic point symmetry. The results of magnetic measurements, performed on polycrystalline and single-crystalline samples of these compounds, revealed in several of them antiferromagnetic ordering in the ground state and strong influence of the crystalline electric field (CEF) effect in both the ordered and paramagnetic regions \( [3-7] \) . In particular, TmAgGe was characterized as an antiferromagnet with the Néel temperature \( 4.2(1) \) K \( [5] \) , easy-plane magnetic anisotropy and distinct metamagnetic features observed for magnetic field applied perpendicular to the c-axis \( [6] \) .
In the present work the magnetic ordering in TmAgGe has been probed by neutron powder diffraction, and the physical properties of the compound have been investigated within wide temperature range by magnetization, electrical resistivity and heat capacity measurements.
1. Introduction
Polycrystalline sample of TmAgGe was synthesized by arc melting high-purity elements (Tm: 3N; Ag: 4N; Ge: 5N) under Physical properties of the compound TmAgGe have been investigated by means of magnetometric, transport, calorimetric as well as neutron diffraction measurements. The compound crystallizes in the hexagonal ZrNiAl-type crystal structure. The reported results indicate that the sample exhibits an antiferromagnetic ordering below \( T_{N}=4.2 \) K. The low temperature behavior of the magnetic susceptibility and the specific heat is in good agreement with the spin-wave theory with linear dispersion relation. In addition, the magnetic structure of TmAgGe was determined by means of neutron diffraction measurements. The Tm moments are equal to \( 6.44(10)\mu_{B} \) at 1.5 K and form a non-collinear magnetic structure within the basal plane. To describe this structure three different propagation vectors: \( \vec{k}=[\frac{1}{2},0,0] \) , \( \vec{k}^{\prime}=[-\frac{1}{2},\frac{1}{2},0] \) and \( \vec{k}^{\prime\prime}=[0,\frac{1}{2},0] \) are required. Such a spin arrangement is analyzed on the basis of group theory.
© 2009 Elsevier B.V. All rights reserved.
titanium-gettered argon atmosphere. In order to ensure appropriate homogeneity the resulting ingot was turned over and remelted several times. Afterwards, the sample was annealed in an evacuated quartz ampoule at \( 600^{\circ} \) C for one week.
The product quality was examined by X-ray powder diffraction at room temperature on a Philips PW-3710 X'PERT diffractometer using \( CuK_{\alpha} \) radiation. The results confirmed the hexagonal ZrNiAl-type crystal structure and indicated almost single-phase character of the prepared sample.
Magnetic measurements were performed within the 1.72–300K temperature range and in external magnetic fields up to 5T using a Quantum Design SQUID magnetometer. The electrical resistivity was measured over the temperature interval of 3.8–290K employing a standard dc four-probe technique and a home-made setup. Heat capacity studies were carried out in the temperature range 0.3–300K using a relaxation method implemented in a Quantum Design PPMS platform.
The neutron powder diffraction patterns were collected on the E6 diffractometer installed at the BERII reactor (Helmholtz-Zentrum Berlin) within the temperature range from 1.5 to 6.1 K. The incident neutron wavelength was 2.452 Å. The neutron diffraction data were analyzed using the Rietveld-type program FullProf [8].
3. Results and discussion
3.1. Crystal structure
The X-ray diffraction data, collected at room temperature, as well as the neutron diffraction data, obtained at 6.1 K
(paramagnetic state), confirmed unambiguously the hexagonal ZrNiAl-type structure (space group P6 \( \overline{2} \) m) of TmAgGe. In this unit cell the particular atoms occupy the following sites:
\[ 3\mathrm{Tm}\mathrm{atoms}\mathrm{at}3(\mathrm{g})\mathrm{site}\quad x_{\mathrm{Tm}},0,\frac{1}{2}\quad0,x_{\mathrm{Tm}},\frac{1}{2}\quad\overline{x}_{\mathrm{Tm}},\overline{x}_{\mathrm{Tm}},\frac{1}{2} \]
\[ 3\mathrm{Ag}\mathrm{atoms}\mathrm{at}3(\mathrm{f})\mathrm{site}\quad x_{\mathrm{Ag}},0,0\quad0,x_{\mathrm{Ag}},0\quad\overline{x}_{\mathrm{Ag}},\overline{x}_{\mathrm{Ag}},0 \]
\[ 2\mathrm{Ge}\mathrm{atoms}\mathrm{at}2(\mathrm{c})\mathrm{site}\quad\frac{1}{3},\frac{2}{3},0\quad\frac{2}{3},\frac{1}{3},0 \]
\[ 1\mathrm{Ge}\mathrm{atom}\mathrm{at}1(\mathrm{b})\mathrm{site}\quad0,0,\frac{1}{2} \]
The values of the lattice parameters and the free positional parameters x derived from the neutron diffraction pattern are listed in Table 1.
3.2. Magnetic behavior
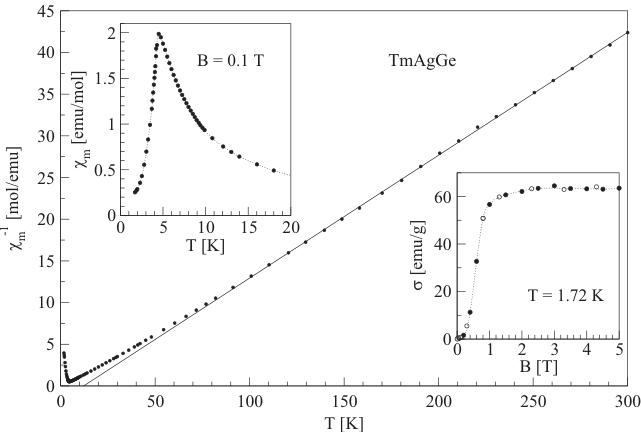
The magnetic properties of TmAgGe are presented in Fig. 1. Above about 80K, the inverse magnetic susceptibility exhibits a linear-in-T behavior. At lower temperatures some curvature of \( \chi^{-1}(T) \) is seen, presumably due to CEF effect. Fitting the Curie–Weiss formula to the experimental data yielded the paramagnetic Curie temperature \( \theta_{p}=12.1(1) \) K and the effective magnetic moment \( \mu_{eff}=7.37(4) \) \( \mu_{B} \) . The experimental value of \( \mu_{eff} \) is close to the free \( Tm^{3+} \) ion value (7.56 \( \mu_{B} \) ). As shown in the upper
Refined structural parameters of TmAgGe together with residuals for profile and integrated intensities.
| a ( \( \textup{\AA} \) ) | 7.026(2) |
| c ( \( \textup{\AA} \) ) | 4.143(2) |
| c/a | 0.5897(4) |
| V ( \( \textup{\AA}^{3} \) ) | 177.1(2) |
| x_{Tm} | 0.576(2) |
| x_{Ag} | 0.250(2) |
| \( \chi^{2} \) | 4.83 |
| R_{profile} (%) | 2.62 |
| R_{Bragg} (%) | 5.95 |
inset in Fig. 1, the compound orders magnetically at 4.2 K and the observed anomaly is typical for antiferromagnets. Very similar result was reported for TmAgGe in Ref. [5]. The antiferromagnetic character of the magnetic ordering is corroborated by behavior of the isothermal magnetisation taken at 1.72 K as a function of magnetic field up to about 5 T. A clear metamagnetic transition is visible at \( B = 0.3 \) T (see the lower inset to Fig. 1). This value is in good agreement with the data found for single crystal (see in Ref. [6, Fig. 18]). The saturation magnetic moment in the field-induced ferromagnetic state at 1.72 K equals \( 3.9(3) \) \( \mu_{B} \) , which is much smaller than the free \( Tm^{3+} \) ion value ( \( 7.0 \mu_{B} \) ) and should be related to the CEF electronic ground state of the compound.
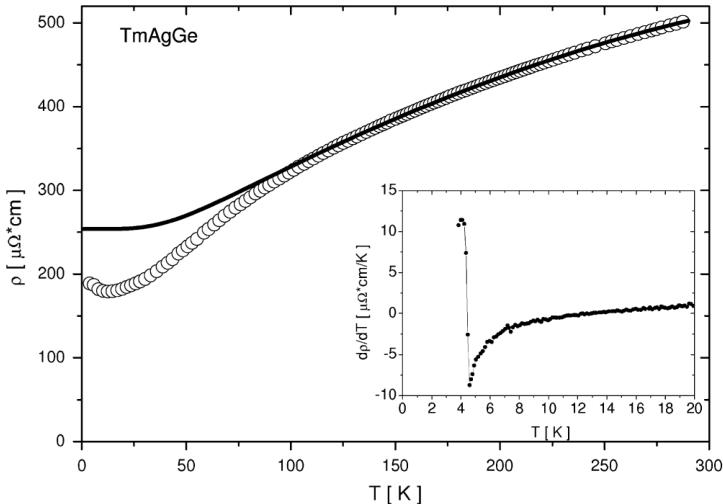
3.3. Electrical resistivity
The results of electrical transport measurements of TmAgGe are presented in Fig. 2. The compound exhibits metal-like electrical conductivity with a faint anomaly at low temperatures due to magnetic ordering at \( T_{N} = 4.2 \) K. The latter feature manifests itself as a sudden drop in the temperature derivative of the resistivity (see the lower inset in Fig. 2). Above the Neel temperature the resistivity goes through a broad local minimum around 15 K. In the region where the magnetic contribution to the electrical resistivity can be assumed to be nearly temperature independent (i.e. where the CEF effects do not play major role), the resistivity data can be described using the Bloch–Grüneisen–Mott (BGM) formula:
\[ \rho(T)=(\rho_{0}+\rho_{\infty})+4R T\left(\frac{T}{\Theta_{D}}\right)^{4}\int_{0}^{\Theta_{D}/T}\frac{x^{5}\mathrm{d}x}{(\mathrm{e}^{x}-1)(1-\mathrm{e}^{-x})}-K T^{3} \quad (1) \]
where the first term is a sum of the residual \( \rho_{0} \) and spin-disorder \( \rho_{\infty} \) resistivities, whereas the electron-phonon scattering processes and the s-d interband scattering processes are described by the second and the third term, respectively. Fitting Eq. (1) to the experimental data in the range 125–290 K gives the following set of parameters: \( (\rho_{0} + \rho_{\infty}) = 253.7 \mu\Omega cm \) , \( R = 1.086 \mu\Omega cm/K \) , \( \Theta_{D} = 257.7 K \) and \( K = 2.19 \times 10^{-6} \mu\Omega cm/K^{-3} \) . The parameter \( \Theta_{D} \) is usually treated as a rough estimation of the Debye temperature, despite its value is somehow influenced by electronic correlations [9]. In the case of TmAgGe, however, the so-obtained \( \Theta_{D} \) appears to

Fig. 1. Inverse magnetic susceptibility of TmAgGe. The solid line shows the Curie–Weiss fit discussed in text. The upper-left corner inset presents magnetic susceptibility at low temperatures. The bottom-right corner inset presents isothermal magnetisation curve during increasing (open symbols) and decreasing (filled symbols) of the magnetic field.

Fig. 2. Electrical resistivity of TmAgGe (open symbols). The solid line shows the fit to the Block–Grüneisen–Mott formula (see main text for details). The inset presents the low-temperature part of the derivative of electrical resistivity with respect to temperature.

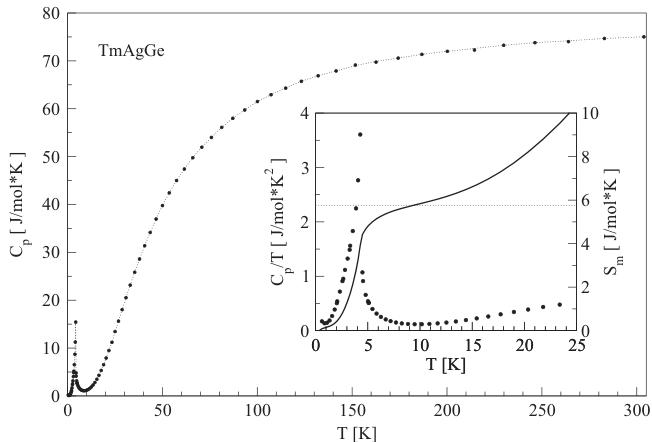
Fig. 3. Temperature dependence of the specific heat of TmAgGe. The inset presents the low-temperature part of \( c_{p}/T \) (dots) and magnetic entropy \( S_{m} \) (solid line). The entropy level \( Rln2 \) is marked by dotted line.
be close to that estimated from the specific heat data for the isostructural LuAgGe ( \( \Theta_{D} \approx 231 \) K) [4]. Gradual depopulation of the crystal field levels with decreasing temperature manifests itself in the reduction of the measured resistivity below 125 K with respect to that calculated assuming constant value of the magnetic contribution in the paramagnetic region (cf. Fig. 2).
3.4. Specific heat
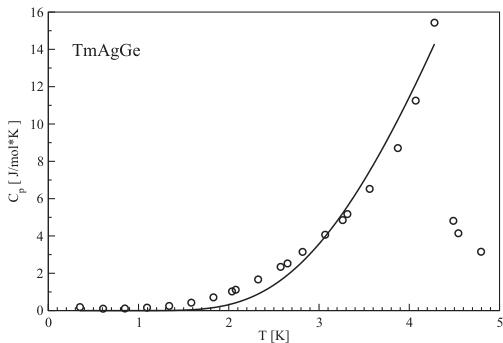
The temperature variation of the specific heat of TmAgGe is presented in Fig. 3. At the temperature of about 4.2 K a sharp lambda-shaped anomaly is seen, which should be related to the antiferromagnetic ordering.
The jump in the specific heat \( \Delta C_{p} \) at \( T_{N} \) equals approximately 14J/molK which is smaller than the theoretical value 20.54J/molK given by the relation \( \Delta C(T_{N}) = 2.5R((2J + 1)^{2} - 1)/(2J + 1)^{2} + 1) \) with J = 6 appropriate for \( Tm^{3+} \) ions.
The magnetic entropy \( S_{m}(T) \) , derived from the \( C_{p}/T \) dependence, has a break in slope close to the transition temperature \( T_{N} \) with entropy reaching a value of \( R\ln2 \) at the point of break. Such a value indicates ground state being a doublet or two closely separated singlets. In the unit cell of TmAgGe, the \( Tm^{3+} \) ions are located at the crystallographic position 3g with the orthorhombic

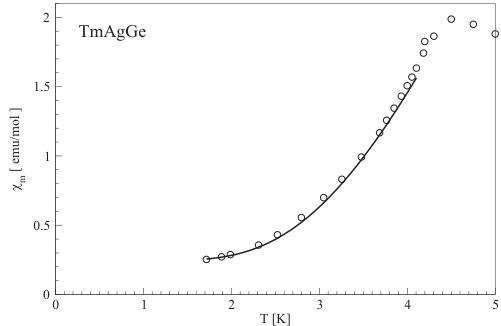
Fig. 4. The fit of the formula given by Eq. (2) to the experimental data of TmAgGe magnetic susceptibility.

Fig. 5. The fit of the formula given by Eq. (3) to the experimental data of TmAgGe specific heat.
symmetry \( C_{2v} \) (mm \( ^{2} \) ). In the crystal field potential of this symmetry the thulium \( {}^{3}H_{6} \) ground multiplet splits into several energy levels, with 13 singlets being the terminal case with total lifting of the \( 2J + 1 = 13 \) degeneracy. Such a distribution of the crystal field levels was found for isostructural TmNiAl [10]. Inelastic neutron diffraction experiment is necessary to conclude on the crystal field splitting scheme in TmAgGe.
3.5. Low temperature thermodynamic properties—AF magnons evidence
The spin-wave theory of antiferromagnetic magnons (AFM) with linear dispersion relation \( \varepsilon^{2}(k)=\varDelta^{2}+Dk^{2} \) , where \( \varDelta \) denotes an energy gap, predicts the following temperature dependence of the magnetic susceptibility [11]
\[ \chi=\frac{1}{3}(\chi_{\parallel}+2\chi_{\perp})=A+B\sqrt{\Delta T}e^{-\varDelta/T}(\varDelta-T) \quad (2) \]
where A and B are constants. It is worth noting that the parameter A is proportional to \( 1/\beta \) , where \( \beta \) is an anisotropy constant.
Fitting Eq. (2) to the experimental data of TmAgGe below 4K (see Fig. 4) gives the following parameters: A = 0.244(8) emu/mol, B = 0.491(11) emu/mol 0.16emK \( ^{2} \) and \( \varDelta = 13.2(3) \) K.
In turn, the formula predicted by the spin-wave theory for the temperature variation of the specific heat in the ordered region is given by expression
\[ C_{T r a n}=C T^{-1/2}e^{-\varDelta/T} \quad (3) \]
where C is a constant [11].
Fitting Eq. (3) to the low-temperature specific heat data of TmAgGe (see Fig. 5) yields the parameters: \( C = 1.15(29) \times 10^{3} \) JK \( ^{1/2} \) /mol and \( \varDelta = 15.7(9) \) K. Although the latter fit is of worse quality than that to the magnetic susceptibility data, the two obtained values of the energy gap \( \varDelta \) are in reasonable agreement. One may thus conclude that both the magnetic and thermodynamic characteristics of TmAgGe fulfil the predictions of the spin-wave theory for antiferromagnets. Similar description of the magnetic susceptibility and the specific was previously proposed for the isostructural compound TbAuln [12]. However, in that latter case the energy gap \( \varDelta \) obtained from the analysis was as large as 58.3 K.

Fig. 6. Differential neutron diffraction pattern of TmAgGe together with Rietveld fit and difference plot. The pattern was made as a difference between patterns collected at 1.5 and 6.1 K. The upper row of vertical ticks indicates the positions of nuclear reflections (it is plotted just as a reference because nuclear reflections are absent in differential pattern). The next row indicates the positions of reflections originating from antiferromagnetic order.
3.6. Magnetic structure
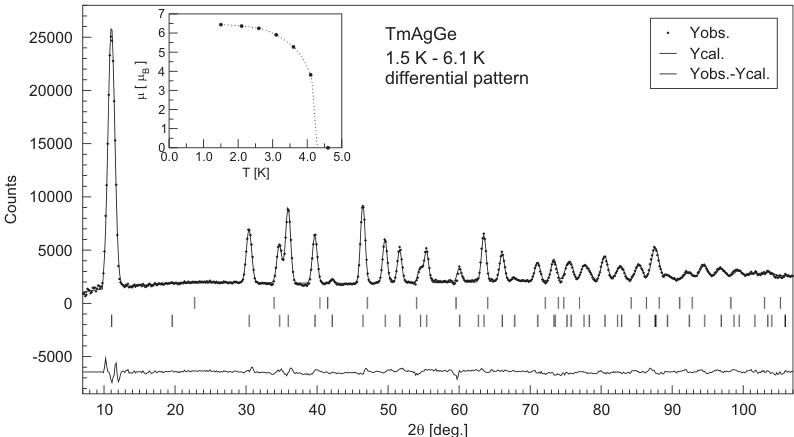
The neutron diffraction patterns of TmAgGe taken below the Néel temperature clearly reveal the presence of some additional reflections due to the magnetic ordering. The magnetic contribution can be easily extracted by making differential pattern, like the one shown in Fig. 6. All the Bragg reflections of magnetic origin can be indexed using the propagation vector \( \vec{k} = [\frac{1}{2}, 0, 0] \) . In order to reduce theoretically infinite number of possible magnetic moment arrangements a group theory analysis was performed. The magnetic structures allowed by symmetry were calculated with the use of computer program MODY [13].
In case of the space group G = P62m and the propagation vector \( \vec{k} = [\frac{1}{2}, 00] \) symmetry allows two other equivalent propagation vectors: \( \vec{k}' = [-\frac{1}{2}, 0] \) and \( \vec{k}'' = [0, \frac{1}{2}, 0] \) . It means that each of the three rare earth magnetic moments present in the unit cell, i.e. \( Tm_{1} \) at \( x_{Tm_{1}} \) , \( 0\frac{1}{2} \) , \( Tm_{2} \) at \( 1 - x_{Tm_{1}} \) , \( 1 - x_{Tm_{1}} \) , \( \frac{1}{2} \) and \( Tm_{3} \) at \( 0, x_{Tm_{1}} \) , \( \frac{1}{2} \) , where \( x_{Tm} = 0.576(2) \) (see Table 1), may propagate with different vectors. The magnetic moments of each allowed by symmetry magnetic structure have to be parallel to basic vectors (BV) of irreducible representations (IR). The basic vectors calculated for the propagation vectors \( \vec{k} \) , \( \vec{k}' \) and \( \vec{k}'' \) are listed in Table 2. For each propagation vector the atoms are divided into so-called orbits. Within one orbit the magnetic moments have to be of the same magnitude while the magnitude of the moments in the other orbit is independent (from symmetry point of view).
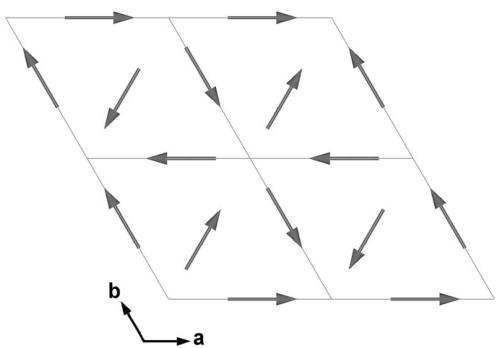
The magnetic structures constructed on the basis of the data shown in Table 2 were compared with the experimental neutron diffraction pattern. It was found that taking into account only one propagation vector one obtains non-physical results (in the magnetic structure model that accounted well for the experimental data the moment in the 2nd orbit was about \( 11 \mu_{B} \) while the moments in the 1st were of zero magnitude). Similarly, non-physical results were obtained while two different propagation vectors were considered. The only magnetic structure that fits well the experimental data and provides reasonable values of the magnetic moments has to be constructed with the use of three different propagations vectors. Particularly, \( Tm_{1} \) magnetic moment propagates with \( \vec{k}^{\prime} = [0, \frac{1}{2}, 0] \) , \( Tm_{2} \) with \( \vec{k}^{\prime} = [-\frac{1}{2}, \frac{1}{2}, 0] \) and \( Tm_{3} \) with \( \vec{k} = [\frac{1}{2}, 0, 1] \) . All the magnetic moments are confined to the basal plane. The magnetic moments directions refer to the basic vectors of \( \tau_{1} \) (or \( \tau_{1}^{\prime} \) ) in case of each propagation vector. The resulting magnetic structure, presented in Fig. 7, is a typical "triangular" magnetic structure often found in magnetically frustrated compounds. At 1.5 K the Tm magnetic moments are equal to \( 6.44(10) \mu_{B} \) . The temperature dependence of this moment is shown in the inset to Fig. 6. The refined magnetic structure parameters are summarized in Table 3.
The derived magnetic structure of TmAgGe is in line with the results of the bulk magnetic studies on single crystals \( [5,6] \) . The latter showed a periodicity of \( 60^{\circ} \) while rotating along the c-axis. That finding led to the conclusion that magnetic moments are aligned along the \( [110] \) direction and its equivalents, i.e. \( [100] \) and \( [010] \) .
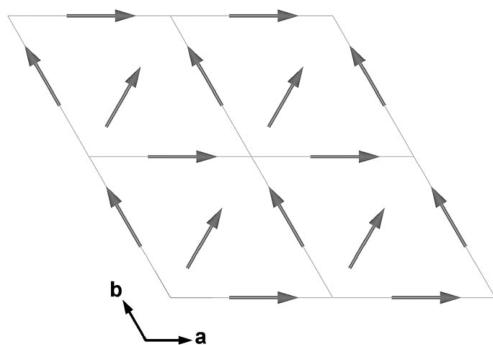
The magnetic moment of \( 6.44(10)\mu_{B} \) at 1.5K found from neutron diffraction is slightly smaller than the free \( Tm^{3+} \) ion which equals \( 7.0\mu_{B} \) , however, it is still much larger than the values found from magnetization measurements: \( 3.9\mu_{B} \) at B = 5T and T = 1.72K for polycrystalline sample (see Magnetic behavior section) and \( 4.92\mu_{B} \) at B = 7T and T = 2K (single-crystal with magnetic field applied along [110] direction [5,6]). The magnetic structure presented in Fig. 7 was derived from neutron diffraction data collected in the absence of external magnetic field. Applying an external magnetic field causes probably transition to a canted ferromagnetic structure as presented in Fig. 8. In such a structure the average Tm magnetic moment is given by formula
Basic vectors (BV) of the irreducible representations (IR).
| PV | \( \vec{k} = [\frac{1}{2}, 0, 0] \ | ||
| IR | 1st orbit | 2nd orbit | |
| Tm1 | Tm2 | Tm3 | |
| \( \tau_{1} \) | [1,0,0] | [1,1,0] | [0,1,0] |
| \( \tau_{1}^{\prime} \) | [0,1,0] | [0,-1,0] | [0,1,0] |
| \( \tilde{\tau}_{2} \) | [0,0,1] | [0,0,1] | - |
| \( \tau_{3} \) | [1,0,0] | [-1,-1,0] | [2,1,0] |
| \( \tau_{3}^{\prime} \) | [0,1,0] | [0,1,0] | [2,1,0] |
| \( \tilde{\tau}_{4} \) | [0,0,1] | [0,0,-1] | [0,0,1] |
| PV | \( \vec{k}^{\prime} = [-\frac{1}{2}, \frac{1}{\gamma}, 0] \ | ||
| IR | 1st orbit | 2nd orbit | |
| Tm1 | |||
| \( \tau_{1} \) | [1,0,0,0] | [0,1,0,0] | [1,1,0,0] |
| \( \tau_{1}^{\prime} \) | [1,0,0,0] | [0,0,-1,0] | [1,1,0,0] |
| \( t_{3}^{\prime} \) | [1,1,0,0] | [-1,-1,0,0] | [0,-1,0,0] |
| \( \tau_{4} \) | [0,0,1,0] | [0,0,1,0] | [0,0,1] |
| PV | \( \vec{k}^{\prime\prime} = [0, \frac{1}{2}, 0] \ | ||
| IR | 1st orbit | ||
| Tm2 | Tm3 | Tm1 | |
| \( \tau_{1} \) | [1,1,0,0] | [0,1,0,0] | [0,0,0,0] |
| \( \tau_{1}^{\prime} \) | [1,0,0,0] | [0,0,0,0] | |
| \( \tau_{3} \) | [1,1,0,0] | [0,-1,0,0] | [1,2,0,0] |
| [1,0,0,0] | [1,0,0,0] | [1,2,0,0] | |
| \( \tau_{4} \) | [0,0,1,0] | [0,0,-1,0] | |
| [0,0,1,0] | [0,0,-1,0] | [0,0,1] | |
Abbreviation PV denotes propagation vector.

Fig. 7. The antiferromagnetic magnetic structure of TmAgGe derived from neutron diffraction.
\( \langle\mu\rangle=(\mu/3)(1+2\cos60^{\circ}) \) . Substituting \( \mu=6.44\ \mu_{B} \) gives \( \langle\mu\rangle \) equal to \( 4.29\ \mu_{B} \) which is in reasonable agreement with the single crystal magnetometric data. The value found for polycrystalline sample is smaller which might be caused by some preferential ordering of crystallites.
Refined parameters of TmAgGe magnetic structure together with residuals for profile and integrated magnetic intensities.
| Atom | Tm1 | Tm2 | Tm3 |
| PV | \( \vec{k}' = [0, \frac{1}{2}, 0] \) | \( \vec{k}' = [-\frac{1}{2}, \frac{1}{2}, 0] \) | \( \vec{k} = [\frac{1}{2}, 0, 0] \) |
| DMM | [10 0] | [11 0] | [0 1 0] |
| \( \mu \) [ \( \mu_{B} \) ] | 6.44(10) | ||
| \( \gamma^{2} \) | 7.73 | ||
| \( R_{\text{profile}} \) (%) | 3.78 | ||
| \( R_{\text{magnetic}} \) (%) | 4.82 |
The parameters were derived from the differential neutron diffraction pattern made as difference between patterns collected at 1.5 and 6.1 K. PV denotes propagation vector while DMM direction of magnetic moment.

Fig. 8. The canted ferromagnetic structure of TmAgGe in the presence of external magnetic field (see discussion at the end of Magnetic structure subsection).
4. Summary
The ternary compound TmAgGe crystallizes in the hexagonal ZrNiAl-type crystal structure. It exhibits an antiferromagnetic ordering below 4.2 K, as derived from the magnetic susceptibility, the electrical resistivity and the specific heat data. The value of Néel temperature is in good agreement with the previously reported result. The neutron diffraction data indicate that this compound exhibits a magnetic structure with "triangular" arrangement of the Tm magnetic moments confined within the basal plane. Three different propagation vectors: \( \vec{k} = [\frac{1}{2}, 0, 0] \), \( \vec{k}' = [-\frac{1}{2}, \frac{1}{2}, 0] \), and \( \vec{k}'' = [0, \frac{1}{2}, 0] \) are necessary to describe the magnetic order. This result follows the group theory predictions and is in good agreement with the single-crystal magnetization data. The low-temperature dependencies of the magnetic susceptibility and the specific heat reveal the presence of antiferromagnetic magnons. The value of magnetic moment derived from the neutron diffraction data is smaller than the free \( Tm^{3+} \) ion value, but well accounts for the value of the average magnetic moment in canted ferromagnetic structure, expected to form in TmAgGe in the presence of strong external magnetic field.
Acknowledgements
This research project has been supported by the European Commission under the Sixth Framework Programme through the Key Action: Strengthening the European Research Area, Research Infrastructures. Contract no: RII3-CT-2003-505925 (NMI3) and by the National Scientific Network “Strongly correlated materials: preparation, fundamental research and applications”.
References
[1] G. Zanicchi, D. Mazzone, V. Contardi, R. Marazza, G. Rambaldi, D. Rossi, Gazz. Chim. Ital. 113 (1983) 257–259.
[2] G. Gibson, R. Pöttgen, R.K. Kremer, A. Simon, K.R.A. Ziebeck, J. Alloys Compd. 239 (1996) 34–40.
[3] S. Baran, M. Hofmann, J. Leciejewicz, B. Penc, M. Ślaski, A. Szytula, J. Alloys Compd. 281 (1998) 92–98.
[4] B.J. Gibson, Investigation of the physical properties of the ternary intermetallic compounds, RETGe (RE = Sc, Y, La–Lu : T = Ag, Au), Doctoral Thesis, Loughborough University, UK, 1998.
[5] E. Morosan, S.L. Bud'ko, P.C. Canfield, M.S. Torikachvili, A.H. Lacerda, J. Magn. Magn. Mater. 277 (2004) 298–321.
[6] E. Morosan, S.L. Bud'ko, P.C. Canfield, Phys. Rev. B 71 (2005) 014445.
[7] G.D. Samolyuk, S.L. Bud'ko, E. Morosan, V.P. Antropov, P.C. Canfield, J. Phys. Condens. Matter 18 (2006) 1473–1482.
[8] J. Rodríguez-Carvajal, Physica B 192 (1993) 55–69.
[9] M. Giovannini, H. Michor, E. Bauer, G. Hilscher, P. Rogl, R. Ferro, J. Alloys Compd. 280 (1998) 26–38.
[10] N.C. Tuan, V. Sechovský, M. Diviš, P. Svoboda, H. Nakotte, F.R. de Boer, N.H. Kim-Ngan, J. Appl. Phys. 73 (1993) 5677–5679.
[11] A.I. Akhiezer, V.G. Baryakhtar, M.I. Kazanov, Usp. Fiz. Nauk 71 (1960) 533.
[12] L. Gondek, A. Szytula, M. Balanda, W. Warkokci, A. Szewczyk, M. Gutowska, Solid State Commun. 136 (2005) 26–31.
[13] W. Sikora, F. Bialas, L. Pytlik, J. Appl. Crystallogr. 37 (2004) 1015–1019.