| Transition Temperature | 0.7 K |
|---|---|
| Experiment Temperature | 0.05 K |
| Parent Space Group | Fd-3m (#227) |
| Magnetic Space Group | FS-43m (#216.77) |
| Magnetic Point Group | -43m1' (31.2.116) |
| Lattice Parameters | 20.37040 20.37040 20.37040 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1088/0953-8984/16/28/l01 |
| Reference | J.R. Stewart, G. Ehlers, A.S. Wills, S.T. Bramwell and J.S. Gardner, Journal of Physics: Condensed Matter (2004) 16 L321-L326. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Gd1_1 | Gd | 4.95 | 0.0 | -4.95 | 7.00 |
| Gd1_2 | Gd | 0.0 | 0.0 | 0.0 | 0.00 |
Title
Phase transitions, partial disorder and multi-k structures in \( Gd_{2}Ti_{2}O_{7} \)
Authors
J R Stewart \( ^{1} \), G Ehlers \( ^{2} \), A S Wills \( ^{3} \), S T Bramwell \( ^{3} \) and J S Gardner \( ^{4,5} \) \( ^{1} \) Institut Max von Laue-Paul Langevin, 6 rue Jules Horowitz, 38042 Grenoble, France \( ^{2} \) SNS Project, Oak Ridge National Laboratory, 701 Scarboro Road, Oak Ridge, TN 37830, USA \( ^{3} \) Department of Chemistry, University College London, 20 Gordon Street, London WC1H 0AJ, UK \( ^{4} \) NIST Center for Neutron Research, NIST, Gaithersburg, MD 20899-8562, USA \( ^{5} \) Physics Department, Brookhaven National Laboratory, Upton, NY 11973, USA
Materials Studied
\( Gd_{2}Ti_{2}O_{7} \) (geometrically frustrated antiferromagnet) \( {}^{160}Gd_{2}Ti_{2}O_{7} \) (isotopically substituted sample, 536 mg)
Key Information
- Crystal structure / space group: Cubic, \( Fd\bar{3}m \)
- Magnetic ordering type and temperature:
- Magnetic ordering commences at \( T_{N} = 1.1 \) K.
- Second magnetic phase transition at \( T' = 0.7 \) K (more precisely \( T' = 0.725 \pm 0.025 \) K).
- Between \( T' \) and \( T_{N} \), the structure is partly ordered (consistent with a 1-k structure variant).
- Below \( T' \), the remaining spins order weakly, forming a 4-k magnetic structure.
- Interstitial spins order in a collinear pattern within the [111] plane.
- Three other spins, arranged in a ‘120°’ pattern parallel to \( \langle 110 \rangle \) in the higher temperature phase, are globally rotated by \( \sim 9^{\circ} \) within the [111] plane below \( T' \).
- In the 4-k structure, all spins are perpendicular to the local trigonal \( \langle111\rangle \) axes.
- Propagation vector(s): \( k = \frac{1}{2} \frac{1}{2} \frac{1}{2} \)
- Magnetic moments:
- Maximum ordered moment of interstitial spins: \( 1.9 \pm 0.1 \mu_{B} \) at \( T = 250 \) mK.
- Refined ordered moment of the three other spins: \( 7.0 \pm 0.1 \mu_{B} \) (close to \( Gd^{3+} \) spin-only moment of \( 7 \mu_{B} \) for \( S = 7/2 \)).
- Disordered moment per weakly ordered spin (derived from diffuse scattering): \( 5.1 \pm 0.1 \mu_{B} \).
- Lattice parameters: \( a = 10.18(1) \) Å at 300 K.
- Any other critical measured values:
- Diffuse scattering peak observed at \( 1.1\ \AA^{-1} \).
- Spin correlation parameters from diffuse scattering fits (Table 1):
- 1-k model: \( S(S+1) = 6.5(3) \), \( \langle S_{0}\cdot S_{1}\rangle/S(S+1) = +0.08(4) \), \( \langle S_{0}\cdot S_{2}\rangle/S(S+1) = +0.29(12) \).
- 4-k model: \( S(S+1) = 6.6(3) \), \( \langle S_{0}\cdot S_{1}\rangle/S(S+1) = -0.48(8) \), \( \langle S_{0}\cdot S_{2}\rangle/S(S+1) = +0.16(9) \).
- \( \chi^{2} \) for 1-k fit: 1.75; for 4-k fit: 1.20.
Synthesis Method
Not available. The paper states: "We used the sample of \( {}^{160}Gd_{2}Ti_{2}O_{7} \) (536 mg) described in detail in [6] (isotopic substitution is necessary to limit neutron absorption)." The synthesis method itself is not described in this paper but referenced to [6].
Abstract
The geometrically frustrated antiferromagnet \( Gd_{2}Ti_{2}O_{7} \) exhibits magnetic behaviour of such complexity that it poses a challenge to both experiment and theory. Magnetic ordering commences at \( T_{N} = 1.1 \) K and there is a further magnetic phase transition at \( T' = 0.7 \) K. Here we use neutron diffraction to definitively establish the nature of the phase transition at \( T' \) and the magnetic structure adopted below this temperature. Between \( T' \) and \( T_{N} \) the structure is partly ordered, as previously reported. Below \( T' \) the remaining spins order, but only weakly. The magnetic structure in this temperature range is shown to be a 4-k structure, closely related to the 1-k structure previously suggested. The 4-k and 1-k variants of the structure are distinguished by analysis of the diffuse scattering, which we believe represents a new method of solving the 'multi-k' problem of magnetic structure determination.
Main Content Summary
The paper investigates the intricate magnetic properties of the geometrically frustrated antiferromagnet \( Gd_{2}Ti_{2}O_{7} \), a material crystallizing in the cubic \( Fd\bar{3}m \) space group with a lattice parameter of \( a = 10.18(1) \) Å at 300 K. Previous studies had identified two magnetic phase transitions at \( T_{N} = 1.1 \) K and \( T' = 0.7 \) K, but the precise nature of the magnetic structures, particularly the distinction between single-k and multi-k variants, remained ambiguous due to the inherent difficulties in neutron diffraction analysis of high-symmetry systems. This study aims to definitively resolve these ambiguities, focusing on the phase transition at \( T' \) and the magnetic ground state.
The research employed neutron diffraction on a polycrystalline sample of isotopically enriched \( {}^{160}Gd_{2}Ti_{2}O_{7} \). Bragg scattering data, collected on the D20 diffractometer, confirmed magnetic reflections below \( T_{N} \), indexing on a propagation vector \( k = \frac{1}{2} \frac{1}{2} \frac{1}{2} \). A key finding was the observation of a weak magnetic reflection at \( hkl = \frac{1}{2} \frac{1}{2} \frac{1}{2} \), which vanishes above \( T' \approx 0.725 \pm 0.025 \) K. This reflection's presence below \( T' \) indicates the ordering of a subset of "interstitial" spins, which were previously thought to remain disordered. Rietveld refinement showed these interstitial spins order collinearly within the [111] plane with a weak ordered moment of \( 1.9 \pm 0.1 \mu_{B} \) at 250 mK. The remaining three-quarters of spins, which form a 120° arrangement in the higher temperature phase, exhibit a robust ordered moment of \( 7.0 \pm 0.1 \mu_{B} \) and undergo a global rotation of \( \sim 9^{\circ} \) within the [111] plane below \( T' \).
A significant contribution of this work is the novel use of magnetic diffuse scattering to distinguish between the 1-k and 4-k magnetic structures, after ruling out 2-k and 3-k variants based on unphysical moment values. Diffuse scattering data, obtained using polarization analysis on the D7 spectrometer, revealed a peak at \( 1.1\ \AA^{-1} \). This peak's position corresponds to a near-neighbor distance of disordered spins of approximately \( 3.5\ \AA \), which is consistent with the \( 3.6\ \AA \) separation in the 4-k structure but not the \( 7.2\ \AA \) in the 1-k structure. Quantitative fits of the diffuse scattering data to a model of spin correlation functions strongly favored the 4-k structure (\( \chi^{2} = 1.20 \)) over the 1-k structure (\( \chi^{2} = 1.75 \)), yielding plausible antiferromagnetic nearest-neighbor correlations for the 4-k model. The disordered moment derived from this analysis, \( 5.1 \pm 0.1 \mu_{B} \), also aligned well with the difference between the full and ordered moments.
The paper concludes by discussing the implications of the established 4-k structure, where all spins are perpendicular to their local trigonal \( \langle111\rangle \) axes, in the context of theoretical models and other experimental observations. This local symmetry is argued to be more physically reasonable for \( Gd^{3+} \) in the pyrochlore structure. The findings successfully reconcile previous discrepancies between calorimetric and neutron scattering studies, providing a definitive experimental determination of the magnetic ground state and introducing a valuable new methodology for resolving multi-k ambiguities in magnetic structure determination.
Conclusion
In summary, our main results are: (1) between \( T_{N} = 1.1 \) K and \( T' = 0.7 \) K the magnetic structure of \( Gd_{2}Ti_{2}O_{7} \) is consistent with that previously described [6]; (2) the phase transition at \( T' \) corresponds to very weak ordering of the subset of spins that were previously thought to remain completely disordered; (3) the magnetic structure at \( T = 46 \) mK is in fact a 4-k structure, not the 1-k structure previously proposed. We have thus fully reconciled the results of calorimetric [7, 8] and neutron scattering studies of this material and paved the way for a full theoretical understanding of its properties [10, 11]. Furthermore, we have demonstrated what we believe to be the first case where single and multi-k variants of a magnetic structure are distinguished by analysis of the diffuse scattering. This may represent a useful addition to the existing experimental methodology.
Phase transitions, partial disorder and multi-k structures in \( Gd_{2}Ti_{2}O_{7} \)
This article has been downloaded from IOPscience. Please scroll down to see the full text article.
2004 J. Phys.: Condens. Matter 16 L321
(http://iopscience.iop.org/0953-8984/16/28/L01)
View the table of contents for this issue, or go to the journal homepage for more
Download details:
IP Address: 136.159.235.223
The article was downloaded on 28/04/2013 at 09:22
Please note that terms and conditions apply.
LETTER TO THE EDITOR
Phase transitions, partial disorder and multi-k structures in \( Gd_{2}Ti_{2}O_{7} \)
J R Stewart \( ^{1} \) , G Ehlers \( ^{2} \) , A S Wills \( ^{3} \) , S T Bramwell \( ^{3} \) and J S Gardner \( ^{4,5} \)
\( ^{1} \) Institut Max von Laue-Paul Langevin, 6 rue Jules Horowitz, 38042 Grenoble, France
\( ^{2} \) SNS Project, Oak Ridge National Laboratory, 701 Scarboro Road, Oak Ridge, TN 37830, USA
\( ^{3} \) Department of Chemistry, University College London, 20 Gordon Street, London WC1H 0AJ, UK
\( ^{4} \) NIST Center for Neutron Research, NIST, Gaithersburg, MD 20899-8562, USA
\( ^{5} \) Physics Department, Brookhaven National Laboratory, Upton, NY 11973, USA
Received 12 March 2004 Published 2 July 2004
Online at stacks.iop.org/JPhysCM/16/L321
doi:10.1088/0953-8984/16/28/L01
Abstract
The geometrically frustrated antiferromagnet \( Gd_{2}Ti_{2}O_{7} \) exhibits magnetic behaviour of such complexity that it poses a challenge to both experiment and theory. Magnetic ordering commences at \( T_{N} = 1.1 \) K and there is a further magnetic phase transition at \( T' = 0.7 \) K. Here we use neutron diffraction to definitively establish the nature of the phase transition at \( T' \) and the magnetic structure adopted below this temperature. Between \( T' \) and \( T_{N} \) the structure is partly ordered, as previously reported. Below \( T' \) the remaining spins order, but only weakly. The magnetic structure in this temperature range is shown to be a 4-k structure, closely related to the 1-k structure previously suggested. The 4-k and 1-k variants of the structure are distinguished by analysis of the diffuse scattering, which we believe represents a new method of solving the 'multi-k' problem of magnetic structure determination.
The technique of neutron diffraction enables the direct determination of complex magnetic structures, but it can be ambiguous when applied to systems of high symmetry, where the problem of 'multi-k' structures arises \( [1] \) . Alternative structures, described by one or several symmetry-related propagation vectors k, give identical diffraction patterns as a result of orientational averaging in powders or 'k-domain' formation in single crystals. To distinguish such structures is difficult, both experimentally (where applying a perturbation can affect the structure) and theoretically (where the structures are often degenerate to several orders in the Landau expansion of the free energy \( [1] \) ). It is these very difficulties that make the problem of multi-k structures an interesting and fundamentally important scientific challenge (see, for example, \( [2–4] \) ).
A case in point is the highly frustrated cubic antiferromagnet \( Gd_{2}Ti_{2}O_{7} \) \( [5–8] \) . This material crystallizes in \( Fd\bar{3}m \) with \( a = 10.18(1) \) Å at 300 K. The \( Gd^{3+} \) spins (spin
\( S = 7/2 \) , make up a pyrochlore lattice of corner-linked tetrahedra, which frustrates the dominant near neighbor antiferromagnetic interactions. \( Gd_{2}Ti_{2}O_{7} \) has a magnetic transition at \( T_{N} = 1.1 \) K [5]. On the basis of powder neutron diffraction, the magnetic structure at T = 50 mK was described as a partly ordered single-k structure, but multi-k variants were not explicitly excluded [6]. Subsequent specific heat investigations demonstrated a second transition at \( T' = 0.7 \) K [7] as well as vanishing entropy in the ground state [8]—suggesting that the neutron diffraction study might be incomplete. At a theoretical level, \( Gd_{2}Ti_{2}O_{7} \) approximates the Heisenberg antiferromagnet with strong dipole–dipole coupling [5, 9], but justification for the experimental magnetic structure has proved surprisingly difficult, and it can be considered to be an important test case [9–11].
To help solve the problem, we have performed further neutron investigations of polycrystalline \( Gd_{2}Ti_{2}O_{7} \) as well as measurements of the diffuse scattering arising from the previously reported magnetic disorder [6]. We used the sample of \( {}^{160}Gd_{2}Ti_{2}O_{7} \) (536 mg) described in detail in [6] (isotopic substitution is necessary to limit neutron absorption). Powder diffraction data were measured on the D20 diffractometer at the ILL, Grenoble, using an incident wavelength of 2.4 Å. In order to refine the magnetic structure, background and nuclear Bragg peaks obtained from a high temperature pattern were subtracted from the data sets.
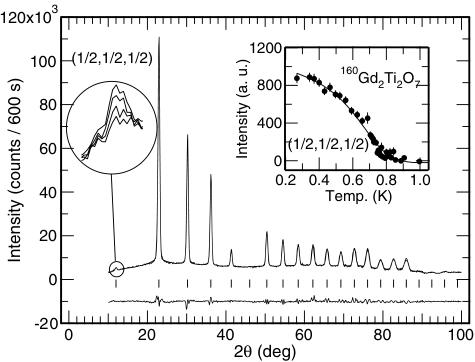
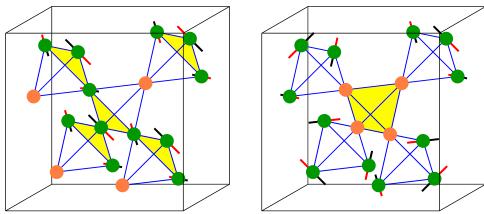
As expected, magnetic Bragg reflections were observed at temperatures below \( T_{N} = 1.1 \) K. These index on the propagation vector \( k = \frac{1}{2} \frac{1}{2} \frac{1}{2} \) , as previously reported [6], but the D20 data reveal a subtle feature that was outside the wavevector range of the previous experiment: the presence of a weak reflection at \( hkl = \frac{1}{2} \frac{1}{2} \frac{1}{\frac{1}{2}} \) . The temperature dependence of this reflection is shown in the inset of figure 1. It disappears at about \( T' = 0.725 \pm 0.025 \) K, corresponding to the transition observed in the specific heat [7]. Above that temperature the data are perfectly consistent with the magnetic structure described in [6]. This 1-k structure is best pictured if the pyrochlore lattice is described as [111] 'Kagomé' planes separated by 'interstitial' sites that form a distinct fcc Bravais sublattice. There is 'q = 0' type order within the Kagomé planes and spin disorder on the interstitial sites (figure 2). Bragg diffraction cannot distinguish this 1-k structure from its 2, 3 and 4-k variants: however, those multi-k possibilities can always be generated from their related 1-k structure [1], so for the moment it is convenient to retain the 1-k structure as a working model.
The \( \frac{1}{2}\frac{1}{2}\frac{1}{2} \) reflection is important because its structure factor is finite only if the interstitial spins are ordered. Hence we can immediately identify the transition reported in [7] as ordering of the interstitial spin: this also explains the zero entropy reported in [8]. Rietveld refinement (figure 1) shows that the interstitial spin orders in a collinear pattern within the [111] plane with a maximum ordered moment of only \( 1.9 \pm 0.1 \mu_{B} \) at \( T = 250 mK \) . The three other spins, parallel to \( \langle 110 \rangle \) in a ‘120°’ arrangement in the higher temperature phase, are globally rotated by an angle of \( \sim 9^{\circ} \) within the [111] plane. They have a refined ordered moment of \( 7.0 \pm 0.1 \mu_{B} \) , close to the spin-only moment of \( 7 \mu_{B} \) expected for \( Gd^{3+} \) with \( S = 7/2 \) . Note that powder diffraction cannot determine the spin direction of the interstitial spin within the [111] plane but it can determine the direction of the three planar spins with respect to \( \langle 110 \rangle \) —a departure from the rules enunciated by Shirane [12] which are applicable to collinear structures only.
The results of [6] implied that roughly \( \frac{1}{4} \) of Gd spins are either statically or dynamically disordered at \( T = 50 mK \) . We now see that this fraction corresponds to the disordered component of the \( \frac{1}{4} \) of spins that are only weakly ( \( \sim27\% \) ) ordered (figure 2). The remaining \( \frac{3}{4} \) of spins are essentially fully ordered by 250 mK, consistent with [6]. Transforming the 1-k structure defined above, we can generate several 2-k, 3-k and 4-k structures that give identical diffraction patterns. However the 2-k and 3-k structures can be ruled out because the refined

Figure 1. Rietveld fit at 250 mK to magnetic-only scattering (magnetic R-factor 4%; the lower line is observed minus calculated intensity). Highlighted on the left of the main figure \( \frac{1}{2}\frac{1}{2}\frac{1}{2} \) magnetic reflection at 420 mK, 540 mK, 670 mK and 750 mK (in order of decreasing intensity). Inset: intensity versus temperature of this reflection, which disappears near the \( T^{\prime} \approx 0.7 \) K phase transition reported in [7].

Figure 2. Comparison of (left) the 1-k structure and (right) its 4-k variant. In each structure the four \( Gd^{3+} \) ions coloured orange are shown as carrying no thermally averaged moment. The phase transition at \( T' = 0.7 \) K involves weak ordering of these four spins and a small canting of the remaining spins away from the positions shown. At \( T \ll 0.7 \) K, only these ions carry a disordered spin component.
moments on some \( Gd^{3+} \) ions come out as much greater than \( 7 \mu_{B} \) , which is unphysical. This leaves only the 1-k and 4-k structures to be distinguished.
These two structures are compared in figure 2. If the pyrochlore unit cell is described as four 'up' tetrahedra, then the 4-k structure consists of three fully ordered spin tetrahedra (with moment \( 7.0 \mu_{B}/spin \) ) and one weakly ordered spin tetrahedron ( \( 1.9 \mu_{B}/spin \) ). These derive, respectively, from the 'planar' and 'interstitial' spin sets of the 1-k structure. In the 4-k structure, all spins (in both sets) are perpendicular to the local trigonal \( \langle111\rangle \) axes (that connect the vertices of the tetrahedra to their centres), while in the 1-k structure the spins are perpendicular to a single global [111] crystallographic direction. However, the disordered spin components—which are associated with only the weakly ordered set—have a completely different spatial distribution in the 1-k and 4-k structures. In the 1-k structure, nearest neighbour disordered spin components are separated by \( 7.2 \AA \) , while in the 4-k structure they are separated


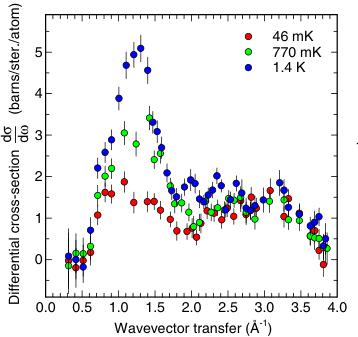
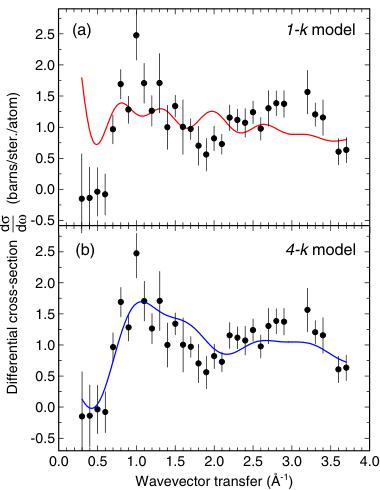
Figure 3. Left: magnetic diffuse scattering measured on D7 as a function of temperature. Right: fits of the \( T = 46 \, mK \) data to the disordered component of (a) the 1-k and (b) the 4-k structures (see figure 2). The data have been binned to \( \Delta Q = 0.1 \, \AA^{-1} \) and fitted to equation (1), using two near neighbour shells (n = 1, 2) and three adjustable parameters: \( (S_{0} \cdot S_{1}) \) , \( (S_{0} \cdot S_{2}) \) and \( S(S + 1) \) . Results of the fits are shown in table 1.
by 3.6 Å. The magnetic diffuse neutron scattering from the two structures must therefore be substantially different.
The diffuse background to the D20 data (not illustrated) revealed a peak at \( 1.1\ \AA^{-1} \) . This peak is typical of pyrochlores [13] and arises from the dominant near neighbour spin correlation. Naively one can invert the peak wavevector \( Q_{max} \) with the relation \( R_{nn} = 4.5/Q_{max} \) (from equation (1), below) where \( R_{nn} \) is the near-neighbour distance of the disordered spins. In the present case this suggests \( R_{nn} = 3.5\ \AA \) , much closer to the \( R_{nn}^{4} = 3.6\ \AA \) of the 4-k structure than to the \( R_{nn}^{1} = 7.2\ \AA \) of the 1-k structure. To be certain that the \( 1.1\ \AA^{-1} \) peak arises from magnetic diffuse scattering, we have isolated the purely magnetic component using polarization analysis techniques (at the cost of poorer statistics). Data were collected on the D7 diffuse scattering spectrometer at the ILL, Grenoble, using three-directional (XYZ) neutron polarization analysis [14] in order to separate the magnetic diffuse scattering from nuclear coherent, nuclear spin-incoherent and background contributions. The data were collected using an incident wavelength of \( 3.1\ \AA \) . The lowest temperature reached in this experiment was 46 mK, but from the magnetic Bragg scattering it is clear that there is no change in magnetic structure between this temperature and the base temperature of the D20 experiment, 250 mK.
Figure 3 shows the D7 diffuse scattering data. They confirm the presence of the peak at \( 1.1 \, \AA \) at all measured temperatures. To analyse the data further we use the expression for the magnetic cross section [15]:
\[ \left(\frac{\mathrm{d}\sigma}{\mathrm{d}\Omega}\right)_{\mathrm{M a g}}=\frac{2}{3}\left(\frac{r_{0}\gamma}{2}\right)^{2}|f(Q)|^{2}g^{2}S(S+1)\sum_{n}\frac{\langle\mathbf{S}_{0}\cdot\mathbf{S}_{\mathrm{n}}\rangle}{S(S+1)}N_{n}\frac{\sin(Q R_{n})}{Q R_{n}} \quad (1) \]
Table 1. Spin correlation parameters (equation (1)) estimated from the fits to the diffuse scattering shown in figure 3.
| Model | S(S+1) | \( \langle S_{0}\cdot S_{1}\rangle \) | \( \langle S_{0}\cdot S_{2}\rangle \) | \( \chi^{2} \) |
| S(S+1) | S(S+1) | |||
| 1-k | 6.5(3) | +0.08(4) | +0.29(12) | 1.75 |
| 4-k | 6.6(3) | -0.48(8) | +0.16(9) | 1.20 |
where the factor \( \frac{2}{3}\left(\frac{\omega\gamma}{2}\right)^{2}=0.049 \) b, g=2 and \( R_{n} \) and \( N_{n} \) are the radii and coordination numbers of the nth near neighbour shells, respectively.
The crudest approximation is to include spin correlations over the near neighbour shell only. Here, the 4-k structure produces a reasonable fit while the 1-k structure cannot fit the data. A more flexible description includes the first two shells. These fits, using the spin correlation functions and \( S(S+1) \) as adjustable parameters, are shown in figure 3 and summarized in table 1. The 4-k structure is again acceptable for such a crude model and gives plausible spin correlation functions: antiferromagnetic nearest neighbours and decreasing with distance. \( S(S+1)=6.6 \) implies a disordered moment per (weakly ordered) spin of \( \sqrt{4\times6.6}=5.1\pm0.1\mu_{B} \) in good agreement with the value \( 7.0-1.9=5.1\mu_{B} \) expected from the D20 refinement at \( T=250mK \) . It is also clear that the 1-k structure is ruled out by this analysis. Even with three adjustable parameters, the best fit is very poor and some parameters derived are implausible: the fit drives the near neighbour spin correlation (which produces a strong peak at \( 0.7\ \AA^{-1} \) ) to zero and replaces it with an unlikely ferromagnetic second near neighbour correlation. Further attempts to fit the data utilized the 'reverse Monte Carlo' method, a very flexible fitting procedure that uses the spins as independent parameters to model the data according to equation (1). Once again this only produced a convincing fit to the 4-k structure, the fit to the 1-k structure remaining very poor.
We have thus obtained strong evidence in favour of the 4-k structure at T = 46 mK. At high temperatures and above \( T_{N} \) (e.g. at 1.4 K, see figure 3) the diffuse scattering pattern is qualitatively the same, but more intense. This is consistent with the near neighbour antiferromagnetic correlation at \( R_{nn}^{4} = 3.6 \AA \) remaining the dominant correlation for all disordered spin components in the sample, as would be expected [5]. Because of this, it is no longer possible to make a clear distinction between the two structures in the temperature range \( T' < T < T_{N} \) where all spins carry a significant disordered component.
The 4-k structure with \( k = \frac{1}{2} \frac{1}{2} \frac{1}{2} \) established here is not the same as the ground state of the Heisenberg Hamiltonian with strong dipolar interactions calculated by Palmer and Chalker [9] which has k = 0. However, the adoption of a \( k = \frac{1}{2} \frac{1}{2} \cdot \frac{1}{2} \) structure below \( T_{N} \) has been justified theoretically for a Hamiltonian with added second and third neighbour couplings [10]. This propagation vector is also selected even without these extra terms, but only in a very narrow temperature range [11]. As shown in this paper, the real material has a fully ordered 4-k structure below \( T' \) and a partially ordered structure of unknown multiplicity above this temperature. In the notation of [10] these correspond to a 4-k variant of the 'D' structure and a variant of the 'B' structure respectively. For a detailed comparison with experiment it will be necessary to calculate the stability of multi-k structures. In this context, we note that the 4-k structure found experimentally would seem more reasonable than the alternative 1-k structure: 3/8 of tetrahedra in the 4-k structure are in the ground state spin configuration of a single tetrahedron [9] while none of the tetrahedra of the 1-k structure are. Perhaps more importantly, every ordered spin in the 4-k structure is perpendicular to its local trigonal axis, which is the axis of point symmetry and crystal field quantization axis of the pyrochlore structure. The dipolar couplings and any weak single ion anisotropy [18] must be symmetric.
with respect to this axis, so it is reasonable to expect that the ordered spin structure will also have this local symmetry. In contrast, the global \( [111] \) axis of the 1-k structure has no local significance for three quarters of the ordered spins.
Bearing these remarks in mind, it would be useful to re-examine the results of Mößbauer \( [16] \) and ESR measurements \( [17] \) . The former support the spins being perpendicular to the local trigonal axis, consistent with the 4-k structure established here. The results of the ESR study \( [17] \) are much less easy to reconcile, either with the present neutron scattering or the recent bulk magnetization study of Petrenko et al \( [8] \) . It was suggested in \( [17] \) that \( Gd_{2}Ti_{2}O_{7} \) has a unique \( [111] \) axis with uniaxial magnetic anisotropy of 16 K. This proposition is compatible with the 1-k structure, but is not supported by crystallographic or magnetometry evidence, nor seemingly consistent with the typical anisotropy of \( Gd^{3+} \) , \( \sim0.3 \) K \( [18] \) . It should also be noted that the ESR results were obtained in high field, at \( T > 4.2 \) K, so may not be directly comparable with our results.
In summary, our main results are: (1) between \( T_{N} = 1.1 \) K and \( T' = 0.7 \) K the magnetic structure of \( Gd_{2}Ti_{2}O_{7} \) is consistent with that previously described [6]; (2) the phase transition at \( T' \) corresponds to very weak ordering of the subset of spins that were previously thought to remain completely disordered; (3) the magnetic structure at \( T = 46 \) mK is in fact a 4-k structure, not the 1-k structure previously proposed. We have thus fully reconciled the results of calorimetric [7, 8] and neutron scattering studies of this material and paved the way for a full theoretical understanding of its properties [10, 11]. Furthermore, we have demonstrated what we believe to be the first case where single and multi-k variants of a magnetic structure are distinguished by analysis of the diffuse scattering. This may represent a useful addition to the existing experimental methodology.
It is a pleasure to thank S Pujol for technical support. STB thanks P J Brown, K A McEwen and M Wilson for useful comments. GE acknowledges support by the Spallation Neutron Source Project (SNS). SNS is managed by UT-Battelle, LLC, under contract DE-AC05-00OR22725 for the US Department of Energy. JSG acknowledges support by Brookhaven, US Department of Energy contract DE-AC02-98CH10886. JSG and STB were partially supported by a NATO Collaborative Linkage Grant, reference number PST.CLG.978705.
References
[1] Rossat-Mignod J 1987 Neutron scattering Methods in Experimental Physics vol 23C, ed K Skjold and D L Price (New York: Academic) p 69
[2] Forgan E M, Gibbons E P, McEwen K A and Fort D 1989 Phys. Rev. Lett. 62 470
[3] Longfield M J, Paião A J, Bernhoeft N and Lander G H 2002 Phys. Rev. B 66 054417
[4] Ader J-P 2002 Phys. Rev. B 66 174414
[5] Raju N P, Dion M, Gingras M J P, Mason T E and Greedan J E 1999 Phys. Rev. B 59 14489
[6] Champion J D M, Wills A S, Fennell T, Bramwell S T, Gardner J S and Green M A 2001 Phys. Rev. B 64 140407(R)
[7] Ramirez A P, Shastry B S, Hayashi A, Krajewski J J, Huse D A and Cava R J 2002 Phys. Rev. Lett. 89 067202
[8] Petrenko O A, Lees M R, Balakrishnan G and Paul D McK 2003 Preprint cond-mat/0307152
[9] Palmer S E and Chalker J T 2000 Phys. Rev. B 62 488
[10] Cepas O and Shastry B S 2003 Preprint cond-mat/0306638
[11] Enjalran M and Gingras M J P 2003 Preprint cond-mat/0307152
[12] Shirane G 1959 Acta Crystallogr. 12 282
[13] Reimers J N 1992 Phys. Rev. B 46 193
[14] Schärpf O and Capellmann H 1993 Phys. Status Solidi a 135 359
[15] Rainford B D 1982 J. Physique 43 C7
[16] Bonville P et al 2003 J. Phys.: Condens. Matter 15 7777
[17] Hassan A K, Lévy L P, Darie C and Strobel P 2003 Phys. Rev. B 67 214432
[18] Buckmaster H A and Shing Y H 1973 Phys. Status Solidi a 12 467