| Transition Temperature | 310 K |
|---|---|
| Experiment Temperature | 2 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | I4/m (#87) |
| Magnetic Space Group | C2' (#5.15) |
| Magnetic Point Group | 2' (3.3.8) |
| Lattice Parameters | 8.01500 8.01500 5.49360 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1103/PhysRevB.102.180403 |
| Reference | X. Liu, K. M. Taddei, S. Li, W. Liu, N. Dhale, R. Kadado, D. Berman, C. Dela Cruz, B. Lv, PHYSICAL REVIEW B (2020) 102 180403(R) |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Fe1_1 | Fe | -1.98 | 0.67 | 0.0 | 2.09 |
| Fe1_2 | Fe | 1.98 | 0.67 | 0.0 | 2.09 |
Canted antiferromagnetism in the quasi-one-dimensional iron chalcogenide BaFe₂Se₄
Xiaoyuan Liu \( ^{1} \) , Keith M. Taddei, \( ^{2} \) Sheng Li, \( ^{1} \) Wenhao Liu, \( ^{1} \) Nikhil Dhale, \( ^{1} \) Rashad Kadado, \( ^{1} \) Diana Berman, \( ^{3} \) Clarina Dela Cruz, \( ^{2} \) and Bing Lv \( ^{1,4,*} \)
\( ^{1} \) Department of Physics, University of Texas at Dallas, Richardson, Texas 75080, USA
\( ^{2} \) Neutron Scattering Division, Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA
\( ^{3} \) Department of Materials Science and Engineering, University of North Texas, Denton, Texas 76203, USA
\( ^{4} \) Department of Materials Science and Engineering, University of Texas at Dallas, Richardson, Texas 75080, USA
We report the synthesis and physical properties studies of quasi-one-dimensional (quais-1D) iron chalcogenide \( BaFe_{2}Se_{4} \) which shares the \( FeSe_{4} \) tetrahedra building motif commonly seen in the iron chalcogenide superconductors. A high-quality polycrystalline sample was achieved by solid-state reaction method and characterized by x-ray diffraction, electrical resistivity, magnetic susceptibility, and neutron diffraction measurements. \( BaFe_{2}Se_{4} \) is a narrow gap semiconductor that magnetically orders at \( \sim310 \) K. Both neutron powder diffraction results and isothermal M-H loops suggest a canted antiferromagnetic structure where Fe sublattices are antiferromagnetically ordered along the c-axis quasi-1D chain direction, resulting in a net ferromagnetic moment in the perpendicular direction along the a axis with tilted angle of \( 18.7^{\circ} \) towards the b axis.
DOI: 10.1103/PhysRevB.102.180403
The discovery of iron-based superconductors \( [1,2] \) has significantly changed the landscape of unconventional superconductivity in the past decade. Among all the iron-based superconductors, two major chalcogenide-based families have been intensively studied. First, the FeSe, with the simplest crystal structure and bulk superconductivity at 8 K at ambient pressure \( [3,4] \) and at 37 K under high pressure \( [5–9] \) , has caught particular research interest in the past few years due to the significantly enhanced interfacial superconductivity with \( T_{c} \) up to 65 K found in the epitaxial single-layer FeSe/SrTiO \( _{3} \) system \( [10–15] \) . The second major family is alkali metal (A = K, Rb, Cs, and Tl) intercalated \( A_{1-x}Fe_{2-y}Se_{2} \) superconductors with \( T_{c} \sim 30 \) K \( [16–22] \) where the interplay of vacancy order, magnetism, orbital-selective Mott phase, and superconductivity have been intensively studied \( [22–26] \) . New chemical intercalation routes \( [27–33] \) also result in several new superconductors with higher \( T_{c} \) such as \( \mathrm{Li_{x}(NH_{2})_{y}(NH_{3})_{1-y}Fe_{2}Se_{2}} \) ( \( x \sim 0.6; y \sim 0.2 \) ) and \( (\mathrm{Li,Fe})OHFeSe \) . Nevertheless, the essential charge-carrier layers of these chalcogenide superconductor, two-dimensional (2D) \( Fe_{2}Se_{2} \) square lattices formed by the edge-sharing \( FeSe_{4} \) tetrahedra, are the fundamental building blocks of all the Fe-based superconductors.
The spin-ladder compound \( BaFe_{2}Se_{3} \) is structurally related to the iron chalcogenide superconductors mentioned above, but with a reduced dimensionality. The structure consists of the same building motif, edge-sharing \( FeSe_{4} \) tetrahedra, but stacked along the b axis thus forming unique quasi-one-dimensional (quasi-1D) double chains of \( [Fe_{2}Se_{3}] \) instead of the 2D \( [Fe_{2}Se_{2}] \) lattice seen in the iron chalcogenide superconductors. It exhibits unique spin-ladder magnetic structure and long-range-ordered antiferromagnetic order below \( T_{N} \sim 250 \) K, and short-range magnetic correlations at room temperature [34,35]. The antiferromagnetism changes from block type in \( BaFe_{2}Se_{3} \) to stripe type in \( BaFe_{2}S_{3} \) , \( KFe_{2}Se_{3} \) , and \( CsFe_{2}Se_{3} \) [36–38]. Interestingly, superconductivity has been reported in both \( BaFe_{2}Se_{3} \) and \( BaFe_{2}S_{3} \) compounds under high pressure, with \( T_{c} \sim 11 \) K [39] above 10 GPa for \( BaFe_{2}Se_{3} \) , and \( T_{c} \sim 24 \) K above 10 GPa for \( BaFe_{2}S_{3} \) [40], respectively. They are the only reported materials so far to exhibit a superconducting phase under pressure in this spin-ladder family. This is rather intriguing as the superconductivity in \( BaFe_{2}Se_{3} \) emerges near a possible orbital-selective Mott insulator [39], which might provide additional insight into the understanding of the 2D iron chalcogenide superconductors.
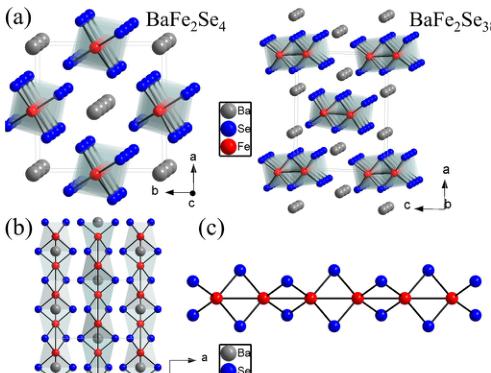
\( BaFe_{2}Se_{4} \) is another new quasi-1D iron chalcogenide based on the \( FeSe_{4} \) tetrahedra building motif but with a simpler and different structure from that of the \( BaFe_{2}Se_{3} \) compound. The difference between the two crystal structures of \( BaFe_{2}Se_{4} \) and \( BaFe_{2}Se_{3} \) is shown in Fig. 1(a). Unlike the spin-ladder double chains in the \( BaFe_{2}Se_{3} \) , the quasi-1D chain in the \( BaFe_{2}Se_{4} \) consists only of single chains of edge-sharing \( FeSe_{4} \) tetrahedra along the c axis separated by Ba atoms. Figures 1(b) and 1(c) are highlighting the quasi-1D chain along different directions. The interlayer chains are well separated from each other, with a Fe–Fe distance between the interlayer neighboring 1D Fe chains of 5.663(1) Å and the closest Se–Se distance of 3.489(8) Å. On the other hand, within the quasi-1D chain [Fig. 1(c)], the Fe–Fe interchain distance is 2.742(9) Å and the Fe–Se distance within the \( FeSe_{4} \) tetrahedra is 2.349(5) Å. Both are pretty comparable with the distances in the \( BaFe_{2}Se_{3} \) and other iron chalcogenide superconductors. The isostructural S analog \( Ba_{1+x}Fe_{2}S_{4} \) , which has interesting infinitely adaptive structural features, has been studied previously where


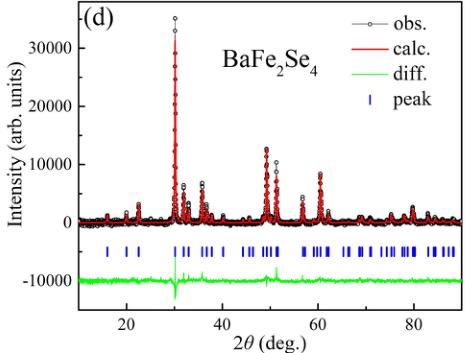
FIG. 1. (a) Schematic crystal structure of \( BaFe_{2}Se_{4} \) and \( BaFe_{2}Se_{3} \) . (b) View from the b axis for \( BaFe_{2}Se_{4} \) . (c) Detailed microstructure of infinite chains of edge-sharing \( FeSe_{4} \) tetrahedra along the c axis for \( BaFe_{2}Se_{4} \) . (d) X-ray diffraction pattern and Rietveld refinement results of the \( BaFe_{2}Se_{4} \) at room temperature.
physical properties of \( Ba_{1+x}Fe_{2}S_{4} \) varies with the excess of Ba atoms [41–47].
However, to date, only the structural determination based on small grains ( \( \sim50\ \mu m \) ) has been reported for this compound [48]. Previous synthesis attempts from pure elements and repeated regrinding/annealing using different temperature profiles up to \( 1100\ ^{\circ}C \) do not yield an x-ray powder pure phase [48]. Therefore, no systematic transport and magnetic characterizations have been carried out on this compound. Band structure calculations, on the other hand, suggest the Fermi level of this compound lies near a local minimum in the density of states and an overall metallic behavior for \( BaFe_{2}Se_{4} \) [48].
In this work, we present our studies on high-quality and x-ray pure phase \( BaFe_{2}Se_{4} \) polycrystalline samples. The \( BaFe_{2}Se_{4} \) polycrystalline sample was synthesized by the solid-state reaction method shown in the Supplemental Material [49]. The x-ray diffraction (XRD) pattern of the synthesized \( BaFe_{2}Se_{4} \) sample and corresponding structural

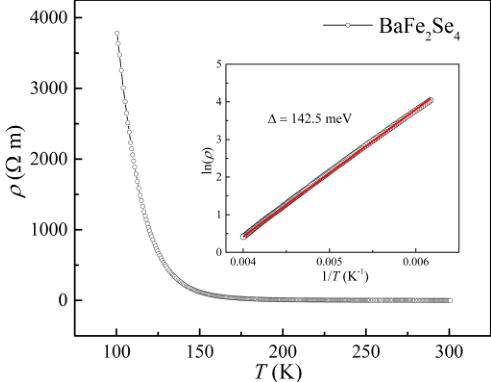
FIG. 2. Temperature dependence of resistivity on \( BaFe_{2}Se_{4} \) and the inset shows fitting results from \( \ln(\rho) \) vs 1/T.
refinement results are presented in Fig. 1(d) and Table SI in the Supplemental Material [49] (see, also, Refs. [50,51] therein). All diffraction peaks for \( BaFe_{2}Se_{4} \) can be well indexed and no impurities are detected within XRD resolution. Together with the good refinement values \( R = 1.71\% \) and \( R_{wp} = 2.52\% \) , this suggests the high quality of our synthesized \( BaFe_{2}Se_{4} \) powder sample.
The temperature-dependent electrical resistivity data are shown in Fig. 2. The resistivity shows an overall semiconducting behavior, which is in contradiction with previous band structure calculations [48], but in agreement with the measurement reported for its isostructural counterpart \( BaFe_{2}S_{4} \) [52]. We note that the resistivity value at room temperature is \( 35.5\ \Omega\ cm \) , which is slightly larger than that of the spin-ladder compound \( BaFe_{2}Se_{3} \) ( \( 17\ \Omega\ cm \) ) [53]. The resistivity can be fit quite well using thermal activation model \( \rho=\rho_{0}\exp(\Delta/k_{B}T) \) , where \( \rho_{0} \) is a prefactor, and \( k_{B} \) is the Boltzmann constant. The inset of Fig. 2 shows the results of linear fitting of \( \ln(\rho) \) vs 1/T. The activation energy estimated from the fitting is \( \Delta=142.5\ meV \) , which is comparable to the reported gap value of \( BaFe_{2}Se_{3} \) ( \( \sim180\ meV \) ) [53].
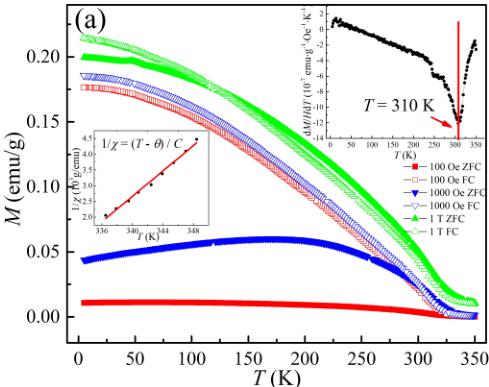
The temperature dependence of the magnetization of \( BaFe_{2}Se_{4} \) from 5 to 350 K under different magnetic fields is presented in Fig. 3(a). A spontaneous magnetization appears at \( \sim310 \) K. Together with the clear splitting of magnetization between the zero-field-cooled (ZFC) and field-cooled (FC) modes, indicates the existence of a ferromagnetic component below the transition temperature. The \( M_{ZFC} \) and \( M_{FC} \) splitting becomes weaker with an increasing magnetic field, eventually nearly overlapping at 1 T. The magnetization starts to saturate to a nearly constant plateau below about 50 K. Increasing the applied magnetic field increases the absolute value of the magnetization, but the change of transition temperature \( T_{c} \) is rather small (<5 K). The exact transition temperature is tracked best in the temperature derivative of the normalized magnetization \( dM/HdT \) , depicted in the inset of Fig. 3(a). No traceable magnetic transition at \( \sim120 \) K from Fe-Se binary phase ( \( Fe_{7}Se_{8} \) ) is observed, further suggesting the success of


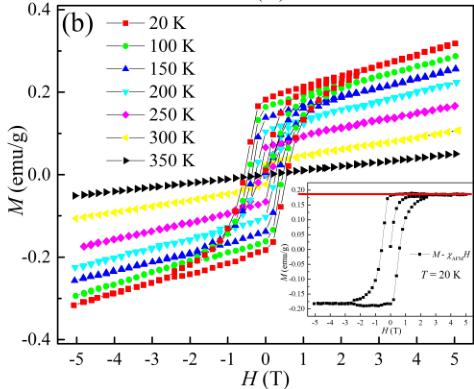
FIG. 3. (a) Magnetization as a function of temperature \( M(T) \) of \( BaFe_{2}Se_{4} \) measured with ZFC and FC modes at different applied magnetic fields. The top right inset shows the transition temperature determined from the \( dM/HdT \) vs T plot. The left inset shows the Curie-Weiss fitting over the high-temperature range. (b) Magnetization as a function of field \( M(H) \) of \( BaFe_{2}Se_{4} \) measured at different temperatures from 20 to 350 K. The inset shows the fitting data after subtracting the linear antiferromagnetic contribution \( \chi_{AFM}H \) at 20 K.
our synthetic approach for high-quality samples. A small blip at \( \sim50 \) K in ZFC data at 1 T was observed which is due to some trapped oxygen in the powder samples, which is a nonintrinsic signal of the \( BaFe_{2}Se_{4} \) sample. To obtain the effective magnetic moment of Fe in \( BaFe_{2}Se_{4} \) , we performed Curie-Weiss fitting over the high-temperature range. To eliminate the influence of ferromagnetic behavior, the temperature range between 330 and 350 K was chosen at which the \( M(T)/H \) curves of 100 Oe, 1000 Oe, and 1 T overlap with each other. The susceptibility does follow the Curie-Weiss law \( \chi = C/(T - \theta) \) quite nicely, as shown in the inset of Fig. 3(a), with Curie constant C = 2.82 emu K/mol and Curie temperature \( \theta = 329 \) K. The resulting Curie constant corresponds to an effective magnetic moment of \( \mu_{eff} = 3.36\mu_{B}/Fe(4.75\mu_{B}/f.u.) \) . The positive \( \theta \) , which is close to the transition temperature, on the other hand, indicates ferromagnetic interactions in the samples.
The field dependence measurements of the magnetization for \( BaFe_{2}Se_{4} \) from -5 to 5 T at different temperatures from 20 to 350 K were carried out to further explore the nature of magnetic orders and are shown in Fig. 3(b). A weak yet clear magnetic hysteresis has been observed below 310 K; however, the magnetization did not saturate at a high magnetic field; instead, linear dependent M-H curves suggest an antiferromagnetic state is observed. The magnetic hysteresis loop is suppressed with increasing temperature and eventually disappears and becomes a straight line by 350 K. This further suggests that the observed concurrence of the ferromagnetic and antiferromagnetic states is an intrinsic property of our samples. For a high-quality pure phase, this M-H behavior is consistent with the canted antiferromagnetic state in the \( BaFe_{2}Se_{4} \) system in which the ferromagnetic order is provided by the small component canted by the magnetic moment of Fe.
The hysteresis loop at 20 K closes up at the field value \( H \sim 2.6 \) T and shows a coercive field of \( H_{c} = 5.6 \) kOe. The linear antiferromagnetic behavior appears to hold up to 5 T, the highest field we have measured. To extract the saturation moment caused by the ferromagnetic component, the \( M(H) \) curve at the high field was fit using \( M(H) = M_{\mathrm{S}} + M_{\mathrm{AFM}} \) , where \( M_{S} \) is the saturation moment which is field independent at the high magnetic field and \( M_{AFM} \) is the antiferromagnetic contribution which has a linear relationship to the magnetic field. Through this fitting, we are able to subtract the linear contribution \( \chi_{AFM}H \) from the experimental data, as shown in the inset of Fig. 3(b). The moment of the ferromagnetic component could also be extracted from the saturated magnetization, from which we obtained \( \sim 0.013\mu_{B}/Fe \) . This value is way smaller than the effective moment calculated by the Curie-Weiss law, which further supports the canted antiferromagnetism scenario in \( BaFe_{2}Se_{4} \) .
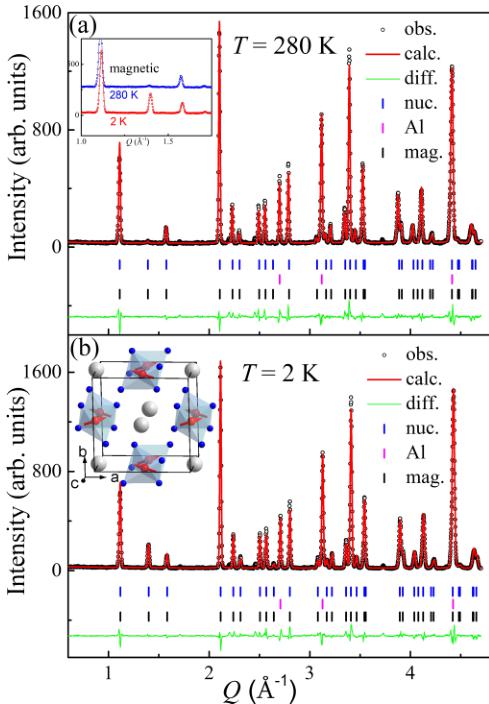
In order to gain further insights into the magnetic order, we performed temperature-dependent neutron powder diffraction (NPD). The highest temperature due to the experimental setup is 280 K [54], which is below the \( T_{N} \) . The magnetic peak is determined through temperature-dependent NPD data. As seen in the inset of Fig. 4(a), when the temperature is decreased from 280 K down to 2 K, we observe a significant increase of the magnetic Bragg intensities on top of the nuclear Bragg peaks. This suggests that the magnetic structure is resultant of a \( k = (0, 0, 0) \) propagation vector which preserves the nuclear lattice's translational symmetry. Figure 4(a) shows a diffraction pattern taken at 280 K along with Rietveld refinement results obtained using FULLPROF [50]. All Bragg peaks can be fit with the Rietveld refinement. The obtained refinement values \( \chi^{2} = 6.10 \) , \( R_{wp} = 13.1 \) , and the R Bragg factors for the refinement of nuclear and magnetic phases are 4.278 and 17.55, respectively. There are three additional Bragg peaks at \( Q \sim 2.7 \) , 3.1, and \( 4.4 \, \AA^{-1} \) , which belong to the aluminum sample holder and were added to the structural refinement as the minor phase.
To identify the magnetic structure, we further performed a full representational analysis for NPD data at 2 K to determine possible irreducible representations (irreps) and basis vectors (BVs) to describe the magnetic structure using the SARAH code [55]. The results are shown in Table SII in the

FIG. 4. (a) Rietveld refinement of neutron powder diffraction data of \( BaFe_{2}Se_{4} \) at 280 K. The inset shows the increased intensity of magnetic peak when the temperature is decreased to 2 K. (b) Rietveld refinement of neutron powder diffraction data of \( BaFe_{2}Se \) at 2 K. The inset shows the schematics of the magnetic structure of \( BaFe_{2}Se_{4} \) .
Supplemental Material [49]. We discriminated between all BVs by comparing the refinement values \( \chi^{2} \) and R factors and found that both \( \Psi_{3} \) and \( \Psi_{5} \) are required in order to obtain the best fit, as shown in Fig. 4(b) and Table SIII in the Supplemental Material [49]. The \( \Psi_{3} \) and \( \Psi_{5} \) here from two different irreps which implies that either there are two transitions or a strong first-order transition. From the M-T plots presented in Fig. 3(a), only one transition was observed, therefore a first-order transition seems more likely to be presented in \( BaFe_{2}Se_{4} \) . The \( \Psi_{5} \) indicates a ferromagnetic moment along the b axis, while \( \Psi_{3} \) suggests an antiferromagnetic moment along the a axis, which further confirms the canted antiferromagnetic spin alignment in \( BaFe_{2}Se_{4} \) . The obtained refinement values are \( \chi^{2}=6.82 \) and \( R_{wp}=12.6 \) . The R Bragg factors for the refinement of nuclear and magnetic phases are 4.898 and 5.758, respectively.
The obtained magnetic structure of \( BaFe_{2}Se_{4} \) can be described as Fe spins aligned perpendicular to the 1D molecular chains, antiferromagnetically correlated along the chain direction (the c axis) as well as the interchain direction (the a axis), with spins along the a axis, and a small ferromagnetic canting along the b axis, as shown in the inset of Fig. 4(b). The magnitude of the magnetic moment estimated from NPD data is \( 2.09\mu_{B}/Fe \) , with \( 1.98\mu_{B}/Fe \) along the a axis and \( 0.67\mu_{B}/Fe \) along the b axis. The magnetic moment canting angle is \( \sim18.7^{\circ} \) from the a axis. Because of thermal fluctuations, a larger tilted angle of \( 63.1^{\circ} \) is observed at 280 K comparing to \( 18.7^{\circ} \) at 2 K. For comparison, in the tetrahedrally coordinated system, due to the crystal field effect, the magnetic moment of a free \( Fe^{3+} \) ion is \( 5.92\mu_{B} \) for the high spin state and \( 1.73\mu_{B} \) for the low spin state taking the Lande factor g=2. The calculated magnetic moment is in between the high spin and low spin states indicating a possible mixed state in this system. The magnitude of the magnetic moment is pretty close to that of single-chain quasi-1D \( TlFeSe_{2} \) material with the same formal \( Fe^{3+} \) valence, but smaller than that of spin-ladder quasi-1D iron chalcogenide \( BaFe_{2}Se_{3} \) with a formal \( Fe^{2+} \) valence. In \( TlFeSe_{2} \) , the \( FeSe_{4} \) tetrahedra also form a quasi-1D structure with Néel temperature at 295 K and the magnetic moment of Fe is \( 2.1\mu_{B}/Fe \) [56–60]. The similar single 1D chain in both \( BaFe_{2}Se_{4} \) and \( TlFeSe_{2} \) , leads one to expect that both materials have similar direct and indirect exchange interactions. However, the Dzyaloshinskii-Moriya interaction also arises, and this anisotropic exchange interaction leads to the canted antiferromagnetic ground state in \( BaFe_{2}Se_{4} \) . On the other hand, this canted antiferromagnetic structure in \( BaFe_{2}Se_{4} \) is quite different from the typical magnetic structures discovered in spin-ladder quasi-1D iron chalcogenides, such as the block-type structure in \( BaFe_{2}Se_{3} \) [34,35], or the stripe-type structure in \( BaFe_{2}S_{3} \) , \( KFe_{2}Se_{3} \) , and \( CsFe_{2}Se_{3} \) [36–38].
The observation of the canted antiferromagnetism in this quasi-1D \( BaFe_{2}Se_{4} \) compound is rather intriguing and could be a playground to further explore the correlations between magnetism and superconductivity. The antiferromagnetic order and/or magnetic spin fluctuations have been universally observed in the iron-based superconductors, and plays an important role for the emergence of superconductivity \( [61-63] \) . \( BaFe_{2}Se_{4} \) , with a simpler structure and higher symmetry than spin-ladder phase \( BaFe_{2}Se_{3} \) , will provide a unique opportunity to reveal the intimate interplay between magnetism, crystal lattice, and electronic structure in \( [FeX_{4}] \) -based materials, and perhaps to understand the mechanism of superconductivity in Fe-based compounds. The \( BaFe_{2}Se_{3} \) becomes superconducting at \( \sim11 \) K at high pressure >10 GPa. The appearance of superconductivity in \( BaFe_{2}Se_{3} \) has a strong correlation with the magnitude of magnetic moments of Fe atoms, and the magnitude of magnetic moments is gradually decreasing with increasing pressure [39]. It will be interesting to investigate how the magnetic structure and moment, canted antiferromagnetic correlation, and ferromagnetic component evolve with chemical doping or high pressure, whether superconductivity could be induced in the vicinity of this canted antiferromagnetism, and how it interplays with the antiferromagnetism or even ferromagnetism when it emerges. This canted antiferromagnetic structure in \( BaFe_{2}Se_{4} \) , is also different from the typical block-type or stripe-type magnetism discovered in the quasi-1D iron chalcogenides such as \( BaFe_{2}Se_{3} \) and \( BaFe_{2}S_{3} \) , and could provide a unique playground to study the interplay between magnetism, crystal lattice, and electronic structure in Fe-based compounds.
This work at University of Texas at Dallas is supported by U.S. Air Force Office of Scientific Research (FA9550-19-1-0037) and National Science Foundation (DMR 1921581). We also acknowledge the support from the Office of Research at University of Texas at Dallas through the Seed Program for Interdisciplinary Research (SPIRe) and the Core Facility
[1] Y. Kamihara, H. Hiramatsu, M. Hirano, R. Kawamura, H. Yanagi, T. Kamiya, and H. Hosono, J. Am. Chem. Soc. 128, 10012 (2006).
[2] Y. Kamihara, T. Watanabe, M. Hirano, and H. Hosono, J. Am. Chem. Soc. 130, 3296 (2008).
[3] F.-C. Hsu, J.-Y. Luo, K.-W. Yeh, T.-K. Chen, T.-W. Huang, P. M. Wu, Y.-C. Lee, Y.-L. Huang, Y.-Y. Chu, D.-C. Yan, and M.-K. Wu, Proc. Natl. Acad. Sci. USA 105, 14262 (2008).
[4] T. M. McQueen, Q. Huang, V. Ksenofontov, C. Felser, Q. Xu, H. Zandbergen, Y. S. Hor, J. Allred, A. J. Williams, D. Qu et al., Phys. Rev. B 79, 014522 (2009).
[5] Y. Mizuguchi, F. Tomioka, S. Tsuda, T. Yamaguchi, and Y. Takano, Appl. Phys. Lett. 93, 152505 (2008).
[6] S. Margadonna, Y. Takabayashi, Y. Ohishi, Y. Mizuguchi, Y. Takano, T. Kagayama, T. Nakagawa, M. Takata, and K. Prassides, Phys. Rev. B 80, 064506 (2009).
[7] S. Medvedev, T. M. McQueen, I. A. Troyan, T. Palasyuk, M. I. Eremets, R. J. Cava, S. Naghavi, F. Casper, V. Ksenofontov, G. Wortmann, and C. Felser, Nat. Mater. 8, 630 (2009).
[8] D. Braithwaite, B. Salce, G. Lapertot, F. Bourdarot, C. Marin, D. Aoki, and M. Hanfland, J. Phys.: Condens. Matter 21, 232202 (2009).
[9] G. Garbarino, A. Sow, P. Lejay, A. Sulpice, P. Toulemonde, M. Mezouar, and M. Núñez-Regueiro, Europhys. Lett. 86, 27001 (2009).
[10] Q.-Y. Wang, Z. Li, W.-H. Zhang, Z.-C. Zhang, J.-S. Zhang, W. Li, H. Ding, Y.-B. Ou, P. Deng, K. Chang et al., Chin. Phys. Lett. 29, 037402 (2012).
[11] D. Liu, W. Zhang, D. Mou, J. He, Y.-B. Ou, Q.-Y. Wang, Z. Li, L. Wang, L. Zhao, S. He et al., Nat. Commun. 3, 1 (2012).
[12] S. He, J. He, W. Zhang, L. Zhao, D. Liu, X. Liu, D. Mou, Y.-B. Ou, Q.-Y. Wang, Z. Li et al., Nat. Mater. 12, 605 (2013).
[13] S. Tan, Y. Zhang, M. Xia, Z. Ye, F. Chen, X. Xie, R. Peng, D. Xu, Q. Fan, H. Xu et al., Nat. Mater. 12, 634 (2013).
[14] J. J. Lee, F. T. Schmitt, R. G. Moore, S. Johnston, Y.-T. Cui, W. Li, M. Yi, Z. K. Liu, M. Hashimoto, Y. Zhang et al., Nature (London) 515, 245 (2014).
[15] Z. Zhang, Y.-H. Wang, Q. Song, C. Liu, R. Peng, K. A. Moler, D. Feng, and Y. Wang, Sci. Bull. 60, 1301 (2015).
[16] J. Guo, S. Jin, G. Wang, S. Wang, K. Zhu, T. Zhou, M. He, and X. Chen, Phys. Rev. B 82, 180520(R) (2010).
[17] A. F. Wang, J. J. Ying, Y. J. Yan, R. H. Liu, X. G. Luo, Z. Y. Li, X. F. Wang, M. Zhang, G. J. Ye, P. Cheng et al., Phys. Rev. B 83, 060512(R) (2011).
[18] Y. Mizuguchi, H. Takeya, Y. Kawasaki, T. Ozaki, S. Tsuda, T. Yamaguchi, and Y. Takano, Appl.Phys. Lett. 98, 042511 (2011).
[19] A. Krzton-Maziopa, Z. Shermadini, E. Pomjakushina, V. Pomjakushin, M. Bendele, A. Amato, R. Khasanov, H.
Voucher Program. The research conducted at ORNL’s High Flux Isotope Reactor was sponsored by the Scientific User Facilities Division, Office of Basic Energy Sciences, U.S. Department of Energy. Support from Advanced Materials and Manufacturing Processes Institute (AMMPI) at the University of North Texas is acknowledged.
Luetkens, and K. Conder, J. Phys.: Condens. Matter 23, 052203 (2011).
[20] M.-H. Fang, H.-D. Wang, C.-H. Dong, Z.-J. Li, C.-M. Feng, J. Chen, and H. Q. Yuan, Europhys. Lett. 94, 27009 (2011).
[21] T. Qian, X.-P. Wang, W.-C. Jin, P. Zhang, P. Richard, G. Xu, X. Dai, Z. Fang, J.-G. Guo, X.-L. Chen, and H. Ding, Phys. Rev. Lett. 106, 187001 (2011).
[22] K. M. Taddei, M. Sturza, D.-Y. Chung, H. B. Cao, H. Claus, M. G. Kanatzidis, R. Osborn, S. Rosenkranz, and O. Chmaissem, Phys. Rev. B 92, 094505 (2015).
[23] M. Yi, D. H. Lu, R. Yu, S. C. Riggs, J.-H. Chu, B. Lv, Z. K. Liu, M. Lu, Y.-T. Cui, M. Hashimoto et al., Phys. Rev. Lett. 110, 067003 (2013).
[24] M. Yi, Z.-K. Liu, Y. Zhang, R. Yu, J.-X. Zhu, J. J. Lee, R. G. Moore, F. T. Schmitt, W. Li, S. C. Riggs et al., Nat. Commun. 6, 1 (2015).
[25] F. Ye, S. Chi, W. Bao, X. F. Wang, J. J. Ying, X. H. Chen, H. D. Wang, C. H. Dong, and M. Fang, Phys. Rev. Lett. 107, 137003 (2011).
[26] E. Dagotto, Rev. Mod. Phys. 85, 849 (2013).
[27] M. Burrard-Lucas, D. G. Free, S. J. Sedlmaier, J. D. Wright, S. J. Cassidy, Y. Hara, A. J. Corkett, T. Lancaster, P. J. Baker, S. J. Blundell, and S. J. Clarke, Nat. Mater. 12, 15 (2013).
[28] X. F. Lu, N. Z. Wang, H. Wu, Y. P. Wu, D. Zhao, X. Z. Zeng, X. G. Luo, T. Wu, W. Bao, G. H. Zhang et al., Nat. Mater. 14, 325 (2015).
[29] X. Dong, H. Zhou, H. Yang, J. Yuan, K. Jin, F. Zhou, D. Yuan, L. Wei, J. Li, X. Wang et al., J. Am. Chem. Soc. 137, 66 (2015).
[30] X. Dong, K. Jin, D. Yuan, H. Zhou, J. Yuan, Y. Huang, W. Hua, J. Sun, P. Zheng, W. Hu et al., Phys. Rev. B 92, 064515 (2015).
[31] L. Zhao, A. Liang, D. Yuan, Y. Hu, D. Liu, J. Huang, S. He, B. Shen, Y. Xu, X. Liu et al., Nat. Commun. 7, 10608 (2016).
[32] Q. Liu, C. Chen, T. Zhang, R. Peng, Y.-J. Yan, Chen-Hao-Ping Wen, X. Lou, Y.-L. Huang, J.-P. Tian, X.-L. Dong et al., Phys. Rev. X 8, 041056 (2018).
[33] C. Chen, Q. Liu, T. Z. Zhang, D. Li, P. P. Shen, X. L. Dong, Z.-X. Zhao, T. Zhang, and D. L. Feng, Chin. Phys. Lett. 36, 057403 (2019).
[34] J. M. Caron, J. R. Neilson, D. C. Miller, A. Llobet, and T. M. McQueen, Phys. Rev. B 84, 180409(R) (2011).
[35] A. Krzton-Maziopa, E. Pomjakushina, V. Pomjakushin, D. Sheptyakov, D. Chernyshov, V. Svitlyk, and K. Conder, J. Phys.: Condens. Matter 23, 402201 (2011).
[36] S. Chi, Y. Uwatoko, H. Cao, Y. Hirata, K. Hashizume, T. Aoyama, and K. Ohgushi, Phys. Rev. Lett. 117, 047003 (2016).
[37] J. M. Caron, J. R. Neilson, D. C. Miller, K. Arpino, A. Llobet, and T. M. McQueen, Phys. Rev. 85, 180405(R) (2012).
[38] F. Du, K. Ohgushi, Y. Nambu, T. Kawakami, M. Avdeev, Y. Hirata, Y. Watanabe, T. J. Sato, and Y. Ueda, Phys. Rev. B 85, 214436 (2012).
[39] J. Ying, H. Lei, C. Petrovic, Y. Xiao, and V. V. Struzhkin, Phys. Rev. B 95, 241109(R) (2017).
[40] T. Yamauchi, Y. Hirata, Y. Ueda, and K. Ohgushi, Phys. Rev. Lett. 115, 246402 (2015).
[41] I. E. Grey, J. Solid State Chem. 11, 128 (1974).
[42] I. E. Grey, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater. 31, 45 (1975).
[43] J. S. Swinnea and H. Steinfink, J. Solid State Chem. 32, 329 (1980).
[44] N. Nakayama, K. Kosuge, and S. Kachi, J. Solid State Chem. 36, 9 (1981).
[45] A. C. Holladay and L. Eyring, J. Solid State Chem. 64, 113 (1986).
[46] J. S. Swinnea and H. Steinfink, J. Solid State. Chem. 41, 124 (1982).
[47] H. Steinfink and J. S. Swinnea, Mater. Res. Soc. Symp. Proc. 97, 371 (1987).
[48] D. Berthebaud, O. Perez, J. Tobola, D. Pelloquin, and A. Maignan, J. Solid State Chem. 230, 293 (2015).
[49] See Supplemental Material at http://link.aps.org/supplemental/10.1103/PhysRevB.102.180403 for canted antiferromagnetism in the quasi-1D iron chalcogenide BaFe_{2}Se_{4}.
[50] J. Rodríguez-Carvajal, Physica B (Amsterdam, Neth.) 192, 55 (1993).
[51] B. H. Toby and R. B. Von Dreele, J. Appl. Cryst. 46, 544 (2013).
[52] J. Gopalakrishnan and K. Nanjundaswamy, Bull. Mater. Sci. 5, 287 (1983).
[53] H. Lei, H. Ryu, A. I. Frenkel, and C. Petrovic, Phys. Rev. B 84, 214511 (2011).
[54] S. Calder, K. An, R. Boehler, C. R. Dela Cruz, M. D. Frontzek, M. Guthrie, B. Haberl, A. Huq, S. A. Kimber, J. Liu et al., Rev. Sci. Instrum. 89, 092701 (2018).
[55] A. S. Wills, Physica B 276, 680 (2000).
[56] Z. Seidov, H.-A. Krug von Nidda, J. Hemberger, A. Loidl, G. Sultanov, E. Kerimova, and A. Panfilov, Phys. Rev. B 65, 014433 (2001).
[57] E. B. Asgerov, N. T. Dang, A. I. Beskrovnyy, A. I. Madadzada, D. I. Ismayilov, R. N. Mehdiyeva, S. H. Jabarov, and E. M. Karimova, Semiconductors 49, 879 (2015).
[58] N. A. Ismayilova, H. S. Orudjev, and S. H. Jabarov, Semiconductors 51, 473 (2017).
[59] Z. Seidov, H.-A. Krug von Nidda, V. Tsurkan, I. Filippova, A. Günther, A. Najafov, M. N. Aliyev, F. G. Vagizov, A. G. Kiiamov, L. R. Tagirov et al. Bull. Russ. Acad. Sci.: Phys. 81, 885 (2017).
[60] E. B. Asgerov, D. I. Ismayilov, R. N. Mehdieva, S. H. Jabarov, M. N. Mirzayev, E. M. Kerimova, and N. T. Dang, J. Surf. Invest.: X-Ray, Synchrotron Neutron Tech. 12, 688 (2018).
[61] J. M. Allred, K. M. Taddei, D. E. Bugaris, M. J. Krogstad, S. H. Lapidus, D. Y. Chung, H. Claus, M. G. Kanatzidis, D. E. Brown, J. Kang et al., Nat. Phys. 12, 493 (2016).
[62] D. N. Basov and A. V. Chubukov, Nat. Phys. 7, 272 (2011).
[63] R. M. Fernandes and A. V. Chubukov, Rep. Prog. Phys. 80, 014503 (2016).