| Transition Temperature | 93 K |
|---|---|
| Experiment Temperature | 4 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | P42/mnm (#136) |
| Magnetic Space Group | Pn'nm (#58.395) |
| Magnetic Point Group | m'mm (8.3.26) |
| Lattice Parameters | 4.58717(9) 4.58717(9) 8.8114(2) 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1103/PhysRevB.92.094419 |
| Reference | M. Zhu, D. Do, C. R. Dela Cruz, Z. Dun, J.-G. Cheng, H. Goto, Y. Uwatoko, T. Zou, H. D. Zhou, S. D. Mahanti, X. Ke, PHYSICAL REVIEW B (2015) 92 094419 |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Cr1 | Cr | 0.0 | 2.47 | 0.0 | 2.47 |
Ferromagnetic superexchange in insulating Cr₂MoO₆ by controlling orbital hybridization
M. Zhu, \( ^{1} \) D. Do, \( ^{1} \) C. R. Dela Cruz, \( ^{2} \) Z. Dun, \( ^{3} \) J.-G. Cheng, \( ^{4,5} \) H. Goto, \( ^{5} \) Y. Uwatoko, \( ^{5} \) T. Zou, \( ^{1} \) H. D. Zhou, \( ^{3} \) Subhendra D. Mahanti, \( ^{1} \) and X. Ke \( ^{1} \)
\( ^{1} \) Department of Physics and Astronomy, Michigan State University, East Lansing, Michigan 48824, USA
\( ^{2} \) Quantum Condensed Matter Division, Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA
\( ^{3} \) Department of Physics and Astronomy, University of Tennessee, Knoxville, Tennessee 37996, USA
\( ^{4} \) Beijing National Laboratory for Condensed Matter Physics and Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China
\( ^{5} \) Institute for Solid State Physics, University of Tokyo, 5-1-5 Kashiwanoha, Kashiwa, Chiba 277-8581, Japan
(Received 20 January 2015; revised manuscript received 24 March 2015; published 11 September 2015)
We report the magnetic and electronic structures of the inverse-triturile compound \( Cr_{2}MoO_{6} \) . Despite the same crystal symmetry and similar bond lengths and bond angles as \( Cr_{2}TeO_{6} \) , \( Cr_{2}MoO_{6} \) possesses a magnetic structure different from that in \( Cr_{2}TeO_{6} \) . ab initio electronic structure calculations show that the sign and strength of the Cr-O-Cr superexchange coupling is strongly influenced by the hybridization between the filled \( O2p \) and empty Mo 4d orbitals: the virtual transfer of an \( O2p \) electron to the empty Mo 4d orbitals leaves the \( O2p \) partially occupied, which leads to ferromagnetic exchange between Cr moments. This result further substantiates our recently proposed mechanism for tuning the exchange interaction between two magnetic atoms by modifying the electronic states of nonmagnetic atoms in the exchange path through orbital hybridization. This approach is fundamentally different from the conventional methods of controlling the exchange interaction by either carrier injection or through structural distortions.
DOI: 10.1103/PhysRevB.92.094419
PACS number(s): 71.15.Mb, 75.25.-j, 75.30.Et
Understanding the origin and nature of exchange interaction between the electrons in magnetic atoms has been a fundamental topic to elucidate a wide range of magnetic phenomena in condensed matter systems for many decades. For instance, the celebrated Hund's rule, which favors the electronic state with the highest multiplicity, arises from the Coulomb exchange of electrons within the d orbitals of the same atom. In transition-metal oxides, the exchange coupling between magnetic cations is prevalently mediated by the intervening nonmagnetic oxygen atoms. This indirect exchange coupling, named superexchange interaction, was first studied by Kramers \( [1] \) and Anderson \( [2] \) in the framework of the perturbation theory, and the sign of the exchange integral is formulated by Goodenough-Kanamori rules based on the symmetry consideration of occupied electron orbitals \( [3,4] \) . To date, magnetic interaction is still a subtle question to investigate in real systems in spite of the great success of the direct and indirect mechanisms proposed in understanding the origin of magnetic coupling in a variety of systems. A well-known example of magnetic exchange that has attracted considerable interest in recent years is the Zener double exchange mechanism, which explains the metallicity and ferromagnetism in the mixed-valence Mn compounds \( [5] \) .
The ordered inverse trirutiles, such as \( Cr_{2}WO_{6} \) and \( Cr_{2}TeO_{6} \) , are a series of materials in which the magnetic coupling cannot be explained only by the antiferromagnetic superexchange interaction based on the Goodenough-Kanamori rules. The space group is \( P4_{2}/mnm \) , and the bond lengths and the bond angles are nearly identical in both compounds [6]. However, their magnetic structures are quite distinct and the Cr-O-Cr magnetic coupling depends on whether the Te or W occupies the nonmagnetic sites [6]. Recently, we presented the sign reversal of the magnetic exchange in the \( \mathrm{Cr}_{2}(\mathrm{Te}_{1-x}\mathrm{W}_{x})\mathrm{O}_{6} \) system at x = 0.7, where both the transition temperature and the average sublattice magnetic moment reach their minimum values, and we argued that the hybridization of unoccupied W 5d orbitals with filled O 2p orbitals played an essential role in determining the nature of Cr-Cr superexchange via O 2p [7]. The competition between the usual antiferromagnetic superexchange and the ferromagnetic interaction induced by the 5d-2p hybridization could account for the sign and strength of the magnetic couplings in this system. To further substantiate the proposed orbital hybridization effect of the nonmagnetic ions with empty d orbitals in determining the exchange interaction, we have studied the magnetic property and the electronic structure of another inverse trirutile, \( Cr_{2}MoO_{6} \) . In this system, the presence of the low-lying unoccupied Mo 4d orbitals hybridizing with the occupied 2p orbitals of the oxygen atom in the Cr-O-Cr superexchange path should give rise to a ferromagnetic coupling between Cr-Cr atoms, as in the W compound. This is precisely what we have observed and report in this paper. As we will discuss later, the physical origin of ferromagnetic exchange in \( \mathrm{Cr}_{2}\mathrm{MoO}_{6} \) and also in \( \mathrm{Cr}_{2}\mathrm{WO}_{6} \) differs fundamentally from the proposed antiferromagnetic exchange mechanisms via the empty Ti 3d orbitals in perovskite \( EuTiO_{3} \) [8] and in double perovskite \( CaCu_{3}Ti_{4}O_{12} \) [9].
Polycrystalline samples of \( Cr_{2}MoO_{6} \) [10] were synthesized under high-pressure and high-temperature conditions using a cubic anvil system. The mixtures of \( Cr_{2}O_{3} \) and \( MoO_{3} \) in the stoichiometric ratio were ground thoroughly and reacted at \( 1000^{\circ}C \) for 30 min under 4 GPa. Phase purity of the obtained product was first examined at room temperature with the powder x-ray diffraction. Magnetic susceptibility was measured using the Quantum Design SQUID magnetometer and specific heat was characterized using the Physical Properties Measurement System (Quantum Design). The neutron power diffraction (NPD) measurements on the sample of \( \sim1g \) were performed on HB2A neutron powder diffractometer at High Flux Isotope Reactor (HFIR) in Oak Ridge National Laboratory. The NPD data were taken with the neutron

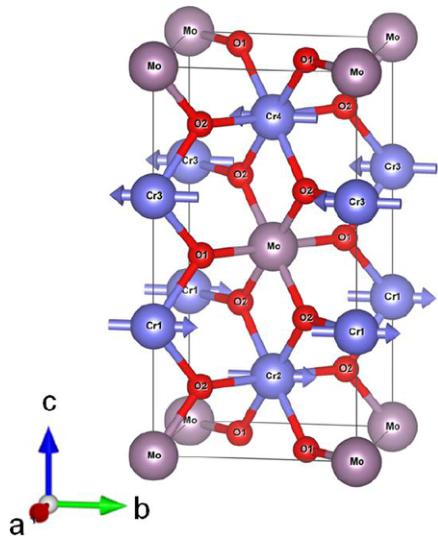
FIG. 1. (Color online) The schematics of the crystal and magnetic structure of \( Cr_{2}MoO_{6} \) . The \( Cr^{3+} \) spins are parallel within the ab plane. The intrabilayer (Cr1-Cr2) coupling is ferromagnetic, while the interbilayer one (Cr2-Cr3) is antiferromagnetic.
wavelength \( \lambda = 2.41 \AA \) and a collimation of 12'-open-6', and were analyzed using the Rietveld refinement program FULLPROF [11].
The schematics of both crystal structure and the obtained magnetic structure of \( Cr_{2}MoO_{6} \) are shown in Fig. 1. It has an inverse-triturile structure with tetragonal symmetry \( P4_{2}/mnm \) , and the lattice parameters are \( a = b = 4.58717(9) \) Å and \( c = 8.81138(22) \) Å at \( T = 4 \) K. As seen in Table I, the Cr-O-Cr bond angles and bond lengths are close to those of \( Cr_{2}WO_{6} \) and \( Cr_{2}TeO_{6} \) due to the similar ionic radii of \( Mo^{6+} \) , \( Te^{0+} \) , and \( W^{6+} \) . As to be shown later, \( Cr_{2}MoO_{6} \) undergoes a paramagnetic-antiferromagnetic transition at \( T_{N} = 93 \) K with the same spin order as \( Cr_{2}WO_{6} \) . One can visualize the magnetic structure in terms of each \( Cr^{3+} \) bilayer separated by a Mo layer. The \( Cr^{3+} \) spins are aligned in parallel within the ab plane but are antiparallel between the bilayers (Cr1-Cr3 and Cr2-Cr4). The intrabilayer coupling between two nearest-neighbor \( Cr^{3+} \) spins (Cr1-Cr2 and Cr3-Cr4) is ferromagnetic as seen in \( Cr_{2}WO_{6} \) , in contrast to the antiferromagnetic coupling in \( Cr_{2}TeO_{6} \) [6,7]. The close similarity in the crystal structures of these compounds with dramatically distinct magnetic structures ( \( Cr_{2}MoO_{6} \) and \( Cr_{2}WO_{6} \) vs. \( Cr_{2}TeO_{6} \) ) underscores the limitations of the Goodenough-Kanamori rules [3,4] in predicting the nature of the exchange interaction in these complex systems with competing exchange mechanisms. The role of other nonmagnetic ions (e.g., Mo, W, and Te) in the superexchange mechanism has to be reexamined in detail.
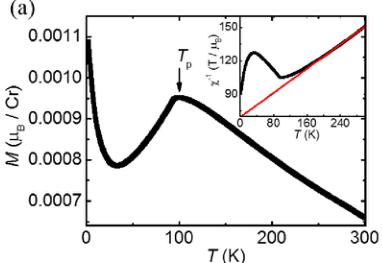
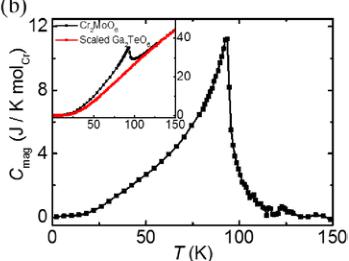
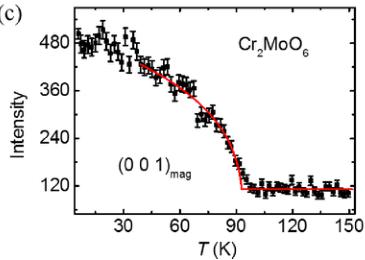
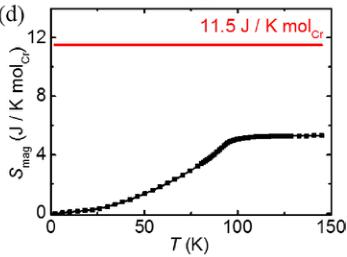
Figure 2(a) shows the temperature dependence of magnetic susceptibility measured in an external field \( H = 1000 \, Oe \) . A broad peak is observed near \( T_{p} \sim 98 \, K \) , implying the presence of short-range antiferromagnetic correlation near and above this temperature. Inset displays the inverse susceptibility and a Curie-Weiss fit is performed in the temperature range 200–300 K. The fitting gives a Weiss temperature \( \theta_{w} \sim -254.4 \, K \) and the effective magnetic moment \( \mu_{eff} \) is estimated to be \( 2.92 \mu_{B}/Cr \) , close to the expected value \( 3 \mu_{B} \) for the \( Cr^{3+} \) spins. The negative \( \theta_{w} \) is consistent with the dominance of antiferromagnetic correlations in Cr1-Cr3 and Cr2-Cr4 dimers [12] in this system. The increase in the susceptibility at low temperatures is presumably due to paramagnetic impurities [7,13]. The magnetic heat capacity as a function of temperature, \( C_{\text{mag}}(T) \) , is shown in Fig. 2(b) with the phonon contribution subtracted by the scaled heat capacity of an isostructural nonmagnetic compound \( Ga_{2}TeO_{6} \) from the total heat capacity measured [see the inset of Fig. 2(b)]. The sharp peak at \( T_{N} \sim 93 \, K \) shown in \( C_{\text{mag}}(T) \) indicates a transition into a long-range ordered antiferromagnetic state. It is noteworthy that the transition temperature \( T_{N} \) is slightly lower than \( T_{p} \) determined from the broad peak in the magnetic susceptibility, which seems to be a common feature in the inverse trirutiles such as \( Cr_{2}TeO_{6} \) , \( Cr_{2}WO_{6} \) , and \( Fe_{2}TeO_{6} \) [7,13]. Such a feature is associated with the presence of short-range low-dimensional magnetic fluctuations prior to entering a three-dimensional long-range antiferromagnetic state. The integrated magnetic entropy is shown in Fig. 2(d) with a saturated value of \( 5.30 \, J/K \, mol_{Cr} \) , which is about 50% of the theoretical value ( \( 11.5 \, J/K \, mol_{Cr} \) ) for spin \( S = 3/2 \, Cr^{3+} \) ions. The presence of resultant residual magnetic entropy implies the existence of magnetic correlation in the system above \( T_{N} \) . Note that residual magnetic entropy ( \( 6.20 \, J/K \, mol_{Cr} \) ) is nearly half of the maximum value and is commonly observed in low dimensional and frustrated magnetic systems with competing interactions.
TABLE I. Structural parameters (\(T = 4\) K) of \(\mathrm{Cr}_{2}\mathrm{TeO}_{6}\), \(\mathrm{Cr}_{2}\mathrm{WO}_{6}\), and \(\mathrm{Cr}_{2}\mathrm{MoO}_{6}\), including lattice parameters, bond length, and bond angles.
| Compound | \( Cr_{2}TeO_{6} \) | \( Cr_{2}WO_{6} \) | \( Cr_{2}MoO_{6} \) | |
| Lattice parameters ( \( \AA \) ) | a | 4.54487(8) | 4.58346(5) | 4.58717(9) |
| b | 4.54487(8) | 4.58346(5) | 导4.58717(9) | |
| c | 8.99539(21) | 8.85319(13) | 导8.81138(22) | |
| Bond length ( \( \AA \) ) | Cr3-Cr1 | 2.968(14) | 2.930(13) | 导2.78(3) |
| Cr3-Cr4 | 3.559(7) | 3.558(6) | 导3.603(8) | |
| Cr3-Cr3 | 4.54487(8) | 4.58346(5) | 導4.58717(9) | |
| Bond angle (degree) | Cr3-O1-Cr1 | 98.5(3) | 97.6(3) | 导96.65(16) |
| Cr3-O2-Cr4 | 127.0(4) | 128.6(3) | 导130.3(3) |
(a)

(b)

(c)

(d)

FIG. 2. (Color online) (a) Temperature dependence of the magnetic susceptibility. Inset shows the inverse susceptibility and the Curie-Weiss fit. (b) Temperature dependence of the magnetic heat capacity. Inset shows the subtraction of the phonon contribution using the scaled heat capacity of \( Ga_{2}TeO_{6} \) . (c) Intensity of the \( (0\ 0\ 1) \) magnetic Bragg peak as a function of temperature. The solid line is a guide to the eyes. (d) Temperature dependence of the integrated magnetic entropy. The horizontal red line denotes the theoretical value for \( S = 3/2 \) .
[14]. It has also been seen in \( Cr_{2}(Te_{1-x}W_{x})O_{6} \) [7], suggesting one of these factors to be present in \( Cr_{2}MoO_{6} \) [15].
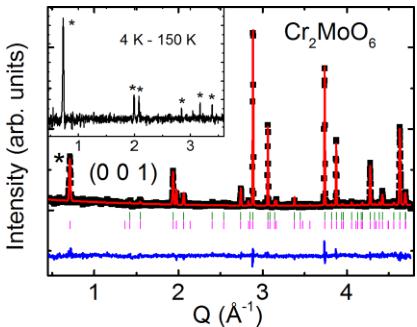
The NPD data measured at T = 4 K are shown in Fig. 3. The magnetic propagation wave vector is determined to be \( (0\ 0\ 1) \) . Representational analysis using the BasIrreps program in FULLPROF [11] suggests that the magnetic structure shown in Fig. 1 is symmetry compatible and the most plausible fit to the data. The R Bragg factors for the refinement of

FIG. 3. (Color online) Neutron powder diffraction data of \( Cr_{2}MoO_{6} \) at T = 4 K. The black symbols are experimental data and the red curve is the Rietveld refinement fit. The difference is represented by the blue. The positions of the nuclear and magnetic peaks are marked by the green and magenta lines, respectively. Inset shows the difference between low- and high-temperature data with the positions of magnetic Bragg peaks denoted by the symbol \( * \) .
nuclear and magnetic phases are 7.44 and 22.6, respectively. This magnetic structure is identical to that of \( Cr_{2}WO_{6} \) , that is, the intrabilayer coupling (for example, Cr1-Cr2) is ferromagnetic. Note that the in-plane spin direction could not be unambiguously determined because of the tetragonal structure of the system and the nature of neutron powder data. The full width at half maximum (FWHM) of the magnetic Bragg peaks is determined by the instrumental resolution according to the refinement, confirming the long-range character of the magnetic order. Inset shows the zoom-in view of the magnetic Bragg peak after subtracting the 150 K neutron diffraction data from the 4 K one. The temperature dependence of the \( (0\ 0\ 1) \) magnetic order parameter (sublattice magnetization) is presented in Fig. 2(c), and the solid curve is a guide to the eyes. The magnetic signal disappears at the antiferromagnetic transition temperature \( T_{N} \sim 93 \) K, consistent with the specific heat measurement. Note that the magnitude of the static magnetic moment ( \( \approx 2.47 \mu_{B}/Cr \) ) extracted from NPD measurement is smaller than the theoretical value of \( 3.0 \mu_{B}/Cr \) , which is attributed to quantum spin fluctuation (at low T) as well as due to the covalence [16–18].
The observed ferromagnetic intrabilayer coupling in \( Cr_{2}MoO_{6} \) is consistent with a mechanism we proposed earlier for the W compound [7]; the nearby unoccupied Mo 4d orbitals (in the place of unoccupied W 5d orbitals) play an essential role in determining the sign of the Cr-Cr exchange by hybridizing with intervening filled O p orbitals. That is, the d-p hybridization induced ferromagnetic exchange dominates the usual superexchange interaction in \( Cr_{2}MoO_{6} \) and \( Cr_{2}WO_{6} \) . In contrast, in \( Cr_{2}TeO_{6} \) , a compound with similar crystal structure but with no empty Te d orbitals, the superexchange
TABLE II. Total energies (in eV) per magnetic unit cell containing four \( Cr^{3+} \) ions of different magnetic configurations.
| Configuration | AF-AF | AF-F | F-AF | F-F |
| GGA | -153.325 | -153.520 | -153.457 | -153.422 |
| GGA+U | -143.649 | -143.671 | -143.562 | -143.635 |
interaction between two intrabilayer Cr moments is antiferromagnetic. However, in spite of the similarity, i.e., the presence of the empty d orbitals, the Neel temperature of \( Cr_{2}MoO_{6} \) is considerably higher than that of the \( Cr_{2}WO_{6} \) , \( T_{N} \sim 45 \) K. Possible explanation of this difference will be discussed later.
To understand the \( Cr_{2}MoO_{6} \) electronic structure and its magnetic properties, we carried out first-principles calculations for four different interbilayer-intrabilayer magnetic configurations, i.e., AF-AF, AF-F, F-AF, and F-F, where AF and F denote antiferromagnetic and ferromagnetic alignments, respectively. Density functional theory (DFT) calculations were done within the generalized gradient approximation (GGA) and GGA+U [19] as implemented in the Vienna ab initio simulation package (VASP) [19–21], using projector-augmented wave (PAW) method [22,23] and Perdew-Burke-Ernzerhof (PBE) exchange-correlation functional [24]. The plane-wave energy cutoff and total energy accuracy are set at 400 and \( 10^{-3}eV \) , respectively. To sample the Brillouin zone, we use the Monkhorst-Pack schemes with the k mesh of \( 14 \times 14 \times 7 \) for self-consistent calculations and \( 20 \times 20 \times 10 \) to get the density of states (DOS). According to the total energies of different magnetic configurations listed in Table II, we can see that both GGA and GGA+U calculations give the ground state as AF-F, consistent with the experimental result. However, unlike \( Cr_{2}WO_{6} \) and \( Cr_{2}TeO_{6} \) [7], GGA gives a small negative band gap (data not shown) in \( Cr_{2}MoO_{6} \) , while the experiment shows an insulating behavior. Note that GGA usually underestimates the band gap in semiconductors [25] and the problem is severe in systems containing 3d electrons such as Cr. This problem can be partially corrected through GGA+U approximation [26,27].
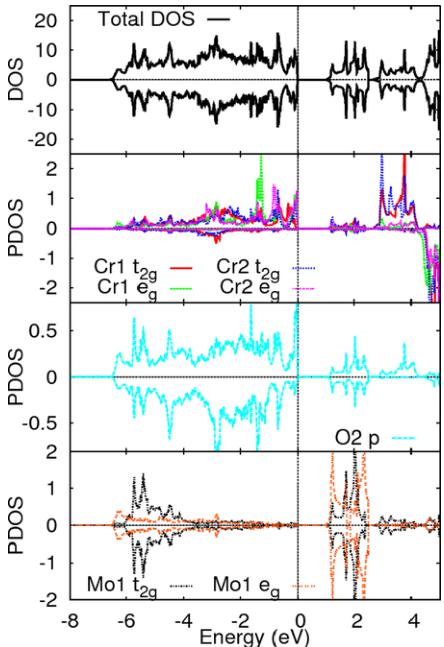
Figure 4 presents the density of state (DOS) and projected DOS of \( Cr_{2}MoO_{6} \) calculated using GGA+U with U = 4 eV for Cr. GGA+U indeed opens up a band gap and increases the \( Cr^{3+} \) magnetic moment from \( \sim2.5\mu_{B} \) for GGA to \( \sim2.9\mu_{B} \) for GGA+U. Reduction from \( 3.0\mu_{B} \) to \( 2.9\mu_{B} \) is due to the covalency and comparison with the experimental value, \( 2.47\mu_{B} \) , suggests that the effect of quantum spin fluctuation is important in this system [16,17,18]. Note that in our electronic structure calculations, the principle axis is along the tetragonal axes, which are not aligned with the cubic axis of the local crystal field of the \( CrO_{6} \) system, giving rise to the mixture of both \( t_{2g} \) and \( e_{g} \) states in the former coordinate system for Cr 3d orbitals. Also note that Mo 3d orbitals were treated as core states and were not a part of the manifold of active orbitals because of the large energy difference ( \( \sim235.45eV \) ) between O 2p and Mo 3d; therefore the notation of d orbitals of Mo hereafter refers to its 4d orbitals. The projected DOS shows that there is strong hybridization between Mo d and O p near the bottom of the O p band ( \( -4 \) to \( -6.5eV \) ), and this hybridization also shows up in the lower part of the conduction

FIG. 4. (Color online) Density of states (DOS) in the units of [number of states / (eV u.c.)] and projected density of states (PDOS) in the units of [number of states / (eV atom)] of \( Cr_{2}MoO_{6} \) calculated by GGA + U.
band [28,29]. This strong hybridization is due to the small distance between Mo and O( \( \sim \) 1.9 Å). The Cr d states, which are mainly in the energy range 0 to -4 eV, do not hybridize strongly with Mo d states due to large Cr-Mo distance ( \( \sim \) 3.0 and \( \sim \) 3.5 Å). However, the perturbed (by mixing with Mo d) O p bands hybridizing with the Cr d states (Cr-O distance is \( \sim \) 1.9 Å) lead to a ferromagnetic interaction between the intrabilayer Cr spins. This physics is very similar to what we found in \( Cr_{2}WO_{6} \) [7]. As elaborated in the cartoon shown in Fig. 5, a simple perturbative way of understanding this ferromagnetic coupling is that hybridization of O p with empty Mo d orbitals creates a virtual hole in the O p-band. This “hole” leads to a ferromagnetic coupling between two \( Cr^{3+}d \) spins, which flank this oxygen atom. In this sense, the empty 5d orbitals of the Mo are responsible for the observed ferromagnetic coupling between nearest-neighbor intrabilayer Cr spins, quite similar to what happens in the W compound.
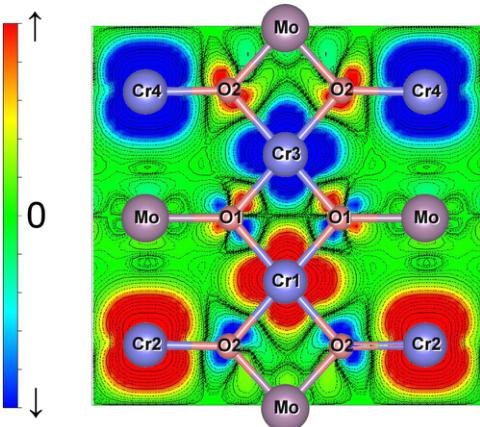
To visualize the magnetic ordering and orbital hybridization effect, we show the spin densities projected onto the \( (110) \) plane in Fig. 6. We can see that the intrabilayer \( (\mathrm{Cr1-Cr2,Cr3-Cr4}) \) Cr spin densities are the same (ferromagnetic ordering, blue-blue, or red-red) and interbilayer \( (\mathrm{Cr1-Cr3,Cr2-Cr4}) \) spin densities are opposite (antiferromagnetic ordering, red-blue), which is very similar to that of

FIG. 5. (Color online) A cartoon illustrating the ferromagnetic coupling between two Cr 3d moments via the orbital hybridization between O 2p orbitals and Mo empty 4d orbitals leading to a virtual electron transfer from O 2p to Mo 4d, leaving O 2p partially occupied which induces a ferromagnetic coupling between two Cr moments via Cr 3d–O 2p hybridization.
\( Cr_{2}WO_{6} \) but in contrast to \( Cr_{2}TeO_{6} \) [7]. The remarkable difference is seen in the spin density associated with the oxygen atom (O2), which mediates the intrabilayer exchange between Mo (W) and Te. In the former, both lobes are of the same polarization, whereas for Te they have opposite polarization (for W and Te please see Ref. [7]), characteristic of ferromagnetic and antiferromagnetic coupling between Cr1 and Cr2, respectively.
We would like to note that the mechanism of the intrabilayer ferromagnetic coupling in \( Cr_{2}MoO_{6} \) and \( Cr_{2}WO_{6} \) via the empty 4d (5d) obitals of Mo (W) discussed above is fundamentally different from the proposed antiferromagnetic exchange mechanisms in \( EuTiO_{3} \) [8] and \( CaCu_{3}Ti_{4}O_{12} \) [9] via the empty 3d orbitals of Ti. In \( EuTiO_{3} \) , the exchange interaction between two nearest-neighbor \( Eu^{f7} \) moments comes from three mechanisms [8]: (i) an antiferromagnetic superexchange through filled oxygen 2p states, (ii) a ferromagnetic coupling through hybridization between Eu f states at one site with empty Eu 5d orbitals at the other (followed by Hunds exchange coupling between Eu f and d at the same site—the well-known Kasuya mechanism [30]), and (iii) an antiferromagnetic

FIG. 6. (Color online) Spin density projected on (110) of \( Cr_{2}MoO_{6} \) calculated using GGA + U where red and blue indicate spin up and down, respectively. Similar results for the W and Te compounds are given (from Ref. [7]). Since the local cubic axes of the \( CrO_{6} \) octahedra are rotated from the chosen tetragonal x-y-z coordinates (see Fig. 1), in the latter coordinate system \( Cr d-t_{2g} \) and \( d-e_{g} \) states are mixed.
superexchange through empty Ti 3d orbitals. (i) is quite small and (ii) and (iii) compete. Small changes in the lattice constant (introduced by strain) can tune this competition and change the nearest-neighbor Eu-Eu interaction from antiferro- to ferromagnetic [31]. In principle, the ferromagnetic exchange coupling proposed by us could also be present in \( EuTiO_{3} \) . The empty Ti 3d orbitals can hybridize with O p, which mediates the superexchange between two Eu moments. However, in this compound, the Eu-O-Eu superexchange is extremely small (zero) due to 90° superexchange path (Eu-O-Eu bond angle). Thus, the mixing of O p with Ti d does not do much to this very small superexchange. In \( CaCu_{3}Ti_{4}O_{12} \) , Toyoda et al. [9] found that the long-range exchange interaction (third nearest neighbor) between two Cu moments is mediated through two O and one Ti atoms in a Cu-O-Ti-O-Cu exchange path where the empty 3d orbitals of Ti introduce an antiferromagnetic exchange between two Cu moments. Similar physics also operates when Ti is replaced by Zr, the empty 4d orbitals of the Zr atom playing the role of Ti 3d orbital.
Finally, we would like to comment the difference in \( T_{N} \) of \( Cr_{2}MoO_{6} \) and \( Cr_{2}\mathrm{WO}_{6} \) . For this purpose, we have calculated the sign and the strength of the interbilayer (J, Cr3-Cr1 distance \( \sim2.780\ \AA \) ) and intrabilayer (j, Cr3-Cr4 distance \( \sim3.604\ \AA \) ) exchange interactions between Cr moments using a simple nearest-neighbor Heisenberg model \( H = -2\sum_{\langle ij\rangle} J_{ij}\vec{S}_{i} \cdot \vec{S}_{j} \) for the two compounds within GGA and GGA+U. The respective values are given in Table III. Note that compared to J and j, further neighbor interactions (e.g., the interaction between two nearest-neighbor Cr3 ions within the layer separated by a distance of \( 4.587\ \AA \) ) is much smaller and thus negligible. A similar approximation was previously made in Ref. [12]. As seen in the table, introduction of U reduces the strengths of the exchange couplings in general. However, because of the competition between ferromagnetic and antiferromagnetic contributions to a given exchange parameter, the introduction
TABLE III. Exchange parameters J and j obtained from the simple isotropic Heisenberg model \( H = -2 \sum_{\langle ij\rangle} J_{ij} \vec{S}_i \cdot \vec{S}_j \) ; \( J_{ij} = j \) for nearest-neighbor (nn) intrabilayer and \( J_{ij} = J \) for nn interbilayer exchange. Values with superscript * are obtained using GGA based on a model proposed in Ref. [12].
| Compound Parameter | \( Cr_{2}MoO_{6} \) | \( Cr_{2}WO_{6} \) | ||
| J (meV) | j (meV) | J (meV) | j (meV) | |
| Theo. (GGA) | -5.4 | 2.7 | -10.4 | 1.0 |
| Theo. (GGA +U) | -1.9 | 0.15 | -1.0 | 0.75 |
| Ref. [12] | -3.8 \( ^{*} \) | 0.12 \( ^{*} \) | ||
of U affects J and j differently, not only for a given system but also between different systems. The precise quantitative values should not be taken seriously but the qualitative trends are consistent with experiment. Nevertheless, one can see that GGA+U seems to give a better description of the observed antiferromagnetic transition temperature \( T_{N} \) (45 and 93 K for W and Mo compounds, respectively) since the energy scale of \( T_{N} \) is primarily set by J. In addition, the smaller j value of \( Cr_{2}MoO_{6} \) than that of \( Cr_{2}WO_{6} \) given by the GGA+U calculation is also consistent with the scenario that the Mo 4d orbital is less extended than the W 5d one, which is expected to contribute to the weaker ferromagnetic interaction induced via a lesser extent of the d-p orbital hybridization. More careful calculations of the total energy using improved approximations to exchange-correlation potential within DFT (both local and nonlocal) are needed to pin down the parameters of the exchange Hamiltonian. Also magnon dispersion measurements and theoretical calculations will help us understand the nature of magnetic exchange in these interesting systems.
In summary, we have studied the magnetic and electronic properties of an inverse-trirutile compound \( Cr_{2}MoO_{6} \) to examine the idea that low-lying empty d bands associated with Mo can induce a ferromagnetic coupling between two Cr moments by perturbing the p orbitals of the O atom, which
[1] H. A. Kramers, Physica 1, 182 (1934).
[2] P. W. Anderson, Phys. Rev. 79, 350 (1950).
[3] J. Kanamori, J. Phys. Chem. Solids 10, 87 (1959).
[4] J. B. Goodenough, Phys. Rev. 100, 564 (1955).
[5] C. Zener, Phys. Rev. 82, 403 (1951).
[6] W. Kunnmann, S. La Placa, L. M. Corliss, J. M. Hastings, and E. Banks, J. Phys. Chem. Solids 29, 1359 (1968).
[7] M. Zhu, D. Do, C. R. Dela Cruz, Z. Dun, H. D. Zhou, S. D. Mahanti, and X. Ke, Phys. Rev. Lett. 113, 076406 (2014).
[8] H. Akamatsu, Y. Kumagai, F. Oba, K. Fujita, H. Murakami, K. Tanaka, and I. Tanaka, Phys. Rev. B 83, 214421 (2011).
[9] M. Toyoda, K. Yamauchi, and T. Oguchi, Phys. Rev. B 87, 224430 (2013).
[10] A. Collomb, J. J. Capponi, M. Gondrand, and J. C. Joubert, J. Solid State Chem. 23, 315 (1978).
[11] J. Rodríguez-Carvajal, Physica (Amsterdam) 192B, 55 (1993).
[12] M. Drillon, L. Padel, and J. C. Bernier, Physica (Amsterdam) 97B+C, 380 (1979).
[13] M. Yamaguchi and M. Ishikawa, J. Phys. Soc. Jpn. 63, 1666 (1994).
[14] R. Moessner and A. P. Ramirez, Phys. Today 59, 24 (2006).
[15] Since the strongest exchange interaction is between the two \( Cr^{3+} \) moments forming dimers Cr1-Cr3, it is possible that above \( T_{N} \) intradimer spin correlations still persist which will lead to a reduction in the magnetic entropy from the free ion (S = 3/2) value.
[16] P. J. Brown, J. B. Forsyth, E. Lelièvre-Berna, and F. Tasser, J. Phys. Condens. Mater. 14, 1957 (2002).
[17] S. D. Mahanti and T. A. Kaplan, J. Appl. Phys. 69, 5382 (1991).
[18] T. A. Kaplan. S. D. Mahanti, and H. Chang, Phys. Rev. B 45, 2565 (1992).
mediates the exchange between these two Cr atoms. The underlying physics is similar to the one we have previously suggested for \( Cr_{2}WO_{6} \) with low-lying empty W5d bands. GGA+U appears to give a better description of the system. However, for a quantitative understanding of the exchange parameters more theoretical work is necessary. Also, inelastic scattering measurements of magnon spectra will be helpful in pinning down the exchange parameters to validate the theoretical predictions.
ACKNOWLEDGMENTS
X.K. acknowledges the support from the start-up funds at Michigan State University. D.D. and S.M. acknowledge support by the Institution for Cyber Enabled Research (ICER), and High Performance Computer Center (HPCC) at Michigan State University. Z.D. and H.D.Z. thank for the support for the support of NSF-DMR-1350002. J.G.C. acknowledges the support of the NSFC and MOST of China (Grants No. 11304371 and No. 2014CB921500) and the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB07020100). Work at ORNL was supported by the Scientific User Facilities Division, Office of Basic Energy Sciences, DOE.
[19] S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys, and A. P. Sutton, Phys. Rev. B 57, 1505 (1998).
[20] G. Kresse and J. Furthmüller, Comp. Mater. Sci. 6, 15 (1996).
[21] G. Kresse and J. Furthmüller, Phys. Rev. B 54, 11169 (1996).
[22] G. Kresse and J. Hafner, Phys. Rev. B 47, 558 (1993).
[23] G. Kresse and D. Joubert, Phys. Rev. B 59, 1758 (1999).
[24] John P. Perdew, Kieron Burke, and Matthias Ernzerhof, Phys. Rev. Lett. 77, 3865 (1996).
[25] R. M. Martin, Electronic Structure Theory: Basic Theory and Practical Methods (Cambridge University Press, Cambridge, UK, 2004).
[26] Vladimir I. Anisimov, Jan Zaanen, and Ole K. Andersen, Phys. Rev. B 44, 943 (1991).
[27] V. I. Anisimov, I. V. Solovyev, M. A. Korotin, M. T. Czyzyk, and G. A. Sawatzky, Phys. Rev. B 48, 16929 (1993).
[28] The dominant mixing between \( O2p \) and Mo d orbitals comes from the latter's 4d orbitals, not from the deep lying 3d orbitals. This is easily seen by looking at the atomic energies of \( O2p \) ( \( E_{O2p} = -0.632 \) au), Mo 4d ( \( E_{Mo4d} = -0.358 \) au), and Mo 3d ( \( E_{Mo3d} = -9.284 \) au). The energy difference between \( O2p \) and Mo 4d is \( \sim7.45 \) eV, whereas that between \( O2p \) and Mo 3d is \( \sim235.45 \) eV. Thus \( O2p \) and Mo 3d mixing is expected to be extremely small. In fact, in our electronic-structure calculations, Mo 3d were treated as core state and not a part of the manifold of active orbitals. In a recent paper on \( \alpha \) -MoO \( _{3} \) [29], the authors stated that the hybridization of \( O2p \) is with Mo 3d. This is just a mistake because they use the same electronic-structure package that we have used and the Mo 3d states are treated as core states.
[29] P.R. Huang, Y. He, C. Cao, and Z. H. Lu, Sci. Rep. 4, 7131 (2014).
[30] T. Kasuya, IBM J. Res. Dev. 14, 214 (1970).
[31] C. J. Fennie and K. M. Rabe, Phys. Rev. Lett. 97, 267602 (2006).