| Transition Temperature | 190 K |
|---|---|
| Experiment Temperature | 110 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | Cmcm (#63) |
| Magnetic Space Group | Cm'cm' (#63.464) |
| Magnetic Point Group | m'm'm (8.4.27) |
| Lattice Parameters | 4.34500 11.01900 4.10800 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1007/s10751-013-0924-4 |
| Reference | R. A. Susilo, J. M. Cadogan, D. H. Ryan, N. R. Lee-Hone, R. Cobas, S. Munoz-Perez, Hyperfine Interactions (2013) 226 257 - 266 |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Gd1 | Gd | 0.0 | 4.6 | 0.0 | 4.60 |
Spin-reorientation in GdGa
R. A. Susilo · J. M. Cadogan · D. H. Ryan ·
N. R. Lee-Hone · R. Cobas · S. Muñoz-Pérez
© Springer Science+Business Media Dordrecht 2013
Abstract We have determined the magnetic structure of the intermetallic compound GdGa by \( {}^{155} \) Gd Mössbauer spectroscopy and neutron powder diffraction. This compound crystallizes in the orthorhombic (Cmcm) CrB-type structure. It orders ferromagnetically at \( T_{c}=190(2) \) K and then undergoes a spin reorientation at \( T_{SR}=68(2) \) K. Between \( T_{c} \) and \( T_{SR} \) , the magnetic structure is characterized by ferromagnetic order of the Gd moments along the b-axis. On cooling below \( T_{SR} \) , the Gd 4c magnetic moments split into two groups (2:2). At 3.6 K, the Gd moment is \( 6.7(4)\mu_{B} \) , and the Gd magnetic moments are in the b c-plane, canted by \( 84(3)^{\circ} \) and \( 46(4)^{\circ} \) with respect to the crystallographic b-axis. This splitting into two magnetically inequivalent sites is confirmed by our 5 K \( {}^{155} \) Gd Mössbauer results.
Keywords Magnetic structure · \( {}^{155} \) Gd Mössbauer spectroscopy · Neutron diffraction · Rare earth intermetallics
1 Introduction
The orthorhombic RGa (R = rare earth) intermetallic compounds crystallise in the CrB-type Cmcm (#63) structure with one R site and one Ga site, both 4c. The
RGa compounds were first prepared in the early 1960's \( [1-4] \) . They order ferromagnetically with a Curie temperature ranging from a high of \( \sim \) 187 K in GdGa \( [5-10] \) to a low of 15 K for TmGa \( [6, 11] \) . Neutron diffraction determinations of the magnetic structures in this system have been reported for TbGa \( [12] \) , ErGa \( [13] \) and HoGa \( [14] \) .
Hyperfine studies of the RGa series have been carried out using \( {}^{119} \) Sn Mössbauer spectroscopy on Sn-doped RGa samples [9, 15], \( {}^{161} \) Dy Mössbauer spectroscopy [16] and Perturbed Angular Correlation spectroscopy [17]. In 1992, Nesterov et al. [15] used \( {}^{119} \) Sn-doped samples to demonstrate that NdGa, HoGa and ErGa undergo spin-reorientations upon cooling. This Mössbauer work was extended by Delyagin et al. [9]. Within the last few years, the RGa compounds have attracted some interest due to their potential for use as magnetocaloric-effect-based low-temperature refrigeration materials [10, 18–20].
In this paper we present the results of our \( {}^{155} \) Gd Mössbauer spectroscopy and neutron powder diffraction work carried out on GdGa. This compound is a ferromagnet with a Curie temperature of 187(4) K \( [5–10] \) and was reported to undergo a spin-reorientation at around 85 K \( [9, 10] \) . Electronic structure calculations on GdGa by Liu and Altounian \( [21] \) predicted a Curie temperature of 187 K, in good agreement with our experimental value of 190(2) K. Our interest in this compound stems from the \( {}^{119} \) Sn Mössbauer work of Delyagin et al. \( [9] \) who found that while a single sextet was sufficient to fit the \( {}^{119} \) Sn spectra of Sn-doped GdGa between \( T_{c} \) and \( T_{SR} \) , below \( T_{SR} \) two equal-area sextets were required, in contrast to the other RGa compounds that they studied where a single sextet was sufficient at all temperatures. The fact that two sextets were required to fit the \( {}^{119} \) Sn spectra obtained below \( T_{SR} \) was interpreted as indicating that the crystallographically equivalent Gd 4c sites split into two magnetically-inequivalent sites with different magnetic orientations within the crystal cell. These authors used the magnitude and temperature dependence of the electric quadrupole splitting to suggest that between \( T_{c} \) and \( T_{SR} \) , the gadolinium moments in GdGa lie in the ab-plane canted by an angle of 57° away from the crystallographic a-axis. In their analysis, the subsequent reorientation leaves the gadolinium moments in the ab-plane, but split into two distinct magnetic sublattices canted by 30(5)° and 64(5)° away from the crystallographic a-axis.
Our aim here is to make a direct measurement of the ordering directions of the Gd moments above and below \( T_{SR} \) using neutron diffraction and \( {}^{155}Gd \) Mössbauer spectroscopy, and to determine if the Gd-4c site does indeed split into two magnetically inequivalent sites below the reorientation temperature.
2 Experimental methods
2.1 Sample preparation and characterization
The polycrystalline GdGa sample was prepared by melting high purity starting elements (Alfa Aesar, (Gd (99.9 %) and Ga (99.999 %)) in an argon-arc furnace under a purified argon gas atmosphere. To promote homogeneity, the sample was wrapped in Tantalum foil and then annealed at \( 850\ ^{\circ}C \) for three weeks in an evacuated quartz tube. The sample purity was checked by x-ray diffraction using a Siemens D5000 diffractometer and \( Cu-K_{\alpha} \) radiation. The a.c. magnetic susceptibility
was measured at a frequency of 377 Hz down to 4 K in a magnetic field of amplitude 1.5 mT.
2.2 Mössbauer spectroscopy
The 50 mCi \( {}^{155} \) Sm source was prepared by neutron activation of \( {}^{154} \) SmPd \( _{3} \) . The source and sample were mounted vertically in a helium flow cryostat and the drive was operated in sinusoidal mode. The 86.55 keV Mössbauer \( \gamma \) -photons were isolated from the various x-rays emitted by the source with a high-purity Ge detector. The drive system was calibrated using a laser interferometer with velocities cross checked against both \( {}^{57} \) CoRh/ \( \alpha \) -Fe at room temperature and \( {}^{155} \) SmPd \( _{3} \) /GdFe \( _{2} \) at 5 K. The sample temperature was monitored with a calibrated Cernox thermometer. The spectra were fitted using a non-linear least-squares minimization routine using an exact solution to the full Hamiltonian [22]. The electric quadrupole coupling constants (ground state) obtained from the fits are referred to as eQV \( _{zz} \) .
2.3 Neutron diffraction
Natural gadolinium is the most powerful neutron absorbing element in the Periodic Table and conventional powder diffraction on a sample such as GdGa, which contains 50 at.% Gd, is impractical. However, we have used a large-area, flat-plate sample holder \( [23] \) to great effect in recent studies of highly-absorbing samples \( [24–28] \) and this method was used in the present study of GdGa. Neutron diffraction experiments were carried out on the C2 multi-wire powder diffractometer (DUALSPEC) at the NRU reactor, Canadian Neutron Beam Centre, Chalk River, Ontario. To prepare the flat-plate samples for the neutron diffraction measurements \( \sim170 \) mg (about a 1/e absorption thickness) of finely powdered material was spread across a 2.4 cm by 8 cm area on a 600 \( \mu \) m thick single-crystal silicon wafer and immobilised using a 1 % solution of GE-7031 varnish in toluene/methanol (1:1). A second silicon wafer was used as a cover. The two plates were mounted in an aluminium frame and loaded into a closed-cycle refrigerator with the sample in a partial pressure of helium to ensure thermal uniformity. The plate was oriented with its surface normal parallel to the incident neutron beam to maximise the total flux onto the sample and the measurements were made in transmission mode. A neutron wavelength ( \( \lambda \) ) of 1.3286(1) Å was used as no long-period antiferromagnetic ordering modes were expected. All full-pattern magnetic and structural refinements employed the FullProf/WinPlotr suite \( [29, 30] \) with neutron scattering length coefficients for natural Gd taken from the tabulation by Lynn and Seeger \( [31] \) . As all of the key magnetic reflections occurred below \( 2\theta = 35^{\circ} \) , no absorption correction was applied, however the data were truncated at \( 2\theta = 35^{\circ} \) to minimise the potential impact of angle-dependent absorption effects.
3 Results
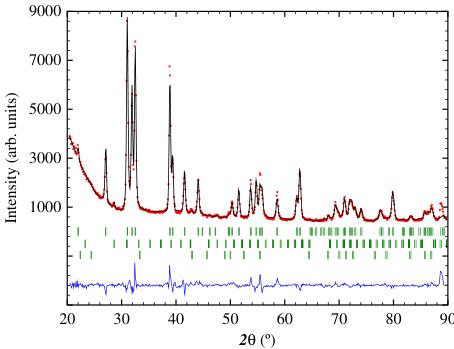
Refinement of the x-ray powder diffraction pattern obtained at 295 K (Fig. 1) confirmed the formation of the CrB-type Cmcm orthorhombic phase. Small amounts (around 3 wt% total) of \( GdGa_{2} \) and \( Gd_{2}O_{3} \) impurity phases were present in the
Fig. 1 X-ray powder diffraction pattern of GdGa obtained at 295 K with \( Cu-K_{\alpha} \) radiation. The sets of Bragg markers (top to bottom) represent GdGa, GdGa \( _{2} \) and \( Gd_{2}O_{3} \)

Table 1 Crystallographic data (at 295 K) for GdGa determined by x-ray diffraction
| Atom | Site | Point symmetry | y |
| Gd | 4c | m2m | 0.3614(3) |
| Ga | 4c | m2m | 0.0785(5) |
| Orthorhombic Cmcm (#63) | |||
| a = 4.345(1) Å | b = 11.019(3) Å | c = 4.108(1) Å | |
| \( R_{\text{Bragg}} = 7.3 \) | \( R_{F} = 8.1 \) | ||
The 4c site is generated by (0, y, \( \frac{1}{4} \) )
sample. The crystallographic data obtained by refinement of the x-ray diffraction pattern are given in Table 1.
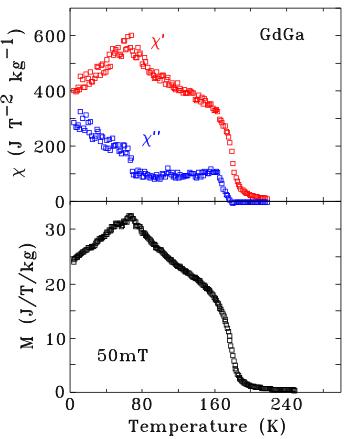
In Fig. 2 we show the temperature dependence of the a.c.-susceptibility and the magnetization (obtained in a field of 50 mT) of GdGa. The Curie temperature of GdGa is 190(2) K and the spin-reorientation of the magnetic structure at 68(2) K is clear in all signals.
3.1 Neutron diffraction
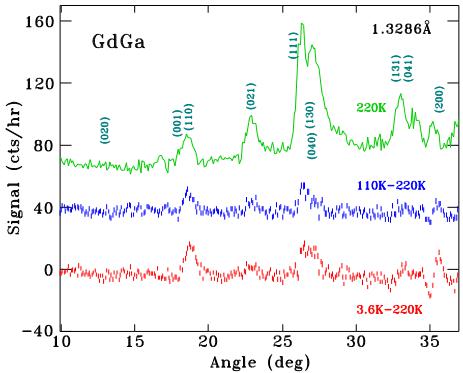
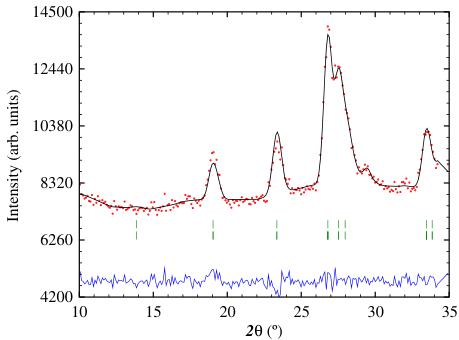
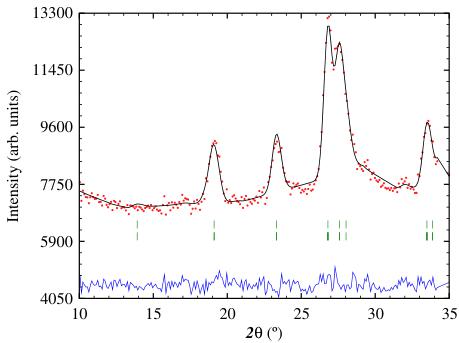
In Fig. 3 we plot the neutron powder diffraction patterns of GdGa, showing the nuclear pattern obtained at 220 K and also the differences between the patterns at 110 K and 220 K and between 3.6 K and 220 K. These difference plots show the magnetic contributions to the overall scattering.
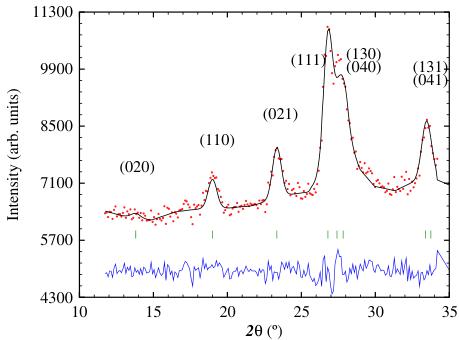
In Fig. 4 we show the refinements of the neutron powder diffraction patterns of GdGa, obtained at 220 K (in the paramagnetic state showing only the nuclear scattering), at 110 K (between \( T_{c} \) and \( T_{SR} \) in the ferromagnetic state) and at 3.6 K (below \( T_{SR} \) ).
The conventional R-factors for the refinement of the nuclear scattering in the 220 K pattern are \( R_{F} = 7.6 \) and \( R_{Bragg} = 10.65 \) .
It is clear from the difference plots in Fig. 3 that the magnetic scattering is rather weak. The diffraction pattern obtained at 110 K (Fig. 4) i.e. magnetically ordered
Fig. 2 (Top) Temperature dependence of the in-phase \( (\chi^{\prime}) \) and out-of-phase \( (\chi^{\prime\prime}) \) a.c.-susceptibility of GdGa obtained at 377 Hz in a magnetic field of 1.5 mT. (Bottom) Magnetization of GdGa obtained in a field of 50 mT

Fig. 3 Neutron powder diffraction pattern of GdGa obtained at 220 K (green, top), the difference between the 110 K and 220 K patterns (blue, middle) and between 3.6 K and 220 K (red, bottom). The neutron wavelength was 1.3286(1) Å. The plots have been offset vertically for clarity

but above the spin-reorientation temperature, shows magnetic contributions from the Gd sublattice. There are no additional peaks that might signal antiferromagnetic order and all magnetic contributions add to the existing Bragg nuclear peaks i.e. the propagation vector k is \( [0\ 0\ 0] \) . The dominant magnetic contributions occur at the \( (110) \) , \( (021) \) and \( (111) \) positions, with scattering angles of \( 2\theta\sim18.7^{\circ} \) , \( 22.9^{\circ} \) , and \( 26.3^{\circ} \) , respectively. The lack of a magnetic contribution at the \( (020) \) position \( (2\theta\sim13.7^{\circ}) \) is significant.
In order to consider all the symmetry-allowed magnetic structures for GdGa, we carried out Representational Analysis for the Gd site using the BASIREPS
Fig. 4 Neutron powder diffraction patterns of GdGa obtained at 220 K, 110 K and 3.6 K, with a neutron wavelength of 1.3286(1) Å. The two sets of Bragg markers represent the nuclear and magnetic contributions of GdGa to the patterns



Table 2 Representational analysis for the Gd(4c) site in GdGa with the space group Cmcm and a propagation vector \( [0\ 0\ 0] \)
| Representation | Ordering mode | Magnetic (Shubnikov) group | Moment arrangement |
| \( \Gamma_{2} \) | \( G_{Y} \) | \( Cm'c'm' \) | \( + - + - \) |
| \( \Gamma_{3} \) | \( F_{Z} \) | \( Cm'c'm \) | \( + + + + \) |
| \( \Gamma_{4} \) | \( G_{X} \) | \( Cm\ c\ m' \) | \( + - + - \) |
| \( \gamma_{5} \) | \( F_{Y} \) | \( Cm'c\ m' \) | \( + + + + \) |
| \( \Gamma_{7} \) | \( F_{X} \) | \( Cm\ c'm' \) | \( + + + + \) |
| \( \gamma_{8} \) | \( G_{Z} \) | \( Cm'c\ m \) | \( + - + - \) |
The respective atomic positions are \( (0, y, \frac{1}{4}) \) , \( (0, \overline{y}, \frac{3}{4}) \) , + the \( (\frac{1}{2}, \frac{1}{2}, 0) \) C-translation
program, part of the FullProf/WinPlotr suite \( [29, 30] \) . The decomposition of the magnetic representation comprises six one-dimensional representations, each appearing once:
\[ \Gamma_{\mathrm{M a g}}^{4\mathrm{c}}=\mathbf{1}\Gamma_{2}+\mathbf{1}\Gamma_{3}+\mathbf{1}\Gamma_{4}+\mathbf{1}\Gamma_{5}+\mathbf{1}\Gamma_{7}+\mathbf{1}\Gamma_{8} \quad (1) \]
and the basis vectors of these irreducible representations are given in Table 2.
We can rule out the antiferromagnetic modes \( \Gamma_{2} \) , \( \Gamma_{4} \) and \( \Gamma_{8} \) on the strength of the magnetometry and susceptibility work that clearly indicates ferromagnetic order. Thus, we are left with ferromagnetic order along one of the orthorhombic crystal axes. The absence of any magnetic intensity at the (020) peak suggests ferromagnetic order along the b-axis, corresponding to the \( \Gamma_{5} \) ( \( Cm'cm' \) ) mode. Our best refinement to the 110 K neutron diffraction pattern of GdGa was achieved with a Gd magnetic moment of \( 4.6(1)\mu_{B} \) oriented along the b-axis. The refined Gd moment is in excellent agreement with the Gd magnetisation data of Zhang et al. [10] ( \( \sim110JT^{-1}kg^{-1}\rightarrow4.5\mu_{B} \) ). The conventional R-factors for the refinement of the 110 K pattern are \( R_{F}=6.2 \) , \( R_{Bragg}=6.2 \) and \( R_{mag}=8.1 \) .
Upon further cooling, we observe a progressive increase in the magnetic contribution to the (110) peak at \( 2\theta = 18.7^{\circ} \) , relative to that of the (021) peak at \( 2\theta = 22.9^{\circ} \) . Similar changes occur at other peaks, indicating that the magnetic order tips away from the crystal b-axis. This spin-reorientation has been observed in a.c.-susceptibility measurements (Fig. 2 and [10]) and also by \( {}^{119} \) Sn Mössbauer spectroscopy [9].
Analysis of the neutron diffraction pattern obtained at 3.6 K (Fig. 4) and the difference pattern between 110 K and 3.6 K (Fig. 3) showed that a single Gd magnetic contribution was insufficient for the refinement of the 3.6 K diffraction pattern. The four Gd magnetic moments in the Cmcm cell split into two (2:2) magnetically inequivalent groups, differing only in their orientations. We find that the Gd moments are within the bc-plane, canted by \( 84(3)^{\circ} \) and \( 46(4)^{\circ} \) from the b-axis, respectively. The refined Gd moment is \( 6.7(4)\mu_{B} \) at 3.6 K, in excellent agreement with the 'free-ion' value of \( 7\mu_{B} \) . The conventional R-factors for the refinement of the 3.6 K pattern are \( R_{F}=7.3 \) , \( R_{Bragg}=7.2 \) and \( R_{mag}=11.7 \) .
3.2 \( ^{155} \) Gd Mössbauer spectroscopy
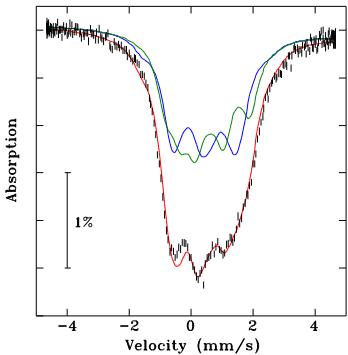
In Fig. 5, we show the \( {}^{155} \) Gd Mössbauer spectrum of GdGa, obtained at 5 K. As with the neutron diffraction pattern taken below \( T_{SR} \) , we found that a single magnetically-
Fig. 5 \( {}^{155} \) Gd Mössbauer spectrum of GdGa, obtained at 5 K. The green (Gd-1) and blue (Gd-2) lines represent the two equal area subspectra, as described in the text

split component was insufficient to fit this spectrum and the fit requires two equal-area components. In this instance, the Mössbauer data provide unequivocal proof of the splitting of the Gd 4c sites. The two subspectra have essentially the same hyperfine parameters, as expected since they originate from the same crystallographic site. The only difference between the two sites is \( \theta \) , the angle between the hyperfine field and the principal axis of the electric field gradient (EFG), \( V_{zz} \) . Due to \( \eta \) being near its maximal value of 1, positive and negative \( eQV_{zz} \) give similar fits with the condition that \( \theta \rightarrow (90^{\circ} - \theta) \) , so while the magnitude of \( eQV_{zz} \) can be found, its sign is indeterminate. In Table 3 we show the values for negative \( eQV_{zz} \) .
The Gd 4c site has m2m point symmetry, which allows for a non-zero EFG asymmetry parameter, \( \eta \) , and forces the EFG axes to align with the crystallographic axes. There is, however, no requirement that the principal axis (z) aligns with any particular crystallographic axis. The hyperfine magnetic field, \( B_{hf} \) , at the Gd site is almost entirely due to the local contribution of the Gd moment, so it is collinear with the Gd moment. The angle, \( \theta \) , between \( V_{zz} \) and \( B_{hf} \) can thus be related to the direction within the crystallographic reference frame if the EFG \( \rightarrow \) crystallographic axis assignment can be established. Therefore, the only remaining issue is whether there is such an assignment which makes the \( {}^{155} \) Gd Mössbauer and neutron diffraction results consistent.
We first consider the results of Table 3, with negative \( eQV_{zz} \) . Directing the z-axis of the EFG along the crystallographic c-axis, and the x-axis along the a-axis, with the fitted azimuthal angle \( (\phi) \) equal to \( 90^{\circ} \) , places the hyperfine field (and hence the Gd moments) in the \( yz-(EFG) \) -plane or b c-(crystallographic)-plane, consistent with the neutron diffraction data presented above. Furthermore, \( \phi = 90^{\circ} \) means that \( \theta \) represents a rotation away from the c-axis so that the angle between the moments and the b-axis is \( 90^{\circ} - \theta \) . Thus, the Gd moment directions obtained from \( {}^{155}Gd \) Mössbauer spectroscopy \( (90(2)^{\circ} = 90^{\circ} - \theta_{Gd-1} \) and \( 41(2)^{\circ} = 90^{\circ} - \theta_{Gd-2}) \) are in excellent agreement with those derived from neutron diffraction \( (84(3)^{\circ} \) and \( 46(4)^{\circ}) \) . The EFG axis \( \rightarrow \) crystallographic axis assignment for negative \( eQV_{zz} \) is thus \( (XYZ) \equiv (ab c) \) . For positive \( eQV_{zz} \) , the angles are \( \theta \rightarrow 90 - \theta \) , so the correct EFG
Table 3 Hyperfine parameters of GdGa obtained by \( {}^{155} \) Gd Mössbauer spectroscopy at 5 K. I. S. = isomer shift, \( B_{hf} \) = hyperfine field, \( \eta \) = EFG asymmetry parameter
| Component | I.S. (mm/s) | eQVzz (mm/s) | Bhf (T) | η | θ | φ | Area (%) |
| Gd-1 | 0.47(1) | -1.45(3) | 39.5(3) | 0.87(1) | 0(2) | 90 | 50 |
| Gd-2 | 0.46(1) | -1.43(3) | 39.8(3) | 0.88(1) | 49(2) | 90 | 50 |
axis → crystallographic axis assignment is \( (-XZY)\equiv(ab\,c) \) , which yields the same moment directions in the crystallographic cell as the negative \( eQV_{zz} \) case.
3.3 \( ^{119} \) Sn Mössbauer spectroscopy
Delyagin et al. [9] used \( {}^{119} \) Sn doping in the RGa compounds to study the magnetic order of the R sublattice by \( {}^{119} \) Sn Mössbauer spectroscopy. Since the Sn replaces Ga which also occupies a 4c site, the EFG constraints discussed with respect to the Gd–4c site in the previous section also apply. There is, however, no reason for the EFG axis → crystallographic axis assignments of the Gd and (Ga/Sn) sites to be the same.
The Sn dopant is non-magnetic, so any hyperfine field at this dopant site is transferred from the neighbouring magnetic order of the R sublattice. Information about the ordering directions can be deduced by determining the orientation of the hyperfine field (assumed collinear with the R magnetic order) within the principal axis frame of the EFG at the \( {}^{119} \) Sn site. The original analysis by Delyagin et al. [9] placed the Gd moments within the ab-plane, at angles of \( 30(5)^{\circ} \) and \( 64(5)^{\circ} \) relative to the a-axis. However, this is inconsistent with our neutron diffraction results that place the Gd moments in the bc-plane.
In light of this, we re-evaluated the \( {}^{119} \) Sn Mössbauer spectrum taken at 5 K. An analysis of all possible EFG → crystallographic axis assignments was undertaken with the angles constrained to \( \theta_{1}=0^{\circ} \) and \( \theta_{2}=45^{\circ} \) within the bc-plane. We found that with the assignment \( (\mathrm{YZX})\equiv(ab\,c) \) , the calculated peak positions were almost indistinguishable from the pattern generated with the \( \theta_{1}=30^{\circ} \) and \( \theta_{2}=64^{\circ} \) angles found by Delyagin et al.. With the \( (\mathrm{YZX})\equiv(ab\,c) \) axis assignment, we obtain agreement between the \( {}^{119} \) Sn Mössbauer spectroscopy, our \( {}^{155} \) Gd Mössbauer spectroscopy and neutron powder diffraction results.
4 Conclusions
We have used \( {}^{155} \) Gd Mössbauer spectroscopy and neutron powder diffraction to show that the magnetic order of the Gd sublattice in GdGa is ferromagnetic along the orthorhombic b-axis below its Curie temperature of 190(2) K. Upon cooling below 68(2) K, the Gd moments split into two magnetically inequivalent sublattices which can't away from the b-axis within the bc-plane, and at 3.6 K make angles of 84(3)° and 46(4)°, relative to the b-axis. This splitting of the Gd 4c site into two subgroups is particularly prominent in the \( {}^{155} \) Gd Mössbauer spectrum which provides unequivocal evidence that such a splitting occurs.
Acknowledgements Activation of the \( {}^{155} \) Gd Mössbauer source was carried out in the National Research Universal (NRU) research reactor, operated by Atomic Energy of Canada, Ltd., at Chalk River, Ontario, by Raghu Rao and Robert Speranzini. JMC acknowledges support from
the Australian Research Council and the University of New South Wales. DHR and NRL-H were supported by grants from Natural Sciences and Engineering Research Council of Canada and Fonds Québécois de la Recherche sur la Nature et les Technologies. Initial parts of this work were carried out at the University of Manitoba where JMC was a faculty member, supported by the Canada Research Chairs programme, the Natural Sciences and Engineering Research Council of Canada, the Canada Foundation for Innovation and the Manitoba Research Infrastructure Fund. RAS acknowledges a University International Postgraduate Award and a University College Postgraduate Research Scholarship. Finally, we are very grateful to Professor Vasily Krylov of the Skobeltsyn Institute of Nuclear Physics, Moscow State University, for sending us the original \( {}^{119} \) Sn Mössbauer spectra of \( {}^{119} \) Sn doped GdGa.
References
-
Iandelli, A.: In: The Physical Chemistry of Metallic Solutions and Intermetallic Compounds, vol. 1, pp. 376. Chemical Publishing Co., Inc, New York (1960)
-
Baenziger, N.C., Moriarty, Jr. J.L.: Acta Cryst. 14, 946–947 (1961)
-
Schob, O., Parthé, E.: Acta Cryst. 19, 214–224 (1965)
-
Dwight, A.E., Downey, J.W., Conner Jr. R.A.: Acta Cryst. 23, 860–862 (1967)
-
Fujii, H., Shohata, N., Okamoto, T., Tatsumoto, E.: J. Phys. Soc. Japan 31, 1592 (1971)
-
Barbara, B., Nguyen, V.N., Siaud, E.: C.R. Acad. Sci. B274, 1053 (1972)
-
Shohata, N.: J. Phys. Soc. Japan 42, 1873–1880 (1977)
-
Leithe-Jasper, A., Hiebl, K.: Phys. Stat. Sol. A 155, 223–231 (1996)
-
Delyagin, N.N., Krylov, V.I., Rozantsev, I.N.: J. Magn. Magn. Mater. 308, 74–79 (2007)
-
Zhang, J.Y., Luo, J., Li, J.B., Liang, J.K., Wang, Y.C., Ji, L.N., Liu, Y.H., Rao, G.H.: J. Alloys Compounds 469, 15–19 (2009)
-
Gao, T., Nishimura, K., Matsumoto, T., Namiki, T., Isikawa, Y.: Solid State Commun. 158, 1–4 (2013)
-
Cable, J.W., Koehler, W.C., Wollan, E.O.: Phys. Rev. 136, A240–A242 (1964)
-
Barbara, B., Bècle, C., Nguyen, N.N., Siaud, E.: Conf. Digest No. 3: Rare-Earths and Actinides, pp. 219–221. Institute of Physics, Durham (1971)
-
Susilo, R.A., Muñoz-Pérez, S., Cobas, R., Cadogan, J.M., Avdeev, M.: J. Phys. Conf. Ser. 340, 012071 (6pp) (2012)
-
Nesterov, V.I., Reiman, S.I., Rozantsev, I.N.: Sov. Phys. Solid State 34, 671–673 (1992)
-
Iraldi, R., Nguyen, V.N., Rossat-Mignod, J., Tcheou, F.L.: Solid State Commun. 15, 1543–1546 (1974)
-
Cavalcante, F.H.M., Pereira, L.F.D., Saitovich, H., Mestnik-Filho, J., Pasquevich, A.F., Forker, M.: Hyperfine Interact. 221, 123–128 (2013)
-
Chen, J., Shen, B.G., Dong, Q.Y., Hu, F.X., Sun, J.R.: Appl. Phys. Lett. 95, 132504 (3pp) (2009)
-
Chen, J., Shen, B.G., Dong, Q.Y., Sun, J.R.: Solid State Commun. 150, 157–159 (2010)
-
Zheng, X.Q., Chen, J., Shen, J., Zhang, H., Xu, Z.Y., Gao, W.W., Wu, J.F., Hu, F.X., Sun, J.R., Shen, B.G.: J. Appl. Phys. 111, 07A917 (3pp) (2012)
-
Liu, X.B., Altounian, Z.: Physica B 406, 710–714 (2011)
-
Voyer, C.J., Ryan, D.H.: Hyperfine Interact. 170, 91–104 (2006)
-
Ryan, D.H., Cranswick, L.M.D.: J. Appl. Cryst. 41, 198–205 (2008)
-
Cadogan, J.M., Ryan, D.H., Napoletano, M., Riani, P., Cranswick, L.M.D.: J. Phys.: Cond. Matter 21, 124201 (8pp) (2009)
-
Ryan, D.H., Cadogan, J.M., Ritter, C., Canepa, F., Palenzona, A., Putti, M.: Phys. Rev. B: Rapid Comm. 80, 220503(R) (4pp) (2009)
-
Ryan, D.H., Cadogan, J.M., Cranswick, L.M.D., Gschneidner Jr. K.A., Pecharsky, V.K., Mudryk, Ya.: Phys. Rev. B 82, 224405 (6pp) (2010)
-
Ryan, D.H., Cadogan, J.M., Xu, S.G., Xu, Z., Cao, G.: Phys. Rev. B 83, 132403 (4pp) (2011)
-
Lemoine, P., Cadogan, J.M., Ryan, D.H., Giovannini, M.: J. Phys.: Cond. Matter 24, 236004 (8pp) (2012)
-
Rodríguez-Carvajal, J.: Physica B 192, 55–69 (1993)
-
Roisnel, T., Rodríguez-Carvajal, J.: Mater. Sci. Forum 378–381, 118–123 (2001)
-
Lynn, J.E., Seeger, P.A.: At. Data Nucl. Data Tables 44, 191–207 (1990)