| Transition Temperature | 66(3) K |
|---|---|
| Experiment Temperature | 45 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | Cmcm (#63) |
| Magnetic Space Group | Cm'c'm (#63.462) |
| Magnetic Point Group | m'm'm (8.4.27) |
| Lattice Parameters | 4.27620 10.75710 4.03440 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1088/1742-6596/340/1/012071 |
| Reference | R. A. Susilo, S. Munoz Perez, R. Cobas, J. M. Cadogan, M. Avdeev, Journal of Physics: Conference Series (2012) 340 012071 |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Ho1 | Ho | 0.0 | 0.0 | 6.2 | 6.20 |
Magnetic order and spin-reorientation in HoGa
R A Susilo \( ^{1} \) , S Muñoz Pérez \( ^{1} \) , R Cobas \( ^{1} \) , J M Cadogan \( ^{1} \) and M Avdeev \( ^{2} \)
\( ^{1} \) Department of Physics and Astronomy, University of Manitoba, Winnipeg, Manitoba, R3T 2N2, Canada
\( ^{2} \) Bragg Institute, ANSTO, PMB 1, Menai, NSW 2234, Australia
E-mail: cadogan@physics.umanitoba.ca
Abstract. We have determined the magnetic structure of the intermetallic compound HoGa by high-resolution neutron powder diffraction. This compound crystallizes in the orthorhombic \( (Cmcm) \) CrB-type structure and the magnetic structure comprises ferromagnetic order of the Ho sublattice along the c-axis. The Curie temperature is 66(3) K. Upon cooling below 20 K, the Ho magnetic moments can't away from the c-axis towards the ab-plane. At 3 K, the Ho moment is 8.8(2) \( \mu_{B} \) and the Ho magnetic moments point in the direction \( \theta = 30(2)^{\circ} \) and \( \phi = 49(4)^{\circ} \) with respect to the crystallographic c-axis. The observation of an ab-plane component at around 50° from the a-axis is in contrast with the suggested magnetic structure of ac order ( \( \theta = 32^{\circ} \) and \( \phi = 0^{\circ} \) ) reported by Delyagin et al. [1] on the basis of a \( {}^{119} \) Sn Mössbauer spectroscopy study of a Sn-doped HoGa sample. However, we find that these two sets of orientations are in fact indistinguishable by Mössbauer spectroscopy.
1. Introduction
The orthorhombic RGa (R = rare earth) compounds crystallize in the CrB-type \( Cmcm\ (\#63) \) structure. There is one R site, the 4c, and one Ga site, also a 4c. The RGa compounds were first prepared in the early 1960's [2, 3, 4, 5]. They order ferromagnetically with a Curie temperature that ranges from a high of 183 K in GdGa [6, 7, 8] to a low of \( \sim \) 15 K in TmGa [9]. Neutron diffraction work on TbGa was reported in 1964 by Cable et al. [10] who showed that the Tb moments order along the c-axis. In 1971, Barbara et al. used neutron diffraction to show that ErGa orders along the b-axis [11]. In 1992, Nesterov et al. [12] used \( {}^{119} \) Sn Mössbauer spectroscopy on Sn-doped samples to show that NdGa, HoGa and ErGa undergo spin-reorientations upon cooling. This Mössbauer work was recently extended by Delyagin et al. [1]. Within the last year or two, the RGa compounds have attracted some interest due to their potential for use as magnetocaloric-effect-based low-temperature refrigeration applications [13, 14, 15].
In this paper we present the results of high-resolution neutron powder diffraction carried out on HoGa to examine the spin-reorientation reported to occur at \( \sim \) 20 K. HoGa is a ferromagnet with a Curie temperature of 66(3) K [1, 6, 12, 15]. Its initial easy direction of order is the c-axis and the reorientation was suggested by Delyagin et al. [1] to involve a canting towards the a-axis, within the ac-plane. We show that the canting actually tips the Ho moments towards an intermediate planar arrangement, which differs from the structure suggested on the basis of \( {}^{119} \) Sn Mössbauer spectroscopy. However, we find that the two magnetic structures are, in fact, indistinguishable by \( {}^{119} \) Sn Mössbauer spectroscopy.
2. Experimental Methods
The HoGa sample was prepared in an argon-arc furnace. Stoichiometric amounts of the pure elements (Ho (99.9%) and Ga (99.999%)) were melted several times under pure (less than 1 ppm impurity) argon to ensure homogeneity. X-ray powder diffraction measurements were made at room temperature using Cu–Kα radiation on a PANalytical X'Pert Pro diffractometer. Neutron diffraction experiments were carried out on the Echidna high-resolution powder diffractometer at the OPAL reactor in Sydney, Australia [16]. The neutron wavelength was \( 1.6220(5) \) Å. The neutron diffraction data were corrected for absorption effects and all patterns were refined using the Rietveld method and the FullProf/WinPlot suite [17, 18].
3. Results
Refinement of the x-ray powder diffraction pattern obtained at 295 K confirmed the formation of the CrB-type Cmcm orthorhombic phase. Any impurity phases present amounted to less than 1 wt%, undetectable in the powder diffraction pattern. The refined lattice parameters are \( a = 4.2794(5) \) Å, \( b = 10.7869(11) \) Å, \( c = 4.0445(5) \) Å.
3.1. Neutron Diffraction
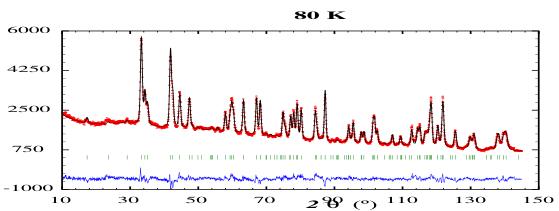
In figure 1 we show the neutron powder diffraction patterns of HoGa, obtained at 80 K, 45 K, 22 K and 3 K. The Curie temperature of HoGa is 66(3) K, as mentioned earlier, so the 80 K pattern represents the nuclear scattering from the orthorhombic Cmcm cell. In Table 1 we show the atomic position parameters for HoGa derived from a refinement to the 80 K nuclear diffraction pattern. The conventional R-factors for this refinement are \( R_{B} = 5.65\% \) and \( R_{F} = 4.06\% \) .
Table 1. Crystallographic data for HoGa in the orthorhombic Cmcm cell, refined from the neutron diffraction patterns. The 4c site occupied by both the Ho and Ga atoms is defined by the atomic positions \( (0\ y\ \frac{1}{4}) \) .
| T(K) | a(Å) | b(Å) | c(Å) | Atom | y |
| 80 | 4.2779(5) | 10.7595(10) | 4.0353(4) | Ho | 0.3592(3) |
| Ga | 0.0750(5) | ||||
| 45 | 4.2762(5) | 10.7571(11) | 4.0344(5) | Ho | 0.3595(4) |
| Ga | 0.0752(6) | ||||
| 22 | 4.2760(5) | 10.7589(11) | 4.0337(5) | Ho | 0.3596(3) |
| Ga | 0 | ||||
| 3 | 4.2758(5) | 10.7582(11) | 4.0337(5) | Ho | 0.0594(3) |
| Ga | 0 0751(6) |
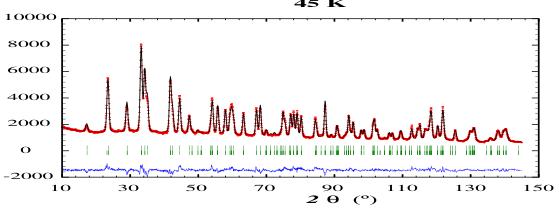
The diffraction patterns obtained at 45 K, 22 K and 3 K show considerable magnetic contributions from the Ho sublattice. There are no additional peaks that would signal antiferromagnetic order and all magnetic contributions simply add to the existing Bragg nuclear peaks i.e. the propagation vector k = 0. The dominant magnetic contributions occur at the \( (020) \) , \( (110) \) and \( (021) \) positions, with scattering angles \( 2\theta \sim 17.3^{\circ} \) , \( 23.6^{\circ} \) and \( 29.1^{\circ} \) , respectively.
In order to consider all possible magnetic structures allowed for HoGa, we carried out Representational Analysis for the Ho site using the BASIREPS program, part of the




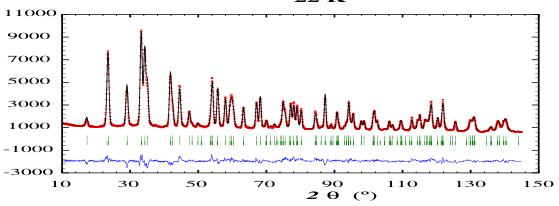
Figure 1. Neutron powder diffraction patterns of HoGa obtained at 80 K, 45 K, 22 K and 3 K, with a neutron wavelength of 1.6220(5) Å. The two sets of Bragg markers represent the nuclear and magnetic contributions to the patterns.
FullProf/WinPlotr suite [17, 18]. The decomposition of the magnetic representation comprises six one-dimensional representations, each appearing once:
\[ \Gamma_{M a g}^{4c}=1\Gamma_{2}+1\Gamma_{3}+1\Gamma_{4}+1\Gamma_{5}+1\Gamma_{7}+1\Gamma_{8} \quad (1) \]
and the basis vectors of these irreducible representations are given in table 2.
We can rule out the antiferromagnetic modes \( \Gamma_{2} \) , \( \Gamma_{4} \) and \( \Gamma_{8} \) on the strength of the magnetometry and susceptibility work which clearly indicates ferromagnetic order. Thus, we are left with ferromagnetic order along one of the orthorhombic crystal axes. The observation of
Table 2. Representational Analysis for the Ho(4c) site in HoGa with a propagation vector k = 0. The respective atomic positions are \( (x, y, z) \) , \( (-x, -y, -z) \) , \( (\frac{1}{2} + x, \frac{1}{2} + y, z) \) , and \( (\frac{1}{2} - x, \frac{1}{2} - y, -z) \) .
| Representation | Ordering Mode | Moment directions |
| \( \Gamma_{2} \) | \( G_{Y} \) | + - + - |
| \( \Gamma_{3} \) | \( F_{Z} \) | + + + + |
| \( \Gamma_{4} \) | \( G_{X} \) | + - + - |
| \( \Gamma_{5} \) | \( F_{Y} \) | + + + + |
| \( \Gamma_{7} \) | \( F_{X} \) | + + + + |
| \( \Gamma_{8} \) | \( G_{Z} \) | + - + - |
substantial magnetic contributions to the (020) and (200) peaks, combined with the absence of any magnetic intensity at the (002) peak, clearly indicates ferromagnetic order along the c-axis, corresponding to the \( \Gamma_{3} \) mode. At 45 K we find a refined Ho magnetic moment of \( 6.2(2)\mu_{B} \) , which increases to \( 8.2(2)\mu_{B} \) by 22 K. The conventional R-factors for the 45 K refinement are \( R_{B}=6.44\% \) , \( R_{F}=4.32\% \) and \( R_{mag}=7.27\% \) . The R-factors for the 22 K refinement are \( R_{B}=7.30\% \) , \( R_{F}=5.29\% \) and \( R_{mag}=6.93\% \) .
Upon further cooling below 22 K we observe an increase in the magnetic intensity at the \( (021) \) peak at \( 2\theta = 29.1^{\circ} \) , relative to the magnetic intensity at the \( (110) \) peak at \( 2\theta = 23.6^{\circ} \) . Similar changes occur at other peaks, indicating that the magnetic order tips away from the crystal c-axis. This spin-reorientation has been observed in ac-susceptibility measurements [15]. At 3 K, the Ho magnetic moments are canted away from the c-axis by \( 30(2)^{\circ} \) . The moments amount to \( 8.8(2)\mu_{B} \) at 3 K, i.e. the 'free-ion' value \( (9\mu_{B}) \) . The R-factors for the 3 K refinement are \( R_{B} = 5.27\% \) , \( R_{F} = 4.04\% \) and \( R_{mag} = 4.38\% \) . Our refinement of the 3 K pattern also shows that the canting Ho moments tip towards an intermediate planar arrangement between the crystal a- and b-axes. We find polar angles of \( \theta = 30(2)^{\circ} \) and \( \phi = 49(4)^{\circ} \) . This reorientation is driven by competition between the different crystal-field orders acting on the \( Ho^{3+} \) ions, with the higher-order \( (4^{th} \) and \( 6^{th}) \) terms becoming significant as the temperature is lowered. The observation of c-axis order just below \( T_{c} \) is consistent with the signs and relative magnitudes of the diagonal and off-diagonal second-order crystal-field terms derived from single-crystal susceptibility measurements by Shohata et al. [7, 8].
3.2. \( ^{119} \) Sn Mössbauer spectroscopy
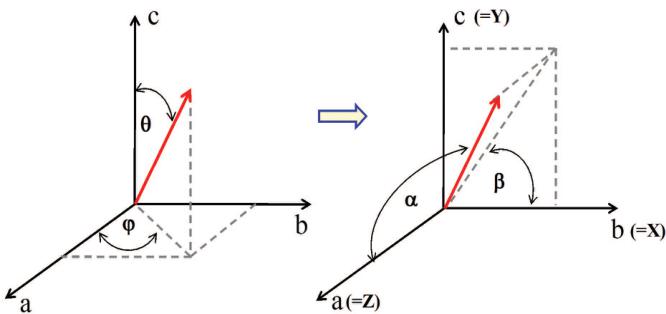
Delyagin et al. [1] used \( {}^{119} \) Sn doping in the RGa compounds to study the magnetic order of the R sublattice by \( {}^{119} \) Sn Mössbauer spectroscopy. The Sn dopant is non-magnetic so any hyperfine field at this dopant site is transferred from the neighbouring magnetic order of the R sublattice. Information about the ordering directions can be deduced by determining the orientation of the hyperfine field (assumed collinear with the R magnetic order) within the principal axis frame of the Electric Field Gradient (EFG) at the \( {}^{119} \) Sn site. Delyagin et al. showed that the EFG axes are aligned along the orthorhombic axes, as expected from the m2m point symmetry of the Ga 4c sites, the location of the \( {}^{119} \) Sn dopant. The particular identification of the EFG axes is \( (xyz)=(bca) \) . Within this EFG frame, the temperature dependence of the quadrupole splitting showed that above about 20 K the hyperfine field makes an angle of \( 90^{\circ} \) with the \( z(\mathrm{EFG}) \) axis, along the \( y(\mathrm{EFG}) \) axis. In other words, Ho magnetic ordering is along the c-axis, as we found by neutron diffraction. Below 20 K, this angle decreases to about \( 58^{\circ} \) at 4 K, with the hyperfine field lying in the \( yz(\mathrm{EFG}) \) plane, i.e. Ho magnetic order in the crystal ac-plane. In figure 2 we show the orientational relationship between the Mössbauer and neutron diffraction measurements, in terms of the crystal (abc) and EFG (xyz) axes.

Figure 2. Orientation of the Ho magnetic moment (and hence hyperfine field at \( {}^{119} \) Sn sites) relative to the crystal (abc) and EFG(xyz) axes, used in the interpretation of the neutron powder diffraction and Mössbauer data.
The quadrupole shift in a magnetically split Mössbauer spectrum, as defined by Delyagin et al., is
\[ QSH=\frac{eQV_{zz}}{8}\times[3cos^{2}\alpha-1+\eta(sin^{2}\alpha)cos(2\beta)] \quad (2) \]
using standard notation. Here, \( \alpha \) and \( \beta \) are the polar angles of the hyperfine magnetic field in the principal axis frame of the EFG at the \( {}^{119} \) Sn nuclei. The asymmetry of the EFG tensor is described by the \( \eta \) parameter. Using the accepted conventions for describing the components of the EFG tensor, Delyagin et al. deduced \( eQV_{zz} = 1.10(8) \) mm/s and \( \eta = 0.65(9) \) . Thus, taking \( \theta = 58^{\circ} \) and \( \phi = 90^{\circ} \) , one obtains the experimentally observed value of QSH i.e. \( -0.087(4) \) mm/s.
As shown earlier, the principal z-axis of the EFG frame lies along the crystal's orthorhombic a-axis. Our neutron diffraction results are determined relative to the crystal c-axis. It is straightforward to show that our angles \( \theta = 30(2)^{\circ} \) and \( \phi = 49(4)^{\circ} \) correspond to \( \alpha = 71(3)^{\circ} \) and \( \beta = 66(3)^{\circ} \) in the EFG frame employed in the Mössbauer work and using equation (2), our magnetic structure yields a QSH value of \( -0.15(4) \) mm/s, fully consistent with the Mössbauer result.
4. Conclusions
We have used high-resolution neutron powder diffraction to show that the magnetic order of the Ho sublattice in HoGa is ferromagnetic along the orthorhombic c-axis below its Curie temperature of \( 66(3) \) K. Below \( \sim20 \) K, the Ho moments can't away from the c-axis towards the ab-plane and at 3 K the Ho magnetic order is defined by the polar angles of \( \theta=30(2)^{\circ} \) and \( \phi=49(4)^{\circ} \) , relative to the orthorhombic abc axes.
Acknowledgments
We are grateful for financial support from the Natural Sciences and Engineering Research Council of Canada and the Canada Foundation for Innovation. JMC acknowledges support from the Canada Research Chairs programme.
References
[1] Delyagin N N, Krylov V I and Rozantsev I N 2007 J. Magn. Magn. Mater. 308 74–9.
[2] Iandelli A 1960 in The Physical Chemistry of Metallic Solutions and Intermetallic Compounds 1 376. New York: Chemical Publishing Co., Inc.
[3] Baenziger N C and Moriarty Jr. J L 1961 Acta Cryst. 14 946–7.
[4] Schob O and Parthé E 1965 Acta Cryst. 19 214–24.
[5] Dwight A E, Downey J W and Conner Jr. R A 1967 Acta Cryst. 23 860–2.
[6] Fujii H, Shohata N, Okamoto T and Tatsumoto E 1971 J. Phys. Soc. Japan 31 1592.
[7] Shohata N, Fujii H and Okamoto T 1974 J. Phys. Soc. Japan 37 567.
[8] Shohata N 1977 J. Phys. Soc. Japan 42 1873–80.
[9] Barbara B., Nguyen V N and Siaud E 1972 C.R. Acad. Sci. B274 1053.
[10] Cable J W, Koehler W C and Wollan E O 1964 Phys. Rev. 136 A240–2.
[11] Barbara B, Bècle C, Nguyen N N and Siaud E 1971 Conf. Digest No. 3: Rare-Earths and Actinides, Institute of Physics, Durham, 219–221.
[12] Nesterov V I, Reiman S I and Rozantsev I N 1992 Sov. Phys. Solid State 34 671–3.
[13] Zhang J Y, Luo J, Li J B, Liang J K, Wang Y C, Ji L N, Liu Y H and Rao G H 2009 J. Alloys and Compounds 469 15–9.
[14] Chen J, Shen B G, Dong Q Y, Hu F X and Sun J R 2009 Appl. Phys. Lett. 95 132504 (3pp).
[15] Chen J, Shen B G, Dong Q Y and Sun J R 2010 Solid State Commun. 150 157–9.
[16] Liss K-D, Hunter B A, Hagen M E, Noakes T J and Kennedy S J 2006 Physica B 385-6 1010-2.
[17] Rodríguez-Carvajal J 1993 Physica B 192 55–69.
[18] Roisnel T and Rodríguez-Carvajal J 2001 Mater. Sci. Forum 378–81 118–23.