| Transition Temperature | 365 K |
|---|---|
| Experiment Temperature | 77 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | Pm-3m (#221) |
| Magnetic Space Group | R-3m' (#166.101) |
| Magnetic Point Group | -3m' (20.5.75) |
| Lattice Parameters | 3.833 3.833 3.833 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1063/1.1709571 |
| Reference | E. Kren, G. Kadar, L. Pal and P. Szabo, Journal of Applied Physics (1967) 38 1265-1266. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Mn1 | Mn | 2.4 | -1.2 | -1.2 | 2.94 |
Investigation of the FirstOrder Magnetic Transformation in Mn3Pt
E. Krén, G. Kádár, L. Pál, and P. Szabó
Citation: Journal of Applied Physics 38, 1265 (1967); doi: 10.1063/1.1709571
View online: http://dx.doi.org/10.1063/1.1709571
View Table of Contents: http://scitation.aip.org/content/aip/journal/jap/38/3?ver=pdfcov
Published by the AIP Publishing
Articles you may be interested in
Kinetic arrest related to a first-order ferrimagnetic to antiferromagnetic transition in the Heusler compound Mn2PtGa
J. Appl. Phys. 113, 17E308 (2013); 10.1063/1.4800687
The Need for a Firstorder Quasi Lorentz Transformation AIP Conf. Proc. 1301, 3 (2010); 10.1063/1.3526639
First-order magnetic phase transition in FeRh–Pt thin films J. Appl. Phys. 105, 07A904 (2009); 10.1063/1.3065973
The firstorder phase transformation in NaCN: A martensite transformation J. Appl. Phys. 54, 6900 (1983); 10.1063/1.331996
XRay and Susceptibility Study of the FirstOrder Magnetic Transformation in Mn 3 Pt J. Appl. Phys. 39, 469 (1968); 10.1063/1.2163485

Investigation of the First-Order Magnetic Transformation in \( Mn_{3}Pt \)
E. Krén, G. Kádár, L. Pál, and P. Szabó
Central Research Institute for Physics, Budapest, Hungary
The effect of composition on the first-order transformation from triangular into collinear antiferromagnetic structure (AF-AF transformation) occurring in ordered \( Mn_{3}Pt \) has been investigated on ternary \( Mn_{3}Pt_{1-x}Rh_{x} \) and binary \( Mn_{3+y}Pt_{1-y} \) alloys using x-ray and neutron-diffraction methods.
On increasing the concentrations x and y, an increase in both the Néel and the transition temperatures with a simultaneous decrease in the lattice parameter were observed. The magnetic moment of Mn remained the same irrespective of the concentration and the AF-AF transformation. The results suggest the existence of a critical lattice-parameter value at which the transformation occurs, like that observed for the \( Mn_{2-x}Cr_{x}Sb \) system.
R CENTLY \( ^{1} \) we observed a first-order magnetic transformation in \( Cu_{3}Au \) -type ordered \( Mn_{3}Pt \) . The magnetic structure transformed from triangular to collinear antiferromagnetic with increasing temperature. The atomic and magnetic unit cells in the triangular structure are identical; therefore, the magnetic neutron scattering appears as a contribution to the
TABLE I. Values of lattice parameter, transition temperatures and magnetic moment.
| Specimen | a ( \( \textup{\AA} \) ) | T_{t} ( \( ^{\circ} \) K) | T_{N} ( \( ^{\circ} \) K) | \( \mu \) ( \( \mu_{B} \) ) |
| Mn_{3}Pt | 3.833 | 365±10 | 475±10 | 3.0±0.3 |
| Mn_{3}Pt_{0.96}Rh_{0.05} | 3.833 | 415±10 | 465±10 | 3.5±0.4 |
| Mn_{3}Pt_{0.9}Rh_{0.1} | 3.832 | ... | 505±10 | 2.8±0.3 |
| Mn_{3}Pt_{0.8}Rh_{0.2} | 3.828 | ... | 555±10 | 3.2±0.4 |
| Mn_{3}Pt_{0.8}Rh_{0.5} | 3.820 | ... | 685±10 | 3.5±0.4 |
| Mn_{3}Rh | 3.813 | ... | 855±10 | 3.6±0.4 |
| Mn_{2.93}Pt_{1.07} | 3.844 | 315±10 | 460±10 | 3.4±0.4 |
| Mn_{3}Pt | 3.833 | 365±10 475±10 | 3.0±0.3 | |
| Mn_{2.09}Pt_{0.91} | 3.827 | 455±10 | 3.2±0.4 |
nuclear reflections. In the collinear structure the magnetic unit cell is doubled, and the neutron diffraction pattern is characterized by magnetic superreflections indexed by half-integers. The transformation can be easily followed up by measuring the temperature dependence of the two types of magnetic reflections. The transition is accompanied by an abrupt change in the lattice parameter, as well as by thermal hysteresis. \( Mn_{3}Rh \) of the same type, however, was found to have triangular structure up to the Néel temperature. \( ^{1,2} \)
Continuing these investigations, the effect of composition on the AF-AF transformation was studied on alloys in the ternary (pseudobinary) \( Mn_{3}Pt_{1-x}Rh_{x} \) and the binary \( Mn_{3+y}Pt_{1-y} \) systems by x-ray and neutron-diffraction methods.

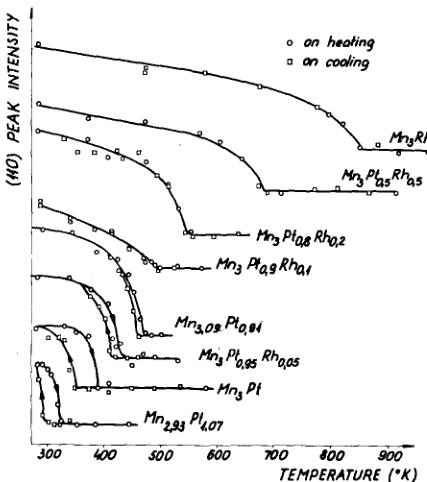
FIG. 1. Temperature dependence of the (110) reflection.
Alloys of x=0, 0.05, 0.1, 0.2, 0.5, 1.0 and y=0.09, -0.07 concentrations were prepared from 99.9% pure metals by melting. The loss in weight was about 0.2% in each case. The Mn concentration was checked by chemical analysis. The ingots were filed, then annealed at 700°C for 120 h in evacuated quartz tube. X-ray diffraction photographs taken at room temperature showed a highly ordered Cu_{3}Au-type single phase with values of lattice parameter a given in Table I.
At 77°K the neutron diffraction patterns of each specimen indicate triangular structure with magnetic moments of Mn listed in Table I. The magnetic moment in the collinear phase could be evaluated only for

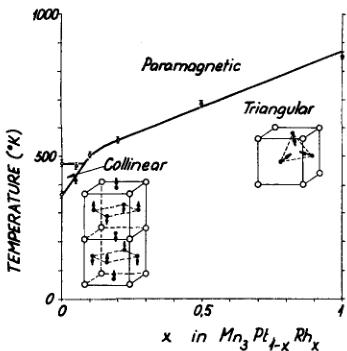
Fig. 2. Magnetic phase diagram of the \( Mn_{3}Pt_{1-x}Rh_{x} \) system.
\( y=0 \) and -0.07 as \( 2.4\pm0.3 \) and \( 2.8\pm0.3\mu_{B} \) at \( 380^{\circ} \) and \( 340^{\circ}K \) respectively. The transition temperature \( T_{t} \) of the AF-AF transformation and the Néel temperature \( T_{N} \) were determined from the temperature dependence of the (110) and \( (10\frac{1}{2}) \) reflections associated with triangular and collinear structures, respectively. The results for (110) are shown in Fig. 1. If observable, \( (10\frac{1}{2}) \) changes oppositely. The values of \( T_{t} \) and \( T_{N} \) are included in Table I. In spite of the abrupt change and thermal hysteresis in (110), \( T_{N} \) could not be determined in the y=0.09 specimen since \( (10\frac{1}{2}) \) could not be observed. This is probably due to the closeness of the values of \( T_{t} \) and \( T_{N} \) . The magnetic phase diagram of the \( Mn_{3}Pt_{1-x}Rh_{x}~ \) system is given in Fig. 2. As seen, the collinear structure is stable only in a limited concentration and temperature range. It would be more stable in the binary alloys at lower Mn concentrations if the ordered crystal structure existed. \( ^{3} \) The variation of a with temperature was measured by high-temperature x-ray diffractometer on specimens of y=0 and -0.07. The curves in Fig. 3 show a discontinuity at \( T_{t} \) as well.

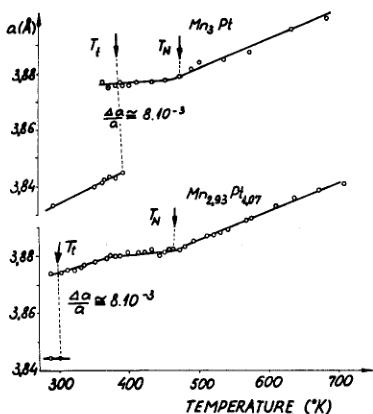
FIG. 3. Temperature dependence of the lattice parameter for y=0 and -0.07.
as a break at \( T_{N} \) . An anomalous behavior between \( T_{t} \) and \( T_{N} \) is apparent for y=0.07.
On increasing the x and y concentrations, an increase in both \( T_{t} \) and \( T_{N} \) with a decrease in a can be observed. Within the experimental accuracy the magnetic moment of Mn does not change with concentration nor during the AF-AF transformation. The simultaneous variation of \( T_{t} \) and a suggests the existence of a critical lattice parameter value at which the transition occurs, similarly to the \( Mn_{2-x}Cr_{x}Sb \) system. \( ^{4} \) The relation between \( T_{t} \) and a is not linear ( \( T_{t} \) is more sensitive to changes in a if close to \( T_{N} \) ), then this may be attributed to the anomaly in a in Fig. 3. The different values of \( T_{t} \) in x=0.2 and y=0.09, for which a is the same, could be explained by different thermal expansion coefficients in the ternary and binary alloys. In order to clarify the role of the lattice parameter in the AF-AF transformation, x-ray measurements on further specimens are in progress.
\( ^{4} \) C. Kittel, Phys. Rev. 120, 335 (1960).