| Transition Temperature | 155 K |
|---|---|
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | P63cm (#185) |
| Magnetic Space Group | P63c'm' (#185.201) |
| Magnetic Point Group | 6m'm' (25.4.94) |
| Lattice Parameters | 5.96520 5.96520 11.70220 90.00 90.00 120.00 |
|---|---|
| DOI | 10.1103/physrevlett.114.217602 |
| Reference | S.M. Disseler, J.A. Borchers, C.M. Brooks, J.A. Mundy, J.A. Moyer, D.A. Hillsberry, E.L. Thies, D.A. Tenne, J. Heron, M.E. Holtz, J.D. Clarkson, G.M. Stiehl, P. Schiffer, D.A. Muller, D.G. Schlom and W.D. Ratcliff, Physical Review Letters (2015) 114. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Fe1 | Fe | 2.9 | 0.0 | 0.0 | 2.90 |
Magnetic Structure and Ordering of Multiferroic Hexagonal LuFeO_{3}
Steven M. Disseler, \( ^{1} \) Julie A. Borchers, \( ^{1} \) Charles M. Brooks, \( ^{2} \) Julia A. Mundy, \( ^{3} \) Jarrett A. Moyer, \( ^{4} \) Daniel A. Hillsberry, \( ^{5} \) Eric L. Thies, \( ^{5} \) Dmitri A. Tenne, \( ^{5} \) John Heron, \( ^{2} \) Megan E. Holtz, \( ^{3} \) James D. Clarkson, \( ^{6} \) Gregory M. Stiehl, \( ^{7} \) Peter Schiffer, \( ^{4} \) David A. Muller, \( ^{3,8} \) Darrell G. Schlom, \( ^{2,8} \) and William D. Ratcliff \( ^{1} \)
\( ^{1} \) NIST Center for Neutron Research, National Institute of Standards and Technology, Gaithersburg, Maryland 20899, USA
\( ^{2} \) Department of Materials Science and Engineering, Cornell University, Ithaca, New York 14853, USA
\( ^{3} \) School of Applied and Engineering Physics, Cornell University, Ithaca, New York 14853, USA
\( ^{4} \) Department of Physics and Frederick Seitz Materials Research Laboratory, University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA
\( ^{5} \) Department of Physics, Boise State University, Boise, Idaho 83725, USA
\( ^{6} \) Department of Materials Science and Engineering, University of California, Berkeley, California 94720, USA
\( ^{7} \) Department of Physics, Cornell University, Ithaca, New York 14853, USA
\( ^{8} \) Kavli Institute at Cornell for Nanoscale Science, Ithaca, New York 14853, USA
(Received 7 November 2014; revised manuscript received 16 March 2015; published 27 May 2015)
We report on the magnetic structure and ordering of hexagonal LuFeO \( _{3} \) films of variable thickness grown by molecular-beam epitaxy on YSZ (111) and Al \( _{2} \) O \( _{3} \) (0001) substrates. These crystalline films exhibit long-range structural uniformity dominated by the polar P6 \( _{3} \) cm phase, which is responsible for the paraelectric to ferroelectric transition that occurs above 1000 K. Using bulk magnetometry and neutron diffraction, we find that the system orders into a ferromagnetically canted antiferromagnetic state via a single transition below 155 K regardless of film thickness, which is substantially lower than that previously reported in hexagonal LuFeO \( _{3} \) films. The symmetry of the magnetic structure in the ferroelectric state implies that this material is a strong candidate for linear magnetoelectric coupling and control of the ferromagnetic moment directly by an electric field.
DOI: 10.1103/PhysRevLett.114.217602
PACS numbers: 77.55.Nv, 61.05.fm, 68.37.Ma, 75.25.-j
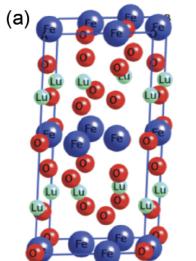
Multiferroic materials display both ferroelectric and magnetic order and have been the subject of intense investigation both from fundamental and applied perspectives \( [1,2] \) . If both order parameters are coupled, these materials would enable new devices ranging from magnetic field sensors to magnetic random access memory. Unfortunately, single-phase multiferroics are extraordinarily rare; thus far only four room-temperature single-phase multiferroics have been reported: \( \mathrm{BiFeO_{3}} \) \( [3] \) , \( \mathrm{BiCoO_{3}} \) \( [4] \) , corundum \( \mathrm{ScFeO_{3}} \) \( [5] \) , and most recently hexagonal \( \mathrm{LuFeO_{3}} \) (h- \( \mathrm{LuFeO_{3}} \) ) \( [6] \) . The latter compound, h- \( \mathrm{LuFeO_{3}} \) was found to be isostructural with \( YMnO_{3} \) \( [Fig. 1(a)] \) \( [7,8] \) when synthesized in thin film form, and antiferromagnetism appears to persist in the ferroelectric state well above room temperature. Our current investigation of the same system reveals that hexagonal \( LuFeO_{3} \) is a multiferroic, but the onset of magnetic order is well below room temperature.
Specifically, \( YMnO_{3} \) and other hexagonal manganites, \( REMnO_{3} \) (RE = Lu, Y, Ho), have been known for some time to exhibit multiferroic properties. Here, ferroelectricity is the result of a structural transition from the nonpolar \( P6_{3}/mmc \) to the polar \( P6_{3}cm \) space group above room temperature ( \( T_{C} \sim 900 \) K in \( YMnO_{3} \) ) [9]. Magnetic order sets in at much lower temperatures ( \( T_{N} \sim 80 \) K in \( YMnO_{3} \) ) [10], which renders these materials unsuitable for multiferroic devices. Even in the magnetically ordered state the coupling between the ferroelectric and magnetic order parameters is weak [11]. Replacing Mn with Fe in this system has been proposed as one way to increase the magnetic transition temperature as well as the coupling between the two order parameters [12], and has been the recent subject of increased interest [6,13]. Theoretical calculations using first-principles suggest that a weak ferromagnetic moment along the c axis may be deterministically switchable by \( 180^{\circ} \) with an electric field [12].
Reports of antiferromagnetic order above room temperature in h-LuFeO \( _{3} \) [6] coupled with theoretical predictions of a weak canted moment along the c axis [12] observed at temperatures below 147 K [13], have generated significant interest in this material for applications. In this Letter, we determine through magnetometry and neutron diffraction measurements the intrinsic magnetic structure of h-LuFeO \( _{3} \) epitaxial films exhibiting uniform \( P6_{3}cm \) structural order. We find that antiferromagnetic order is evident as previously reported [6] but occurs only below 155 K for h-LuFeO \( _{3} \) films of variable thickness on several substrates (i.e., Al \( _{2} \) O \( _{3} \) and cubic zirconia). Furthermore, its onset occurs simultaneously with the onset of the weak ferromagnetic canting of the moments. From Raman scattering we demonstrate that h-LuFeO \( _{3} \) is ferroelectric at room temperature, with a paraelectric-to-ferroelectric transition temperature \( T_{C} = 1020 \) K ± 50 K. Solving the magnetic structure we confirm that the films magnetically order in the ferroelectric state in a manner consistent with




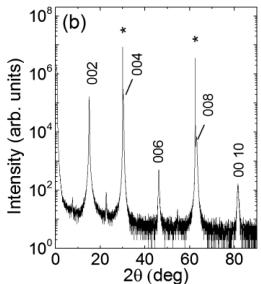
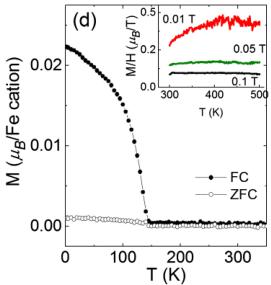
FIG. 1 (color online). Characterization of a 250 nm thick film of h-LuFeO \( _{3} \) on YSZ (YSZ-250 nm). (a) Schematic of the crystal structure of h-LuFeO \( _{3} \) with the \( P6_{3}cm \) space group. (b) XRD at room temperature, with h-LuFeO \( _{3} \) 00l reflections labeled accordingly; substrate peaks are denoted by (*). (c) STEM image along the [110] direction highlighting the positions of the Lu-ions in the "up down down" pattern demonstrating the \( P6_{3}cm \) structure. (d) Magnetization at 0.01 T under FC (closed circles) and ZFC (open circles) conditions. Inset: high temperature magnetization for magnetic fields 0.01, 0.05, and 0.1 T applied parallel to the c axis.
magnetoelectric theoretical predictions such that electric field-induced reversal of the ferromagnetic moment direction should be achievable below the magnetic ordering temperature \( (T < 155\ \text{K}) \) . Our results thus contrast with previous reports of room-temperature antiferromagnetic ordering in comparable h-LuFeO \( _{3} \) films [6]. Subtle, but significant, deviations of the structure from the \( P6_{3}cm \) phase in the films of the previous study are key to interpreting these differences in magnetic ordering temperatures.
We used oxide molecular-beam epitaxy (MBE) to grow six high-quality, single-crystalline films of h-LuFeO \( _{3} \) with thicknesses from 20 to 250 nm on 10 mm × 10 mm substrates of either (111)-oriented yttria-stabilized cubic zirconia (YSZ) or (0001) Al \( _{2} \) O \( _{3} \) [13]. The list of samples is provided in Table 1. For simplicity, each sample considered will be designated by their substrate and LuFeO \( _{3} \) thickness (e.g., YSZ-200 nm).
In Fig. 1(b), we show as an example a \( \theta \) -2 \( \theta \) XRD scan for YSZ-250 nm. The intense narrow peaks come from the substrate, while the other reflections from the film
TABLE I. Lattice parameters and Néel temperatures for each sample determined from neutron diffraction. Errors in parenthesis represent one standard deviation of the last digit as obtained from least-squares fitting.
| Sample | a( \( \textup{\AA} \) ) | c( \( \textup{\AA} \) ) | \( T_{N} \) |
| 200 nm on YSZ | 5.989(5) | 11.70(3) | 155(5) K |
| 250 nm on YSZ | 5.979(5) | 11.81(3) | 150(1) K |
| 200 nm on Al \( _{2} \) O \( _{3} \) | 5.985(5) | 11.77(2) | 140(2) K |
| 250 nm on Al \( _{2} \) O \( _{3} \) | 5.994(5) | 11.78(2) | 139(1) K |
| 70 nm on Al \( _{2} \) O \( _{3} \) | 6.050(30) | 11.97(5) | 115(20) K |
| 20 nm on Al \( _{2} \) O \( _{3} \) | 6.015(10) | 11.84(5) | 130(15) K |
demonstrate that it is single phase. Only 00l reflections with even l are observed indicating the (001) orientation of the film and consistent with the \( P6_{3}cm \) space group shown in Fig. 1(a). Similar patterns are observed for the remaining samples [14]. From STEM images along the [110] zone axis of h-LuFeO \( _{3} \) in Fig. 1(c) we find this film is also nearly free of extra Fe-O layers (syntactic intergrowths of LuFe \( _{2} \) O \( _{4} \) ) [13], which are occasionally observed in similar films [14]. These images reveal that the Lu atoms in each plane are displaced in an “up down down” pattern over extended length scales consistent with the noncentrosymmetric, polar \( P6_{3}cm \) structural phase. TEM images (Fig. S2, Ref. [6]) from previous investigations of related h-LuFeO \( _{3} \) films show local regions with the Lu atoms in the “up down down” pattern. These areas are interspersed within larger regions that exhibit a “up middle down” pattern consistent with closely related structural phases such as antipolar \( P\bar{3}c \) [15], suggesting that these nonpolar regions are intermixed with the polar \( P6_{3}cm \) phase [15].
The lattice parameters for each sample in the current study were obtained from neutron diffraction measurements of the 300 and 004 nuclear reflections at 5 K (Table 1). These values appear to be independent of both sample thickness and substrate and are within error of previously reported values for stoichiometric films [6,13]. Films with thicknesses \( \geq \) 200 nm or greater exhibit resolution-limited peak shapes at nuclear reflections [14] indicating no distribution of lattice parameters from strain or finite-size effects, while films of 20 and 70 nm are broadened only along 00l in accordance with reduced physical dimensions along that direction. It thus does not appear that the strain, potentially induced by the substrate-film interface, plays any significant role in determining the crystallographic, ferroelectric, or magnetic properties of this system regardless of film thickness.
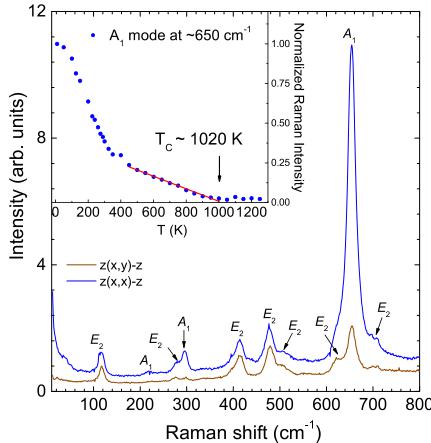
Raman measurements, shown for YSZ-200 nm in Fig. 2, reveal that the ferroelectric transition occurs well above room temperature. The observed peak positions in the Raman spectra and relative intensities are very similar to that of hexagonal \( LuMnO_{3} \) [16], as opposed to those reported for orthorhombic \( LuFeO_{3} \) [17]. We are able to distinguish at least 10 phonon modes out of the 23 that are

FIG. 2 (color online). Raman spectra of 200 nm thick h-LuFeO_{3} (YSZ-200 nm) measured at 10 K using both polarizations [14] demonstrating the Raman active phonon modes in the ferroelectric state of h-LuFeO_{3}. Inset: Normalized Raman intensity of the A_{1} mode (peak around 650 cm^{-1}) as a function of temperature, solid line is a linear fit over the temperature region 400 K < T < 1050 K.
active in the scattering geometries used, consistent with its ferroelectric structure of h-LuFeO_{3} [14]. The temperature dependence of the integrated Raman intensity of the strongest A_{1} peak, near 655 cm^{-1} [normalized by the Bose factor \( n + 1 = 1/(1 - e^{-h\omega/kT}) \) ] is shown in the inset. The intensity decreases linearly with increasing temperature between 400 and 1000 K, above which no change is observed; a linear fit of the intensity over this temperature region demonstrates a clear transition to a nonpolar phase at \( T_{c} = 1020 K \pm 50 K \) . Piezoelectric force microscopy measurements confirmed ferroelectricity at room temperature in these films through switching of the ferroelectric polarization [14].
As expected from theory [12], bulk magnetization measurements indicate that the onset of ferromagnetic order is not coincident with the ferroelectric transition, instead occurring well below room temperature. Magnetization measurements along the c axis of YSZ-250 nm are shown in Fig. 1(d). A clear transition is evident in the field-cooled data at 143 K. While the magnetization magnitude is small ( \( \sim0.02\mu_{B} \) ), it is clear evidence for weak ferromagnetism occurring in the ordered phase. The presence of weak ferromagnetism is common among all samples in this study, with onset temperatures between 118 and 150 K [14]. The offset between FC and ZFC at higher temperatures in some samples is indicative of trace amounts of \( Fe_{3}O_{4} \) or a similar impurity phase that occurs in conjunction with syntactic intergrowths seen in TEM [14]. Beyond this, we find no evidence for additional magnetic transitions at or above room temperature in measurements of the magnetic susceptibility, as shown in the inset of Fig. 1(d). Similar susceptibilities have been measured for magnetic fields applied parallel to the plane of the film indicating isotropic magnetic susceptibility above room temperature, in contrast to the previous report [6].
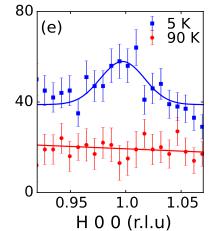
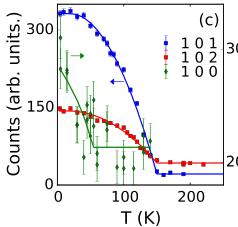
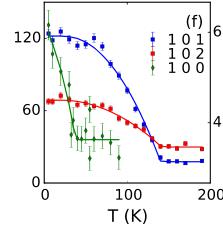
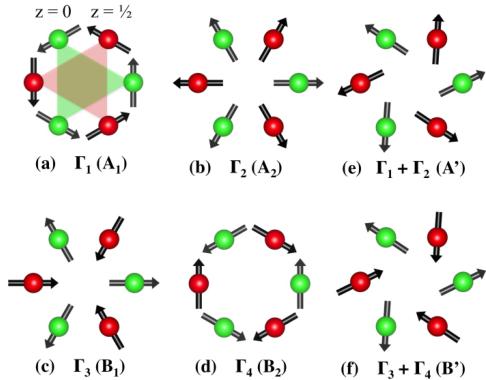
We now turn our focus to the neutron diffraction results, which provide a full picture of the corresponding antiferromagnetic order. We measured the temperature dependence (Fig. 3) of several reflections including the 101, 100, and 102, which are predominantly (or entirely) of magnetic origin. Interpretation of the differences among the temperature dependence of these reflections, however, first requires an understanding of the possible magnetic structures consistent with the \( P6_{3}cm \) space group. Representational analysis reveals that the magnetic and crystallographic unit cells of these materials are identical (q = 0) and that the magnetic structure may fall into six representations: four one-dimensional and two two-dimensional [18–20]. For the hexagonal manganites, the materials measured thus far have been well described by the one-dimensional representations which contain the classic \( 120^{\circ} \) arrangement of spins in a given plane, labeled as \( \Gamma_{1} \) to \( \Gamma_{4} \) as shown in Figs. 4(a)–4(d), respectively. Planes can either be coupled ferromagnetically ( \( \Gamma_{3} \) and \( \Gamma_{4} \) ) or antiferromagnetically ( \( \Gamma_{1} \) and \( \Gamma_{2} \) ) along the c axis, and the moments may lie along the a or b crystallographic axes with respect to the \( 120^{\circ} \) arrangement of the spins. Furthermore, only the \( \Gamma_{2} \) representation allows for a net moment along the c axis. Unfortunately, the Fe atoms lie at the \( (\frac{1}{3}00) \) position, such that the \( \Gamma_{1} \) and \( \Gamma_{3} \) representations form a homometric pair, as do the \( \Gamma_{2} \) and \( \Gamma_{4} \) representations. Members of the same homometric pair cannot be distinguished by unpolarized neutron scattering [19]. Different homometries may still be distinguished through unpolarized diffraction by the presence of the 100 magnetic reflection which is found only for the \( \Gamma_{1} \) and \( \Gamma_{3} \)
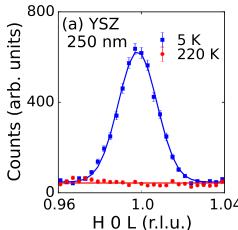
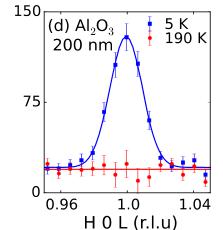
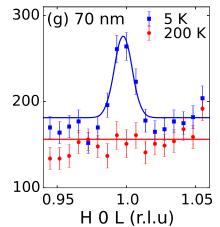
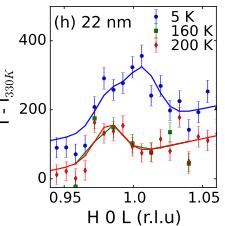
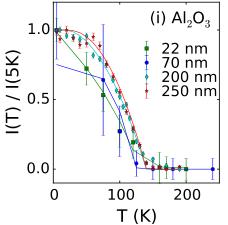
In Figs. 3(a)–3(f) we show detailed neutron diffraction results for YSZ-250 nm and \( Al_{2}O_{3} \) -200 nm as examples, noting that similar measurements were made on all six films [14]. The 101 reflection, which is entirely of magnetic origin, is present at low temperatures for all films on both YSZ and \( Al_{2}O_{3} \) substrates, including films with thicknesses of only 70 and 20 nm as shown in Figs. 3(g) and 3(h), respectively, and clearly absent above the transition temperature determined by magnetometry. Our measurements show no evidence of magnetic scattering above 155 K regardless of thickness, as demonstrated in Fig. 3(i) in which the temperature dependence of the 101 reflection is shown for films fabricated on \( Al_{2}O_{3} \) with thicknesses from 20 to 250 nm.
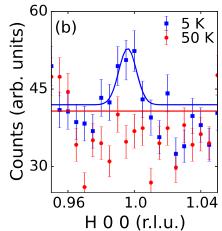
The temperature dependence of several other magnetic reflections measured on warming is shown in Figs. 3(c) and 3(f). The antiferromagnetic ordering temperature \( T_{N} \) is determined by fitting the 101 and 102 reflections









FIG. 3 (color online). Determination of the antiferromagnetic structure using neutron diffraction. The scattered intensity of the magnetic 101 and 100 reflections above and below \( T_{N} \) and temperature dependence for the (a)–(c) YSZ-250 nm and (d)–(f) \( Al_{2}O_{3} \) -200 nm. (g)–(h) Intensity of the 101 reflection \( Al_{2}O_{3} \) -70 nm and \( Al_{2}O_{3} \) -20 nm, respectively. (i) Temperature dependent intensity of the 101 reflection for films deposited on \( Al_{2}O_{3} \) . Solid lines in (c), (f), and (i) are fits with mean-field order parameter function, while others are Gaussian.
with a mean-field order parameter, from which we find \( 115(20) \) K < \( T_{N} < 155(5) \) K for all samples (Table 1). These ordering temperatures agree well with the onset of ferromagnetism obtained from magnetometry, indicating that both in-plane magnetic order and canted moments develop simultaneously and only well below room temperature in these stoichiometric h-LuFeO \( _{3} \) films.
These results directly contradict the interpretation of the temperature dependence of the 102 reflection in a stack of 20 nm films detailed in a previous report [6]. The intensity of the 102 reflection is extremely sensitive to the precise symmetry of the structural phase. For example, relative to that expected for the polar \( P6_{3}cm \) phase, the structural contribution to the 102 intensity is larger for the nonpolar, centrosymmetric \( P\bar{3}c \) phase (which is consistent with the arrangement of the Lu atoms in the TEM images for their samples [6]) and smaller for the \( P6_{3}mmc \) , and \( P6_{3}mmc \) phases. It is plausible that the apparent transition reported in Ref. [6] is not magnetic in nature, but rather represents a structural transition near or above room temperature. As in that study many films were coaligned, only a small fraction of the structure in any particular film would have to transform to change the 102 peak intensity substantially.
Significant intensity is also observed at the 100 reflection for the films in Ref. 6 though it vanishes near 130 K, which is roughly consistent with \( T_{N} \) for the films in our current study. Several of our films also have temperature-dependent 100 scattering [Figs. 3(b) and 3(e)], though this reflection does not emerge simultaneously with the 101 and 102 magnetic reflections. Rather, the appearance of the 100 reflection is consistent with a reorientation of the moments within the hk0 plane below \( T_{N} \) [20]. The reorientation temperature, \( T_{R} \) , is again determined from a fit of a mean-field order parameter of the 100 intensity, from which we find \( T_{R} = 53 \pm 3 \) K(YSZ-250 nm) and \( 38 \pm 3 \) K(Al \( _{2} \) O \( _{3} \) -200 nm), while no such reorientation is discernable for YSZ-200 nm or Al \( _{2} \) O \( _{3} \) -250 nm [14]. For YSZ-250 nm and Al \( _{2} \) O \( _{3} \) -200 nm, the ground state magnetic structure can be described by a combination of the \( \Gamma_{1} + \Gamma_{2} \) representations as shown in Fig. 4(e), and is

FIG. 4 (color online). (a)–(d) Illustration of the four one-dimensional representations for h-LuFeO_{3}. The magnetic structures below \( T_{R} \) are shown in (e) and (f) and consist of combinations of the representations in (a)–(d). Labels in parenthesis refer to the equivalent notation used in Ref. [12], for example.
consistent with that suggested previously [6], while a single \( \Gamma_{2} \) representation alone is adequate to describe \( Al_{2}O_{3}-250 \) nm. From the relative intensities of the 100 and 101 reflections we find this effect is quite small, with a maximum possible rotation of only \( 15^{\circ} \) in plane and with no effect on the ferromagnetic moment we observe. Determination of the structural origin of the variation (or absence) of \( T_{R} \) in our samples would require a precise crystallographic refinement of the Fe position and distortion of the O bipyramid [21,22] that is not feasible due to the geometric characteristics of these epitaxial films.
As no spin reorientation was observed in \( Al_{2}O_{3}-250 \) nm, we may easily refine the magnetic structure including the magnitude of the ordered Fe moments at 5 K from the integrated intensities of several magnetic and structural peaks. The in-plane magnetic structure is refined using the \( \Gamma_{2} \) representation, from which we extract an ordered magnetic moment of \( 2.9(5)\mu_{B}/Fe \) [14]. The moment is reduced from that expected for the \( S=5/2~Fe^{3+} \) , but follows similar observations of reduced moments in hexagonal manganites [18,19]. While this refinement was performed using only a single magnetic domain, we note that including equal populations of magnetic domains [12] produces a statistically similar refinement of the data with a comparable magnetic moment on the Fe site.
We conclude that uniform films with variable thickness of metastable h-LuFeO \( _{3} \) can be stabilized on different substrates. Our films exhibit robust canted antiferromagnetic order below 155 K, which is substantially below the value (440 K) previously reported [6]. Furthermore, we have demonstrated that the magnetic structure in the ordered state of h-LuFeO \( _{3} \) does not depend on the underlying substrate or film thickness and that the canting and Néel state appear as a single transition; the differences (in \( T_{N} \) , for example) that do occur among our samples cannot be attributed to differences in strain. The universal appearance of a ferromagnetically canted antiferromagnet in the ferroelectric state indicates that the films contain the proper symmetries to support coupling of the ferromagnetic moment directly to an electric field as theoretically proposed [12]. In future work, it will prove interesting to determine whether this observed canted magnetic moment is indeed switchable with electric field, since the films are ferroelectric at temperatures well above room temperature. If so, then further efforts will be warranted to determine if it is possible to increase the magnetic transition temperature in this system, or whether the lessons we learn from this material can be applied in the hunt for materials with similar magnetic properties, but with higher transition temperatures.
The authors would like to thank Hena Das, Craig Fennie, Jeffrey Lynn, Leland Harriger and Daniel Parshall for helpful discussions. Research supported by the U.S. Department of Energy, Office of Basic Energy Sciences under Award No. DE-SC0002334. Work performed at the electron microscopy facility of the Cornell Center for Materials Research was supported by the National Science Foundation (NSF) Materials Research Science and Engineering Centers program (DMR 1120296) and NSF No. IMR-0417392. This work was performed in part at the Cornell NanoScale Facility, a member of the National Nanotechnology Infrastructure Network, which is supported by the NSF (Grant No. ECCS-0335765). Raman studies at Boise State University have been supported by NSF under Grant No. DMR-1006136, and by the M.J. Murdock Charitable Trust “Partners in Science” program (E.L.T.).
[1] S.-W. Cheong and M. Mostovoy, Nat. Mater. 6, 13 (2007).
[2] R. Ramesh and N. A. Spaldin, Nat. Mater. 6, 21 (2007).
[3] J. Wang, J. B. Neaton, H. Zheng, V. Nagarajan, S. B. Ogale, B. Liu, D. Viehland, V. Vaithyanathan, D. G. Schlom, U. V. Waghmare, N. A. Spaldin, K. M. Rabe, M. Wuttig, and R. Ramesh, Science 299, 1719 (2003).
[4] A. A. Belik, S. Iikubo, K. Kodama, N. Igawa, S. Shamoto, S. Niitaka, M. Azuma, Y. Shimakawa, M. Takano, F. Izumi, and E. Takayama-Muromachi, Chem. Mater. 18, 798 (2006).
[5] M. R. Li, U. Adem, S. R. C. McMitchell, Z. Xu, C. I. Thomas, J. E. Warren, D. V. Giap, H. Niu, X. Wan, R. G. Palgrave, F. Schiffmann, F. Cora, B. Slater, T. L. Burnett, M. G. Cain, A. M. Abakumov, G. Tendeloo, M. F. Thomas, M. J. Rosseinsky, and J. B. Claridge, J. Am. Chem. Soc. 134, 3737 (2012).
[6] W. Wang, J. Zhao, W. Wang, Z. Gai, N. Balke, M. Chi, H. N. Lee, W. Tian, L. Zhu, X. Cheng, D. J. Keavney, J. Yi,
T. Z. Ward, P. C. Snijders, H. M. Christen, W. Wu, J. Shen, and X. Xu, Phys. Rev. Lett. 110, 237601 (2013).
[7] A. A. Bossak, I. E. Graboy, O. Y. Gorbenko, A. R. Kaul, M. S. Kartavtseva, V. L. Svetchnikov, and H. W. Zandbergen, Chem. Mater. 16, 1751 (2004).
[8] Y. K. Jeong, J.-H. Lee, S.-J. Ahn, and H. M. Jang, Chem. Mater. 24, 2426 (2012).
[9] G. A. Smolenskii and V. A. Bokov, J. Appl. Phys. 35, 915 (1964).
[10] T. Katsufuji, S. Mori, M. Masaki, Y. Moritomo, N. Yamamoto, and H. Takagi, Phys. Rev. B 64, 104419 (2001).
[11] B. B. Van Aken, T. T. M. Palstra, A. Filippetti, and N. A. Spaldin, Nat. Mater. 3, 164 (2004).
[12] H. Das, A. L. Wysocki, Y. Geng, W. Wu, and C. J. Fennie, Nat. Commun. 5, 2998 (2014).
[13] J. A. Moyer, R. Misra, J. A. Mundy, C. M. Brooks, J. T. Heron, D. A. Muller, D. G. Schlom, and P. Schiffer, APL Mater. 2, 012106 (2014).
[14] See Supplemental Material at http://link.aps.org/supplemental/10.1103/PhysRevLett.114.217602 for detailed descriptions of experimental methods as well as additional characterization information of several samples.
[15] F.-T. Huang, X. Wang, S. M. Griffin, Y. Kumagai, O. Gindele, M.-W. Chu, Y. Horibe, N. A. Spaldin, and S.-W. Cheong, Phys. Rev. Lett. 113, 267602 (2014).
[16] A. Ghosh, J. R. Sahu, S. V. Bhat, and C. N. R. Rao, Solid State Sci. 11, 1639 (2009).
[17] S. Venugopalan and M. M. Becker, J. Chem. Phys. 93, 3833 (1990).
[18] S. Quezel, J. Rossat-Mignod, and E. F. Bertaut, Solid State Commun. 14, 941 (1974).
[19] P. J. Brown and T. Chatterji, J. Phys. Condens. Matter 18, 10085 (2006).
[20] A. Munoz, J. A. Alonso, M. J. Martinez-Lope, M. T. Casais, J. T. Martinez, and M. T. Fernandez-Diaz, Phys. Rev. B 62, 9498 (2000).
[21] H. Wang, I. V. Solovyev, W. Wang, X. Wang, P. J. Ryan, D. J. Keavney, J.-W. Kim, T. Z. Ward, L. Zhu, J. Shen, X. M. Cheng, L. He, X. Xu, and X. Wu, Phys. Rev. B 90, 014436 (2014).
[22] X. Fabrèges, S. Petit, I. Mirebeau, S. Pailhès, L. Pinsard, A. Forget, M. T. Fernandez-Díaz, and F. Porcher, Phys. Rev. Lett. 103, 067204 (2009).