| Transition Temperature | 35 K |
|---|---|
| Experiment Temperature | 1.85 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | P21/c (#14) |
| Magnetic Space Group | P21/c (#14.75) |
| Magnetic Point Group | 2/m (5.1.12) |
| Lattice Parameters | 4.79740 8.38150 7.89560 90.00 121.83 90.00 |
|---|---|
| DOI | 10.1021/ic401280e |
| Reference | M. Reynaud, G. Rousse, J.-N. Chotard, J. Rodriguez-Carvajal and J.-M. Tarascon, Inorganic Chemistry (2013) 52 10456-10466. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Fe1 | Fe | 0.0 | 0.02 | 4.33 | 4.33 |
Marinite Li_{2}M(SO_{4}){2} (M = Co, Fe, Mn) and Li{1}Fe(SO_{4})_{2}: Model Compounds for Super-Super-Exchange Magnetic Interactions
Marine Reynaud, \( ^{\dagger} \) Gwenaëlle Rousse, \( ^{*,\ddagger} \) Jean-Noël Chotard, \( ^{\dagger} \) Juan Rodríguez-Carvajal, \( ^{\S} \) and Jean-Marie Tarascon \( ^{\dagger} \)
\( ^{\dagger} \) Laboratoire de Réactivité et Chimie des Solides (LRCS), Université de Picardie Jules Verne, CNRS UMR 7314, 33 rue Saint Leu, 80039 Amiens cedex, France
\( ^{\ddagger} \) Institut de Minéralogie et de Physique des Milieux Condensés (IMPMC), Université Pierre et Marie Curie, UPMC Univ Paris 06, CNRS UMR 7590, 4 Place Jussieu, 75252 Paris cedex 05, France
\( ^{8} \) Institut Laue-Langevin (ILL), BP 156, 6 rue Jules Horowitz, 38042 Grenoble cedex 9, France
Supporting Information
ABSTRACT: New materials initially designed for battery electrodes are often of interest for magnetic study, because their chemical compositions include 3d transition metals. We report here on the magnetic properties of marinite phases \( \mathrm{Li}_{2}\mathrm{M}(\mathrm{SO}_{4})_{2} \) (M = Fe, Co, Mn) and \( \mathrm{Li}_{1}\mathrm{Fe}(\mathrm{SO}_{4})_{2} \) , which all order antiferromagnetically at low temperature. From neutron powder diffraction, we propose a model for their ground-state magnetic structures. The magnetism of marinite \( \mathrm{Li}_{2}\mathrm{M}(\mathrm{SO}_{4})_{2}^{\cdot} \) compounds unambiguously results from super-super-exchange interactions; therefore, these materials can be considered as a model case for which the Goodenough–Kanamori–Anderson rules can be tested.
■ INTRODUCTION
Since the discovery of \( LiFePO_{4} \) as a promising positive electrode material for Li-ion batteries, \( ^{1} \) there has been a growing interest in polyanionic compounds among the battery research community, and numerous new materials have been proposed. \( ^{2-4} \) In this context, our group has been reporting over the years on a wide family of fluorosulfates, with general formula \( AMSO_{4}F \) (A = Li, Na; M = Fe, Co, Ni, Mn, Zn, Mg). \( ^{5-12} \) Among them, the favorite and triplet forms of \( LiFeSO_{4}F \) have drawn particular attention, because they display the highest potentials ever obtained for the \( Fe^{III+}/Fe^{II+} \) redox couple in inorganic compounds (3.6 and 3.9 V versus \( Li^{+}/Li^{0} \) , respectively). \( ^{5,8,10} \) Following this work, we investigated the bimetallic sulfates and we isolated two new compounds— \( Li_{2}M(SO_{4})_{2} \) (M = Fe, Co)—among which the iron phase also demonstrates a high potential of 3.83 V vs \( Li^{+}/Li^{0} \) for the \( Fe^{III+}/Fe^{II+} \) redox couple. \( ^{13} \) We recently prepared the manganese equivalent \( Li_{2}Mn(SO_{4})_{2} \) which is presented herein along with the accurate structural determination of the delithiated \( Li_{1}Fe(SO_{4})_{2} \) phase.
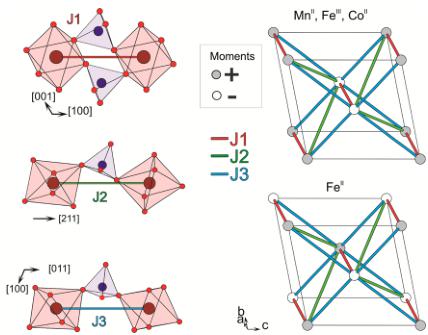
Aside from being attractive electrode materials for Li-ion batteries, these new \( \mathrm{Li_{2}M(SO_{4})_{2}} \) (x = 1, 2; M = Fe, Co, Mn) phases can constitute model compounds for magnetic studies as the particular arrangement of \( MO_{6} \) octahedra and \( SO_{4} \) tetrahedra of their structure should solely enable super-super-exchange interactions. Among polyanionic compounds, few iron-based materials (e.g., \( FePO_{4} \) \( ^{14} \) , \( Fe_{2}(SO_{4})_{3} \) \( ^{15,16} \) , \( Fe_{2}(MoO_{4})_{3} \) \( ^{17} \) , \( Li_{3}Fe_{2}(PO_{4})_{3} \) \( ^{18,19} \) , \( LiFeP_{2}O_{7} \) \( ^{20} \) , \( AFe(SO_{4})_{2} \) (A = K, Cs,

Rb) \( ^{21,22} \) present such singular structures in which interactions between magnetic atoms are only possible via M–O–O–M pathways. They generally lead to antiferromagnetic long-range ordering, \( ^{14-20} \) but can also result in more-complex magnetic structures (e.g., helical) due to topologically frustrated interactions. \( ^{21,22} \) Other works compare the magnetism of different 3d metals within isostructural sulfate-based compounds, in which both M–O–M super-exchange interactions and M–O–O–M super-super-exchange interactions are likely to occur. One can cite, in particular, the works on the antiferromagnetic anhydrous metal sulfates \( MSO_{4} \) (M = Fe, Ni, Co), \( ^{23} \) on the antiferromagnetic fluorosulfates \( AMSO_{4}F \) (A = Li, Na; M = Fe Co), \( ^{7,12,24} \) on the ferrimagnetic hydroxysulfates \( M_{3}(OH)_{2}(SO_{4})_{2}(H_{2}O)_{2} \) (M = Co, Mn, Ni), \( ^{25-27} \) and on the jarosite \( AM_{3}(SO_{4})_{2}(OH)_{6} \) (A = Na, K, Ag, Rb, H, \( NH_{4} \) etc.; M = Fe, Cr, V) whose Kagomé lattice leads to strong frustration and exotic magnetic structures. \( ^{28-30} \)
We present here a detailed report on the temperature-dependent magnetic susceptibility of the four marinite compounds \( \mathrm{Li_{2}Co^{II}(SO_{4})_{2}} \) , \( \mathrm{Li_{2}Mn^{II}(SO_{4})_{2}} \) , \( \mathrm{Li_{2}}Fe^{II}(SO_{4})_{2} \) , and \( \mathrm{Li_{1}}Fe^{III}(SO_{4})_{2} \) , and we further use low-temperature neutron powder diffraction to determine their magnetic structures. Finally, we perform an analysis of the super-super-exchange
interactions and discuss the relative strengths required to obtain the observed magnetic structures as the ground state.
EXPERIMENTAL SECTION
Sample Preparation. The \( \mathrm{Li_{2}M(SO_{4})_{2}} \) samples (M = Co, Fe, Mn) were prepared following the previously reported procedure \( ^{13} \) which consists of three steps: (i) stoichiometric amounts of \( Li_{2}SO_{4} \) and \( MSO_{4} \) are thoroughly mixed using a Spex Miller 8000M, (ii) the resulting powder is pressed into a pellet, (iii) the latter is annealed at \( 325\ ^{\circ}C \) for 12–48 h, either under air (M = Co, Mn) or in a quartz tube sealed under vacuum (M = Fe). In contrast to the Fe phase, neither the Co compound nor the Mn compound are electrochemically active, with respect to Li metal. Thus, only the delithiated phase \( \mathrm{Li_{2}Fe(SO_{4})_{2}} \) was obtained through chemical oxidation of \( \mathrm{Li_{2}Fe(SO_{4})_{2}} \) , using an excess of \( NO_{2}BF_{4} \) (>2 equiv) as an oxidizing agent in acetonitrile.
Structural Characterization. Purity of the samples was checked by laboratory powder X-ray diffraction (XRD), with a Bruker D8 diffractometer equipped with an X-ray tube providing Cu Kα radiation and a LynxEye detector.
Neutron powder diffraction (NPD) was performed on the D2B and D20 diffractometers at the Institut Laue Langevin (ILL, Grenoble, France). The D2B diffractometer has a very high resolution and, therefore, was used to precisely refine the nuclear structure of \( Li_{1}Fe(SO_{4})_{2} \) at room temperature, using a wavelength of \( \lambda = 1.594 \) Å. The high-intensity D20 diffractometer has a good resolution at low angles and was used to determine the magnetic structures of the title compounds. NPD patterns on D20 were recorded either under high-flux conditions (takeoff angle = \( 42^{\circ} \) ), using a wavelength of \( \lambda = 2.418 \) Å, or in the high-resolution mode (takeoff angle = \( 90^{\circ} \) ) with two different wavelengths ( \( \lambda = 1.543 \) and \( 2.416 \) Å).
Synchrotron powder X-ray diffraction data ( \( \lambda = 0.4139 \) Å) were obtained through the mail-in service of the 11-BM beamline at the Advanced Photon Source (Argonne National Laboratory, Argonne, IL, USA).
Nuclear and magnetic structures were refined using the Rietveld method \( ^{31} \) as implemented in the FullProf program. \( ^{32,33} \) For the magnetic structure determination, Bertaut symmetry analyses \( ^{34} \) were carried out using the program BasIReps within the same suite of software. The structures were drawn and examined with the help of the FullProf Studio program, as well as the VESTA visualization program. \( ^{35} \)
Magnetic measurements. Susceptibility measurements were carried out using either a SQUID SS or a SQUID XL magnetometer (Quantum Design), in zero-field-cooled (ZFC) and field-cooled (FC) modes, under applied magnetic fields of 10 kOe and 100 Oe. Magnetization curves \( (M = f(H)) \) were recorded at 2 K. Powder samples of roughly 20–30 mg were placed into gel caps for the measurement.
■ RESULTS
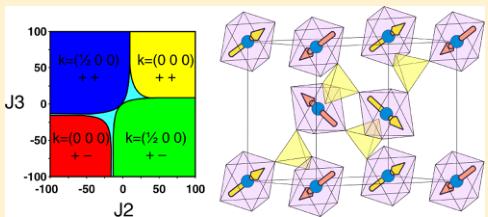
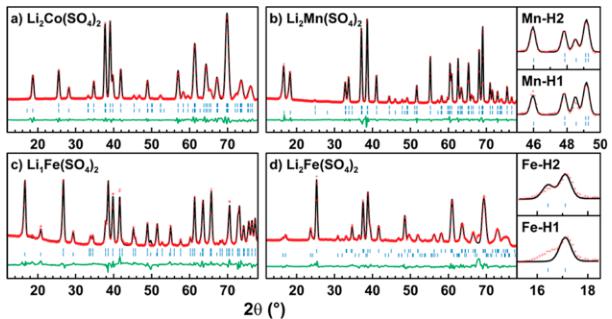
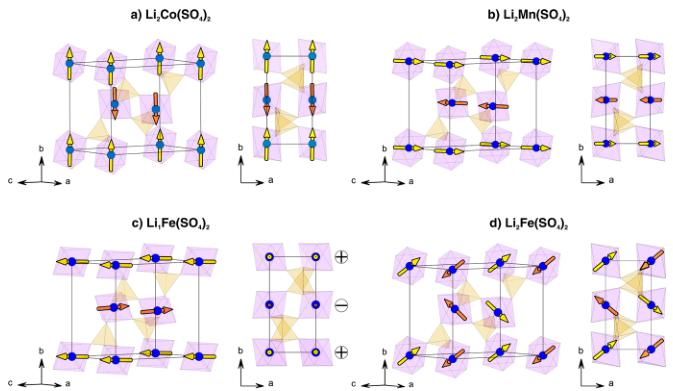
Crystal Structures. We reported on the synthesis, electrochemical properties, and structures of the new \( \mathrm{Li_{2}Co(SO_{4})_{2}} \) and \( \mathrm{Li_{2}Fe(SO_{4})_{2}} \) compounds in a previous communication. \( ^{13} \) Unlike the lithium nickel sulfate \( \mathrm{Li_{2}Ni(SO_{4})_{2}} \) , which has an orthorhombic structure \( (Pbca) \) , \( ^{36} \) the cobalt and iron analogues crystallize in a monoclinic unit cell (space group \( P2_{1}/c \) ). Their structure is built upon \( MO_{6} \) octahedra, which are connected to each other through their six vertices by \( SO_{4} \) tetrahedra (Figure 1a). Each sulfate tetrahedron is linked to three different \( MO_{6} \) octahedra; its fourth corner points to a large tunnel along the a-axis, in which the Li atoms sit.
Later, we were able to synthesize a manganese equivalent \( \mathrm{Li_{2}Mn(SO_{4})_{2}} \) using the same procedure as the one previously described for the cobalt analogue. The high similarity of their two XRD patterns suggested that this new lithium manganese sulfate crystallizes in the same structure as the iron and cobalt compounds. This was confirmed with a Rietveld refinement of

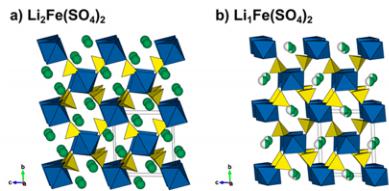
Figure 1. Comparison of the structures of (a) \( \mathrm{Li_{2}Fe(SO_{4})_{2}} \) and (b) \( \mathrm{Li_{1}Fe(SO_{4})_{2}} \) . Projections along the a-axis. \( FeO_{6} \) octahedra and \( SO_{4} \) tetrahedra are displayed in blue and yellow, respectively. The Li atoms are shown as green balls. In the delithiated phase, the lithium is on a half-occupied site as represented by the half-colored balls.
the XRD data, whose results are given in the Supporting Information (Figure SI-1 and Table SI-1).
We previously reported the lattice parameters of \( \mathrm{Li_{1}Fe(SO_{4})_{2}} \) , prepared by chemical delithiation from \( \mathrm{Li_{2}Fe(SO_{4})_{2}} \) , but X-ray laboratory data were not ideal to precisely determine the structure, and, in particular, the position of the Li atoms within the unit cell. \( ^{13} \) To accurately determine its crystal structure, we performed NPD on the high-resolution powder diffractometer D2B at ILL (Grenoble, France) using a wavelength of \( \lambda = 1.594 \) Å. Starting from a refinement of the NPD pattern of \( \mathrm{Li_{1}Fe(SO_{4})_{2}} \) and using the \( FeO_{6} \) octahedra and \( SO_{4}^{-} \) tetrahedra framework pertaining to \( \mathrm{Li_{2}Fe(SO_{4})_{2}} \) structure, we were able to precisely localize the position of the Li atoms in the center of the channels described above, using Fourier differential maps calculations, which were performed with the GFourier program of the FullProf Suite \( ^{32,33} \) (Figure SI-2a). Refinement of the structure with one Li atom placed in the special position \( \left(^{1}/_{2}0^{1}/_{2}\right) \) (2d Wyckoff site) resulted in an important anisotropic displacement (equivalent isotropic temperature factor \( B \approx 8 \mathring{A}^{2} \) ), with the main direction of the ellipsoid elongated along \( \langle 5 1 2 \rangle \) (see Figure SI-2b in the Supporting Information). This suggested that the Li ions are more likely distributed on a general position 4e located in the vicinity of the 2d position, with half occupancy. This led to a much lower temperature factor \( B \approx 1.1 \mathring{A}^{2} \) ). The resulting position of Li is shown in Figures SI-2c and SI-2d in the Supporting Information. The two half-occupied positions for Li around the \( \left(^{1}/_{2}0^{1}/_{2}\right. \) site are then separated by a distance of 0.7 Å, which is consistent with the anisotropic displacement calculated with the first model. Finally, a joint refinement of the structure was performed against both D2B NPD data and 11-BM Synchrotron XRD data. The results of this refinement are presented in the Supporting Information (Figure SI-3 and Table SI-2). A bond valence sum analysis, using \( b_{0} \) parameters from Brown, \( ^{37} \) indicates that the Fe–O bond lengths are in excellent agreement with iron in the III+ oxidation state, also confirmed by Mössbauer data (see the Supporting Information, Figure SI-4). As a result, the structure of \( \mathrm{Li_{1}Fe(SO_{4})_{2}} \) ; presents the same framework of \( FeO_{6} \) octahedra and \( SO_{4}^{+} \) tetrahedra as the lithiated phase (Figure 1b), but the octahedra and tetrahedra in \( \mathrm{Li_{1}Fe(SO_{4})_{2}} \) are slightly tilted compared to \( \mathrm{Li_{2}Fe(SO_{4})_{2}} \) . After the removal of one Li ion, the remaining Li ion of \( \mathrm{Li_{1}Fe(SO_{4})_{2}} \) . shifts toward the middle of the tunnel in a split position with half occupancy. As a consequence, the Li ions are coordinated by five O atoms, which is more preferable than the highly elongated octahedral coordination that lithium would adopt in the \( \left(^{1}/_{2}0^{1}/_{2}\atop2d\ \mathrm{Wyckoff\ position}\right) \) . Moreover, this five-coordination is geometrically similar to the coordination of the lithium in the pristine \( \mathrm{Li_{2}Fe(SO_{4})_{2}} \) compound.
In short, the four studied compounds \( (\mathrm{Li}_{2}\mathrm{Co}(\mathrm{SO}_{4})_{2}, \mathrm{Li}_{2}\mathrm{Mn}(\mathrm{SO}_{4})_{2}, \mathrm{Li}_{2}\mathrm{Fe}(\mathrm{SO}_{4})_{2}) \) , and \( \mathrm{Li}_{1}\mathrm{Fe}(\mathrm{SO}_{4})_{2}) \) present the same framework of \( MO_{6} \) octahedra and \( SO_{4} \) tetrahedra, in which the metal atoms are all isolated from each other and are only interconnected through the sulfate tetrahedra. Such a specific connectivity suggests that the magnetic properties are only due to super-super-exchange interactions, hence our interest to study the magnetic properties of these materials as described next.
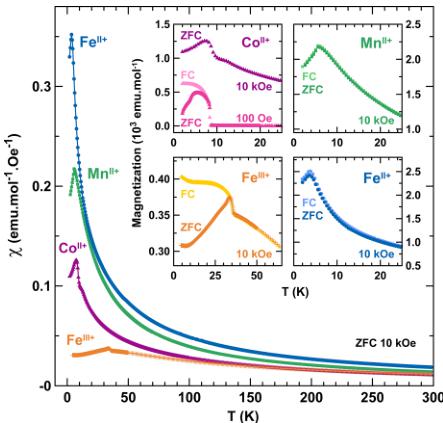
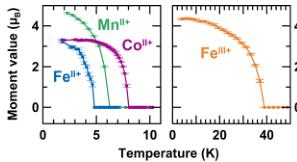
Magnetic Properties. The macroscopic magnetic properties of the title compounds were determined with a SQUID magnetometer in both ZFC and FC conditions under 10 kOe. Curves of the temperature dependence of the ZFC magnetic susceptibility are shown in Figure 2. All compounds show cusps

Figure 2. Temperature dependence of the magnetic susceptibility ( \( \chi \) ) of the title compounds, measured under zero-field-cooled (ZFC) conditions with a field of 10 kOe between 300 and 2 K. Purple triangles, green squares, orange crosses, and blue circles are assigned to \( \mathrm{Li}_{2}\mathrm{Co}^{\mathrm{II}}(\mathrm{SO}_{4})_{2} \) , \( \mathrm{Li}_{2}\mathrm{Mn}^{\mathrm{II}}(\mathrm{SO}_{4})_{2} \) , \( \mathrm{Li}_{1}\mathrm{Fe}^{\mathrm{II}}(\mathrm{SO}_{4})_{2} \) and \( \mathrm{Li}_{2}\mathrm{Fe}^{\mathrm{II}}(\mathrm{SO}_{4})_{2} \) respectively. Insets show enlargement of the ZFC (dark colors) and field-cooled (FC) (light colors) magnetization curves at low temperatures. For \( \mathrm{Li}_{2}\mathrm{Co}^{\mathrm{II}}(\mathrm{BO}_{4})_{2} \) only the 10-kOe ZFC curve is shown (purple triangles) and compared to the ZFC (dark pink) and FC (light pink) curves measured with a field of 100 Oe.
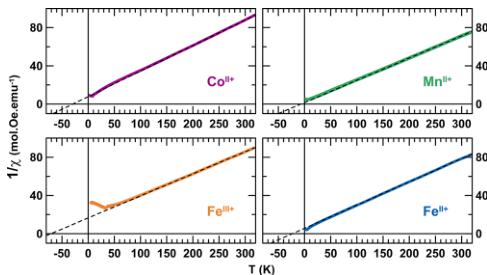
of a long-range antiferromagnetic ordering, which occurs at a Néel temperature \( (T_{\mathrm{N}}) \) of \( \sim7 \) K for \( \mathrm{Li}_{2}\mathrm{Co}^{\mathrm{II}}(\mathrm{PO}_{4})_{2} \) , \( \sim6 \) K for \( \mathrm{Li}_{2}\mathrm{Mn}^{\mathrm{II}}(\mathrm{PO}_{4})_{2} \) , \( \sim4 \) K for \( \mathrm{Li}_{2}\mathrm{Fe}^{\mathrm{II}}(\mathrm{PO}_{4})_{2} \) , and \( \sim35 \) K for \( \mathrm{Li}_{1}\mathrm{Fe}^{\mathrm{III}}(\mathrm{PO}_{4})_{2} \) . The high-temperature region (200–300 K) of the inverse susceptibility was fitted to the Curie–Weiss equation \( \chi = C/(T - \theta_{\mathrm{CW}}) \) (see Figure 3). We deduced the Curie–Weiss temperatures to be approximately \( -30 \) K, \( -8 \) K, \( -23 \) K, and \( -71 \) K, and the effective moments were determined to be \( 5.4 \mu_{\mathrm{B}} \) , \( 5.9 \mu_{\mathrm{B}} \) , \( 5.7 \mu_{\mathrm{B}} \) , and \( 5.8 \mu_{\mathrm{B}} \) for \( \mathrm{Li}_{2}\mathrm{Co}^{\mathrm{II}}(\mathrm{O}_{4})_{2} \) , \( \mathrm{Li}_{2}\mathrm{Mn}_{\mathrm{II}}^{\mathrm{II}}(\mathrm{PO}_{4})_{2} \) , \( \mathrm{Li}_{2}\mathrm{Fe}^{\mathrm{II}}(\mathrm{BO}_{4})_{2} \) , and \( \mathrm{Li}_{1}\mathrm{Fe}^{\mathrm{III}}(\mathrm{BO}_{4})_{2} \) , respectively. These results are summarized in Table 1, together with the frustration parameter \( |\theta_{\mathrm{CW}}|/T_{\mathrm{N}} \) .
Usually, the value of the effective moment of a given cation can be calculated using the following formula: \( \mu_{\mathrm{eff}} = g_{1} \cdot [J(J + 1)]^{1/2} \) , where \( g_{1} \) is the Landé gyromagnetic factor and J is the total angular momentum (the sum of the spin angular momentum S and the orbital angular momentum L). However, the effective moment is often affected by the crystal field and thus differs from the expected value for the free ion. Two models are actually used

Figure 3. Evolution of the inverse of the magnetic susceptibility \( (1/\chi) \) of the title compounds as a function of the temperature. Purple, green, orange, and blue colors are assigned to \( \mathrm{Li}_{2}\mathrm{Co}^{\mathrm{II}}\left(\mathrm{SO}_{4}\right)_{2} \) , \( \mathrm{Li}_{2}\mathrm{Mn}^{\mathrm{III}}\left(\mathrm{SO}_{4}\right)_{2} \) , \( \mathrm{Li}_{1}\mathrm{Fe}^{\mathrm{III}}\left(\mathrm{SO}_{4}\right)_{2} \) , and \( \mathrm{Li}_{2}\mathrm{Fe}^{\mathrm{II}}\left(\mathrm{SO}_{4}\right)_{2} \) , respectively. Experimental curves are fitted with the ideal Curie–Weiss law in the temperature range of 200 K \( \leq T \leq 300 \) K (dashed lines).
to account for this phenomenon: (i) the orbital moment L may be fully decoupled from the spin contribution S (i.e., the spin–orbit coupling L·S is null), thus leading to an effective moment given by the equation \( \mu_{\mathrm{eff}} = [4S(S + 1) + L(L + 1)]^{1/2} \) ; (ii) the orbital contribution L may be completely quenched and the system would then present a spin-only effective moment, which is calculated from the formula \( \mu_{\mathrm{eff}} = 2 \cdot [S(S + 1)]^{1/2} \) (or \( \mu_{\mathrm{eff}} = [n(n + 2)]^{1/2} \) , with n being the number of unpaired electrons). Table 1 shows that the experimental effective moments deduced from the magnetic measurements of \( \mathrm{Li}_{2}\mathrm{Co}^{\mathrm{II}}(\mathrm{VO}_{4})_{2} \) and \( \mathrm{Li}_{2}\mathrm{Be}^{\mathrm{II}}(\mathrm{SO}_{4})_{2} \) are consistent with the expected effective moment of a single 3d metal cation in a high-spin octahedral environment with an unquenched orbital moment, which is fully decoupled from the spin contribution. However, one should note that the case of \( Co^{II} \) is always pretty tricky, as high-spin \( Co^{II} \) samples are known to exhibit significant spin–orbit coupling that manifests itself in the population of the Kramers \( S = \pm^{1/2} \) doublet ground state, and these samples can be regarded as carrying an effective spin of \( S = ^{1/2} \) with a large Landé factor. We cannot rule out such a possibility and further experiments such as EPR or magnetization measurements on single crystals could be of interest. In fact, as discussed below, the refined magnetic moment of \( Co^{II} \) ions (3.3 \( \mu_{B} \) ) is slightly higher than the spin-only value ( \( 3.0 \mu_{B} \) ). In the case of \( \mathrm{Li}_{2}\mathrm{Mn}^{\mathrm{II}}(\mathrm{VO}_{4})_{2} \) and \( \mathbf{Li}_{1}\mathbf{Fe}^{\mathrm{III}}(\mathrm{SO}_{4})_{2} \) , the orbital moment is null and the experimental values for the effective moment are in good agreement with a spin-only effective moment calculated for a \( d^{5} \) transition metal.
The inset of Figure 2 shows an enlargement of the magnetization curves at low temperatures for ZFC and FC measurements under 10 kOe, as well as the ZFC/FC curves for the \( Co^{II} \) -based sample under 100 Oe. \( \mathrm{Li}_{2}\mathrm{Mn}^{\mathrm{II}}(\mathrm{BO}_{4})_{2} \) and \( \mathrm{Li}_{2}\mathrm{Re}^{\mathrm{II}}(\mathrm{SO}_{4})_{2} \) present a typical antiferromagnetic behavior, with the ZFC and FC curves that are superimposed. Concerning \( \mathrm{Li}_{1}\mathrm{Fe}^{\mathrm{III}}(\mathrm{SO}_{4})_{2} \) , the ZFC and FC curves deviate at temperatures below \( T_{N} \) , which may result from either a ferromagnetic impurity or some ferromagnetic/ferrimagnetic contributions. Since neither the XRD nor the NPD patterns reveal the presence of a secondary phase, the latter hypothesis is more probable. A similar behavior is observed for \( \mathrm{Li}_{2}\mathrm{Co}^{\mathrm{II}}(\mathrm{S}\mathrm{O}_{4})_{2} \) , with, in addition, a nonlinearity of the moment versus the applied field, as the curves recorded under a field of 100 Oe lead to magnetization larger than expected from the value obtained at 10 kOe.
Table 1. Magnetic Parameters of the Title Compounds Deduced from Magnetic Measurements and Neutron Diffraction, and Compared to Some Expected Theoretical Values
| Li4CoII(SO4)2 | Li2MnII(SO4)2 | Li3FeII(SO4)2 | Li1FeII(SO4)2 | |
| electronic configuration | d7:t2g5e2 | d5:t2g5e2 | d6:t2g4e2 | d5:t2g5e2 |
| S = 3/2, L = 3 | S = 5/2, L = 0 | S = 2, L = 2 | S = 5/2, L = 0 | |
| Experimental Values Deduced from Magnetic Measurements (H = 10 kOe) | ||||
| Néel temperature, TN | 7 K | 6 K | 4 K | 35 K |
| Curie constant, C | 3.7 emu K mol−1 | 4.3 emu K mol−1 | 4.1 emu K mol−1 | 4.3 emu K mol−1 |
| Curie–Weiss temperature, θCW | −30 K | −8 K | −23 K | −71 K |
| frustration parameter, |θCW|/TN | 4.29 | 1.33 | 5.75 | 2.03 |
| effective moment, μeff | 5.4 μB | 5.9 μB | 5.7 μB | 5.8 μB |
| Experimental Values Deduced from Neutron Diffraction | ||||
| Néel temperature, TN | 8 K | 6 K | 5 K | 39 K |
| magnetic moment at 1.85 K | 3.3 μB | 4.6 μB | 3.2 μB | 4.3 μB |
| Expected Theoretical Values | ||||
| effective moment, μeff | ||||
| μeff = g·[J(J + 1)]1/2 | 6.6 μB | 5.9 μB | 6.7 μB | 5.9 μB |
| μeff = [4S(S + 1) + L(L + 1)]1/2 | 5.2 μB | 5.9 μB | 5.5 μB | 5.9 μB |
| μeff = 2·[S(S + 1)]1/2 | 3.9 μB | 5.9 μB | 4.9 μB | 5.9 μB |
| magnetic moment, m = g·S | 3 μB | 5 μB | 4 μB | 5 μB |

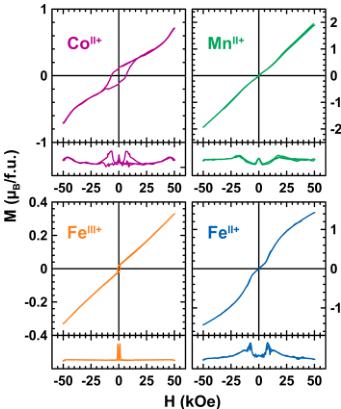
Figure 4. Magnetization curves of \( \mathrm{Li_{2}Co^{II}(SO_{4})_{2}} \) (purple), \( \mathrm{Li_{2}Mn^{II}(SO_{4})_{2}} \) (green), \( \mathrm{Li_{3}Fe^{III}(SO_{4})_{2}} \) (orange), and \( \mathrm{Li_{3}Fe^{II}(SO_{4})_{2}} \) (blue), as a function of the applied field measured at 2 K. Derivative curves are displayed in the lower part of each diagram.
To test this point, we recorded the magnetization curves at 2 K for the four samples (Figure 4). The magnetization curve of \( \mathrm{Li_{2}Co^{II}(SO_{4})_{2} \) clearly shows a hysteresis loop, which indicates a weak ferromagnetic behavior with a remnant magnetization \( (M_{\mathrm{t}}) \) of \( 0.12 \mu_{B} \) and a coercive field \( (H_{\mathrm{c}}) \) of 6.5 kOe. This can explain the discrepancy between the ZFC and FC curves previously mentioned. Close inspection of the data for \( \mathrm{Li_{2}Mn^{II}(SO_{4})_{2}} and \mathrm{Li_{3}Fe^{III}(SO_{4})_{2}} \) also reveals a tiny weak ferromagnetism, and the remnant magnetization is \( \sim0.02 \mu_{B} \) . The absence of any hysteresis loop on the magnetization curve of \( \mathrm{Li_{2}Fe^{II}(SO_{4})_{2}} \) confirms a pure antiferromagnetic ground state, which is consistent with the ZFC/FC curves that are neatly superimposed. Switching to higher fields, the evolution of the magnetization of \( \mathrm{Li_{3}Fe^{III}(SO_{4})_{2}} is linear with the applied field, while an interesting feature is observed for \( \mathrm{Li_{2}Fe^{II}(SO_{4})_{2}} and \mathrm{Li_{2}Co^{II}(SO_{4})_{2}} \) . The magnetization for the latter presents an inflection point of \( \sim45 \) kOe (seen in the derivative curve in Figure 4), which may suggest a metamagnetic behavior; therefore, this point must be confirmed by magnetization measurements at higher field for checking the feasibility to saturate the magnetization, and single-crystal experiments would be needed to confirm this. A similar inflection point can be seen for the \( Fe^{II} \) -based compound, but the field at which it occurs is much lower ( \( \sim10 \) kOe); therefore, this could result from a canted magnetic structure that becomes colinear under the effect of the magnetic field. To figure this out, we embarked into an NPD study to determine the magnetic structures of each counterpart.
Magnetic Structures. NPD measurements were performed on the four title compounds at the D20 diffractometer of the Institut Laue-Langevin (ILL). With a high resolution at low \( 2\theta \) angles, the D20 diffractometer is a choice instrument for magnetic structure determination. NPD patterns of the \( \mathrm{Li_{2}(SO_{4})_{2}} \) and \( \mathrm{Li_{2}Fe(SO_{4})_{2}} \) samples were acquired in a high flux configuration using a \( \lambda = 2.418 \AA \) wavelength, while the newly reported \( \mathrm{Li_{2}Mn(SO_{4})_{2}} \) and \( \mathrm{Li_{1}Fe(SO_{4})_{2}} \) phases were measured in high-resolution mode at two different wavelengths: \( \lambda = 1.543 \AA \) and \( \lambda = 2.416 \AA \) .
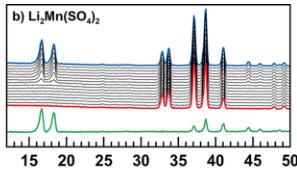
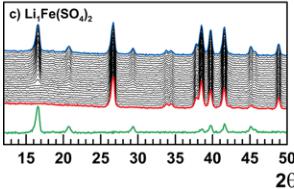
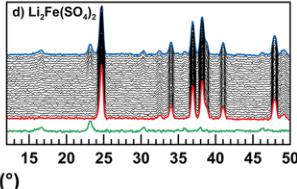
Crystallographic data obtained from the Rietveld refinement of the NPD patterns acquired above the Neel temperature of each compound are summarized in Tables 2–5, and the results of these refinements for \( \mathrm{Li_{2}Mn(SO_{4})_{2}} \) are presented in Figure 5. Upon cooling the powder samples (Figure 6), we observed the growth of new peaks, which indicates a long-range ordering of the magnetic moments. These extra peaks are better observed when plotting the difference patterns (green lines in Figure 6) of a diagram recorded above \( T_{N} \) (red patterns in Figure 6) and of another one recorded below \( T_{N} \) (blue patterns in Figure 6).
Next, NPD patterns were recorded at 1.85 K in order to determine the magnetic structure of each compound. We found that the magnetic reflections observed for \( \mathrm{Li_{2}Co(SO_{4})_{2}} \) , \( \mathrm{Li_{2}Mn(SO_{4})_{2}} \) , and \( \mathrm{Li_{1}Fe(SO_{4})_{2}} \) can be indexed in the same unit cell as their nuclear structure. The propagation vector is the gamma-point of the Brillouin zone: \( \mathbf{k} = (0, 0, 0) \) . A symmetry analysis was then performed using Bertaut's method, \( ^{34} \) as implemented in the program BasIReps in order to determine all possible spin configurations compatible with the crystal symmetry of the nuclear structure. The results of this analysis are
Table 2. Nuclear and Magnetic Structures of \( Li_{2}Co(SO_{4})_{2} \) . Results from a Bond Valence Sum Analysis \( ^{37} \) (BVS) are Reported
| Nuclear Structure | |||||
| D20 Diffractometer in High-Flux Mode, \( \lambda = 2.418 \) Å, T = 15 K | |||||
| space group: \( P2_{1}/c \) | \( R_{\text{Bragg}} = 1.86\% \) , \( \chi^{2} = 76.7 \) | ||||
| a = 4.9671(2) Å, b = 8.0908(3) Å, c = 8.7639(3) Å, \( \beta = 121.855(5)^{\circ} \) , V = 299.162(17) Å \( ^{3} \) | |||||
| atom | Wyckoff position | occupancy | x | y | z |
| Co | 2a | 1.0 | 0 | 0 | 0 |
| Li | 4e | 1.0 | 0.014 (3) | 0.6352(12) | 0.1015(18) |
| S | 4e | 1.0 | 0.3388(18) | 0.3021(12) | 0.3046(10) |
| O1 | 4e | 1.0 | 0.1810(13) | 0.4176(5) | 0.1507(6) |
| O2 | 4e | 1.0 | 0.2005(10) | 0.1342(7) | 0.2463(5) |
| O3 | 4e | 1.0 | 0.2861(9) | 0.3510(4) | 0.4465(5) |
| O4 | 4e | 1.0 | 0.6854(9) | 0.3018(4) | 0.3764(5) |
| Magnetic Structure | |||||
| D20 Diffractometer in High-Flux Mode; \( \lambda = 2.418 \) Å, T = 1.85 K | |||||
| k = (0, 0, 0), \( \Gamma_{3} \) | |||||
| atom | \( M_{x} \) ( \( \mu_{B} \) ) | \( M_{y} \) ( \( \mu_{B} \) ) | \( M_{z} \) ( \( \mu_{B} \) ) | \( M_{\text{tot}} \) ( \( \mu_{B} \) ) | |
| Co (0 0 0) | 0.12 | 3.33(3) | 0 | 3.33(3) | |
| Co (0 \( \frac{1}{2} \) \( \frac{1}{2} \) ) | 0.12 | -3.33(3) | 0 | 3.33(3) | 0 |
Table 3. Nuclear and Magnetic Structures of \( Li_{2}Mn(SO_{4})_{2} \) . Results from a Bond Valence Sum Analysis \( ^{[37]} \) (BVS) are Reported
| Nuclear Structure | |||||
| D20 Diffractometer in High-Resolution Mode, \( \lambda = 1.543 \) Å, T = 15 K | |||||
| space group: \( P2_{1}/c \( | \) R_{\text{Bragg}} = 3.38\%, \chi^{2} = 16.4 \( | ||||
| a = 4.9811 (1) Å, b = 8.3140 (2) Å, c = 8.8382 (2) Å, \) \beta = 121.250 (5) \( ^{\circ}, V = 312.910 (9) \) Å \( ^{3} \) | |||||
| atom | Wyckoff position | occupancy | x | y | z |
| Mn | 2a | 1.0 | 0 | 0 | 0.66 (8) |
| Li | 4e | 1.0 | 0.0175 (16) | 0.6299 (8) | 0.1044 (9) |
| S | 4e | 1.0 | 0.3286 (10) | 0.3026 (6) | 0.2975 (6) |
| O1 | 4e | 1.0 | 0,1756 (6) | 0.4145 (3) | 0.1497 (3) |
| O2 | 4e | 1.0 | 0,1928 (5) | 0.1391 (3) | 0.2449 (3) |
| O3 | 4e | 1.0 | 0,2886 (6) | 0.3533 (3) | 0.4448 (3) |
| O4 | 4e | 1.0 | 0,6711 (6) | 0.2980 (3) | 0.3630 (3) |
| Magnetic Structure | |||||
| D20 Diffractometer in High-Resolution Mode; \( \lambda = 2.416 \) Å, T = 1.85 K | |||||
| k = (0, 0, 0), \( \Gamma_{1} \) | |||||
| atom | \( M_{x} \) ( \( \nu_{B} \) ) | \( M_{y} \) ( \( \nu_{B} \) ) | \( M_{z} \) ( \( \nu_{B} \) ) | \( M_{\text{tot}} \) ( \( \nu_{B} \) ) | |
| Mn (0 0 0) | 3.97 (8) | 0.02 | -1.03 (12) | 4.59 (18) | |
| Mn (0 \( \frac{1}{2} \) \( \frac{1}{4} \) ) | -3.97 (8) | 0.02 | 1.03 (12) | 4.59 (18) | |
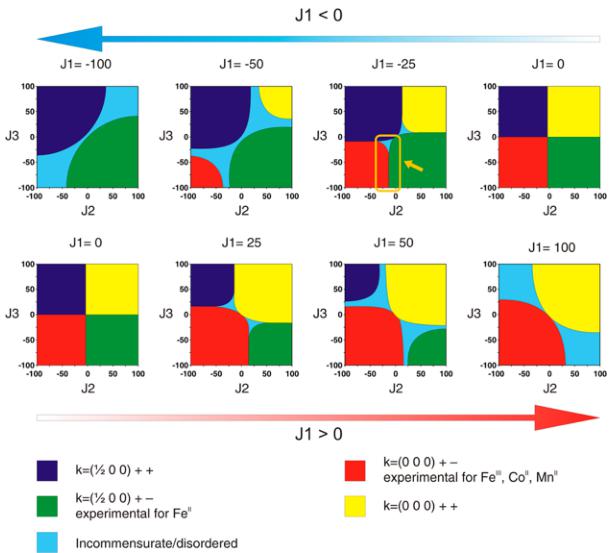
summarized in Table 6. Two irreducible representations were found to be associated with the 2a Wyckoff site (0 0 0) which is occupied by the 3d metals: \( \Gamma_{magetic} = 3\Gamma_{1} + 3\Gamma_{3} \) . These representations are built with three basis vectors which are collinear to the a, b, and c unit cell directions, respectively. In the \( \Gamma_{1} \) representation, the magnetic moments of the two metal atoms, which are nonrelated by lattice translations ( \( M_{1} \) in (0 0 0) and \( M_{2} \) in (0 \( \frac{1}{2} \) \( \frac{1}{3} \) ) are constrained to be \( (u, v, w) \) and \( (-u, v, -w) \) for \( M_{1} \) and for \( M_{2} \) , respectively. The corresponding Shubnikov group is \( P2_{1}/c \) . In the \( \Gamma_{3} \) representation, the directions of the magnetic moments of the \( M_{1} \) and \( M_{2} \) atoms become of the form \( (u, v, w) \) and \( (u, -v, w) \) , respectively. The corresponding Shubnikov group is \( P2_{1}^{\prime}/c^{\prime} \) . For the three phases \( Li_{2}Co(SO_{4})_{2} \) , \( Li_{2}Mn(SO_{4})_{2} \) , and \( Li_{1}Fe(SO_{4})_{2} \) , we tested all the possibilities given by these two irreducible representations against the NPD patterns recorded at 1.85 K, and we determined the magnetic structure for each compound. First, we found that the magnetic moments of \( Li_{2}Co(SO_{4})_{2} \) align antiferromagnetically along the b-axis, as allowed by the \( \Gamma_{3} \) representation. In agreement with the SQUID measurements, a weak ferromagnetic component can be added in the \( (ac) \) plane, since it is indeed allowed by symmetry; however, because of the weakness of these ferromagnetic components, they cannot be refined from NPD data. The results of this refinement are shown in Figure 7a and in the lower part of Table 2. The refined value of the magnetic moment of the cobalt is then \( 3.33(3) \) \( \mu_{B} \) . The magnetic structure of \( Li_{2}Co(SO_{4})_{2} \) is illustrated in Figure 8a. It shows the alternate orientations \( (+ -) \) of the moments along the [011] direction while the sequence of the moments is \( (+ +) \) along the [100] and [001] directions.
Unlike the cobalt phase, the best agreement with the magnetic reflections observed for \( \mathrm{Li_{2}Mn(SO_{4})_{2}} \) and \( \mathrm{Li_{1}Fe(SO_{4})_{2}} \) was obtained using the irreducible representation \( \Gamma_{1} \) . For the manganese analogue, a magnetic moment aligned along the a-
Table 4. Nuclear and Magnetic Structures of \( Li_{1}Fe(SO_{4})_{2} \) . Results from a Bond Valence Sum Analysis \( ^{37} \) (BVS) are Reported
| Nuclear Structure | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| D20 Diffractometer in High-Resolution Mode, \( \lambda = 1.543 \) Å, \( T = 50 \) K | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| space group: \( P2_{1}/c \) | \( R_{\text{Bragg}} = 2.67\% \) , \( \chi^{2} = 13.5 \) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a = 4.7974(2) Å, b = 8.3815(2) Å, c = 7.8956(2) Å, \( \beta = 121.835(5)^{\circ} \) , V = 269.721(10) ų | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| atom | Wyckoff position | occupancy | x | y | z | B_{\text{iso}} (Ų) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Fe | 2a | 1.0 | 0 | 0 | 0 | 0.31(6) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Li | 4e | 0.5 | 0.581(5) | 0.025(3) | 0.524(4) | 1.5(5) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| S | 4e | 1.0 | 0.2974(16) | 0.1797(7) | 0.7592(8) | 0.09(12) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| O1 | 4e | 1.0 | 0.0413(7) | 0.1296(4) | 0.7985(4) | 0.25(7) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| O2 | 4e | 1.0 | 0.2602(8) | 0.1067(4) | 0.5871(5) | 0.30(7) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| O3 | 4e | 1.0 | 0.2876(7) | 0.3564(4) | 0.7391(5) | 0.36(7) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| O4 | 4e | 1.0 | 0.3781(7) | 0.6428(4) | 0.5594(5) | 0.53(7) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Magnetic Structure | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| D20 Diffractometer in High-Resolution Mode | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| k = (0, 0, 0), \( \Gamma_{1} \) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| atom | \( M_{x} \) ( \( \mu_{B} \) ) | \( M_{y} \) ( \( \mu_{B} \) ) | \( M_{z} \) ( \( \mu_{B} \) ) | \( M_{tot} \) ( \( \mu_{B} \) ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Fe (0 0 0) | 0 | 0.02 | 4.33(4) | 4.33(4) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Fe (0 1/2 1/2) | 0 | 0.02 | -4.33(4) | 4.33(4) | } \endtable> Table 5. Nuclear and Magnetic Structures of \( Li_{2}Fe(SO_{4})_{2} \) . Results from a Bond Valence Sum Analysis\(^{37}\) (BVS) are Reported | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Nuclear Structure | ||||||
| D20 Diffractometer in High-Flux Mode, \( \lambda = 2.418 \) Å, \( T = 10 \) K | ||||||
| space group: \( P2_{1}/c \( | \( R_{\text{Bragg}} = 6.4\% \) , \( \chi^{2} = 87.4 \) | |||||
| a = 4.9836(7) Å, b = 8.1910(13) Å, c = 8.8108(11) Å, \( \beta = 121.915(9)^{\circ} \) , V = 305.30(7) ų | ||||||
| atom | Wyckoff position | occupancy | x | y | z | |
| Fe | 2a | 1.0 | 0 | 0 | 0 | |
| Li | 4e | 1.0 | 0.020(5) | 0.645(3) | 0.102(4) | 1.11(4) |
| S | 4e | 1.0 | 0.334(5) | 0.293(3) | 0.315(3) | 5.83(17) |
| O1 | 4e | 1.0 | 0 | 0.183(3) | 0.4139(10) | 1.66(6) |
| O2 | 4e | 1.0 | 0 | 0.194(2) | 0.1379(12) | 2.19(9) |
| O3 | 4e | 1.0 | 0 | 0.2841(16) | 0.3569(8) | 0.4482(11) |
| O4 | 4e | 1.0 | 0 | 0.6884(19) | 0.3016(8) | 0.3782(12) |
| Magnetic Structure | ||||||
| D20 Diffractometer in High-Flux Mode, \( \lambda = 2.41 \) Å, \( T = 1.85 \) K | ||||||
| k = (1/2, 0, 0), \( \Gamma_{1} \) | ||||||
| Atom | \( M_{x} \) ( \( \mu_{B} \) ) | \( M_{y} \) ( \( \mu_{B} \) ) | \( M_{z} \) ( \( \mu_{B} \) ) | \( M_{\text{tot}} \) ( \( \mu_{B} \) ) | ||
| Fe (0 0 0) | 2.97(6) | 1.25(10) | 0 | 3.23(12) | ||
| Fe (0 1/2 1/2) | -2.97(6) | 1.25(10) | 0 | 3.23(12) | ||
| k = (0, 0, 0) | k = (1/2, 0, 0) | ||||||
| Γ1(++++) | (x y z) | (-x y + 1/2 -z + 1/2) | Γ1(++++) | (x y z) | (-x y + 2/2 -z + 1/2) | ||
| Ψ1 | (1 0 0) | (Γ 0 0) | Ψ1 | (1 0 0) | (Γ 0 00) | ||
| Ψ2 | (0 1 0) | (0 1 0) | Ψ2 | (0 1 0) | (0 1 00) | ||
| Ψ3 | (0 0 1) | (0 0 Γ) | Ψ3 | (0 0 1) | (0 0 Γ0) | ||
| Γ3(+-+-) | (x y z) | (-x y + 1/2 -z +1/2) | Γ3(+-+-) | (x y z) | (-x y +1/2 -z +1/2) | ||
| Ψ1 | (1 00) | (1 0 0) | Ψ1 | (1 00) | (1 0 0)0 | ||
| Ψ2 | (0 1 0)0 | (0 Γ 0) | Ψ2 | (0 1 0) | (00 1 0) | ||
| Ψ3 | (0 0 1 | (0 0 1) | Ψ3 | (0 0 1) | (0 01) | ||