| Transition Temperature | 9.5 K |
|---|---|
| Experiment Temperature | 1.6 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | P63/mmc (#194) |
| Magnetic Space Group | Cmcm' (#63.461) |
| Magnetic Point Group | m'mm (8.3.26) |
| Lattice Parameters | 8.8300 8.8300 9.4296 90.0000 90.0000 120.0000 |
|---|---|
| DOI | 10.1103/physrevb.85.064412 |
| Reference | R. Troc, M. Pasturel, O. Tougait, A.P. Sazonov, A. Gukasov, C. Sulkowski and H. Noël, Physical Review B (2012) 85. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| U1_1 | U | 0.0 | -2.5 | 0.0 | 2.50 |
| U1_2 | U | -2.5 | -2.5 | 0.0 | 2.50 |
Single-crystal study of the kagome antiferromagnet U_{3}Ru_{4}Al_{12}
R. Troč, \( ^{1,*} \) M. Pasturel, \( ^{2} \) O. Tougait, \( ^{2} \) A. P. Sazonov, \( ^{3} \) A. Gukasov, \( ^{3} \) C. Sulkowski, \( ^{1} \) and H. Noël \( ^{2} \)
\( ^{1} \) Institute of Low Temperature and Structure Research, Polish Academy of Sciences, P.O. Box 1410, 50-950 Wrocław 2, Poland
\( ^{2} \) Sciences Chimiques de Rennes, Université de Rennes 1, UMR CNRS 6226, Campus de Beaulieu, 263 av. Général Leclerc, 35042 Rennes Cedex, France
\( ^{3} \) CEA, Centre de Saclay, DSM/IRAMIS/Laboratoire Léon Brillouin, F-91191 Gif-sur-Yvette, France (Received 25 July 2011; revised manuscript received 3 October 2011; published 21 February 2012)
A ternary intermetallic compound, \( U_{3}Ru_{4}Al_{12} \) in a single-crystal form, was studied by measurement of susceptibility, magnetization, electrical resistivity, magnetoresistivity, thermopower, and heat capacity, as well as neutron diffraction, revealing that this aluminide is an antiferromagnetically ordered ( \( T_{N} = 9.5 \) K) dense Kondo system ( \( T_{K} \approx 30 \) K) with a considerable enhancement of the Sommerfeld coefficient \( \gamma(0) \) of about 200 mJ mol \( ^{-1} \) K \( ^{-2} \) . The electrical resistivity and thermopower of \( U_{3}Ru_{4}Al_{12} \) show characteristic features of the interplay between anisotropic magnetic exchange, Kondo, and crystal field effects. A pronounced in-plane anisotropy and a unique noncollinear antiferromagnetic structure in the \( (a,b) \) hexagonal plane, found by neutron diffraction, are discussed in view of the effect of geometrical frustration caused by the distorted kagome lattice of a \( Gd_{3}Ru_{4}Al_{12} \) -type crystal structure. Thus, the overall behavior of \( U_{3}Ru_{4}Al_{12} \) resembles that observed for the orthorhombic compound \( UCu_{5}In \) , reported earlier as a spin density wave material.
DOI: 10.1103/PhysRevB.85.064412
PACS number(s): 71.27.+a, 75.20.Hr, 72.15.Eb, 72.15.Jf
I. INTRODUCTION
Investigation into the magnetic properties of various families of solids containing magnetic atoms forming geometrical frustration, as in triangular, kagome-like spinels and pyrochlore lattices, is a hot topic for physicists today. Because of the complicated geometrical frustrations induced by specific crystal structures, a number of unusual behaviors take place, such as multiple-phase transitions, complex magnetic structures (e.g., with coexistence of magnetic and nonmagnetic sites), and suppression of magnetic ordering temperatures. \( ^{1-3} \) We will only mention here some examples of rare earth–(R) or uranium-based intermetallic antiferromagnets in which R or U atoms are connected in a two-dimensional (2D) network of triangles sharing vertices, forming a kagome-like network in the hexagonal basal plane. \( ^{4,5} \) For the latter case, the triangular lattice of Er or U ions in \( ErNiAl^{6} \) and \( UNi_{4}B_{7} \) , respectively, means their magnetic moments, which lie in the basal hexagonal plane, can only form an angle between one another. For example, the phenomenon of frustration occurs fairly often in the antiferromagnetic ternary aluminides like \( R(Ni,Pd,Pt)Al \) and \( UNiAl \) , which crystallize like \( ErNiAl \) in the hexagonal \( ZrNiAl \) -type structure, where all R or U atoms are located on crystallographically equivalent 3f sites. Thus, the symmetry of the triangular lattice of this site in the \( (a,b) \) plane resembles that of the kagome lattice. \( ^{8} \) As expected, many representative compounds containing R atoms forming this kind of network are characterized by a complex magnetic structure, like that reported, for example, for \( PrPdAl \) , from the interplay between frustrated anisotropic exchange interactions and magnetocrystalline anisotropy of the hexagonal structure. In isostructural 5f compounds, the antiferromagnetic coupling of moments usually occurs along the c axis; thus, no frustration takes place. The close packing of U and T (transition metal) atoms in the basal plane of the \( ZrNiAl \) -type structure results in a strong 5f-d hybridization that, as a consequence, leads to an Ising-like system of strongly ferromagnetically coupled moments in this plane. Nevertheless, a notable exception is UNiAl, in which the magnetic moments are arranged parallel to the c axis but their amplitude forms in the basal plane a modulated, frustrated structure with magnetic propagation vector \( \mathbf{k} = (0.1, 0.1, 0.5) \) . \( ^{10} \)
Also within the \( Gd_{3}Ru_{4}Al_{12} \) structure type (space group \( P6_{3}/mmc \) , no. 194), \( ^{11,12} \) the f element located at the 6h site forms a distorted 2D kagome lattice, wherein small \( [U3] \) triangles share vertices with larger ones, and vice versa. Knowing that uranium magnetic moments have a strong tendency to order collinearly along the c axis in hexagonal structures, wherein moments lie ferromagnetically ordered perpendicular to the network of nearest neighbor (n-n) links between uranium atoms in basal planes, \( ^{13} \) it was obvious that this geometry, in the case of (n-n) antiferromagnetic-type interactions in the basal plane, will be responsible for magnetic frustrations (e.g., inducing a spin-glass behavior in \( U_{3}Fe_{4}Al_{12} \) [Ref. 14 and \( U_{3}Co_{4+x}Al_{12-x} \) [Refs. 15,16]) crystallizing in the above structure type. In this context, it was quite surprising that the isostructural \( U_{3}Ru_{4}Al_{12} \) exhibits an antiferromagnetic ordering at \( T_{N} = 8.4 \) K in the presence of Kondo-like interactions. \( ^{17} \)
To further investigate the physical properties of the latter aluminide, a single crystal of \( U_{3}Ru_{4}Al_{12} \) was grown and analyzed by conducting magnetic, electrical transport (resistivity in magnetic fields from 0 up to 8 T), thermopower, and specific heat measurements, as well as neutron diffraction. The aim of this paper is to present the various results and try to understand the formation of the antiferromagnetically ordered state in the kagome-like network. Elhajal et al. \( ^{18} \) have shown that antisymmetric Dzyaloshinsky–Moriya interactions are present in such a lattice type and that they can drive the system to ordered states.
II. EXPERIMENTAL DETAILS
A single crystal of \( U_{3}Ru_{4}Al_{12} \) is grown by the Czochralski pulling method in a tetra-arc furnace under an argon atmosphere. The starting components were high-purity elements (U-3N, Ru-4N, and Al-5N). The obtained crystal was
a cylinder 4 mm in diameter and 15 mm in length. It was easily pulled along the twofold a axis. The crystal was not given any additional heat treatment. The sixfold symmetry clearly appears on the Laue pattern taken from the plane perpendicular to the c axis. The x-ray diffraction (XRD) performed on powdered small crystals enlarged the lattice parameters slightly \( (a = 0.8838[5] \) and \( c = 0.9439[5] \) nm) compared with those reported previously. \( ^{[17]} \) The specimens for microanalysis and physical measurements were cut from an x-ray-oriented crystal using a wire saw.
Magnetic properties of the oriented single crystals were investigated in a temperature range of 2–400 K and magnetic fields up to 5 T using a superconducting quantum interference device magnetometer. Unpolarized neutron diffraction studies were performed at \( T = 1.6 \) and 10 K on the 6C2 diffractometer ( \( \lambda = 0.9 \) Å) at the Orphée reactor of the Laboratoire Léon Brillouin, Saclay, France. The MAGLSQ program from the Cambridge Crystallography Subroutine Library \( ^{19} \) was used to refine the parameters of the nuclear and magnetic structures.
Electrical resistivity measurements were performed with the usual DC four-probe technique from room temperature (RT) down to 350 mK, whereas the magnetoresistivity was measured in the temperature range 4.2–35 K in magnetic fields up to 8 T. External magnetic field was always applied perpendicular to the current j. Specific heat was determined using a relaxation calorimeter in the temperature range 4–70 K. Finally, the Seebeck coefficient was measured in the temperature range 5–300 K with a steady-state method.
III. RESULTS AND DISCUSSION
A. Magnetic properties
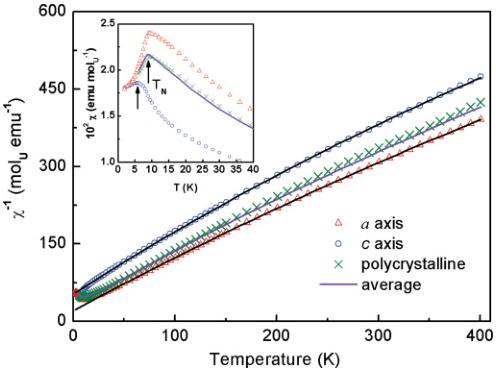
The thermal variation of the magnetic susceptibility (inset) of \( U_{3}Ru_{4}Al_{12} \) and its inverse, measured along the a and c axes, are presented in Fig. 1 and compared with the polycrystalline sample data.
As expected from the hexagonal \( Gd_{3}Ru_{4}Al_{12} \) structure type of this intermetallic compound, a remarkable anisotropy is observed between measurements along both crystallographic directions. Despite this anisotropy, the high temperature of the \( \chi^{-1} \) vs. T curves, measured in fields oriented along the \( a \) ( \( \chi_{a} \) ) and \( c \) ( \( \chi_{c} \) ) axes, follow a modified Curie–Weiss law in the temperature range 30–400 K: \( \chi_{i} = C_{i}/(T - \theta_{p}^{i}) + \chi_{0}^{i} \) (where C is a Curie constant, \( \theta_{p} \) is the paramagnetic Curie temperature, \( \chi_{0} \) is the temperature-independent susceptibility, and i = a and c) with the following fitting parameters:
\[ \begin{aligned}\chi_{a}^{0}&=3.60(5)10^{-4}emu mol^{-1};\mu_{\mathrm{eff}}^{a}=2.72\mu_{\mathrm{B}}\\\mathrm{and}\quad&\theta_{\mathrm{p}}^{a}=-19.1(3)\mathrm{K}(along the a axis);\\\chi_{0}^{c}&=4.20(8)10^{-4}emu mol^{-1};\mu_{\mathrm{eff}}^{c}=2.45\mu_{\mathrm{B}}\\\mathrm{and}\quad&\theta_{\mathrm{p}}^{c}=-40.5(3)\mathrm{K}(along the c axis).\end{aligned} \]
The moderately negative values of \( \theta_{p}^{i} \) are characteristic of the presence of antiferromagnetic interactions. Thus, the derived values \( \theta_{p}^{i} < 0 \) for both crystallographic directions provide an estimate for the strength of magnetic interactions for an antiferromagnet and set a scale for magnetic anisotropy according to the following definition of the frustration parameter f, where \( f^{i} = |\theta_{p}^{i}| / T_{N} \) . The obtained values \( f^{i} > 2-5 \) indicate a

FIG. 1. (Color online) Temperature dependencies of reverse molar susceptibility measured under a magnetic field of 0.5 T applied parallel to the a and c axes. Solid lines represent fits to the modified Curie–Weiss law of the experimental data above about 20 K. Dependencies for average susceptibility for the polycrystalline sample are also displayed. The inset shows all these susceptibilities at low temperature.
suppression of ordering temperature as a result of frustration. \( ^{1} \) The small values of \( \chi_{0} \) found for both axes highlight a small curvature of both \( \chi_{i}^{-1}=f(T) \) curves, which mainly originates from the presence of the crystal electric field (CEF) acting on the uranium ion in this aluminide. Also note in Fig. 1 that the average inverse susceptibility data of \( 1/(^{2}/_{3}\chi_{a}+^{1}/_{3}\chi_{c}) \) match quite well the polycrystalline sample data, with a mean maximum value located at \( T_{\mathrm{N}}(\mathrm{average})=T_{\mathrm{N}}(\mathrm{poly})=8.4\;\mathrm{K} \) (Ref. 17; i.e., about 1 K lower than the value found from measurements on the single crystal, i.e., \( T_{N}=9.5\;K \) ).
The low-temperature thermal variations of the magnetic susceptibility are shown in the inset to Fig. 1. Susceptibility along the a axis ( \( \chi_{a} \) ) presents rather a sharp maximum at \( T_{N} \) , characteristic of an antiferromagnetic transition, whereas along the c axis ( \( \chi_{c} \) ), the transition is much less visible, and only a broad small hump appears with its maximum, however, at 6(1) K. This signals a noncollinear magnetic structure formed within the hexagonal basal plane in which none of the components of the susceptibility is expected to show a tendency to fall to zero, far below \( T_{N} \) . Also, the overall magnitudes of susceptibilities \( \chi_{a} > \chi_{c} \) indicate that the ordering of magnetic moments is confined just in the \( (a,b) \) hexagonal basal plane (i.e., in the uranium-distorted kagome net plane). This finding is in accord with the neutron diffraction data presented below. As one expects in the case of an existing kagome plane, various antiferromagnetic arrangements of the uranium moments are possible.
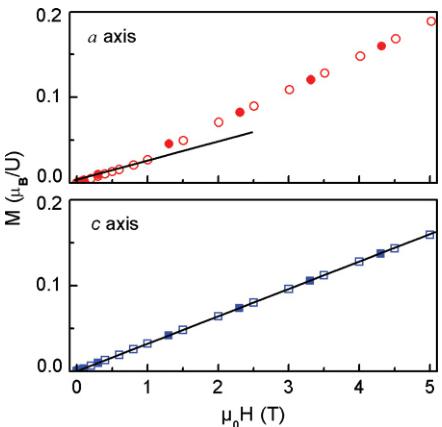
The magnetic field dependencies of the magnetization taken at 2 K along the a and c axes are presented in Fig. 2. As seen along the c axis, the magnetization \( M_{c}(B\|c) \) measured up to \( \mu_{0}H = 5 \) T is linear and fully reversible, as expected for a paramagnetic or an antiferromagnetic state. However at this temperature, the susceptibility \( \chi_{c} \) (taken as the slope of the \( M_{c} \) vs. B straight line) is greater than \( \chi_{a} \) if one compares the slope for this direction below about \( \mu_{0}H \approx 1 \) T. Above

FIG. 2. (Color online) Magnetization isotherms with field parallel to the a and c axes taken at 2 K. Solid lines show straight-line behavior below 1 T along the a axis and up to 5 T along the c axis. The open and closed symbols are the measured increasing and decreasing magnetic fields, respectively.
this field, \( M_{a}(B\|a) \) increases in a manner we have already observed for the polycrystalline sample, \( ^{17} \) keeping, however, a slope similar to \( M_{c}(B\|c) \) . We think that some tendency to moderate the field-induced metamagnetic transition in the \( (a,b) \) plane can explain this observation. Therefore, the increase in slope of \( M_{a}(B\|a) \) mentioned above may be ascribed to the partial release of magnetic frustration, as, for example, that reported for another kagome-like system, namely YbAgGe, \( ^{20} \) crystallizing in the ZrNiAl-type structure, for which a change in the initial slope of \( M(B\|a) \) was observed above 4.5 T.
B. Neutron diffraction
To determine the precise magnetic structure of \( U_{3}Ru_{4}Al_{12} \) , single-crystal neutron diffraction measurements were performed. As many as 136 Bragg reflections were collected up to \( \sin\theta/\lambda = 0.45 \, \AA^{-1} \) at 1.6 K. The nuclear structure parameters were deduced from the measurements at 10 K, corroborating these obtained at room temperature by single-crystal XRD. The integrated intensities of the measured reflections were used to refine the components of the uranium magnetic moments using the symmetry constraints described below. All the observed reflections at 1.6 K can be indexed with a magnetic propagation vector \( k = 0 \) . This means no loss in translational symmetry from the magnetic moment arrangement and identity of the magnetic and chemical cells. To analyze the possible magnetic structure of \( U_{3}Ru_{4}Al_{12} \) , a systematic search was performed based on the theory of representations of space groups proposed by Bertaut \( ^{21} \) and Izyumov and Naish. \( ^{22} \) It allows one to consider all possible models of magnetic structures consistent with a given crystal structure of space group G. According to this method, the magnetic structure can be expressed via the basis vectors of the irreducible representations of group G. To calculate the irreducible representations, the program SARAh \( ^{23} \) was used. The magnetic representation for the U ions occupying the 6b site in the \( P6_{3}/mmc \) space group with \( k = 0 \) can be written as \( \Gamma_{U} = 1\Gamma_{2}^{(1)} + 1\Gamma_{3}^{(1)} + 1\Gamma_{4}^{(1)} + 1\Gamma_{5}^{(1)} + 1\Gamma_{6}^{(1)} + 1\Gamma_{7}^{(1)} + 2\Gamma_{9}^{(2)} + 1\Gamma_{10}^{(2)} + 1\Gamma_{11}^{(2)} + 2\Gamma_{12}^{(2)} \) , following the numbering scheme of Kovalev. \( ^{24} \) The basis vectors describing moments of the \( U^{3+} \) ions, which transform according to the irreducible representations from \( \Gamma_{2} \) to \( \Gamma_{11} \) , can be ruled out because they do not allow any contribution to the strongest measured magnetic reflection (001) and provide a poor description of other magnetic reflections ( \( \chi^{2} = 2.1-2.5 \) ). In contrast, only the 2D representation \( \Gamma_{12} \) yields a correct description of our neutron diffraction data ( \( \chi^{2} = 1.2 \) ).
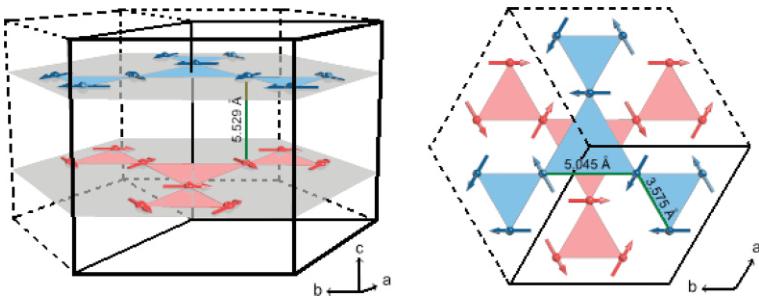
The planar triangular noncollinear magnetic structure resulting from the refinement in \( \Gamma_{12} \) is illustrated in Fig. 3. The relatively large \( U^{3+} \) magnetic moments of \( 2.5(2)\mu_{B} \) , lie in the \( (a,b) \) plane, as expected. They are parallel, either to the a axis or the b axis, as well as to the shortest diagonal of the rhombus formed by those axes. The three uranium moments form an angle \( \alpha=2\pi/3=120^{\circ} \) at the three apexes of the smallest [U3] triangles of the kagome network. The interatomic distances in this triangle are \( d_{U-U}=3.575(1)\mathring{A} \) , a value not far from the 3.5- \( \mathring{A} \) Hill criterion for appearance of magnetic ordering. This and the other \( d_{U-U} \) distances are visualized in Fig. 3. It should be noted that the classical ground state of a kagome lattice antiferromagnet is an ordered state in which the three spins around any triangle are oriented 120 degrees apart, such

FIG. 3. (Color online) Magnetic structure (left panel) of \( U_{3}Ru_{4}Al_{12} \) and its projection on the basal \( (a,b) \) plane (right panel). For clarity, only the uranium atoms are presented.
that the sum of these three spins shows no net moment on the triangle. Surprisingly, the magnetic structure found for \( U_{3}Ru_{4}Al_{12} \) features a net moment on each triangle, in which the spins are rotated \( -60^{\circ} \) , \( 0^{\circ} \) , and \( +60^{\circ} \) from the b axis. Thus, two thirds of all nearest neighbor bonds are slightly ferromagnetic, whereas one third are antiferromagnetic, leading to the ferromagnetic-like component in the layer. The nearest neighbor layers are coupled in such a way that their ferromagnetic-like components compensate each other, which results in an overall antiferromagnetic structure. This unique noncollinear magnetic order arises as a result of a compromise between the various anisotropic interactions.
C. Electrical transport
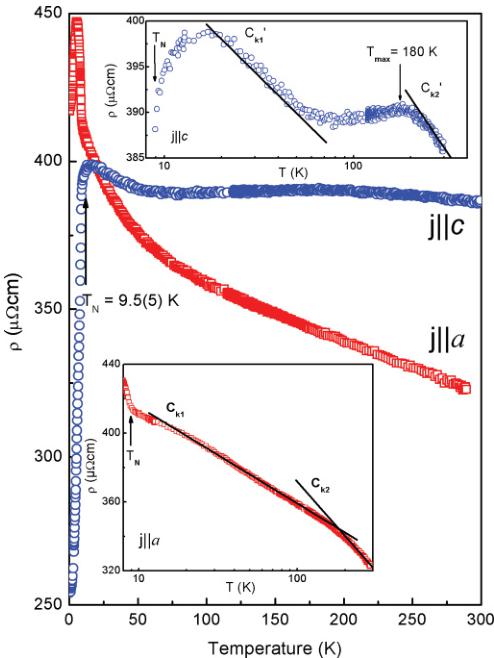
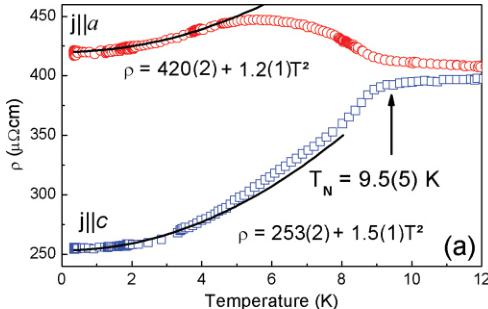
The thermal variations of the electrical resistivity for \( U_{3}Ru_{4}Al_{12} \) measured along the main crystallographic axes are presented in Fig. 4. As can be seen, resistivity in the high-temperature region measured along the a axis ( \( \rho_{a} \) ) first increases slowly with decreasing temperature below RT. Then, at about 100 K, it begins to rise more rapidly, finally reaching the Néel temperature found from susceptibility measurements [i.e., \( T_{N} = 9.5(5) \) K]. As in the case of the polycrystalline sample, \( ^{[17]} \) we tend to describe this behavior with CEF effects in

FIG. 4. (Color online) Temperature dependencies of electrical resistivity measured with current flowing along the two main crystallographic directions. Upper and lower insets present resistivity for current flowing along the c and a axes, respectively, versus \( \log T \) . Solid lines show logarithmic behavior, with slopes \( c_{ki} \) for resistivity in the paramagnetic state.
the presence of Kondo interactions, as highlighted in the lower inset to Fig. 4, showing -1g T behavior of \( \rho_{a}(T) \) . As is seen, this function behaves with different logarithmic slopes \( c_{k1} \) and \( c_{k2} \) in two regions (i.e., between 20 and 180 K and 180 and 300 K, respectively). According to Cornut and Coqblin, \( ^{25} \) who combined the influence of the Kondo effect and crystal field interactions on the electrical properties of cerium intermetallic compounds, the logarithmic slopes \( c_{i} \) may be proportional to the squared effective degeneracy of the thermally populated crystal field levels. Such an observation has been made for many \( Ce^{3+} \) -containing compounds, as, for example, in the case of the tetragonal \( Ce_{2}T_{2}In \) -type (T = Pd, Cu, Au) compounds \( ^{26} \) that were shown to behave quantitatively according to the theory of Cornut and Coqblin. \( ^{25} \) Furthermore, the transport studies \( ^{27} \) of the solid solutions between antiferromagnetically ordered \( Ce_{2}Cu_{2}In \) ( \( T_{N} = 5.5 \) K) and intermediate valence system \( Ce_{2}Ni_{2}In \) , where the effect of delocalization of 4f electrons increases with increasing Ni concentration, have revealed many similarities in the logarithmic characteristics of resistivity between some intermediate compositions and those presented here for \( U_{3}Ru_{4}Al_{12} \) .
In turn, the \( \rho_{a}(T) \) dependence of \( U_{3}Ru_{4}Al_{12} \) , after passing a kink at \( T_{N} \) , forms a sharp peak at \( T_{max} = 5.6(5) \) K and then decreases to a large value of the residual resistivity \( \rho_{0} = 420 \mu\Omega cm \) . An overall behavior found below \( T_{N} \) in \( \rho_{a}(T) \) for this compound is similar to a few examples determined earlier for the rare earth and uranium compounds. For the latter cases, we only mention here the occurrence of a similar sharp peak in \( \rho(T) \) just below the temperature of a given phase transition, as for \( UCu_{2}Sn \) , \( ^{28} \) \( UCu_{5} \) , \( ^{29} \) and \( UNi_{2}Ge_{2} \) . \( ^{30} \) Thus, for all cases, a low-temperature gapping of the Fermi surface (FS) has been postulated. In general such a drastic change in the FS may be caused by (i) the difference between the unit cells of the crystal and magnetic structures brought about by the occurrence of new Brillouin superzone boundaries \( ^{31} \) or (ii) the rise of a spin density wave (SDW) state like that in \( Cr_{3} \) , \( ^{32} \) where the FS becomes partially gapped. Initially, the situation in \( UCu_{2}Sn \) , crystallizing in the hexagonal \( ZrCu_{2}Al \) -type structure, was attributed to the first (i) origin, but later, the sharp peak in \( \rho(T) \) observed just below the phase transition for \( UCu_{2}Sn \) was explained by a nonmagnetic effect at \( T_{Q} = 16 \) K, caused by a quadrupolar ordering \( ^{33} \) in a way similar to those reported earlier for \( UPd_{3} \) \( ^{34} \) and \( URu_{2}Si_{2} \) . \( ^{35} \) The second (ii) possibility was described in detail (e.g., in the case of \( UCu_{5} \) \( ^{36} \) crystallizing in the cubic AuBe \( _{5} \) -type structure), which shows a coherent Kondo state with antiferromagnetic (AFM) ordering below \( T_{N} = 15 \) K. In view of the additional 1 K phase transition existing in this compound, \( ^{36} \) the muon spin resonance ( \( \mu SR \) ) data \( ^{37} \) have revealed that, except for conventional antiferromagnetism with 4q- and 1q-type magnetic structures realized below the higher and lower temperature phase transitions, respectively, \( ^{38} \) a quasi-independent subsystem with very small ordered moments associated with static SDW sets in at the lowest temperatures by the heavy quasiparticles. \( ^{37} \)
However, electrical transport properties most similar to that reported in this paper for the aluminide were found for the medium-heavy fermion antiferromagnet \( UCu_{5}In \) ( \( T_{N} = 25 \, K \) ) crystallizing in the orthorhombic \( CeCu_{5}Au \) -type structure. \( ^{[39]} \) The resistivity measurements performed along the a, b, and c directions revealed negative Kondo-like
temperature coefficients and pronounced maxima of a similar shape, centered at about 15 K along all three axes, practically independent of an applied pressure up to 2.2 GPa in both the shape and \( T_{N} \) value. \( ^{39} \) This indicates unambiguously that the observed feature is not a Kondo coherence peak, but it may originate from the SDW formation, as suggested earlier in Ref. 39. Such a conclusion comes from the fact that \( UCu_{5}In \) exhibits a noncollinear antiferromagnetic structure of uranium moments confined to the \( (a,c) \) plane with a magnetic unit cell of the same size as that of the chemical unit cell. \( ^{39} \)
We found quite different behavior from that of \( \rho_{a}(T) \) for \( \rho_{c}(T) \) in both the paramagnetic and ordered temperature regions. As Fig. 4 demonstrates, this dependence with decreasing temperature below RT manifests, first, a very diffuse maximum (on the scale of this figure) and then, below about 100 K, it goes through a distinct knee to fall rapidly at \( T_{N} \) . From the upper inset of this figure, where the above behavior is presented as \( -\log T \) on an enlarged scale, it becomes clear that for this case we also have two different logarithmic slopes \( c_{ki} \) . One may compare these two features with those we have described above for the \( \rho_{a}(T) \) curve, but it happens to be true in slightly different temperature ranges. Because we also show the curves containing the phonon contribution [the magnetic part \( \rho_{\mathrm{m}}(T) \) could not be isolated], we restrict ourselves only to pointing out that this phenomenon has not been detected earlier for any other uranium compound. Although it was not strictly said, such a behavior can also be seen for \( UCu_{5}In \) from Fig. 1 of Ref. 39. It is worthwhile noting that the magnetic and transport properties of single-crystal \( UNi_{2}Ge_{2} \) are also very close to those of \( U_{3}Ru_{4}Al_{12} \) . This tetragonal germanide ( \( ThCr_{2}Si_{2} \) -type) exhibits AFM ordering ( \( T_{N} = 78 K \) ) and large anisotropy in resistivity. The difference appears mainly in the crystallographic directions. Here, resistivity shows a Kondo-type behavior and a sharp resistivity peak along the c axis. \( ^{30} \)
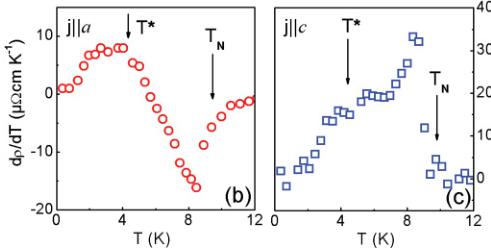
We have also analyzed the resistivity behavior of \( U_{3}Ru_{4}Al_{12} \) in the low-temperature region down to 0.3 K within the AFM state. In Fig. 5, we present the resistivities [Fig. 5(a)] and their derivatives [Figs. 5(b) and 5(c)], \( d\rho_{i}(T)/dT \) , as functions of temperature. As seen from Fig. 5(a), the Fermi liquid behavior [i.e., \( \rho_{i}(T)=\rho_{0i}+A_{i}T^{2} \) ] is followed for current j flowing along both main crystallographic directions. The corresponding parameters are given in the figure. However, the above equation for both \( \rho_{a}(T) \) and \( \rho_{c}(T) \) is obeyed only below 4.5 K. Along the a axis, the electrical resistivity is characterized by a distinct negative anomaly in \( d\rho_{a}(T)/dT \) , appearing close to \( T_{N} \) [Fig. 5(b)], as previously observed for \( UCu_{5} \) (Fig. 5 in Ref. 36). Bernasconi et al. \( ^{36} \) took a similar approach for \( UCu_{5} \) as that in \( Cr^{32} \) to show the effect of AFM ordering on the FS in \( UCu_{5} \) . This effect gives rise to gapping of a part of the FS due to additional Brillouin-zone boundaries. In contrast, along the c axis, the picture is typical of that in the usual, magnetically ordered f-electron system but shows additionally the presence of SDW-like fluctuations evidenced by a diffuse peak at \( T^{*} \) (as is, e.g., the case of \( UGe_{2} \) ) \( ^{40} \) [Fig. 5(c)]. Almost the same general behavior of \( d\rho_{i}(T)/dT \) , but with the axes reversed (the c-axis is here the direction of antiferromagnetically ordered magnetic moments below \( T_{N}=36 \) K), is presented in Ref. 41 for single-crystal \( UPt_{2}Si_{2} \) crystallizing in the tetragonal \( CaBe_{2}Ge_{2} \) -type structure.


FIG. 5. (Color online) (a) Low-temperature variations of the electrical resistivity of \( U_{3}Ru_{4}Al_{12} \) measured along the a and c directions (upper panel). (b) and (c) Temperature derivatives of resistivity calculated for both crystallographic directions (lower panel). Explanation of \( T^{*} \) is given in the text.
The whole discussion given above leads to the conclusion that a number of uranium binary and ternary intermetallics show transport behavior reminiscent of that first described for metallic chromium, independent of their crystal structures. However, the simultaneous presence of conventional, local AFM ordering makes it experimentally difficult to understand clearly the existence of two quasi-independent electronic subsystems. They originate from a dual character of the \( 5f \) electrons in some uranium metallic compounds (one is itinerant and the other is more localized in character). This requires more sophisticated studies in the future than have been done up to now to explain the roles played by each subsystem separately.
D. Transverse magnetoresistivity
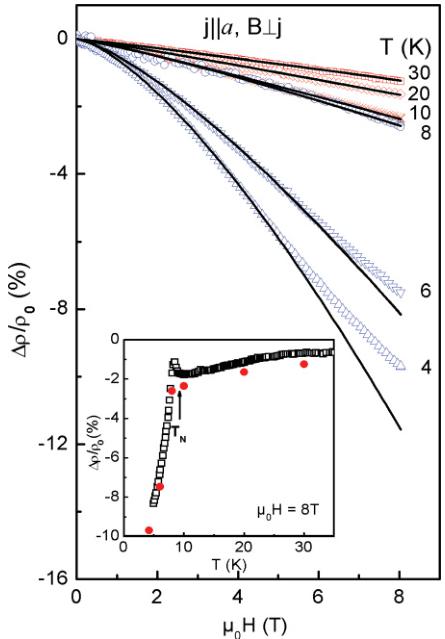
The transverse magnetoresistivity (TMR), defined as \( \Delta\rho/\rho_{0}=(\rho_{BT}-\rho_{0T})/\rho_{0T} \) , were measured as a function of an applied magnetic field perpendicular to j at several temperature values and as a function of temperature at \( \mu_{0}H=8 \) T. The results for j along the a and c axes are depicted in Figs. 6 and 7, respectively. Along the a axis, the field-dependent variation of TMR shows a slight negative curvature above \( T_{N} \) , following the \( -\alpha(T)B^{n} \) function, with fitting parameters \( \alpha \) and n presented in Table I. Below \( T_{N} \) , the negative curvature is more pronounced, and a deviation from the above variation is observed at high magnetic fields.
As Table I demonstrates, the power factor n varies from 1.08 to 1.42 and yields smaller values than the expected value n = 2,
TABLE I. Fit parameters of transverse magnetoresistivity along the \(a\) axis to the \(-\alpha(T)B^{n}\) law.
| T (K) | 4 | 6 | 8 | 10 | 20 | 30 |
| \( \alpha(T^{-n}) \) | 0.600(5) | 0.500(5) | 0.225(5) | 0.235(5) | 0.175(5) | 0.130(5) |
| n | 1.42(2) | 1.34(2) | 1.17(2) | 1.11(2) | 1.08(2) | 1.08(2) |
showing the coexistence of at least two different components in TMR. This result is a little surprising as long as the polycrystalline sample strictly follows the \( -\alpha(T)B^{2} \) law. \( ^{[17]} \) In turn, the thermal variation of TMR, taken at a constant magnetic field of 8 T and presented in the inset to Fig. 6, confirms the negative character in the entire studied temperature range. The TMR behavior of \( U_{3}Ru_{4}Al_{12} \) , measured for the configuration \( j\parallel a \) and \( B\parallel c \) in the paramagnetic range of temperatures, changes only weakly with temperature. Subsequently, just below \( T_{N} \) , \( \Delta\rho/\rho_{0}(T) \) first goes through a small negative maximum and then it falls rapidly with decreasing temperature, achieving at 4.2 K a large value of about \( -10\% \) . As is further seen from this inset, the slope of magnetoresistivity changes radically below \( T_{N} \) after formation of the above peak, which proves the

FIG. 6. (Color online) Transverse magnetoresistivity \( \Delta\rho/\rho_{0} \) for the current j flowing along the a axis in a magnetic field applied perpendicular to the current and measured for several temperatures between 4.2 and 30 K. Blue and red points show differences between AFM ordered and paramagnetic regions of measured temperatures. The inset shows magnetoresistivity taken at 8 T along this axis and measured as a function of temperature. The filled red dots in the inset correspond to the values obtained at 8 T on the main graph. The solid lines are fittings to the \( -\alpha(T)B^{n} \) function (see Table I).
existence of the gap in a part of the FS attributed to SDW and surviving even in an applied magnetic field as large as 8 T. It is interesting to recall here the high magnetic field study performed by Andraka et al. \( ^{42} \) on \( UCu_{5} \) also was regarded as exhibiting SDW properties below \( T_{N} \) . It turned out that even the 10-T field had only a negligible effect on the resistivity hump formed in the vicinity of \( T_{N} \) .
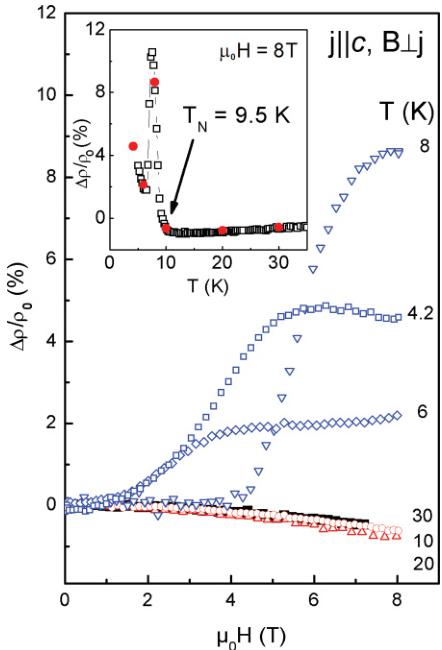
The TMR behavior along the c axis, is displayed in Fig. 7. As this figure illustrates, in the temperature range above \( T_{N} \) , there is a tiny negative curvature in \( \Delta\rho/\rho_{0}(B) \) with increasing magnetic field strength, but the \( \Delta\rho/\rho_{0} \) magnitudes measured at T = 10, 20, and 30 K are almost the same, in agreement with the temperature variations of TMR at 8 T (see the inset to Fig. 7). Nevertheless, below \( T_{N} \) , this variation changes radically: at T = 8 K, a sharp increase from almost 0% to positive values of TMR is observed, but only above a critical field \( \mu_{0}H_{c} = 4.2 \) T. Then, this quantity above about 6 T begins to show a tendency to form a maximum, reaching a value of about 9% at \( \mu_{0}H = 8 \) T. A further decrease in temperature results in a decrease in the \( \Delta\rho/\rho_{0} \) magnitudes, shifting a

FIG. 7. (Color online) Same as in Fig. 6, but for current j flowing along the c axis.
weakly marked wide maximum to lower magnetic fields. Also, the initial \( \mu_{0}H_{c} \) field required for their rise falls to about 1 T for the 6-K and 4.2-K magnetoresistivity isotherms. As depicted in the inset to Fig. 7, these observations are correlated to the presence of a sharp peak below \( T_{N} \) in the thermal variation of TMR taken for this direction at \( \mu_{0}H = 8 \) T. The SDW state postulated in this work, owing to the resistivity peak apparent along the a axis just below \( T_{N} \) in the absence of a magnetic field, seems thus to propagate along the c axis above a certain critical magnetic field, \( \mu_{0}H_{C} > \sim 1 \) T, depending on the temperature of measurements. This aspect of measurements has to be investigated further (e.g., by making \( \mu \) SR or neutron diffraction studies in applied magnetic fields). Such data are necessary to infer more conclusive explanations of the TMR results presented in this paper.
Now we can only conclude that in the ordered state of \( U_{3}Ru_{4}Al_{12} \) , the SDW state can also be generated along the c axis by applying an external magnetic field. As mentioned above, the SDW hump is seen along all three main directions in the case of the orthorhombic \( UCu_{5}In \) . \( ^{39} \) Furthermore, in the ordered magnetic state, an applied magnetic field also seems to enhance the electrical conductivity in the \( (a,b) \) plane containing the magnetic moments and to decrease this conductivity perpendicular to this plane.
E. Seebeck coefficient
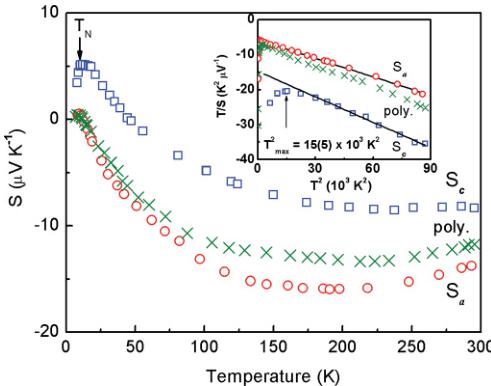
Thermal variation of the thermoelectric power (TEP), \( S_{i} \) , shown in Fig. 8, demonstrates remarkable anisotropy between the a and c axes. Moreover, it presents many common features with that of the \( S_{\mathrm{poly}}(T) \) behavior, \( ^{17} \) whose overall values are located rather closer to the \( S_{a}(T) \) variation, as is also the case for the corresponding temperature dependencies of the resistivity.
At high temperatures, the Seebeck coefficient is negative for both main axes and goes through a broad minimum at 200 K and 230 K, attaining values of -16.0 and -8.5 \( \mu \) V

FIG. 8. (Color online) Temperature dependencies of thermoelectric power \( S_{i} \) measured along the a and c axes and for the polycrystalline sample (Ref. 17). The inset shows \( T/S_{i} \) as a function of temperature squared. Solid lines show the straight-line behavior of this dependence.
\( K^{-1} \) , for \( S_{a}(T) \) and \( S_{c}(T) \) , which in turn become positive below T = 12 and 46 K, respectively. Finally, both of these curves go through a positive maximum at the vicinity of \( T_{N} \) , and afterward, their extrapolations drop to zero at T = 0 K. It should be noted that if the former maximum is only very weakly marked, the latter one, at the same time, is fairly well pronounced. These variations are in line with those previously reported for the polycrystalline sample and were attributed to Kondo-like interactions in the presence of CEF effects, as well as to a change in the density of states (DOS) at the Fermi level at temperatures close to \( T_{N} \) , owing to the change in sign of \( S_{i}(T) \) . It should be emphasized here that the sign change and the subsequent positive low-temperature increase of TEP forming a maximum are typical features of a Kondo system. \( ^{43} \) At the same time, in such a system with an AFM ground state, \( S(T) \) reaches a maximum at \( T_{N} \) together with a tendency to reach a Kondo resonance as the temperature is lowered. Finally, this results in the occurrence of a positive maximum in \( S(T) \) . For confirmation of this conclusion, one can find almost identical behavior of \( S(T) \) in \( UCu_{5}In \) .
In a procedure similar to that applied to the polycrystalline sample, the T/S vs. \( T^{2} \) plots have been drawn in the inset to Fig. 8, highlighting the linear variation of those plots at high temperature in the paramagnetic state. This linear variation is followed by \( S_{a} \) just for \( T > T_{N} \) , while in the case of \( S_{c} \) this is only true above 170 K. As shown for both of the crystallographic axes, the above linearity means that \( S_{i}(T) \) of \( U_{3}Ru_{4}Al_{12} \) satisfies the single Lorentzian band model \( ^{44} \) described by Eq. (1),
\[ S(T)=\frac{A T}{B^{2}+T^{2}} \quad (1) \]
\[ with\quad A=\frac{2\Delta}{\left|e\right|}\quad and\quad B^{2}=\frac{3(\Delta^{2}+\Gamma^{2})}{(\pi k_{B})^{2}}, \]
where \( \Delta_{t}=\varepsilon_{5f}-\varepsilon_{F} \) is a measure of the position \( \varepsilon_{5f} \) of the 5f DOS peak with respect to the Fermi level \( \varepsilon_{F} \) , and \( \Gamma_{t} \) is the width of the Lorentzian-shaped 5f band. The fitting of experimental data to Eq. (1) gives the following values: \( \Gamma_{a}=27.9 \) meV and \( \Delta_{a}=-2.82 \) meV along the a axis and \( \Gamma_{c}=38.4 \) meV and \( \Delta_{c}=-2.06 \) meV along the c axis. These values are comparable to those observed for different aluminides like \( CeAl_{2} \) or \( UAl_{2} \) \( ^{45} \) being moderately heavy fermions. It is worth adding that a number of uranium compounds crystallizing in different hexagonal structures, like \( UPt_{2}In \) , \( UNi_{4}B \) , \( UNi_{2}Al_{3} \) , \( UPd_{2}Al_{3} \) , and \( UCu_{3}Ga_{2} \) \( ^{46} \) have positive TEP in a whole range of temperatures below RT, and this quantity can only be described with the use of a two-Lorentzian band model.
F. Specific heat
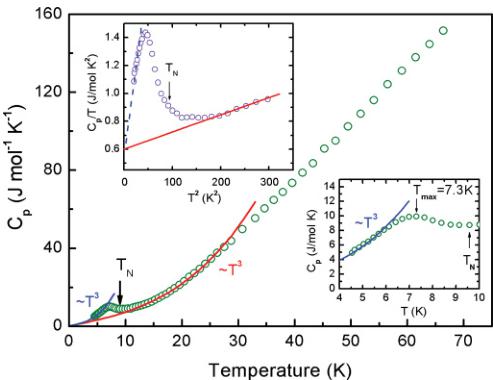
The thermal dependence of specific heat \( C_{\mathrm{p}}(T) \) of \( U_{3}Ru_{4}Al_{12}o \) was measured in the temperature range 4–66 K, and the results are presented in Fig. 9 and in the lower inset, where \( C_{\mathrm{p}}(T) \) is shown in the vicinity of \( T_{N} \) on an enlarged scale. As shown, the temperature AFM ordering \( T_{N} \) (=9.5 K) for this aluminide lies at a minimum of \( C_{\mathrm{p}}(T) \) just before going by this function through a faint hump with \( T_{max} = 7.3 \) K. This hump is better seen in the upper inset of this figure, where the function \( C_{\mathrm{p}}/T = f(T^{2}) \) is plotted at low temperatures. Unfortunately, we were not able to determine

FIG. 9. (Color online) Temperatures dependence of the specific heat \( C_{p} \) measured between 4.2 and 66 K. Both solid lines (blue and red) show \( C_{p} \) vs. \( T^{3} \) behavior with a different coefficient \( \beta \) . Upper and lower insets present \( C_{p}/T \) vs. \( T^{2} \) and \( C_{p} \) vs. T on expanded scales, respectively. Note a large \( \gamma(0) \) value of 200 mJ mol \( _{U}^{-1} \) K \( ^{-2} \) . The solid line at the lower inset shows the \( T^{3} \) behavior of specific heat in the antiferromagnetic state.
the magnetic entropy at \( T_{N} \) for \( U_{3}Ru_{4}Al_{12} \) for lack of a proper corresponding phonon reference. Our numerous attempts to obtain \( Th_{3}Ru_{4}Al_{12} \) , regarded as a good reference in this case, ended in failure. It is highly probable that such a compound does not exist. Nevertheless, removing magnetic entropy by AFM ordering, obtained by considering only the peak in the \( C_{p}/T \) vs. \( T^{2} \) dependence of \( U_{3}Ru_{4}Al_{12} \) and limited by the red straight line (see the upper inset of Fig. 9), is rather small and amounts only to \( 0.22R \) in 2. Therefore, we judge that it is the reason for the large Sommerfeld coefficient \( \gamma(0)=200\ mJ\ mol_{U}^{-1}\ K^{-2} \) per U atom, as derived from the formula \( C_{p}/T=\gamma+\beta T^{2} \) , where the first term accounts for the electronic contribution and the second term accounts for both the phonon and spin wave contributions, for which \( C_{p}(T) \) follows the same simple \( T^{3} \) law. As the upper inset to Fig. 9 demonstrates, both curves extrapolated from above \( T_{N}^{2} \) and below \( T_{max}^{2} \) to T=0 K show the expected linear behavior, yielding the same value \( \gamma(0) \) . The high magnitude of this coefficient classifies this uranium intermetallic compound as a moderately heavy fermion system, probably because of the presence of Kondo-like interactions. Almost the same \( C_{p}(T) \) behavior as that found above for \( U_{3}Ru_{4}Al_{12} \) has been reported for \( UCu_{5}In \) . \( ^{39} \) The latter compound revealed \( \gamma(0)=210\ mJ\ mol_{U}^{-1}\ K^{-2} \) per U atom and only a small, very broad anomaly, which, as in our case, started to develop just below \( T_{N} \) . These two high values of \( \gamma(0) \) gives almost the same \( T_{K}\approx30\ K \) for both compounds discussed here using the well-known Eq. (2) given by Oliveira and Wilkins, \( ^{47} \)
\[ T_{\mathrm{K}}\approx0.68\ R/\gamma(0). \quad (2) \]
The lack of a distinct \( \lambda \) -type anomaly in \( C_{\mathrm{p}}(T) \) at \( T_{N} \) for these two compounds despite large ordered magnetic moments of 2.5 and 1.55 \( \mu_{B} \) , respectively, is quite puzzling. Quite opposite results to the above data have been reported (e.g., for \( UCu_{2}Sn^{28,33} \) or \( UPd_{3}^{34} \) ). The quadrupolar ordering of the non-Kramers \( \Gamma_{5} \) ground state doublet in these two compounds causes a pronounced, sharp \( \lambda \) -type anomaly, and entropy attains exactly a value of R ln 2 expected for a doublet at \( T_{Q} \) . In turn, \( UCu_{5} \) , also regarded as a SDW system, does develops a \( \lambda \) -type anomaly in \( C_{\mathrm{p}}(T) \) , but the magnetic entropy at \( T_{N} \) achieves a rather low value of \( 0.6R\ln2 \) , but with a very high \( \gamma(0)=380\ mJ\ mol_{U}^{-1}\ K^{-2} \) , inferred from the temperature region just above 1 K and extrapolated to T=0 K. Below 1 K, another first-order transition takes place. \( ^{29} \)
IV. CONCLUSIONS
As previous investigations have pointed out, the distorted kagome lattice of uranium atoms, characteristic of \( U_{3}T_{4}Al_{12} \) -type compounds (when T = Fe and Co), induces a spin glass behavior. Contrary to this observation, the antiferromagnetic ordering first reported for the polycrystalline sample of \( U_{3}Ru_{4}Al_{12} \) is now confirmed by single-crystal investigations with a neutron diffraction study. The geometrical frustration of the hexagonal structure in which the above three compounds crystallize, in the case of a domination of AFM-type interactions between uranium moments, leads to magnetic ordering in the \( (a,b) \) hexagonal plane. A noncollinear magnetic structure is formed because the system cannot satisfy all possible couplings, so the resulting magnetic structure is a compromise between various anisotropic interactions. Because of this, a number of interesting anomalous behaviors take place at low temperatures, which have been investigated here by magnetic, electrical transport, and thermal measurements.
For example, instead of a rapid decrease of electrical resistivity below \( T_{N} \) , as expected from a decrease of spin disorder resistivity, as is indeed observed along the c axis, we found a sharp peak just below \( T_{N} \) along the a axis, highlighting a strong modification of the Fermi surface in the vicinity of \( T_{N} \) , probably because of a gap opening in the FS, which in turn is induced by SDW excitations similar to that observed in \( UCu_{5} \) . The latter conclusion has been inferred for this compound from a study \( ^{48} \) of absorption in the far infrared that develops below \( T_{N} \) . It is interesting to note that the transverse magnetoresistivity measurements prove that this spin-density wave gap survives in \( U_{3}Ru_{4}Al_{12} \) in applied magnetic fields up to 8 T but also starts to propagate along the c direction below \( T_{N} \) and above 2 T. Both the low-temperature sharp maximum in \( \rho(T) \) and the hump in \( C_{\mathrm{p}}(T) \) just below \( T_{N} \) , observed previously for \( UCu_{5}In^{39} \) and now for \( U_{3}Ru_{4}Al_{12} \) , become a hallmark of a gap opening in the FS from SDW formation in these ternaries. The exciting findings presented here for \( U_{3}Ru_{4}Al_{12} \) call for further experimental and theoretical studies of this aluminide.
ACKNOWLEDGMENTS
The authors are grateful to T. Komatsubara for his valuable advice and help concerning the single-crystal growth technique. We thank B. Coqblin for his helpful discussion. We are also indebted to A. Hackemer, R. Wawryk, R. Gorzelniak, and D. Badurski for their assistance in thermal and transport measurements.
\( ^{r} \) .troc@int.pan.wroc.pl
\( ^{1} \) L. Balents, Nature 464, 199 (2010).
\( ^{2} \) See, e.g., Highly Frustrated Magnetism 2008 conference proceedings in J. Phys.: Conf. Ser. 145, 011001 (2009).
\( ^{3} \) A. P. Ramirez, in: Handbook on Magnetic Materials, edited by K. H. J. Buschow (Elsevier, North-Holland, Amsterdam, 2001), vol. 13, p. 421.
\( ^{4} \) R. Ballou, J. Alloy Compd. 275–277, 510 (1998).
\( ^{5} \) D. Gignoux and D. Schmitt, J. Alloy Compd. 326, 143 (2001).
\( ^{6} \) P. Javorsky, P. Burlet, E. Ressouche, V. Sechovsky, H. Michor, and G. Lapertot, Physica B 225, 230 (1996).
\( ^{7} \) S. A. M. Mentink, A. Drost, G. J. Nieuwenhuys, E. Frikkee, A. A. Menovsky, and J. A. Mydosh, Phys. Rev. Lett. 73, 1031 (1994).
\( ^{8} \) G. Ehlers, C. Ritter, A. Krutjakow, W. Miekeley, N. Stüßer, Th. Zeiske, and H. Maletta, Phys. Rev. B 59, 8821 (1999), and references therein.
\( ^{9} \) L. Keller, A. Dönni, H. Kitazawa, J. Tang, F. Fauth, and M. Zolliker, Physica B 241–243, 660 (1998).
\( ^{10} \) K. Prokeš, E. Brück, and V. Sechovsky, Physica B 404, 3025 (2009).
\( ^{11} \) R. E. Gladyshevskij, O. R. Strusievicz, K. Cenzual, and E. Parthé, Acta. Cryst. B 49, 474 (1993).
\( ^{12} \) J. Niermann and W. Jeitschko, Z. Anorg. Allg. Chem. 628, 2549 (2002).
\( ^{13} \) R. A. Robinson, A. C. Lawson, V. Sechovsky, L. Havela, Y. Kergadallan, H. Nakotte, and F. R. de Boer, J. Alloys Compd. 213–214, 528 (1994).
\( ^{14} \) A. P. Gonçalves, A. P. Waerenborgh, P. Gaczyński, H. Noël, and O. Tougait, Intermetallics 17, 25 (2009).
\( ^{15} \) O. Tougait, H. Noël, and R. Troc, J. Solid State Chem. 177, 2053 (2004).
\( ^{16} \) O. Tougait, R. Troc, A. Zaleski, and H. Noël, Phil. Mag. 87, 1085 (2007).
\( ^{17} \) M. Pasturel, O. Tougait, M. Potel, T. Roisnel, K. Wochowski, H. Noël, and R. Troc, J. Phys.: Condens. Matter 21, 125401 (2009).
\( ^{18} \) M. Elhajal, B. Canals, and C. Lacroix, Physica B 312–313, 716 (2002).
\( ^{19} \) P. J. Brown and J. C. Matthewman, “The Cambridge crystallography subroutine library,” CCSL Documentation, 2009, http://www.ill.eu/sites/ccsl/html/ccsldoc.html (5 May 2009).
\( ^{20} \) H. Kubo, K. Umeo, K. Katoh, A. Ochiai, and T. Takabatake, J. Phys. Soc. Jpn. 79, 64715 (2010).
\( ^{21} \) E. F. Bertaut, Acta Cryst. A 24, 217 (1968).
\( ^{22} \) Y. A. Izyumov and V. E. Naish, J. Magn. Magn. Mater. 12, 239 (1979).
\( ^{23} \) A. S. Wills, Physica B 276–278, 680 (2000).
\( ^{24} \) O. V. Kovalev, Irreducible Representations of the Space Groups (Gordon and Breach, New York, 1965).
\( ^{25} \) B. Cornut and B. Coqblin, Phys. Rev. B 5, 4541 (1972).
\( ^{26} \) D. Kaczorowski, P. Rogl, and K. Hiebl, Phys. Rev. B 54, 9891 (1996).
\( ^{27} \) A. Pikul and D. Kaczorowski, J. Phys.: Cond. Matter. 23, 456002 (2011).
\( ^{28} \) T. Takabatake, H. Iwasaki, H. Fujii, S.-I. Ikeda, S. Nishigori, Y. Aoki, T. Suzuki, and T. Fujita, J. Phys. Soc. Jpn. 61, 778 (1992).
\( ^{29} \) H. R. Ott, H. Rudigier, E. Felder, Z. Fisk, and B. Batlogg, Phys. Rev. Lett. 55, 1595 (1985).
\( ^{30} \) Y. B. Ning, J. D. Garrett, C. V. Stager, and W. R. Datars, Phys. Rev. B 46, 8201 (1992).
\( ^{31} \) R. J. Elliot and F. A. Wedgwood, Proc. Phys. Soc. 81, 846 (1963).
\( ^{32} \) A. S. Barker Jr., B. I. Halperin, and T. M. Rice, Phys. Rev. Lett. 20, 384 (1968).
\( ^{33} \) T. Suzuki, I. Ishii, N. Okuda, K. Katoh, T. Takabatake, T. Fujita, and A. Tamaki, Phys. Rev. B 62, 49 (2000).
\( ^{34} \) S. W. Yun, H. Sugawara, J. Itoh, M. Takashita, T. Ebihara, N. Kimura, P. Swoboda, R. Settai, Y. Onuki, and H. Sato, J. Phys. Soc. Jpn. 63, 1518 (1994).
\( ^{35} \) D. A. Bonn, J. D. Garrett, and T. Timusk, Phys. Rev. Lett. 61, 1305 (1988).
\( ^{36} \) A. Bernasconi, M. Mombelli, Z. Fisk, and H. R. Ott, Z. Phys. B 94, 423 (1994).
\( ^{37} \) A. Schenck, P. Birrer, F. N. Gygax, B. Hitti, E. Lippelt, M. Weber, P. Boni, P. Fischer, H. R. Ott, and Z. Fisk, Phys. Rev. Lett. 65, 2454 (1990).
\( ^{38} \) H. Nakamura, Y. Kitaoka, M. Inoue, K. Asayama, and Y. Onuki, J. Magn. Magn. Mat. 90–91, 459 (1990).
\( ^{39} \) D. Kaczorowski, R. Troc, T. Kagayama, F. Honda, and G. Oómi, Solid State Commun. 122, 527 (2002); D. Kaczorowski, R. Troc, T. Komatsubara, C. Sulkowski, and H. Misiorek, Physica B 312–313, 300 (2002); D. Kaczorowski, R. Troc, A. Czopnik, A. Jeżowski, Z. Henkie, and V. I. Zaremba, Phys. Rev. B 63, 144401 (2001); V. H. Tran, D. Kaczorowski, R. Troc, G. André, F. Bourée, and V. Zaremba, Solid State Comm. 117, 527 (2001).
\( ^{40} \) V. Taufour, D. Aoki, G. Knebel, and J. Flouquet, Phys. Rev. Lett. 105, 217201 (2010); S. Watanabe and K. Miyake, J. Phys. Soc. Jpn. 71, 2489 (2002).
\( ^{41} \) S. Süllow, A. Otop, A. Loose, J. Klenke, O. Prokhnenko, R. Feyerherm, R. W. A. Hendrikx, J. A. Mydosh, and H. Amitsuka, J. Phys. Soc. Jpn. 77, 024708 (2008).
\( ^{42} \) B. Andraka, J. Dapprich, M. Baldus, P. Kumar, and G. R. Stewart, Phys. Rev. B 45, 7481 (1992).
\( ^{43} \) V. Zlatić, R. Monnier, and J. Freericks, Physica B 378–380, 661 (2006).
\( ^{44} \) U. Gottwick, K. Gloos, S. Horn, F. Steglich, and N. Grewe, J. Magn. Magn. Mater. 47–48, 536 (1985).
\( ^{45} \) J.-G. Park and M. Očko, J. Phys.: Condens. Matter 9, 4627 (1997).
\( ^{46} \) Y. Bando, T. Suemitsu, T. Takagi, H. Tokushima, Y. Echizen, K. Katoh, K. Umeo, Y. Maeda, and T. Takabatake, J. Alloy Compd. 313, 1 (2000).
\( ^{47} \) L. N. Oliveira and J. W. Wilkins Phys. Rev. Lett. 47, 1553 (1981).
\( ^{48} \) L. Degiorgi, St. Thierne, H. R. Ott, M. Dressel, G. Grüner, Y. Dalichaouch, M. B. Maple, Z. Fisk, C. Geibel, and F. Steglich, Z. Phys. B 102, 367 (1997).