| Transition Temperature | 120 K |
|---|---|
| Experiment Temperature | 4.2 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | R-3 (#148) |
| Magnetic Space Group | R-3' (#148.19) |
| Magnetic Point Group | -3' (17.3.64) |
| Lattice Parameters | 5.01250 5.01250 14.29860 90.00 90.00 120.00 |
|---|---|
| DOI | 10.1143/jpsj.37.1242 |
| Reference | K. Tsuzuki, Y. Ishikawa, N. Watanabe and S. Akimoto, Journal of the Physical Society of Japan (1974) 37 1242-1247. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Mn1 | Mn | 0.0 | 0.0 | 4.6 | 4.60 |
Neutron Diffraction and Paramagnetic Scattering from a High Pressure Phase of \( MnGeO_{3} \) (Ilmenite)
Kazuo Tsuzuki, \( ^{*} \) Yoshikazu Ishikawa, Noboru Watanabe and Syuniti Akimoto \( ^{\dagger} \)
Department of Physics and Laboratory of Nuclear Science, Tohoku University, Sendai
\( ^{\dagger} \) Institute for Solid State Physics, University of Tokyo, Tokyo
(Received May 22, 1974)
The magnetic structure as well as the exchange parameters in \( MnGeO_{3} \) with the ilmenite structure have been investigated by neutron diffraction and paramagnetic scattering using powder sample prepared at \( 1000^{\circ}C \) under high pressure of 50 kbar. It has been found that the crystal has the same antiferromagnetic structure as \( MnTiO_{3} \) ; the spins are directed along the [111] rhombohedral axis and are aligned in antiparallel in the layer. The nearest neighbor \( Mn^{2+} \) distance is \( 3.02\AA \) and the exchange integral \( J_{1} \) between them is found to be \( 0.84\pm0.01 \) meV.
§ 1. Introduction
Manganese germanate \( MnGeO_{8} \) with the ilmenite structure is a stable phase at high pressure and high temperature. The structure is metastably conserved even at room temperature when it is quenched from high temperatures in the high pressure cell. \( ^{1} \) The magnetic susceptibility has been studied by Sawaoka et al. and it has been found that the susceptibility has a broad maximum around 120 K, \( ^{2} \) just like \( MnTiO_{3} \) . \( ^{8} \) Therefore it has been anticipated that \( MnGeO_{8} \) has the same antiferromagnetic structure as \( MnTiO_{3} \) , \( ^{4} \) the spins are aligned in antiparallel in the basal plane and the magnetic interaction in the layer which is the nearest neighbor (n.n.) interaction predominates over the interlayer interactions, so that it behaves as a quasi-two dimensional system. \( ^{6} \) The magnetic interaction in the layer has been supposed to be the direct cation-cation interaction which depends strongly on the interatomic distance. \( ^{8} \) Since in \( MnGeO_{8} \) the distance between the nearest neighbor \( Mn^{2+} \) ions is the shortest of the manganese oxides, the direct interaction would be the largest.
We have prepared a sufficient amount of the sample (about 45 gr.) and the n.n. exchange parameter was determined by the neutron paramagnetic scatterings and the static magnetic susceptibility measurement. Neutron diffraction has also been carried out to determine the magnetic structure. The investigation is a part of the large program of the study of the feasibility of the pulsed neutron source produced by an electron linac for the neutron scattering experiments. \( ^{7} \)
§ 2. Sample Preparation
It has been reported that \( MnGeO_{3} \) with the pyroxene structure is transformed to the ilmenite structure under high pressures above about 30 kbar at \( 700^{\circ}C \) . \( ^{1)} \) Polycrystalline specimens of \( MnGeO_{3} \) having the pyroxene structure were prepared by firing the mixture of MnO and \( GeO_{2} \) at about \( 1100^{\circ}C \) for two hours in air, followed by quenching to room temperature. In order to transform the pyroxene structure to the ilmenite structure, we used a tetrahedral anvil-type high pressure-apparatus described previously. \( ^{8)} \) A powered sample of \( MnGeO_{3} \) (pyroxene) was subjected to the desired pressure (about 50 kbar) at about \( 1000^{\circ}C \) for about 40 minutes in the apparatus. After being maintained at a desired pressure and temperature for a desired time, the sample was quenched isobarically to room temperature. Since one run of procedure produces only 0.2 to 0.3 grs. of \( MnGeO_{3} \) with the ilmenite structure, we repeated the procedure 220 times to get the sample of about 45 grs.
X-ray analysis with a G-M method showed that the sample obtained was the single phase with the ilmenite structure, and no pyroxene structure was found.
§ 3. Magnetic Susceptibility Measurement
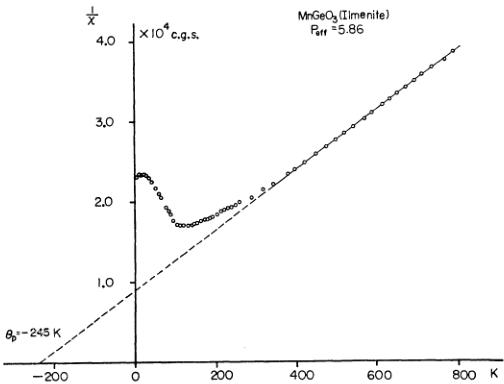
Magnetic susceptibility of \( MnGeO_{3} \) (ilmenite) was measured with a Cahn's type magnetic balance over a temperature range from 4.2 K
to 800 K in a magnetic field of 4 kOe. The result is shown in Fig. 1 which confirms that the magnetic susceptibility of \( MnGeO_{3} \) has a broad maximum near 120 K as reported previously. \( ^{[2]} \) The asymptotic Curie temperature \( \theta_{p} \) and the effective Bohr magneton number \( P_{eff} \) are -245 K and 5.86 \( \mu_{B} \) respectively. These values are different from the previous results, because they measured the susceptibility up to room temperature, but the Curie-Weiss relation holds

Fig. 1. Reciprocal of susceptibility vs temperature of \( MnGeO_{3} \)
only above 300 K as shown in the figure.
§ 4. Neutron Diffraction Study
In order to determine the magnetic structure of \( MnGeO_{3} \) with the ilmenite structure, we carried out a powder neutron diffraction study with the TOF method using the pulsed neutron source produced by the Tohoku electron linac. \( ^{9} \)
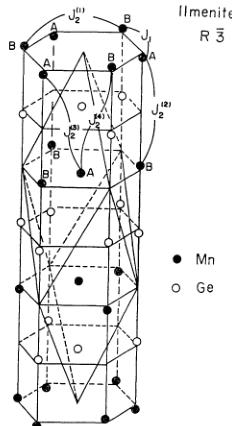
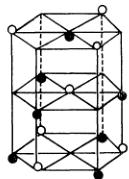
The crystal structure of this substance is shown in Fig. 2, where the hexagonal metallic sites are displayed, together with the rhombohedral unit cell. The crystal has the space group of \( R\bar{3} \) and the crystal parameters \( a_{R} \) and \( \alpha \) of the rhombohedral lattice are 5.576 \( \mathring{A} \) and 53.42° in arc respectively. The unit cell contains two molecules of \( MnGeO_{3} \) , the atomic position of which are given by following five parameters;
\[ 2\mathrm{Mn}^{2+}\mathrm{~a t~}\pm(u_{1},u_{1},u_{1}), \]
\[ 2\mathrm{Ge}^{4+}\mathrm{~a t~}\pm(u_{2},u_{2},u_{2}), \]
\[ 60^{\circ-}\mathrm{~a t~}\pm(x,y,z),\quad\pm(y,z,x),\quad\pm(z,x,y). \]
These parameters have been determined by the single crystal X-ray analysis to be \( ^{10)} \)
\[ u_{1}=0.6383,\quad u_{2}=0.15694,\quad x=0.56029, \]
\[ y=-0.04086,\quad z=0.20396. \]
The integrated intensity \( I_{hkl} \) of the powder neutron diffraction patterns at a fixed scattering angle \( 2\theta_{0} \) is given by \( ^{[11]} \)
\[ I_{h k l}=\frac{I(\lambda_{h k l})\lambda_{h k l}^{2}j_{h k l}|F_{h k l}|^{2}}{\sin^{3}\theta_{0}}\mathbf{e}^{-2B_{h k l}}\cdot A(\lambda_{h k l})\cdot K, \quad (1) \]
where \( I(\lambda_{hkl}) \) is the energy spectrum of the incident neutron, \( j_{hkl} \) is the multiplicity factor of the reflection hkl, \( A(\lambda_{hkl}) \) is the absorption factor and K is a constant independent of \( \lambda_{hkl} \) .

Fig. 2. Cation sites in \( MnGeO_{3} \) with the rhombohedral unit cell.
\(\lambda_{hkl}\) is the Bragg reflection wave length given by \(\lambda_{hkl}=2d_{hkl}\sin\theta_{0}\), all other notations have conventional meanings.
If the magnetic order develops below the Néel temperature, the structure factor \( |F_{hkl}|^{2} \) is given by the sum of the nuclear and magnetic form factor;
(2)
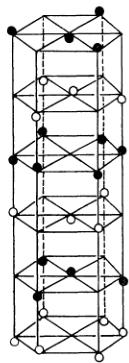
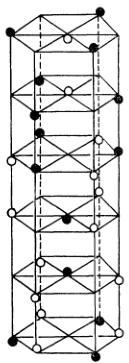
where q is the magnetic interaction vector determined by the spin direction with respect to the scattering vector. The ilmenite has in general three possible antiferromagnetic structures \( ^{4)} \) which are illustrated in Fig. 3. The magnetic unit cells of models (a) and (b) are larger than the chemical unit cell, while in model (c), which has been predicted for \( MnGeO_{3} \) as well as \( MnTiO_{3} \) , the unit cell is not modified by spin ordering.
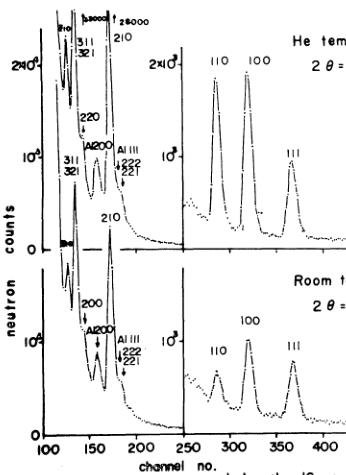
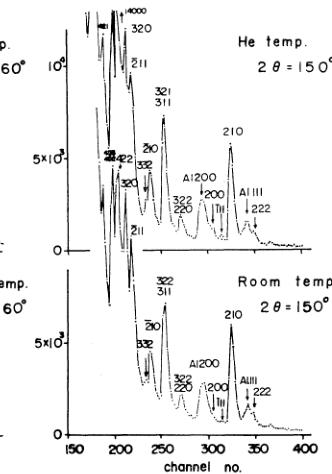
Powder neutron diffraction patterns were obtained at room temperature and 4.2 K and are shown in Fig. 4. The abscissa is the neutron flight time from the source to the detectors,

(a)

(b)


(c)
Fig. 3. Three possible antiferromagnetic structures for the ilmenite structure.


Fig. 4. Powder neutron diffraction patterns of \( MnGeO_{3} \) measured by TOF method at fixed scattering angles of \( 60^{\circ} \) and \( 150^{\circ} \) at 4.2 K and room temperature.
which is proportional to the wave length of the neutrons. The sample was packed in a cylindrical aluminium container 20 mm in diameter. The scattering angles were fixed with \( 30^{\circ} \) , \( 60^{\circ} \) and \( 150^{\circ} \) . The data for \( 2\theta_{0}=60^{\circ} \) is appropriate for evaluating the diffraction with low index, while that for \( 2\theta_{0}=150^{\circ} \) gives a good resolution for the high index reflections. The observed integrated intensities \( I_{obs} \) are normalized by that of the 100 reflection at room temperature and is listed in Table I. The integrated
Table I. Observed and calculated neutron diffraction intensities for MnGeO_{3}.
\[ \mu_{\mathrm{M n}}=4.6\mu_{\mathrm{B}}. \]
| I_{\mathrm{obs}} | I_{\mathrm{cal.}} | I_{\mathrm{obs}} | ||||
| hkl | 298 K | Nucl. | Mag. | Total | 4.2 K | |
| 111 | 84 | 85 | 0 | 85 | 85 | |
| 100 | 100 | 100 | 70 | 170 | 170 | |
| 110 | 31 | 31 | 88 | 119 | 119 | |
| 1\bar{1}0 | 21 | 14 | 0 | 14 | 30 | |
| 210 | 773 | 707 | 24 | 731 | 801 | |
| 1\bar{1}1 | 5 | 5 | 26 | 31 | 68 | |
| 322 | 88 | 111 | 2 | 113 | 129 | |
| 320 | ||||||
| 321 | 517 | 534 | 25 | 559 | 620 | |
| 311 | 208 | 196 | 15 | 211 | 277 | |
| 210 | ||||||
| R factor | 7.3% | 7.4% |
spin direction [111]
intensities are also calculated using the crystal parameters determined by X-ray analysis \( ^{9} \) and are also tabulated in the table. The temperature factors \( e^{-2B} \) were omitted in the calculation considering the accuracy of the measurement. The agreement between the observation at 298 K and the calculated values are satisfactory. This confirms the accuracy of the crystal parameters. The distance \( a_{1} \) between the nearest neighbor \( Mn^{2+} \) ions calculated using these parameters is \( a_{1}=3.022\mathring{A} \) . The magnetic reflection intensities are also calculated by assuming the model c with the moment \( 4.6\mu_{B} \) at 4.2 K aligned in the [111] direction. It was found that the observed intensities can be reproduced by the model c, which is the antiferromagnetic structure established in \( MnTiO_{3} \) . It is noted that the value of the moment \( 4.6\mu_{B} \) for \( Mn^{2+} \) moment is only 92% of the value for S=5/2. This is not due to the existence of the \( Mn^{2+} \) state but presumably to the two dimensional character of the antiferromagnetic state, \( ^{4)} \) because the effective magnetic moment evaluated from the susceptibility is very close to the theoretical value for S=5/2.
§ 5. Paramagnetic Scattering Study
The neutron paramagnetic scattering experiment was performed on the same sample to determine the magnetic interactions in the substance. The neutron differential cross section for the paramagnetic scattering from the Heisenberg system is given by
\[ \begin{aligned}\frac{\mathrm{d}^{2}\sigma}{\mathrm{d}\Omega\mathrm{d}\omega}&=\frac{2}{3}\left(\frac{e^{2}\gamma}{mc^{2}}\right)^{2}|f(\theta)|^{2}\\&\quad\times\frac{k_{f}}{k_{0}}N S(S+1)\frac{1}{\sqrt{2\pi\langle\omega^{2}\rangle}}\mathrm{e}^{-\frac{\omega^{2}}{2\langle\omega^{2}\rangle}},\end{aligned} \quad (3) \]
for the powder specimen with high momentum transfer of \( Qa > \pi,^{12)} \) a being a distance between the interacting atoms. The second moment of the energy distribution \( \hbar^{2}\langle\omega^{2}\rangle \) is related with the exchange integrals \( J_{i} \) between the i-th neighbors to be
\[ \hbar^{2}\langle\omega^{2}\rangle=\frac{8}{3}S(S+1)\sum_{i}Z_{i}J_{i}^{2}, \quad (4) \]
with \( Z_{i} \) the number of i-th neighbors. If we neglect the interactions further than the second neighbors, we can evaluate the values of \( J_{1} \) and \( J_{2} \) from eq. (4) and the paramagnetic Curie temperature \( \theta_{p} \) which is given in the molecular field approximation by
\[ k_{\mathrm{B}}\theta_{\mathrm{p}}=\frac{2}{3}S(S+1)\sum_{i}Z_{i}J_{i}. \quad (5) \]
A new type of spectrometer has been installed to the pulse neutron source produced by the Tohoku electron linear accelerator. The monochromatized pulse neutron beams with the energy of 3.75 meV and 14.5 meV were obtained by the Bragg reflection from a quasi-bent pyrolytic graphite. The details of the spectrometer is reported separately. \( ^{[18]} \) The neutrons scattered from the samples of about 45 grs. in weight contained in an aluminium case were detected by a set of four \( BF_{3} \) counters and the scattered neutron energy is measured by the TOF technique.
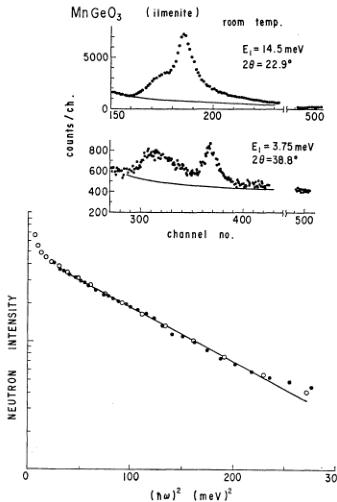
The TOF spectra obtained at different scattering angles and different incident neutrons are shown in the upper part of Fig. 5. These spectra were converted to the energy spectra after correcting for various instrumental factors discussed in detail in another paper \( ^{13} \) and \( k_{f}/k_{0} \) and \( f(Q) \) in eq. (3) and are plotted in the semi-
logarithmic scale against \( \hbar^{2}\omega^{2} \) in the lower part of the figure. The figure shows that the energy spectra of the scattered neutrons are well expressed by a Gaussian with the second moment independent of both of scattering angles and incident energies. The value of \( \hbar^{2}\langle\omega^{2}\rangle \) estimated from the slope of the linear part in Fig. 5 is \( 51.5\ (\mathrm{meV})^{2} \) .

Fig. 5. Raw TOF spectra for paramagnetic scatterings measured with the incident neutron energies of 14.5 meV and 3.75 meV (upper part) and semi-logarithmic plot of scattered neutron intensity against square of energy transfer \( (\hbar\omega)^{2} \) (●: \( E_{i}=3.75 \) meV, \( 2\theta_{0}=38.8^{\circ} \) , ○: \( E_{i}=14.5 \) meV, \( 2\theta_{0}=22.9^{\circ} \) ).
§ 6. Discussion
In the ilmenite structure, there are five different types of exchange interactions, which are denoted as \( J_{1} \) , \( J_{2}^{(1)} \) , \( J_{2}^{(2)} \) , \( J_{2}^{(3)} \) and \( J_{2}^{(4)} \) in Fig. 2. \( ^{14,15} \) The nearest neighbor interaction \( J_{1} \) consists of two kinds of mechanisms. One is the \( 90^{\circ} \) cation-anion-cation interaction and another is the direct cation-cation interaction due to the overlapping of the \( d\varepsilon \) orbitals of neighboring cations. \( ^{5} \) All other interactions are the indirect interactions intervened by two anion layers and is expected to be weak compared with \( J_{1} \) . If we assume that the interlayer interactions \( J_{2}^{(3)} \) and \( J_{2}^{(4)} \approx J_{2}^{(4)} \) are the same order of magnitude and the same sign with each other, the antiferromagnetic structure is determined by the interaction \( J_{2}^{(2)} \) which should be negative.
In order to estimate the magnitude of these interactions from the paramagnetic scatterings and the magnetic susceptibility, we assumed that \( J_{z}^{(1)}=J_{z}^{(3)}=J_{z}^{(4)}=\bar{J}_{z} \) and \( J_{z}^{(2)}=n\bar{J}_{z} \) with \( n\geq1 \) , because atomic configurations giving rise to the exchange integrals \( J_{z}^{(1)} \) , \( J_{z}^{(3)} \) and \( J_{z}^{(4)} \) are quite similar. Then the eqs. (4) and (5) are reduced to be
\[ \begin{aligned}&\hbar^{2}\langle\omega^{2}\rangle=\frac{8}{3}S(S+1)[3J_{1}^{2}+(15+n)\bar{J}_{z}^{2}]\\&k\theta_{p}=\frac{2}{3}S(S+1)[3J_{1}+(15+n)\bar{J}_{z}]\\ \end{aligned} \quad (6) \]
Using the values of \( \hbar^{2}\langle\omega^{2}\rangle \) and \( k\theta_{p} \) experimentally determined, we estimated \( J_{1} \) and \( \bar{J}_{z} \) to be
\[ \begin{aligned}&J_{1}=-0.84meV,\\&\bar{J}_{z}=-0.07meV,\quad for\quad n=1\\&and\\&J_{1}=-0.845meV,\\&\bar{J}_{z}=-0.06meV.\quad for\quad n=4\\ \end{aligned} \]
and
Although there is an ambiguity for the value of n, we can derermine the value of \( J_{1} \) with a reasonable accuracy to be \( J_{1} = -0.84 \pm 0.01 \) meV. \( ^{*} \) The value should be compared with \( J_{1} = -0.63 \pm 0.02 \) meV \( ^{18} \) in \( MnTiO_{3} \) with the n.n. distance \( a_{1} = 3.04 \AA \) and \( J_{1} = -0.38 \pm 0.02 \) meV and \( \partial J_{1}/\partial r = -2.5 \pm 0.15 \) meV/ \( \AA \) in MnO with \( a_{1} = 3.14 \AA \) . \( ^{17} \) The steep increase in the exchange interaction with decreasing the atomic distance may be understood by the increase of the overlapping between the \( d\varepsilon \) orbitals of the neighboring \( Mn^{2+} \) atoms and this will be an experimental evidence to show that the direct-cation-cation interaction predominates in the n.n. interaction. It is remarked that the molecular field \( H_{\varepsilon} \) acting on a \( Mn^{2+} \) spin from the neighboring layers which establishes the three dimensional order is given in our approximation to be
\[ H_{2}=(n-3)\bar{J}_{2}\langle S\rangle/g\mu_{\mathrm{B}}. \quad (7) \]
The relation shows that the interlayer interaction becomes accidentally very small if n is close to 3. This is the reason why the substance displays the typical two dimensional character. The ratio of the intralayer molecular
field \( H_{1} \) to \( H_{2} \) , \( H_{1}/H_{2}=3J_{1}/(n-3)J_{2}\simeq36 \) for \( MnGeO_{8} \) if n=4. This ratio is 29 for \( MnTiO_{8} \) . Therefore two dimensional character is more pronounced in \( MnGeO_{8} \) than in \( MnTiO_{8} \) .
Acknowledgements
The authors would thank Professor Y. Syono and Professor M. Tokonami for their information of the result of the single crystal X-ray analysis prior to publication. The work was partly supported by the Grant-in-Aid for Scientific Research from the Ministry of Education.
References
1) A. E. Ringwood and M. Seabrook: J. geophys. Res. 68 (1963) 4601.
2) A. Sawaoka, S. Miyahara, S. Akimoto and H. Fujisawa: J. Phys. Soc. Japan 19 (1964) 1750; 21 (1966) 185.
3) G. S. Heller: Proc. Intern. Conf. Magnetism, Nottingham (1964)
4) G. Shirane, J. Pickart and Y. Ishikawa: J. Phys. Soc. Japan 19 (1959) 1298.
5) J. Akimitsu and Y. Ishikawa: Solid State Commun. 8 (1970) 87.
6) K. Motida and S. Miyahara: J. Phys. Soc.
Japan 28 (1970) 1188.
7) M. Kimura, Y. Ishikawa and N. Watanabe: EUR 4954e (1973) 11.
8) S. Akimoto, H. Fujisawa and T. Katsura: J. geophys. Res. 70 (1965) 1969.
9) M. Kimura, M. Sugawara, M. Oyamada, Y. Yamada, S. Tomiyoshi, T. Suzuki, N. Watanabe and S. Takeda: Nuclear Instrum. and Method 71 (1969) 102.
10) M. Tokonami and Y. Syono: private communication.
11) B. Lebech and K. Mikke: Risö Report No. 164 (1967).
12) P. D. De Genne: J. Phys. Chem. Solids 4 (1958) 223.
13) N. Watanabe, Y. Ishikawa and K. Tsuzuki: to be published in Nuclear Itstrum. and Method.
14) Y. Ishikawa and S. Akimoto: J. Phys. Soc. Japan 13 (1958) 1298.
15) J. B. Goodenough and J. J. Stickler: Phys. Rev. 164 (1967) 768.
16) Y. Ishikawa, N. Watanabe, K. Tsuzuki: Research Rep. of Lab. Nuclear Science 5 (1973) 106; to be published in J. Phys. Soc. Japan.
17) M. Kohgi, Y. Ishikawa, I. Harada, and K. Motizuki: J. Phys. Soc. Japan 36 (1974) 112.