| Transition Temperature | 7.9 K |
|---|---|
| Experiment Temperature | 1.6 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | Pnma (#62) |
| Magnetic Space Group | Pm'c21' (#26.68) |
| Magnetic Point Group | m'm2' (7.3.22) |
| Lattice Parameters | 7.62900 6.87600 14.57300 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1103/physrevb.92.054425 |
| Reference | M. Hase, H. Kuroe, V.Y. Pomjakushin, L. Keller, R. Tamura, N. Terada, Y. Matsushita, A. Donni and T. Sekine, Physical Review B (2015) 92. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Cu1 | Cu | 0.085 | 0.0 | 0.0 | 0.09 |
| Cu2_1 | Cu | 0.555 | 0.0 | 0.283 | 0.62 |
| Cu2_2 | Cu | 0.555 | 0.0 | -0.283 | 0.62 |
| Cu3_1 | Cu | 0.555 | 0.0 | 0.283 | 0.62 |
| Cu3_2 | Cu | 0.555 | 0.0 | -0.283 | 0.62 |
Magnetic structure of the spin- \( \frac{1}{2} \) frustrated quasi-one-dimensional antiferromagnet \( Cu_{3}Mo_{2}O_{9} \) : Appearance of a partially disordered state
Masashi Hase, \( ^{1,*} \) Haruhiko Kuroe, \( ^{2} \) Vladimir Yu. Pomjakushin, \( ^{3} \) Lukas Keller, \( ^{3} \) Ryo Tamura, \( ^{1} \) Noriki Terada, \( ^{1} \)
Yoshitaka Matsushita, \( ^{1} \) Andreas Dönni, \( ^{1} \) and Tomoyuki Sekine \( ^{2} \)
\( ^{1} \) National Institute for Materials Science (NIMS), 1-2-1 Sengen, Tsukuba, Ibaraki 305-0047, Japan
\( ^{2} \) Department of Physics, Sophia University, 7-1 Kioi-cho, Chiyoda-ku, Tokyo 102-8554, Japan
\( ^{3} \) Laboratory for Neutron Scattering and Imaging, Paul Scherrer Institut (PSI), CH-5232 Villigen PSI, Switzerland (Received 22 April 2015; revised manuscript received 2 July 2015; published 13 August 2015)
We investigated the crystal and magnetic structures of the spin- \( \frac{1}{2} \) frustrated antiferromagnet \( Cu_{3}Mo_{2}O_{9} \) in which the spin system consists of antiferromagnetic chains and dimers. The space group at room temperature has been reported to be orthorhombic Pnma (No. 62). We infer that the space group above \( T_{N} = 7.9 \) K is monoclinic \( P2_{1}/m \) (No. 11) from the observation of reflections forbidden in Pnma in x-ray powder diffraction experiments at room temperature. We determined the magnetic structure of \( Cu_{3}Mo_{2}O_{9} \) in neutron powder diffraction experiments. Magnetic moments on dimer sites lie in the ac planes. The magnitudes are \( (0.50 \sim 0.74)\mu_{\mathrm{B}} \) . Moments on chain sites may exist but the magnitudes are very small. The magnetic structure indicates that a partially disordered state is realized. We consider the origin of the magnetic structure, weak ferromagnetism, and electric polarization.
DOI: 10.1103/PhysRevB.92.054425
PACS number(s): 75.10.Jm, 75.10.Pq, 75.25.-j, 75.47.Lx
I. INTRODUCTION
Several frustrated antiferromagnets exhibit intriguing magnetic states such as the quantum spin-liquid state \( [1] \) , the chiral ordered state \( [2,3] \) , the spin nematic or the multipolar state \( [4,5] \) , and the spin-gel state \( [6] \) . Among frustrated antiferromagnets, frustrated spin chains provide grounds for studies of exotic quantum phases caused by combination of frustration and quantum fluctuation. In the Heisenberg spin- \( \frac{1}{2} \) chain with antiferromagnetic (AF) nearest-neighbor (NN) and next-nearest-neighbor (NNN) exchange interactions ( \( J_{NN} \) and \( J_{NNN} \) interactions, respectively), the ground state(s) are a gapless spin-singlet state designated as Tomonaga-Luttinger liquid and two-folded-degenerated gapped spin-singlet states for \( 0 \leqslant J_{NNN} < 0.241 J_{NN} \) and \( 0.241 J_{NN} < J_{NNN} \) , respectively \( [7–9] \) . In the spin-Peierls substance \( CuGeO_{3} \) \( [10–12] \) , both the interactions are considered to exist \( [13–15] \) . It is inferred that a large spin gap observed in Raman scattering experiments of 3.5% Mg-doped \( CuGeO_{3} \) under high pressures is generated not only by the spin-Peierls transition but also by the frustration between the two interactions \( [16] \) . In the spin- \( \frac{1}{2} \) chain with ferromagnetic \( J_{NN} \) and AF \( J_{NNN} \) interactions in the presence of magnetic fields, theoretical studies predict various quantum phases including the vector chiral phase, the spin nematic phase, phases with multipole order, and the spin-density-wave phases \( [17–26] \) . Several model substances have been found and are summarized in Table I in Ref. \( [27] \) or Fig. 5 in Ref. \( [28] \) . Experimental results are compared with theoretical results \( [22,26] \) . In the frustrated diamond-chain system, three ground states appear according to relative intensities among exchange interactions \( [29] \) . A spin-liquid ground state and a 1/3 magnetization plateau were found in the model compound \( \mathrm{Cu}_{3}(\mathrm{CO}_{3})_{2}(\mathrm{OH})_{2} \) \( [30] \) .
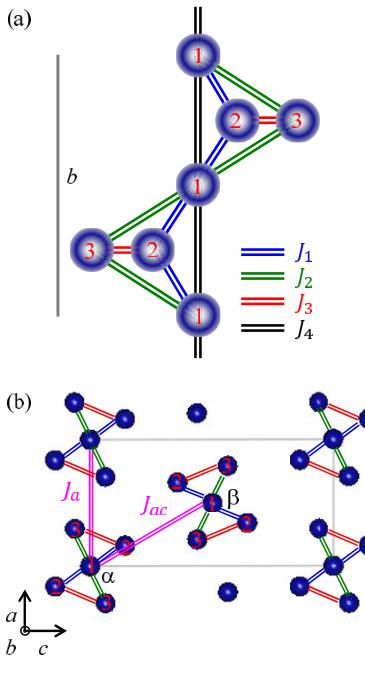
\( Cu_{3}Mo_{2}O_{9} \) provides a different frustrated spin- \( \frac{1}{2} \) AF chain [31]. Figure 1 shows schematically the spin system in \( Cu_{3}Mo_{2}O_{9} \) . Here, we assume that the space group SG is orthorhombic \( P_{nma} \) (No. 62) [32,33]. There are three crystallographic \( Cu^{2+} \) sites having spin- \( \frac{1}{2} \) . Four types of NN exchange interactions between Cu spins exist. The \( J_{4} \) interaction forms AF chains parallel to the b axis of Cu1 spins. The \( J_{3} \) interaction forms AF dimers in ac planes of Cu2 and Cu3 spins. The \( J_{1} \) and \( J_{2} \) interactions connect chains and dimers. The four NN interactions form distorted tetrahedral spin chains. Magnetic frustration exists in each distorted tetrahedral spin chain. We also consider interchain interactions ( \( J_{ac} \) and \( J_{a} \) interactions) shown in Fig. 1(b). As will be described later, we infer that the space group above the transition temperature \( T_{N} = 7.9 \) K is monoclinic $ P_{2
We determined dispersion relations of magnetic excitations from inelastic neutron scattering results [34] of a single crystal synthesized using the continuous solid-state crystallization method [35]. We observed hybridization of magnetic excitations of the chains and dimers. The dispersion relations can be explained using the above spin model with \( J_{4}=4.0 \) meV, \( J_{3}=5.8 \) meV, \( J_{1}\sim1 \) meV, \( J_{2}\sim1 \) meV, \( J_{ac}=0.19 \) meV (AF), and \( J_{a}=-0.19 \) meV (ferromagnetic) based on a chain mean-field theory with random phase approximation [34,36–38] or with \( J_{4}=6.50 \) meV, \( J_{3}=5.70 \) meV, \( |J_{1}-J_{2}|=3.06 \) meV, \( J_{ac}=0.04 \) meV, and \( J_{a}=-0.04 \) meV based on a spin-wave theory [39].
\( Cu_{3}Mo_{2}O_{9} \) exhibits both AF long-range order and electric polarization below \( T_{N}=7.9 \) K, meaning that \( Cu_{3}Mo_{2}O_{9} \) is a multiferroic substance [40]. Weak ferromagnetism appears only in finite magnetic fields parallel to the a or c axis [31]. The weak ferromagnetism disappears by slight substitution of Zn (0.5%) for Cu sites [41]. The electric polarization appears parallel to the c axis at zero magnetic field and becomes parallel to the a axis in the magnetic field parallel to the c axis with H>8T. Several magnetic-field-induced phase transitions and 2/3 magnetization plateau appear in the magnetization curves up to 74 T [42,43]. The magnetic and dielectric properties
(a)

FIG. 1. (Color online) The spin system in \( Cu_{3}Mo_{2}O_{9} \) . Here, we assume that the space group is orthorhombic \( P_{nma} \) (No. 62) [32,33]. There are three crystallographic \( Cu^{2+} \) sites having spin- \( \frac{1}{2} \) . Gray lines correspond to lattice constants. (a) A distorted tetrahedral spin chain parallel to the b axis formed by the four types of nearest-neighbor exchange interactions. The \( J_{4} \) interaction forms AF chains of Cu1 spins. The \( J_{3} \) interaction forms AF dimers of Cu2 and Cu3 spins. The \( J_{1} \) and \( J_{2} \) interactions connect the chains and dimers. (b) Corner \( (\alpha) \) and center \( (\beta) \) distorted tetrahedral spin chains projected on the ac plane. To explain dispersion relations of magnetic excitations, we consider \( J_{ac} \) and \( J_{a} \) interchain interactions in addition to \( J_{1} \sim J_{4} \) interactions. We infer that the space group above \( T_{N} = 7.9 \) K is monoclinic \( P2_{1}/m \) (No. 11), although deviations from the average symmetry (Pnma) are very small. The a,b, and c axes in Pnma correspond to the a,b, and c axes in \( P2_{1}/m \) , respectively. In the crystal structure with \( P2_{1}/m, \alpha \) and \( \beta \) distorted tetrahedral spin chains are inequivalent.
change simultaneously at the transition fields. Temperature–magnetic field phase diagrams have been obtained [43]. Raman scattering experiments were performed [44]. The Raman scattering spectra did not change at \( T_{N} \) . Therefore, change of the crystal structure caused by the multiferroic transition is negligibly small.
It is important to determine the magnetic structure of \( Cu_{3}Mo_{2}O_{9} \) to understand the above-mentioned results. Another group performed neutron powder diffraction experiments and reported the magnetic structure of \( Cu_{3}Mo_{2}O_{9} \) \( [45] \) . Ferromagnetic behavior parallel to the b axis is expected in the result, whereas the ferromagnetic behavior parallel to the a or c axis was observed in our magnetization results of single crystals \( [31] \) . We considered that reinvestigation of the magnetic structure is necessary. Accordingly, we performed neutron powder diffraction experiments.
II. EXPERIMENTAL METHODS
We synthesized \( Cu_{3}Mo_{2}O_{9} \) powder using a solid-state-reaction method at 1023 K in air for 150 h with intermediate grindings. We performed x-ray powder diffraction experiments at room temperature using a RIGAKU RINT-TTR III diffractometer. The wavelength \( \lambda \) is 1.542 Å (Cu \( K_{\alpha} \) ). We carried out neutron powder diffraction experiments at the Swiss spallation neutron source (SINQ) at Paul Scherrer Institute (PSI). We used the high-resolution powder diffractometer for thermal neutrons (HRPT) in the high-intensity mode ( \( \Delta d/d \geqslant 1.8 \times 10^{-3} \) ) [46] and the high-intensity cold neutron powder diffractometer (DMC). We used neutrons with \( \lambda = 1.886 \) and 4.507 Å at HRPT and DMC diffractometers, respectively. Powder was filled into a vanadium container with 8 mm diameter and 55 mm height for the HRPT experiments and that with 10 mm diameter and 55 mm height for the DMC experiments.
We performed Rietveld refinements of the crystal and magnetic structures using the FULLPROF SUITE program package \( [47] \) with its internal tables for scattering lengths and magnetic form factors. Symmetry analysis was done by using ISODISTORT tool based on ISOTROPY software \( [48,49] \) and BASIREP program of FULLPROF SUITE.
III. RESULTS AND ANALYSES
A. Reinvestigation into the crystal structure above \( T_{N} \)
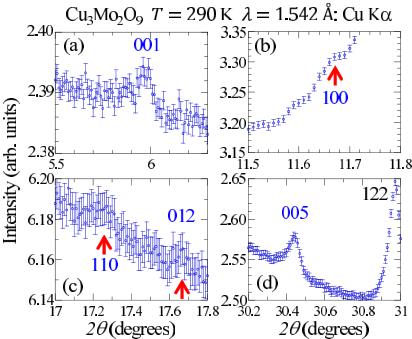
The space group of \( Cu_{3}Mo_{2}O_{9} \) at room temperature has been reported to be orthorhombic Pnma (No. 62) [32,33]. As will shown later, the symmetry of the crystal structure is important to consider weak ferromagnetism and electric polarization. Therefore, we reinvestigated the crystal structure above \( T_{N} \) . We measured high-statistics x-ray powder diffraction patterns at 290 K to investigate whether reflections forbidden in Pnma were present or not. As shown in Fig. 2, we found five weak reflections that were forbidden in Pnma. We estimated the

FIG. 2. (Color online) X-ray powder diffraction patterns of \( Cu_{3}Mo_{2}O_{9} \) at 290 K measured using a RIGAKU RINT-TTR III diffractometer ( \( \lambda = 1.542 \, \AA \) , Cu \( K_{\alpha} \) ). Five reflections forbidden in Pnma were observed at 001, 100, 110, 012, and 005.
d values of the five reflections as 14.8(2), 7.59(2), 5.14(3), 5.02(2), and 2.936(3) Å from lower to higher 2θ. Assuming an orthorhombic crystal structure, we calculated the lattice constants as \( a = 7.685(2) \) , \( b = 6.878(1) \) , and \( c = 14.650(3) \) Å from an x-ray diffraction pattern at 290 K between \( 2\theta = 5 \) and \( 80^{\circ} \) . We obtained the d values as 14.650(3), 7.685(2), 5.125(2), 5.014(2), and 2.930(1) Å for forbidden reflections at 001, 100, 110, 012, and 005. We consider that we can assign the indices to the five reflections. The diffraction results suggest that the space group at 290 K could have a lower symmetry than Pnma. In maximal subgroups of Pnma, only monoclinic \( P2_{1}/m \) (No. 11) can have all the forbidden reflections. The a, b, and c axes in Pnma correspond to the a, b, and c axes in \( P2_{1}/m \) , respectively. We detected, however, neither a split of reflections nor a broadening of reflections caused by a very small split. We observed no phase transition above \( T_{N} \) in the specific heat of \( Cu_{3}Mo_{2}O_{9} \) [31]. Consequently, we tentatively suggest that the space group above \( T_{N} \) is \( P2_{1}/m \) . The five reflections forbidden in Pnma are very weak. For example, the forbidden 005 reflection is weaker than the weak allowed 122 reflection shown in Fig. 2(d), which is only 0.72% of the largest Bragg reflection at 020. Accordingly, deviations from the average symmetry are very small. We have to evaluate 48 coordinates of the atomic positions except for special coordinates in \( P2_{1}/m \) instead of 24 coordinates in Pnma. It is practically impossible to determine the atomic positions of \( Cu_{3}Mo_{2}O_{9} \) in Rietveld refinements using \( P2_{1}/m \) . We cannot rigorously prove that the space group at 290 K is \( P2_{1}/m \) .
The circles in Fig. 3 show a neutron powder diffraction pattern of \( Cu_{3}Mo_{2}O_{9} \) at 12 K just above \( T_{N}=7.9 \) K recorded using the HRPT diffractometer with \( \lambda=1.886 \) Å. We observed no reflection forbidden in Pnma. It is difficult to obtain reliable converged results in Rietveld refinements for the neutron data at 12 K using \( P2_{1}/m \) with a lower symmetry than Pnma. We performed Rietveld refinements using Pnma to evaluate crystal structure parameters at 12 K. The line on the experimental pattern indicates the result of Rietveld refinements. The line agrees well with the experimental pattern. The refined crystal structure parameters are presented

FIG. 3. (Color online) A neutron powder diffraction pattern of \( Cu_{3}Mo_{2}O_{9} at 12 K \) (above the transition temperature \( T_{N} = 7.9 K \) ) measured using the HRPT diffractometer ( \( \lambda = 1.886 \AA \) ). Lines on the observed pattern and at the bottom show a Rietveld refined pattern obtained using the crystal structure with Pnma (No. 62) and the difference between the observed and the Rietveld refined patterns, respectively. Hash marks represent positions of nuclear reflections.
TABLE I. Structural parameters of \( Cu_{3}Mo_{2}O_{9} \) derived from Rietveld refinements of the HRPT neutron powder diffraction pattern at 12 K. We used orthorhombic Pnma (No. 62). The lattice constants at 12 K are \( a = 7.629(1) \) Å, \( b = 6.876(1) \) Å, and \( c = 14.573(1) \) Å. Estimated standard deviations are shown in parentheses. The reliability indexes of the refinement are \( R_{p} = 3.26\% \) , \( R_{wp} = 4.16\% \) , \( R_{exp} = 2.75\% \) , and \( \chi^{2} = 2.29 \) .
| Atom | Site | x | y | z | B_{\text{iso}}(\text{\AA}^{2}) |
| Cu1 | 4a | 0 | 0 | 0 | 0.23(3) |
| Cu2 | 4c | 0.1620(2) | 0.75 | 0.1430(1) | 0.09(3) |
| Cu3 | 4c | 0.2064(2) | 0.25 | 0.4373(1) | 0.14(3) |
| Mo1 | 4c | 0.2657(3) | 0.25 | 0.1696(1) | 0.18(3) |
| Mo2 | 4c | 0.1547(3) | 0.75 | 0.3885(1) | 0.19(4) |
| O1 | 4c | 0.0875(3) | 0.75 | 0.0159(1) | 0.22(5) |
| O2 | 4c | 0.2075(3) | 0.75 | 0.2715(2) | 0.32(4) |
| O3 | 4c | 0.4310(3) | 0.75 | 0.0969(2) | 0.27(5) |
| O4 | 8d | 0.2481(2) | 0.9636(2) | 0.4397(1) | 0.31(3) |
| O5 | 8d | 0.1410(2) | 0.0369(2) | 0.1373(1) | 0.42(3) |
| O6 | 4c | 0.3029(3) | 0.25 | 0.2857(2) | 0.44(4) |
| O7 | 4c | 0.4692(3) | 0.25 | 0.1103(2) | 0.33(5) |
in Table I. We performed symmetry analysis and Rietveld refinements based on both \( P2_{1}/m \) and Pnma to determine the magnetic structure. We expected that atomic positions determined using \( P2_{1}/m \) would be almost the same as those determined using Pnma because the forbidden reflections are very weak in the x-ray powder diffraction patterns. Therefore, we used the values in Table I for the following Rietveld refinements to determine the magnetic structure. We describe below the relation between the positions in Pnma and \( P2_{1}/m \) . The basis transformation is given by identity matrix without origin shift. The Cu1 (4a) position in Pnma is split into Cu11 (2a) and Cu12 (2d) positions in \( P2_{1}/m \) . The Cu2 and Cu3 (4c) positions are split into Cu21 and Cu22 (2e), and Cu31 and Cu32 (2e) positions, respectively. In \( P2_{1}/m \) , the corner ( \( \alpha \) ) and center ( \( \beta \) ) distorted tetrahedral spin chains are inequivalent.
B. Magnetic structure
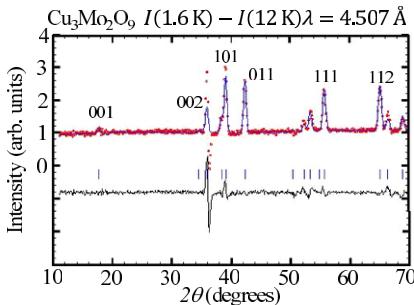
We measured neutron powder diffraction patterns at 1.6 and 12 K (below and above \( T_{N} = 7.9 \) K, respectively) using the DMC diffractometer with \( \lambda = 4.507 \) Å. Figure 4 shows the difference pattern made by subtracting the 12 K diffraction pattern from the 1.6 K one. Several magnetic reflections are apparent at 1.6 K. All the reflections can be indexed in the chemical cell with the propagation vector k = 0.
The magnetic reflections are much weaker than major nuclear reflections. Therefore, we have performed the analysis for the difference pattern shown in Fig. 4 to determine the magnetic structure of \( Cu_{3}Mo_{2}O_{9} \) . For \( k = 0 \) , there are four one-dimensional (1D) real irreducible representations (IRs) that enter the magnetic representation decomposition, resulting in four possible Shubnikov groups based on \( P2_{1}/m \) . The best-fit candidate is \( P2_{1}/m' \) , which corresponds to \( m\Gamma_{1}^{-} \) ( \( \tau_{2} \) ). The nomenclature for the IR is given according to Ref. [49] with Kovalev's notation in the parentheses. The a and c components of magnetic moments are allowed on the dimer sites (2e), whereas the magnetic moments on the chain sites (2a and 2d) are zero by symmetry of \( m\Gamma_{1}^{-} \) . There are two IRs.

FIG. 4. (Color online) A difference pattern made by subtracting a neutron powder diffraction pattern of \( Cu_{3}Mo_{2}O_{9} \) at 12 K from that at 1.6 K ( \( T_{N} = 7.9 \) K). The diffraction patterns were measured using the DMC diffractometer ( \( \lambda = 4.507 \) Å). Lines on the observed pattern show a Rietveld refined pattern obtained using \( m\Gamma_{1}^{-} \) ( \( \tau_{2} \) ) in \( P2_{1}/m \) . Lines at the bottom show the difference between the observed and the Rietveld refined patterns. Hash marks represent positions of magnetic reflections. We described indices of several magnetic reflections.
even by inversion operator \( m\Gamma_{2}^{+}(\tau3) \) and \( m\Gamma_{1}^{+}(\tau1) \) , that allow nonzero chain moments. We performed Rietveld refinements using \( m\Gamma_{1}^{-} \) for dimer moments and \( m\Gamma_{2}^{+} \) or \( m\Gamma_{1}^{+} \) for chain moments. In both cases, the reliability indexes are smallest for the chain moments close to zero.
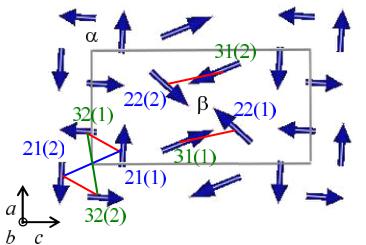
As shown in Fig. 4, the experimental pattern can be explained well by the line calculated using \( P2_{1}/m' \) . The reliability indexes are \( R_{wp} = 4.90\% \) , \( R_{exp} = 2.85\% \) , and \( \chi^{2} = 2.95 \) . The magnetic structure is shown in Fig. 5. Magnetic moments on dimer sites are \( \mathbf{M}_{21} = (0.57(2), 0, 0.04(3))\mu_{\mathrm{B}} \) on Cu21 sites, \( \mathbf{M}_{22} = (0.46(3), 0, -0.50(3))\mu_{\mathrm{B}} \) on Cu22 sites, \( \mathbf{M}_{31} = (0.27(4), 0, 0.69(3))\mu_{\mathrm{B}} \) on Cu31 sites, and \( \mathbf{M}_{32} = (0.04(4), 0, -0.50(3))\mu_{\mathrm{B}} \) on \( Cu_{32} \) sites. The magnitude of the moments is \( M_{21} = 0.57(2)\mu_{\mathrm{B}} \) , \( M_{22} = 0.69(3)\mu_{\mathrm{B}} \) , \( M_{31} = 0.74(4)\mu_{\mathrm{B}} \) , and \( M_{32} = 0.50(3)\mu_{\mathrm{B}} \) . The angle between two moments in Cu21-Cu32 and Cu22-Cu31 dimers is \( 90(8)^{\circ} \) and \( 116(6)^{\circ} \) , respectively. Two neighboring dimer moments in each

FIG. 5. (Color online) The magnetic structure of \( Cu_{3}Mo_{2}O_{9} \) obtained using \( P2_{1}/m' \) . Magnetic moment vectors in dimers are \( \mathbf{M}_{21} = (0.57(2), 0.04(3))\mu_{\mathrm{B}} \) on \( \mathrm{Cu}_{21}(1) \) sites, \( \mathbf{M}_{22} = (0.46(3), 00, -0.50(3))\mu_{\mathrm{B}} \) on \( \mathrm{Cu}_{22}(1) \) sites, \( \mathbf{M}_{31} = (0.27(4), 00, 0.69(3))\mu_{\mathrm{B}} \) on \( \mathrm{Cu}_{31}(1) \) sites, and \( \mathbf{M}_{32} = (0.04(4), -0, -0.50(3))\mu_{\mathrm{B}} \) on \( \mathbf{Cu}_{32}(1) \) sites. Symmetry operators of moments are shown in Table II. The chain moments are very small if they exist.
TABLE II. Symmetry operators of magnetic moments in the two Shubnikov groups. The u, v, and w indicate the a, b, and c components of ordered magnetic moments.
| Shubnikov group | Site | (1) | (2) |
| \( P2_{1}/m' \) (11.53) | 2e (dimer) | [u,0,w] | [ \( \bar{u} \) ,0, \( \bar{w} \) ] |
| 2a,2d (chain) | [0,0,0] | [0,0,0] | |
| \( Pm' \) (6.20) | 1a,1b (dimer) | [u,0,w] | |
| 2c (chain) | [u,v,w] | [u, \( \bar{v} \) ,w] |
distorted tetrahedral spin chain are antiparallel to each other as indicated by the blue or green line. The chain moments may exist but the magnitudes are very small, meaning that spins in chains are nearly disordered. The magnetic structure indicates that a partially disordered (PD) state is realized. The magnetic entropy S is shown in Fig. 6(b) in [31]. The value of S/R ln2 is about 0.1 at \( T_{N} \) where R is the gas constant. The small magnetic entropy is consistent with the nearly disordered chain moments. In the previous papers [31,41], we inferred that the main component of ordered moments in chains was the b component and that spins in dimers were nearly spin singlet. The previous inferences are incorrect.
We investigated the magnetic structure assuming \( P_{nma} \) that has been reported as the space group at room temperature. As described below, the obtained magnetic structures are similar to that in Fig. 5. In the case of \( k=0 \) , there are eight 1D real IRs, resulting in eight Shubnikov groups based on \( P_{nma} \) . The best-fit candidate is \( P_{nm}a \) , which corresponds to \( m\Gamma_{4}^{-}(\tau4) \) . The a and c components of ordered magnetic moments can be finite on dimer sites (4c), whereas no ordered magnetic moment on chain sites (4a) is allowed by symmetry of \( m\Gamma_{4}^{-} \) . In addition, the 001 magnetic reflection observed at \( 2\theta=17.7^{\circ} \) is forbidden in \( m\Gamma_{4}^{-} \) . There are four IRs even by inversion operator that enter the magnetic representation decomposition for the chain moments. Among the four, the 001 magnetic reflection is allowed in \( m\Gamma_{2}^{+}(\tau7) \) and \( m\Gamma_{1}^{+}(\tau1) \) . In refinements using \( m\Gamma_{4}^{-} \) and \( m\Gamma_{2}^{+} \) for dimer and chain moments, respectively, we obtained magnetic moments as \( \mathbf{M}_{1}=(0.085(9),0,0)\mu_{\mathrm{B}} \) on Cu1 sites, \( \mathbf{M}_{2}=(0.555(8),0,0.283(6))\mu_{\mathrm{B}} \) on Cu2 sites, and \( \mathbf{M}_{3}=(0.132(7),0,0.604(6))\mu_{\mathrm{B}} \) on Cu3 sites. The reliability indexes are \( R_{wp}=5.02\% \) , \( R_{exp}=2.86\% \) , and \( \chi^{2}=3.08 \) . The magnitude of the Cu2 and Cu3 moments is \( 0.62(1)\mu_{\mathrm{B}} \) . The angle between two moments in each dimer is \( 105(2)^{\circ} \) . In refinements using \( m\Gamma_{4}^{-} \) and \( \mathbf{m}\Gamma_{1}^{+} \) for dimer and chain moments, respectively, we obtained magnetic moments as \( \mathrm{M}_{1}=(0,0.085(9),0.13(2))\mu_{\mathrm{B}} \) on Cu1 sites, \( \mathbf{M}_{2}=0.543(9),0,0.289(7))\mu_{\mathrm{B}} \) on Cu2 sites, and \( \mathbf{M}_{\mathrm{3}}=0.141(7),0,0.593(8))\mu_{\mathrm{B}} \) on Cu3 sites. The reliability indexes are \( \mathbf{R}_{wp}=4.97\% \) , \( R_{exp}=2.86\% \) , and \( \mathbf{\chi}^{2}=3.02 \) . The magnitude of the Cu1, Cu2, and Cu3 moments is \( 0.16(2),0.62(1) \) , and \( 0.61(1)\mu_{\mathrm{B}} \) , respectively. The angle between two moments in each dimer is \( 105(2)^{\circ} \) .
IV. DISCUSSION
A. Origin of the magnetic structure
We consider the origin of the magnetic structure in \( Cu_{3}Mo_{2}O_{9} \) . To avoid complicated explanations, we use Cu1,
Cu2, and Cu3 to indicate Cu sites. As described, the four types of NN interactions \( (J_{1} \sim J_{4} \) interactions) shown in Fig. 1 generate magnetic frustration. Six NN interactions influence each Cu1 spin, whereas only three NN interactions influence each Cu2 or Cu3 spin. Probably, the frustration is more effective for Cu1 spins than Cu2 and Cu3 spins. Therefore, Cu1 spins are nearly disordered, whereas Cu2 and Cu3 spins can be ordered.
In addition to the magnetic frustration, the magnetic structure of the Cu2 and Cu3 moments allows the nearly disordered state of Cu1 spins. Two neighboring Cu2 (Cu3) moments in each distorted tetrahedral spin chain are antiparallel to each other as indicated by the blue (green) line in Fig. 5. The internal magnetic fields generated by Cu2 or Cu3 ordered moments are canceled out on Cu1 sites in the magnetic structure. Therefore, classical magnetic energy is independent of the direction of Cu1 moments in the absence of magnetic anisotropy. Cu1 spins can be disordered.
A similar PD state is seen in the frustrated three-legged ladder Heisenberg antiferromagnets \( \mathrm{Cu}_{3}(\mathrm{OH})_{4}\mathrm{AO}_{4} \) (A = S or Se) [50,51]. Cu moments within the inner leg remain random, whereas Cu moments within the two outer legs are ordered. Six NN interactions influence each inner Cu spin, whereas four NN interactions influence each outer Cu spin. The frustration may be more effective for inner Cu spins than outer Cu spins as expected in \( Cu_{3}Mo_{2}O_{9} \) . In addition to \( \mathrm{Cu}_{3}(\mathrm{OH})_{4}\mathrm{AO}_{3} \) (A = S or Se), a part of spins are perfectly or nearly disordered in the ordered state in several frustrated Heisenberg antiferromagnets such as the spinel antiferromagnet \( GeNi_{2}O_{4} \) [52], the pyrochlore antiferromagnet \( Gd_{2}Ti_{2}O_{7} \) [53], and the triangular lattice antiferromagnets \( CuFeO_{2} \) [54] and \( Ag_{2}CrO_{2} \) [55]. Exchange interactions in long M-M bonds, where M represents a magnetic ion, play an important role in the occurrence of the PD states.
Table III shows possible Shubnikov magnetic groups appearing as a result of mixing of two IRs. Among them, bond alternation of the \( J_{4} \) interaction is possible in Pm (No. 6) and \( Pmc2_{1} \) (No. 26) [56]. The bond alternation of the \( J_{4} \) interaction may be the origin of the very small Cu1 moment. Bond alternation of NN interactions generates a gapped spin-singlet ground state in an AF spin chain as in
TABLE III. Possible ferromagnetic moment (FM) and electric polarization (EP) in the Shubnikov groups obtained by mixing of two IRs of the parent space groups. The columns indicate A: the parent space group to be considered initially, B: the two mixed IRs, C: the Shubnikov group obtained by the mixing with the number in BNS settings [49], and D and E: the direction of the possible FM and EP, respectively, in the basis of the parent space group of the column A (the Shubnikov group of the column C). The symbol “-” means no FM or EP. The third and sixth lines are added to indicate that FM and EP are impossible in Shubnikov group based on single IR.
| A | B | C | D: FM | E: EP |
| \( P2_{1}/m \) | \( m\Gamma_{1}^{-},m\Gamma_{2}^{+} \) | \( Pm' \) (6.20) | \( \perp b \) ( \( \perp b \) ) | \( \perp b \) ( \( \perp b \) ) |
| \( m\Gamma_{1}^{-},m\Gamma_{1}^{+} \) | \( P2_{1} \) (4.7) | \( \parallel b \) ( \( \parallel b \) ) | \( \parallel b \) ( \( \parallel b \) ) | |
| \( m\Gamma_{1}^{-} \) | \( P2_{1}/m' \) (11.53) | - (-) | - (-) | |
| \( Pnma \) | \( m\Gamma_{4}^{-},m\Gamma_{2}^{+} \) | \( Pm'c2_{1}' \) (26.68) | \( \parallel c \) ( \( \parallel b \) ) | \( \parallel a \) ( \( \parallel c \) ) |
| \( m\Gamma_{4}^{-},m\Gamma_{1}^{+} \) | \( Pna2_{1} \) (33.144) | - (-) | \( \parallel b \) ( \( \parallel c \) ) | |
| \( m\Gamma_{4} \) | \( Pnm'a \) (62.444) | - (-) | - (-) |
the spin-Peierls system. The values of \( S^{T} \) and \( S_{z}^{T} \) are 0 in a spin-singlet ground state. Here, \( S^{T} \) and \( S_{z}^{T} \) represent a value and a z value, respectively, of the sum of spin operators. Other \( S_{z}^{T}=0 \) states can be hybridized with the spin-singlet ground state of an AF alternating spin chain by other interactions [57]. States with \( S^{T}>0 \) and \( S_{z}^{T}=0 \) are magnetic. For example, \( S_{z}^{T}=0 \) is zero in a collinear two-sublattice AF ordered state, although the state is not an eigenstate of the AF Heisenberg models. As a result, the ground state of the AF alternating spin chain can be magnetic by the hybridization of plural \( S_{z}^{T}=0 \) states. When AF long-range order occurs, the magnitude of the ordered moments is expected to be larger for a smaller spin gap. The alternation ratio is probably very close to 1 and a spin gap is very small. The spin gap of Cu1 spins is less than 0.2 meV in inelastic neutron scattering results of \( Cu_{3}Mo_{2}O_{9} \) . Accordingly, the bond alternation of the \( J_{4} \) interaction is not the origin of the very small Cu1 moment.
The moments in AF dimers are reduced from a classical value ( \( \sim1\mu_{B} \) ). Probably, the magnetic frustration generates the reduction of the moments. In addition, character of a spin-singlet pair may be overlapped and may cause the reduction of the moments [58]. We do not understand the reason that the angle between two moments in AF dimers \( [90(8)^{\circ} \) or \( 116(6)^{\circ}] \) is different from \( 180^{\circ} \) (antiparallel configuration). As described, long-distance interactions exist in several frustrated Heisenberg antiferromagnets showing a PD state. Long-distance interactions may exist in \( Cu_{3}Mo_{2}O_{9} \) and may affect determination of the angle between two moments in AF dimers. The 2/3 magnetization plateau appears in the magnetization curves of \( Cu_{3}Mo_{2}O_{9} \) [43]. In a Heisenberg model with bilinear and biquadratic terms \( [S_{i}\cdot S_{j} \) and \( (S_{i}\cdot S_{j})^{2} \) terms, respectively], the magnetization plateau can appear as in \( CdCr_{2}O_{4} \) [59]. We are seeking a model that can explain the magnetic excitations, the magnetization curves, and the magnetic structure.
B. Consideration of other experimental results
We comment on the signs of the exchange interactions between spins on chain sites. From the dispersion relations of the magnetic excitations, the \( J_{4} \) interaction forming Cu1 spin chains parallel to the b axis and the interchain \( J_{ac} \) interaction are antiferromagnetic, whereas the interchain \( J_{a} \) interaction is ferromagnetic [34,39]. The signs of the interactions agree with the signs of the b components on 2a and 2d sites for \( m\Gamma_{2}^{+} \) in \( P2_{1}/m \) and the signs of the a and c components on 2a and 2d sites for \( m\Gamma_{1}^{+} \) in \( P2_{1}/m \) , although the chain moments are nearly disordered. Spin chains can show dispersive magnetic excitations even in the absence of magnetic long-range order. The disordered component generates the magnetic excitations of the chains.
We consider the weak ferromagnetism in magnetic fields parallel to the a or c axis [31] and the electric polarization parallel to the c axis at zero magnetic field [40] below \( T_{N} = 7.9 \) K in \( Cu_{3}Mo_{2}O_{9} \) . As described in Table III, if the IR for the chain moments is \( m\Gamma_{2}^{+} \) in \( P2_{1}/m, \) the Shubnikov group for the magnetic structure is \( Pm' \) from the mixing of \( m\Gamma_{1}^{-} \) and \( m\Gamma_{2}^{+} \) . As described in Table II, dimer sites are 1a or 1b sites. The a and c components (u and w, respectively) of ordered moments can be finite. The weak ferromagnetism
perpendicular to the b axis is possible on the dimer sites because all the dimer sites are independent. Chain sites are 2c sites. According to the symmetry operators of magnetic moments, the weak ferromagnetism perpendicular to the b axis is possible also on the chain sites, whereas the sum of b components is zero on 2c sites. In \( P2_{1}/m' \) , the a and c components of ordered moments on dimer (2e) sites can be finite. The sum of a components and that of c components are zero. Therefore, the weak ferromagnetism is impossible in any direction. The electric polarization perpendicular to the b axis is possible in the crystal structure with the space group Pm. Considering the basis transformation, the b axis in Pm corresponds to the b axis in \( P2_{1}/m \) . Consequently, the experimental results of the weak ferromagnetism and electric polarization may be explained by the \( Pm' \) model described in the first line in Table III [60]. The other models in Table III, on the other hand, cannot explain the experimental results.
We consider that the origin of the weak ferromagnetism is the dimer moments because of the following reasons. The chain moments are very small if they exist. It may be doubtful that the chain moments can have the observable weak ferromagnetism. The weak ferromagnetism disappears by substitution of Zn for Cu sites [41]. We performed neutron powder diffraction experiments on \( Cu_{2.88}Zn_{0.12}Mo_{2}O_{9} \) and \( Cu_{2.85}Zn_{0.15}Mo_{2}O_{9} \) using the HRPT diffractometer. We observed a few magnetic reflections. Probably, the propagation vector is \( k=0 \) as in \( Cu_{3}Mo_{2}O_{9} \) . We evaluated crystal structure parameters above \( T_{N} \) assuming Pnma. Most of Zn ions enter Cu3 sites, the remaining Zn ions enter Cu2 sites, and almost no Zn ions enter Cu1 sites. Influence of Zn substitution is more effective for Cu2 and Cu3 sites than for Cu1 sites. The results suggest that Cu2 and Cu3 moments (dimer moments) are responsible for the weak ferromagnetism. We will determine the magnetic structure of \( Cu_{3-x}Zn_{x}Mo_{2}O_{9} \) to investigate the origin of the weak ferromagnetism and the reason that the weak ferromagnetism disappears by substitution of Zn for Cu sites.
V. CONCLUSION
We investigated the crystal and magnetic structures of the spin- \( \frac{1}{2} \) frustrated antiferromagnet \( Cu_{3}Mo_{2}O_{9} \) in which the spin system consists of antiferromagnetic chains and dimers.
[1] P. W. Anderson, Mater. Res. Bull. 8, 153 (1973).
[2] S. Miyashita and H. Shiba, J. Phys. Soc. Jpn. 53, 1145 (1984).
[3] S. Onoda and N. Nagaosa, Phys. Rev. Lett. 99, 027206 (2007).
[4] H. Tsunetsugu and M. Arikawa, J. Phys. Soc. Jpn. 75, 083701 (2006).
[5] M. E. Zhitomirsky, Phys. Rev. B 78, 094423 (2008).
[6] H. Kawamura, A. Yamamoto, and T. Okubo, J. Phys. Soc. Jpn. 79, 023701 (2010).
[7] F. D. M. Haldane, Phys. Rev. B 25, 4925 (1982).
[8] F. D. M. Haldane, Phys. Rev. B 26, 5257 (1982).
[9] K. Okamoto and K. Nomura, Phys. Lett. A 169, 433 (1992).
The space group at room temperature has been reported to be orthorhombic Pnma (No. 62). We observed reflections forbidden in Pnma in x-ray powder diffraction experiments at room temperature. We infer that the space group above \( T_{N} = 7.9 \) K is monoclinic \( P2_{1}/m \) (No. 11) that is one of maximal subgroups of Pnma. We determined the magnetic structure of \( Cu_{3}Mo_{2}O_{9} \) in neutron powder diffraction experiments. The experimental diffraction pattern can be explained well by the line calculated using the irreducible representation (IR) \( m\Gamma_{1}^{-} \) ( \( \tau2 \) ) in \( P2_{1}/m \) . Magnetic moments on dimer sites lie in the ac planes. The magnitudes are \( (0.50 \sim 0.74)\mu_{\mathrm{B}} \) . The angle between two moments in dimers is \( 90(8)^{\circ} \) or \( 116(6)^{\circ} \) . The moments on chain sites may exist but the magnitudes are very small. The magnetic structure indicates that a partially disordered state is realized. Probably, magnetic frustration influences the magnetic structure. If the IR for the chain moments is \( m\Gamma_{2}^{+} \) ( \( \tau3 \) ) in \( P2_{1}/m \) , the Shubnikov group for the magnetic structure is \( Pm' \) from the mixing of \( m\Gamma_{1}^{-} \) and \( m\Gamma_{2}^{+} \) . The weak ferromagnetism perpendicular to the b axis is possible in \( Pm' \) . The electric polarization perpendicular to the b axis is possible in the crystal structure with the space group \( Pm \) (No. 6). The b axis in \( Pm \) corresponds to the b axis in \( P2_{1}/m \) and Pnma. Consequently, the experimental results of the weak ferromagnetism and electric polarization may be explained by the Pm' model, although we cannot prove that the Shubnikov group below \( T_{N} \) is \( Pm' \) .
ACKNOWLEDGMENTS
We are grateful to H. Eisaki, T. Goto, T. Ito, K. Kaneko, Y. Kawamura, R. Kiyanagi, M. Kohno, T. Masuda, M. Matsuda, M. Matsumoto, S. Matsumoto, Y. Noda, K. Oka, T. Suzuki, K. Tomiyasu, and O. Zaharko for fruitful discussion or experimental support. The neutron powder diffraction experiments were performed by using the DMC and HRPT diffractometers at SINQ, Paul Scherrer Institut, Switzerland (Proposals No. 20131441 and No. 20131464, respectively). The experiments were transferred from 5G:PONTA at JRR-3 with the approval of Institute for Solid State Physics, The University of Tokyo (Proposals No. 14806 and No. 14807) and Japan Atomic Energy Agency, Tokai, Japan. This work was partially supported by grants from National Institute for Materials Science.
[10] M. Hase, I. Terasaki, and K. Uchinokura, Phys. Rev. Lett. 70, 3651 (1993).
[11] M. Hase, I. Terasaki, Y. Sasago, K. Uchinokura, and H. Obara, Phys. Rev. Lett. 71, 4059 (1993).
[12] M. Hase, I. Terasaki, K. Uchinokura, M. Tokunaga, N. Miura, and H. Obara, Phys. Rev. B 48, 9616 (1993).
[13] J. E. Lorenzo, K. Hirota, G. Shirane, J. M. Tranquada, M. Hase, K. Uchinokura, H. Kojima, I. Tanaka, and Y. Shibuya, Phys. Rev. B 50, 1278 (1994).
[14] G. Castilla, S. Chakravarty, and V. J. Emery, Phys. Rev. Lett. 75, 1823 (1995).
[15] J. Riera and A. Dobry, Phys. Rev. B 51, 16098 (1995).
[16] Y. Tanokura, Y. Oono, S. Ikeda, H. Kuroe, T. Sekine, T. Masuda, and K. Uchinokura, Phys. Rev. B 68, 054412 (2003).
[17] A. V. Chubukov, Phys. Rev. B 44, 4693 (1991).
[18] A. Kolezhuk and T. Vekua, Phys. Rev. B 72, 094424 (2005).
[19] F. Heidrich-Meisner, A. Honecker, and T. Vekua, Phys. Rev. B 74, 020403(R) (2006).
[20] T. Vekua, A. Honecker, H.-J. Mikeska, and F. Heidrich-Meisner, Phys. Rev. B 76, 174420 (2007).
[21] L. Kecke, T. Momoi, and A. Furusaki, Phys. Rev. B 76, 060407(R) (2007).
[22] T. Hikihara, L. Kecke, T. Momoi, and A. Furusaki, Phys.Rev. B 78, 144404 (2008).
[23] J. Sudan, A. Luscher, and A. M. Läuchli, Phys. Rev. B 80, 140402(R) (2009).
[24] M. Sato, T. Momoi, and A. Furusaki, Phys. Rev. B 79, 060406(R) (2009).
[25] F. Heidrich-Meisner, I. P. McCulloch, and A. K. Kolezhuk, Phys. Rev. B 80, 144417 (2009).
[26] M. Sato, T. Hikihara, and T. Momoi, Phys. Rev. B 83, 064405 (2011).
[27] M. Hase, H. Kuroe, K. Ozawa, O. Suzuki, H. Kitazawa, G. Kido, and T. Sekine, Phys. Rev. B 70, 104426 (2004).
[28] S.-L. Drechsler, O. Volkova, A. N. Vasiliev, N. Tristan, J. Richter, M. Schmitt, H. Rosner, J. Málek, R. Klingeler, A. A. Zvyagin, and B. Büchner, Phys. Rev. Lett. 98, 077202 (2007).
[29] K. Okamoto, T. Tonegawa, Y. Takahashi, and M. Kaburagi, J. Phys.: Condens. Matter 15, 5979 (2003).
[30] H. Kikuchi, Y. Fujii, M. Chiba, S. Mitsudo, T. Idehara, T. Tonegawa, K. Okamoto, T. Sakai, T. Kuwai, and H. Ohta, Phys. Rev. Lett. 94, 227201 (2005).
[31] T. Hamasaki, T. Ide, H. Kuroe, T. Sekine, M. Hase, I. Tsukada, and T. Sakakibara, Phys. Rev. B 77, 134419 (2008).
[32] U. Steiner and W. Reichelt, Acta Crystallogr. Sect. C 53, 1371 (1997).
[33] W. Reichelt, U. Steiner, T. Söhnel, O. Oeckler, V. Duppel, and L. Kienle, Z. Anorg. Allg. Chem. 631, 596 (2005).
[34] H. Kuroe, T. Hamasaki, T. Sekine, M. Hase, K. Oka, T. Ito, H. Eisaki, K. Kaneko, N. Metoki, M. Matsuda, and K. Kakurai, Phys. Rev. B 83, 184423 (2011).
[35] K. Oka, T. Ito, H. Eisaki, M. Hase, T. Hamasaki, H. Kuroe, and T. Sekine, J. Cryst. Growth 334, 108 (2011).
[36] F. H. L. Essler, A. M. Tsvelik, and G. Delfino, Phys. Rev. B 56, 11001 (1997).
[37] M. Kenzelmann, A. Zheludev, S. Raymond, E. Ressouche, T. Masuda, P. Bóni, K. Kakurai, I. Tsukada, K. Uchinokura, and R. Coldea, Phys. Rev. B 64, 054422 (2001).
[38] A. Zheludev, S. Raymond, L.-P. Regnault, F. H. L. Essler, K. Kakurai, T. Masuda, and K. Uchinokura, Phys. Rev. B 67, 134406 (2003).
[39] M. Matsumoto, H. Kuroe, T. Sekine, and M. Hase, J. Phys. Soc. Jpn. 81, 024711 (2012).
[40] H. Kuroe, R. Kino, T. Hosaka, M. Suzuki, S. Hachiuma, T. Sekine, M. Hase, K. Oka, T. Ito H. Eisaki, M. Fujisawa, S. Okubo, and H. Ohta, J. Phys. Soc. Jpn. 80, 083705 (2011).
[41] M. Hase, H. Kitazawa, K. Ozawa, T. Hamasaki, H. Kuroe, and T. Sekine, J. Phys. Soc. Jpn. 77, 034706 (2008).
[42] T. Hamasaki, H. Kuroe, T. Sekine, M. Hase, and H. Kitazawa, J. Phys.: Conf. Ser. 150, 042047 (2009).
[43] H. Kuroe, K. Aoki, R. Kino, T. Sato, H. Kuwahara, T. Sekine, T. Kihara, M. Akaki, Y. Kohama, M. Tokunaga, A. Matsuo, K. Kindo, M. Hase, K. Takehana, H. Kitazawa, K. Oka, T. Ito, and H. Eisaki, JPS Conf. Proc. 3, 014036 (2014).
[44] T. Sato, K. Aoki, R. Kino, H. Kuroe, T. Sekine, M. Hase, K. Oka, T. Ito and H. Eisaki, JPS Conf. Proc. 3, 014035 (2014).
[45] S. Vilminot, G. André, and M. Kurmoo, Inorg. Chem. 48, 2687 (2009).
[46] P. Fischer, G. Frey, M. Koch, M. Koennecke, V. Pomjakushin, J. Schefer, R. Thut, N. Schlumpf, R. Buerge, U. Greuter, S. Bondt, and E. Berruyer, Physica B 276-278, 146 (2000); http://sinq.web.psi.ch/hrpt.
[47] J. Rodriguez-Carvajal, Physica B 192, 55 (1993); http://www.ill.eu/sites/fullprof.
[48] H. T. Stokes and D. M. Hatch, Isotropy Subgroups of the 230 Crystallographic Space Groups (World Scientific Publishing, Singapore, 1988).
[49] B. J. Campbell, H. T. Stokes, D. E. Tanner, and D. M. Hatch, J. Appl. Crystallogr. 39, 607 (2006).
[50] S. Vilminot, M. Richard-Plouet, G. André, D. Swierczynski, M. Guillot, F. Bourée-Vigneron, and M. Drillon, J. Solid State Chem. 170, 255 (2003).
[51] S. Vilminot, G. André, F. Bourée-Vigneron, M. Richard-Plouet, and M. Kurmoo, Inorg. Chem. 46, 10079 (2007).
[52] M. Matsuda, J.-H. Chung, S. Park, T. J. Sato, K. Matsuno, H. Aruga Katori, H. Takagi, K. Kakurai, K. Kamazawa, Y. Tsunoda, I. Kagomiya, C. L. Henley, and S.-H. Lee, Europhys. Lett. 82, 37006 (2008).
[53] J. R. Stewart, G. Ehlers, A. S. Wills, S. T. Bramwell, and J. S. Gardner, J. Phys.: Condens. Matter 16, L321 (2004).
[54] M. Mekata, N. Yaguchi, T. Takagi, T. Sugino, S. Mitsuda, H. Yoshizawa, N. Hosoito, and T. Shinjo, J. Phys. Soc. Jpn. 62, 4474 (1993).
[55] M. Matsuda, C. de la Cruz, H. Yoshida, M. Isobe, and R. S. Fishman, Phys. Rev. B 85, 144407 (2012).
[56] Bond alternation of the \( J_{4} \) interaction is expected crystallographically. Cu1 sites are 4a in Pnma. A 4a position in Pnma is split into two 2c positions in Pm (No. 6). The symmetry operators are (1) x, y, z and (2) x, \( \bar{y} \) , z. Bond alternation is possible except for y = 0.25. Each 2c position forms each linear chain. Therefore, Cu sites in each linear chain are equivalent. A 4a position in Pnma corresponds to a 4c position in \( Pmc2_{1} \) (No. 26, in the standard setting). The symmetry operators are (1) x, y, z, (2) \( \bar{x} \) , \( \bar{y} \) , z + 1/2, (3) x, \( \bar{y} \) , z + 1/2, and (4) \( \bar{x} \) , y, z. The linear chain is parallel to the a axis. Bond alternation is possible except for x = 0.25.
[57] T. Masuda, K. Kakurai, and A. Zheludev, Phys. Rev. B 80, 180412(R) (2009).
[58] K. Tomiyasu, M. K. Crawford, D. T. Adroja, P. Manuel, A. Tominaga, S. Hara, H. Sato, T. Watanabe, S. I. Ikeda, J. W. Lynn, K. Iwasa, and K. Yamada, Phys. Rev. B 84, 054405 (2011).
[59] K. Penc, N. Shannon, and H. Shiba, Phys. Rev. Lett. 93, 197203 (2004).
[60] There are too many (twenty-two) independent components of magnetic moments in \( Pm' \) . Rietveld refinements using \( Pm' \) are not practically possible.