| Transition Temperature | 16 K |
|---|---|
| Experiment Temperature | 1.4 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | R-3c (#167) |
| Magnetic Space Group | R3c (#161.69) |
| Magnetic Point Group | 3m (19.1.68) |
| Lattice Parameters | 9.1314 9.1314 10.5817 90.0000 90.0000 120.0000 |
|---|---|
| DOI | 10.1103/physrevlett.100.047601 |
| Reference | Y.J. Choi, H.T. Yi, S. Lee, Q. Huang, V. Kiryukhin and S.-W. Cheong, Physical Review Letters (2008) 100. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Mn | Mn | 0.0 | 0.0 | 1.93 | 1.93 |
| Co | Co | 0.0 | 0.0 | 0.66 | 0.66 |
Ferroelectricity in an Ising Chain Magnet
Y. J. Choi, \( ^{1} \) H. T. Yi, \( ^{1} \) S. Lee, \( ^{1} \) Q. Huang, \( ^{2} \) V. Kiryukhin, \( ^{1} \) and S.-W. Cheong \( ^{1} \)
\( ^{1} \) Rutgers Center for Emergent Materials and Department of Physics & Astronomy,
136 Frelinghuysen Road, Piscataway, New Jersey, 08854, USA
\( ^{2} \) NIST Center for Neutron Research, NIST, Gaithersburg, Maryland 20899, USA (Received 13 September 2007; published 29 January 2008)
We report discovery of collinear-magnetism-driven ferroelectricity in the Ising chain magnet \( Ca_{3}Co_{2-x}Mn_{x}O_{6} \) ( \( x \approx 0.96 \) ). Neutron diffraction shows that \( Co^{2+} \) and \( Mn^{4+} \) ions alternating along the chains exhibit an up-up-down-down ( \( \uparrow\downarrow\downarrow \) ) magnetic order. The ferroelectricity results from the inversion symmetry breaking in the \( \uparrow\downarrow\downarrow \) spin chain with an alternating charge order. Unlike in spiral magneto-electrics where antisymmetric exchange coupling is active, the symmetry breaking in \( Ca_{3}(Co, Mn)_{2}O_{6} \) occurs through exchange striction associated with symmetric superexchange.
DOI: 10.1103/PhysRevLett.100.047601
PACS numbers: 77.80.−e, 75.10.Pq, 75.80.+q, 77.22.Ej
The concept of magnetism-driven ferroelectricity has recently drawn a significant attention \( [1,2] \) . In magnetism-driven ferroelectrics, development of inversion-symmetry-breaking magnetic order leads to the loss of the lattice inversion symmetry through exchange striction, thereby leading to the development of ferroelectricity. In these materials, external magnetic field influences the configuration of the magnetic order, naturally leading to changes in ferroelectric or dielectric properties. Spectacular cross-coupling effects, such as reversible flipping of ferroelectric polarization or drastic change of dielectric constant in applied magnetic fields, have been recently observed in magnetism-driven ferroelectrics \( [3–5] \) . Spiral magnetic order, resulting from magnetic frustration, is a common way to induce the loss of inversion symmetry, and ferroelectricity has been recently observed in a number of spiral magnets such as \( TbMnO_{3} \) , \( Ni_{3}V_{2}O_{8} \) , \( CuFeO_{2} \) , \( (\mathrm{Ba},\mathrm{Sr})_{2}\mathrm{Zn}_{2}\mathrm{Fe}_{12}\mathrm{O}_{22} \) , \( CoCr_{2}O_{4} \) , \( MnWO_{4} \) , and \( LiCu_{2}O_{2} \) \( [6–12] \) . In the spiral magnets, the relevant exchange striction is associated with the antisymmetric part of the exchange coupling, which constitutes the so-called Dzyaloshinski-Moriya (DM) interaction \( [13–16] \) .
Spiral magnetic order is not the only possible route towards magnetism-induced ferroelectricity. In \( RMn_{2}O_{5} \) (R = Tb-Lu), for example, a nearly-collinear acentric magnetic order with broken inversion symmetry was proposed to be responsible for the ferroelectricity [17]. In this mechanism, the ferroelectricity results from lattice relaxation through exchange striction associated with the symmetric superexchange coupling. However, a model where ferroelectricity is induced by a spiral spin configuration along the \( Mn^{4+} \) spin chain has been also discussed for \( RMn_{2}O_{5} \) [18,19]. Thus, the true origin of multiferroicity in \( RMn_{2}O_{5} \) is currently uncertain. Another promising example is the so-called E-type magnetic order. This collinear order, combined with alternating oxygen cage rotations, has been suggested as the origin of ferroelectricity in the orthorhombic \( HoMnO_{3} \) [20]. Polycrystalline \( HoMnO_{3} \) has been experimentally studied to test this theoretical prediction [21], but the induced polarization turned out to be too small to support the proposed theory. Identification of nonspiral magnetism-driven ferroelectrics remains, therefore, an important task. Among those, systems driven by the potentially large symmetric superexchange are, clearly, of special interest.
A simple and conceptually important model in which a collinear spin order induces ferroelectricity through symmetric superexchange can be constructed using an Ising spin chain with competing nearest-neighbor ferromagnetic \( (J_{F}) \) and next-nearest-neighbor antiferromagnetic \( (J_{\mathrm{AF}}) \) interactions [2]. For \( |J_{\mathrm{AF}}/J_{F}| > 1/2 \) , the ground state mag-
(a)

(b)
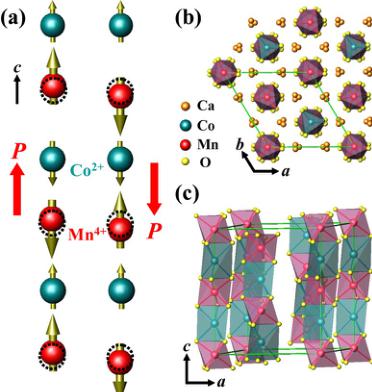
FIG. 1 (color online). (a) Ising chains with the up-up-down-down spin order and alternating ionic order, in which electric polarization is induced through symmetric exchange striction. The two possible magnetic configurations leading to the opposite polarizations are shown. The atomic positions in the undistorted chains are shown with dashed circles. (b,c) The crystal structure of the \( Ca_{3}CoMnO_{6} \) chain magnet. The green boxes represent the crystallographic unit cell.
netic order is of the up-up-down-down ( \( \uparrow\uparrow\downarrow\downarrow \) ) type [22]. If the charges of magnetic ions alternate along the chain, this magnetic ordering breaks inversion symmetry on magnetic sites and can induce electric polarization via exchange striction. This mechanism is illustrated in Fig. 1(a). The exchange striction associated with symmetric superexchange shortens the bonds between the parallel spins, while stretching those connecting the antiparallel spins. As a result, electric polarization, P, is induced in the direction of the chain. As shown in Fig. 1(a), there are two ways to combine the \( \uparrow\downarrow\downarrow \) order with the ionic charge order, giving rise to the opposite electrical polarization vectors. Experimental realization of such a simple model system would be of a significant importance in the field. Herein, we report discovery of a chain magnet in which this model is remarkably realized.
To find the appropriate experimental system, we have identified \( Ca_{3}Co_{2}O_{6} \) -derived compounds as possible candidates because \( Ca_{3}Co_{2}O_{6} \) is an Ising chain magnet where about a half of Co ions can be replaced by Mn ions [23,24]. The structure of \( Ca_{3}Co_{2-x}Mn_{x}O_{6} \) , as depicted in Figs. 1(b) and 1(c), contains spin chains consisting of magnetic ions with alternating oxygen cages of face-shared trigonal prisms and octahedra along the c axis. The spin chains are separated by Ca ions and form a triangular lattice in the ab plane. Mn ions have a strong tendency to avoid the trigonal prismatic oxygen coordination. Thus, for example, for x = 1, all the Co ions are located in the trigonal prismatic sites, and all the Mn ions occupy the octahedral sites [24]. We prepared single-phase polycrystalline \( Ca_{3}Co_{2-x}Mn_{x}O_{6} with x \) up to 1 by using standard solid state reaction method [23]. Since single crystals are necessary for conclusive measurements of the ferroelectric properties, we have attempted to grow single crystals of \( Ca_{3}(Co, Mn)_{2}O_{6} \) by utilizing the known technique (KCl- \( K_{2}CO_{3} \) flux method) for the growth of \( Ca_{3}Co_{2}O_{6} \) crystals [25]. With increasing Mn concentration, the crystal growth was found to be increasingly more difficult. However, single crystals with maximum x approaching 0.96 (as determined by comparing x-ray diffraction patterns of crushed crystals with those of polycrystalline samples) were grown successfully.
DC magnetic susceptibility ( \( \chi = M/H \) ) was measured in a SQUID magnetometer, specific heat (C) and AC magnetic susceptibility ( \( \chi' \) and \( \chi'' \) ) measurements were carried out in the Quantum Design PPMS, and dielectric constant ( \( \epsilon \) ) was measured using an LCR meter at f = 44 kHz. The temperature (T) dependence of electric polarization (P) was obtained by the integration of pyroelectric current with the T variation of 2 K/min after poling a specimen from 40 to 2 K in a static electric field of \( E \approx 6.7 \) kV/cm. For \( \epsilon \) and P measurements, a c-axis needle-shaped crystal was cut and polished with the ab plane cross section of \( \sim 0.64 \) mm \( ^{2} \) and thickness of \( \sim 0.15 \) mm, and then annealed at 650 °C for 5 hours to remove strain built up during polishing. Neutron powder diffraction measurements were performed on polycrystalline \( Ca_{3}Co_{2-x}Mn_{x}O_{5} \) (x = 0.95) at the BT-1 beam line at NIST Center for Neutron Research. Monochromatic neutrons ( \( \lambda = 2.079 \) Å) were produced by a Ge(311) monochromator, and the data were collected for T = 1.4, 8, and 20 K.
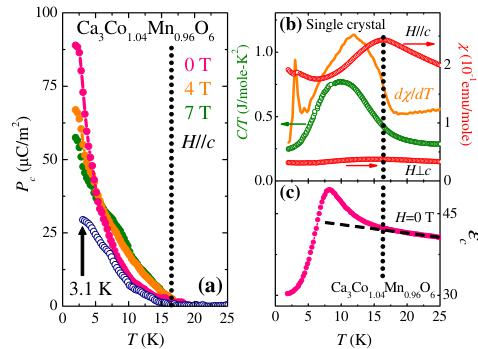
Search for the ferroelectricity was performed in the crystal with the highest Mn concentration, x = 0.96, and ferroelectric polarization along the chain direction was indeed found. Figure 2(a) shows that the polarization smoothly emerges below the transition temperature of 16.5 K, increases rapidly below \( \sim \) 10 K, and reaches \( \sim \) 90 \( \mu \) C/m \( ^{2} \) at 2 K. The appearance of the polarization at 16.5 K coincides with the onset of the magnetic order, which is signified [24] by a broad peak in the magnetic susceptibility, \( \chi(T) \) , shown in Fig. 2(b). Specific heat also exhibits an upturn at this temperature. The temperature dependence of the dielectric constant along the c axis, \( \epsilon_{c}(T) \) , starts deviating from its high-temperature behavior at the onset temperature of the polarization without showing any sharp anomaly, see Fig. 2(c). Instead, \( \epsilon_{c}(T) \) reveals a broad peak at \( \sim \) 8 K followed by a sharp decrease at lower temperatures. The electric polarization decreases in a magnetic field applied along the c axis. There is an additional magnetic anomaly at \( T \approx 3 \) K, which can be seen in the behavior of the derivative \( d\chi(T)/dT \) shown in Fig. 2(b); it is discussed in more detail below. The Ising

FIG. 2 (color online). (a) Electric polarization of single crystal \( Ca_{3}Co_{1-x}Mn_{x}O_{6} \) (x = 0.96) along the chain direction ( \( P \parallel c \) ), taken upon warming. The samples were poled upon cooling from 40 K to 2 K (filled circles), and to 3.1 K (open circles) before the measurement. The data for the 2 K poled sample were collected in various applied magnetic fields, as shown. (b) Temperature dependence of magnetic susceptibility, \( \chi(T) = M/H \) , measured in an applied magnetic field H = 0.2 T along and perpendicular to the chain direction. The temperature derivative \( d\chi/dT \) , and zero-field heat capacity (C/T) are also shown. (c) The c-axis dielectric constant, \( \epsilon_{c} \) . Dashed line shows the high-temperature behavior of \( \epsilon_{c} \) .
character of this compound is clearly reflected in the large anisotropy of \( \chi(T) \) .
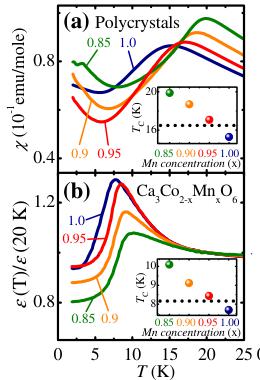
Studies of \( Ca_{3}Co_{2-x}Mn_{x}O_{6} \) polycrystalline samples suggest that a similar behavior is expected in a wide range of x near x = 1. Figures 3(a) and 3(b) display \( \chi(T) \) and \( \epsilon(T)/\epsilon(T = 20\ \mathrm{K}) \) for various Mn concentrations, x = 0.85, 0.9, 0.95, and 1.0. These data exhibit the same features as those of the corresponding quantities of the x = 0.96 single crystal, strongly suggesting that the observed properties of the single crystal are representative for large Mn concentrations. The temperatures of the maxima in \( \chi(T) \) and \( \epsilon(T) \) , shown in the insets in Figs. 3(a) and 3(b), decrease with increasing x, indicating the corresponding decrease in the magnetic transition temperature. The corresponding temperatures in the single crystal (dotted lines in the insets) agree well with the Mn concentration x = 0.96, corroborating our x-ray results.
The structure of \( Ca_{3}Co_{2-x}Mn_{x}O_{6}\ (x=0.95) \) was determined using neutron powder diffraction. The possible magnetic structures (including those with ab-plane components) were constructed using the magnetic symmetry analysis, and the diffraction data were refined using the FULLPROF program package [26]. The spins point along the c axis, as indicated by the absence of (003) magnetic peak, and the structure is of the \( \uparrow\uparrow\downarrow \) type. The accuracy of the


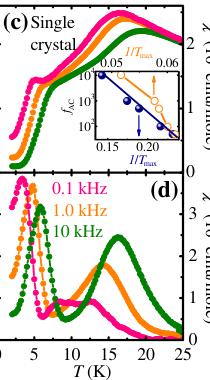
FIG. 3 (color online). (a) \( \chi(T) \) of polycrystalline \( Ca_{3}Co_{1-x}Mn_{x}O_{6} \) for H = 0.2 T. (b) \( \epsilon(T) \) of polycrystalline \( Ca_{3}Co_{1-x}MnxO_{6} \) for H = 0, normalized at T = 20 K. The insets in (a) and (b) show peak positions of \( \chi(T) \) and \( \epsilon(T) \) , respectively, for different Mn concentrations. The dashed lines indicate the corresponding peak positions in the x = 0.96 single crystal. (c,d) Real and imaginary parts of the AC susceptibility, \( \chi'(T) \) , and \( \chi''(T) \) , of the x = 0.96 single crystal. The AC magnetic field is 5 Oe, and the frequencies are 0.1, 1 and 10 kHz, as shown. The inset in Fig. 3(c) shows \( \log[f] \) vs inverse temperature for the peaklike features of \( \chi' \) . The low-temperature feature is shown with filled circles, and the high-temperature feature with open circles.
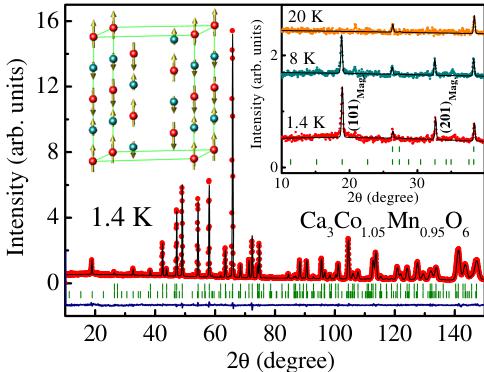
final refinement result was independently estimated by the Simulated Annealing process, which shows that the deviation of the spins from the c axis cannot exceed \( 3^{\circ} \) . The refinement results for T = 1.4 K are shown in Fig. 4: good agreement factors, \( \chi^{2} = 1.44 \) , \( R_{B} = 2.4\% \) , \( R_{f} = 2.7\% \) , and \( R_{mag} = 9.8\% \) , are obtained. The obtained three-dimensional magnetic structure is shown in the inset in Fig. 4. In agreement with [24], the Mn ions occupy the octahedral sites. The ordered magnetic moments of Co and Mn ions are \( 0.66(3)\mu_{B} \) and \( 1.93(3)\mu_{B} \) , respectively, and the estimated valences of the cations from Bond-Valence calculation are 1.814(2) for Co and 3.997(3) for Mn. Thus, the magnetic chains consist of alternating low-spin \( Co^{2+} \) and high-spin \( Mn^{4+} \) ions. Combined with the \( \uparrow\downarrow\downarrow \) spin order, this makes \( \mathrm{Ca}_{3}(\mathrm{Co},\mathrm{Mn})_{2}\mathrm{O}_{6} \) an experimental realization of the magnetoelectric model system described above. In the unit cell shown in Fig. 4, all the chains possess the same polarization direction according to this model. We note that the (101) magnetic peak appears to be slightly broadened (see the inset in Fig. 4). This indicates that the magnetic order is not truly long-ranged. Measurements on yet unavailable large single crystals are needed to determine the magnetic correlation length with any adequate precision. On warming to T = 8 K, no qualitative changes are observed in the magnetic structure, and no magnetic order is present at T = 20 K.
While the magnetic origin of the ferroelectricity and its description in the framework of the \( \uparrow\uparrow\downarrow \) chain with alternating ions are established by the above data, the tempera-

FIG. 4 (color online). Observed (symbols) and calculated (line) powder neutron diffraction patterns for polycrystalline \( Ca_{3}Co_{1-x}Mn_{x}O_{5} \) (x = 0.95) for T = 1.4 K. The first row of bars below the diffraction pattern indicates the positions of the nuclear Bragg peaks, and the second row depicts the locations of the magnetic Bragg peaks. The blue line shows the difference between the observed and calculated diffraction patterns. The insets show the low-angle patterns for T = 1.4 K, 8 and 20 K, and the refined spin structure.
ture dependences of both the electric and the magnetic properties are rather complicated. To gain insight into this complexity, we have measured temperature-dependent AC magnetic susceptibility in the x = 0.96 single crystal. Figures 3(c) and 3(d) reveal that both of the magnetic temperature anomalies (peaks) exhibit strong frequency dependence, shifting to higher temperature with increasing frequency. This behavior is indicative of magnetic freezing, which may range from simple superparamagnetism to complex spin-glass transition [27]. As shown in the inset in Fig. 3(c), the lower-temperature peak \( T_{\mathrm{max}} \) of \( \chi'(T) \) exhibits the Arrhenius behavior, \( f = f_{0} \exp[-E_{a}/k_{B}T_{\mathrm{max}}] \) , with physically reasonable values of the activation energy, \( E_{a}/k_{B} \approx 60 \) K, and \( f_{0} \approx 60 \) MHz [27]. This behavior with \( E_{a}/T_{\mathrm{max}} \approx 20 \) , together with the numerical value of the slope parameter \( \Delta T_{\mathrm{max}}/T_{\mathrm{max}} \ln[f] \) of 0.21, signals superparamagnetic blocking (freezing of poorly-correlated magnetic clusters) at low temperatures [27]. The behavior of the higher-temperature anomaly, associated with the magnetic ordering transition, is more complicated. For example, \( T_{\mathrm{max}} (> 16 \) K) of \( \chi'(T) \) does not exhibit the simple Arrhenius behavior [see the inset of Fig. 3(c)]. The data of Fig. 3, combined with the neutron data, show that only finite-size magnetic domains develop at the magnetic transition and that these domains exhibit an additional freezing at a lower temperature. This behavior deserves further investigation since it is likely related to the one dimensionality of the magnetic chains and the geometrical frustration in the ab-plane triangular lattice.
While complicated, the observed magnetic behavior provides a consistent explanation of the unconventional temperature dependence of the electric polarization in Fig. 2(a). Magnetic disorder and freezing naturally lead to the corresponding phenomena for the ferroelectric properties in our system. Local clusters exhibiting the two different variants of the spin order shown in Fig. 1(a) give rise to the opposite electrical polarization vectors. Thus, on warming from 2 K, the frozen poled magnetoelectric domains should quickly become dynamic, leading to decreased macroscopic polarization. This is consistent with the rapid reduction of the polarization with increasing temperature. An additional confirmation of this scenario is obtained by observation of thermal history effects, which are characteristic to frozen states. As shown in Fig. 2(a), the polarization of the system poled on cooling down to T = 2 K (filled circles) significantly exceeds the polarization of the sample poled at T = 3.1 K (open circles), when the polarization is subsequently measured on warming in zero field. This is a typical behavior of a frozen system undergoing slow relaxation processes. This scenario is also consistent with the absence of any sharp anomaly of \( \epsilon_{e}(T) \) at the magnetic transition. We conclude, therefore, that in \( \mathrm{Ca}_{3}(\mathrm{Co}, \mathrm{Mn})_{2}\mathrm{O}_{6} \) , thermal fluctuations of the magnetoelectric clusters tend to suppress the macroscopic polarization, leading to the complex temperature dependences and thermal history effects observed in the experiments.
In summary, we report discovery of an unambiguous example of magnetism-driven ferroelectricity with a collinear magnetic order in the Ising chain magnet \( Ca_{3}Co_{2-x}Mn_{x}O_{6} \) ( \( x \approx 0.96 \) ). The ferroelectricity originates from the simultaneous presence of the alternating order of Co and Mn ions and the spin order with the \( \uparrow\downarrow\downarrow \) configuration. This provides the first experimental realization of theoretically predicted ferroelectricity in a frustrated Ising chain with an ionic order. Unlike in well-known spiral magnetoelectrics, symmetric exchange striction is expected to drive the ferroelectricity in this system.
Work at Rutgers was supported by the DOE under Grant No. DE-FG02-07ER46382. S. L. was partially supported by the Korea Science and Engineering Foundation through the Center for Strongly Correlated Materials Research at Seoul National University.
[1] D. I. Khomskii, J. Magn. Magn. Mater. 306, 1 (2006).
[2] S.-W. Cheong and M. Mostovoy, Nat. Mater. 6, 13 (2007).
[3] N. Hur et al., Nature (London) 429, 392 (2004).
[4] T. Goto et al., Phys. Rev. Lett. 92, 257201 (2004).
[5] N. Hur et al., Phys. Rev. Lett. 93, 107207 (2004).
[6] T. Kimura et al., Nature (London) 426, 55 (2003).
[7] G. Lawes et al., Phys. Rev. Lett. 95, 087205 (2005).
[8] T. Kimura et al., Phys. Rev. B 73, 220401(R) (2006).
[9] T. Kimura et al., Phys. Rev. Lett. 94, 137201 (2005).
[10] Y. Yamasaki et al., Phys. Rev. Lett. 96, 207204 (2006).
[11] K. Taniguchi et al., Phys. Rev. Lett. 97, 097203 (2006).
[12] S. Park et al., Phys. Rev. Lett. 98, 057601 (2007).
[13] H. Katsura et al., Phys. Rev. Lett. 95, 057205 (2005).
[14] M. Mostovoy, Phys. Rev. Lett. 96, 067601 (2006).
[15] I. A. Sergienko and E. Dagotto, Phys. Rev. B 73, 094434 (2006).
[16] A. B. Harris et al., Phys. Rev. B 73, 184433 (2006).
[17] L. C. Chapon et al., Phys. Rev. Lett. 96, 097601 (2006).
[18] Y. Noda et al., Physica B (Amsterdam) 385–386, 119 (2006).
[19] H. Kimura et al., J. Phys. Soc. Jpn. 75, 113701 (2006).
[20] I. A. Sergienko et al., Phys. Rev. Lett. 97, 227204 (2006).
[21] B. Lorentz et al., Phys. Rev. B 76, 104405 (2007).
[22] M. E. Fisher and W. Selke, Phys. Rev. Lett. 44, 1502 (1980).
[23] S. Rayaprol et al., Solid State Commun. 128, 79 (2003).
[24] V. G. Zubkov et al., Solid State Commun. 160, 293 (2001).
[25] A. Maignan et al., Eur. Phys. J. B 15, 657 (2000).
[26] J. Rodr guez-Carvajal, Physica B (Amsterdam) 192, 55 (1993).
[27] J. A. Mydosh, Spin Glasses. An Experimental Introduction. (Taylor & Francis, London, 1993).