| Transition Temperature | 19 K |
|---|---|
| Experiment Temperature | 1.7 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | Pnnm (#58) |
| Magnetic Space Group | Pnn'm' (#58.398) |
| Magnetic Point Group | m'm'm (8.4.27) |
| Lattice Parameters | 6.0362(3) 7.1195(2) 7.4455(2) 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1103/physrevb.67.144406 |
| Reference | A. Lappas, A.S. Wills, M.A. Green, K. Prassides and M. Kurmoo, Physical Review B (2003) 67. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Fe1 | Mn | -3.99 | 1.01 | 0.0 | 4.12 |
Magnetic ordering in the rutile molecular magnets \( M^{\mathrm{II}}[\mathrm{N}(\mathrm{CN})_{2}]_{2} \)
\( (M=\mathrm{Ni}, \mathrm{Co}, \mathrm{Fe}, \mathrm{Mn}, \mathrm{Ni}_{0.5}\mathrm{Co}_{0.5}, \mathrm{and} \mathrm{Ni}_{0.5}\mathrm{Fe}_{0.5}) \)
Alexandros Lappas, \( ^{1,*} \) Andrew S. Wills, \( ^{2,3} \) Mark A. Green, \( ^{2,3} \) Kosmas Prassides, \( ^{4} \) and Mohamedally Kurmoo \( ^{5} \)
\( ^{1} \) Institute of Electronic Structure and Laser, Foundation for Research and Technology—Hellas,
P.O. Box 1527, 711 10 Heraklion Crete, Greece
\( ^{2} \) Department of Chemistry, Christopher Ingold Laboratories, University College London, 20 Gordon Street, London, WC1H 0AJ, United Kingdom
\( ^{3} \) The Davy-Faraday Research Laboratory, The Royal Institution of Great Britain, 21 Albermarle Street, London, W1S 4BS, United Kingdom
\( ^{4} \) School of Chemistry, Physics and Environmental Science, University of Sussex, Brighton BN1 9QJ, United Kingdom
\( ^{5} \) Institut de Physique et Chimie des Matériaux de Strasbourg, CNRS-UMR 7504, 23 rue de Loess, F-67037 Strasbourg Cedex, France
(Received 25 September 2002; revised manuscript received 2 December 2002; published 7 April 2003)
Rietveld refinement of powder neutron diffraction data, combined with group theory considerations, is used to determine the magnetic structures of the binary metal dicyanamide, \( M^{\mathrm{II}}[\mathrm{N}(\mathrm{CN})_{2}]_{1} \) where M=Ni, Co, Fe, Mn, \( Ni_{0.5}Co_{0.5} \) , and \( Ni_{0.5}Fe_{0.5} \) . Compounds with M=Mn or Fe show a canted antiferromagnetic arrangement of spin oriented in the ab crystallographic plane, with antiparallel components of the two sublattices along the a axis and parallel along the b axis. Symmetry considerations forbid an additional moment, whether compensated or not, to be present along the c axis. The compounds with fewer unpaired electrons (Co and Ni) are ferromagnets, with all moments oriented along the c axis. The mixed composition of \( Ni_{0.5}Co_{0.5} \) displays the same collinear ferromagnetic structure as its parent compounds. However, the composition with \( M=Ni_{0.5}Fe_{0.5} \) , whose parent compounds show different magnetic behavior, does not exhibit long-range magnetic ordering down to 1.7 K. Magnetostriction was observed for the ferromagnets for which we investigated the variable temperature powder neutron diffraction. The cobalt-rich compounds show more pronounced effects, consistent with their increasing magnetocrystalline anisotropy.
DOI: 10.1103/PhysRevB.67.144406
I. INTRODUCTION
Over the past 20 years magnetic ground states that are more commonly associated with elements or alloys have been discovered in a variety of extended lattices involving molecule-based solids. \( ^{1} \) The observation of properties such as ferromagnetism and superconductivity in these systems has created a lot of interest because their high degree of chemical flexibility allows direct structural control of their electronic properties. \( ^{1,2} \) The range of accessible organic connectors enables the tailoring of properties for specific applications such as magnetic and/or photonic devices for information storage media. The molecular magnetic systems are often composed of a number of different chemical constituents, namely a central transition-metal ion, its coordinating ligand, charge-balancing ions, and solvent molecules. The coordinating ligand plays an important role in the connectivity of the magnetic metal ions, as well as playing a direct active role in the interaction between the localized magnetic moments or conduction electrons. The versatility of the structure and bonding in these systems enables one to synthesize materials exhibiting dual properties, such as superconductivity and magnetism, or coupling of properties, e.g., optical sensitivity and magnetism.
Magnets based on the Prussian blue family \( ^{3} \) have been extensively studied as the linear metal-cyanide-metal connectivity gives rise to three-dimensional (3D) structures with high Curie temperatures, for example, \( T_{C}=315 \) K in \( V[Cr(CN)_{6}]_{0.86}\cdot2.8H_{2}O \) . \( ^{4} \) While work has concentrated on
PACS number(s): 75.25.+z, 61.12.-q, 75.10.-b
varying the oxidation and spin states of the metal centers, it has also been shown that an effective replacement of the bridging cyanide ligand, \( CN^{-} \) , may be afforded by the dicyanamide anion, \( \mathrm{N}(\mathrm{CN})_{2}^{-} \) . The new family of isostructural compounds with the general formula \( M^{\mathrm{II}}[\mathrm{N}(\mathrm{CN})_{2}]_{3} \) (M is a transition-metal ion) exhibits particularly interesting magnetic properties. \( ^{5-12} \) They crystallize in a distorted rutile-like 3D structure in which the connectivity between the metals is through \( (\mathrm{N}\equiv\mathrm{C}-\mathrm{N}-\mathrm{C}\equiv\mathrm{N})^{-} \) and \( N-C-N \) linkages. The structural features of importance for magnetism are the near-orthogonal arrangement of the octahedral \( MN_{6} \) units connected through three atoms and the presence of the \( \pi \) electrons. \( ^{5,6} \) Bulk magnetic susceptibility \( ^{5-11} \) and muon-spin relaxation \( ^{12} \) ( \( \mu^{+}SR \) ) measurements of the \( M^{\mathrm{II}}[\mathrm{N}(\mathrm{CN})_{2}]_{5} \) series have revealed a plethora of electronic ground states as a function of transition-metal ion, including paramagnetism, ferromagnetism, and canted antiferromagnetism. Application of pressure has different effects on each of these compounds. \( ^{13} \) An important aspect in this area of research is the determination of the key structural or electronic characteristics that control the resulting magnetic ground states.
In this paper, we employ high-resolution and high-intensity neutron powder diffraction measurements together with the implementation of symmetry-allowed models, to determine the magnetic structure of \( M[\mathrm{N}(\mathrm{CN})_{2}]_{2} \) . The properties of the mixed metal systems, \( Ni_{0.5}Co_{0.5}[N(CN)_{2}]_{2} \) and \( Ni_{0.5}Fe_{0.5}[N(CN)_{2}]_{2} \) , are also explored; the former shows ferromagnetism, analogous to the parent compositions,
whereas the latter shows no evidence of long-range magnetic ordering (LRO) down to 1.7 K. These mixed metal compositions show unambiguously that the bond angles and distances, which greatly influence the superexchange interactions, are not the only factors that control the resultant magnetic ground states.
II. EXPERIMENTAL DETAILS
The synthesis procedure has been adequately described elsewhere. \( ^{5-11,14} \) However, it is important to note that samples containing iron require the use of degassed distilled water and manipulation under an inert-gas atmosphere. Powder x-ray diffraction on Siemens D5000 (Cu Kα) and D500 (Co Kα) diffractometers confirmed phase purity and allowed indexing of the observed reflections in the space group Pnnm. Bulk dc magnetic susceptibilities were measured using superconducting quantum-interference device (SQUID) magnetometers (Quantum Design, MPMS-XL and MPMS-7). Powder neutron diffraction was performed with a combination of the medium-resolution, high-intensity D20 ( \( \lambda = 2.418 \, \AA \) ) and the high-resolution D2b ( \( \lambda = 1.5938 \, \AA \) ) instruments at the Institut Laue Langevin (ILL), France. Diffraction patterns were recorded in the \( 2\theta \) range \( 5^{\circ} - 150^{\circ} \) (scan step \( 0.05^{\circ} \) ) for D2b and \( 0^{\circ} - 130^{\circ} \) (scan step \( 0.1^{\circ} \) ) for D20. Measurements were performed every 60 s with the D20 diffractometer on heating from 1.7 to 30 K (at 10 K/h) and from 30 to 275 K (at 30 K/h). Measurements on D2b were performed over a 9-h time interval at each selected temperature. Polycrystalline samples were placed in 9-mm-diameter cylindrical vanadium cans inside a continuous-flow ILL “orange” helium cryostat. Analysis of the neutron data was carried out with the Rietveld method \( ^{15} \) using the General Structure Analysis System (GSAS) \( ^{16} \) suite of programs. Sequential refinements were performed using a script file, which allowed GSAS to run in cyclic mode using the final refined parameters from each pattern as the starting model for the next. Magnetic structure factors were calculated with the GENLES routine of this suite with symmetry-allowed moment orientations controlled outside GSAS using the reverse Monte Carlo front-end SARAh-Refine program. \( ^{17} \) Group theory calculations were carried out using the program SARAh-Representational Analysis. \( ^{17,18} \) During the refinements of the magnetic structures, the parameters of the nuclear structure were fixed at the values refined at 25 K. Comparison of refined parameters of the atomic positions for the antiferromagnets at 2 and 25 K showed that this assumption introduced no significant error.
III. MAGNETIZATION MEASUREMENTS
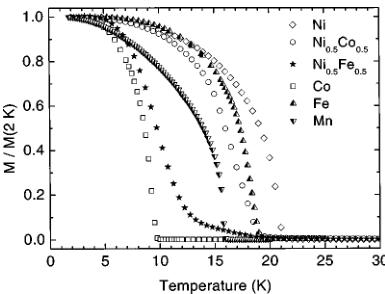
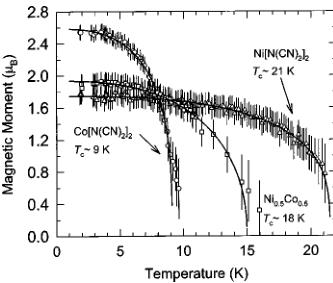
The previously reported magnetization measurements of \( M[\mathrm{N}(\mathrm{CN})_{2}]_{2} \) (M=Ni, Co, Fe, and Mn) have shown the compounds with M=Co and Ni to be ferromagnets, whereas those with M=Mn and Fe to be canted antiferromagnets. \( ^{6,8,10} \) The magnetization measurements of M=Fe, \( Ni_{0.5}Co_{0.5} \) , and \( Ni_{0.5}Fe_{0.5} \) are shown in Fig. 1, together with those of previously reported systems for comparison. \( \mathrm{Fe}[\mathrm{N}(\mathrm{CN})_{2}]_{2} \) shows similar behavior to the Mn ana-

FIG. 1. Temperature dependence of the normalized dc magnetization, \( M(T)/M(2\mathrm{K}) \) of \( M^{\mathrm{II}}[\mathrm{N}(\mathrm{CN})_{2}]_{2} \) (M=Ni; Co; Fe; Mn; \( Ni_{0.5}Co_{0.5} \) , and \( \mathrm{Ni}_{0.5}\mathrm{Fe}_{0.5} \) ) measured on cooling in a small applied magnetic field (H<10 Oe).
log, displaying spontaneous magnetization at 19 K, a linear dependence of the magnetization on the applied field, and a negative Weiss temperature when the high-temperature data are fitted with the Curie-Weiss law. \( (\mathrm{Ni}_{0.5}\mathrm{Co}_{0.5})[\mathrm{N}(\mathrm{CN})_{2}]_{2} \) shows a large, spontaneous increase of the magnetization around 18 K, indicating the onset of ferromagnetism. This is expected, as it is composed of two ions whose parent compositions, \( \mathrm{Co}[\mathrm{N}(\mathrm{CN})_{2}]_{2} \) and \( \mathrm{Ni}[\mathrm{N}(\mathrm{CN})_{2}]_{2} \) , both show bulk ferromagnetism.
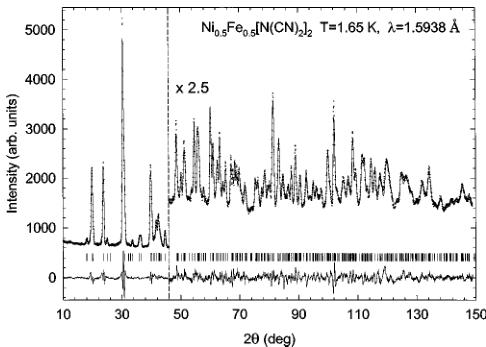
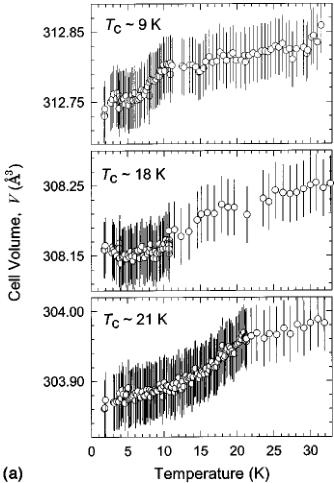
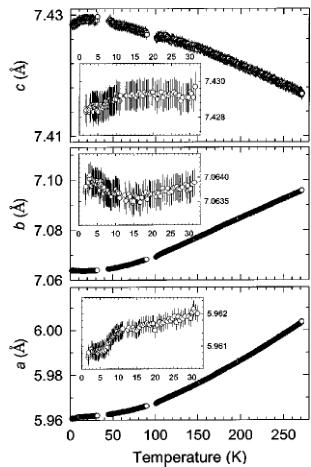
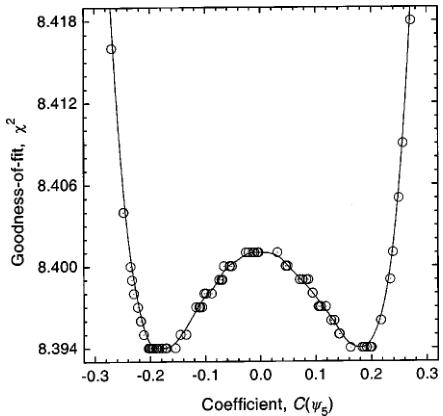
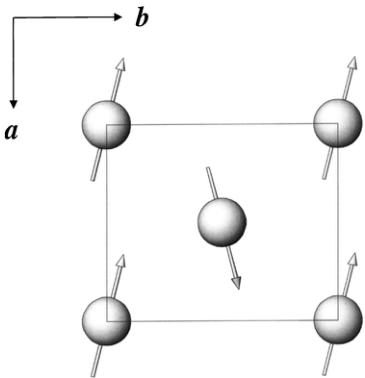
To further investigate the relative strength of the antiferromagnetic and ferromagnetic competing interactions, we synthesized the composition \( \left(\mathrm{Ni}_{0.5}\mathrm{Fe}_{0.5}\right)\left[\mathrm{N}(\mathrm{CN})_{2}\right]_{2} \) , whose parent compounds, \( \mathrm{Ni}\left[\mathrm{N}(\mathrm{CN})_{2}\right]_{2} \) and \( \mathrm{Fe}\left[\mathrm{N}(\mathrm{CN})_{2}\right]_{2} \) , are ferromagnetic and canted antiferromagnetic, respectively. The dc susceptibility of \( \left(\mathrm{Ni}_{0.5}\mathrm{Fe}_{0.6}\right)\left[\mathrm{N}(\mathrm{CN})_{2}\right]_{2} $ , shown in Fig. 1, displays a slower onset to a broader transition, over a range of 10 K, which finally reaches a maximum magnetization only below \( \sim5 \) K. While the Curie temperature of the \( \left(\mathrm{Ni}_{0.5}\mathrm{Co}_{0.5}\right)\left[\mathrm{N}(\mathrm{CN})_{2}\right)_{2} \) ferromagnet falls between those of the parent compounds, the transition temperature of \( \left(\mathrm{Ni}_{0.5}\mathrm{Fe}_{0,5}\right)\left[\mathrm{N}(\mathrm{CN})_{2}\right]_{2}\right. \) lies lower than those of the respective parent compounds. Further isothermal magnetization measurements, not shown in Fig. 1, indicate that while the 20 K data are typical of a paramagnet, below 15 K a small hysteresis is observed, reaching 1300 Oe at 2 K. Fits to the Curie-Weiss law give a Curie constant on the order of 1.70(6) cm \( ^{3} \) K/mol and a temperature-dependent Weiss constant of \( +13\pm7 \) K, depending on the temperature range of the fit. A summary of the magnetic data, including the Curie and Weiss constants from fitting to the Curie-Weiss law over the temperature range \( T_{C} Rietveld refinement of the data, taken on the D20 instrument, was carried out by employing (a) a two-phase model that accounts for both the nuclear and magnetic structures below \( T_{C} \) and (b) a single-phase model, describing only the nuclear structure for temperatures above \( T_{C} \) . The atomic position parameters were kept constant to the values deter- TABLE I. Bulk magnetic parameters determined from fits of the dc magnetization to the Curie-Weiss law, \(\chi=C/(T-\theta)\), over the temperature range \(T_{C} mined from long counting scans at 1.7(1) K using the D2b diffractometer. During these sequential refinements and in order to control the stability of the least-squares procedure, only the following parameters were refined in each cycle: scale factor, background (cosine Fourier series of six terms), lattice size, overall isotropic temperature factors, and magnetic moment (below \( T_{C} \) ). Neither the D20 measurements nor complementary measurements on the higher-resolution D2b diffractometer at 1.7 and 25 K showed deviation from the previously reported orthorhombic Pnnm space group. \( ^{5-11} \) Therefore, this work will concentrate on the temperature variation of the structural parameters as well as the additional magnetic scattering observed at low temperature for all but the \( \mathrm{Ni}_{0.5}\mathrm{Fe}_{0.5}[\mathrm{N}(\mathrm{CN})_{2}]_{2} \) composition. The Rietveld refinement of the high-resolution powder neutron diffraction data of \( \mathrm{Ni}_{0.5}\mathrm{Fe}_{0.5}N(\mathrm{CN})_{2}]_{2} \) collected at 1.65 K on diffractometer D2b is shown in Fig. 2 as an indication of the typical quality of the experimental data and fits. The relevant occupancy of the metal sites was refined as \( n_{\mathrm{Fe}} = 0.61(17) \) and \( n_{\mathrm{Ni}} = 0.39(17) \) . The resulting structural parameters for the compounds, \( \mathrm{Fe}^{II}[\mathrm{N}(\mathrm{CN})_{2}]_{2} \) , \( \mathrm{Ni}_{0.5}\mathrm{Fe}_{0.5} \mathrm{N}(\mathrm{CN})_{2}]_{2} \) , and \( \mathrm{Ni}_{0.5}\mathrm{Co}_{0.5}[\mathrm{N}(\mathrm{CN})_{2}]_{2} \) , not reported before, are compiled in Table II, together with those for \( \mathrm{Ni}^{II}[\mathrm{N}(\mathrm{CN})_{2}]_{2} \) , $ \mathrm{Co}^{II}[\mathrm{N}(\mathrm{CN})_{2}]_{2} �MATH90� \mathrm{Mn}^{II}[\mathrm{N}(\mathrm{CN})_{2}]_{2} $ . Thermal expansion was investigated in three selected members of the \( M[N(CN)_{2}]_{2} \) series. Figure 3(a) shows the temperature dependence of the unit-cell volume of \( M[N(CN)_{2}]_{2} \) (M=Co, \( Ni_{0.5}Co_{0.5} \) , and Ni) and Fig. 3(b) the variation of the unit-cell parameters of \( \mathrm{Co}[N(CN)_{2}]_{2} \) with FIG. 2. Observed (points), calculated (line), and difference neutron powder diffraction profiles for the nuclear structure of \( Ni_{0.5}Fe_{0.5}[N(CN)_{2}]_{2} \) . The vertical lines mark the position of the Bragg reflections for the Pnnm space group. temperature. Expanded views, Fig. 3(a) and the inset to Fig. 3(b), show the subtle changes around the \( T_{C} \) . The refinements lead to the conclusion that above \( T_{C} \) , the monotonic increase in the average unit-cell volume with increasing temperature, observed in the series, results from a monotonic expansion along the a and b axes, coupled with a contraction along the c axis. A summary of the thermal expansion coefficients, \( \alpha_{I}=(l_{T_{2}}-l_{T_{1}})/[l_{T_{1}}(T_{2}-T_{1})] \) , where l is the length in consideration, T is the sample temperature, and \( T_{2}>T_{1} \) is given in Table III. Close inspection of the evolution of the lattice parameters around the magnetic ordering temperature reveals magnetostriction effects. These correlate with the spontaneous changes in the magnetic properties and correspond to the force exerted on the lattice at the magnetic transition. They can be characterized by the magnetostriction constant, \( \lambda_{s}=\Delta L/L_{0} \) , where \( \Delta L \) is the difference between the lengths in the magnetized \( L_{m} \) and the nonmagnetized \( L_{0} \) state. In the present case, the zero-field linear striction in the \( \mathrm{Co}[\mathrm{N}(\mathrm{CN})_{2}]_{2} \) ferromagnet is more noticeable for the a axis. As the temperature decreases from \( T_{C} \) to 6.5 K, the a axis contracts by 0.0005(2) Å. The “step-like” changes in the same temperature region are \( \Delta L_{a}/L_{a}\approx-8\times10^{-5} \) , \( \Delta L_{b}/L_{b}\approx3\times10^{-5} \) , and \( \Delta L_{c}/L_{c}\approx-4\times10^{-5} \) , in good comparison with the reported value of \( \lambda_{s}=5\times10^{-5} \) for the magnetostriction effect in polycrystalline specimens of ferromagnetic cobalt metal. \( ^{19} \) We note that despite the opposite sign of the striction along the b axis, the \( \mathrm{Co}[\mathrm{N}(\mathrm{CN})_{2}]_{1} \) molecular ferromagnet displays an overall anisotropic magnetostriction, which results in a volume shrinkage, \( \Delta V/V=(V_{m}-V_{0})/V_{0}\cong-9\times10^{-5} \) (where \( V_{m} \) and \( V_{0} \) denote the crystal volume in the magnetic and nonmagnetic states, respectively). As it may be expected from its higher moment and larger anisotropy, the effect is most pronounced in the cobalt compound, which shows a sizable jump in all three lattice parameters at \( T_{C} \) . The magnitude of the distortion is gradually suppressed as we move towards the larger ions, that is to say, it is weakest in the nickel-rich composition where only a change in the slope, from positive to negative, in the temperature evolution of the c lattice constant marks the magnetostriction effects when the material is warmed up. Table III details the effective magnetostriction constants associated with the three crystallographic axes. For their calculation we took into account the lattice constant changes between \( T_{C}-4 \) K and the corresponding \( T_{C} \) as quoted in Table III. The negative (positive) values for \( \lambda_{s} \) imply a fairly rapid diminution (increase) in the lattice constant with sample cooling below \( T_{C} \) . Previous neutron diffraction studies made on the series \( M[N(CN)_{2}]_{2} \) (M=Co, Ni, Fe, Mn) showed the presence of TABLE II. Structural parameters derived from Rietveld refinements of the \( M[\mathrm{N}(\mathrm{CN})_{2}]_{2} \) series, where \( M=Ni \) , Co, Fe, Mn, \( Ni_{0.5}Fe_{0.5} \) , and \( Ni_{0.5}Co_{0.5} \) . N and P represent the total number of observations and basic variables, respectively. C is the number of constraints. The atoms were refined in the Pnmm space group with M at (0,0,0), N(1) at \( (x,y,z) \) , C at \( (x,y,z) \) , and N(2) at \( (x,y,0) \) . \( ^{*} \) NA=not applicable. collinear ferromagnetism \( ^{20} \) in the Co and Ni members and canted antiferromagnetism \( ^{21} \) in the Fe and Mn salts. All of these materials order with magnetic structures that propagate through space with the same periodicity as the nuclear cell, that is to say, they can be described by the propagation vector \( \mathbf{k}=(0,0,0) \) . A useful first step in the examination of magnetic ordering is to perform symmetry analysis using the technique of representational analysis. Its calculations are reported in the present study of the \( M[\mathrm{N}(\mathrm{CN})_{2}]_{2} \) , series. They involve first the determination of the irreducible representations (IR's) of the translational group made up of the symmetry operations of the nuclear cell that leave the wave vector k invariant. For this series, \( \mathbf{k}=(0,0,0) \) , and consequently these IR's are in fact those of the space group Pnmm itself. The second step of the analysis entails projection of the basis functions of the magnetic moments, described by axial vectors, at the equivalent positions of a given crystallographic site. The decomposition of the magnetic representation at the \( M^{II} \) position is \( ^{17,18} \) \[ \begin{aligned}\Gamma_{\mathrm{mag}}=&1\Gamma_{1}^{(1)}+0\Gamma_{2}^{(1)}+2\Gamma_{3}^{(1)}+0\Gamma_{4}^{(1)}+2\Gamma_{5}^{(1)}\\&+0\Gamma_{6}^{(1)}+1\Gamma_{7}^{(1)}+0\Gamma_{8}^{(1)}.\end{aligned} \quad (1) \] The magnetic structures characteristic of a given IR may be produced from linear combinations of its associated basis vectors, or equivalently by defining those of all other IR's to be zero. For second-order transitions, as it is the case for these materials, Landau theory states that a magnetic structure can be the result of only one IR becoming critical. Thus, the different symmetry-allowed magnetic structures can involve only the basis vectors within a single IR. The basis vectors for the nonzero IR's at the M site are presented in Table IV. Inspection of the four IR's with nonzero basis vectors on the M site reveals that \( \Gamma_{1} \) and \( \Gamma_{7} \) correspond to simple collinear antiferromagnetism and ferromagnetism, respectively, with the moments confined by symmetry to be along the c axis. Both \( \Gamma_{3} \) and \( \Gamma_{5} \) have the moments constrained to be in the ab plane. In \( \Gamma_{3} \) the components of the moments along the a axis are ferromagnetically and along the b axis are antiferromagnetically aligned. These relations are reversed in \( \Gamma_{5} \) , i.e., the components along a are antiferromagnetic and along b are ferromagnetic. The collinear ferromagnetic structures found in Co and Ni, with moments oriented along the c axis, obey the restriction of ordering according to a single IR \( (\Gamma_{7}) \) . However, the noncollinear canted antiferromagnetic structure proposed for the Mn salt does not, \( ^{21} \) as it has nonzero components along each of the a, b, and c directions and consequently it is not a valid magnetic structural model. We therefore reexamined the magnetic ordering of \( \mathrm{Mn}[\mathrm{N}(\mathrm{CN})_{2}]_{2} \) in terms of the different symmetry-allowed models presented. In the language of basis vectors, the refinement of a structure involves varying the mixing coefficients, \( C_{i} \) , of its associated basis vectors, \[ \mathbf{M}=C_{1}\psi_{1}+\cdots+C_{n}\psi_{n}, \quad (2) \] where M is the function that contains the components of the moments of all the equivalent positions for a crystallographic (a) (b) FIG. 3. Temperature dependence of the (a) unit-cell volume for \( M[\mathrm{N}(\mathrm{CN})_{2}]_{2} \) (from top: Co, \( Ni_{0.5}Co_{0.5} \) , and Ni, respectively) around the ferromagnetic transition temperature \( T_{C} \) and (b) lattice parameters for \( \mathrm{Co}[\mathrm{N}(\mathrm{CN})_{2}]_{2} \) ; the insets show subtle changes close to \( T_{C} \) . site. For convenience, during the refinement we restricted the sum of the moduli of the mixing coefficients to be unity, \( \Sigma_{i}|C_{i}|=1 \) . To better examine the fit hyperspace, our refinement of the mixing coefficients was carried out using a reverse Monte Carlo algorithm. The values of the moments on the two Mn equivalent positions were refined using conventional least-squares methods subject to the constraint of their being equal. The data are only adequately fitted using a collinear ferromagnetic arrangement of moments along the c axis ( \( \Gamma_{7} \) ). We will not elaborate on the magnetic structure of these purely ferromagnetic systems, as it has already been discussed elsewhere. \( ^{5-10,20} \) We confirmed that the mixed metal compound that arises from elements where the parent compounds are themselves ferromagnets, has its moment pointing along the same direction with a magnitude approximately equal to the average of the two components. However, we note a discrepancy in the value of the ordered sublattice moment with those previously published. This is likely to arise as a consequence of the difficulty in the partitioning of the nuclear and magnetic scattering intensity. As the magnetic intensities in the previous studies were extracted by fitting Gaussian functions to the individual peaks, \( ^{20} \) their deviations are expected to be greater than those of this work where full pattern-matching Rietveld analysis was employed. From the long statistics runs, the average magnetic moment per Co ion is found to be \( \langle\mu\rangle=2.86(7)\mu_{B} \) , (T=2 K) compared with \( \langle\mu\rangle=1.82(12)\mu_{B} \) (T=1.8 K) for the Ni compound, and \( \langle\mu\rangle=1.98(12)\mu_{B} \) (T=1.8 K) for the mixed metal composition, \( M=Ni_{0.5}Co_{0.5} \) . The temperature evolution of the magnitude of the moments for these ferromagnetic compounds, as determined from the lower statistics sequential Rietveld refinements, is given in Fig. 4. The high resolution data collected using the instrument D2b for \( \mathrm{Fe}[\mathrm{N}(\mathrm{CN})_{2}]_{2} \) could only be well fitted by the basis vectors of \( \Gamma_{5} \) , i.e., \( \psi_{4} \) and \( \psi_{5} \) . The plot of goodness-of-fit factor, \( \chi^{2} \) , determined from Rietveld analysis as a function of \( C(\psi_{5}) \) , is shown in Fig. 5. It shows well-defined minima either side of \( C(\psi_{5})=0 \) , giving clear evidence for the canting of the moments. The final values of the mixing coefficients were \( C(\psi_{4})=0.82(3) \) and \( C(\psi_{5})=0.18(3) \) , which indicates that the moments are tilted away from the ac plane by an angle of \( \theta\approx14^{\circ} \) . Taking the ordered sublattice magnetization as \( \langle\mu(\mathrm{Fe})\rangle=4.12(5)\mu_{B} \) , leads to a value for the ferromagnetic component along the b axis of \( 1.01(17)\mu_{B} \) , in very good agreement with that reported earlier by bulk magnetization measurements. \( ^{6} \) The sublattice magnetization is also in perfect agreement with that expected for a high-spin divalent iron ion \( (gS=4\mu_{B}) \) . \( ^{22} \) The canted antiferromagnetic structure of \( \mathrm{Fe}[\mathrm{N}(\mathrm{CN})_{2}]_{2}\mathrm{~is~shown~in~Fig.~6~with~the~two~Fe~moments~restricted~in~the~ab~plane~.~Their~components~along~the~a~direction~are~antiferromagnetically~related~} \) \( (\psi_{4}) \) and a small canting along the b direction \( (\psi_{5}) \) is responsible for the observed ferromagnetism. The size of the ferromagnetic moment of \( \mathrm{Mn}[\mathrm{N}(\mathrm{CN})_{2}]_{2} \) , as determined from maximum remanant magnetization measurements at 2 K, is \( \mu_{ferro}=0.002\mu_{B} \) . The magnitude of this ferromagnetic component is too small to be determined from the powder neutron data. Contrary to the previous report, \( ^{21} \) we find that the sublattice magnetization is equal to the spin- TABLE III. Coefficients, \( \alpha_{I} \) , for linear thermal expansion and effective magnetostriction constants, \( \lambda_{s} \) , along the three crystallographic axes of \( M[\mathrm{N}(\mathrm{CN})_{2}]_{2} \) compounds. The \( \alpha_{I} \) coefficients were determined in the temperature range where the crystal size evolves almost linearly and in all cases above the ferromagnetic phase transitions ( \( T_{C} \) ). Negative thermal expansion is identified for the c axis in all compositions. only value, \( gS=2\times\frac{5}{2}=5\mu_{B} \) , and that no delocalization of spin densities from the metal onto its coordinating ligands is observed. Canting of the type discussed above is commonly attributed to the Dzyaloshinsky-Moriya (DM) interaction. \( ^{23} \) This antisymmetric exchange is a consequence of spin-orbit coupling and its value follows \( D\cdot[S_{1}\times S_{2}] \) . As it is described by a vectorial product of spins, it favors moments that are related by \( 90^{\circ} \) . Symmetry restrictions show that for a chemical bond linking two moments to mediate this coupling, its center cannot be an inversion center. As this criterion is met in the Pnmm structure of the \( M[N(CN)_{2}]_{2} \) series, the DM mechanism will be present; however, without explicit calculation of the electron transfer integrals that describe the exchange, its value is difficult to estimate. We note that as the DM coupling involves terms of order 2, it is compatible with Landau theory and the rule of ordering according to a single IR does not need to be adjusted for it to be taken into account. An alternative effect that can give rise to canting is single-ion anisotropy. However, as the coordination octahedra are distorted and tilted in the \( M[N(CN)_{2}]_{2} \) structure, it is difficult to envisage how this will cause moments to order. TABLE IV. The basis vectors at the metal positions of the space group Pnmm with \( \mathbf{k}=(0,0,0) \) . The numbering of the IR's follows the scheme used by Kovalev (Ref. 21). The positions are defined as \( M_{1}=(0,0,0) \) and \( M_{2}=(0.5,0.5,0.5) \) . The components of the basis vectors are given with respect to the crystallographic axes a, b, and c. along the c axis or in the ab plane, as required by the symmetry of the exchange Hamiltonian. The magnetic ground state of \( M[N(CN)_{2}]_{2} \) results from the subtle balance of competing antiferromagnetic and ferromagnetic superexchange interactions, as direct overlap is negligibly small due to the large distances involved. It has been shown that the \( e_{g}-e_{g} \) and \( t_{2g}-t_{2g} \) interactions are ferromagnetic, whereas the exchange between \( e_{g} \) and \( t_{2g} \) electrons is antiferromagnetic. \( ^{[10,13]} \) The resultant magnetic structure is further influenced by the relative strengths of the superexchange interactions, in other words, the magnitude of the overlap that changes as a function of the crystallographic bond distances and bond angles. \( ^{[24]} \) The question remains as to what are the major factors which determine the resultant magnetic ground state. The superexchange occurs via interactions through the N(1)-C-N(2) unit. The rigidity of the bridging dicyanamide and the size of the cation cause the chains to tilt. Consequently, the magnitude of the superexchange interactions, between metal ions of the same chemical type, changes. In fact, it has been proposed that the tilting FIG. 4. The temperature evolution of the average ordered magnetic moment per transition metal site in \( M[\mathrm{N}(\mathrm{CN})_{2}]_{2} \) (M=Ni, \( Ni_{0.5}Co_{0.5} \) , and Co); a line is included as a guide to the eye. FIG. 5. The goodness-of-fit parameter \( \chi^{2} \) as a function of the basis vector mixing coefficient \( C(\psi_{5}) \) obtained from reverse Monte Carlo refinement. A clear minimum is seen at \( C(\psi_{5}) \cong \pm 0.18 \) . Only the size of the moment for the powder neutron diffraction data of the \( \mathrm{Fe}[\mathrm{N}(\mathrm{CN})_{2}]_{2} \) was refined by conventional Rietveld method. The line is a guide to the eye. angle, \( \alpha \) , between M-C-M atoms, represents the dominant superexchange angle and it is this angle that is responsible for controlling the magnetism, with a crossover from ferromagnetism to antiferromagnetism occurring at \( \alpha = 142.0(5)^{\circ} \) . \( ^{21} \) For compositions containing mixed transition-metal elements, where the parent compounds are themselves ferromagnets, the mixed systems are also collinear ferromagnets with the spin oriented along the crystallographic c axis. However, when one of the parent compounds is ferromagnetic (Ni) and the other antiferromagnetic (Fe), the mixed system, \( Ni_{0.5}Fe_{0.5} \) does not show long-range magnetic order. The lack of long-range magnetic order in \( Ni_{0.5}Fe_{0.5}[N(CN)_{2}]_{2} \) is evident from inspection of the differ- FIG. 6. The canted antiferromagnetic structure of Fe[N(CN) \( _{2} \) ] \( _{2} \) . ence plot between the 1.65 and 24.5 K neutron data, which shows no evidence for either extra peaks or enhancement at the nuclear Bragg positions. This is an important observation towards the understanding of the balance between structural and electronic effects, which influence the resultant magnetic ground state. The tilt angle affecting the superexchange interaction, \( \alpha \) , in \( \mathrm{Ni}_{0.5}\mathrm{Fe}_{0.5}[\mathrm{N}(\mathrm{CN})_{2}]_{2} \) was determined to be \( \alpha=141.73^{\circ} \) at 1.7 K. This angle is extremely similar in magnitude to the pure iron-containing compound ( \( \alpha=141.78^{\circ} \) ). This is despite the observation of the large change in volume from 319.97(2) Å \( ^{3} \) (Fe) to 310.12(2) Å \( ^{3} \) ( \( Ni_{0.5}Fe_{0.5} \) ). This information, along with the lack of evidence of neutron diffraction peak broadening, confirms the homogeneous mixture of the two metals on the same site within the length scale of the diffraction experiment. This tilting angle is within the regime of the canted antiferromagnetic systems; however, we obtain a much-increased Weiss constant of 13(7) K, reflecting enhanced ferromagnetic interaction compared to the parent Fe compound. The observation of no long-range magnetic order and bulk magnetic susceptibility showing short-range spin correlations demonstrates that other factors together with site randomness and/or local structure play a crucial role in determining the resultant magnetic ground state. Therefore, the different electronic configurations created by mixing ions of different metals will tune the relative number and strength of magnetic exchange interactions, i.e., ferromagnetic ( \( e_{g}-e_{g} \) and \( t_{2g}-t_{2g} \) ) versus antiferromagnetic ( \( e_{g}-t_{2g} \) ). Chemical methods can thus be used to directly influence the macroscopic magnetic behavior. Previous work on \( \mathrm{Mn}[\mathrm{N}(\mathrm{CN})_{2}]_{2} \) has established the major compensated moment to be along the a axis, with a second compensated moment lying along the c axis, whose contribution increases with application of an external magnetic field. \( ^{[21]} \) The ferromagnetic component was then predicted to lie along the b axis, although confirmation with Rietveld refinement was outside the resolution of the data. \( ^{[21]} \) In the present work, the use of high-resolution and high-intensity powder neutron diffraction, in combination with group theory techniques, has allowed the correct symmetry-allowed magnetic structure for the \( Fe^{II} \) - and \( Mn^{II} \) -containing compounds to be derived, with both the present canted antiferromagnetic structures possessing uncompensated moments along the b axis. In each case, the moments are restricted to the ab plane with any inclusion of a component along the c axis being forbidden by symmetry. As the local symmetry axes of the coordination octahedron of the metal ions do not correspond to the crystallographic axes of the unit cell, it is difficult to ascribe the fixing of the spin direction in space for the canted antiferromagnets to single ion effects. Rather, the DM interaction appears to be responsible because by its very nature the direction along which it induces canting is defined by the local bond geometry. As the unit cell symmetry is lower than tetragonal, it would thus distinguish between the a and b axes. Financial support by EPSRC, UK, CNRS, France, and a NATO collaborative linkage research grant is acknowledged. \( ^{*} \) Electronic address: lappas@iesl.forth.gr \( ^{1} \) For a recent review in this area see J. S. Miller, Inorg. Chem. 39, 4392 (2000). \( ^{2} \) Magnetism: A Supramolecular Function, edited by O. Kahn (Kluwer Academic, 1996); Supramolecular Engineering of Synthetic Metallic Materials, Conductors and Magnets, NATO ASI Series, edited by J. Veciana, C. Rovira, and D. B. Amabilino (Kluwer Academic, Dordrecht, 1998), Vol. C518; Molecular Magnetism, New Magnetic Materials, edited by K. Itoh and M. Minoshita (Gordon Breach-Kodansha, Tokyo, 2000); Organic Superconductors (Including Fullerenes): Synthesis, Structure, Properties and Theory, edited by J. M. Williams, J. R. Ferraro, R. J. Thorn, K. D. Carlson, U. Geiser, H. H. Wang, A. M. Kini, and M.-H. Whangbo (Prentice-Hall, New Jersey, 1992). \( ^{3} \) F. Herren, P. Fischer, A. Ludi, and W. Hälg, Inorg. Chem. 19, 956 (1980); M. Schierber, in Experimental Magnetochemistry, edited by E. P. Wohlfarth (North-Holland, Amsterdam, 1967), p. 476. \( ^{4} \) S. Ferlay, T. Mallah, R. Ouahès, P. Veillet, and M. Verdaguer, Nature (London) 378, 701 (1995). \( ^{5} \) S. R. Batten, P. Jensen, B. Moubaraki, K. S. Murray, and R. Robson, Chem. Commun. (Cambridge), 439 (1998). \( ^{6} \) M. Kurmoo and C. J. Kepert, New J. Chem. 22, 1515 (1998). \( ^{7} \) M. Kurmoo, P. Day, and C. J. Kepert, in Supramolecular Engineering of Synthetic Metallic Materials: Conductors and Magnets, edited by J. Veciana, C. Rovira and D. B. Amabilino, NATO ASI Series (Kluwer Academic, Dordrecht, 1998), Vol. C518, p. 271. \( ^{8} \) J. L. Manson, C. R. Kmety, Q. Huang, J. W. Lynn, G. M. Bendele, S. Pagola, P. W. Stephens, L. M. Liable-Sands, A. L. Rheingold, A. J. Epstein, and J. S. Miller, Chem. Mater. 10, 2552 (1998). \( ^{9} \) M. Kurmoo and C. J. Kepert, Mol. Cryst. Liq. Cryst. 334, 693 (1999). \( ^{10} \) S. R. Batten, P. Jansen, C. J. Kepert, M. Kurmoo, B. Moubaraki, We would like to thank the ILL for provision of neutron beam time, Dr. T. Hansen for help with the neutron experiments, and Dr. C. Brown for preliminary data collection on the cobalt complex. K. S. Murray, and D. J. Price, J. Chem. Soc. Dalton Trans. 1999, 2987. \( ^{11} \) J. L. Manson, C. R. Kmety, A. J. Epstein, and J. S. Miller, Inorg. Chem. 38, 2552 (1999). \( ^{12} \) T. Jestadt, M. Kurmoo, S. J. Blundel, F. L. Pratt, C. J. Kepert, K. Prassides, B. W. Lovett, I. M. Marshall, A. Husmann, K. H. Chow, R. M. Valladares, C. M. Brown, and A. Lappas, J. Phys.: Condens. Matter 13, 2263 (2001). \( ^{13} \) C. J. Nuttall, T. Takenobu, Y. Iwasa, and M. Kurmoo, Mol. Cryst. Liq. Cryst. 343, 227 (2000). \( ^{14} \) H. Kohler, Z. Anorg. Allg. Chem. 331, 237 (1964). \( ^{15} \) H. M. Rietveld, J. Appl. Crystallogr. 2, 65 (1969). \( ^{16} \) A. C. Larson and R. B. von Dreele, General Structure Analysis System (GSAS), Los Alamos National Laboratories Report LAUR 86-748 (2000) (unpublished). \( ^{17} \) A. S. Wills, Physica B 276–278, 680 (2000); A. S. Wills, Phys. Rev. B 63, 064430 (2001). (Program SARAh available from ftp://ftp.ill.fr/pub/dif/sarah.) \( ^{18} \) O. V. Kovalev, Irreducible Representations of the Space Groups (Gordon and Breach, New York, 1961); W. Opechowski and R. Guccione, in Magnetism, edited by G. T. Rado and H. Suhl (Academic, New York, 1965), Vol. IIa, Chap. 3. \( ^{19} \) E. du Tremolet de Lacheisserie, Magnetostriction (CRC Press, Boca Raton, 1993). \( ^{20} \) C. R. Kmety, J. L. Manson, Q. Huang, J. W. Lynn, R. W. Erwin, J. S. Miller, and A. J. Epstein, Phys. Rev. B 60, 60 (1999). \( ^{21} \) C. R. Kmety, Q. Huang, J. W. Lynn, R. W. Erwin, J.L. Manson, S. McCall, J. E. Crow, K. L. Stevenson, J. S. Miller, and A. J. Epstein, Phys. Rev. B 62, 5576 (2000). \( ^{22} \) A. Herpin, Theorie du Magnetisme (Presse Universitaire de France, Paris, 1968). \( ^{23} \) I. Dzyaloshinsky, J. Phys. Chem. Solids 4, 241 (1958); T. Moriya, Phys. Rev. 120, 91 (1960). \( ^{24} \) J. B. Goodenough, Magnetism and the Chemical Bond (Wiley, New York, 1963).IV. POWDER NEUTRON DIFFRACTION MEASUREMENTS
Ni Ni_{0.5}Co_{0.5} Ni_{0.5}Fe_{0.5} Co Fe Mn C (cm^{3} K/mol) 1.21(3) 2.02(6) 1.70(6) 2.85(8) 3.36(10) 4.42(14) \( \theta \) (K) 23(1) 10(3) 13(7) -2(6) -22(1) -25(1) T_{C} (K) 21 18 No LRO 9 19 16 
V. SYMMETRY-ALLOWED MAGNETIC ORDERINGS
M[N(CN)2]2 M=Ni M=Ni0.5Co0.5 M=Ni0.5Fe0.5 M=Co M=Fe M=Mn T(K) 1.8 1.8 1.7 2 1.7 1.7 a(Å) 5.9064(5) 5.9224(6) 5.9800(3) 5.9559(5) 6.0362(3) 6.1096(2) b(Å) 7.0148(5) 7.0486(6) 7.0479(3) 7.0583(6) 7.1195(2) 7.2675(2) c(Å) 7.3133(9) 7.3688(11) 7.3577(2) 7.4230(9) 7.4455(2) 7.5708(2) V(Å3) 303.01(5) 307.61(6) 310.12(2) 312.05(5) 319.97(2) 336.15(2) M x=y=z 0 0 0 0 0 0 N(1) x 0.2075(3) 0.2082(4) 0.2122(4) 0.2068(3) 0.2165(3) 0.2188(3) y -0.0933(3) -0.0930(4) -0.0944(3) -0.0936(3) -0.0933(2) -0.0893(2) z 0.2037(4) 0.2066(5) 0.2063(2) 0.2106(4) 0.2085(2) 0.2128(2) N(2) x 0.1631(5) 0.1619(6) 0.1573(5) 0.1608(5) 0.1573(4) 0.1545(5) y 0.2709(5) 0.2713(6) 0.2759(4) 0.2746(5) 0.2793(4) 0.2876(4) z 0 0 0 0 0 0. C x 0.2667(7) 0.2656(8) 0.2697(6) 0.2682(6) 0.2724(5) 0.2732(5) y -0.1494(5) -0.1490(6) -0.1479(5) -0.1492(5) -0.1454(4) -0.1421(3) z 0.3431(5) 0.3454(6) 0.3480(3) 0.3473(5) 0.3493(3) 0.3520(3) Rwp(%) Rρ(%) 2.95, 2.01 3.98, 2.60 3.68, 2.74 4.35, 3.04 4.75, 3.65 4.48, 3.35 Rmag(%) 2θ(deg) 19.02, 22°-58° 12.91, 22°-58° NA* 13.43, 22°-58° 16.22, 10°-53° 14.56, 10°-53° No. magnetic 38 40 NA 40 114 119 reflections ⟨μ⟩ 1.82(12) 1.98(12) 0 2.86(7) 4.12(5) 5.01(6) N, P, C 1080, 15, 2 1080, 15, 2 2740, 33, 2 1080, 15, 2 2760, 33, 1 2745, 33, 2


A. Ferromagnetism in Ni, Co, and Ni_{0.5}Co_{0.5}
B. Canted antiferromagnetism in Fe[N(CN)₂]₂ and Mn[N(CN₂)]₂
\( \alpha_{I} \) ( \( 10^{-5} \) K \( ^{-1} \) ) Temperature range (K) Ni[N(CN) \( _{2} \) ] \( _{2} \) Ni \( _{0.5} \) Co \( _{0.5} \) [N(CN) \( _{2} \) ] \( _{2} \) Co[N(CN) \( _{2} \) ] \( _{2} \) \( \alpha_{a} \) 100-271 3.4 3.6 3.5 \( \alpha_{b} \) 100-271 1.8 1.9 2.2 \( \alpha_{c} \) 25-271 -0.55 -0.66 -0.71 \( \lambda_{s} \) (units of \( 10^{-4} \) ) 17-21 K 14-18 K 5-9 K \( T_{C}=21 \) K \( T_{C}=18 \) K \( T_{C}=9 \) K \( \lambda_{a} \) -0.5 -0.7 -0.9 \( \lambda_{b} \) 0.0 0.3 0.4 \( \lambda_{c} \) -0.3 -0.5 -0.7 IR Basis vector \( M_{1} \) \( M_{2} \) \( M_{1a} \) \( M_{1b} \) \( M_{1c} \) \( M_{2a} \) \( M_{2b} \) \( M_{2c} \) \( \Gamma_{1} \) \( \psi_{1} \) 0 0 1 0 0 -1 \( \Gamma_{3} \) \( \psi_{2} \) 1 0 0 1 0 0 \( \psi_{3} \) 0 1 0 0 -1 0 \( \Gamma_{5} \) \( \psi_{4} \) 1 0 0 -1 0 0 \( \psi_{5} \) 0 1 0 0 1 0 \( \Gamma_{7} \) \( \psi_{6} \) 0 0 1 0 0 1 VI. DISCUSSION



VII. SUMMARY
ACKNOWLEDGMENTS