| Transition Temperature | 4.1 K |
|---|---|
| Experiment Temperature | 1.4 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | Pnma (#62) |
| Magnetic Space Group | Pnm'a (#62.444) |
| Magnetic Point Group | m'mm (8.3.26) |
| Lattice Parameters | 5.8163(5) 8.1854(6) 5.7816(5) 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1088/0953-8984/26/9/095401 |
| Reference | M. Avdeev, B.J. Kennedy and T. Kolodiazhnyi, Journal of Physics: Condensed Matter (2014) 26 095401. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Eu1 | Eu | 7.3 | 0.0 | 0.0 | 7.30 |
Neutron powder diffraction study of the magnetic structure of \( EuZrO_{3} \)
This content has been downloaded from IOPscience. Please scroll down to see the full text.
2014 J. Phys.: Condens. Matter 26 095401
(http://iopscience.iop.org/0953-8984/26/9/095401)
View the table of contents for this issue, or go to the journal homepage for more
Download details:
IP Address: 93.180.53.211
This content was downloaded on 14/02/2014 at 09:19
Please note that terms and conditions apply.
Neutron powder diffraction study of the magnetic structure of EuZrO_{3}
Maxim Avdeev \( ^{1} \) , Brendan J Kennedy \( ^{2} \) and Taras Kolodiazhnyi \( ^{3} \)
\( ^{1} \) Australian Nuclear Science and Technology Organisation, New Illawarra Road, Lucas Heights, New South Wales, 2234, Australia
\( ^{2} \) School of Chemistry, The University of Sydney, Sydney, NSW 2006, Australia
\( ^{3} \) National Institute for Materials Science, Namiki 1-1, Tsukuba, Ibaraki 305-0044, Japan
E-mail: b.kennedy@chem.usyd.edu.au
Received 13 November 2013, revised 5 January 2014
Accepted for publication 7 January 2014
Published 13 February 2014
Abstract
Neutron powder diffraction experiments on the orthorhombic perovskite \( EuZrO_{3} \) show it to have an antiferromagnetic G-type magnetic structure with the magnetic moments aligned parallel to the a-axis. The orthorhombic crystal structure is a consequence of cooperative rotations of the corner-sharing \( ZrO_{6} \) octahedra. The crystal structure does not change significantly below the Néel temperature, \( \sim4.1 \) K, showing there to be only weak magnetoelastic coupling.
Keywords: perovskite, EuZrO_{3}, magnetic structure
☑ Online supplementary data available from stacks.iop.org/JPhysCM/26/095401/mmedia
(Some figures may appear in colour only in the online journal)
1. Introduction
Divalent europium perovskite oxides with the chemical formula \( EuMO_{3} \) (M = Ti and Zr) are of considerable interest as a consequence of their diverse and often intriguing physical properties. There is increasing evidence that the large magnetic moments of the \( Eu^{2+} \) ion, which stem from the half-filled 4f shell, can couple to electrical polarization of the soft-mode optical phonons, leading to fascinating properties in \( EuTiO_{3} \) [1–6]. Surprisingly, a magnetoelectric effect is observed in \( EuZrO_{3} \) , albeit on a smaller scale, despite the absence of an analogous soft mode [7]. In agreement with experimental data, recent theoretical efforts indicate that the microscopic origin of the spin–lattice coupling in \( EuMO_{3} \) perovskites is driven by a non-zero hybridization between the Eu 4f and M \( n d \) electronic orbitals, which, in turn, depend on the degree of the oxygen octahedral rotations [8, 9].
\( EuTiO_{3} \) is isostructural with \( SrTiO_{3} \) at room temperature, and both have a simple cubic perovskite structure (space group \( Pm3m \) ) with a lattice constant of \( \sim3.9 \) Å. As established in the early neutron diffraction study of McGuire et al [3], the localized 4f spins of the \( Eu^{2+} \) ions (S = 7/2) in \( EuTiO_{3} \) show G-type antiferromagnetic (AFM) ordering below 5.3 K; the spin of each \( Eu^{2+} \) cation is opposite to that of all of its nearest neighbours. This magnetic structure was confirmed recently by Scagnoli et al [10]. Since the radii of the 4f orbitals are much smaller than those of the 5s or 5p orbitals, the Eu f bands are narrow and the Néel temperature is low.
It was recently reported that \( EuZrO_{3} \) is isostructural with \( SrZrO_{3} \) and that it adopts an orthorhombic perovskite structure in space group Pnma [11–14]. The Eu sites in \( EuZrO_{3} \) form a pseudo simple cubic lattice similar to that seen in \( EuTiO_{3} \) , and it has been widely assumed that the Eu 4f spins would exhibit a G-type AFM ordering below 4.1 K [9, 15]. It was not obvious, however, whether the G-type AFM ordering survives under strong rotations of the oxygen octahedra reported for \( EuZrO_{3} \) . In an effort to understand the microscopic origin of the magnetoelectric effect in \( EuMO_{3} \) perovskites, we have studied the magnetic structure of \( EuZrO_{3} \) using powder neutron diffraction. This paper provides experimental proof of a G-type magnetic ground state of \( EuZrO_{3} \) .
2. Experimental details
\( EuZrO_{3} \) was prepared by solid-state reaction between \( Eu_{2}O_{3} \) and \( ZrO_{2} \) under hydrogen flow, following the previously

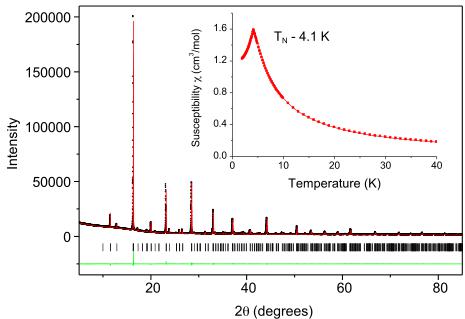
Figure 1. Observed (black symbols), calculated (red line), and difference (green line) synchrotron x-ray diffraction pattern for \( EuZrO_{3} \) at room temperature. The structure was refined in space group \( P_{nma} \) . The inset shows the temperature dependence of the magnetic susceptibility of \( EuZrO_{3} \) between 2 and 40 K.
reported method [16]. Field-cooled and zero-field-cooled magnetic susceptibilities were measured with an applied field of 100 Oe in the temperature range 2–40 K range using a commercial superconducting quantum interference device (Quantum Design, MPMS, USA). Neutron powder diffraction (NPD) data were collected on the high-resolution diffractometer Echidna at the OPAL facility (Lucas Heights, Australia) using neutrons of wavelength 1.6215 Å [17]. For the measurements, 2.5927 g of the powder sample was loaded into an annular vanadium can with outer diameter 10.58 mm and a gap of 0.55 mm between the walls, and data were collected at 1.4 and 7 K, i.e., above and below the magnetic transition, using a liquid helium cryostat. Rietveld analysis of the data was performed using the Fullprof suite [18] with default neutron scattering lengths and \( Eu^{2+} \) magnetic form-factor. Since an analytical description of a transmission curve for an annular can is not available in the code and it differs substantially from that for a cylinder, the data were corrected numerically [19] prior to the analysis using a packing density (49%) estimated geometrically. Synchrotron x-ray diffraction patterns were recorded using the powder diffractometer at BL-10 of the Australian Synchrotron, using x-rays with wavelength 0.82554 Å [20]. Data were collected at room temperature in the angular range \( 5^{\circ} \leq 2\theta \leq 85^{\circ} \) from a finely ground sample housed in a 0.2 mm diameter capillary that was rotated during the measurements.
3. Results
Rietveld refinement of the structure of \( EuZrO_{3} \) using synchrotron x-ray powder diffraction data confirmed the orthorhombic Pnma structure, and the refined lattice parameters \( (a = 5.81920(2) \) Å, \( b = 8.19580(3) \) Å, and \( c = 5.79580(2) \) Å) are in good agreement with values reported previously [11, 12], noting the change in setting from Pbnm to Pnma. In the Pnma model, the Eu is at the 4c site \( (x 1/4 y) \) , and the Zr is at the 4a origin site \( (0 0 0) \) . Magnetic susceptibility measurements demonstrated the material to be

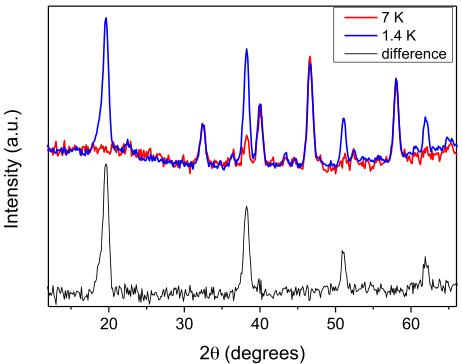
Figure 2. NPD patterns for \( EuZrO_{3} \) collected at 1.4 K (blue) and 7 K (red), and their difference (black).
antiferromagnetic, with a Néel temperature of 4.1 K. These results are summarized in figure 1.
Neutron diffraction data collected at 7 K, i.e., above the magnetic transition observed in the magnetic susceptibility measurements, were successfully analysed using the same orthorhombic model employed in the analysis of the room-temperature synchrotron x-ray diffraction pattern. We note that structural refinements gave a small and positive value of the refined thermal parameter (0.34(6) Ų). Since this is well known to strongly correlate with absorption, this value suggests that the effect of absorption in the sample in an annular can was accurately estimated. The final Rietveld plot and crystallographic information are presented in figure S1 and table S1 (available at stacks.iop.org/JPhysCM/26/095401/mmedia) of the supplementary data, respectively. Selected interatomic distances, metal–oxygen–metal distances, and bond valence sums, given in table S2 (available at stacks.iop.org/JPhysCM/26/095401/mmedia), are unexceptional, and are in good agreement with previously published data [11, 12].
Comparison of the NPD patterns collected at 1.4 and 7 K revealed additional intensity due to magnetic ordering (figure 2). This is consistent with the magnetic susceptibility data, which suggested an AFM transition at \( \sim \) 4.1 K. All the diffraction peaks that contained a magnetic scattering contribution could be indexed by the chemical unit cell, i.e., with the propagation vector \( k = (0, 0, 0) \) . Representational analysis performed with BasIReps [18] showed that, for the 4c (x, 0.25, z) Wyckoff site of the Pnma space group, the magnetic representation decomposes in terms of eight one-dimensional irreducible representations (irreps) as \( \Gamma = \Gamma_{1} + 2\Gamma_{2} + 2\Gamma_{3} + \Gamma_{4} + \Gamma_{5} + 2\Gamma_{6} + 2\Gamma_{7} + \Gamma_{8} \) . The associated basis vectors are listed in table S3 (available at stacks.iop.org/JPhysCM/26/095401/mmedia).
Examination of the reflections allowed by symmetry for the different irreps immediately narrowed down the list of possible solutions to \( \Gamma2 \) , \( \Gamma6 \) , and \( \Gamma8 \) . Furthermore, for the irreps \( \Gamma2 \) and \( \Gamma6 \) , the data showed no evidence of the scattering corresponding to the Ax and Az basis vectors, respectively (table 2). Therefore only the Cz, Cx, and Cy basis vectors

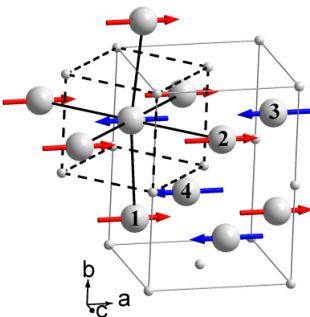
Figure 3. View of the magnetic structure of \( EuZrO_{3} \) . The europium atoms are shown as large balls with the labels corresponding to the numbering scheme of table S2 (available at stacks.iop.org/JPhysCM/26/095401/mmedia). The grey and black dashed lines show an orthorhombic unit cell and a cell of the cubic perovskite aristotype, respectively. Black solid lines emphasize G-type antiferromagnetic coupling of nearest neighbours to a selected \( Eu^{2+} \) atom.
Table 1. Crystal structural parameters for EuZrO₃ based on the Rietveld refinement against NPD data collected at 1.4 K. Space group Pnma(#62), a = 5.8163(5) Å, b = 8.1854(6) Å, c = 5.7816(5) Å, V = 275.25(4) ų, B₀v = 0.34(6) Ų.
| Atom | Wyckoff site | x | y | z | BVS \( ^{a} \) |
| Eu | 4c | 0.0283(12) | 0.25 | 0.499(4) | 1.82(4) |
| Zr | 4a | 0 | 0 | 0 | 3.84(3) |
| O1 | 4c | 0.485(2) | 0.25 | 0.578(2) | 1.89(3) |
| O2 | 8d | 0.2908(14) | 0.0330(10) | 0.2147(15) | 1.88(3) |
\( ^{a} \) Bond valence sums (BVS) calculated with Fullprof using distance cutoff 3.0 Å and constants published in [21].
of the irreps \( \Gamma2 \) , \( \Gamma6 \) , and \( \Gamma8 \) , describing a G-type magnetic structure with the magnetic moment parallel to the c-axis, a-axis, and b-axis, respectively, were considered further.
Although the considered irreps \( \Gamma2 \) , \( \Gamma6 \) , and \( \Gamma8 \) gave similar agreement between experimental and calculated NPD patterns, the \( R_{mag} \) factors, 10.8%, 8.85%, and 11.1%, respectively slightly favour the \( \Gamma6 \) model. The model (equivalent to the \( Pnm'a \) Shubnikov group, Opechowski–Guccione #62.4.505) describes a G-type magnetic structure with the magnetic moments parallel to the a-axis, as shown in figure 3. The Rietveld plot and crystallographic information are presented in figure 4 and table 1, respectively. The refined value of the moment, \( 7.3(1) \) \( \mu_{B} \) , is close to that expected for \( S = 7/2 \) \( Eu^{2+} \) and recently determined for a G-type ordered \( EuTiO_{3} \) [13].
4. Discussion
We have demonstrated, for the first time, that \( EuZrO_{3} \) has a G-type antiferromagnetic structure. This is the same magnetic structure as observed in \( EuTiO_{3} \) , despite the difference in space group symmetry; \( EuZrO_{3} \) is orthorhombic, space group Pnma, and at low temperatures \( EuTiO_{3} \) is tetragonal, space group I4/mcm. The symmetry lowering is a consequence of

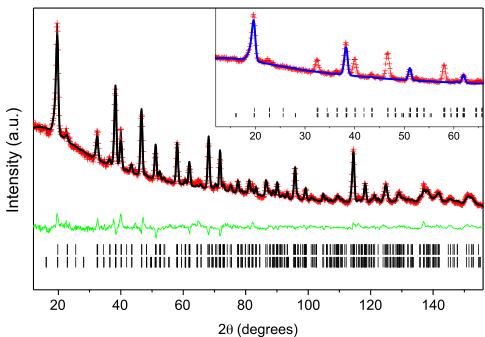
Figure 4. Rietveld plot for the \( EuZrO_{3} \) neutron powder diffraction data collected at 1.4 K. The red crosses and black and green solid lines indicate the observed and calculated patterns and their difference, respectively. The tick marks indicate the positions of the diffraction peaks. \( R_{p}=2.17\% \) , \( R_{wp}=2.92\% \) , \( R_{F}=8.77\% \) , and \( R_{mag}=8.85\% \) . The blue curve in the inset shows the magnetic contribution.
Table 2. Representational analysis for the 4c (x, 0.25, z) Eu site of the Pnma space group and the propagation vector k = (0, 0, 0). The atomic positions are (x, y, z), \( (-x + 1/2, -y, z + 1/2) \) , \( (-x, y + 1/2, -z) \) , and \( (x + 1/2, -y + 1/2, -z + 1/2) \) . The ordering modes are defined as \( \mathrm{F}(++++) \) , \( \mathrm{C}(++--) \) , \( \mathrm{G}(+-+-) \) , and \( \mathrm{A}(+-+) \) . The model providing the best agreement with the experimental NPD data is highlighted in bold font.
| Irreps | Basis vectors | Shubnikov group |
| \( \Gamma1 \) | Gy | Pnma |
| \( \Gamma2 \) | AxCz | Pn'm'a' |
| \( \Gamma3 \) | GxFz | Pn'm'a |
| \( \Gamma4 \) | Ay | Pnma' |
| \( \Gamma5 \) | Fy | Pn'm'a' |
| \( \Gamma6 \) | CxAz | Pnm'a |
| FxGz | Pnm'a' | |
| \( \Gamma7 \) | FxGz | Pnm'a' |
| \( \gamma8 \) | Cy | Pn'ma |
cooperative rotations of the corner-sharing \( MO_{6} \) octahedra. The presence of such tilting is often predicted using the tolerance factor \( t = (r_{\mathrm{A}} + r_{\mathrm{O}} / \sqrt{2}(r_{\mathrm{B}} + r_{\mathrm{O}}) \) , where \( r_{i} \) is the ionic radius of the A-, B-, and O-type ions, with the tilts increasing in magnitude as the tolerance factor decreases. The magnitude of the rotations are estimated from the refined atomic coordinates [22]; for EuZrO \( _{3} \) the in-phase tilts are estimated to be 8.7° and the out-of-phase tilts are estimated to be 10.6°. These values are, as expected, greater than those observed at room temperature, and are comparable with the values observed in SrZrO \( _{3} \) [14].
Although octahedral rotations in perovskites generally occur in order to optimize the bonding of the two cations, Akamatsu et al [9] have argued that these also impact on the strength of the superexchange interactions in \( EuMO_{3} \) perovskites. An important consequence of the strong spin–lattice coupling in \( EuMO_{3} \) perovskites is the increase in the energy gap between the antiferromagnetic G-type and
ferromagnetic F-type magnetic structures upon rotation of the \( MO_{6} \) octahedra. In \( EuZrO_{3} \) , the octahedral rotations will facilitate spatial overlap between the Eu 4f and Zr d orbitals, although the larger band gap in \( EuZrO_{3} \) , compared to \( EuTiO_{3} \) , will limit the extent of hybridization between the Eu f and Zr d orbitals. The octahedral rotations also reduce the effective coordination of the Eu from 12 in the archetypal cubic structure to effectively 8, which increases the covalent bonding strength and hybridization between the Eu and oxygen anions. They will partially remove the degeneracy of the Zr–O bond distances (see table S2 available at stacks.iop.org/JPhysCM/2/6/095401/mmedia), allowing for anisotropic spreading of the Zr 4d orbitals, enhancing the AFM superexchange interaction.
Comparison of the structure immediately above and below the Néel temperature, \( \sim4.1 \) K, shows that although the cell volume remains essentially constant there is a small expansion in the b lattice parameter, from 8.1816(7) Å at 7 K to 8.1854(6) Å at 1.4 K, which is offset by a contraction in the c lattice parameter from 5.7832(5) to 5.7816(5) Å. Evidently there is weak magnetoelastic coupling in \( EuZrO_{3} \) .
Acknowledgments
This work has been partially supported by the Australian Research Council. This work was, in part, performed at the powder diffraction beamline at the Australian Synchrotron with the assistance of Dr Helen Brand. TK was supported by the Japan Society for the Promotion of Science.
References
[1] Lee J H et al 2010 Nature 466 954
[2] Katsufuji T and Takagi H 2001 Phys. Rev. B 64 054415
[3] McGuire T R, Shafer M W, Joenk R J, Alperin H A and Pickart S J 1966 J. Appl. Phys. 37 981
[4] Fennie C J and Rabe K M 2006 Phys. Rev. Lett. 97 267602
[5] Shvartsman V V, Borisov P, Kleemann W, Kamba S and Katsufuji T 2010 Phys. Rev. B 81 064426
[6] Birol T and Fennie C J 2013 Phys. Rev. B 88 094103
[7] Kolodiazhnyi T, Fujita K, Wang L, Zong Y, Tanaka K, Sakka Y and Takayama-Muromachi E 2010 Appl. Phys. Lett. 96 252901
[8] Ke X, Birol T, Misra R, Lee J H, Kirby B J, Schlom D G, Fennie C J and Freeland J W 2013 Phys. Rev. B 88 094434
[9] Akamatsu H, Kumagai Y, Oba F, Fujita K, Tanaka K and Tanaka I 2013 Adv. Funct. Mater. 23 1864
[10] Scagnoli V, Allieta M, Walker H, Scavini M, Katsufuji T, Sagarna L, Zaharko O and Mazzoli C 2012 Phys. Rev. B 86 094432
[11] Viallet V, Marucco J F, Saint J, Herbst-Ghysel M and Dragoe N 2008 J. Alloys Compounds 461 346
[12] Zong Y, Fujita K, Akamatsu H, Murai S and Tanaka K 2010 J. Solid State Chem. 183 168
[13] Akamatsu H, Fujita K, Hayashi H, Kawamoto T, Kumagai Y, Zong Y, Iwata K, Oba F, Tanaka I and Tanaka K 2012 Inorganic Chem. 51 4560
[14] Howard C J, Knight K S, Kennedy B J and Kisi E H 2000 J. Phys.: Condens. Matter 12 L677
[15] Alho B P, Nóbrega E P, de Sousa V S R, Carvalho A M G, de Oliveira N A and von Ranke P J 2011 J. Appl. Phys. 109 083942
[16] Kolodiazhnyi T, Valant M, Williams J R, Bugnet M, Botton G A, Ohashi N and Sakka Y 2012 J. Appl. Phys. 112 083719
[17] Liss K D, Hunter B, Hagen M, Noakes T and Kennedy S 2006 Physica B 385/86 1010
[18] Rodríguez-Carvajal J 1993 Physica B 192 55
[19] Bowden M and Ryan M 2010 J. Appl. Crystallogr. 43 693
[20] Wallwork K S, Kennedy B J and Wang D 2007 AIP Conf. Proc. 879 879
[21] Brown I D and Altermatt D 1985 Acta Crystallogr. B 41 244
[22] Kennedy B J, Howard C J and Chakoumakos B C 1999 J. Phys.: Condens. Matter 11 1479