| Transition Temperature | 4.4 K |
|---|---|
| Experiment Temperature | 1.5 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | Pnma (#62) |
| Magnetic Space Group | Pn'm'a' (#62.449) |
| Magnetic Point Group | m'm'm' (8.5.28) |
| Lattice Parameters | 5.8172(2) 8.1805(2) 5.7833(2) 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1103/physrevb.93.014409 |
| Reference | R. Saha, A. Sundaresan, M.K. Sanyal, C.N.R. Rao, F. Orlandi, P. Manuel and S. Langridge, Physical Review B (2016) 93. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Eu1 | Eu | 0.0 | 0.0 | 6.40 | 6.40 |
Neutron scattering study of the crystallographic and spin structure in antiferromagnetic EuZrO_{3}
Rana Saha, \( ^{1} \) A. Sundaresan, \( ^{1} \) Milan K. Sanyal, \( ^{1,2} \) C. N. R. Rao, \( ^{1} \) Fabio Orlandi, \( ^{3,4} \) Pascal Manuel, \( ^{4} \) and Sean Langridge \( ^{4,*} \)
\( ^{1} \) Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkur P.O., Bangalore 560064, India
\( ^{2} \) Saha Institute of Nuclear Physics, Bidhannagar, Kolkata 700064, India
\( ^{3} \) Dipartimento di Chimica, Università degli Studi di Parma, Parco Area delle Scienze 17A, I-43124 Parma, Italy
\( ^{4} \) ISIS Facility, STFC Rutherford Appleton Laboratory, Harwell Science and Innovation Campus, Oxon OX11 0QX, United Kingdom (Received 22 September 2015; revised manuscript received 25 November 2015; published 8 January 2016)
High-resolution neutron powder diffraction is used to demonstrate that the \( Eu^{2+} \) moments in \( EuZrO_{3} \) are oriented along the c axis, in contrast to \( EuTiO_{3} \) where the moments lie within the ab plane. By applying a Landau theory analysis to the Ti and Zr system we are able to contrast the differing magnetoelectric coupling symmetries resulting from the magnetic space groups of the two ordered structures. The observed order parameter is consistent with the asymptotic three-dimensional Ising model.
DOI: 10.1103/PhysRevB.93.014409
I. INTRODUCTION
Multiferroic materials have opened up the desirable possibility of controlling ferroelectric polarization with a magnetic field and magnetization by an electric field. These fascinating, technologically relevant materials with unique magnetoelectric properties also allow us to investigate the fundamental interplay of magnetic and electric order parameters. Most commonly known multiferroics are perovskite oxides having a general formula \( ABO_{3} \) . Unambiguous magnetoelectric coupling at room temperature has been demonstrated in \( BiFeO_{3} \) , where weak ferromagnetism arises from the canting of the antiferromagnetically aligned spins [1,2]. Perovskite oxides based on divalent europium ions, such as \( EuTiO_{3} \) and \( EuZrO_{3} \) , with localized spin S = 7/2, are also being extensively investigated experimentally and theoretically to understand the intriguing correlation of magnetic and dielectric properties which give rise to the magneto-electric effects. \( EuTiO_{3} \) has a cubic structure at room temperature with the space group \( Pm\overline{3}m \) and a small optical band gap of 0.8 eV, while \( EuZrO_{3} \) has an orthorhombic structure with the space group Pnma and possesses a much higher optical band gap of about 2.4 eV [3,4]. These two compounds exhibit similar magnetic properties where the A-site \( Eu^{2+} \) (S = 7/2) ion undergoes a paramagnetic-to-antiferromagnetic (AFM) transition in the temperature range of 4–5 K. In \( Eu^{2+} \) containing perovskite oxides, nearest-neighbor magnetic exchange interactions are antiferromagnetic (AFM) while the interaction with the next-nearest neighbor is ferromagnetic (FM). It has been shown that there is a delicate balance between the AFM and FM states in these materials. For example, one can obtain a FM metallic state instead of the AFM insulator state in \( EuTiO_{3} \) by strain [5] and hydride substitution [6]. Interestingly, \( EuZrO_{3} \) shows a strong magnetodielectric effect at the antiferromagnetic ordering temperature [7]. Neutron scattering and magnetic resonant x-ray diffraction techniques have been used to study the magnetic structure of \( EuTiO_{3} \) , and it is observed that G-type AFM ordering takes place below 5.3 K, with the moments lying within the ab plane along the plane diagonal [8]. Neutron powder diffraction experiments revealed G-type AFM ordering in the orthorhombic perovskite \( EuZrO_{3} \) though the spin direction along the crystallographic axis could not be determined unambiguously. A better agreement was obtained when the magnetic moments were assumed to be aligned parallel to the a axis in the \( Pnm'a \) magnetic space group [9]. It has been shown theoretically in a recent paper [10] that the possible magnetic structure of \( EuZrO_{3} \) could be isotropic G-AFM or anisotropic A-AFM. It is therefore extremely important to determine the spin-orientation with respect to the crystallographic directions in the orthorhombic perovskite \( EuZrO_{3} \) , as directional spin-orbit coupling plays a pivotal role in determining the magnetoelectric coupling in these materials [1,2]. Here we show with high-resolution neutron diffraction data collected as a function of temperature that the magnetic moments are oriented along the c axis, corresponding to the \( Pn'm'a' \) symmetry, as the temperature drops below the AFM transition temperature of 4.4 K. We also show that the \( Eu^{2+} \) ions attain a moment of \( 6.40\mu_{B} \) along the c axis at 1.5 K following the asymptotic three-dimensional (3D) Ising model with a critical exponent \( \beta = 0.29 \) .
II. EXPERIMENTAL METHODOLOGY
Polycrystalline \( EuZrO_{3} \) was prepared by the conventional solid state reaction in a reducing atmosphere of pure \( H_{2} \) (99.9995%) starting from the binary oxides, namely \( Eu_{2}O_{3} \) (Sigma Aldrich, 99.9%) and \( ZrO_{2} \) (Fluka Chemika, 97%). Stoichiometric amounts of the precursors were mixed together, ground, and heated in a reducing atmosphere at 1400 °C for 24 hrs with several intermediate grindings. X-ray diffraction (XRD) patterns of the samples were recorded with a PANalytical monochromatic laboratory x-ray diffractometer ( \( \lambda = 1.5406 \) Å) to confirm the phase purity. The FULLPROF suite [11] was used to refine the crystallographic structural parameters obtained from x-ray diffraction. DC magnetization measurements were carried out using a superconducting quantum interference device (SQUID) Magnetometer (MPMS3, Quantum Design, USA) in the temperature range of 2–390 K under zero-field-cooled (ZFC) and field-cooled (FC) conditions in the presence of different magnetic fields. Isothermal magnetization measurement was carried out in the magnetic field range of \( \pm70 \) kOe. Neutron powder diffraction measurements were performed on the high-resolution
long-wavelength diffractometer WISH [12] at the ISIS facility in zero applied magnetic field. The powder sample was loaded in a 3 mm diameter thin-walled vanadium can, lightly packed to minimize absorption. Rietveld analysis of the neutron data was performed with the JANA2006 [13] software using standard scattering length densities and the \( Eu^{2+} \) form factor. The effect of neutron absorption was treated in the standard linear absorption coefficient manner and was not found to be significant.
III. RESULTS AND DISCUSSION
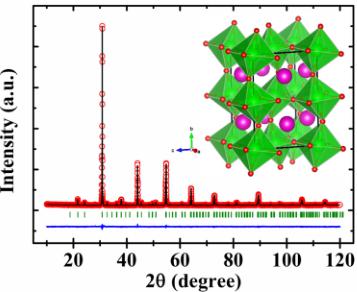
Figure 1(a) shows the Rietveld refinement of the x-ray diffraction pattern of polycrystalline \( EuZrO_{3} \) collected at room temperature using monochromatic (Cu \( K\alpha_{1} \) ) radiation. From the Rietveld refinement it is confirmed that this compound has an orthorhombic perovskite structure with the space group Pnma at room temperature. The sample contains a small amount of \( Eu_{2}Zr_{2}O_{7} \) as an impurity phase. \( EuZrO_{3} \) does not show any symmetry lowering or structural phase transition down to 10 K. \( EuTiO_{3} \) shows a structural phase from cubic \( Pm\bar{3}m \) to a tetragonal 14/mcm structure at 235 K [14]. Neutron diffraction data of \( EuZrO_{3} \) also show that the compound retains the orthorhombic space group Pnma down to the lowest temperature (T = 1.5 K), which will be discussed later. For the structural refinement, we have used the Pnma standard settings where Eu, Zr, O1, and O2 are located at the 4c, 4a, 8d, and 4c Wyckoff sites respectively. The structure of \( EuZrO_{3} \) consists of corner shared \( ZrO_{6} \) octahedra forming a perovskite network with the \( Eu^{2+} \) ions occupying the interstitial sites as shown in the inset of Fig. 1(a). In \( EuZrO_{3} \) the smaller tolerance factor, as compared to \( EuTiO_{3} \) leads to a rotation of the \( ZrO_{6} \) octahedra, resulting in a \( GdFeO_{3} \) type structural distortion.
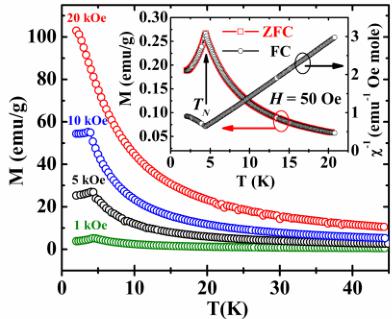
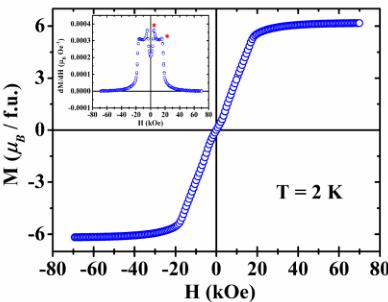
Temperature-dependent DC magnetization measurements on \( EuZrO_{3} \) at different magnetic fields are shown in Fig. 1(b). The temperature-dependent zero-field-cooled (ZFC) and field-cooled (FC) data recorded in the presence of an applied magnetic field of 50 Oe show a sharp kink at 4.4 K without any divergence between the ZFC and FC data down to our lowest temperature, as shown in the inset of Fig. 1(b). The kink at 4.4 K indicates the second-order magnetic phase transition from the paramagnetic to the antiferromagnetic state, which is also evident from the inverse susceptibility vs temperature plot shown in the inset of Fig. 1(b). Interestingly, the sharp kink gradually becomes broader with increasing magnetic field and it completely disappears at about 20 kOe, as is evident from the temperature-dependent magnetization data shown in Fig. 1(b). Isothermal magnetization data as a function of magnetic field recorded at 2 K [Fig. 1(c)] shows approximately linear behavior up to 20 kOe and then it tends toward saturation, indicating the appearance of a ferromagnetic state with the saturation magnetization value around \( 6.2\mu_{B} \) per formula unit, which is close to the spin-only moment of \( Eu^{2+} \) ( \( 7\mu_{B} \) ) ions. From Fig. 1(c) we see that initially the slope of the M vs H curve increases with magnetic field and then the slope changes at around 5 kOe, which is prominent from an inspection of the derivative plot as shown in the inset of Fig. 1(c). This phenomenon is similar to the spin-flop transition, where spins start orienting from the antiferromagnetic to ferromagnetic state. This continues with
(a)

(b)

(c)

FIG. 1. (a) Rietveld refinement of the XRD pattern of polycrystalline \( EuZrO_{3} \) acquired at room temperature using monochromatic (Cu \( K\alpha_{1} \) ) laboratory x rays. (Red open circles and black solid line indicates the experimental data and calculated profile, green ticks indicate the Bragg positions for the space group Pnma, and the blue line below is the difference between the observed and calculated profile). The inset shows the crystal structure of \( EuZrO_{3} \) . (b) Temperature-dependent DC magnetization data recorded at various magnetic fields under FC conditions. The inset shows the ZFC and FC magnetization and inverse susceptibility as a function of temperature at H = 50 Oe. (c) Isothermal magnetization data recorded at 2 K showing the spin-flop behavior at moderate magnetic field. The inset shows the first derivative of magnetization with respect to magnetic field plotted as a function of magnetic field.
increasing magnetic field up to 20 kOe, where all the spins are ferromagnetically aligned. In this context, it is to be noted

FIG. 2. The Rietveld refinement of the neutron data acquired at T = 10 K. The black crosses represent the neutron data and the red and blue lines represent the calculated spectrum and its difference to the data respectively. The black lines show the positions of the Bragg peaks. The agreement factors are \( R_{p} = 1.82\% \) , \( R_{wp} = 2.03\% \) , and Goodness of Fit, GoF = 1.65.
that the kink in the temperature-dependent magnetization data disappears in the presence of a magnetic field of 20 kOe. This spin flop behavior at moderate magnetic fields is attributed to the weak intersublattice interaction and the small magnetic anisotropy of the \( Eu^{2+} \) ion (S = 7/2, L = 0) [3].
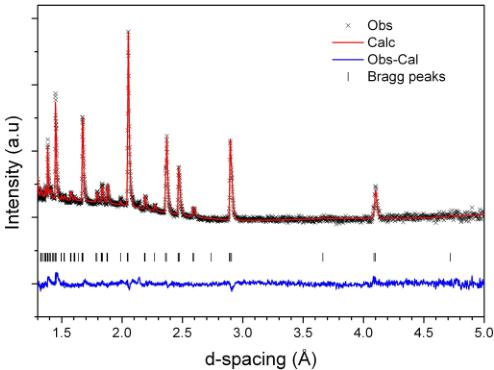
The Rietveld refinement of the neutron diffraction pattern recorded at 10 K (Fig. 2), above the peak in the magnetic susceptibility [Fig. 1(b)], confirms the orthorhombic structure with the Pnma space group [15]. The crystal structure parameters are reported in Table I. The refined thermal parameters (see Table I) are consistent with manageable absorption effects for our transmission geometry, as is the absence of a large sloping background in the diffraction data.
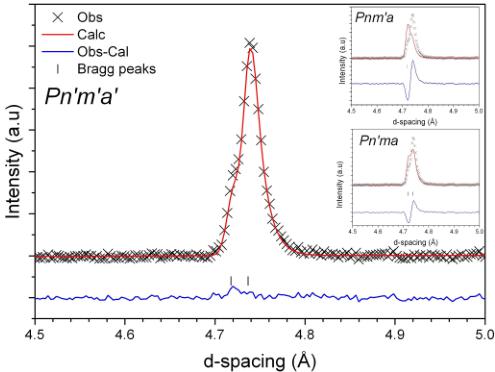
In Fig. 3 we show the high d-spacing region of the neutron powder diffraction data collected at 1.5 K. As the magnetically ordered phase appears in the \( EuZrO_{3} \) structure, magnetic contributions to some of the Bragg peaks become apparent, indicating a \( \mathbf{k} = (000) \) propagation vector. Neutron diffraction is an ideal technique for the internal calibration of the magnetic moment, as the magnetic scattering contribution gets added to the nuclear scattering as the temperature approaches the AFM transition. Although the presented data in Fig. 3 is broadly consistent with the earlier report [9], the higher resolution of our time-of-flight data allows us to distinguish the (110) and
TABLE I. Crystal structure parameters for \( EuZrO_{3} \) at 10 K in the Pnma space group. The refined cell parameters are \( a = 5.8172(2) \) Å, \( b = 8.1805(2) \) Å, \( c = 5.7833(2) \) Å.
| Atom | x | y | z | U_{\text{iso}}(\text{Å}^{2}) |
| Eu | 0.0237(11) | 0.25 | 0.4853(15) | 0.002(1) |
| Zr | 0 | 0 | 0 | 0.002(1) |
| O1 | 0.2784(9) | 0.0427(6) | 0.2123(9) | 0.007(2) |
| O2 | 0.4807(16) | 0.25 | 0.5702(16) | 0.007(2) |

FIG. 3. The experimental data (black) for the (110) and (011) reflections. In the main panel's Rietveld refinement, the red and blue lines represent the calculated spectrum and its difference from the data respectively. The neutron data were acquired at \( T = 1.5 \, K \) . The refinement indicates the alignment of spins on the \( Eu^{2+} \) ions along the c axis ( \( Pn'm'a' \) ). The right inset shows the calculated profile assuming that the spins are oriented along the a axis ( \( Pnm'a \) ) or b axis ( \( P'n'ma \) ), upper and lower curves respectively. Both of these models fail to accurately represent the data.
(011) reflections and becomes crucial to the magnetic structure solution presented here.
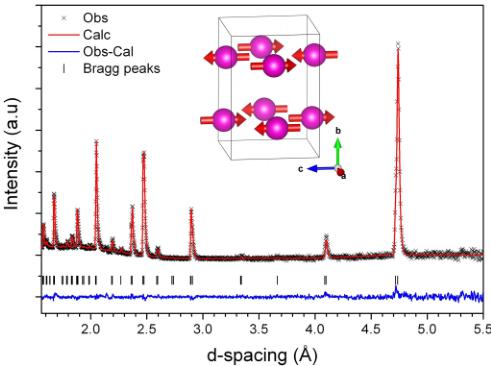
The best refinement of the 1.5 K data shown in Fig. 4 yields a G-type antiferromagnetic structure for the \( Eu^{2+} \) ions in the \( Pn'm'a' \) space group, with a moment of \( 6.40(2)\mu_{B} \) along the c direction, and this is quite close to the theoretically predicted moment of \( 6.82\mu_{B} \) for \( Eu^{2+} \) ions [16]. There is also agreement

FIG. 4. The Rietveld refinement of the neutron data acquired at \(T=1.5\ \mathrm{K}\). The black crosses represent the neutron data and the red and blue lines represent the calculated spectrum and its differences from the data respectively. The black lines show the positions of the Bragg peaks. The inset shows a schematic of the \(G\)-type magnetic structure in the \(Pn'm'a'\) magnetic space group. The agreement factors are \(R_{p}=1.99\%\), \(R_{wp}=2.25\%\), and GoF=1.62.
with our magnetometry measurements. The relative intensities of the (110) and (011) Bragg reflections were found to be strongly dependent on the preferred orientation of the spin of the \( Eu^{2+} \) ions along a particular axis of this orthorhombic structure. In the right panel of Fig. 3, we show the result of our refinements assuming different orientations of the \( Eu^{2+} \) magnetic moments, corresponding to the different magnetic space groups. The calculated data agree with the measured intensity profile only when we assume the spins are oriented along the c axis of this G-AFM magnetic structure. It is noteworthy that the closeness of the d spacing (and respective neutron wavelength) for these two reflections minimizes the effect of sample absorption on the subsequent interpretation. In the inset of Fig. 4 we show a schematic of this preferred spin orientation. It is clear from the calculated profiles that the assumption of spin orientation along the a axis ( \( Pnm'a \) ) and b axis ( \( P'n'ma \) ), presented in the right inset of Fig. 3, does not reproduce the measured data. It should be mentioned here that in the previous neutron diffraction measurement [9] the R factors for these three different magnetic structures were fairly similar, and the authors pointed out that the Eu moment lying along the a axis gives a slightly better fit. However, the better resolution of the data presented here clearly indicates that the moments lie along the c axis as shown in Figs. 3 and 4. Based on the aforementioned magnetic structure refinement, we determine that the Shubnikov group for the \( EuZrO_{3} \) magnetic structure is \( Pn'm'a'(mGM1-) \) where G-AFM is along the c direction instead of the earlier reported Shubnikov group \( Pnm'a(mGM4-) \) , where the magnetic moment is along the a direction [9]. Of these two magnetic space groups, the symmetry of the first one allows a linear magnetoelectric effect while the latter does not [17]. It is important to highlight the difference between the moment direction in the two compounds \( EuZrO_{3} \) and \( EuTiO_{3} \) . In order to avoid misunderstanding due to the different cell choice and space group of the two compounds, it is worthwhile to describe the moment direction with respect to the \( BO_{6} \) octahedra. In the case of the \( EuTiO_{3} \) compound the \( Eu^{2+} \) moments point towards the void left by the octahedra networks, whereas in the case of the \( EuZrO_{3} \) the \( Eu^{2+} \) moments point towards the apical oxygen of the \( BO_{6} \) polyhedra.
To gain more insight on the magnetoelectric coupling in the \( EuBO_{3} \) (B = Ti,Zr) compounds and to describe the different symmetries of the coupling constants observed in the literature [8,17], we perform a magnetic symmetry analysis. By writing the Landau theory free energy F in terms of the ith component of an applied magnetic field H and an applied electric field E, one can describe the magnetoelectric effect.
The magnetic structure of the \( EuTiO_{3} \) compound was solved by means of neutron and x-ray magnetic scattering as a G-type structure along the diagonal of the tetragonal ab plane \( ^{[8]} \) . The parent nuclear structure of the \( EuTiO_{3} \) compound has tetragonal symmetry with the \( I4/mcm \) space group; in Table II the atom positions from Ref. [14] are reported. Using the ISODISTORT software [18], we find that this solution corresponds to the \( Fm^{\prime}mm \) symmetry with a cell related to the parent one by the transformation \( (\bar{1}\bar{1}0,\bar{1}10,00\bar{1}) \) and an origin shift of \( (\frac{1}{2},0,\frac{1}{2}) \) . The phase transition is therefore driven by the mGM5- representation with order parameter direction \( P3(a,a) \) . Using the invariant polynomials of the
TABLE II. Crystal structure parameters for EuTiO₃ taken from Ref. [14] in the I4/mcm space group with cell parameters a = 5.507642(9) Å, c = 7.805161(25) Å.
| Atom | x | y | z |
| Eu | 0 | 0.5 | 0.25 |
| Ti | 0 | 0 | 0 |
| O1 | 0 | 0 | 0.25 |
| O2 | 0.2353(4) | 0.7353(4) | 0 |
magnetic point group we construct the free energy up to fourth order:
\[ \begin{aligned}F(E,H)&=\epsilon_{ik}E_{i}E_{k}+\chi_{ik}H_{i}H_{k}\\&\quad+\alpha_{ik}E_{i}H_{k}+\delta_{iklm}E_{i}E_{k}H_{l}H_{m}.\end{aligned} \quad (1) \]
The expansion of the free energy indicates the possibility of linear and biquadratic magnetoelectric coupling in the system. Regarding the linear magnetoelectric tensor \( \alpha_{ik} \) , the only allowed coefficients from the \( m^{\prime}mm \) magnetic point group are the off-diagonal terms \( \alpha_{23} \) and \( \alpha_{32} \) . The fourth-rank tensor \( \delta_{iklm} \) is related to the giant magnetocapacitance effect at the magnetic transition [19]. It transforms as a polar fourth-rank tensor, and the allowed components are reported in Table III in the contracted matrix form [17].
Regarding \( EuZrO_{3} \) , our magnetic symmetry analysis indicates a G-type structure with the magnetic symmetry \( Pn'm'a'(mGM1- \) representation with order parameter direction \( P1(a) \) ). The Landau free energy, constructed on the basis of the magnetic point group, is the same as for the \( EuTiO_{3} \) compound and, as a consequence, linear and biquadratic magnetoelectric coupling are also allowed. Given that the magnetic point group symmetry is different in the two cases, the symmetries of the allowed linear magnetoelectric tensors are dissimilar. Indeed, for \( EuZrO_{3} \) , only the diagonal \( \alpha_{ii} \) terms are different from zero. Conversely the \( \delta_{iklm} \) tensor has the same internal symmetry for the two materials, though, of course, the values of the tensor components may be different. This symmetry analysis indicates the different nature of the magnetoelectric coupling in these two systems, caused by the different magnetic space groups of the ordered structure. Not surprisingly, the symmetry analysis cannot predict the strength of the magnetoelectric coupling, given that this depends on the specific microscopic coupling mechanism.
TABLE III. Magnetoelectric tensor components \(\alpha_{ik}\) and \(\delta_{iklm}\) for \(\mathrm{EuBO}_{3}\) (\(B=\mathrm{Ti}, \mathrm{Zr}\)).
| EuTiO3 | EuZrO3 | |||
| Magnetic point group | m'mm | m'm'm' | ||
| αik | (0 0 0) | (α11 0 0) | (α11 0 0) | (α22 0 0) |
| (0 α32 0) | (0 0 α33) | (0 0 α33) | (α33 0 0) | |
| δiklm | (δ11 δ12 δ13 0 0 0) | (δ12 δ22 δ23 0 0 0) | (δ21 δ32 δ33 0 0 0) | (δ31 δ32 δ33 0 0 0) |
| (0 0 0) | (0 0 0) | (δ44 0 0) | (δ55 0 0) | |
| (0 0 0) | (0 0 0) | (δ66 0 0) | ||

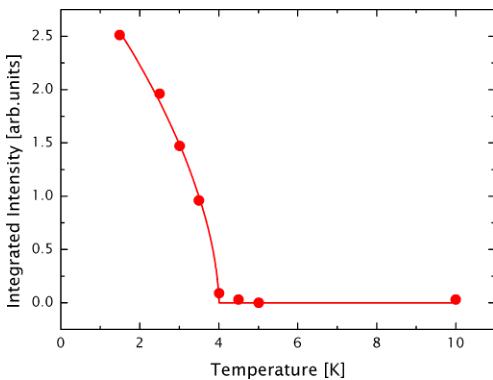
FIG. 5. The background corrected integrated intensity of the (110) and (011) reflections is plotted as a function of temperature. The intensity increases below the AFM transition temperature of 4.1 K. The solid line is the power-law fit described in the text.
For example, the partially covalent Ti-O bond in \( EuTiO_{3} \) favors a soft phonon mode which then couples to the magnetic excitations [20], in contrast to the more ionic-like Zr-O bond in \( EuZrO_{3} \) [7]. This then suggests a larger magnetoelectric coupling in the Ti system over the Zr one, as observed experimentally.
Finally, we now analyze the magnetic scattering as the temperature is lowered by plotting the background corrected integrated intensity of the (110) and (011) peaks combined, as shown in Fig. 5. The obtained data have been fitted with a power law (the red curve) of the form \( I \propto \left(\frac{T - T_{c}}{T_{c}}\right)^{2\beta} \) yielding a \( T_{c} \) of 4.0(1) K and \( \beta = 0.29(4) \) . The critical exponent \( \beta = 0.29(4) \) is consistent with the asymptotic three-dimensional (3D) Ising model. It may be noted here that the
[1] J. T. Heron, J. L. Bosse, Q. He, Y. Gao, M. Trassin, L. Ye, J. D. Clarkson, C. Wang, J. Liu, S. Salahuddin, D. C. Ralph, D. G. Schlom, J. Iniguez, B. D. Huey, and R. Ramesh, Deterministic switching of ferromagnetism at room temperature using an electric field, Nature (London) 516, 370 (2014).
[2] I. A. Sergienko and E. Dagotto, Role of the Dzyaloshinskii-Moriya interaction in multiferroic perovskites, Phys. Rev. B 73, 094434 (2006).
[3] H. Akamatsu, K. Fujita, H. Hayashi, T. Kawamoto, Y. Kumagai, Y. Zong, K. Iwata, F. Oba, I. Tanaka, and K. Tanaka, Crystal and electronic structure and magnetic properties of divalent europium perovskite oxides \( EuMO_{3} \) (M = Ti, Zr, and Hf): Experimental and first-principles approaches, Inorg. Chem. 51, 4560 (2012).
[4] B. J. Kennedy, G. Murphy, E. Reynolds, M. Avdeev, H. E. R. Brand, and T. Kolodiazhnyi, Studies of the antiferrodistortive transition in \( EuTiO_{3} \) , J. Phys.: Condens. Matter 26, 495901 (2014).
[5] J. H. Lee, L. Fang, E. Vlahos, X. Ke, Y. W. Jung, L. F. Kourkoutis, J.-W. Kim, P. J. Ryan, T. Heeg, M. Roeckerath, V. Goian, M.
AFM order of an epitaxial \( EuTiO_{3} \) film was found to follow either the 3D Heisenberg model with an exponent of \( \beta = 0.385 \) or larger \( \beta = 0.496 \) , depending upon the strain induced by the substrate [21]. This compares with 0.373 in a bulk single crystal [22]. The \( Eu^{2+} \) moments in both the Zr [22] and Ti [23] are treated as Heisenberg-like, given their spin-only moment. Interestingly, in our zero field data we see evidence of a reduced \( \beta \) consistent with an Ising-like symmetry. This interpretation is supported by the weak spin-flop transition which is seen in the magnetometry data and implies a weak uniaxial anisotropy which is easily overcome with an applied field > 5 kOe. As reported, this is only a weak anisotropy given the isotropic nature of the \( 4f \) electrons and the weak sublattice interactions [3].
In conclusion, our results of a high-resolution neutron powder diffraction study clearly demonstrate that the moments of the \( Eu^{2+} \) ions in \( EuZrO_{3} \) are oriented along the c axis; this is in contrast to the spin orientation along diagonal of ab plane in the case of \( EuTiO_{3} \) . Moreover, by applying Landau theory we indicate the symmetry allowed magnetoelectric coupling in the \( EuBO_{3} \) (B = Ti,Zr) compounds, and highlight the different tensor properties in the two materials induced by the different magnetic point groups which describe the differing magnetoelectric behaviors. The presented magnetic structure obtained (see inset of Fig. 4) in this perovskite oxide is intriguing given that first-principles calculations [24,25] have revealed that these materials are critically balanced between the anti- and ferro-magnetic states and show a spin-flop transition at moderate magnetic fields [Fig. 1(c)]. It will be interesting to study the magnetic structure of \( EuZrO_{3} \) as a function of strain [5] and hydride substitution [6] as demonstrated for \( EuTiO_{3} \) .
ACKNOWLEDGMENT
We wish to thank Science and Technology Facilities Council for the provision of neutron beamtime.
Bernhagen, R. Uecker, P. C. Hammel, K. M. Rabe, S. Kamba, J. Schubert, J. W. Freeland, D. A. Muller, C. J. Fennie, P. Schiffer, V. Gopalan, E. Johnston-Halperin, and D. G. Schlom, A strong ferroelectric ferromagnet created by means of spin-lattice coupling, Nature (London) 466, 954 (2010).
[6] T. Yamamoto, R. Yoshii, G. Bouilly, Y. Kobayashi, K. Fujita, Y. Kususe, Y. Matsushita, K. Tanaka, and H. Kageyama, An antiferro-to-ferromagnetic transition in \( EuTiO_{3-x}H_{x} \) induced by hydride substitution, Inorg. Chem. 54, 1501 (2015).
[7] T. Kolodiazhnyi, K. Fujita, L. Wang, Y. Zong, K. Tanaka, Y. Sakka, and E. Takayama-Muromachi, Magnetodielectric effect in \( EuZrO_{3} \) , Appl. Phys. Lett. 96, 252901 (2010).
[8] V. Scagnoli, M. Allieta, H. Walker, M. Scavini, T. Katsufuji, L. Sagarna, O. Zaharko, and C. Mazzoli, \( EuTiO_{3} \) magnetic structure studied by neutron powder diffraction and resonant x-ray scattering, Phys. Rev. B 86, 094432 (2012).
[9] M. Avdeev, B. J. Kennedy, and T. Kolodiazhnyi, Neutron powder diffraction study of the magnetic structure of \( EuZrO_{3} \) , J. Phys.: Condens. Matter 26, 095401 (2014).
[10] H. Ai-Yuan, Q. Guo-Ping, W. Zhi-Min, and C. Yu-Ting, Possible magnetic structures of \( EuZrO_{3} \) , Chin. Phys. B 24, 067501 (2015).
[11] J. Rodríguez-Carvajal, Recent advances in magnetic structure determination by neutron powder diffraction, Physica B: Condens. Matter 192, 55 (1993).
[12] L. C. Chapon, P. Manuel, P. G. Radaelli, C. Benson, L. Perrott, S. Ansell, N. J. Rhodes, D. Raspino, D. Duxbury, E. Spill, and J. Norris, Wish: The new powder and single crystal magnetic diffractometer on the second target station, Neutron News 22, 22 (2011).
[13] V. Petříček, M. Dušek, and L. Palatinus, Crystallographic computing system JANA2006: General features, Z. Kristallogr. 229, 345 (2014).
[14] M. Allieta, M. Scavini, L. J. Spalek, V. Scagnoli, H. C. Walker, C. Panagopoulos, S. S. Saxena, T. Katsufuji, and C. Mazzoli, Role of intrinsic disorder in the structural phase transition of magnetoelectric \( EuTiO_{3} \) , Phys. Rev. B 85, 184107 (2012).
[15] V. Viallet, J.-F. Marucco, J. Saint, M. Herbst-Ghysel, and N. Dragoe, Structural, magnetic and electrical properties of a perovskite containing divalent europium \( EuZrO_{3} \) , J. Alloys Compd. 461, 346 (2008).
[16] Z.-L. Zhu, J.-H. Gu, Y. Jia, and X. Hu, Antiferromagnetism of perovskite \( EuZrO_{3} \) from a first-principles study, Physica B: Condens. Matter 406, 3985 (2011).
[17] International Tables for Crystallography Volume D: Physical Properties of Crystals, edited by A. Authier (International Union of Crystallography, Chester, UK, 2013).
[18] B. J. Campbell, H. T. Stokes, D. E. Tanner, and D. M. Hatch, ISODISPLACE: A web-based tool for exploring structural distortions, J. Appl. Crystallogr. 39, 607 (2006).
[19] V. V. Shvartsman, P. Borisov, W. Kleemann, S. Kamba, and T. Katsufuji, Large off-diagonal magnetoelectric coupling in the quantum paraelectric antiferromagnet \( EuTiO_{3} \) , Phys. Rev. B 81, 064426 (2010).
[20] V. Goian, S. Kamba, J. Hlinka, P. Vaněk, A. A. Belik, T. Kolodiazhnyi, and J. Petzelt, Polar phonon mixing in magnetoelectric \( EuTiO_{3} \) , Eur. Phys. J. B 71, 429 (2009).
[21] P. J. Ryan, J.-W. Kim, T. Birol, P. Thompson, J.-H. Lee, X. Ke, P. S. Normile, E. Karapetrova, P. Schiffer, S. D. Brown, C. J. Fennie, and D. G. Schlom, Reversible control of magnetic interactions by electric field in a single-phase material, Nat. Commun. 4, 1334 (2013).
[22] J.-W. Kim, P. Thompson, S. Brown, P. S. Normile, J. A. Schlueter, A. Shkabko, A. Weidenkaff, and P. J. Ryan, Emergent Superstructural Dynamic Order Due to Competing Antiferroelectric and Antiferrodistortive Instabilities in Bulk \( EuTiO_{3} \) , Phys. Rev. Lett. 110, 027201 (2013).
[23] T. Katsufuji and H. Takagi, Coupling between magnetism and dielectric properties in quantum paraelectric \( EuTiO_{3} \) , Phys. Rev. B 64, 054415 (2001).
[24] C. J. Fennie and K. M. Rabe, Magnetic and Electric Phase Control in Epitaxial \( EuTiO_{3} \) from First Principles, Phys. Rev. Lett. 97, 267602 (2006).
[25] R. Ranjan, H. S. Nabi, and R. Pentcheva, Electronic structure and magnetism of \( EuTiO_{3} \) : A first-principles study, J. Phys.: Condens. Matter 19, 406217 (2007).