| Transition Temperature | 0.15 K |
|---|---|
| Experiment Temperature | 0.052 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | Fd-3m (#227) |
| Magnetic Space Group | I41/am'd' (#141.557) |
| Magnetic Point Group | 4/mm'm' (15.6.58) |
| Lattice Parameters | 10.2766(5) 10.27660 10.27660 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1103/physrevlett.110.127207 |
| Reference | A. Yaouanc, P.D. de Reotier, P. Bonville, J.A. Hodges, V. Glazkov, L. Keller, V. Sikolenko, M. Bartkowiak, A. Amato, C. Baines, P.J.C. King, P.C.M. Gubbens and A. Forget, Physical Review Letters (2013) 110. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Yb1 | Yb | -0.13 | -0.13 | 1.03 | 1.05 |
Title
Dynamical Splayed Ferromagnetic Ground State in the Quantum Spin Ice \( Yb_{2}Sn_{2}O_{7} \)
Authors
A. Yaouanc,\(^{1,*}\) P. Dalmas de Réotier,\(^{1}\) P. Bonville,\(^{2}\) J. A. Hodges,\(^{2}\) V. Glazkov,\(^{1,3}\) L. Keller,\(^{4}\) V. Sikolenko,\(^{4}\) M. Bartkowiak,⁵ A. Amato,⁶ C. Baines,⁶ P. J. C. King,⁷ P. C. M. Gubbens,⁸ and A. Forget²
\( ^{1} \) Institut Nanosciences et Cryogénie, SPSMS, CEA and Université Joseph Fourier, F-38054 Grenoble, France \( ^{2} \) CEA/DSM, Institut Rayonnement Matière de Saclay, SPEC, 91191 Gif-sur-Yvette, France \( ^{3} \) P.L. Kapitza Institute for Physical Problems, RAS, 119334 Moscow, Russia \( ^{4} \) Laboratory for Neutron Scattering, Paul Scherrer Institute, CH-5232 Villigen-PSI, Switzerland \( ^{5} \) Laboratory for Developments and Methods, Paul Scherrer Institute, CH-5232 Villigen-PSI, Switzerland \( ^{6} \) Laboratory for Muon-Spin Spectroscopy, Paul Scherrer Institute, CH-5232 Villigen-PSI, Switzerland \( ^{7} \) Rutherford Appleton Laboratory, ISIS Facility, Chilton OX11 0QX, United Kingdom \( ^{8} \) FAME, R3, Applied Sciences, Delft University of Technology, 2629JB Delft, The Netherlands \( ^{*} \) Also at Laboratory for Muon-Spin Spectroscopy, Paul Scherrer Institute, CH-5232 Villigen-PSI, Switzerland.
Materials Studied
\( Yb_{2}Sn_{2}O_{7} \) (polycrystalline)
Key Information
- Crystal structure / space group: Cubic \( Fd\bar{3}m \)
- Magnetic ordering type and temperature:
- First order transition at \( T_t \approx 0.15 \) K.
- Long-range magnetically ordered ground state.
- Splayed ferromagnetism: moments are noncoplanar, directed away from a common fourfold cubic axis along four different directions.
- Net ferromagnetic exchange interaction.
- Propagation vector(s): \( k = 0 \)
- Magnetic moments:
- Ordered moment per \( Yb^{3+} \) ion: \( 1.1\mu_{B} \) (Mössbauer), \( 1.05(2)\mu_{B} \) (neutron diffraction).
- Paramagnetic moment: \( m_{para}=3.05(5)\mu_{B}/Yb \).
- Moment direction: Lies at \( \approx10^{\circ} \) to a common fourfold cubic axis.
- Angle relative to local \( \langle 111 \rangle \) direction: \( \phi = 65^{\circ} \).
- Lattice parameters: \( a = 10.2766(5) \) Å
- Any other critical measured values:
- Curie-Weiss temperature: \( \theta_{CW}=0.53(5) \) K.
- Oxygen position parameter (2mm site): \( x = 0.340(1) \).
- Spectroscopic g factors of \( Yb^{3+} \) ground state Kramers doublet: \( g_{z} \simeq 1.1 \) and \( g_{\perp} \approx 4.2 \).
- Anisotropy ratio \( r = g_{\perp} / g_{z} \): 3.8.
- Hyperfine field magnitude: 110 (2) T.
- Spin fluctuation rate in ordered state ( \( \mu \) SR): \( \nu_{c,\mu} \approx 3 \times 10^{6} s^{-1} \) (megahertz range).
- Spin fluctuation rate in ordered state (Mössbauer upper bound): \( 10^{8} \) s \( ^{-1} \).
- Activation energy for fluctuations above \( T_t \): 0.20 K.
- Root-mean-square of dipolar field distribution at muon site: \( \Delta_{para}\simeq73\;mT \).
Synthesis Method
Not available
Abstract
From magnetic, specific heat, \( {}^{170} \) Yb Mössbauer effect, neutron diffraction, and muon spin relaxation measurements on polycrystalline \( Yb_{2}Sn_{2}O_{7} \) , we show that below the first order transition at 0.15 K all of the \( Yb^{3+} \) ions are long-range magnetically ordered and each has a moment of \( 1.1\mu_{B} \) which lies at \( \approx10^{\circ} \) to a common fourfold cubic axis. The four sublattice moments have four different directions away from this axis and are therefore noncoplanar. We term this arrangement splayed ferromagnetism. This ground state has a dynamical component with a fluctuation rate in the megahertz range. The net ferromagnetic exchange interaction has an anisotropy that favors the local threefold axis. We discuss our results in terms of the phase diagram proposed by Savary and Balents [Phys. Rev. Lett. 108, 037202 (2012)] for a pyrochlore lattice of Kramers 1/2 effective spins.
Main Content Summary
This paper presents a comprehensive experimental study of the pyrochlore compound \( Yb_{2}Sn_{2}O_{7} \), investigating its low-temperature magnetic properties using a combination of macroscopic and microscopic techniques. The motivation stems from the interest in pyrochlore lattices as potential quantum spin liquid candidates, with \( Yb_{2}Sn_{2}O_{7} \) being considered a better test case than \( Yb_{2}Ti_{2}O_{7} \) due to potentially simpler exchange interactions. The study aims to characterize the ground state and its dynamics, relating the findings to theoretical predictions for quantum spin ice systems.
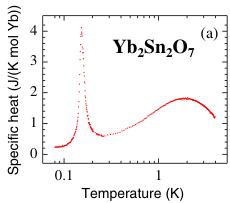
Macroscopic measurements reveal a net ferromagnetic exchange interaction, indicated by a positive Curie-Weiss temperature \( \theta_{CW}=0.53(5) \) K and a paramagnetic moment \( m_{para}=3.05(5)\mu_{B}/Yb \). Specific heat measurements show a sharp, fairly symmetric peak at \( T_t \approx 0.15 \) K, signaling a phase transition, and a broad hump centered around 2 K, attributed to exchange splitting and magnetic correlations. This broad hump is a common feature in frustrated magnets and is not a crystal-field Schottky anomaly.
Microscopic probes, including \( {}^{170} \) Yb Mössbauer spectroscopy and powder neutron diffraction, confirm a first-order magnetic phase transition at \( T_t \). Mössbauer data show the coexistence of paramagnetic and magnetically ordered moments around \( T_t \), and below \( \approx 0.09 \) K, all \( Yb^{3+} \) ions carry a spontaneous magnetic moment of \( m_{sp} = 1.1\mu_{B} \). This moment is tilted at an angle \( \phi = 65^{\circ} \) relative to the local \( \langle 111 \rangle \) direction, implying an easy-plane g-tensor anisotropy but a strong easy-axis exchange anisotropy. Neutron diffraction confirms long-range magnetic order with a \( k=0 \) propagation vector in the cubic \( Fd\bar{3}m \) structure, yielding \( m_{sp} = 1.05(2)\mu_{B} \) and a lattice parameter \( a = 10.2766(5) \) Å. The magnetic structure is identified as "splayed ferromagnetism," where the four magnetic moments within a tetrahedron are noncoplanar, directed away from a common fourfold cubic axis.
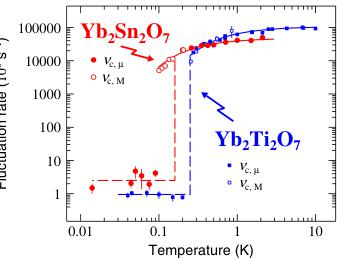
Muon spin relaxation ( \( \mu \) SR) measurements provide crucial insights into the spin dynamics. Above \( T_t \), the system is in a fast fluctuation limit, with the relaxation rate increasing upon cooling, consistent with slowing down of exchange-coupled moments. Below \( T_t \), despite long-range order, the spectral shape shows persistent dynamics, with a fluctuation rate in the megahertz range ( \( \nu_{c,\mu} \approx 3 \times 10^{6} s^{-1} \)). This abrupt decrease in fluctuation rate at \( T_t \) is similar to that observed in \( Yb_{2}Ti_{2}O_{7} \). The persistent dynamics in the ordered state is a key finding, suggesting that the ground state is not static but possesses a dynamical component.
Conclusion
In summary the pyrochlore \( Yb_{2}Sn_{2}O_{7} \) is characterized by the following low temperature properties. The net interactions between the \( Yb^{3+} \) moments are weakly ferromagnetic \( [\theta_{\mathrm{CW}}=0.53(5)\mathrm{K}] \) . Owing to the small size of the ordered magnetic moments \( (1.1\mu_{\mathrm{B}}) \) the dipolar interaction energy is small. Together with an easy-plane g-tensor anisotropy and a strong easy-axis exchange anisotropy, these properties qualify \( Yb_{2}Sn_{2}O_{7} \) as a quantum or exchange spin ice candidate. The system undergoes a first order phase transition at \( T_{t}\simeq0.15~K \) associated with a degeneracy lifting whose characteristics are controlled by the specific exchange and g-factor anisotropies. The \( Yb^{3+} \) magnetic moments which are not coplanar are nevertheless nearly ferromagnetically aligned along a cubic fourfold axis—the canting angle is \( \arctan(\sqrt{(m_{\mathrm{sp}}^{3})^{2}+(m_{\mathrm{sp}}^{7})^{2}}/m_{\mathrm{sp}}^{7})\simeq10^{\circ} \) —while the components transverse to this axis are oriented along twofold axes and cancel in a unit cell. We term this type of order splayed ferromagnetism.
The \( Yb_{2}Sn_{2}O_{7} \) ground state properties are closely related to the CFM and Higgs FM phases recently predicted [7]. A robust evidence for the presence or absence of an energy gap and its characterization would help to distinguish between these two phases [44]. The analysis of the broad hump measured by specific heat around 2 K, besides the sharp peak at \( T_{t} \) [10], as well as the constraint imposed by the \( 65^{\circ} \) angle between the \( Yb^{3+} \) moment and the local trigonal axis should provide clues for the Hamiltonian parameters and the location of \( Yb_{2}Sn_{2}O_{7} \) in the phase diagram. A further challenge for the theory is to find a physical mechanism for the persistent spin dynamics which is observed as the temperature goes to zero.
Dynamical Splayed Ferromagnetic Ground State in the Quantum Spin Ice \( Yb_{2}Sn_{2}O_{7} \)
A. Yaouanc,\(^{1,*}\) P. Dalmas de Réotier,\(^{1}\) P. Bonville,\(^{2}\) J. A. Hodges,\(^{2}\) V. Glazkov,\(^{1,3}\) L. Keller,\(^{4}\) V. Sikolenko,\(^{4}\)
M. Bartkowiak,⁵ A. Amato,⁶ C. Baines,⁶ P. J. C. King,⁷ P. C. M. Gubbens,⁸ and A. Forget²
\( ^{1} \) Institut Nanosciences et Cryogénie, SPSMS, CEA and Université Joseph Fourier, F-38054 Grenoble, France
\( ^{2} \) CEA/DSM, Institut Rayonnement Matière de Saclay, SPEC, 91191 Gif-sur-Yvette, France
\( ^{3} \) P.L. Kapitza Institute for Physical Problems, RAS, 119334 Moscow, Russia
\( ^{4} \) Laboratory for Neutron Scattering, Paul Scherrer Institute, CH-5232 Villigen-PSI, Switzerland
\( ^{5} \) Laboratory for Developments and Methods, Paul Scherrer Institute, CH-5232 Villigen-PSI, Switzerland
\( ^{6} \) Laboratory for Muon-Spin Spectroscopy, Paul Scherrer Institute, CH-5232 Villigen-PSI, Switzerland
\( ^{7} \) Rutherford Appleton Laboratory, ISIS Facility, Chilton OX11 0QX, United Kingdom
\( ^{8} \) FAME, R3, Applied Sciences, Delft University of Technology, 2629JB Delft, The Netherlands
(Received 14 November 2012; revised manuscript received 24 January 2013; published 20 March 2013)
From magnetic, specific heat, \( {}^{170} \) Yb Mössbauer effect, neutron diffraction, and muon spin relaxation measurements on polycrystalline \( Yb_{2}Sn_{2}O_{7} \) , we show that below the first order transition at 0.15 K all of the \( Yb^{3+} \) ions are long-range magnetically ordered and each has a moment of \( 1.1\mu_{B} \) which lies at \( \approx10^{\circ} \) to a common fourfold cubic axis. The four sublattice moments have four different directions away from this axis and are therefore noncoplanar. We term this arrangement splayed ferromagnetism. This ground state has a dynamical component with a fluctuation rate in the megahertz range. The net ferromagnetic exchange interaction has an anisotropy that favors the local threefold axis. We discuss our results in terms of the phase diagram proposed by Savary and Balents [Phys. Rev. Lett. 108, 037202 (2012)] for a pyrochlore lattice of Kramers 1/2 effective spins.
DOI: 10.1103/PhysRevLett.110.127207
PACS numbers: 75.40.−s, 75.25.−j, 76.75.+i, 76.80.+y
There is much interest in the pyrochlore lattice compounds \( R_{2}M_{2}O_{7} \) , where R is a rare earth and M is a transition or sp metal. The chief motivation is that the R ions form corner-sharing tetrahedra such that the interionic interactions are prone to geometrical frustration. A number of different situations have been encountered depending on the form, sign, size, and anisotropy of the various possible interionic interactions [1]. The quest for the spin liquid state, namely a ground state where the spins are strongly correlated while they show no long-range order and are dynamical, has motivated important theoretical and experimental efforts. For example, pyrochlores like \( Ho_{2}Ti_{2}O_{7} \) , where the R = Ho ion has a large axial anisotropy and where there is a net ferromagnetic interaction, evidence magnetic frustration which shows analogies with the positional fluctuations of the protons in ice. Such systems have been labeled “spin ice” [2]. Their behavior is essentially driven by the classical dipolar interaction between the spins [3]. More recently, the interest has focused on the quantum spin liquid model where exchange interactions determine the low temperature behavior [4–6] and the possibility has been raised that the pyrochlore \( Yb_{2}Ti_{2}O_{7} \) is a physical realization of this model [7–10]. Even more striking, four phases are predicted from a gauge mean field theory depending on values of the symmetry dictated nearest neighbor Hamiltonian parameters: two Higgs phases either ferromagnetic (FM) or antiferromagnetic (AFM), the quantum spin liquid phase, and a new exotic phase, the Coulombic ferromagnetic (CFM) phase [7]. Three types of magnetic excitations which are either gapped or not can be observed: they are respectively associated with an effective electric charge (gapped), an effective magnetic charge (gapped), and an artificial photon (gapless) [9]. Fractional spin excitations are present in the CFM phase.
The Higgs FM phase has recently been proposed for \( Yb_{2}Ti_{2}O_{7} \) at low temperature [11]. However, a long-standing controversy exists as to the intrinsic presence of magnetic Bragg reflections in this compound [11–17]. In this respect, recent studies show the variability of the low temperature physical response of this system [11,18,19].
Beside the \( R_{2}Ti_{2}O_{7} \) series, the pyrochlore rare earth stannates \( R_{2}Sn_{2}O_{7} \) have also attracted strong interest [1,20] since both series share similar R anisotropies and a nonmagnetic M sublattice. As an illustration of the similarities of the two families of pyrochlores, \( Ho_{2}Sn_{2}O_{7} \) is a dipolar spin ice, like \( Ho_{2}Ti_{2}O_{7} \) [21]. Comparing the two series, it seems that the titanates are more influenced by exchange interactions beyond the nearest neighbors than the stannates [22,23]. Therefore \( Yb_{2}Sn_{2}O_{7} \) could be a better test case than \( Yb_{2}Ti_{2}O_{7} \) for the current theoretical works dedicated to quantum spin liquids which consider a nearest neighbor Hamiltonian on the pyrochlore lattice [7,8,10,11].
Here we present a detailed study of \( Yb_{2}Sn_{2}O_{7} \) . Its ground state is a long-range magnetically ordered phase, essentially of the ferromagnetic type, i.e., one of the FM or CFM phases predicted by the gauge mean field theory. We first report bulk macroscopic properties, followed by
microscopic results obtained from \( {}^{170}Yb \) Mössbauer spectroscopy, powder neutron diffraction, and muon spin relaxation ( \( \mu \) SR).
The low temperature inverse susceptibility follows a Curie-Weiss law: \( \chi^{-1}(T)=(\nu/\mu_{0})[3k_{\mathrm{B}}(T-\theta_{\mathrm{CW}})]/m_{\mathrm{para}}^{2} \) , where \( \nu \) is the volume per \( Yb^{3+} \) ion. Fitting the data between 2 and 10 K we measure for the paramagnetic moment \( m_{para}=3.05(5)\mu_{B}/Yb \) and the Curie-Weiss temperature \( \theta_{CW}=0.53(5) \) K, indicating a net ferromagnetic exchange interaction as found previously [20].
The heat capacity, measured by the dynamic adiabatic method in the range 0.08–4 K, is presented in Fig. 1(a). Its main features are a fairly symmetric narrow peak signaling a transition at \( T_{r} \approx 0.15 \) K, and a broad hump centered at about 2 K. As this hump cannot correspond to a crystal-field Schottky anomaly (the lowest excited crystal field doublet lies at \( \approx 50 \) meV above the ground level [24]), it is attributed to the exchange splitting of the ground Kramers doublets associated with the onset of magnetic correlations. This is a commonly observed feature in frustrated magnets [25]. A tentative analysis of the low temperature heat capacity is presented in the Supplemental Material [26].
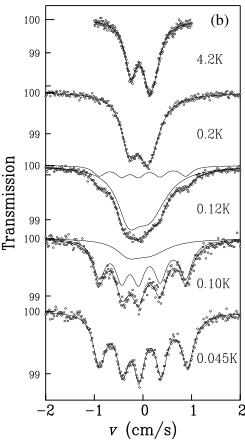
The \( {}^{170} \) Yb Mössbauer spectroscopy measurements [see Fig. 1(b)] were made down to 0.045 K. The experimental details and analysis protocol are given in Refs. [12,27].


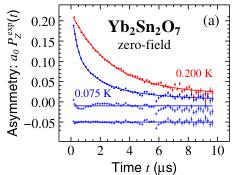
FIG. 1 (color online). (a) Low temperature heat capacity of \( Yb_{2}Sn_{2}O_{7} \) . (b) \( {}^{170}Yb \) absorption Mössbauer spectra at selected temperatures. The decomposition of the spectra at 0.12 and 0.10 K in terms of two subspectra, pure quadrupole and quadrupole with magnetic hyperfine interactions, is indicated. (c) Thermal evolution of the magnitude of the \( Yb^{3+} \) magnetic moments detected by Mössbauer spectroscopy and (d) the percentage fraction of the \( Yb^{3+} \) ions carrying a magnetic moment. Here the lines are guides to the eye. The behaviors shown in panels (c) and (d) are the signature of a first order transition.
At 4.2 K a pure quadrupole hyperfine spectrum is observed [26]. The size and symmetry of the quadrupole hyperfine interaction are independent of temperature. On decreasing the temperature, the line shapes broaden progressively [see Fig. 1(b) at 0.2 K] due to the build up of short range correlations amongst the \( Yb^{3+} \) moments as also evidenced by the specific heat measurements. These correlations lead to a decrease of the \( Yb^{3+} \) spin fluctuation rate \( \nu_{c,M} \) so that it enters the \( {}^{170}Yb \) Mössbauer frequency window. \( \nu_{c,M}(T) \) is displayed in Fig. 2. As the temperature is lowered through \( T_{f} \) , an additional magnetic hyperfine interaction initially appears on some of the \( Yb^{3+} \) spins. The relative weight of this fraction increases as the temperature is decreased [see Fig. 1(d)] such that below \( \approx 0.09 \) K the pure quadrupole subspectrum has disappeared and only the mixed quadrupole with magnetic hyperfine spectrum remains. This behavior evidences that paramagnetic and magnetically ordered moments coexist in a small temperature range around the transition; this is the hallmark of a first order transition. Below the transition, the fluctuation rate is below the sensitivity limit of the technique ( \( 10^{8} \) s \( ^{-1} \) ), but it may be assessed by \( \mu \) SR (see below). The hyperfine field magnitude, proportional to the magnetic order parameter, i.e., to the spontaneous magnetic moment \( m_{sp} \) , is 110 (2) T. It corresponds to \( m_{sp} = 1.1\mu_{B} \) , a value common to all the \( Yb^{3+} \) moments of the compound and which is temperature independent [see Fig. 1(c)]. These moments which are parallel to the hyperfine field lie at an angle \( \phi = 65^{\circ} \) relative to their local \( \langle 111 \rangle \) direction [26].
Since \( m_{para} \) , \( m_{sp} \) and \( \phi \) have been determined, we can deduce the spectroscopic g factors of the anisotropic \( Yb^{3+} \) ground state Kramers doublet [26]. We find \( g_{z} \simeq 1.1 \) and

FIG. 2 (color online). Temperature dependence of the fluctuation rates of the correlated \( Yb^{3+} \) moments in \( Yb_{2}Sn_{2}O_{7} \) obtained from \( {}^{170}Yb \) Mössbauer and \( \mu \) SR spectroscopies, and comparison with the \( Yb_{2}Ti_{2}O_{7} \) data [38]. The full lines above the transition temperatures result from fits to activation laws. The dashed lines are guides to the eye. At the temperature of the respective specific heat peaks they are vertical, indicating a sharp change in the spin dynamics at those temperatures. The few points below \( T_{f} \) for \( Yb_{2}Sn_{2}O_{7} \) correspond to paramagnetic moments which coexist with ordered moments [see Fig. 1(c)].

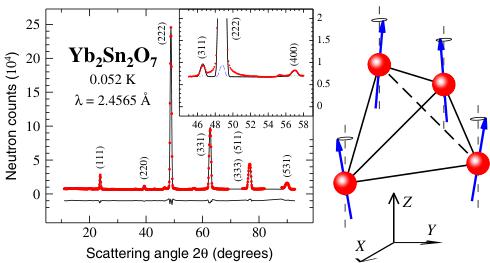
FIG. 3 (color online). Neutron scattering intensity from a powder of \( Yb_{2}Sn_{2}O_{7} \) at 0.052 K versus the scattering angle \( 2\theta \) . Neutrons of wavelength 2.4565 Å were used. To ensure a good thermal contact, the powder was placed in a copper container filled at room temperature with 10 bars of helium and sealed. Data nearby \( 2\theta = 72^{\circ} \) and \( 85^{\circ} \) are not shown because they are strongly influenced by neutrons scattered from the container. The solid black line results from a Rietveld refinement of the sum of intensities associated with the nuclear and magnetic structures. The lattice parameter of the cubic \( Fd\bar{3}m \) structure is \( a = 10.2766(5) \) Å and the parameter controlling the oxygen position at the 2mm site is \( x = 0.340(1) \) . The difference between the experimental data and the refinement is shown at the bottom. The insert displays the details of the central part of the pattern. The green dotted, blue dashed, and black full lines correspond to the nuclear, magnetic, and total scattering intensities, respectively. The measured intensity is essentially of magnetic origin at Bragg positions (311) and (400), while the nuclear intensity is overwhelming at position (222). The side panel represents the magnetic structure.
\( g_{\perp} \approx 4.2 \) . This means that the XY anisotropy is stronger in \( Yb_{2}Sn_{2}O_{7} \) than in \( Yb_{2}Ti_{2}O_{7} \) ; i.e., \( r = g_{\perp} / g_{z} \) is larger for the stannate (3.8 versus 2.4).
While the ground state g-tensor anisotropy favors the plane perpendicular to the local threefold z axis, \( m_{sp} \) is tilted towards this axis by the exchange field which is oriented at an angle arctan( \( \tan\phi/r^{2} \) ) \( \simeq8^{\circ} \) from it. This result directly evidences the strong easy-axis anisotropy of the exchange in \( Yb_{2}Sn_{2}O_{7} \) , as already noticed for \( Yb_{2}Ti_{2}O_{7} \) [27,28] and \( Yb_{2}GaSbO_{7} \) [29].
The neutron diffraction measurements were performed at the cold neutron powder diffractometer DMC of the SINQ facility, Paul Scherrer Institute (PSI), Switzerland (see Fig. 3). Remarkably, magnetic reflections are observed at the position of the nuclear Bragg peaks. Therefore a long-range magnetic order is found characterized by a \( k = 0 \) propagation wave vector. A Rietveld refinement [30] was performed according to a linear combination of two basis vectors of the sixth order irreducible representation (IR) \( \Gamma_{9+} \) [22]. \( \Gamma_{9+} \) is indeed the only one of the four possible IRs for a \( k = 0 \) magnetic structure in the \( Fd\bar{3}m \) space group allowing for an angle between the ordered moment and the local \( \langle 111 \rangle \) axis different from \( 0^{\circ} \) and \( 90^{\circ} \) . Setting this angle to \( \phi = 65^{\circ} \) we obtain a very good fit of TABLE I. Components of the four magnetic moments of the \( Yb^{3+} \) ions in a tetrahedron. The site positions X, Y, and Z and the moment coordinates \( m_{Sp}^{X} \) , \( m_{Sp}^{Y} \) , \( m_{Sp}^{Z} \) , given in Bohr magneton units at the temperature of 52 mK, are expressed respective to the cubic axes.
| Site | X | Y | Z | \( m_{Sp}^{X} \) | \( m_{Sp}^{Y} \) | \( m_{Sp}^{Z} \) |
| 1 | \( \frac{1}{2} \) | \( \frac{1}{2} \) | \( \frac{1}{4} \) | -0.13(1) | -0.13(1) | 1.03(1) |
| 2 | \( \frac{1}{2} \) | \( \frac{1}{3} \) | \( \frac{1}{4} \) | 0.13(1) | -0.13(1) | 1.13(1) |
| 3 | \( \frac{1}{4} \) | \( \frac{1}{2} \) | \( \frac{3}{4} \) | -0.13(1) | 0.13(1) | 1.03(1) |
| 4 | \( \frac{1}{4} \) | \( \frac{1}{4} \) | \( \frac{1}{3} \) | 0.13(1) | 0.13(1) | 1.03 |
the data (see Fig. 3) with \( m_{sp} = 1.05(2)\mu_{B} \) , a value close to the Mössbauer spectroscopy result. The \( Yb^{3+} \) magnetic moment components are reported in Table I [31]. While the main moment component lies along one of the fourfold cubic axis, a small component transverse to it and parallel to a twofold axis is present. This means the four magnetic moments of a tetrahedron are directed away from a common fourfold axis along four different directions (see Fig. 3). We term this arrangement a splayed ferromagnetic structure [34].
The profile of the magnetic reflections is Gaussian and very slightly broader than the instrument resolution, pointing to a rather long correlation length of the magnetic order. This is in contrast to \( Tb_{2}Sn_{2}O_{7} \) for which a quasi-Lorentzian profile was found for the magnetic intensity [32,36].
Further information was derived from \( \mu \) SR measurements which were performed at the ISIS facility (Rutherford Appleton Laboratory, United Kingdom) and at the Swiss Muon Source (S \( \mu \) S) of PSI, in the temperature range 0.014–2 K. These measurements give access to the so-called asymmetry \( a_{0}P_{Z}^{\mathrm{exp}}(t) \) , where \( a_{0} \) is an experimental parameter and \( P_{Z}^{\mathrm{exp}}(t) \) the muon polarization function which reflects the physics of the compound under study [37]. All the spectra were fitted to \( a_{0}P_{Z}^{\mathrm{exp}}(t) = a_{s}P_{Z}(t) + a_{\mathrm{bg}} \) , where the second time-independent component accounts for the muons implanted in the sample surroundings, essentially the silver backing plate.
Above \( T_{t} \) we found \( P_{Z}(t) \) to be an exponential function, i.e., \( P_{Z}(t) = \exp(-\lambda_{Z}t) \) , where \( \lambda_{Z} \) is the muon spin-lattice relaxation rate [see Fig. 4(a)]. This means the system is in the fast fluctuation limit; i.e., the fluctuation rate \( \nu_{c,\mu} \) of the \( Yb^{3+} \) dipolar field at the muon site verifies the relation \( \nu_{c,\mu} \gg \gamma_{\mu} \Delta_{para} \) , where \( \Delta_{para} \) is the root-mean-square of the field distribution at the muon site and \( \gamma_{\mu} = 851.6 \, M rad s^{-1} T^{-1} \) is the muon gyromagnetic ratio. We find that \( \lambda_{Z} \) increases on cooling. This is a usual behavior reflecting the slowing down of the fluctuations of exchange coupled \( Yb^{3+} \) moments. In this temperature range, \( \Delta_{para} \) can be taken to be temperature independent. As in Refs. [12,29], to extract \( \nu_{c,\mu} \) from \( \lambda_{Z} \) , we first identify it with \( \nu_{c,M} \) . Since at 0.2 K we have \( \nu_{c,M} \simeq 2.08 \times 10^{10} \, s^{-1} \)


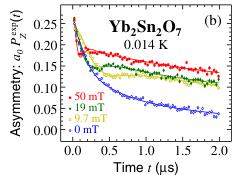
FIG. 4 (color online). \( \mu \) SR spectra. (a) Zero external field data recorded at ISIS shown together with fits to an exponential (0.200 K) and a Gaussian-broadened Gaussian (GBG) (0.075 K) function [45]. The lower sets show the difference between the 0.075 K data and the best fits to an exponential (top) and a GBG (bottom) function. (b) Weak longitudinal field dependence recorded at 0.014 K at \( S\mu S \) and fitted with the GBG function (see text).
and \( \lambda_{Z}\simeq0.37\;\mu s^{-1} \) , we infer \( \Delta_{para}\simeq73\;mT \) using the motional-narrowing relation limit \( \lambda_{Z}=2\gamma_{\mu}^{2}\Delta_{para}^{2}/\nu_{c,\mu} \) [37]. This \( \Delta_{para} \) value is very close to that obtained in the isomorphous compound \( Yb_{2}Ti_{2}O_{7} \) (80 mT) [38]. Figure 2 displays \( \nu_{c,\mu}(T) \) deduced from the above analysis together with \( \nu_{c,\mathrm{M}}(T) \) . An activation law is rather well obeyed, with an activation energy of 0.20 K in temperature units.
Below \( T_{t} \) , i.e., in the presence of long-range magnetic order, it might be expected that the spectral shape would show rapid depolarization or pronounced oscillations due to muon spin precession in the spontaneous field [37]. Instead the spectral shape shows little change on crossing \( T_{t} \) [see Fig. 4(a)]. A similar unusual behavior was already found in \( Er_{2}Ti_{2}O_{7} \) and \( Tb_{2}Sn_{2}O_{7} \) [32,39,40] and explained by a persistent dynamics in the ordered state, with a fluctuation rate larger than the muon precession frequency. Persistent spin dynamics which is ubiquitous in rare earth pyrochlores has been observed by different techniques [41] and we believe that it is spin dynamics and not muon diffusion [42] that is evidenced here. In \( Yb_{2}Sn_{2}O_{7} \) , since \( \nu_{c,\mu} \approx 3 \times 10^{6} s^{-1} \) (see below) the spontaneous field at the muon site would be on the order of 1 mT or less, a small value which could only be explained by a near cancellation of the dipole field produced by the \( Yb^{3+} \) spins at the muon site. An alternative explanation would be the presence of fluctuation modes coexisting with and faster than the mode at \( \approx 3 \times 10^{6} s^{-1} \) , which would have escaped detection by the Mössbauer and \( \mu \) SR techniques. This mode could be looked for with inelastic neutron scattering techniques.
Although there is no evidence of spontaneous precession below \( T_{t} \) , the spectral shape has changed and it no longer follows a simple exponential form [see Fig. 4(a)]. This means that the fast fluctuation limit no longer applies and therefore the \( Yb^{3+} \) spins have undergone a drastic slowing down at \( T_{t} \) . This is confirmed by weak longitudinal field measurements [see Fig. 4(b)]. The weak minimum seen below \( 1 \mu s \) indeed reveals the presence of a field distribution at the muon site with dynamics in the microsecond time scale. The shape of the spectra recorded below \( T_{t} \) is reminiscent of the dynamical Kubo-Toyabe function [43], however with a slight modification as in Ref. [12] (see also Ref. [26]). We find \( \nu_{c,\mu}(T) \) in the \( 10^{6}-10^{7} s^{-1} \) range (see Fig. 2).
The chief result of the \( \mu \) SR study is the abrupt decrease of \( \nu_{c,\mu} \) to an essentially temperature independent value in the megahertz range below \( T_{t} \) . It is consistent with the upper bound of \( 10^{8} \) s \( ^{-1} \) derived from Mössbauer spectroscopy measurements. This unusual transition in the dynamics is similar to that in \( Yb_{2}Ti_{2}O_{7} \) (see Fig. 2).
In summary the pyrochlore \( Yb_{2}Sn_{2}O_{7} \) is characterized by the following low temperature properties. The net interactions between the \( Yb^{3+} \) moments are weakly ferromagnetic \( [\theta_{\mathrm{CW}}=0.53(5)\mathrm{K}] \) . Owing to the small size of the ordered magnetic moments \( (1.1\mu_{\mathrm{B}}) \) the dipolar interaction energy is small. Together with an easy-plane g-tensor anisotropy and a strong easy-axis exchange anisotropy, these properties qualify \( Yb_{2}Sn_{2}O_{7} \) as a quantum or exchange spin ice candidate. The system undergoes a first order phase transition at \( T_{t}\simeq0.15~K \) associated with a degeneracy lifting whose characteristics are controlled by the specific exchange and g-factor anisotropies. The \( Yb^{3+} \) magnetic moments which are not coplanar are nevertheless nearly ferromagnetically aligned along a cubic fourfold axis—the canting angle is \( \arctan(\sqrt{(m_{\mathrm{sp}}^{3})^{2}+(m_{\mathrm{sp}}^{7})^{2}}/m_{\mathrm{sp}}^{7})\simeq10^{\circ} \) —while the components transverse to this axis are oriented along twofold axes and cancel in a unit cell. We term this type of order splayed ferromagnetism.
The \( Yb_{2}Sn_{2}O_{7} \) ground state properties are closely related to the CFM and Higgs FM phases recently predicted [7]. A robust evidence for the presence or absence of an energy gap and its characterization would help to distinguish between these two phases [44]. The analysis of the broad hump measured by specific heat around 2 K, besides the sharp peak at \( T_{t} \) [10], as well as the constraint imposed by the \( 65^{\circ} \) angle between the \( Yb^{3+} \) moment and the local trigonal axis should provide clues for the Hamiltonian parameters and the location of \( Yb_{2}Sn_{2}O_{7} \) in the phase diagram. A further challenge for the theory is to find a physical mechanism for the persistent spin dynamics which is observed as the temperature goes to zero.
We are grateful to M. J. P. Gingras for useful discussions. This research project has been partially supported by the European Commission under the 6th Framework Programme through the Key Action: Strengthening the European Research Area, Research Infrastructures (Contract No. RII3-CT-2003-505925) and under the 7th Framework Programme through the 'Research Infrastructures' Action of the 'Capacities' Programme (Contract No. CP-CSA_INFRA-2008-1.1.1 and No. 226507-NMI3). Part of this work was performed at the Swiss Muon Source and the Swiss Spallation Neutron Source, Paul Scherrer Institute, Villigen, Switzerland, and the ISIS facility, Rutherford Appleton Laboratory, Chilton, United Kingdom.
\( ^{*} \) Also at Laboratory for Muon-Spin Spectroscopy, Paul Scherrer Institute, CH-5232 Villigen-PSI, Switzerland.
[1] J. S. Gardner, M. J. P. Gingras, and J. E. Greedan, Rev. Mod. Phys. 82, 53 (2010).
[2] M. J. Harris, S. Bramwell, D. McMorrow, T. Zeiske, and K. Godfrey, Phys. Rev. Lett. 79, 2554 (1997).
[3] M. J. P. Gingras, in Introduction to Frustrated Magnetism, edited by C. Lacroix, P. Mendels, and F. Mila (Springer-Verlag, Berlin, 2011), Vol. 164, Chap. 12.
[4] M. Hermele, M. P. A. Fisher, and L. Balents, Phys. Rev. B 69, 064404 (2004).
[5] H. R. Molavian, M. J. P. Gingras, and B. Canals, Phys. Rev. Lett. 98, 157204 (2007).
[6] L. Balents, Nature (London) 464, 199 (2010).
[7] L. Savary and L. Balents, Phys. Rev. Lett. 108, 037202 (2012).
[8] N. Shannon, O. Sikora, F. Pollmann, K. Penc, and P. Fulde, Phys. Rev. Lett. 108, 067204 (2012).
[9] O. Benton, O. Sikora, and N. Shannon, Phys. Rev. B 86, 075154 (2012).
[10] R. Applegate, N. R. Hayre, R. R. P. Singh, T. Lin, A. G. R. Day, and M. J. P. Gingras, Phys. Rev. Lett. 109, 097205 (2012).
[11] L.-J. Chang, S. Onoda, Y. Su, Y.-J. Kao, K.-D. Tsuei, Y. Yasui, K. Kakurai, and M. R. Lees, Nat. Commun. 3, 992 (2012).
[12] J. A. Hodges et al., Phys. Rev. Lett. 88, 077204 (2002).
[13] Y. Yasui et al., J. Phys. Soc. Jpn. 72, 3014 (2003).
[14] P. Bonville, J. A. Hodges, E. Bertin, J.-Ph. Bouchaud, P. Dalmas de Réotier, L.-P. Regnault, H. M. Rønnow, J.-P. Sanchez, S. Sosin, and A. Yaouanc, Hyperfine Interact. 156/157, 103 (2004).
[15] J. S. Gardner, G. Ehlers, N. Rosov, R. W. Erwin, and C. Petrovic, Phys. Rev. B 70, 180404(R) (2004).
[16] K. A. Ross, J. P. C. Ruff, C. P. Adams, J. S. Gardner, H. A. Dabkowska, Y. Qiu, J. R. D. Copley, and B. D. Gaulin, Phys. Rev. Lett. 103, 227202 (2009).
[17] K. A. Ross, L. Savary, B. D. Gaulin, and L. Balents, Phys. Rev. X 1, 021002 (2011).
[18] A. Yaouanc, P. Dalmas de Réotier, C. Marin, and V. Glazkov, Phys. Rev. B 84, 172408 (2011).
[19] K. A. Ross, Th. Proffen, H. A. Dabkowska, J. A. Quilliam, L. R. Yaraskavitch, J. B. Kycia, and B. D. Gaulin, Phys. Rev. B 86, 174424 (2012).
[20] K. Matsuhira, Y. Hinatsu, K. Tenya, H. Amitsuka, and T. Sakakibara, J. Phys. Soc. Jpn. 71, 1576 (2002).
[21] H. Kadowaki, Y. Ishii, K. Matsuhira, and Y. Hinatsu, Phys. Rev. B 65, 144421 (2002).
[22] A. S. Wills, M. E. Zhitomirsky, B. Canals, J. P. Sanchez, P. Bonville, P. Dalmas de Réotier, and A. Yaouanc, J. Phys. Condens. Matter 18, L37 (2006).
[23] T. Yavors'kii, T. Fennell, M. Gingras, and S. Bramwell, Phys. Rev. Lett. 101, 037204 (2008).
[24] A. Bertin et al. (to be published).
[25] P. Dalmas de Réotier, A. Yaouanc, P. Gubbens, C. Kaiser, C. Baines, and P. King, Phys. Rev. Lett. 91, 167201 (2003).
[26] See Supplemental Material at http://link.aps.org/supplemental/10.1103/PhysRevLett.110.127207 for details about the analyses of the low temperature heat capacity and the Mössbauer spectroscopy and muon spin
relaxation data, as well as formulas linking the spectroscopic factors and the paramagnetic and ordered magnetic moments.
[27] J. A. Hodges, P. Bonville, A. Forget, M. Rams, K. Królas, and G. Dhalenne, J. Phys. Condens. Matter 13, 9301 (2001).
[28] H. Cao, A. Gukasov, I. Mirebeau, P. Bonville, C. Decorse, and G. Dhalenne, Phys. Rev. Lett. 103, 056402 (2009).
[29] J. A. Hodges, P. Dalmas de Réotier, A. Yaouanc, P. C. M. Gubbens, P. J. C. King, and C. Baines, J. Phys. Condens. Matter 23, 164217 (2011).
[30] The nuclear pattern was accurately determined from a measurement independently performed on the same sample at 0.50 K.
[31] Formally the magnetic structure of \( Tb_{2}Sn_{2}O_{7} \) [32,33] and \( Yb_{2}Sn_{2}O_{7} \) are similar. However the common ferromagnetic component represents 37% of the total moment in the former compound while it is 98% for the latter.
[32] P. Dalmas de Réotier et al., Phys. Rev. Lett. 96, 127202 (2006).
[33] I. Mirebeau, A. Apetrei, J. Rodríguez-Carvajal, P. Bonville, A. Forget, D. Colson, V. Glazkov, J. Sanchez, O. Isnard, and E. Suard, Phys. Rev. Lett. 94, 246402 (2005).
[34] We note that the term splayed ferromagnetism has been used in a recent preprint \( [35] \) for the description of magnetic orders derived for systems described by isotropic exchange interactions in the absence of single ion anisotropy, in contrast to our physical case.
[35] S. R. Sklan and C. L. Henley, arXiv:1209.1381.
[36] Y. Chapuis, A. Yaouanc, P. Dalmas de Réotier, S. Pouget, P. Fouquet, A. Cervellino, and A. Forget, J. Phys. Condens. Matter 19, 446206 (2007).
[37] A. Yaouanc and P. Dalmas de Réotier, Muon Spin Rotation, Relaxation, and Resonance: Applications to Condensed Matter (Oxford University, New York, 2011).
[38] A. Yaouanc, P. Dalmas de Réotier, P. Bonville, J. A. Hodges, P. C. M. Gubbens, C. T. Kaiser, and S. Sakarya, Physica (Amsterdam) 326B, 456 (2003).
[39] J. Lago, T. Lancaster, S. J. Blundell, S. T. Bramwell, F. L. Pratt, M. Shirai, and C. Baines, J. Phys. Condens. Matter 17, 979 (2005).
[40] P. Dalmas de Réotier, A. Yaouanc, Y. Chapuis, S. H. Curnoe, B. Grenier, E. Ressouche, C. Marin, J. Lago, C. Baines, and S. R. Giblin, Phys. Rev. B 86, 104424 (2012).
[41] E. Bertin et al., Eur. Phys. J. B 27, 347 (2002).
[42] P. Quémerais, P. McClarty, and R. Moessner, Phys. Rev. Lett. 109, 127601 (2012).
[43] R. S. Hayano, Y. Uemura, J. Imazato, N. Nishida, T. Yamazaki, and R. Kubo, Phys. Rev. B 20, 850 (1979).
[44] According to the classical approach developed in the supplemental material attached to Ref. [7] the angle \( \phi \) determined in our study places \( Yb_{2}Sn_{2}O_{7} \) on the line of the equation \( 8y/\tan2\phi + 2x = -1 \) where \( x \equiv J_{\pm}/J_{zz} \) and \( y \equiv J_{zz}/J_{zz} \) , in the phase diagram which is obtained for the fourth Hamiltonian parameter \( J_{\pm\pm} \) set to 0. This line intercepts the FM and CFM phases (see Fig. 3 of Ref. [7] supplemental material).
[45] D. R. Noakes and G. M. Kalvius, Phys. Rev. B 56, 2352 (1997).