| Transition Temperature | 15 K |
|---|---|
| Experiment Temperature | 2 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | C2/c (#15) |
| Magnetic Space Group | C2'/c (#15.87) |
| Magnetic Point Group | 2'/m (5.3.14) |
| Lattice Parameters | 10.27940 9.17560 5.47140 90.00 104.24 90.00 |
|---|---|
| DOI | 10.1103/physrevb.93.064423 |
| Reference | L. Ding, C.V. Colin, C. Darie, J. Robert, F. Gay and P. Bordet, Physical Review B (2016) 93. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Mn1 | Mn | 4.30 | 0.0 | 1.14 | 4.17 |
One-dimensional short-range magnetic correlations in the magnetoelectric pyroxene CaMnGe_{2}O_{6}
L. Ding, \( ^{1,2} \) C. V. Colin, \( ^{1,2,*} \) C. Darie, \( ^{1,2} \) J. Robert, \( ^{1,2} \) F. Gay, \( ^{1,2} \) and P. Bordet \( ^{1,2,\dagger} \)
\( ^{1} \) Université Grenoble Alpes, Institut NEEL, F-38000 Grenoble, France
\( ^{2} \) CNRS, Institut NEEL, F-38000 Grenoble, France
(Received 3 August 2015; revised manuscript received 23 December 2015; published 23 February 2016)
We have investigated the magnetic and magnetoelectric properties of \( CaMnGe_{2}O_{6} \) by means of powder neutron diffraction, magnetic susceptibility, heat capacity, and electrical polarization measurements. The presence of one-dimensional short-range magnetic correlations within the \( MnO_{6} \) octahedra chains well above long-range antiferromagnetic ordering (15 K) was evidenced. A one-dimensional antiferromagnetic correlation model along the zigzag chains was developed to fit the diffuse magnetic scattering. The linear magnetoelectric effect and pertinent ferrotoroidicity, allowed by the magnetic symmetry \( (C2^{\prime}/c) \) , have been verified experimentally and theoretically.
DOI: 10.1103/PhysRevB.93.064423
I. INTRODUCTION
Magnetoelectric materials have been the subject of a considerable amount of research activity for their fundamental scientific interest \( [1] \) and potential applications in technology, such as magnetoelectric random access memory (MERAM) \( [2] \) . The cross coupling of magnetization and polarization to their conjugate fields, E and H, is known as the magnetoelectric (ME) effect \( [3] \) . The linear ME effect was first experimentally verified on antiferromagnetic \( Cr_{2}O_{3} \) \( [4] \) after the theoretical prediction by Landau and Lifshitz \( [5] \) . They found that specific symmetry elements, namely spatial inversion and time reversal, must be broken. Thus, the linear ME effect could be predicted by symmetry consideration in a specific material. Unlike the electric polarization yielded in typical type I multiferroics, linear ME materials are characterized by weak polarization values. However, this does not impede their possible applications on random access memory since the small linear ME effect has recently been shown to control spintronic devices very efficiently in a magnetoelectric exchange bias system \( [6] \) . Nevertheless, the underlying mechanism leading to a linear ME coupling is still unclarified, but apparently it is strongly material-dependent.
Ferrotoroidicity is related to the antisymmetric part of the linear magnetoelectric tensor, thus it is present only when the tensor of the linear ME effect is nondiagonal \( [7] \) . From macroscopic symmetry considerations, ferrotoroidic order gives rise to antisymmetric contributions to the ME effect, indicating that the indirect evidence for the presence of a spontaneous toroidal moment in a system can be obtained by measuring the linear ME effect.
Recently, clinopyroxenes containing magnetic cations have attracted revitalized interest because some of them were found to present rich multiferroic and magnetoelectric properties. Pyroxenes have the general formula \( AMX_{2}O_{6} \) , where A is an alkali or alkali-earth ion, M is a transition-metal ion (+II or +III), while X = Si, Ge. Their structures consist of edge-shared \( MO_{6} \) octahedra forming zigzag chains that are well separated by nonmagnetic \( XO_{4} \) tetrahedra. These compounds are well known for their importance in mineralogy and their low-dimensional properties: the spin-singlet ground state [8], the spin-Peierls transition [9], and quasi-one-dimensional (Q1D) magnetic behavior [10].
The renewed interest arose from the recent observation of magnetically driven ferroelectricity in \( \mathrm{NaFe(Si/Ge)_{2}O_{6}} \) [11,12], the magnetoelectric effect in \( \mathrm{LiCr(Si/Ge)_{2}O_{6}} \) [13], \( \mathrm{NaCrSi_{2}O_{6}} \) [14], and \( \mathrm{LiFeSi_{2}O_{6}} \) [11], and the expected ferrotoroidal order in \( \mathrm{LiFe(Si/Ge)_{2}O_{6}} \) [15]. These intriguing physical properties are attributed to the existence and possible interplay of low dimensionality and magnetic frustration [13].
The vast majority of compounds mentioned previously are pyroxenes containing an \( A^{+1} \) cation, however much less investigation has been devoted to the magnetoelectric property of \( Ca^{2+} \) -bearing pyroxenes. Most of these compounds crystallize into monoclinic \( C2/c \) symmetry. Magnetic clinopyroxenes \( \mathrm{Ca(Mn, Fe, Co, Ni)Ge_{2}O_{6}} \) [16,17] order all in commensurate collinear antiferromagnetic structures. Among the reported \( Ca^{2+} \) -bearing pyroxenes, only \( CaMnGe_{2}O_{6} \) allows for the linear magnetoelectric effect.
In this contribution, we present an investigation of the magnetic and magnetoelectric properties of \( CaMnGe_{2}O_{6} \( by means of neutron diffraction, magnetization, heat capacity, and electrical polarization measurements. These techniques coincidentally reveal the presence of one-dimensional (1D) short-range spin correlations appearing well above the long-range antiferromagnetic order at \) T_{N}=15 \( K. Consistent with the determination of the magnetic structure \) (C2^{\prime}/c) \( , the magnetic-field dependence of the electrical polarization signals a clear linear magnetoelectric effect below \) T_{N} \( . We also propose that \) CaMnGe_{2}O_{6} \( should be a pure ferrotoroidic compound by considering the antisymmetric tensor of the linear ME effect and the responding electric polarization under a magnetic field. The toroidization of \) CaMnGe_{2}O_{6} $ is also evaluated by considering the crystal and magnetic structure parameters.
II. EXPERIMENT
Polycrystalline \( CaMnGe_{2}O_{6} \) was synthesized by solid-state reaction. The stoichiometric mixture of reagent-grade \( CaCO_{3} \) , \( MnO_{2} \) , and \( GeO_{2} \) was ground in an agate mortar and pestle and then pelletized. The pellets were placed in a platinum
boat and heated in air to 1373 K at 2 K/min, then held at 1373 K for 100 h and cooled down to room temperature. Intermediate regrinding and reheating were required in order to obtain a high-purity phase \( CaMnGe_{2}O_{6} \) sample. Nonmagnetic analog \( CaZnGe_{2}O_{6} \) was prepared in the same conditions using \( CaCO_{3} \) , ZnO, and \( GeO_{2} \) as starting materials. The sample was characterized by x-ray powder diffraction (XRPD) using a Bruker D8 diffractometer with Cu Kα1 radiation (1.5406 Å) selected by a Ge (111) primary beam monochromator in the range \( 10^{\circ}-90^{\circ} \) with a \( 0.02^{\circ} \) step size.
To investigate the nuclear and magnetic structures, a neutron powder diffraction (NPD) experiment was carried out on the two-axis diffractometer D1B at Institut Laue Langevin (ILL), between 1.7 K and room temperature. For nuclear structure refinement, NPD patterns were recorded at 100 and 300 K with the 1.28 Å wavelength corresponding to the (311) Bragg reflection of a germanium monochromator. The 2.52 Å wavelength corresponding to the (002) Bragg reflection of a pyrolytic graphite monochromator was used for magnetic structure investigation, with longer data collections at 2, 20, and 50 K as well as a temperature ramp between 2 and 300 K on heating. The XRPD and NPD data were analyzed by the Rietveld method using the FULLPROF suite programs [18].
The temperature-dependent magnetic susceptibility was measured on a Quantum Design Magnetic Property Measurement System (MPMS). The dc magnetic susceptibility was measured from 2 to 350 K in zero-field-cooled (ZFC) and field-cooled (FC) procedures under magnetic fields of 1 T. Field-dependent magnetization was measured between 2 and 350 K with a field sweep from 0 to 5 T. The specific-heat measurement was carried out using a relaxation technique with a Quantum Design Physical Property Measurement System (PPMS) in the temperature range of 2–100 K. The pelletized sample was mounted on a sample platform with Apiezon N-grease for better thermal contact.
To study the magnetoelectric properties of \( CaMnGe_{2}O_{6} \) , the temperature dependence of electric polarization was measured under various magnetic fields (0, 2, 4, 6, and 8 T). The sample was sintered to improve grain connectivity by heat treatment of a pressed pellet (thickness 0.29 mm and surface 19 mm \( ^{2} \) ) at 1073 K for 10 h. Then, the pellet was coated with silver epoxy on both sides to make conducting electrodes. Electrical polarization was then determined by using the pyroelectric current measurement technique. The magnetoelectric annealing was performed by simultaneously applying an electric field E of 690 kV/m and a magnetic field \( \mu_{0}H \) of \( \pm8 \) T in perpendicular directions at 100 K and then cooling the sample down to 2 K. Then, the pyroelectric current curves under various magnetic fields were recorded using a Keithley 6514A electrometer while increasing the temperature at a rate of 3 K/min. Electric polarization was obtained by integration of the time dependence of the pyroelectric current.
III. RESULTS AND DISCUSSION
A. Crystal structure
The crystal structure of \( CaMnGe_{2}O_{6} \) has been previously reported [16]. It crystallizes with monoclinic C2/c symmetry corresponding to the high clinopyroxene structure type. In

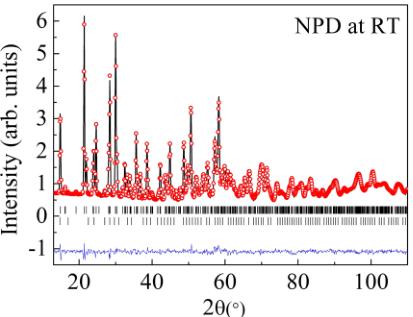
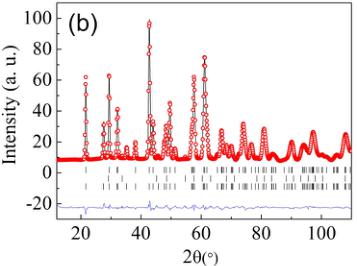
FIG. 1. Rietveld refinement of \( CaMnGe_{2}O_{6} \) from NPD data taken at room temperature. Observed (open circles), calculated (line), and difference plots (bottom line) are shown. Bragg reflections are denoted by tick marks. The lower set of tick marks belongs to a \( Ca_{3}Mn_{2}Ge_{3}O_{12} \) impurity phase.
most pyroxene compounds, the long-range magnetic ordering stems from the competition of intrachain and interchain interactions. The precise description of crystal structure is thus of great importance to understand the magnetic properties. The final Rietveld plot for the room-temperature NPD pattern of \( CaMnGe_{2}O_{6} \) is shown in Fig. 1. The background was described by linear interpolation of selected points in the pattern. A Thomson-Cox-Hastings model of the reflection profile was used. Low-angle peak asymmetry was taken into account using the Berar-Baldinozzi model [19]. \( Ca_{3}Mn_{2}Ge_{3}O_{12} \) , was the only phase detected as an impurity; it was introduced in the pattern description, and its cell parameters and scale factor were refined. The final refinement yielded a weight fraction of 0.15(1)% for this phase. The refinement results are presented in Table I. They are in good agreement with previously reported values [16].
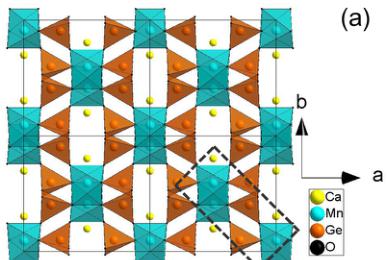
The crystal structure of \( CaMnGe_{2}O_{6} \( is shown in Fig. 2. It is characterized by the alternate stacking perpendicular to the a axis of layers made of \( MnO_{6} \) octahedra and layers of \( GeO_{4} \) tetrahedra. In the octahedral layer, \( MnO_{6} \) octahedra share their O1-O1 edges to form zigzag infinite chains along the c axis. Within the octahedra chains, the shortest (intrachain) Mn-Mn distance is 3.249 Å. According to the band-structure calculations of exchange interactions for pyroxenes [20], the edge-sharing character of \( MO_{6} \) with M-O-M angle close to
TABLE I. Agreement factors and refined structural parameters for \( CaMnGe_{2}O_{6} \) ( \( \chi^{2}=23.99 \) , \( R_{wp}=4.72 \) , and \( R_{Bragg}=3.65 \) ). Lattice parameters: \( a=10.2794(3) \) Å, \( b=9.1756(3) \) Å, \( c=5.4714(2) \) Å, \( \beta=104.244(2)^{\circ} \) .
| Name | Position | x | y | z | B ( \( \textup{\AA}^{2} \) ) |
| Ca | 4e | 0.0 | 0.3075(8) | 0.25 | 0.9(1) |
| Mn | 4e | 0.0 | 0.905(1) | 0.25 | 1.4(2) |
| Ge | 8f | 0.2860(3) | 0.0958(3) | 0.2319(4) | 0.20(4) |
| O1 | 8f | 0.1133(3) | 0.0949(5) | 0.14443(1) | 0.17(6) |
| O2 | 8f | 0.3668(4) | 0.2532(4) | 0.3545(8) | 0.55(6) |
| O3 | 8f | 0.3565(4) | 0.0324(5) | 0.9802(8) | 0.51(6) |

(a)

(b)
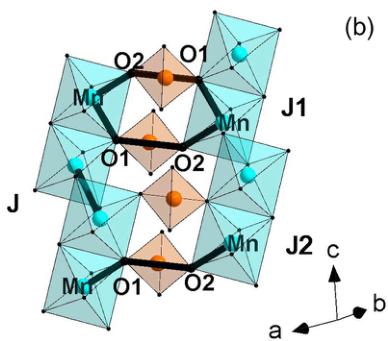
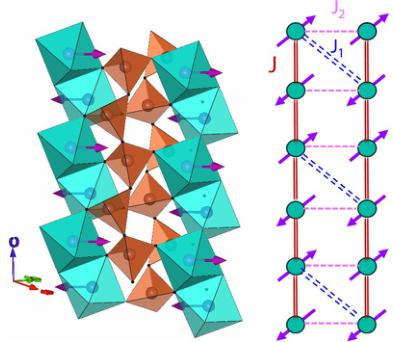
FIG. 2. (a) Projection of the \( CaMnGe_{2}O_{6} \) structure along the c axis. Note that the dashed rectangle marks the nearest-neighbor octahedra chains, which are responsible for the magnetic interaction. (b) The \( MnO_{6} \) zigzag chains separated by \( GeO_{4} \) tetrahedra via corner sharing, derived from NPD at room temperature. Magnetic interaction pathways are triangular geometry in \( CaMnGe_{2}O_{6} \) . J represents the interaction along the zigzag chain and connects \( NN~Mn^{2+} \) sites; J1 denotes the possible exchanges between adjacent octahedra chains but via two tetrahedra; J2 shows the possible exchange between octahedra chains through one tetrahedron.
\( 90^{\circ} \) results in a competition between direct and superexchange magnetic interactions. In \( CaMnGe_{2}O_{6} \) , the Mn-O1-Mn angle was obtained as \( 94^{\circ} \) from the NPD data, substantially deviating from the ideal \( 90^{\circ} \) value. As marked with a dashed rectangle in Fig. 2(a), the \( MnO_{6} \) octahedra chains are linked by corner-sharing \( GeO_{4} \) chains along the a axis. From the viewpoint of magnetism, the structural arrangement leads to two possible magnetic super-super-exchange pathways between \( Mn^{2+} \) cations belonging to adjacent octahedra chains through a \( GeO_{4} \) tetrahedron edge. They were marked with dotted and dashed lines in Fig. 2(b); an equivalent schematic drawing of considered exchange interactions is also shown in Fig. 6. As shown in Fig. 2(b), the J1 interaction is mediated through two different paths (Mn-O1-O2-Mn and Mn-O2-O1-Mn), while for J2 only a single path exists.
B. Magnetic properties
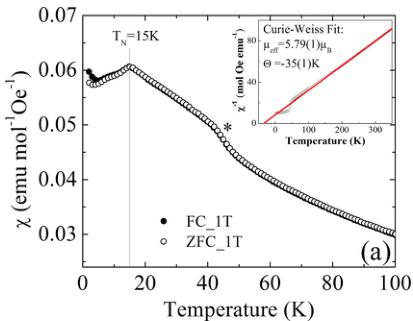
The temperature dependence of magnetization of \( CaMnGe_{2}O_{6} \) was measured with ZFC and FC processes under a magnetic field of 1 T. As shown in Fig. 3(a), we observed


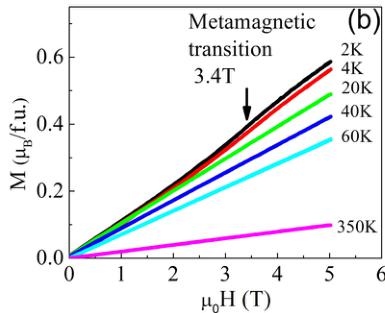
FIG. 3. (a) Temperature dependence of the magnetic susceptibility of \( CaMnGe_{2}O_{6} \) under different magnetic fields. The inset shows the Curie-Weiss fit for inverse magnetic susceptibility (red line). The star symbol indicates the magnetic transition of the \( Mn_{3}O_{4} \) ferrimagnetic impurity. (b) Isothermal magnetization curves of \( CaMnGe_{2}O_{6} \) collected at T = 2, 4, 20, 40, 60, and 350 K.
a cusp at \( T_{N} = 15 \) K, indicating a long-range AFM ordering transition. A change of slope around 45 K was observed in all magnetization curves. It is attributed to the presence of the strongly ferrimagnetic impurity \( Mn_{3}O_{4} \) . Considering \( Mn_{3}O_{4} \) saturation magnetization, we evaluate the impurity amount of less than 0.8% mol, and this impurity was not observed by diffraction. In the previous report [16], the susceptibility curve measured at 0.5 T was shown up to 50 K and did not display any feature around 45 K; only one transition at 12 K was observed. As shown in the inset of Fig. 3(a), the inverse magnetic susceptibility at 0.1 T was fitted with the Curie-Weiss law between 175 and 350 K. This yields an effective moment \( \mu_{eff} = 5.79(1)\mu_{B} \) , consistent with the expected spin-only value of \( 5.92\mu_{B} \) for \( Mn^{2+} \) cations in the high-spin state, in agreement with the previous report. The negative Weiss temperature of \( -35(1) \) K indicates that antiferromagnetic interactions are predominant in this system. Field-dependent magnetization isotherms \( M(H) \) were measured between 2 and 350 K and are presented in Fig. 3(b). The field-induced magnetization is linear up to applied fields of 5 T above \( T_{N} \) . However, on the curves at 2 and 4 K, a change of slope can be seen at 3.4 T determined by the maximum of derivative of dM/dH, as denoted by an arrow. This is indicative of a


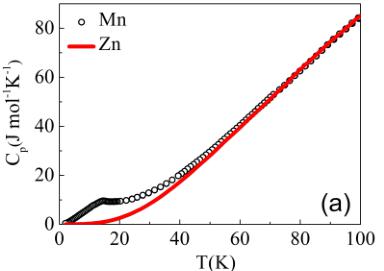
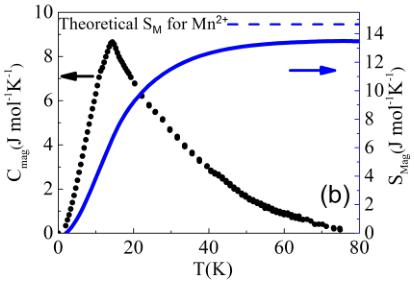
FIG. 4. (a) Specific-heat capacity of \( CaMnGe_{2}O_{6} \) and \( CaZnGe_{2}O_{6} \) , which is used as a lattice standard. (b) (Black) The magnetic component of the specific-heat capacity of \( CaMnGe_{2}O_{6} \) ; (blue) the entropy released through magnetic ordering. The blue dashed line represents the theoretical maximum.
field-induced metamagnetic transition. No saturation can be achieved with the maximum field applied \( (M \leqslant 0.6\mu_{B}/\mathrm{Mn}^{2+} \) at 5 T).
A characterization of the magnetic transition via measurement of the heat capacity was carried out. Figure 4(a) shows the temperature dependence of the specific heat for \( CaMnGe_{2}O_{6} \) . The presence of a cusp in \( C_{p} \) around 15 K indicates the magnetic ordering transition. This temperature is consistent with the Néel temperature observed in magnetic susceptibility and the appearance of the magnetic reflection peaks in neutron diffraction (see below). The magnetic component of the specific-heat capacity of \( CaMnGe_{2}O_6 \) , \( C_{mag} \) , as shown in Fig. 4(b), was obtained by subtracting the phonon contribution with a nonmagnetic analog \( CaZnGe_{2}O_{6} \) . The plotted \( C_{mag} \) versus T clearly shows that only the transition observed at around 15 K in the magnetic susceptibility can also be seen in the specific-heat data, evidencing the nature of long-range order at \( \sim15 \) K. The experimental magnetic entropy with \( S_{m}=13.5 \) J mol \( ^{-1} \) K \( ^{-1} \) at 75 K, derived from the \( C_{mag}-T \) curve, is about 91% of the theoretical value of 14.9 J mol \( ^{-1} \) K \( ^{-1} \) for the spin S=5/2 Mn \( ^{2+} \) ions given by \( R\ln(2S+1) \) , as seen in Fig. 4(b). The magnetic entropy first decreases slowly upon cooling over a broad temperature range between 60 K and Néel temperature \( T_{N}=15 \) K; then below \( \sim15 \) K a rapid decrease is observed. The former phenomenon corresponds to a considerable entropy release; indeed, about half of the magnetic entropy (51%) is released above \( T_{N} \) . A similar phenomenon occurs in \( NaMnGe_{2}O_{6} \) , \( LiFeSi_{2}O_{6} \) , and \( NaFeSi_{2}O_{6} \) [21,22], which was suggested to be the signature of short-range magnetic correlations within chains far above the long-range-ordering temperature.
C. Magnetic structure
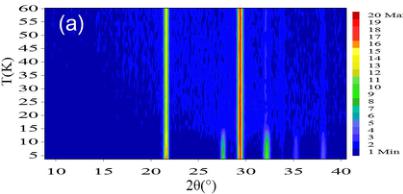
Figure 5(a) shows temperature-dependent NPD patterns below 60 K for \( CaMnGe_{2}O_{6} \) . One can easily observe the appearance of magnetic reflections below 15 K. At low temperature, as seen in Figs. 5(a) and 5(b), all reflections can be indexed with the crystallographic unit cell. Neither the (010) nor the (100) magnetic reflections are observed, which shows that the C centering is preserved. This leads to a commensurate magnetic propagation vector \( k = (0,0,0) \) . The determination of the magnetic structure was done by symmetry analysis.



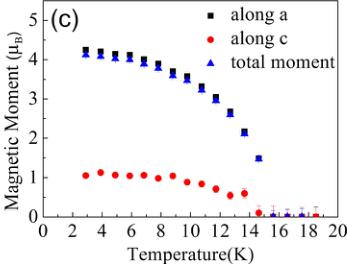
FIG. 5. (a) Plot of neutron powder diffraction scans showing up the magnetic transition at 15 K using a wavelength of 2.52 Å. (b) Observed (open circles) and calculated (line) powder neutron diffraction patterns for \( CaMnGe_{2}O_{6} \) at 2 K. The lowest tick marks show the magnetic reflections. The nuclear reflections are denoted by upper tick marks. The reflections marked in the middle belong to a \( Ca_{3}Mn_{2}Ge_{3}O_{12} \) impurity phase. The bottom line shows the difference between the observed and calculated diffraction patterns. (c) Evolution of the refined \( Mn^{2+} \) magnetic moment components with temperature.
TABLE II. Basis vector for \( Mn^{2+} \) at the 4e site [indicating the position of \( Mn1(0, 0.905, 0.25) \) and \( Mn2(0, 0.095, 0.75) \) ]. Notations: \( F = S1 + S2 \) , \( C = S1 - S2 \) .
| IR | Basis vector | Space group |
| \( \Gamma_{1} \) | \( (0, Fy, 0) \) | \( C2/c \) |
| \( \Gamma_{2} \) | \( (0, Cy, 0) \) | \( C2/c' \) |
| \( \Gamma_{3} \) | \( (Fx, 0, Fz) \) | \( C2'/c' \) |
| \( \Gamma_{4} \) | \( (Cx, 0, Cz) \) | \( C2'/c \) |
following the representation analysis technique described by Bertaut [23]. Calculations were carried out using version 2 K of the program SARAh-Representation analysis [24] and BasIreps integrated in the FULLPROF suite [18]. For the \( Mn^{2+} \) cations on the 4e Wyckoff position of space group C2/c, the decomposition of magnetic representation is
\[ \Gamma_{\mathrm{m a g}}=1\Gamma_{1}^{1}+1\Gamma_{2}^{1}+2\Gamma_{3}^{1}+2\Gamma_{4}^{1}. \quad (1) \]
The different basis vectors calculated using the projection operator technique associated with each IR are presented in Table II. There are four magnetic ions in the cell, but only two possible magnetic couplings. Indeed, because of the C centering, which is preserved by the k vector, the magnetic moments carried by the two \( Mn^{2+} \) cations symmetrically related by the C translation are automatically identical. Consequently, the two magnetic coupling possibilities are a ferromagnetic and an antiferromagnetic one. According to the magnetization measurements, the possible antiferromagnetic structure models determined from the symmetry analysis were tested by Rietveld refinement. The best fit was achieved with the model described by the IR \( \Gamma_{4} \) with the magnetic space group C2'/c. The final refinement for the 2 K NPD pattern is shown in Fig. 5(b). ( \( \chi^{2} = 90.8 \) , \( R_{wp} = 3.13 \) , \( R_{nucl} = 2.28 \) , and \( R_{mag} = 5.04 \) .)
A representation of the magnetic structure is shown in Fig. 6. The magnetic ordering corresponds to antiferromagnetic \( Mn^{2+} \) zigzag chains coupled ferromagnetically

FIG. 6. Left: representation of the magnetic structure of \( CaMnGe_{2}O_{6} \) ; right: the schematic drawing of exchange interactions, and here magnetic moments were added arbitrarily in order better to exhibit the triangular exchange interaction.
with neighboring chains. The \( Mn^{2+} \) magnetic moment is constrained by symmetry in the \( (a,c) \) plane, aligned mainly along the a axis with an angle of \( 14.1(1)^{\circ} \) , and almost perpendicular to the c axis [with an angle of \( 89.9(1)^{\circ} \) ], with \( m_{a}=4.30(1)\mu_{B} \) and \( m_{c}=1.14(3)\mu_{B} \) . Note that this result differs from the magnetic structure reported previously [16] with a magnetic moment component along the b axis of \( 0.78(9)\mu_{B} \) . This would require the use of the two \( \Gamma_{2} \) and \( \Gamma_{4} \) IR leading to the \( C2/c' \) magnetic space group. Contrary to \( C2'/c \) , this space group is not compatible with the observation of the linear magnetoelectric effect reported below. The total ordered magnetic moment refined at 2 K is \( 4.17(5)\mu_{B} \) , which is smaller than the theoretical spin-only ordered value for \( Mn^{2+} \) . The temperature dependence of the magnetic moment is shown in Fig. 5(c) and confirms the \( T_{N}=15 \) K value for the magnetic ordering temperature, in agreement with our magnetic susceptibility measurements.
D. Short-range spin correlations
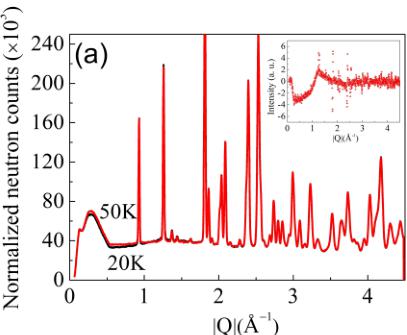
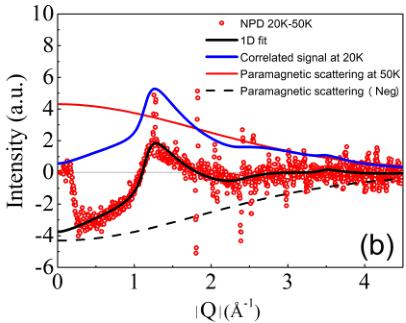
Evidence for short-range spin correlations can be obtained when one checks carefully the background intensity of NPD as a function of temperature. Figure 7(a) shows the comparison of NPD data between 20 and 50 K. The NPD difference


FIG. 7. (a) Comparison between NPD data collected at 20 and 50 K in \( CaMnGe_{2}O_{6} \) . The inset shows the NPD difference pattern between 20 and 50 K. (b) Diffuse neutron scattering is obtained by subtracting the NPD pattern at 50 K from the pattern at 20 K. The fit corresponds to a 1D AFM correlation model along the zigzag chains (see the text).
pattern between 20 and 50 K [the inset of Fig. 7(a)] displays clearly a maximum in the magnetic diffuse scattering at about \( d = 5.4(1) \) Å with asymmetric shape, signifying the existence of short-range magnetic correlations. This broad asymmetric peak featured by the sharp rise at low Q (high-d value) and a gradual decrease toward high Q (low-d value) is characteristic of low-dimensional short-range order. Few numerical models have previously been developed to describe these kinds of feature. In particular, the Warren function, describing the scattering from random layer stacking systems (2D), has been used to describe diffuse magnetic scattering from a layered magnet in which there are long-range correlations within a plane but no correlation between them [25–27]. The comparison of the diffraction theory between randomly oriented line gratings, which are defined as a periodic linear structure, and the three-dimensional crystals and two-dimensional arrays shows that the long tails at the high-Q side in the patterns are characteristic of both randomly oriented two-dimensional arrays and randomly oriented line gratings [28]. In the case of the two-dimensional arrays, the intensity in the tail varies as a function of \( Q^{-2} \) , whereas with the line gratings the intensity in the tail varies as \( Q^{-1} \) [28].
Inspection of this asymmetric peak reveals the slow decay at the high-Q side, thus suggesting the one-dimensional nature of diffuse magnetic scattering in \( CaMnGe_{2}O_{6} \) . Compared to the next-nearest \( Mn^{2+} \) intrachain distance of 5.4 Å, this scattering can be attributed to the presence of short-range magnetic correlations between \( Mn^{2+} \) cations along the octahedra chains with vanishing interchain interaction.
A simple model describing the diffuse scattering at 20 K associated with 1D AFM correlations along the zigzag chains is presented hereafter. In this approach, the powder-averaged scattering function, which can be expressed as a radial Fourier transform of the spin-pair correlations, is given by \( [29–32] \)
\[ S(Q)=f(Q)^{2}\sum_{i}\langle S_{0}S_{i}\rangle\frac{\sin(Q R_{i})}{Q R_{i}}, \quad (2) \]
where \( f(Q) \) is the magnetic form factor in the dipole approximation, in which all the coefficients were taken from the International Tables for Crystallography [33], \( R_{i} \) represents the distance between the sites along the 1D chain and the AFM spin pair correlations, and
\[ \langle S_{0}S_{i}\rangle=(-1)^{i}S^{2}\exp\left(-\frac{d_{i}}{\xi}\right) \quad (3) \]
are considered to decrease exponentially with distance \( d_{i} \) according to the correlation length \( \xi \) . Then, the diffuse scattering data presented in Fig. 7(b) can be fitted by the following expression:
\[ I_{\mathrm{e x p e r i m e n t a l}}=I_{l}S_{T=20\mathrm{~k~}(\mathcal{Q})}-I_{h}S_{T=50\mathrm{~k~}(\mathcal{Q})}, \quad (4) \]
where the first and second terms, respectively, correspond to the low-temperature correlated diffuse scattering and the paramagnetic scattering given by \( S_{T=50}\kappa(Q)=nS(S+1)f^{2}(Q) \) [34], with n the number of spins. Consequently, the free parameters of this fitting procedure are the correlation length \( \xi \) as well as the intensities \( I_{l} \) and \( I_{h} \) of the low- and high-temperature signals. The best fit is given in Fig. 7(b). The fit gives at 20 K a correlation length \( \xi=10\pm1 \) Å for

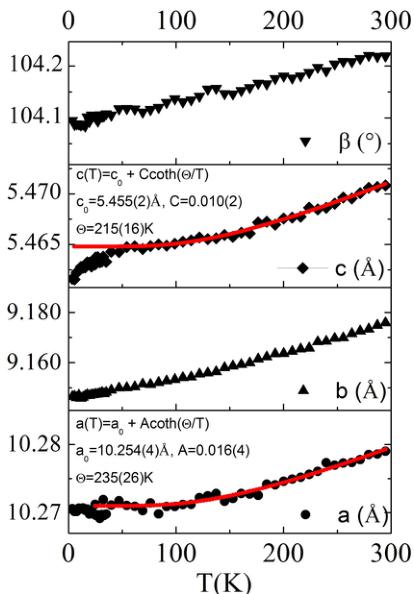
FIG. 8. Lattice parameters of \( CaMnGe_{2}O_{6} \) as a function of temperature from refinement of NPD.
the magnetic correlations along the c axis, evidencing the short-range characteristic.
The signature of this 1D short-range magnetic correlation can also be observed in the temperature dependence of the lattice parameters for \( CaMnGe_{2}O_{6} \) extracted from Rietveld refinement of NPD data collected in the 2–300 K temperature range. They are shown in Fig. 8. The solid line is a fit to \( a(T) = a_{0} + A \coth(\theta / T) \) , which is an approximation to the bare thermal expansion due to thermal vibrations of a solid as derived in Ref. [35]. ( \( \theta \) equals half the Einstein temperature.) Deviations from this temperature dependence signal the occurrence of anomalous lattice strain. The a and b parameters as well as the monoclinic \( \beta \) angle follow a standard evolution in the whole temperature range. No anomaly can be detected at the Néel temperature. On the contrary, the c parameter exhibits a strong anomaly at \( \sim60 \) K, with a notable decrease down to the lowest temperature. This can be attributed to a magnetostrictive effect related to the short-range magnetic correlations appearing at \( \sim60 \) K. This anomaly being detected only along the c axis supports the fitting results of diffuse neutron scattering that this short-range order is due to 1D intrachain antiferromagnetic correlations between the \( Mn^{2+} \) cations.
E. Linear magnetoelectric effect
The magnetic structure determined from neutron diffraction with space group \( C2^{\prime}/c \) allows the linear magnetoelectric effect, and this can be verified by the symmetry consideration mentioned below. The linear magnetoelectric effect can be


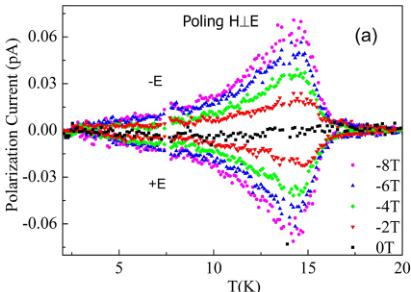
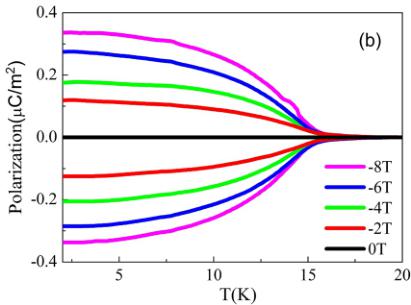
FIG. 9. Temperature dependence of the pyroelectric current (a) and polarization (b) under various magnetic fields.
established in the form
\[ P_{i}=\alpha_{i j}H_{j}. \quad (5) \]
We have seen that antiferromagnetic \( CaMnGe_{2}O_{6} \) has a magnetic point group \( 2^{\prime}/m \) below 15 K. Accordingly, the generating symmetry elements are twofold rotation accompanied by time reversal ( \( 2^{\prime} \) ) parallel to the b axis, and a mirror plane perpendicular to the b axis. By applying Neumann's principle, the matrix representation of the tensor characterizing the linear magnetoelectric effect is expressed as
\[ \alpha_{ij}=\begin{pmatrix}0&\alpha_{12}&0\\\alpha_{21}&0&\alpha_{23}\\0&\alpha_{32}&0\end{pmatrix}. \quad (6) \]
The off-diagonal character indicates that the perpendicular configuration between H and E for ME annealing must be used in order to measure the effect.
The evolution of electric polarization versus magnetic field was followed by measuring the pyroelectric current. It can be clearly seen from Fig. 9(a) that no polarization current is observed in the absence of an external magnetic field. However, the induced current appears under a magnetic field just below the AFM transition, and the current becomes stronger with the increase of the magnetic field. By reversing the annealing electric field, we were able to change the sign of the induced current. The temperature dependence of electric polarization was obtained by integrating the pyroelectric current with respect to time. As shown in Fig. 9(b), no

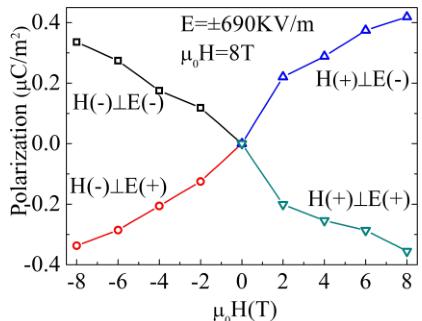
FIG. 10. The induced electric polarization as a function of applied magnetic field with different ME annealing manners.
polarization is observed with zero magnetic field, while a magnetically induced polarization monotonically increases with an increasing magnetic field. The induced electric polarization increases linearly with the increase of the magnetic field at a rate of \( \sim0.05(1)\;\muC/m^{2}/T \) (see Fig. 10). The observed maximum polarization value ( \( 0.42\;\muC/m^{2} \) under 8 T) is smaller in magnitude as compared to the typical magnetoelectric material, such as the first reported ME effect in \( Cr_{2}O_{3} \) [4]. However, it is comparable to the ME polarization value observed in \( LiCrSi_{2}O_{6} \) (single crystal) and \( LiCrGe_{2}O_{6} \) (polycrystalline), which was measured under a simultaneously applied magnetic and electric field.
The temperature dependence of the induced current was also recorded under inverse magnetic fields. This measurement was performed after ME annealing with a perpendicular configuration of \( (\pm)E \) and \( (+)H \) . The temperature dependence of pyroelectric current and electric polarization becomes stronger with increasing magnetic field. And again, the sign of the pyroelectric current and polarization switches simultaneously with the polarity of the ME annealing electric field. The polarization reversal is only achieved by varying the polarity of the ME annealing electric field but not the magnetic field alone, as represented in Fig. 10.
F. Ferrotoroidicity
In addition, it is worth noting that this nondiagonal ME tensor has, in principle, an antisymmetric part that results in a toroidic moment and provides a pure ferrotoroidic compound, i.e., the alignment of toroidic moments. This has been observed recently in the \( MnPS_{3} \) compound with the same magnetic point group \( 2^{\prime}/m \) [36]. It has been found that in \( MnPS_{3} \) , AFM domains can be simply manipulated by cooling the sample under crossed magnetic and electrical fields, as evidenced by neutron polarimetry.
According to \( \alpha_{ij} \propto \sum_{k} \epsilon_{ijk} T_{k} \) , derived from the free-energy expansion by considering the couplings between toroidization, magnetization, and polarization [37], a toroidic moment can always be represented by the antisymmetric part of the linear magnetoelectric effect tensor. A significant volumetric toroidic moment could be estimated in the monoclinic unit cell based on the definition of spontaneous toroidization,
which has been described as the toroidic moment per unit cell volume [37]. Considering the experimental parameters listed in Table I, the spontaneous toroidization of \( CaMnGe_{2}O_{6} \) is given by
\[ T_{s}=(-0.004,0,0.015)\mu_{B}/\mathring{\mathrm{A}}^{2}. \quad (7) \]
Actually, this result is very similar in magnitude to the toroidization found experimentally in MnPS \( _{3} \) [36].
The availability of large single crystals would be highly invaluable to measure the individual terms of the ME tensor and perform neutron polarimetry experiments that could allow a direct observation of the ferrotoroidic order.
IV. DISCUSSION
The neutron diffraction experiments confirm the nature of long-range antiferromagnetic order at 15 K. The magnetic structure of \( CaMnGe_{2}O_{6} \) can be described with a commensurate vector \( k = (0,0,0) \) . The determined magnetic space group, \( C2^{\prime}/c \) , allows for the linear ME effect, in good agreement with the one we observe. The magnetic structure can be described as AFM chains that are coupled ferromagnetically.
Let us first examine the AFM intrachain exchange J. The edge-sharing octahedra make Mn-O-Mn angles close to \( 94^{\circ} \) , which leads to the competition between direct and superexchange (SE) interactions within the chain. To determine which interaction is dominant, the \( Mn^{2+} \) orbital occupancy has to be taken into account. The \( Mn^{2+} \) cations have the simple configuration \( d^{5}(t_{2g}^{3}e_{g}^{2}) \) without any orbital degeneracy, thus the exchange is uniform along the chain. The direct exchange originates from the overlap integral between singly occupied \( t_{2g} \) and \( e_{g} \) orbitals, and this exchange is relatively weakly ferromagnetic. With regard to superexchange, either half-filled \( t_{2g} \) and \( e_{g} \) or half-filled \( t_{2g} \) and \( t_{2g} \) orbital overlaps via the same oxygen 2p orbital will give rise to strong AFM exchange. The dominant coupling within the chains should then be AFM, which is in accordance with our magnetic measurements and neutron diffraction results. Note that this is contrary to the results obtained for \( CaMg_{2}O_{6} \) compounds, where M = Fe, Co, Ni [16,17], for which ferromagnetic ordering of the chains is observed. This may be attributed to the different orbital occupancies and also marginally to different distances and angles within the chains. It makes the case of this \( Mn^{2+} \) containing pyroxene quite unique.
Now, we will consider interchain couplings. In \( CaMnGe_{2}O_{6} \) , the \( MnO_{6} \) octahedra chains are well-bridged by the chains of \( GeO_{4} \) tetrahedra. The two leading interchain exchanges are super-super-exchange (SSE) via double bridges of \( GeO_{4} \) tetrahedra for J1 and a single bridge for J2, as presented in Fig. 2. As a result, the general topology of the three J, J1, and J2 exchanges turns out to be triangular-like, as shown in Fig. 6. According to the topology of the spin lattice determined by neutron diffraction, the coupling through exchange integrals J and J1 is AFM, whereas J2 links two \( Mn^{2+} \) cations that are coupled ferromagnetically. If the exchange interaction J2 is antiferromagnetic, then it is not satisfied and a magnetic frustration is produced accordingly. It is worth noticing that DFT and quantum Monte Carlo calculations for the \( LiCrGe_{2}O_{6} \) pyroxene compound [38] show that the two interchain exchange integrals are antiferromagnetic with the same order of magnitude as the intrachain one. Further work to determine the strengths of the various exchange integrals in \( CaMnGe_{2}O_{6} \) will be very helpful to gain insight into the origin and role of frustration in that particular compound. As for now, the observed magnetic structure indicates a \( J > J1 > J2 \) hierarchy of the magnetic exchange couplings. Note also that this reasoning about frustration does not apply to compounds such as \( CaFeGe_{2}O_{6} \) , \( CaCoGe_{2}O_{6} \) , and \( CaNiGe_{2}O_{6} \) , since their magnetic structures are described by antiferromagnetically arranged ferromagnetic chains, which satisfy all the magnetic exchanges.
Several of our experimental results indicate that strong 1D short-range spin correlations exist at temperatures far above the long-range magnetic ordering. No peak can be detected above the Néel temperature in the heat-capacity measurements, but a large release of magnetic entropy is observed between 15 and 60 K. No magnetic reflection can be seen by neutron diffraction above \( T_{N}=15 \) K, however diffuse magnetic scattering is observed well above \( T_{N} \) and can be characterized as one-dimensional by considering its line shape. Furthermore, an abnormal variation of the c lattice parameter as a function of temperature is observed below about 60 K, which can be attributed to magnetostriction caused by the onset of magnetic correlations along the octahedra chains. To account for these observations, we constructed a phenomenological 1D magnetic correlation model based on exponentially decaying AFM correlations with the analytical form of \( S(Q) \) in this system, which produced a satisfactory fit to the diffuse neutron scattering data, yielding a quite small correlation length \( \xi=10\pm1 \) Å at 20 K. Here again, such intrachain 1D short-range correlations are not observed for pyroxenes of other 3D divalent cations, for which the intrachain interactions are ferromagnetic. In the case of \( CaMnGe_{2}O_{6} \) , the competition between interchain antiferromagnetic interactions might prevent the system from reaching three-dimensional magnetic order above 15 K, despite the onset of strong intrachain AFM correlations at about 60 K.
V. CONCLUSION
In summary, the magnetic and magnetoelectric properties of \( CaMnGe_{2}O_{6} \) were specifically investigated by combining powder neutron diffraction, magnetic susceptibility, heat capacity, and electrical polarization measurements. Far above the Néel ordering at \( T_{N}=15 \) K, we observed the appearance of 1D short-range AFM correlations with a correlation length at \( 10\ \AA \) at 20 K. A 1D AFM correlation model was developed to fit the diffuse magnetic scattering. The electrical polarization measurement performed on polycrystalline \( CaMnGe_{2}O_{6} \) evidences the linear magnetoelectric effect below \( T_{N} \) , which was allowed by considering the magnetic space-group symmetry \( (C2^{\prime}/c) \) . The experimental results reveal that no spontaneous polarization arises below \( T_{N} \) until an external magnetic field is applied. Furthermore, the linear magnetoelectric effect has an antisymmetric part that could result in a toroidic moment, and it makes \( CaMnGe_{2}O_{6} \) a pure ferrotoroidic compound.
ACKNOWLEDGMENTS
We would like to acknowledge scientific and technical support we received during the neutron powder diffraction experiment on the CRG-D1B (ILL) operated by the CNRS: V. Nassif, L. Laversenne, and S. Djellit. This
[1] M. Fiebig, J. Phys. D 38, R123 (2005).
[2] M. Bibes, Nat. Mater. 7, 425 (2008).
[3] H. Schmid, Ferroelectrics 162, 317 (1994).
[4] D. N. Astrov, Sov. Phys. JETP 11, 708 (1960).
[5] L. D. Landau and E. M. Lifshitz, Electrodynamics of Continuous Media (Pergamon Press, Oxford, 1960).
[6] X. Chen, A. Hochstrat, P. Borisov, and W. Kleemann, Appl. Phys. Lett. 89, 202508 (2006).
[7] A. A. Gorbatsevich and Y. V. Kopaev, Ferroelectrics 161, 321 (1994).
[8] Y. Sasago, M. Hase, K. Uchinokura, M. Tokunaga, and N. Miura, Phys. Rev. B 52, 3533 (1995).
[9] M. Isobe, E. Ninomiya, A. N. Vasil'ev, and Y. Ueda, J. Phys. Soc. Jpn. 71, 1423 (2002).
[10] R. Valentí, T. Saha-Dasgupta, and C. Gros, Phys. Rev. B 66, 054426 (2002).
[11] S. Jodlauk, P. Becker, J. A. Mydosh, D. I. Khomskii, T. Lorenz, S. V. Streltsov, D. C. Hezel, and L. Bohatý, J. Phys.: Condens. Matter 19, 432201 (2007).
[12] I. Kim, B. G. Jeon, D. Patil, S. Patil, G. Nénert, and K. H. Kim, J. Phys.: Condens. Matter 24, 306001 (2012).
[13] G. Nénert, M. Isobe, I. Kim, C. Ritter, C. V. Colin, A. N. Vasiliev, K. H. Kim, and Y. Ueda, Phys. Rev. B 82, 024429 (2010).
[14] G. Nénert, I. Kim, M. Isobe, C. Ritter, A. N. Vasiliev, K. H. Kim, and Y. Uedaa, Phys. Rev. B 81, 184408 (2010).
[15] C. Lee, J. Kang, J. Hong, J. H. Shim, and M. H. Whangbo, Chem. Mater. 26, 1745 (2014).
[16] G. J. Redhammer, G. Roth, W. Treutmann, W. Paulus, G. André, C. Pietzonka, and G. Amthauer, J. Solid State Chem. 181, 3163 (2008).
[17] G. J. Redhammer, G. Roth, A. Senyshyn, G. Tippelt, and C. Pietzonka, Z. Kristallogr. 228, 140 (2013).
[18] J. Rodríguez-Carvajal, Z. Phys. B 192, 55 (1993).
[19] J. F. Bérar and G. Baldinozzi, J. Appl. Crystallogr. 26, 128 (1993).
work has benefited from the financial support of ANR Contract Projet No. ANR-13-BS04-0013-01 Dymage. L.D. thanks the China scholarship council (CSC) for scholarship support. We are also grateful to V. Simonet for useful discussions.
[20] S. V. Streltsov and D. I. Khomskii, Phys. Rev. B 77, 064405 (2008).
[21] P. J. Baker, H. J. Lewtas, S. J. Blundell, T. Lancaster, I. Franke, W. Hayes, F. L. Pratt, L. Bohatý, and P. Becker, Phys. Rev. B 81, 214403 (2010).
[22] J. G. Cheng, W. Tian, J. S. Zhou, V. M. Lynch, H. Steinfink, A. Manthiram, A. F. May, V. O. Garlea, J. C. Neuefeind, and J. Q. Yan, J. Am. Chem. Soc. 135, 2776 (2013).
[23] E. F. Bertaut, Acta Crystallogr. Sect. A 24, 217 (1968).
[24] A. S. Wills, Z. Phys. B 276-278, 680 (2000).
[25] B. E. Warren, Phys. Rev. 59, 693 (1941).
[26] A. S. Wills, G. S. Oakley, D. Visser, J. Frunzke, A. Harrison, and K. H. Andersen, Phys. Rev. B 64, 094436 (2001).
[27] J. E. Greedan, N. P. Raju, and I. J. Davidson, J. Solid State Chem. 128, 209 (1997).
[28] R. C. Jones, Acta Crystallogr. 2, 252 (1949).
[29] C. Lacroix, Ph. Mendels, and F. Mila, Introduction to Frustrated Magnetism: Materials, Experiments, Theory (Springer Science & Business Media, Berlin, 2011), Vol. 164.
[30] B. D. Rainford, J. Phys. (Paris) Colloq. 43, C7-33 (1982).
[31] T. M. Sabine, Aust. J. Phys. 33, 565 (1980).
[32] B. Fák, F. C. Coomer, A. Harrison, D. Visser, and M. E. Zhitomirsky, Europhys. Lett. 81, 17006 (2008).
[33] P. J. Brown, in International Tables for Crystallography, edited by A. J. C. Wilson (International Union of Crystallography, Chester, UK, 2006), Chap. 4.4.5, p. 391.
[34] W. Marshall and S. W. Lovesey, Theory of Thermal Neutron Scattering: The Use of Neutrons for the Investigation of Condensed Matter (Oxford University Press, London, 1971).
[35] S. A. Hayward, S. A. T. Redfern, and E. K. H. Salje, J. Phys.: Condens. Matter 14, 10131 (2002).
[36] E. Ressouche, M. Loire, V. Simonet, R. Ballou, A. Stunault, and A. Wildes, Phys. Rev. B 82, 100408(R) (2010).
[37] C. Ederer and N. A. Spaldin, Phys. Rev. B 76, 214404 (2007).
[38] O. Janson, G. Nénert, M. Isobe, Y. Skourski, Y. Ueda, H. Rosner, and A. A. Tsirlin, Phys. Rev. B 90, 214424 (2014).