| Transition Temperature | 3.6 K |
|---|---|
| Experiment Temperature | 0.25 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | Pbnm (#62) |
| Magnetic Space Group | Pn'm'a' (#62.449) |
| Magnetic Point Group | m'm'm' (8.5.28) |
| Lattice Parameters | 5.16420 5.41650 7.38020 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1016/j.solidstatesciences.2013.12.001 |
| Reference | K. Knizek, Z. Jirak, P. Novak and C. de la Cruz, Solid State Sciences (2014) 28 26-30. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Dy1 | Dy | -4.3 | 8. | 0.0 | 9.08 |
Non-collinear magnetic structures of TbCoO_{3} and DyCoO_{3}
K. Knížek \( ^{a,*} \) , Z. Jiráš \( ^{a} \) , P. Novák \( ^{a} \) , Clarina de la Cruz \( ^{b} \)
\( ^{a} \) Institute of Physics ASCR, Cukrovarnická 10, 162 00 Prague 6, Czech Republic
\( ^{b} \) Neutron Scattering Science Division, ORNL, Oak Ridge, TN 37831, United States
ARTICLE INFO
Article history: Received 29 September 2013 Received in revised form 21 November 2013 Accepted 3 December 2013 Available online 11 December 2013
Keywords: Neutron diffraction Crystal fields level splitting TbCoO_{3} DyCoO_{3} Magnetic structure
A B S T R A C T
The orthoperovskites TbCoO \( _{3} \) and DyCoO \( _{3} \) with Co \( ^{3+} \) in a non-magnetic low-spin state have been investigated by neutron diffraction down to 0.25 K. Magnetic ordering is evidenced below \( T_{N}=3.3 \) K and 3.6 K, respectively, and the ordered arrangements are of canted type, \( A_{x}G_{y} \) for TbCoO \( _{3} \) and \( G_{x}A_{y} \) for DyCoO \( _{3} \) in Bertaut's notation. The experiments are confronted with the first-principle calculations of the crystal field and magnetism of Tb \( ^{3+} \) and Dy \( ^{3+} \) ions, located in the Pbnm structure on sites of \( C_{s} \) point symmetry. Both these ions exhibit an Ising behavior, which originates in the lowest energy levels, in particular in accidental doublet of non-Kramers Tb \( ^{3+} \) ( \( 4f^{9} \) configuration) and in ground Kramers doublet of Dy \( ^{3+} \) ( \( 4f^{9} \) ) and it is the actual reason for the non-collinear AFM structures. Very good agreement between the experiment and theory is found. For comparison, calculations of the crystal field and magnetism for other systems with Kramers ions, NdCoO \( _{3} \) and SmCoO \( _{3} \) , are also included.
© 2013 Elsevier Masson SAS. All rights reserved.
1. Introduction
The perovskite cobaltites of \( LaCoO_{3} \) type are systems with closeness in energy of different local state of the octahedrally coordinated cobalt ions. The ground state is generally based on non-magnetic low spin state of \( Co^{3+} \) (LS, \( S = 0 \) , \( t_{2g}^{6}e_{g}^{0} \) ), and the paramagnetic high spin \( Co^{3+} \) (HS, \( S = 2 \) , \( t_{2g}^{4}e_{g}^{2} \) ) species are populated by thermal excitation, which process becomes observable for \( LaCoO_{3} \) above \( \sim40 \) K and achieves the highest rate at \( T_{mgn} = 70 \) K as documented by a maximum of the specific heat excess and anomalous expansion. The resulting non-uniform phase is characterized by HS/LS nearest neighbor correlations [1,2]. A further change is observed at about 530 K where the correlations are melted by thermal agitation, which is accompanied with a drop of electrical resistivity reminding the insulator–metal transition. In related systems with smaller rare-earth or yttrium ions, the magnetic transition shifts to higher temperatures and finally merges with the electrical transition, in particular for \( TbCoO_{3} \) and \( DyCoO_{3} \) at \( T_{mgn} = 735 \) K and 740 K, respectively [3]. Such increased stability of \( LS Co^{3+} \) means that the low-temperature magnetic properties are governed by \( Tb^{3+} \) and \( Dy^{3+} \) local moments and depend on the crystal field splitting of respective \( 4f^{8} \) and \( 4f^{9} \) levels, as well as on the rare-earth intersite interactions. Early studies have shown that \( TbCoO_{3} \) and \( DyCoO_{3}\cdot \) undergo a non-collinear antiferromagnetic (AFM) ordering below \( T_{N}=3.3 \) K and 3.6 K due to interactions that are for the most part of a classical dipole–dipole nature [4,5]. The present study revisits both systems. The crystal and magnetic structures are refined based on the high-resolution powder neutron diffraction, and the electronic levels of rare-earth ions are determined together with their magnetic characteristics, using a novel ab-initio approach. It appears that the observed magnetic arrangements reflect the Ising nature of rare-earths moments associated with the lowest energy levels, namely the ground Kramers doublet of \( Dy^{3+} \) and accidental doublet of non-Kramers \( Tb^{3+} \) .
2. Experiment and calculations
Samples \( TbCoO_{3} \) and \( DyCoO_{3}) \) were prepared by a solid state reaction from stoichiometric amounts of \( Co_{2}O_{3} \) and respective oxides \( Tb_{4}O_{7} \) and \( Dy_{2}O_{3} \) . The precursor powders were mixed, pressed in the form of pellets and sintered at \( 1200\ ^{\circ}C \) for 100 h under air. The product was checked for phase purity and its structural and physical properties were extensively probed. Both compounds were identified as distorted perovskite structure of the orthorhombic Pbnm symmetry.
The powder neutron diffraction was performed on diffractometer Hb2a at Oak Ridge National Laboratory. The scans were recorded at selected temperatures between the 0.25 and 150 K. Two crystal monochromators (Ge113 and Ge115) were used, providing neutron wavelengths \( \lambda = 2.408 \) Å and 1.537 Å.
respectively. Data were collected between \( 8^{\circ} \) and \( 126^{\circ} \) of \( 2\theta \) with the step of \( 0.08^{\circ} \) . To overcome the problem with rather high absorption of dysprosium, the neutrons path length through the \( DyCoO_{3} \) sample was minimized by use of an annular container, where the powder was placed between two concentric aluminum cylinders. Structural refinements were done by Rietveld profile analysis using program FULLPROF (Version 5.30-Mar2012-ILL JRC).
The determination of the \( Tb^{3+} \) and \( Dy^{3+} \) electronic structure was performed in two steps. First, the crystal field parameters were calculated using a novel method based on the first-principles band structure and Wannier projection [6]. The model depends on a single parameter \( \Delta \) , which adjusts relative position of the 4f and oxygen energy levels. In the present calculations \( \Delta \) was fixed at 8.2 eV, which value yields very good agreement between the calculated and experimental values of the multiplet splittings of \( Pr^{3+} \) , \( Nd^{3+} \) , \( Tb^{3+} \) and \( Er^{3+} \) in the orthoperovskites [6,7]. Then the local Hamiltonian operating on the 4f states in a determinantal basis of one-electron wavefunctions was constructed, including the electron–electron repulsion, spin–orbit coupling, crystal field and Zeeman interaction terms. The eigenvalue problem was solved for different orientation and strength of the applied field, in which not only the crystal field splitting of the multiplets, but also their magnetic characteristics (anisotropic g-factors and/or van Vleck susceptibilities) were determined. These calculations were done with the modified 'lanthanide' program [8].
3. Results
3.1. Crystal structure
For \( TbCoO_{3} \) and \( DyCoO_{3} \) the single orthorhombic Pbnm structure is observed over the whole experimental temperature range. For three selected temperatures the complete data including atomic coordinates, Co–O bonding lengths and Co–O–Co angles are presented in Table 1. The relation between lattice parameters, \( b > c/\sqrt{2} > a \) is typical for perovskites \( ABO_{3} \) with smaller A cations (and smaller tolerance factor), for which the tilting of \( CoO_{6} \) octahedra is the dominant source of the orthorhombic distortion. The extent of octahedral tilting is quantified by the average bond angle Co–O–Co, which is close to \( 150^{\circ} \) for both the compounds. The rare-earth cations are located on mirror plane of the Pbnm structure, on the site of low symmetry ( \( C_{s} \) point group), which is coordinated by twelve oxygen atoms. The RE–O distances could be divided into a group of eight short (bonding) lengths within a range 2.2–2.6 Å, and a group of four long distances 3.0–3.4 Å that should be considered as non-bonding ones since they increase with decreasing A size.
3.2. Electronic levels of \( Tb^{3+} \) and \( Dy^{3+} \)
Tb^{3+} in electronic configuration 4f^{8} is a non-Kramers ion. The lowest lying free-ion term is \( ^{7}F_{6} \) (L = 3, S = 3, J = 6), and in the solid it is split by crystal field effects. In Pbnm perovskites with the rare-earth sites of low symmetry \( C_{s} \) , the degeneracy is completely removed, yielding 13 singlets. The analysis of optical transitions available for TbAlO_{3} of the same Pbnm symmetry show that the ground and first excited states of Tb^{3+} ion are formed of 90% by two conjugate J = 6 wavefunctions, |6, +6⟩ + |6, −6⟩ and |6, +6⟩ − |6, −6⟩, and their eigenenergies differ by only 0.025 meV, representing a quasi-doublet [9]. This specific kind of accidental degeneracy has important consequences. Firstly, a relatively modest magnetic field of external or molecular nature will mix the eigenstates into a form of two pseudospins with the main weight of |6, +6⟩ and |6, −6⟩ ionic states, respectively. This results in large magnetic moment of Tb^{3+} ions of about 8.4 μ_{B}. Secondly, these moments have essentially an Ising-like character, which is a source of large local anisotropy.
In the case of \( Dy^{3+} \) in electronic configuration \( 4f^{9} \) , the lowest lying free-ion term is \( ^{6}H_{15/2} \) (L = 5, S = 5/2, J = 15/2), and it is split by the low-symmetry crystal field to 8 Kramers doublets. The ground doublet is spanned by two pseudospins with dominant contribution of \( |15/2, +15/2\rangle \) and \( |15/2, -15/2\rangle \) ionic states, pointing also to the Ising character.
The results of present first-principle approach are summarized in Appendix, where the calculated single-electron CFP for non-Kramers \( Tb^{3+} \) and Kramers \( Dy^{3+} \) are displayed including two other ions possessing Kramers degeneracy, \( Nd^{3+} \) ( \( 4f^{9} \) ) and \( Sm^{3+} \) ( \( 4f^{5} \) ) (see Table A.3). Using these parameters in the 'lanthanide' program, the splitting of \( 4f^{n} \) levels for each rare-earth ion is determined. It is seen below in Table A.7 that the two lowest singlets for \( Tb^{3+} \) in \( TbCoO_{3} \) are separated in energy by only 0.002 meV. Next two singlets are situated at much larger energy, 22.9 and 23.1 meV. For \( Dy^{3+} \) all the states are true doublets and the first excited doublet is situated at energy of 29.8 meV above the ground doublet. Similar separation between the ground and excited doublet is found for \( Sm^{3+} \) , 29.6 meV, while a somewhat lower separation 13.2 meV is obtained for \( Nd^{3+} \) (see also Ref. [7]).
The crystallographic data summary for \( TbCoO_{3} \) and \( DyCoO_{3}^{+} \) at selected temperatures. Space group Pbnm.
| TbCoO3 | DyCoO3 | |||||
| T(K) | 0.25 | 5.5 | 150 | 0.25 | 5.5 | 150 |
| a(Å) | 5.2034(3) | 5.2034(3) | 5.1995(2) | 5.1642(3) | 5.1650(3) | 5.1655(3) |
| b(Å) | 5.3890(3) | 5.3898(3) | 5.3945(2) | 5.4165(4) | 5.4161(3) | 5.4143(4) |
| c(Å) | 7.4050(4) | 7.4052(4) | 7.4102(3) | 7.3802(4) | 7.3813(4) | 7.3866(5) |
| V(Å3) | 207.64(2) | 207.68(2) | 207.84(2) | 206.44(2) | 206.48(2) | 206.59(2) |
| Atom coordinates: TbDy 4c(x,y,1/4), Co 4b(1/2,0,0), O1 4c(x,y,1/4), O2 8d(x,y,z). | ||||||
| x,TbDy | -0.0124(7) | -0.0121(6) | -0.0134(4) | -0.0157(4) | -0.0156(4) | -0.0114(8) |
| y,TbDy | 0.0633(4) | 0.0597(4) | 0.0608(3) | 0.0662(4) | 0.0656(3) | 0.0641(4) |
| x,O1 | 0.0924(9) | 0.0919(7) | 0.0921(5) | 0.4051(10) | 0.0928(9) | 0.0940(14) |
| y,O1 | 0.4779(8) | 0.4772(6) | 0.4776(4) | -0.0193(9) | 0.4796(8) | 0.4844(12) |
| x,O2 | -0.3008(6) | -0.3000(4) | -0.2994(3) | -0.3006(7) | -0.3003(7) | -0.3132(11) |
| y,O2 | 0.2970(6) | 0.2976(4) | 0.2971(3) | 0.3028(8) | 0.3033(7) | 0.3051(10) |
| z,O2 | 0.0446(4) | 0.0461(3) | 0.0454(2) | 0.0448(5) | 0.0447(5) | 0.0483(6) |
| Selected bond distances and angles. | ||||||
| Co-O1(Å) × 2 | 1.916(2) | 1.916(1) | 1.917(1) | 1.912(2) | 1.910(2) | 1.911(2) |
| Co-O2(Å) × 2 | 1.935(4) | 1.935(3) | 1.932(2) | 1.913(5) | 1.910(4) | 1.946(6) |
| Co-O2(Å) × 2 | 1.938(4) | 1.942(3) | 1.942(2) | 1.965(5) | 1.968(5) | 1.964(6) |
| Co-O1-Co(-) × 1 | 150.0(4) | 150.1(3) | 150.1(2) | 149.6(5) | 150.1(4) | 150.1(6) |
| Co-O2-Co(-) × 2 | 150.5(4) | 150.1(3) | 150.5(2) | 149.6(4) | 149.6(4) | 146.2(6) |
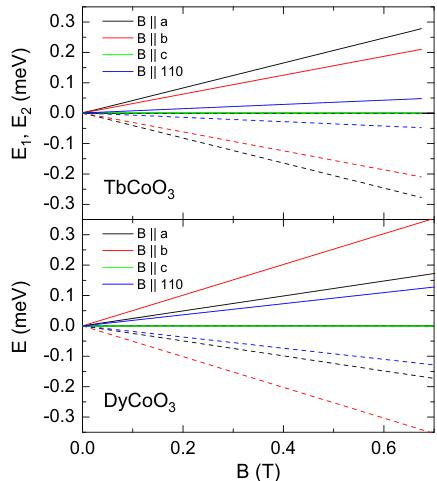
The application of external magnetic field brings two effects on the rare-earth electronic levels (see e.g. Ref. [7]). One is a linear splitting of the doublets that defines the relevant magnetic moments and represents Zeeman energy. Except very low fields, the splitting of the \( Tb^{3+} \) pseudodoublet is also linear, as illustrated for several orientations of applied field in upper panel of Fig. 1. The corresponding g-factors are strongly anisotropic, they are in fact of Ising character with principal components \( g_{x} = 17.78 \) , \( g_{y} \sim 0 \) , \( g_{z} \sim 0 \) , where the local z-axis is defined by symmetry along the perovskite c axis and the Ising x-axis in c-plane makes an angle \( \alpha_{g} = \pm 37.1^{\circ} \) with the orthorhombic a axis. (Here \( \pm \) refers to two inequivalent rare-earth sites in the structure.)
An analogous calculation for the ground doublet of \( Dy^{3+} \) (see lower panel of Fig.1) gives principal components \( g_{x}=19.44 \) , \( g_{y}\sim0 \) , \( g_{z}\sim0 \) and orientation of the Ising axis in c-plane under the angle \( \alpha_{g}=\pm64.0^{\circ} \) to the a-axis.
The g-factors for \( Sm^{3+} \) and \( Nd^{3+} \) are much less anisotropic with principal in-plane components \( g_{x}=0.703 \) , \( g_{y}=0.588 \) , out-of-plane component \( g_{z}=0.322 \) and orientation of the x-axis under the angle \( \alpha_{g}=\pm33.2^{\circ} \) for \( SmCoO_{3} \) . The respective values for \( NdCoO_{3} \) are \( g_{x}=2.818 \) , \( g_{y}=1.228 \) , \( g_{z}=3.015 \) and angle \( \alpha_{g}=\pm62.3^{\circ} \) .
The second effect, visible in high fields only, is a small downward shift of the doublet gravity center that varies quadratically with the field magnitude. This energy decrease arises from the mixing of ground singlets or doublets with higher lying states and is at the root of van Vleck paramagnetism. In systems with non-Kramers ions, this term is generally manifested at low temperatures as a practically constant susceptibility, independent up to very high fields. The well known example is the paramagnetic contribution of \( Pr^{3+} \) [10]. Similar contribution exists also for Kramers ions, where van Vleck susceptibility represents a small addition to dominant, strongly temperature dependent Curie susceptibility that arises due to thermal redistribution within the split levels of ground doublet. In particular for \( DyCoO_{3} \) , the principal values of the van Vleck susceptibility tensor associated with \( Dy^{3+} \) are calculated to \( \chi_{\xi}=0.0143 \) , \( \chi_{\eta}\sim0 \) for the in-plane components, \( \chi_{\zeta}=0.0526\mu_{B} \) T for the out-of-plane component and the orientation of \( \xi \) axis is

Fig. 1. Zeeman splitting of the \( TbCoO_{3} \) low-energy pseudodoublet and the \( DyCoO_{3} \) ground doublet.
defined by \( \alpha_{vV}=\pm22.2^{\circ} \) with respect to the a-axis. Let us note that there is also van Vleck contribution of \( LS\ Co^{3+} \) , which is of the order \( \sim0.0004\ \mu_{B}/T \) ( \( \sim0.0002\ \mu_{B}\ mol^{-1}\ Oe^{-1} \) ) and brings thus little effect.
3.3. Magnetic ordering
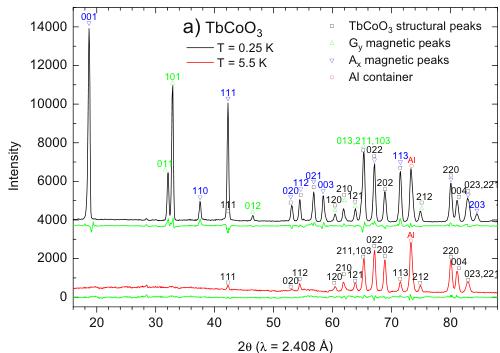
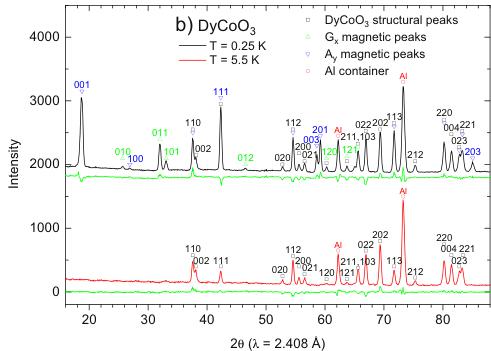
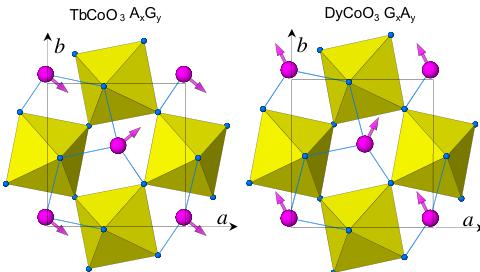
The neutron diffraction data at the lowest temperature \( (T=0.25\ \mathrm{K}) \) and above \( T_{N}(T=5.5\ \mathrm{K}) \) are displayed in Fig. 2. Presence of AFM ordering is manifested in appearance of magnetic peaks below \( T_{N} \) at positions hkl with \( h+k=2n+1 \) , in particular \( 100+010 \) and \( 101+011 \) . These peaks are indicative for the A- and G-types of AFM arrangement in the sample, depending whether \( l=2n \) or \( 2n+1 \) . Let us note that the presence of both components indicates a canting, which is an inevitable consequence of the Ising character of \( Tb^{3+} \) and \( Dy^{3+} \) moments, and the inclination of easy axes \( \pm\alpha \) in the ab-plane of the orthoperovskite structure [9].
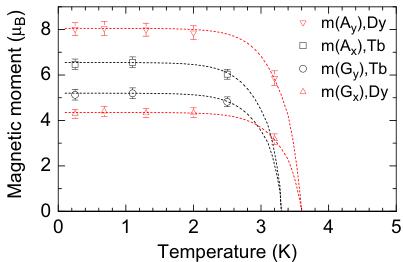
The results of the Rietveld refinement of the rare-earth moments are presented in Fig. 3. The estimated Néel temperatures of the AFM ordering \( T_{N} = 3.3 \) K and 3.6 K for \( TbCoO_{3} \) and \( DyCoO_{3} \) , respectively, are in agreement with previous studies [4,5,11]. The ordered moments are oriented in the a,b-plane of the orthoperovskite structure and reach \( m(A_{\mathrm{x}}) = 6.5 \mu_{\mathrm{B}} \) and \( m(G_{\mathrm{y}}) = 5.1 \mu_{\mathrm{B}} \) for \( TbCoO_{3} \) and \( m(G_{\mathrm{x}}) = 4.3 \mu_{\mathrm{B}} \) and \( m(A_{\mathrm{y}}) = 8.0 \mu_{\mathrm{B}} \) for \( DyCoO_{3} \) . The goodness of final fit is manifested by the difference curves \( I_{obs} - I_{calc} \) in Fig. 2 and for the measurements taken at 0.25 K by R-factors values \( R_{p} = 7.8\% \) , \( R_{wp} = 10.7\% \) , \( R_{bragg} = 5.68\% \) and \( R_{mag} = 14.4\% \) for


Fig. 2. Neutron diffraction patterns of \( TbCoO_{3} \) and \( DyCoO_{3}\ at\ 0.25\ and\ 5.5\ K \) ( \( \lambda = 2.408\ \AA \) ). The difference curve \( I_{obs} - I_{calc} \) is displayed below each pattern.

Fig. 3. The AFM ordered moments deduced from neutron diffraction patterns of \( TbCoO_{3} \) and \( DyCoO_{3} \) . The dashed lines are guides to the eyes.
TbCoO_{3} and R_{p}=8.7%, R_{wp}=11.6%, R_{Bragg}=9.84% and R_{mag}=14.3% for DyCoO_{3}. The rather high magnetic R-factors may be related to the anisotropy of rare-earth's form factors, which is not included in the FullProf Rietveld package.
4. Discussion
Based on the present study, Néel temperatures of the AFM ordering in TbCoO_{3} and DyCoO_{3} is estimated to T_{N}=3.3 K and 3.6 K, and the ordering is of A_{x}G_{y} and G_{x}A_{y} type, respectively. This is in agreement with earlier findings on these cobaltites [5,11] and is also close to AFM temperatures in analogous aluminates [12,13]. The arrangements in the a,b-plane of the orthoperovskite structure are depicted in Fig. 4 and the coupling along the c-axis is purely AFM. The ordered moments for TbCoO_{3} have a magnitude of m=8.3 \( \mu_{B} \) and are inclined from the orthoperovskite a-axis to angle \( \pm38^{\circ} \) . For DyCoO_{3}, the magnitudes of moments is m=9.1 \( \mu_{B} \) and their inclination is \( \pm62^{\circ} \) .
The experimental magnitudes and directions of the magnetic moments are confronted with calculated values in Table 2. Calculated magnitudes of the moments are by 7 and 6% larger than the experimental ones in TbCoO \( _{3} \) and DyCoO \( _{3} \) , respectively. Taking into account that theory contains no parameter to fit the experiment the agreement may be regarded as good for the magnitudes of the moments and excellent for their directions. As pointed out by Bidaux and Meriel for DyAlO \( _{3} \) [12], there are two variants depending in which sense the moments could be inclined, which cannot be distinguished in neutron diffraction experiment. On the other hand, theory allows an unambiguous assignment of the sign of angle \( \alpha_{g} \) to the RE crystal site. Regarding the agreement of the experimentally determined angles and the orientation of Ising axes

Fig. 4. Schematic view of octahedral tilts and the magnetic structures of TbCoO₃ and DyCoO₃. The CoO₆ octahedrons are centered at the c = 0 level; the displayed rare-earth moments are located at c = 1/4 while those at c = 3/4 are oppositely oriented.
Table 2
Comparison of the rare-earth magnetic moment (\(m_{\mathrm{RE}}\)) and its inclination from the orthoperovskite \(a\)-axis (\(a_{g}\)) obtained by neutron diffraction refinement (ND) and electronic structure calculation (calc.) for the reference position (\(\sim0,\sim0.1/4\)).
| TbCoO_{3} | DyCoO_{3} | |||
| ND | Calc. | ND | Calc. | |
| \( \alpha_{g} \) ( \( ^{\circ} \) ) | \( \pm38(1) \) | -37.1 | \( \pm62(1) \) | -64.0 |
| \( m_{\mathrm{RE}} \) ( \( \mu_{B} \) ) | 8.3(2) | 8.9 | 9.1(2) | 9.7 |
in our calculations, we may state that, with respect to \( CoO_{6} \) tilts, the actual orientation is as shown in Fig. 4.
As mentioned above, the origin of observed AFM arrangement, \( A_{x}G_{y} \) for \( TbCoO_{3} \) and \( G_{x}A_{y} \) for DyCoO \( _{3} \) in Bertaut's notation, can be associated with dipolar interactions, which dominant role can be understood in view of large magnitude of the \( Tb^{3+} \) and \( Dy^{3+} \) long-range ordered moments, \( \sim8 \) and \( 9\ \mu_{B} \) , respectively. There are, however, strong indications that the superexchange interactions of purely spin nature must be also acting and may eventually decide on final magnetic arrangement in the rare-earth cobaltites, aluminates or gallets. In particular, AFM ordering at \( T_{N}=1.5 \) K is stabilized for \( SmCoO_{3} \) , though the spin and orbital components of the \( Sm^{3+} \) moment nearly cancel ( \( L=5, S=5/2, J=L-S=5/2 \) ), and dipolar interactions are thus negligible.
Acknowledgments
This work was supported by Project No. P204/11/0713 of the Grant Agency of the Czech Republic. We acknowledge the Oak Ridge National Laboratory (Tennessee, United States) for providing access to the neutron beams and for all technical support during the experiments.
Appendix A. Electron states and magnetism of lanthanide ions in orthocobaltites
The crystal field parameters, obtained by first-principle calculations with a use of experimental crystallographic data for \( NdCoO_{3} \) [14], \( SmCoO_{3} \) [15], \( TbCoO_{3} \) and \( DyCoO_{3}) \) (see Table 1), are summarized in Table A.3. The energies of Kramers doublets and respective \( \widehat{g} \) and \( \widehat{\chi}^{\nu V} \) tensor components for \( Nd^{3+} \) , \( Sm^{3+} \) and \( Dy^{3+} \) are presented in Tables A.4, A.5 and A.6. The diagonal tensor components refer to axes a, b and c of the orthorhombic space group \( Pbnm \) , while the index \( \omega \) stands for the field orientation along 110.
The energies of thirteen levels of the \( {}^{t}F_{6} \) multiplet of the non-Kramers \( Tb^{3+} \) are given in Table A.7. It appears that there are five pairs of states with close energy possessing a quasi-doublet character, i.e. allowing sizeable Zeeman splitting when the strength of external field exceeds the energy gap. The remaining three singlets are non-magnetic and their response to external field is of the van Vleck character.
Table A.3
Nonzero parameters of the crystal field (in meV) in four compounds studied. They hold for the rare-earth position close to \( (\sim0, \sim0, 1/4) \) .
| k | q | NdCoO_{3} | SmCoO_{3} | TbCoO_{3} | DyCoO_{3} |
| 2 | 0 | 28.27 | -37.47 | -21.73 | -65.93 |
| 2 | 2 | 6.47 + 94.6 \mathrm{o}i | 8.31 + 104.64 \mathrm{i} | -9.42 + 62.64 \mathrm{i} | -63.09 + 121.03 \mathrm{i} |
| 4 | 0 | -60.52 | -58.65 | -35.01 | -40.22 |
| 4 | 2 | -9.92 + 120.83 \mathrm{i} | -40.05 + 83.35 \mathrm{i} | -22.50 + 62.48 \mathrm{i} | -59.49 + 52.97 \mathrm{i} |
| 4 | 4 | 46.45 - 64.44 \mathrm{i} | 33.15 - 93.32 \mathrm{i} | 19.07 - 93.94 \mathrm{i} | 12.53 - 128.77 \mathrm{i} |
| 6 | 0 | -121.36 | -66.87 | -54.23 | -41.20 |
| 6 | 2 | 8.78 + 63.53 \mathrm{i} | 11.67 + 33.29 \mathrm{i} | 14.34 + 25.77 \mathrm{i} | 11.46 + 22.01 \mathrm{i} |
| 6 | 4 | -195.90 + 6.00 \mathrm{i} | -136.29 - 0.34 \mathrm{i} | -115.29 - 6.27 \mathrm{i} | -92.65 - 4.13 \mathrm{i} |
| 6 | 6 | 11.63 + 0.48 \mathrm{i} | 11.68 - 3.65 \mathrm{i} | 11.18 + 1.53 \mathrm{i} | 2.55 + 2.49 \mathrm{i} |
Table A.4
\( Nd^{3+} \) ion in \( NdCoO_{3} \) . Energy of five Kramers doublets originating from \( {}^{4}I_{9/2} \) multiplet, \( \tilde{g} \) and \( \tilde{\chi}^{\nu\nu} \) tensor components along the orthorhombic axes and \( \omega \) direction. Energy \( \varepsilon(0) \) is in meV, \( \tilde{\chi}^{\nu\nu} \) is units of \( \mu_{B}/T \) .
| Doublet | \( \varepsilon(0) \) | \( g_{aa} \) | \( g_{bb} \) | \( g_{cc} \) | \( g_{\omega} \) | \( \chi_{aa}^{\nu\nu} \) | \( \chi_{bb}^{\nu\nu} \) | \( \chi_{cc}^{\nu\nu} \) | \( \chi_{\omega}^{\nu\nu} \) |
| 1 | 0.00 | 1.701 | 2.560 | 3.015 | 1.442 | 0.0149 | 0.0106 | 0.0118 | 0.0024 |
| 2 | 13.19 | 1.773 | 2.208 | 2.432 | 0.813 | -0.0072 | -0.0020 | 0.0040 | 0.0054 |
| 3 | 25.66 | 3.596 | 2.524 | 1.666 | 3.800 | 0.0026 | 0.0018 | -0.0062 | -0.0013 |
| 4 | 64.37 | 2.964 | 3.950 | 1.659 | 4.372 | -0.0012 | -0.0022 | 0.0008 | 0.0016 |
| 5 | 84.60 | 2.576 | 2.152 | 3.009 | 1.605 | -0.0068 | -0.0057 | -0.0081 | -0.0063 |
Table A.5
Sm \( ^{3+} \) ion in SmCoO \( _{3} \) . Energy of three Kramers doublets originating from \( {}^{6}H_{5/2} \) multiplet, \( \tilde{g} \) and \( {\tilde{\chi}}^{\nu\nu} \) tensor components along the orthorhombic axes and \( \omega\omega \) direction. Energy \( \varepsilon(0) \) is in meV, \( \tilde{\chi}^{\nu\nu} \) is units of \( \mu_{b}/T \) .
| Doublet | \( \varepsilon(0) \) | \( g_{aa} \) | \( g_{bb} \) | \( g_{CC} \) | \( g_{\omega} \) | \( \chi_{aa}^{\nu} \) | \( \chi_{bb}^{\nu} \) | \( \chi_{CC}^{\nu} \) | \( \chi_{\omega}^{\nu} \) | |
| 1 | 0.00 | 0.671 | 0.625 | 0.322 | 0.593 | 0.0017 | 0.0013 | 0.0019 | 0.0012 | |
| 2 | 29.63 | 1.525 | 0.963 | 0.464 | 0.398 | 0.0012 | 0.0017 | 0.0012 | 0.0011 | |
| 3 | 61.79 | 1.141 | 1.362 | 0.067 | 0.328 | 0.0013 | 0.0010 | 0.0008 | 0.0012 | |
Table A.6
\( Dy^{3+} \) ion in \( DyCoO_{3} \) . Energy of eight Kramers doublets originating from \( {}^{6}H_{15/2} \) multiplet, \( \tilde{g} \) and \( {}^{3}\chi^{\nu\nu} \) tensor components along the orthorhombic axes and \( \omega\ddot{\omega} \) direction. Energy \( \varepsilon(0) \) is in meV, $ \tilde{\chi}^{\nu\nu} $ is units of \( \mu_{B}/T \) .
| Doublet | \( \varepsilon(0) \) |
Table A.7
\( Tb^{3+} \) ion in \( TbCoO_{3} \) . Energy of five magnetic quasidoublets and three singlets originating from \( {}^{7}F_{6} \) multiplet, \( \tilde{g} \) tensor components along the orthorhombic axes and \( \omega \) diretion, in high field ( \( \sim1 \) T) limit. Energy \( \varepsilon(0) \) is in meV.
| Singlet | \( \varepsilon(0) \) | \( g_{aa} \) | gbb | gcc | \( g_{\omega} \) |
| 1 + 2 | 0.000 + 0.002 | 14.18 | 10.71 | 0 | 2.40 |
| 3 + 4 | 22.897 + 23.063 | 1.59 | 4.34 | 0 | 0.08 |
| 5 | 33.264 | — | — | — | — |
| 6 | 35.889 | — | — | — | — |
| 7 + 8 | 41.325 + 41.334 | 3.82 | 0.39 | 0 | 1.76 |
| 9 | 43.185 | — | — | — | — |
| 10 + 11 | 43.59 + 44.491 | 0 | \( \sim \) 0.04 | 0.31 | 0 |
| 12 + 13 | 68.797 + 68.824 | 13.30 | 5.97 | 0 | 14.66 |
References
[1] J.B. Goodenough, J. Phys. Chem. Solids 6 (1958) 287.
[2] K. Knížek, Z. Jirák, J. Hejtmánek, P. Novák, W. Ku, Phys. Rev. B 79 (2009) 014430.
[3] K. Knížek, Z. Jirák, J. Hejtmánek, M. Veverka, M. Maryško, G. Maris, T.T.M. Palstra, Eur. Phys. J. B 47 (2005) 213.
[4] J. Mareschal, J. Sivardíére, G.F. De Vries, E.F. Bertaut, J. Appl. Phys. 39 (1968) 1364.
[5] A. Kappatsch, A. Quezel-Ambrunaz, J. Sivardiére, J. Phys. France 31 (1970) 369. [6] P. Novák, K. Knížek, J. Kunes, Phys. Rev. B 87 (2013) 205139.
[7] P. Novák, K. Knížek, M. Maryško, Z. Jirák, J. Kunes, J. Phys. Condens. Matter 25 (2013) 446001.
[8] S. Edvardsson, D. Aberg, Comput. Phys. Commun. 133 (2001) 396.
[9] J.B. Gruber, K.L. Nash, R.M. Yow, D.K. Sardar, U.V. Valiev, A.A. Uzokov, G.W. Burdick, J. Lumin. 128 (2008) 1271.
[10] R.M. Thomas, V. Skumryev, J.M.D. Coey, S. Wirth, J. Appl. Phys. 85 (1999) 5384.
[11] A. Muñoz, M.J. Martínez-Lope, J.A. Alonso, M.T. Fernández-Díaz, Eur. J. Inorg. Chem. 2012 (2012) 5825.
[12] R. Bidaux, P. Meriel, J. Phys. 29 (1968) 220.
[13] L. Holmes, R. Sherwood, L.G. Van Uitert, J. Appl. Phys. 39 (1968) 1373.
[14] K. Knížek, J. Hejtmánek, Z. Jirák, P. Tomes, P. Henry, G. André, Phys. Rev. B 79 (2009) 134103.
[15] J. Pérez-Cacho, J. Blasco, J. García, R. Sanchez, J. Solid State Chem. 150 (2000) 145.