| Transition Temperature | 21 K |
|---|---|
| Experiment Temperature | 4.2 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | Pbam (#55) |
| Magnetic Space Group | Pbam' (#55.356) |
| Magnetic Point Group | m'mm (8.3.26) |
| Lattice Parameters | 7.56000 8.67000 5.80000 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1016/0022-3697(70)90326-4 |
| Reference | G. Buisson, Journal of Physics and Chemistry of Solids (1970) 31 1171-1183. |
ETUDE PAR RAYONS X ET NEUTRONS DE LA SERIE ISOMORPHE AtTiO \( _{5} \)
(A = Cr, Mn, Fe, T = TERRES RARES)
G. BUISSON
Centre d'études Nucleaires, Cedex 85, 38-Grenoble-Gare, France
(Received 15 July 1969)
Résumé—Les composés \( AtTiO_{5} \) sont isomorphes à \( Mn_{2}HoO_{5} \) pour les terres rares de la première série dont le rayon ionique \( r(T) \) est compris entre \( r(Pr) \) et \( r(Gd) \) . Dans les préparations cette structure est en compétition avec celles du type pyrochlorite et pérovskite de formule respectivite \( Ti_{2}Ti_{2}O_{7} \) et \( ATO_{3} \) . Un des buts de cette étude fut de déterminer dans \( AtTiO_{5} \) la distribution des ions \( A^{3+} \) et \( Ti^{4+} \) sur les deux sites possibles, dont l'un possède un environnement octaédrique en oxygène et l'autre un environnement de cinq oxygènes disposés au sommet d'une pyramide à base carrée. Une étude par diffraction de neutron sur \( CrTiNdO_{5} \) et \( FeTiNdO_{5} \) a montré que 95% du \( Cr^{3+} \) et 57% du \( Fe^{3+} \) vont respectivement sur le site octaédrique. Ce comportement s'explique facilement par des considérations de champ cristallin. Dans \( CrTiNdO_{5} \) , à 13°K \( Cr^{3+} \) et Nd \( ^{3+} \) s'ordonnent magnétiquement en même temps pour donner naissance à une structure non colinéaire où les moments de Nd sont dans le plan XY (+Gx-Ay) ainsi que les moments de 5% d'atome de \( Cr^{3+} \) sur le site pyramidé à base carrée (+Ay) mais les 95% des moments des atomes de \( Cr^{3+} \) sur le site octaédrique sont suivant z (+Az), couplés dans une même représentation. Le groupe de Shubnikov est Pbam'. Dans \( FeTiNdO_{5} \) , Nd n'est pas ordonné et les moments magnétiques de Fe sont dans le plan XY avec une configuration non colinéaire CxPy sur les deux sites. Le groupe de Shubnikov est \( P_{2c}b^{3} \) am'. La direction des moments de Nd \( ^{3+} \) dans \( CrTiNdO_{5} \) et de Fe \( ^{3+} \) dans \( FeTiNdO_{5} \) fait un angle voisin de 12° avec l'axe des Y. On ne peut expliquer la direction des moments dans \( CrTiNdO_{5} \) que par couplage anisotrope antisymétrique. Nous n'avons pas observé d'ordre magnétique pour \( MnTiNdO_{5} \) à 1·5°K.
Abstract—The compounds \( AtTiO_{5} \) are isomorphous with \( HoMn_{2}O_{5} \) when the rare earth ionic radius is intermediate between that of Gd and Pr. Pyrochlore \( (T_{2}Ti_{2}O_{7}) \) and perovskite \( (ATO_{3}) \) structures are found simultaneously. A purpose of this study was to investigate the distribution of \( A^{3+} \) and \( Ti^{4+} \) in \( AtTiO_{5} \) over the two different available sites having an octahedral and square pyramid oxygen environment. A neutron diffraction study of Nd compounds has shown that \( A^{3+} \) occupation of the octahedral site was 95% and 57% when \( A^{3+} \) is \( Cr^{3+} \) and \( Fe^{3+} \) respectively. This is easily interpreted using crystal field theory. In \( CrTiNdO_{5} \) both Cr and Nd spins become ordered below \( 13^{\circ}K \) Nd \( ^{3+} \) spins lie in the XY plane (+Gx-Ay). \( Cr^{3+} \) ions in octahedral sites (95%) have spins along the z axis (+Az) while the remaining \( Cr^{3+} \) ions square pyramid sites (5%) have spins in the XY plane (+Ay). Shubnikov group is Pbam'. In \( FeTiNdO_{5} \) , Nd \( ^{3+} \) spins are not ordered at \( 1\cdot5^{\circ}K \) \( Fe^{3+} \) spins lie in XY plane with a CxPy configuration for both sites. Shubnikov group is \( P_{2c}b^{3} \) am'. For these two compounds the spin direction in the XY plane makes an angle of approximately 12° with the Y axis. In \( CrTiNdO_{5} \) the spin direction can be explained only by assuming anisotropic exchange. No magnetic ordering was observed for \( MnTiNdO_{5} \) .
UN NOUVEAU composé de formule \( TMn_{2}O_{5} \) avec T = terre rare, a été décrit pour la première fois en 1964 \( ^{[1,2]} \) . Ce composé était caractérisé par la coéxistence de \( Mn^{3+} \) et de \( Mn^{4+} \) en proportion stoéchimétrique dans la structure.
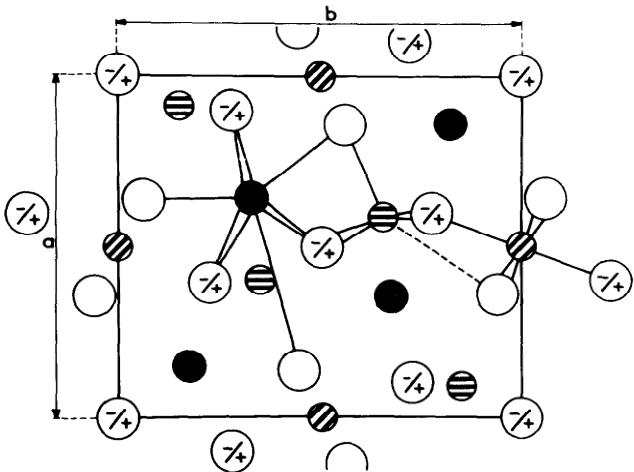
L'étude cristalline révélait que ces atomes de Mn étaient disposés sur deux sites distincts, dont l'environnement était octaédrique pour l'un, et de 5 oxygènes disposés au sommet d'une pyramide à base carrée pour l'autre (Fig. 1).
La structure magnétique du composé isomorphé \( BiMn_{2}O_{5} \) [3] démontrait la complexité des interactions magnétiques et permettait de préciser la place des \( Mn^{3+} \) et \( Mn^{4+} \) sur les deux sites correspondants.

Fig. 1. Projection de la structure de \( HoMn_{2}O_{5} \) dans le plan b.
Nous nous proposons dans ce mémoire* de faire l'étude par rayons X et par Neutrons des propriétés chimiques et physiques des composés ATiTO \( _{5} \) isomorphes à Mn \( _{2} \) TO \( _{5} \) (A \( ^{3+} \) = Cr, Mn, Fe) (T = terres rares)
1. DOMAINE DE STABILITE
Le mélange des oxydes de \( A^{3+} \) ( \( Cr_{2}O_{3} \) , \( Fe_{2}O_{3} \) , \( Fe_{2}O_{3}O \) ou \( Mn_{2}O_{3} \) ) avec \( TiO_{2} \) et \( T_{2}O_{3} \) en proportion stoéchimétrique est finement broyé et porté au four pendant 48 hr à température fixe.
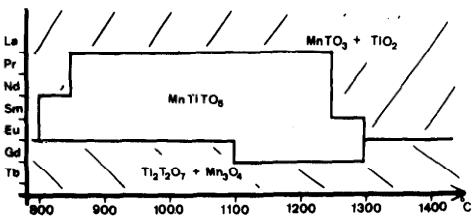
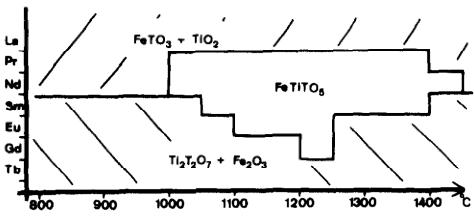
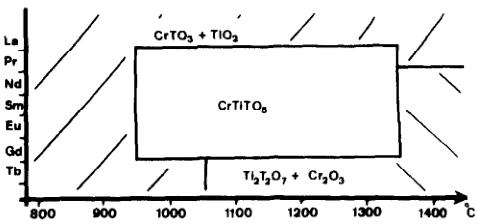
La poudre est analysée par rayons X. La Fig. 2 résume les résultats des produits obtenus en fonction des différentes terres rares et de la température. Nous obtenons les composés isomorphes de formule ATiTO \( _{5} \) avec les terres rares dont le rayon ionique est compris entre celui de Pr et de Gd inclus, dans des domaines de températures variables suivant le cation A \( ^{3+} \) mais en moyenne entre 1000° et 1300°C. Ces composés isomorphes à Mn \( _{2} \) TO \( _{5} \) sont en compétition avec deux autres structures, pyrochlore et pérovskite de formules respectives T \( _{2} \) Ti \( _{2} \) O \( _{7} \) et TAO \( _{3} \) .
On peut remarquer sur la Fig. 2 que pour les terres rares de petits rayons ioniques, c'est la structure pyrochlore qui est la plus stable, la limite de formation dépendant à la fois de la température et du cation \( A^{3+} \) . Pour les terres rares de grands rayons ioniques c'est la structure pérovskite qui est la plus stable.
Il est difficile d'obtenir des produits purs et il existe toujours un mélange entre ces trois structures et les produits de départ. C'est entre 1200° et 1300° que nous avons préparé les composés les plus purs en recuisant et rebroyant le mélange des oxydes pendant plusieurs jours. Les composés ATiTO \( _{5} \) étant formés, ils se décomposent au point de fusion en donnant lieu soit à la pérovskitc soit au pyrochlore.
Nous avons cherché à obtenir les composés isomorphes avec d'autres cations \( A^{3+} \) . Nos résultats n'ont pas été concluants avec \( A^{3+} \)



Fig. 2. Diagrammes de phase \( A_{2}O_{3}-TiO_{2}-T_{2}O_{3} \) en fonction de la température.
= Ga, Al, Ti, Co, Rh. Nous avons d'autre part essayé de remplacer le \( Ti^{4+} \) par \( Ge^{4+} \) et \( Zr^{4+} \) sans obtenir les produits isomorphes cherchés.
2. DONNEES CRISTALLOGRAPHIQUES PAR Rx
Nous avons indéxé les clichés de poudre de rayon X sur chambre de 360 mm avec la longueur d'onde du chrome. La maille est orthorombique. Les groupes d'espaces possibles sont Pbam ou Pba2 ce qui confirme l'isomorphie avec \( TMn_{2}O_{5} \) .
Le Tableau I donne la valeur des paramètres pour les différentes terres rares et pour les différents cations \( A^{3+} \) . Le Tableau 2 résume l'indexation d'un cliché de poudre pour la longueur d'onde du Cr.
3. ETUDE PAR DIFFRACTION NEUTRONIQUE
L'étude de la structure aux Rx aurait certainement permis de situer avec précision la place de la terre rare ainsi que celle des cations de transition 3d. mais les facteurs de diffusion des cations \( A^{3+} \) et \( Ti^{4+} \) étant voisins, il ne nous aurait pas été possible de différencier sur les sites correspondants.
Par contre, avec les neutrons, la longueur de Fermi b(Ti) étant négative, et celle b(Fe) et b(Cr) positive nous pouvons prévoir qu'il sera facile de déterminer la position res-
Tableau 1. Paramètres des mailles orthorhombiques de ATiTO \( _{5} \)
| Cr | Fe | Mn | |||||||||
| b | b | c | a | b | c | a | b | c | |||
| Pr | 7,58 | 8,68 | 5,81 | 7,57 | 8,72 | 5,855 | 7,59 | 8,72 | 5,83 | ||
| Nd | 7,56 | 8,67 | 5,80 | 7,54 | 8,71 | 5,85 | 7,55 | 8,69 | 5,82 | ||
| Sm | 7,50 | 8,62 | 5,79 | 7,50 | 8,69 | 5,83 | 7,49 | 8,65 | 5,81 | ||
| Eu | 7,475 | 8,60 | 5,785 | 7,47 | 8,67 | 5,825 | 7,46 | 8,60 | 5,805 | ||
| Gd | 7,45 | 8,59 | 5,785 | 7,43 | 8,65 | 5,82 | 7,43 | 8,56 | 5,795 | ||
pective de ces cations. Quant aux ions d'oxygène il est bien connu que \( b(0) \) est suffisamment grand pour permettre leur positionnement. A basse température, nous avons d'autre part la contribution dû à l'ordre des atomes magnétiques; par leurs moments magnétiques nous pourrons ainsi confirmer les paramètres des sites dans lesquels ils se placent et déterminer la structure magnétique du composé.
1. CrTiNdO_{5}
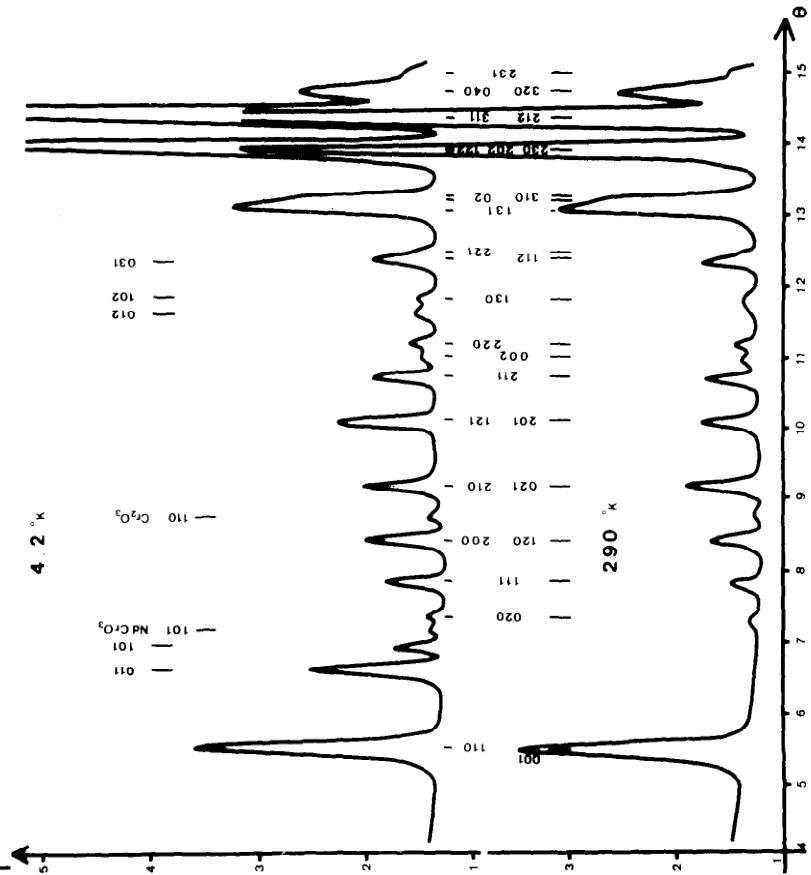
La Fig. 3 représente les diagrammes de neutrons à la longueur d'onde \( \lambda = 1,106 \) A enregistrés à la température ambiante et à 4,2°K.
Affinement de la structure cristalline. Il est difficile d'affiner avec précision la structure en considérant le faible nombre de raies nucléaires non multiples par rapport au grand nombre de paramètres qui-interviennent. D'autre part nous ne connaîsson pas le pourcentage de Cr ou de Ti sur les 2 sites 4h et 4f (voir le Tableau 3 pour les différents sites ou ils peuvent se trouver); nous devons donc introduire une variable supplémentaire qui fixe la distribution de ces cations.
Pour affiner la structure nous avons employé un programme spécialement écrit pour les raies multiples par BASSI du CEN/G. Nous l'avons utilisé en introduisant succés-sivement différents pourcentages de Cr sur le site 4h ou son complément sur le site 4f. Par itérations nous n'avons observé une convergence des valeurs que pour des pour-centages compris entre 0 et 6% de \( Cr^{3+} \) sur le site 4h. Le résidu cristallographique le plus bas correspond à 0% de \( Cr^{3+} \) sur le site 4h et 100 pour cent sur le site 4f. Cependant le calcul montre certaines incompatibilités des distances interatomiques en particulier sur les sites 4f et 4h. Les distances interatomiques les plus vraisemblables, correspondent à un affinement avec 5% de \( Cr^{3+} \) et 95% de \( Ti^{4+} \) sur le site 4h et 95% de \( Cr^{3+} \) et 5% de \( Ti^{4+} \) sur le site 4f.
Le Tableau 3 donne le résultat de cet affinement.
Structure magnétique. Par mesure magnétique nous observons à 13°K un point de transition qui correspond à un ordre magnétique coopératif du Cr et de la terre rare. La transition correspondant à l'ordre du Cr seul n'est pas appréciable. Pour observer l'ordre du Cr seul nous avons dû opérer en diffraction neutronique à plus haute température, dans un vase à température variable. Le diagramme obtenu à 30°K est sensiblement identique à celui correspondant à la température ambiante, aux impuretés près, qui sont \( Cr_{2}O_{3} \) et \( NdCrO_{3} \) ordonnés magnétiquement à ces températures et représentés sur la Fig. 3
Nous en déduisons qu'à 30°K le \( Cr^{3+} \) n'est pas ordonné. Le diagramme à 4,2°K qui correspond à l'ordre du Cr et de la terre rare, permet d'observer des intensités magnétiques qui s'indexent dans la maille cristalline, donc k = 000.
Théorie macroscopique de Bertaut. Les cations en position 4g sont numérotés de
Tableau 2. Indexation d'un cliché de poudre de FeTiSmO_{5} ( \( \lambda \) CR)
| HKL | Sin² θobs. (× 10⁻⁴) | Sin² θcalc (× 10⁻⁴) | HKL | Sin² θobs. (× 10⁻⁴) | Sin² θcalc (× 10⁻⁴) | |
| 001 | 391 | 386 | 251 | 5670 | 5663 | |
| 110 | 407 | 510 | 6014 | 6005 | ||
| 111 | 802 | 793 | 152 | 6133 | 6121 | |
| 120 | 940 | 928 | 323 | 6273 | 6268 | |
| 021 | 1092 | 1081 | 350 | 6462 | 6443 | |
| 210 | 1117 | 1107 | 143 | 6487 | ||
| 201 | 1325 | 1319 | 440 | 6512 | ||
| 121 | 1314 | 520 | 6512 | 6526 | ||
| 211 | 1502 | 1493 | 160 | 6488 | ||
| 002 | 1552 | 1544 | 061 | 6661 | 6641 | |
| 220 | 1638 | 1628 | 432 | 6840 | ||
| 130 | 1806 | 1797 | 351 | 6829 | ||
| 112 | 1960 | 1951 | 441 | 6918 | 6898 | |
| 221 | 2029 | 2014 | 521 | 6912 | ||
| 131 | 2197 | 2183 | 333 | 7141 | 7137 | |
| 310 | 2251 | 2272 | 403 | 7219 | 7206 | |
| 022 | 2239 | 062 | 7810 | 7799 | ||
| 230 | 2485 | 2497 | ||||
| 202 | 2477 | 423 | 7907 | 7901 | ||
| 311 | 2664 | 2659 | 134 | 7974 | 7973 | |
| 212 | 2650 | 442 | 8065 | 8056 | ||
| 140 | 3030 | 3013 | 360 | 8359 | 8354 | |
| 222 | 3188 | 3172 | 343 | 8353 | ||
| 321 | 3180 | 451 | 8451 | 8462 | ||
| 132 | 3347 | 3341 | 314 | 8449 | ||
| 141 | 3414 | 3399 | 540 | 8625 | 8611 | |
| 003 | 3480 | 3474 | 170 | 8756 | 8746 | |
| 330 | 3672 | 3663 | 433 | 8770 | ||
| 400 | 3740 | 3732 | 532 | 8943 | 8939 | |
| 113 | 3884 | 3881 | 611 | 8957 | ||
| 331 | 4050 | 4049 | 541 | 9001 | 8997 | |
| 232 | 4041 | 144 | 9189 | 9189 | ||
| 401 | 4128 | 4118 | 270 | 9454 | 9446 | |
| 042 | 4334 | 4324 | 063 | 9732 | 9729 | |
| 123 | 4412 | 4402 | 271 | 9832 | ||
| 150 | 4582 | 4577 | 334 | 9839 | ||
| 332 | 5214 | 5207 | 404 | 9903 | 9908 | |
| 402 | 5284 | 5276 | 362 | 9898 | ||
| 412 | 5462 | 5450 | ||||
1 à 4 ainsi que ceux en position 4h; ceux en cristallographique (et magnétique) du cristal. position 4f de 5 à 8 Les modes magnétiques compatibles avec la
\[ \begin{array}{c|ccc}\mathbf{X}\mathbf{Y}\mathbf{0}&-1-&\mathbf{X}\mathbf{Y}\mathbf{0},5&0,5\mathbf{O}\mathbf{Z}-5\\\overline{\mathbf{X}}\overline{\mathbf{Y}}\mathbf{0}&-2-&\overline{\mathbf{X}}\overline{\mathbf{Y}}\mathbf{0},5&0,5\mathbf{O}\overline{\mathbf{Z}}-6\\0,5-\mathbf{X},0,5+\mathbf{Y},0-3-0,5-\mathbf{X},0,5+\mathbf{Y},0,5\mathbf{O}0,5\mathbf{Z}-7&\\0,5+\mathbf{X},0,5-\mathbf{Y},0-4-0,5+\mathbf{X},0,5-\mathbf{Y},0,5\mathbf{O}0,5\overline{\mathbf{Z}}-8\end{array} \]
L'énergie est invariante dans le groupe symétrie du cristal sont vecteurs de base

Tableau 3. Paramètres cristallins de CrTiNdO_{5}
| X | Y | Z | Pbam | |
| Nd | 0.142 | 0.172 | 0.0 | 4g |
| 5% Cr 95% Ti | 0.124 | -0.134 | 0.5 | 4h |
| 95% Cr 5% Ti | 0.0 | 0.5 | 0.252 | 4f |
| 0 | 0.111 | -0.285 | 0.260 | 8i |
| 0 | 0.186 | 0.433 | 0.0 | 4g |
| 0 | 0.156 | 0.444 | 0.5 | 4h |
| 0 | 0.0 | 0.0 | 0.300 | 4e |
des représentations du groupe. Une méthode pour trouver les vecteurs de base est celle de l'opérateur de projection, connaissant les représentations irréductibles du groupe. Lorsque k = 0, il suffit d'utiliser les représentations du groupe ponctuel m m m. Le Tableau 4 donne la transformation des spins sur l'action des opérateurs de symétrie. Le Tableau 5 donne les modes compatibles suivant les 8 représentations correspondant
Tableau 4. Transformations des spins par les opérateurs de symétrie.
| e | 2_{1}x | 2_{1}y | 2z | \( \overline{1} \) | \( \overline{1}2_{1}x \) | \( \overline{1}2_{1}y \) | \( \overline{1}2z \) |
| S_{1}x | +S_{4}x | -S_{3}x | -S_{2}x | +S_{2}x | +S_{3}x | -S_{4}x | -S_{1}x |
| S_{1}y | -S_{4}y | +S_{3}y | -S_{2}y | +S_{2}y | -S_{3}y | +S_{4}y | -S_{1}y |
| S_{1}z | -S_{4}z | -S_{3}z | +S_{2}z | +S_{2}z | -S_{3}z | -S_{4}z | +S_{1}z |
| S_{2}x | +S_{3}x | -S_{3}x | -S_{3}x | +S_{3}x | +S_{3}x | -S_{2}y | -S_{3}x |
| S_{3}y | -S_{3}y | +S_{3}y | -S_{3}y | +S_{3}y | -S_{2}y | +S_{3}y | -S_{3}y |
| S_{3}z | -S_{3}z | -S_{3}z | +S_{3}z | +S_{3}z | -S_{3}z | -S_{3}z | +S_{2}z |
Tableau 5. Représentations irréductibles du groupe Pbam pour k = 000 et k = 00 \( \frac{1}{2} \)
| Site 4g et 4h | Site 4f | k = 000 Groupes de Shubnikov | |
| \( \Gamma_{1} \) | Cz | Cz Pbam | |
| \( \Gamma_{2} \) | Cx | Fy | Cx Fy Pbam |
| \( \Gamma_{3} \) | Fx | Cy | Fx Cy Pbam |
| \( \Gamma_{4} \) | Fz | Fz Pbam | |
| \( \Gamma_{5} \) | Ax | Gy | Gz Pbam |
| \( \Gamma_{6} \) | Gz | Ax | Gy Pbam |
| \( \Gamma_{7} \) | Az | Gx | Ay Pbam |
| \( \Gamma_{8} \) | Gx | Ay | Az Pbam |
à P 222 × T. Les lettre F G C A correspondent aux arrangements bien connus des spins.
\[ \begin{array}{l}\mathbf{F}=\mathbf{S}_{1}+\mathbf{S}_{2}+\mathbf{S}_{3}+\mathbf{S}_{4}\quad\mathbf{C}=\mathbf{S}_{1}+\mathbf{S}_{2}-\mathbf{S}_{3}-\mathbf{S}_{4}\\\mathbf{G}=\mathbf{S}_{1}-\mathbf{S}_{2}+\mathbf{S}_{3}-\mathbf{S}_{4}\quad\mathbf{A}=\mathbf{S}_{1}-\mathbf{S}_{2}-\mathbf{S}_{3}+\mathbf{S}_{4}\end{array} \]
Il en est de même pour \( S_{5} \) , \( S_{6} \) , \( S_{7} \) , \( S_{8} \)
Configurations magnétiques observées. Lorsque l'énergie est d'ordre deux dans les spins les modes couplés doivent appartenir à une même représentation irréductible.
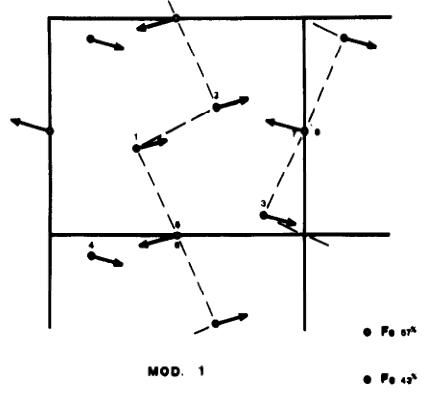
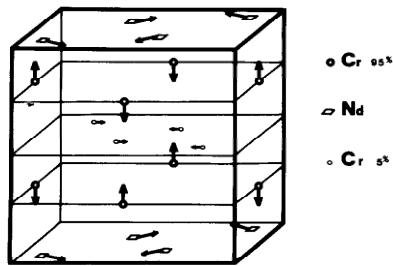
La seule structure compatible avec les intensités observées correspond à la représentation \( \Gamma_{8} \) . En effet nous expliquons les intensités magnétiques observées, en admettant l'existence des modes +Gx et -Fy sur les sites 4g (Nd \( ^{3+} \) ) et Ay sur le site 4h (5% Cr \( ^{3+} \) ) et +Az sur le site 4f (95% de Cr). Les moments magnétiques font un angle de 12° avec l'axe des y pour le site 4g; ils sont suivant y pour le site 4h et suivant z sur le site 4f.
La Fig. 4 représente la direction des moments magnétiques sur les différents sites.

Fig. 4. Structure magnétique de CrTiNdO_{5}.
Le Tableau 6 donne la correspondance entre Iobs. et I théorique pour les différentes réflexions.
Nous avons pris les valeurs du facteur de forme f de Nd de [4] et pour \( Cr^{3+} \) de [5]. Nous devons remarquer que la décroissance des facteurs f des références citées ci-dessus n'est pas assez prononcée puisque les intensités théoriques restent systématique-
ment plus élevées aux grands angles que celles observées.
La précision sur le site à 5% de \( Cr^{3+} \) est insuffisante pour pouvoir préciser l'angle des spins avec l'axe des y.
2. FeTiNdO_{5}
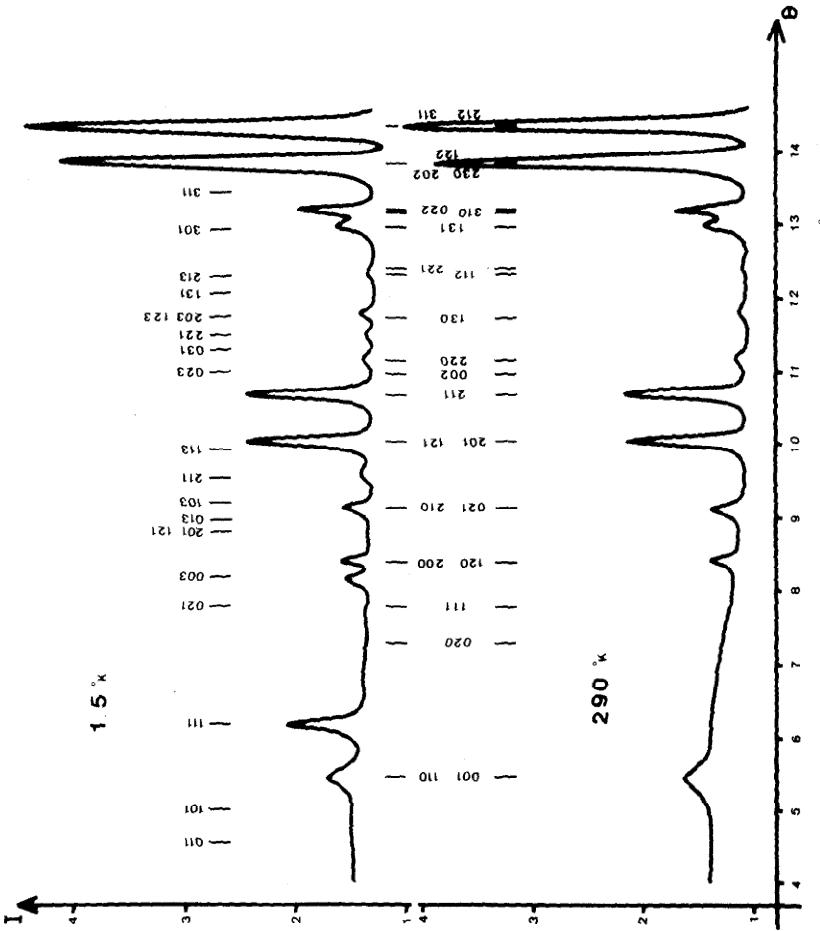
La Fig. 5 représente les diagrammes obtenus par diffraction neutronique ( \( \lambda = 1,106 \) Å) à la température ambiante et à 1,5°K.
Affinement de la structure cristalline. Le problème est identique à celui du produit CrTiNdO_{5}. Nous n'avons que peu de raies de diffraction, un grand nombre de paramètres à affiner, et le pourcentage de Fe^{3+} sur le site 4h et 4f n'est pas connu. Par affinements successifs, en faisant varier le pourcentage de Fe sur le site 4h, nous avons observé une
Tableau 6. Intensités magnétiques observées et calculées pour CrTiNdO_{5}
| Hkl | I cal. | I obs. |
| 001 | 31 | 28 |
| 110 | ||
| 020 | 4 | 0 |
| 011 | 353 | 355 |
| 101 | 97 | 99 |
| 111 | 78,6 | 75 |
| 120 | 125,5 | 130 |
| 200 | ||
| 021 | 13 | 25 |
| 210 | ||
| 121 | 320 | 292 |
| 201 | ||
| 211 | 118 | 99 |
| 002 | 0 | 0 |
| 220 | 46,4 | 37 |
| 012 | 179,6 | 146 |
| 130 | 23 | 15 |
| 102 | ||
| 221 | 220,4 | 180 |
| 031 | ||
| 112 |
\[ R = 10,5\%; \quad \mu N d = 2,89 \quad \mu B \pm 0,15; \quad \mu C r = 2,95 \mu B \pm 0,15. \]
convergence des valeurs pour des pour- centages de Fe compris entre 48 et 40 pour cent.
Les distances interatomiques les plus vraisemblables correspondent à 43% de \( Fe^{3+} \) ou 57% de \( Ti^{4+} \) sur le site 4h, et 57% de \( Fe^{3+} \) ou 43% de \( Ti^{4+} \) sur le site 4f.
Le Tableau 7 résume le résultat de cet affinement.
Tableau 7. Paramètres cristallins de FeTiNdO_{5}
| X | Y | Z | Pbam | |
| Nd | 0,136 | 0,184 | 0,0 | 4g |
| 43%Fe \( ^{a1} \) 57%Ti \( ^{a1} \) | 0,088 | -0,156 | 0,5 | 4h |
| 57%Fe \( ^{a3} \) 43%Ti \( ^{a4} \) | 0,0 | 0,5 | 0,238 | 4f |
| 0 | 0,107 | -0,296 | 0,247 | 8i |
| 0 | 0,206 | 0,429 | 0,0 | 4g |
| 0 | 0,179 | 0,404 | 0,5 | 4h |
| 0 | 0,0 | 0,0 | 0,285 | 4e |
Structure magnétique. Le diagramme à 1,5°K s'indexe en doublant la maille cristalline suivant C. Le vecteur de propagation est donc \( \vec{k} = (00\frac{1}{2}) \) .
Théorie Macroscopique de Bertaut. Les cations sont numérotés de 1 à 4 dans la position 4h et de 5 à 8 dans la position 4f comme pour CrTiNdO_{5}.
On emploie la même méthode que précédemment, c'est à dire celle de l'opérateur de projection, mais il faut trouver les représentations irréductibles correspondant au vecteur \( k = 00\frac{1}{2} \) . On emploie alors la méthode d'Olbrychski, qui étudie les relations entre éléments générateurs
\[ \begin{array}{l l l}{2_{1x}=(2_{x}|\frac{1}{2}\frac{1}{2}0)}&{(2_{1x})^{2}=(\epsilon|100)}\\ {2_{1y}=(2_{y}|\frac{1}{2}\frac{1}{2}0)}&{(2_{11y})^{2}=(\epsilon|010)}\\ {\overline{1}=(\overline{1}|000)}&{(\overline{1})^{2}=(\epsilon|000)}\end{array} \]
\[ \begin{array}{l l}{2_{1x}2_{1y}=(\epsilon|\overline{1}\overline{0})2_{1y}2_{1x}}\\ {2_{1x}\overline{1}=(\epsilon|110)\overline{1}2_{1x}}\\ {2_{1y}\overline{1}=(\epsilon|110)\overline{1}2_{1y}}\end{array} \]
ce qui donne les relations suivantes entre

matrices représentatives pour \(h = 00\ 0,5\)
\[ \begin{align*} (D(2_{1x}))^2 &= +1 \quad (D(2_{1y}))^2 = +1 \\ (D(\bar{1}))^2 &= +1 \\ D(2_{1x}) D(2_{1y}) &= D(2_{1y}) D(2_{1x}) \\ D(2_{1x}) D(\bar{1}) &= D(\bar{1}) D(2_{1x}) \\ D(2_{1y}) D(\bar{1}) &= D(\bar{1}) D(2_{1y}) \end{align*} \]
Ces matrices commutent, donc les représentations irreductibles sont de dimension 1 et comme il y a 8 éléments dans le groupe ponctuel, il y aura 8 représentations irréductibles. Ceci était prévisible, car il n'y a pas d'élément générateur de translation suivant \(z\). Par la méthode de l'opérateur de projection on obtient ainsi les mêmes modes compatibles que dans le cas de CrTiNdO\(_5\) (Tableau 5).
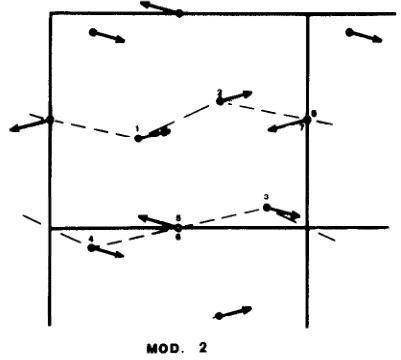
Configurations magnétiques observées. La seule structure compatible avec les intensités observées correspond à la représentation \(\Gamma 2\) (Tableau 5) Le groupe de Shubnikov est \(P_{2c}\) b'am'. Nous expliquons les intensités magnétiques observées, en admettant l'existence des modes \(-Cx+FY\) sur le site \(4h\) (43% de Fe), et \(+Cx-Fy\) sur le site \(4f\) (57% Fe). La faiblesse des intensités observées ne nous permet pas de trancher entre ces modes et \(-Cx+FY\) sur \(4h\) et \(-Cx+FY\) sur \(4f\). Les moments magnétiques sur les 2 sites font un angle de 15° avec l'axe des \(y\).
La Fig. 6 représente la direction des moments sur les différents sites. Le Tableau 8 donne la correspondance entre I obs. et I calculées.
Nous avons pris les valeurs de \(f\) pour le fer, de [6].
3. MnTiNdO\(_5\)
Pour ce composé l'étude est différente, en effet les \(b(Mn)\) et \(b(Ti)\) sont négatifs et de valeurs identiques. Il sera donc impossible de les distinguer par affinement sur les intensités nucléaires.


Il reste uniquement la détermination de la structure magnétique. Or le diagramme de Diffraction Neutronique à 1,5°K est identique à celui obtenu à température ambiante. Les Mn\(^{3+}\) ne sont pas encore ordonnés magnétiquement.
Tableau 8. Intensités magnétiques, observées et calculées pour FeTiNdO_{5}
| Hkh | I cal_{1} | I obs | I cal_{2} |
| 001 | 0 | 0 | 0 |
| 011 | 0,3 | 5 | 5,4 |
| 101 | 2,3 | 0 | 0 |
| 111 | 87 | 87 | 87 |
| 021 | 5,6 | 0 | 5,6 |
| 003 | 55,6 | 55,1 | 55,6 |
| 201 | 5,2 | 15 | 5,2 |
| 121 | 7,7 | 1 | 1,7 |
| 013 | 4,6 | 0 | 0 |
| 103 | 0 | 0 | 5 |
| 211 | 18,5 | 24 | 30,6 |
| 113 | 12,1 | 15 | 12,1 |
| 023 | 4,9 | 0 | 4,9 |
| 031 | 5 | 0 | 0 |
| 221 | 18,9 | 23 | 18,9 |
| 203 | 41,9 | 44 | 41,9 |
| 123 | 6,9 | 8 | 8,3 |
| 131 | 0 | 0 | 0 |
| 213 | 24 | 26 | 16,5 |
| 301 | 0 | 0 | 0 |
| 311 | 24,9 | 30 | 24,9 |
S(eff) = 0,935 (théorique); \( R_{1} = 15\% \) ; \( R_{2} = 18\% \) .
4. DISCUSSIONS
Environment des atomes de transition 3d
La structure possèdent deux sites différents, l'un octaédrique l'autre "pyramide à base carrée" est assez exceptionnelle pour que l'on se demande quels sites vont choisir les différents cations.
Basolo et Pearson (7) donnent les valeurs théoriques des niveaux d'énergie des orbitales d dans des champs cristallins de différentes symétries en particulier pour un octaèdre, une pyramide à base carrée et un tétraèdre (Tableau 9).
Ces calculs ont été faits par la méthode du champ cristallin, en assimilant les ligands à des charges ponctuelles et pour des symétries idéales que nous n'observons que très rarement dans les composés.
D'après ce tableau on peut calculer l'énergie de stabilisation due à l'action du champ cristallin sur les électrons 3d. Cette énergie dépend de la symétrie et du nombre des électrons 3d, donc variera pour les différents cations (Tableau 10).
Ti^{4+} ne possède aucun électron 3d et l'énergie de stabilisation sera donc nulle pour n'importe quelle symétrie. Seules interviennent alors les hybridations d'orbitales s, p, d, la covalence et la taille des rayons ioniques. Donc, théoriquement, Ti^{4+} peut aller sur n'importe quel des deux sites. L'expérience montre qu'il va dans un octaèdre (structure pérovskite) mais aussi sur des sites bipyramides à base triangulaire (8) comme l'énergie de stabilisation est sensiblement la même pour une bipyramide et une pyramide à base carrée nous pouvons donc penser une dans les composés ATiTO_{5}, la position du Ti^{4+} sur les 2 sites est indifférente, et il pourra donc aussi bien se trouver dans la site octaédrique que dans le site pyramidide à base carrée. C'est ce que nous observons dans nos différents composés.
Si nous considérons maintenant \( Cr^{3+} \) , nous pouvons observer de la même façon qu'il est peu probable de le trouver dans un
Tableau 9. Niveaux d'énergie des orbitales d dans des champs cristallins de différentes symétrie (d'après Basolo et Pearson)
| dx^{2}-y^{2} | dy^{2} | dxy | dxz | dyz | |
| Pyramide à base carrée | 9,14 dq | 0,86 dq | -0,86 dq | -4,57 dq | -4,57 dq |
| Octaèdre | 6 dq | 6 dq | -4 dq | -4 dq | -4 dq |
| Tétraèdre | -2,67 dq | -2,67 dq | 1,78 dq | 1,78 dq | 1,78 dq |
Tableau 10. Energie de stabilisation du champ cristallin pour différents cations
| Cr^{3+} | Mn^{3+} | Fe^{3+} | Ti^{4+} | |
| Octaèdre | -12 dq | -6 dq | 0 | 0 |
| Tétraèdre | -3,56 dq | -1,78 dq | 0 | 0 |
| Pyramide à base carrée | -10 dq | -9,14 dq | 0 | 0 |
tétraèdre, puisqu'il perd 8,44Dq par rapport à l'octaèdre, de même dans notre cas, \( Cr^{3+} \) aura tendance à rester sur le site octaédrique plutôt que sur le site "pyramide à base carrée", puisqu'il perd alors 2Dq d'énergie. C'est ce que nous observons, mais alors que l'on ne connaît pas de \( Cr^{3+} \) sur un site tétraèdrique, nous en observons 5 pour cent sur le site "pyramide à base carrée", ce qui peut s'expliquer par la faible différence de stabilisation.
En ce qui concerne \( Fe^{3+} \) , les énergies de stabilisation sont identiques pour tous les sites, et nous pouvons en tirer les mêmes conclusions que pour \( Ti^{4+} \) . C'est ce que nous observons puisqu'il y a pratiquement équipartition du \( Fe^{3+} \) sur les 2 sites. Il faut cependant remarquer une légère préférence du \( Fe^{3+} \) pour le site octaédrique (57%), qui ne peut pas s'expliquer par une différence de rayon ionique, ceux du \( Fe^{3+} \) et \( Ti^{4+} \) étant sensiblement identiques ou bien \( Fe^{3+} \) préferait donc l'environnement octaédrique, ou bien \( Ti^{4+} \) le site "pyramide à base carrée".
Quant à \( Mn^{3+} \) , théoriquement il préferera nettement le site pyramidé à base carrée (gain de 3,14 Dq par rapport à l'octaèdre). Nous n'avons pu le vérifier sur les composés avec Ti, mais nous avons observé que sur le composé isomorphé \( BiMn_{2}O_{5} \) , les ions \( Mn^{3+} \) vont sur ce site. D'autre part le fait que le composé \( MnTiNdO_{5} \) ne soit pas ordonné à 1,5°K peut être dû à l'isolement des \( Mn^{3+} \) dans la structure, puisqu'ils ne sont situés que sur le site 4h (pyramide à base carrée): la liaison magnétique entre les plans des Mn distants de c = 5,81 devient alors très faible, le site 4f étant occupé par \( Ti^{4+} \) diamagnétique.
Interactions magnétiques
La première remarque concerne l'angle que font les spins avec l'axe des y: 12° pour le spin de Nd dans \( CrNdTiO_{5} \) et 15° pour celui de Fe dans \( FeNdTiO_{5} \) . Si l'on ajoute que nous avions trouvé un angle de 13° entre la direction des spins avec l'axe des X dans \( BiMn_{2}O_{5} \) , on se rend compte que la direction d'anisotropie différe de 90°. Elle correspond à la symétrie des sites: en effet dans \( BiMn_{2}O_{5} \) les moments magnétiques sont dirigés à peu près dans la direction de l'axe de la pyramide à base carrée, pour le composé avec le fer ils sont parallèles au plan de base de la pyramide, et pour Nd dans \( NdCrTiO_{5} \) où l'environnement est constitué de 8 oxygènes voisins de la terre rare, la direction des moments magnétiques reste parallèle au plan de symétrie de la terre rare et à la base carée de la pyramide.
La deuxième remarque se rapporté aux interactions Cr–Nd Deux Cr en z=0,25 et -0,25 sont couplés entre eux par de fortes interactions négatives à 90°. Ces deux atomes de Cr sont de part et d'autre d'un plan d'atome de Nd (z=0) et les interactions par pont d'oxygène sont identiques, ils devraient donc se coupler de la même façon par rapport à Nd dans le cas d'interactions isotopes: or leurs moments étant opposés nous devons en conclure que les interactions Cr–Nd doivent être anisotropes et antisymétriques.
La troisième remarque est relative aux interactions Fe-Fe entre les atomes des sites 4h et 4f. Les deux atomes de fer du site 4f (57% de Fe) qui sont situés symétriquement par rapport au Fe du site 4h (z=0,5), dont les interactions d'échange s'effectuent par le même oxygène avec un angle voisin de 120°, ont leurs moments magnétiques de même sens et opposés à ceux de ce deuxième site. L'échange est donc isotrope et s'effectue suivant les lignes parallèles de la Fig. 6. La quatrième remarque est, que deux
atomes de \( Fe^{3+} \) du site 4h, situé en XY et \( \bar{X}\bar{Y} \) sont couplés ferromagnétiquement comme dans \( Fe_{2}CaO_{4} \) et \( UFeO_{4} \) (9) et (10) à l'opposé de ceux de \( Cr^{3+} \) et de \( Mn^{3+} \) dans \( CrTiNdO_{5} \) et \( Mn_{2}BiO_{5} \) .
Il faut remarquer que cette interaction se fait par pont d'oxygène légèrement supérieur à 90° (Fe_{7}O_{7}Fe_{7} = 1000° 18') et pour des distances entre atomes de fer de 3,04 Å. On retrouve cette distance 3,06 Å entre deux atomes de fer sur le site 4f couplés parallèlement, alors qu'elle est de 2,78 Å entre les 2 atomes couples antiparallèlement (Fe_{3}O_{5}Fe_{3} = 78°22') où cette courte distance suggère un échange direct comme dans (9) et (10).
Remerciements—Nous remercions Monsieur le Professeur Bertaut pour l'attention qu'il a apporté à ce travail, nous remercions mademoiselle Martin pour son aide pour la préparation chimique des drivers composés.
REFERENCES
-
QUEZEL-AMBRUNAZ S., BERTAUT E. F. et BUISSON G., C.r. hebd. Seanc Acad. Sci., Paris 258, 3025 (1964).
-
BERTAUT E. F., BUISSON G., DURIF A., MARESCHAL J., MONTMORY M. C. QUEZEL-AMBRUNAZ S., Bull. Soc. Chim. France 1132 (1965).
-
BERTAUT E. F., BUISSON G., QUEZEL-AMBRUNAZ S. et QUEZEL G., Solid State Commun. 5, 25, (1967).
-
KOEHLER W. C. et WOLLAN E. O., Phys. Rev. 92, 1380 (1953).
-
TAKEI W. J., COX D. E. et SHIRANE G., Phys. Rev. 129, 2008, (1963).
-
BROCKHOUSE et al., Phys. Rev. 98, 1721, (1955).
-
BASOLO F. et PEARSON R. G., Mechanism of Inorganic Reaction, p. 55. Wiley, New York (1958).
-
GUILLEN M. et BERTAUT E. F., Cr. hebd. Seanc Acad. Sci., Paris 262, 962 (1966).
-
BERTAUT E. F., CHAPPERT J., APOSTOLOV A. et SEMENOV V., Bull. Sté Franc. Min. et Crist., 89, 206, (1966).
-
BACMANN M., BERTAUT E. F. et BLAISE A., Cr. hebd, Seanc Acad. Sci., Paris 266, 45 (1968).