| Transition Temperature | 0.56 K |
|---|---|
| Experiment Temperature | 0.1 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | R-3m (#166) |
| Magnetic Space Group | R-3m' (#166.101) |
| Magnetic Point Group | -3m' (20.5.75) |
| Lattice Parameters | 7.42200 7.42200 17.50200 90.00 90.00 120.00 |
|---|---|
| DOI | 10.1103/physrevb.93.180407 |
| Reference | A. Scheie, M. Sanders, J. Krizan, Y. Qiu, R.J. Cava and C. Broholm, Physical Review B (2016) 93. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Nd1 | Nd | 0.88 | 1.76 | -0.93 | 1.79 |
Effective spin- \( \frac{1}{2} \) scalar chiral order on kagome lattices in Nd \( _{3} \) Sb \( _{3} \) Mg \( _{2} \) O \( _{14} \)
A. Scheie, \( ^{1} \) M. Sanders, \( ^{2} \) J. Krizan, \( ^{2} \) Y. Qiu, \( ^{3} \) R. J. Cava, \( ^{2} \) and C. Broholm \( ^{1,3,4} \)
\( ^{1} \) Institute for Quantum Matter and Department of Physics and Astronomy, Johns Hopkins University, Baltimore, Maryland 21218, USA
\( ^{2} \) Department of Chemistry, Princeton University, Princeton, New Jersey 08544, USA
\( ^{3} \) NIST Center for Neutron Research, National Institute of Standards and Technology, Gaithersburg, Maryland 20899, USA
\( ^{4} \) Department of Materials Science and Engineering, Johns Hopkins University, Baltimore, Maryland 21218, USA
(Received 13 April 2016; published 20 May 2016)
We introduce \( Nd_{3}Sb_{3}Mg_{2}O_{14} \) with ideal kagome lattices of neodymium ions in ABC stacking. Thermodynamic measurements show a Curie-Weiss temperature of \( \Theta_{CW} = -0.12 \) K, a \( Nd^{3+} \) spin- \( \frac{1}{2} \) Kramers doublet ground state, and a second-order phase transition at \( T_{N} = 0.56(2) \) K. Neutron scattering reveals noncoplanar scalar chiral k = 0 magnetic order with a correlation length exceeding \( 400 \AA = 55a \) and an ordered moment of \( 1.79(5)\mu_{B} \) . This order includes a canted ferromagnetic component perpendicular to the kagome planes favored by Dzyaloshinskii-Moriya interactions.
DOI: 10.1103/PhysRevB.93.180407
Composed of corner-sharing triangles that frustrate conventional magnetic order, the kagome lattice supports exotic forms of magnetism. The Ising kagome model is paramagnetic \( [1] \) , the quantum spin- \( \frac{1}{2} \) model forms a quantum spin liquid \( [2–6] \) , while fluctuation induced order is expected for the classical Heisenberg model \( [7,8] \) . While there may not be an “ideal” experimental realization of any of these particular models, each kagome related magnet presents opportunities to explore the effects of distinct interactions on an underlying massively degenerate manifold \( [9–16] \) . Here we report the discovery of an effective spin- \( \frac{1}{2} \) kagome magnet \( Nd_{3}Sb_{3}Mg_{2}O_{14} \) , with scalar chiral spin order that supports topologically protected quantum transport \( [17] \) .
Just like the celebrated herbertsmithite kagome system \( [14,15] \) , \( Nd_{3}Sb_{3}Mg_{2}O_{14} \) is based on selective nonmagnetic doping of the \( (Fd3m) \) pyrochlore lattice of corner-sharing tetrahedra \( [18] \) . The parent compound is the disordered pyrochlore \( Nd_{2}SbMgO_{7} \) , which features an ordered \( (\mathrm{Nd}^{3+}) \) and a disordered \( (\mathrm{Mg}^{3+} \) and \( Sb^{5+}) \) sublattice of corner-sharing tetrahedra. But while the nominally nonmagnetic zinc sublattice of herbertsmithite contains 15% magnetic copper ions, the different charge and size of \( Sb^{5+} \) ( \( r \approx 74~pm \) ) and \( Nd^{3+} \) ( \( r \approx 125~pm \) ) lead to an ordered layered rhombohedral structure for \( Nd_{3}Sb_{3}Mg_{2}O_{14} \) with \( Nd^{3+} \) on a crystallographically ideal kagome lattice and \( Mg^{3+} \) and \( Sb^{5+} \) cations segregated onto fully occupied nonmagnetic triangular lattices. These intervening layers should reduce magnetic interactions between kagome planes \( [19–21] \) . The magnetism is based on \( Nd^{3+} \) where spin-orbit coupling prevails over crystal fields to produce a Kramers doublet protected by time-reversal symmetry. Thus we have in \( Nd_{3}Sb_{3}Mg_{2}O_{14} \) a rare opportunity to study spin- \( \frac{1}{2} \) kagome magnetism without significant quenched disorder.
\(\mathrm{Nd}_{3}\mathrm{Sb}_{3}\mathrm{Mg}_{2}\mathrm{O}_{14}\) is isostructural to three recently reported compounds, \(\mathrm{Er}_{3}\mathrm{Sb}_{3}\mathrm{Mg}_{2}\mathrm{O}_{14}\), \(\mathrm{Dy}_{3}\mathrm{Sb}_{3}\mathrm{Mg}_{2}\mathrm{O}_{14},\) and \(\mathrm{Gd}_{3}\mathrm{Sb}_{3}\mathrm{Mg}_{2}\mathrm{O}_{{14}}\) [22], which also form crystallographically ideal ordered kagome lattices. An isostructural series based on Zn in place of Mg was also recently communicated [23]. This Rapid Communication reports the determination of a magnetic ordered structure in this family of materials. This compound can also be compared to the jarosites, which form ideal ABC stacked kagome lattices [9] with semiclassical spins and long-range magnetic order [24–26], and the langasites, which have “breathing” rare-earth kagome lattices with long-range interactions leading to incommensurate magnetism [27,28].
Polycrystalline \( Nd_{3}Sb_{3}Mg_{2}O_{14} \) was synthesized from a stoichiometric mixture of \( Nd_{2}O_{3} \) , \( \mathrm{Mg(OH)_{2}} \) , and \( Sb_{2}O_{3} \) using standard solid state methods. To determine the crystal structure, high-resolution x-ray powder diffraction data were acquired at room temperature using beamline 11-BM at the Advanced Photon Source (APS) at Argonne National Laboratory ( \( \lambda = 0.414183 \) Å) and analyzed through the Rietveld method as implemented in FULLPROF [29]. The magnetic susceptibility of \( Nd_{3}Sb_{3}Mg_{2}O_{14} \) was measured between 1.8 and 300 K in a Quantum Design Physical Properties Measurement System (PPMS) in an applied field of 0.5 T [30]. The magnetization was found to be proportional to the magnetic field for all temperatures above 1.8 K and fields less than 1 T. Therefore \( M/H \) at \( \mu_{0}H = 0.5 \) T was used as a measure of the susceptibility. The heat capacity \( C(T) \) was measured between 0.1 and 300 K in zero applied magnetic field in a PPMS equipped with a Quantum Design dilution refrigerator [30]. The sample was a dense polycrystalline pellet with a mass of 0.72 mg.
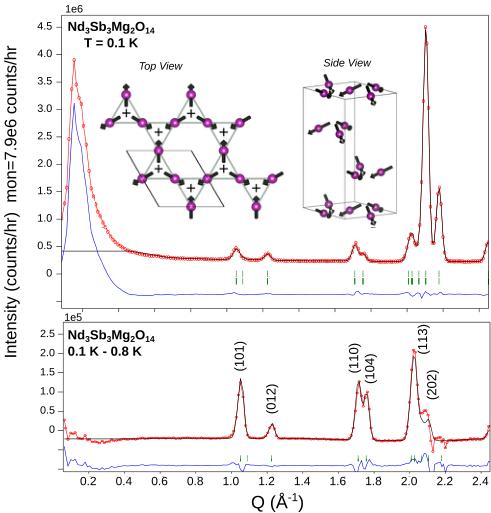
To investigate the magnetic order of \( Nd_{3}Sb_{3}Mg_{2}O_{14} $ , neutron diffraction measurements were carried out on MACS at the NCNR [31]. The monochromator was set for vertical focusing of 5 meV neutrons and the horizontal beam divergence was defined by a 50-mm-wide beam aperture before the monochromator and the 20 mm sample diameter to be 1.5°. 10.2 g of loose \( Nd_{3}Sb_{3}Mg_{2}O_{14} \) powder was loaded into an aluminum can under 10 bars of helium gas at room temperature. The can was closed with an indium sealed copper lid and cooled to the 50 mK base temperature of a KelvinOx-100 dilution fridge with 100 \( \mu \) W cooling power at 100 mK [30]. A 0.02 Tesla magnetic field was applied throughout to maintain aluminum in the normal state. We acquired diffraction data for 24 h at base temperature ( \( T < 0.1 K \) ) and for 24 h at \( T = 0.8 K \) . The neutron diffraction data were analyzed using the FULLPROF [29] and SARAH [32] programs.
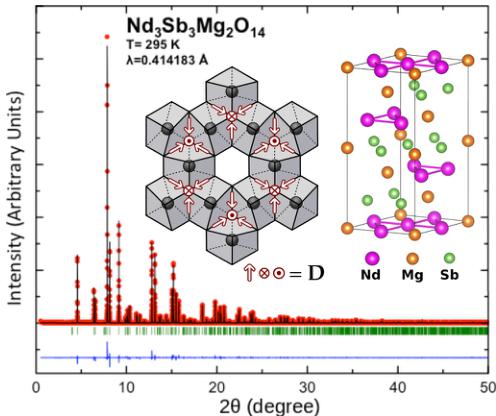
Figure 1 shows a high quality fit of the x-ray diffraction pattern of \( Nd_{3}Sb_{3}Mg_{2}O_{14} to the layered kagome crystal structure with an ideal kagome plane of Nd and nonmagnetic neighboring planes. The rhombohedral lattice parameters of \( Nd_{3}Sb_{3}Mg_{2}O_{14} [a = 7.422(9) \AA \text{ and } c = 17.502(4) \AA] \) are

FIG. 1. Rietveld refinement of 11-BM x-ray diffraction data from \( Nd_{3}Sb_{3}Mg_{2}O_{14} \) at T = 295 K, showing the experimental data points (red), the Rietveld profile (black), and their difference (blue). The green marks indicate Bragg reflections. Also displayed are the stacked kagome planes of Nd atoms in \( Nd_{3}Sb_{3}Mg_{2}O_{14} \) , and the nearest-neighbor coordination relevant to spin-anisotropy, superexchange, and Dzyaloshinskii-Moriya (DM) interactions within kagome planes. The oxygen atoms around each Nd site form scalenohedrons that tilt in alternating directions allowing for the indicated directions of D that define the DM interactions: \( \mathbf{D} \cdot (\mathbf{J}_{1} \times \mathbf{J}_{j}) \) .
closely related to those of the cubic pyrochlore \( Nd_{2}ScNbO_{7} \) \( [a_{p}=10.5336(3)\ \mathring{\mathrm{A}}] \) : by \( a=b\approx a_{p}/\sqrt{2} \) and \( c\approx\sqrt{3}a_{p} \) [19]. The broken symmetries associated with the cubic to rhombohedral transition reflect the loss of intersecting kagome planes in the pyrochlore lattice due to the planar ordering of \( Nd^{3+} \) , \( Sb^{5+} \) , and \( Mg^{2+} \) . In the kagome compound, Nd is found in an eight-coordinated distorted cube (a “scalenohedron”) of O atoms with Nd-O bond distances ranging from 2.342(3) to 2.580(4) Å.
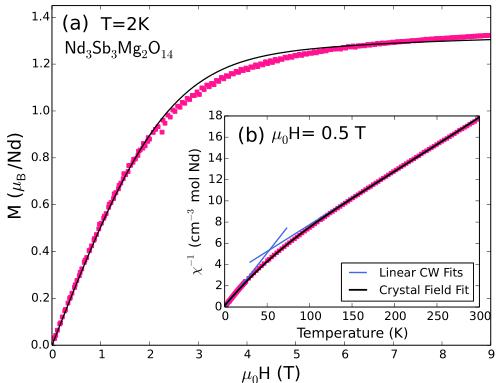
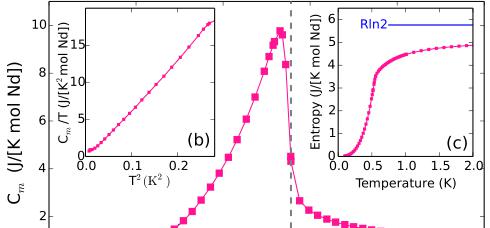
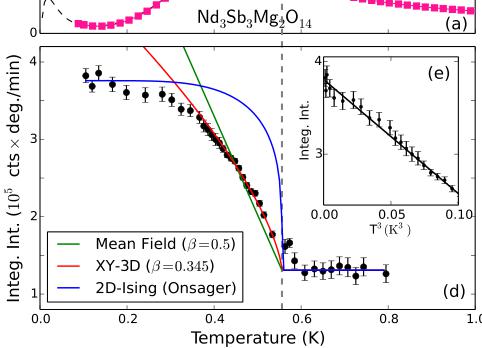
Our first aim is to establish the nature of the spin Hamiltonian in \( Nd_{3}Sb_{3}Mg_{2}O_{14} \( through high-temperature and high-field measurements. Figure 2(b) shows the temperature dependence of the inverse susceptibility. Curie-Weiss fits in the low T and high T ranges yield effective moments of \) \mu_{\mathrm{eff}}(1.8\ \mathrm{K}<T<10\ \mathrm{K})=2.50(5)\mu_{B} \( and \) \mu_{\mathrm{eff}}(150\ \mathrm{K}<T<300\ \mathrm{K})=3.56(5)\mu_{B} \( . The latter value is similar to the free ion value of \) g_{J}\sqrt{J(J+1)}\mu_{B}=3.62\mu_{B} \( for the J=9/2 multiplet of \) Nd^{3+} \( . The ratio between the high and low T effective moments is 0.70(2), which is consistent with the value of \) 1/\sqrt{2}\approx0.707 \( for an easy-plane ion in the large J limit with a random orientation distribution. Similar low T effective moments have been observed for several other easy-plane neodymium pyrochlore oxides, such as \) Nd_{2}ScSbO_{7} \( (2.58 \( \mu_{B} \) ), \( Nd_{2}Pb_{2}O_{7} \) (2.55 \( \mu_{B} \) ), \( Nd_{2}Zr_{2}O_{7} \) (2.54 \( \mu_{B} \) ), and \( Nd_{2}Sn_{2}O \) (2.63 \( \mu_{B} \) ) [33–36]. The energy scale (Curie-Weiss temperature) extracted from the high T fit \( \Theta(150\ \mathrm{K} FIG. 2. Magnetization data for a powder sample of \( Nd_{3}Sb_{3}Mg_{2}O_{14} \) . (a) Magnetization as a function of applied field. (b) Inverse susceptibility H/M in an applied field of 0.5 T. The blue lines are linear fits to distinct T ranges. For \( 1.8~K < T < 10~K \) we find an effective moment of \( 2.50(5)\mu_{B} \) and a Curie-Weiss temperature \( \Theta_{\mathrm{CW}} = -0.12(1) \) K. The higher-temperature fit for \( 150~K < T < 300~K \) yields the full effective moment of \( 3.56(5)\mu_{B} \) and a large negative intercept of -54.5(5) K, which is indicative of the crystal-field energy scale. The black lines are a single consistent fit to the data in (a) and (b) based on a mean-field model described in the text. Weiss fit, we extract an estimate for the sum of all exchange constants associated with each Nd site of \( \Theta(1.8\;\mathrm{K} To quantify anisotropy and exchange parameters, a consistent fit was carried out to \( \chi(T) \) and \( M(H) \) based upon the following mean-field Hamiltonian: \( \mathcal{H}=D_{\mathrm{CF}}J_{z}^{2}+g_{J}\mu_{B}\mu_{0}\mathbf{H}_{\mathrm{eff}}\cdot\mathbf{J} \) . Here \( D_{CF}>0 \) represents the crystal-field easy-plane anisotropy energy, and \( g_{J} \) is the Landé factor. The effective field is \( \mathbf{H}_{\mathrm{eff}}=(H+\lambda M)\hat{\mathbf{H}} \) where \( H=H\hat{H} \) is the applied field, M the induced magnetization per volume unit, \( \lambda=(V/N)(g_{J}\mu_{B})^{-2}\mathcal{J}_{\mathrm{tot}} \) , and \( \mathcal{J}_{\mathrm{tot}}=(1/2N)\Sigma_{ij}\mathcal{J}_{ij} \) is the total exchange energy per spin. The corresponding fitted parameters are \( D_{CF}=28.5(3) \) meV, \( g_{J}=0.7235(9) \) , and \( \mathcal{J}_{\mathrm{tot}}=-23(1)\mu\mathrm{eV} \) . The excellent and consistent description of the data (solid lines in Fig. 2) and consistency with \( g_{J}=0.7273 \) for the \( Nd^{3+} \) ion indicate the low-temperature magnetism of \( Nd_{3}Sb_{3}Mg_{2}O_{14}} \) can be described in terms of FIG. 3. (a) Low-temperature heat capacity of \( Nd_{3}Sb_{3}Mg_{2}O_{14} \) . The low T upturn results from hyperfine enhanced nuclear heat capacity from \( {}^{143}Nd \) and \( {}^{145}Nd \) . The dashed line shows calculated nuclear contribution with a fitted ordered Nd moment of \( 1.5(1)\mu_{B} \) . (b) \( C_{m}/T \) versus \( T^{2} \) after subtracting the low T nuclear contribution to the heat capacity. (c) Change in electronic entropy obtained through an integral of \( C_{m}/T \) . (d) Integrated intensity of the (101) peak versus T along with several fits using various critical exponents \( \beta \) while fixing \( T_{N} \equiv 0.56 \) K as determined from the heat capacity data (vertical dashed line). (e) Integrated intensity versus \( T^{3} \) in the low T regime where the reduction in sublattice magnetization is given by spin wave theory to be \( \propto T^{3} \) . Error bars represent one standard deviation. an easy-plane Kramers doublet with net antiferromagnetic interactions. Turning to collective phenomena, Fig. 3(a) shows low-temperature heat capacity data. Below 0.6 K, the heat capacity strongly increases, with an inflection point at 0.56(2) K. The \( \lambda \) -like anomaly indicates a second-order phase transition at \( T_{N}=0.56(2) \) K, which we shall shortly show is to a three-dimensional long-range-ordered canted antiferromagnetic state that carries a finite scalar chirality. The lattice contribution to heat capacity was removed by subtracting the heat capacity of a nonmagnetic analog, \( La_{3}Sb_{3}Mg_{2}O_{14} \) . For temperatures below 0.2 K a slight upturn in \( C(T) \) is ascribed to a hyperfine field enhanced nuclear Schottky anomaly. The dashed line in this T regime was fit based on this hypothesis and the known hyperfine parameters [37] for the stable spin-full isotopes of neodymium (12.18% \( {}^{143}Nd \) and 8.29% \( {}^{145}Nd \) both with spin- \( \frac{7}{2} \) ) and indicates an ordered Nd moment of \( 1.5(1)\mu_{B} \) . By integrating C/T, the T-dependent change in entropy (computed after subtracting the nuclear Schottky contribution to the heat capacity) was inferred [Fig. 3(c)]. While significant FIG. 4. Rietveld refined neutron diffraction data for \( Nd_{3}Sb_{3}Mg_{2}O_{14} \) (a) Low T data along with images of the corresponding scalar chiral umbrella-like spin structure. (b) Magnetic diffraction data at \( T = 0.1~K \) isolated from nuclear scattering by subtracting nuclear diffraction data acquired at \( T = 0.8~K > T_{N} \) . entropy is liberated at the magnetic phase transition, the amount falls short of R ln 2 anticipated for a ground state doublet. Neglecting any low T configurational entropy, this indicates significant spin correlations for \( T > T_{N} \) K. Figure 3(b) shows a detail of the electronic low T heat capacity (after subtraction of the nuclear term). The limiting \( T^{3} \) behavior is consistent with linear dispersive spin wave excitations in three dimensions. The corresponding average spin-wave velocity extracted from a low T fit to \( C_{m}(T) = (2\pi^{2}/15)R(k_{B}T/\hbar v_{\mathrm{sw}})^{3}v_{0} \) is \( v_{\mathrm{sw}} = 33(2) \) m/s. Here \( v_{0} \) is the volume per Nd ion. This estimate of the spin-wave velocity is consistent with the value of \( v_{sw} = 1/\sqrt{3}|J_{\mathrm{tot}}|Ja/\hbar = 34(1) \) m/s derived from an ABC stacked kagome model with isotropic exchange constants, using \( J_{tot} \) inferred from the low T Curie-Weiss fit. To directly probe the magnetic order parameter we acquired high statistics neutron diffraction data at 0.1 and 0.8 K. The temperature difference in Fig. 4(b) reveals increased intensity at the location of several nuclear Bragg peaks upon cooling below \( T_{N} \) . This is consistent with long-range magnetic order with a propagation vector of \( \mathbf{k} = (0,0,0) \) . Fitting the excess diffraction at (101) to the convolution of a Lorentzian peak with a Gaussian peak that fits the high T (101) peak and so accounts for the instrumental resolution, we obtain a lower bound on the magnetic correlation length at \( T = 0.1 \, K \) of \( \xi > 400 \, \AA = 55a \) . Figure 3(d) shows the peak area (extracted from Gaussian fits) of the (101) peak versus T. The onset for \( T < T_{N} \) links the extra diffraction intensity to the squared order parameter of the phase transition. Knowing the critical temperature from the heat capacity data, we compare the T-dependent diffraction to that anticipated for phase transitions of different universality classes. The data are inconsistent with mean-field criticality and exclude a two-dimensional (2D) Ising transition. Fitting the data within 20% of \( T_{N} \) yields a critical exponent \( \beta = 0.34(4) \) which is consistent with three-dimensional (3D) Ising, XY, and Heisenberg criticality. Both the diffraction line shape and the experimental value for \( \beta \) , however, exclude a 2D transition. To determine the magnetic structure we carried out a Rietveld refinement of the \( T = 0.1 \, K \) data, which contains nuclear as well as magnetic diffraction. Refinement of the nuclear component started from the high T structure determined by x-ray diffraction (Fig. 1). We used representation analysis as implemented in the SARAH program to classify magnetic structures according to the three irreducible representations (IRs) of the \( R\bar{3}m \) space group. Only the three-dimensional representation denoted \( \Gamma_{3} \) provides an acceptable fit (Fig. 4). For comparison the goodness of fit parameter \( \chi^{2} \) increases by a factor of 20 and 59 for the six-dimensional \( \Gamma_{5} \) irrep and the one-dimensional \( \Gamma_{1} \) irrep, respectively. The magnetic diffraction intensity was isolated from the nuclear component by subtracting the 0.8 K data from the 0.1 K data in Fig. 4(b). Apart from a slight discrepancy near (202), which results from systematic errors associated with subtracting intense nuclear peaks acquired at different temperatures, the intensity of magnetic and nuclear diffraction associated with the fit in Fig. 4(a) is consistent with the difference data. With moments canted along a common c direction and pointing either “all-into” or “all-out” from their triangles, the \( \Gamma_{3} \) magnetic structure has an umbrella-like character and carries a net moment along c. The ordered magnetic moment extracted from refinement is \( 1.79(5)\mu_{B} \) . This is consistent with the observed saturation magnetization assuming an easy-plane moment and with the ordered moment inferred from the nuclear Schottky anomaly. Related umbrella-like structures were previously reported in jarosite compounds with \( S \geqslant 3/2 \) . For \( \mathrm{KFe_{3}(OH)_{6}(SO_{4})_{2}} \) the out-of-plane spin component alternates between layers so the unit cell is doubled [38,39], while \( \mathrm{KCr_{3}(OH)_{6}(SO_{4})_{2}} \) appears to have the same structure as \( Nd_{3}Sb_{3}Mg_{2}O_{14} \) though spin canting was not reported [25]. We find a spin canting angle of \( \eta = 30.6(5)^{\circ} \) for \( Nd_{3}Sb_{3}Mg_{2}O_{14} \) , which corresponds to a net ferromagnetic moment of \( 0.93(3)\mu_{B}/Nd \) . This dwarfs the canting angle of \( \eta \approx 2^{\circ} \) found for the jarosites. The magnetic umbrella structure for \( Nd_{3}Sb_{3}Mg_{2}O_{14} $ is different from the structures proposed for \( Gd_{3}Sb_{3}Mg_{2}O_{14} \) , \( Er_{3}Sb_{3}Mg_{2}O_{14} \) , and \( Dy_{3}Sb_{3}Mg_{2}O_{14} \) [22]. The proposed Gd and Er \( 120^{\circ} \) structure corresponds to irrep \( \Gamma_{1} \) , which is inconsistent with the diffraction data for \( Nd_{3}Sb_{3}Mg_{2}O_{14} \( as noted above. The “two-in-one-out” structure proposed for Dy corresponds to a combination of irreps \( \Gamma_{3} \) and \( \Gamma_{5} \) . With a ) \chi^{2} \( value 32 times larger than that for our umbrella structure, the Dy model can also be excluded for \) Nd_{3}Sb_{3}Mg_{2}O_{14} \( . In addition, the presence of two irreps would require a first-order phase transition, which \) Nd_{3}Sb_{3}Mg_{2}O_{14} \( does not have.
Dzyaloshinskii-Moriya (DM) interactions are allowed by symmetry when the midpoint between magnetic ions is not a point of inversion. In jarosites, DM interactions favor the alternating umbrella structure \( [26,39–41] \) . Likewise in \( Nd_{3}Sb_{3}Mg_{2}O_{14} \) ; oxygen atoms surrounding each Nd site are tilted in an alternating pattern that allows DM vectors in the midplane between interacting spins with the orientations indicated in Fig. 1. The corresponding interactions \( \mathbf{D}\cdot(\mathbf{J}_{i}\times\mathbf{J}_{j}) \) favor the \( \Gamma_{3} \) uniform umbrella structure that we infer from diffraction data \( [26,39,41] \) . Given the strongly anisotropic nature of the \( [9/2,\pm1/2) \) state, the large canting angle is to be expected. For semiclassical spins \( \eta \) is related to a ratio of interactions as follows \( [40] \) : \[ \sin2\eta=\left|\frac{2D_{\perp}}{\sqrt{3}J-D_{z}}\right|. \quad (1) \] Here \( D_{\perp} = |D \times \hat{\mathbf{z}}| \) , \( D_{z} = D \cdot \hat{\mathbf{z}} \) , and \( J = J_{1} + J_{2} \) is the sum of near- and next-nearest-neighbor exchange interactions. If we were to use this expression for quantum spins and neglect \( D_{z} \) , the expression yields \( D_{\perp}/J = 0.8 \) for \( Nd_{3}Sb_{3}Mg_{2}O_{1} \) . While there is presently insufficient information to determine all relevant interactions for \( Nd_{3}Sb_{3}Mg_{2}O_{1}4 \) , it is interesting to note that a classical spin model with DM interactions on the kagome lattice should undergo a finite temperature 2D phase transition [40–42]. The phase transition in \( Nd_{3}Sb_{3}Mg_{2}O_{1}4 at T_{N} = 0.56(2) \) K is clearly a 3D transition but the reduced change in entropy at \( T_{N} \) is consistent with a quasi-2D regime for \( T > T_{N} \) that could be a 2D quantum spin liquid [43,44]. Through detailed bulk and neutron scattering experiments on \( Nd_{3}Sb_{3}Mg_{2}O_{14} \) ,we have provided an atomic scale view of magnetism in a new family of rare-earth kagome magnets. The noncoplanar \( k = 0 \) umbrella structure we observe carries uniform magnetization along c and is favored by the staggered Dzyaloshinkii-Moriya interactions anticipated for rare-earth ions on this lattice. The corresponding scalar chiral spin structure implies Berry curvature, which should produce an anomalous thermal Hall effect and topologically protected edge states below and possibly even above \( T_{N} \) [45]. We thank Elizabeth Seibel and Quinn Gibson for helpful discussions. We also thank Ovi Garlea and Stuart Calder for their help during early stages of the project. This work was supported through the Institute for Quantum Matter at Johns Hopkins University, by the US Department of Energy, Division of Basic Energy Sciences, Grant No. DE-FG02-08ER46544. A.S. was supported through the Gordon and Betty Moore Foundation under the EPIQS program GBMF4532. Use of the Advanced Photon Source at Argonne National Laboratory was supported by the US Department of Energy, Office of Science, Office of Basic Energy Sciences, under Contract No. DE-AC02-06CH11357. Use of the NCNR facility was supported in part by the National Science Foundation under Agreement No. DMR-1508249. [3] M. Punk, D. Chowdhury, and S. Sachdev, Nat. Phys. 10, 289 (2014). [4] S. Yan, D. A. Huse, and S. R. White, Science 332, 1173 (2011). [5] S. S. Gong, W. Zhu, L. Balents, and D. N. Sheng, Phys. Rev. B 91, 075112 (2015). [6] K. Essafi, O. Benton, and L. D. C. Jaubert, Nat. Commun. 7, 10297 (2016). [7] A. Chubukov, Phys. Rev. Lett. 69, 832 (1992). [8] I. Ritchey, P. Chandra, and P. Coleman, Phys. Rev. B 47, 15342(R) (1993). [9] M. Takano, T. Shinjo, and T. Takada, J. Phys. Soc. Jpn. 30, 1049 (1971). [10] X. Obradors, A. Labarta, A. Isalgué, J. Tejada, J. Rodriguez, and M. Pernet, Solid State Commun. 65, 189 (1988). [11] A. P. Ramirez, G. P. Espinosa, and A. S. Cooper, Phys. Rev. Lett. 64, 2070 (1990). [12] I. S. Hagemann, Q. Huang, X. P. A. Gao, A. P. Ramirez, and R. J. Cava, Phys. Rev. Lett. 86, 894 (2001). [13] Z. Hiroi, M. Hanawa, N. Kobayashi, M. Nohara, H. Takagi, Y. Kato, and M. Takigawa, J. Phys. Soc. Jpn. 70, 3377 (2001). [14] M. P. Shores, E. A. Nytko, B. M. Bartlett, and D. G. Nocera, J. Am. Chem. Soc. 127, 13462 (2005). [15] J. S. Helton, K. Matan, M. P. Shores, E. A. Nytko, B. M. Bartlett, Y. Yoshida, Y. Takano, A. Suslov, Y. Qiu, J.-H. Chung, D. G. Nocera, and Y. S. Lee, Phys. Rev. Lett. 98, 107204 (2007) [16] Y. Okamoto, H. Yoshida, and Z. Hiroi, J. Phys. Soc. Jpn. 78, 033701 (2009). [17] K. Ohgushi, S. Murakami, and N. Nagaosa, Phys. Rev. B 62, R6065(R) (2000). [18] J. S. Gardner, M. J. P. Gingras, and J. E. Greedan, Rev. Mod. Phys. 82, 53 (2010). [19] S. Zouari, R. Ballou, A. Cheikh-Rouhou, and P. Strobel, Mater. Lett. 62, 3767 (2008). [20] W. T. Fu and D. J. W. IJdo, J. Solid State Chem. 213, 165 (2014). [21] K. Li, Y. Hu, Y. Wang, T. Kamiyama, B. Wang, Z. Li, and J. Lin, J. Solid State Chem. 217, 80 (2014). [22] Z. L. Dun et al., Phys. Rev. Lett. 116, 157201 (2016). [23] M. B. Sanders, J. W. Krizan, and R. J. Cava, J. Mater. Chem. C 4, 541 (2016). [24] T. Inami, M. Nishiyama, S. Maegawa, and Y. Oka, Phys. Rev. B 61, 12181 (2000). [25] S.-H. Lee, C. Broholm, M. F. Collins, L. Heller, A. P. Ramirez, Ch. Kloc, E. Bucher, R. W. Erwin, and N. Lacevic, Phys. Rev. B 56, 8091 (1997). [26] R. Ballou, B. Canals, M. Elhajal, C. Lacroix, and A. S. Wills, J. Magn. Magn. Mater. 262, 465 (2003). [27] P. Bordet, I. Gelard, K. Marty, A. Ibanez, J. Robert, V. Simonet, B. Canals, R. Ballou, and P. Lejay, Pr. J. Phys. Condens. Matter 18, 5147 (2006). [28] V. Simonet, R. Ballou, J. Robert, B. Canals, F. Hippert, P. Bordet, P. Lejay, P. Fouquet, J. Ollivier, and D. Braithwaite, Phys. Rev. Lett. 100, 237204 (2008). [29] Rietveld refinements were performed using the program FULLPROF. J. Rodriguez-Carvajal, Physica B 192, 55 (1993); Program Fullprof, LLB-JRC, Laboratoire Léon Brillouin, CEA-Saclay, France, 1996 (www.ill.eu/sites/fullprof/). [30] The identification of any commercial product or trade name does not imply endorsement or recommendation by the National Institute of Standards and Technology. [31] J. A. Rodriguez, D. M. Adler, P. C. Brand, C. Broholm, J. C. Cook, C. Brocker, R. Hammond, Z. Huang, P. Hundertmark, J. W. Lynn, N. C. Maliszewskyj, J. Moyer, J. Orndorff, D. Pierce, T. D. Pike, G. Scharfstein, S. A. Smee, and R. Vilaseca, Meas. Sci. Technol. 19, 034023 (2008) [32] A. S. Wills, Physica B 276, 680 (2000). [33] M. C. Hatnean, M. R. Lees, O. A. Petrenko, D. S. Keeble, G. Balakrishnan, M. J. Gutmann, V. V. Klekovkina, and B. Z. Malkin, Phys. Rev. B 91, 174416 (2015). [34] A. M. Hallas, A. M. Arevalo-Lopez, A. Z. Sharma, T. Munsie, J. P. Attfield, C. R. Wiebe, and G. M. Luke, Phys. Rev. B 91, 104417 (2015). [35] P. Strobel, S. Zouari, R. Ballou, A. Cheikh-Rouhou, J. Jumas, and J. Olivier-Fourcade, Solid State Sci. 12, 570 (2010). [36] K. Matsuhira, Y. Hinatsu, K. Tenya, H. Amitsuka, and T. Sakakibara, J. Phys. Soc. Jpn. 71, 1576 (2002). [37] B. Bleaney, J. Appl. Phys. 34, 1024 (1963). [38] M. Nishiyama, S. Maegawa, T. Inami, and Y. Oka, Phys. Rev. B 67, 224435 (2003). [39] K. Matan, B. M. Bartlett, J. S. Helton, V. Sikolenko, S. Matas, K. Prokes, Y. Chen, J. W. Lynn, D. Grohol, T. J. Sato, M. Tokunaga, D. G. Nocera, and Y. S. Lee, Phys. Rev B 83, 214406 (2011). [40] T. Yildirim and A. B. Harris, Phys. Rev. B 73, 214446 (2006). [41] M. Elhajal, B. Canals, and C. Lacroix, Phys. Rev. B 66, 014422 (2002). [42] M. Rigol and R. R. P. Singh, Phys. Rev. B 76, 184403 (2007). [43] Y. Huh, L. Fritz, and S. Sachdev, Phys. Rev. B 81, 144432 (2010). [44] L. Messio, O. Cépas, and C. Lhuillier, Phys. Rev. B 81, 064428 (2010). [45] M. Hirschberger, R. Chisnell, Y. S. Lee, and N. P. Ong, Phys. Rev. Lett. 115, 106603 (2015).