| Transition Temperature | 19 K |
|---|---|
| Experiment Temperature | 4.2 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | Pnma (#62) |
| Magnetic Space Group | Pnma (#62.441) |
| Magnetic Point Group | mmm (8.1.24) |
| Lattice Parameters | 7.021(1) 7.441(1) 10.007(2) 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1016/0038-1098(85)90192-9 |
| Reference | G. Ferey, M. Leblanc, R. De Pape, J. Pannetier, Solid State Communications (1985) 53 559 - 563 |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Fe1 | Fe | 3.86 | 1.00 | 1.07 | 4.13 |
| Fe2 | Fe | 0.0 | 3.12 | 0.0 | 3.12 |
FRUSTRATED MAGNETIC STRUCTURES: II.* ANTIFERROMAGNETIC STRUCTURE OF THE ORDERED MODIFIED PYROCHLORENE NH₄Fe³⁺Fe³⁺F₆ AT 4.2 K
G. Ferey, M. Leblanc, R. De Pape and J. Pannetier \( ^{*} \)
Laboratoire des Fluorures et Oxyfluorures Ioniques, ERA 609 Faculté des Sciences, Route de Laval - 72017 Le Mans Cedex, France
\( ^{*} \) Institut Laue-Langevin, 156X, 38042 Grenoble Cedex, France
(Received 20 February 1984, in revised form 17 September 1984 by E.F. Bertaut)
The nuclear and magnetic structures of the ordered modified pyrochlore \( NH_{4}Fe^{2+}Fe^{3+}F_{6} \) were solved at 4.2 K. \( NH_{4}^{+} \) tetrahedra are almost regular ( \( \langle N-H\rangle = 0.924\ \AA \) ) and the fluorinated skeleton at 4.2 K does not exhibit large deviations from the room-temperature positions ( \( R_{N} = 0.042 \) ). Below \( T_{N} = 19 \pm 1 \) K the magnetic and nuclear cells are identical. The strictly antiferromagnetic arrangement of \( Fe^{2+} \) spins ( \( \mu = 3.12(9)\ \muB \) ) along the \( [0\ 1\ 0] \) direction contrasts with the canted antiferromagnetic sublattice of \( Fe^{3+} \) ions ( \( \mu = 4.13\ [8]\ \muB \) ) which is quasi-orthogonal ( \( \alpha = 76^{\circ} \) ) to the \( Fe^{2+} \) sublattice ( \( R_{mag} = 0.078 \) ). The main component of \( Fe^{3+} \) moments lies along a. The antiferromagnetism of \( NH_{4}Fe^{2+}Fe^{3+}F_{6}^{-} \) is compared to the spin-glass like behaviour which occurs when \( M^{2+} \) and \( M^{3+} \) ions are randomly distributed on the cationic sites.
INTRODUCTION
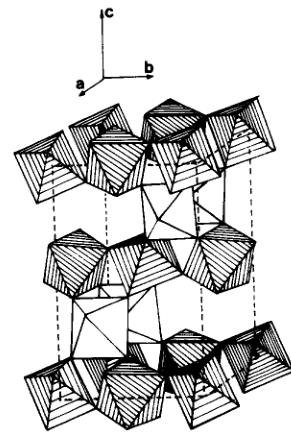
RECENTLY, BESIDE THE LARGE amount of work devoted to metallic spin glasses, interest has been taken in crystalline or amorphous insulating spin glasses, particularly in the \( AM^{2+}M^{3+}F_{6} \) modified pyrochlore structural family \( [1-5] \) . In the cubic cell, \( (SG Fd3m) \) , the random distribution of divalent an trivalent ions on a network of corner sharing octahedra leads to a magnetic behaviour which can be explained either in spin glass \( [2,3] \) or in cluster \( [4,5] \) terms. However, \( M^{2+}-M^{3+} \) cationic order, associated with antiferromagnetic properties, may occur in the structure if the same metal (e.g. Fe) exists with two valence states. We previously described the structure of orthorhombic \( NH_{4}Fe^{III}Fe^{III}F_{6} \) \( [6] \) \( (SG:Pma):Fe^{3+} \) and \( Fe^{2+} \) , in octahedral coordination, form chains, respectively along the \( [0\ 1\ 0] \) and \( [1\ 0\ 0] \) directions (Fig. 1). The consequences of this order on the magnetic structure of this compound ( \( T_{N}=19\ K \) ) will be discussed in contrast with the usual spin glass like behaviour of the other pyrochlores.
EXPERIMENTAL
Powder samples of \( NH_{4}Fe_{2}F_{6} \) were obtained by heating a stoichiometric mixture of elementary fluorides in sealed gold tubes at \( 400^{\circ}C \) during 24 hours, followed by an identical treatment at \( 600^{\circ}C \) . Attempts to obtain the pure deuterated compound were unsuccessful: the

Fig. 1. Perspective view of \( NH_{4}Fe^{III}Fe^{III}F_{6} \)
final product was always contaminated by small amounts of the hexagonal bronze \( (\mathrm{NH}_{4})_{x}\mathrm{FeF}_{3}(x\sim0.30) \) . Neutron diffraction patterns were collected on the DIA high resolution powder diffractometer of the HFR of the Laüe-Langevin Institute using the wavelength \( \lambda=2,98\ \AA \) . The dark brown sample was inserted in a cylindrical vanadium ( \( \phi\ 15\ \mathrm{mm} \) ) can held in a vanadium-tailed liquid helium cryostat. Data were collected in the range \( 8^{\circ}\leqslant20\leqslant150^{\circ} \) in steps of \( 0.05^{\circ} \) . The 30 K pattern was used to localize the hydrogen atoms in the
Table 1. Refined cell parameters and atomic coordinates at 30 K (first line) and 4.2 K (second line).
| a(Å) | b(Å) | c(Å) | |
| 30 K | 7.021(1) | 7.441(1) | 10.011(2) |
| 4.2 K | 7.021(1) | 7.441(1) | 10007(2) |
| X | Y | Z | |
| N | -0.0045(9) | 1/4 | 0.6174(7) |
| -0.0046(9) | 1/4 | 0.6190(6) | |
| H1 | -0.0304(25) | 1/4 | 0.5315(19) |
| -0.0324(25) | 1/4 | 0.5308(19) | |
| H2 | 0.1341(30) | 1/4 | 0.6030(20) |
| 0.1337(30) | 1/4 | 0.6018(21) | |
| H3 | -0.0458(18) | 0.1502(12) | 0.6592(12) |
| -0.0468(18) | 0.1498(12) | 0.6598(12) | |
| Fe3+ | 0 | 0 | 0 |
| Fe2+ | 0.1973(8) | 1/4 | 0.2686(7) |
| 0.1975(8) | 1/4 | 0.2682(7) | |
| F1 | 0.9451(11) | 1/4 | 0.3372(11) |
| 0.9448(11) | 1/4 | 0.3385(11) | |
| F2 | 0.0626(11) | 1/4 | 0.9776(11) |
| 0.0627(11) | 1/4 | 0.9760(11) | |
| F3 | 0.1243(5) | 0.4903(13) | 0.1696(7) |
| 0.1246(5) | 0.4882(13) | 0.1692(7) | |
| F4 | 0.7661(8) | 0.4392(16) | 0.0837(7) |
| 0.7665(8) | 0.4405(16) | 0.0832(7) |
nuclear cell and check the absence of any structural phase transition between room temperature and the Neel temperature \( (T_{N}=19\mathrm{K}) \) ; a second diffraction pattern at 4.2 K was used to determine the magnetic structure at this temperature. The temperature dependence of magnetic reflections intensities was not recorded.
The diffraction patterns were analyzed by the Rietveld method \( [7] \) as modified by Hewat \( [8] \) . The nuclear scattering lengths and magnetic form factors were taken from \( [9 \) and \( [10] \) respectively. Absorption corrections were applied \( [11] \) .
RESULTS
1. Nuclear structure
It has been refined using 64 peaks which correspond to 95 (hkl) triplets. The final values of cell parameters and atomic coordinates at 30 and 4.2 K are given in Table 1. The incoherent scattering from hydrogen atoms gives rise to a high background in the diffraction patterns and the isotropic thermal parameters are rather poorly defined; they were fixed to 2, 2, 3 and 6 Ų respectively for nitrogen, iron, fluorine and hydrogen atoms.
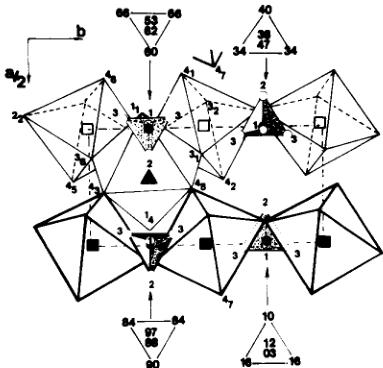
A part of the \( (00\ 1) \) projection of the structure at 4.2 K appears in Fig. 2. \( H_{1} \) and \( H_{3} \) hydrogen atoms of

Fig. 2. Part of the \( (00\ 1) \) projection of the structure of \( NH_{4}Fe_{2}F_{6} \) showing the disposition of \( NH_{4}^{+} \) tetrahedra. N and H are indicated as full and empty circles respectively. The number near the H circles refer to the type of hydrogen indicated in Table 1. Their z coordinates appear in the triangles above and below the projection itself. \( Fe^{3+} \) ions correspond to the squares, empty at z = 0 and full at \( z = \frac{1}{2} \) . \( Fe^{2+} \) are black triangles. F ions are noted with the same two numbers as in [6].
the \( NH_{4}^{+} \) tetrahedron are strongly bonded to \( F_{1} \) , \( F_{3} \) and \( F_{4} \) atoms of the octahedral network with short \( H\ldots F \) distances between 1.93 and 2.32 Å and \( N\ldots F \) shorter than 3.0 Å. \( H_{2} \) atom is less bonded to the fluorinated skeleton (Table 2). In the tetrahedron, the pyramid \( H_{3}H_{1}H_{3}N \) is regular and the hydrogenated basal triangle is equilateral.
2. Magnetic structure
At 4.2 K, the intensity of many nuclear peaks is increased and additional magnetic peaks appear in the spectrum.
All new reflections can be indexed on the nuclear cell. The magnetic structure can be sought using Bertaut's macroscopic theory \( [12] \) . \( \hat{z}_{x} \) , \( \hat{z}_{z} \) and \( \hat{I} \) will be considered as the three independent symmetry elements. If \( S_{i} \) and \( R_{i} \) (i = 1, 4) are the magnetic moments of \( Fe^{3+} \) and \( Fe^{2+} \) corresponding to the atomic coordinates reported in Table 3, it is possible to define in each sublattice four linear combinations of the moments: \( F = M_{1} + M_{2} + M_{3} + M_{4} \) , \( G = M_{1} - M_{2} + M_{3} - M_{4} \) , \( C = M_{1} + M_{2} - M_{3} - M_{4} \) and \( A = M_{1} - M_{2} - M_{3} + M_{4} \) (M = S, R) which represent the ferromagnetic and antiferromagnetic modes of coupling. The base vectors, in the irreducible representation of space group Pnma, lead (Table 3) to the four modes which are suitable with both \( Fe^{2+} \) and \( Fe^{3+} \) sublattices.
The best fit \( (R = 0.078) \) between observed and calculated magnetic intensities (the list of observed and
Table 2. Bond distances ( \( \AA \) ) and angles in the \( NH_{4}^{+} \) tetrahedron and between it and the fluorinated skeleton (4.2 K). The two numbers which affect fluorine atoms refer to the notation of [6]. Standard deviations are about 0.007 Å for N–H distances, 0.010 Å for H…F and N…F distances, and 0.1° for angles.
| 1 × N−H1 | 0.904 | H1−N−H2 | 22.47 |
| 1 × N−H2 | 0.986 | 2 × H1−N−H3 | 111.79 |
| 2 × N−H3 | 0.902 | 2 × H2−N−H3 | 113.71 |
| dN−H | 0.924 | H3−N−H3 | 111.98 |
| H1−H2 | 1.366 | 2 × H1−H2−H3 | 60.45 |
| 2 × H1−H3 | 1.495 | 2 × H2−H1−H3 | 66.92 |
| 2 × H2−H3 | 1.581 | 2 × H2−H3−H1 | 52.63 |
| H3−H3 | 1.495 | 2 × H3−H3−H1 | 60.00 |
| dH−H | 1.502 | 2 × H3−H3−H2 | 61.78 |
| H3−H1−H3 | 60.00 | ||
| H3−H2−H3 | 56.43 | ||
| H1−F11 | 1.931 | N−F11 | 2.830 |
| H3−F32 | 2.119 | N−F32 | 2.950 |
| H3−F47 | 2.319 | N−F47 | 2.967 |
Standard deviations: distances N-H 0,007 Å, H...F and N...F 0,01 Å; angles 0,1°
Table 3. Coordinates of the magnetic ions \( S_{1}(Fe^{3+}) \) and \( R_{1}(Fe^{2+}) \) and part of the irreducible representation of \( Fe^{2+} \) and \( Fe^{3+} \) in the Pnma group. This part corresponds to the representations suitable for the two sublattices.
| Fe3+ | Fe2+ | |||||||
| S1 | : | 0 | 0 | 0 | R1 | : | x | 1/4 |
| S2 | : | 0 | 1/2 | 0 | R2 | : | x | 3/4 |
| S3 | : | 1/2 | 1/2 | 1/2 | R3 | : | 1/2 - x, | 3/4, |
| S4 | : | 1/2 | 0 | 1/2 | R4 | : | 1/2 + x, | 1/4, |
| Mode | x | y | z | x | y | z | ||
| Γ1(+++) | Gx | Cy | Az | Cy | ||||
| Γ2(+-+) | Fx | Ay | Cz | Fx | Cz | |||
| Γ3(-++) | Cx | Gy | Fz | Cx | Fz | |||
| Γ4(--+) | Ax | Fy | Gz | Fy | ||||
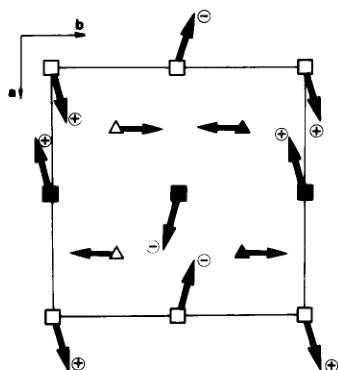
calculated magnetic intensities can be obtained on request to the authors) is obtained for the \( \Gamma_{1} \) mode with signs \( +G_{x} \) , \( +C_{y} \) , \( +A_{z} \) for \( Fe^{3+} \) components and \( +C_{y} \) for \( Fe^{2+} \) . Other combinations of signs do not fit (110), (012), (100) and (122) reflections. All the interactions are antiferromagnetic. Moments of \( Fe^{2+} \) ( \( \mu = 3.12 \) [9] \( \mu B \) ) lie along [010]; the spins of \( Fe^{3+} \) ( \( \mu = 4.13 \) [8] \( \mu B \) ) deviate from the a axis, creating a canted antiferromagnetic sublattice; with respect to the a axis, the angle of canting of \( Fe^{3+} \) spins is \( 20.8^{\circ} \) or \( 15^{\circ} \) from the xy plane. The components of the magnetic moments \( M(M = S, R) \) on the three axes of the cell are listed in Table 4.
The two magnetic sublattices of \( Fe^{2+} \) and \( Fe^{3+} \) , are quasiorthogonal, the angle between \( \mu_{Fe^{2+}} \) and \( \mu_{Fe^{3+}} \) being \( 76^{\circ} \) (Fig. 3). Magnetic dipolar energy calculations carried out in the real space inside a sphere of \( 50 \AA \) radius, show that \( Fe^{3+}-Fe^{3+} \) coupling ( \( -4.8 J.mole^{-1} \) ) is predominant (Table 5).
DISCUSSION
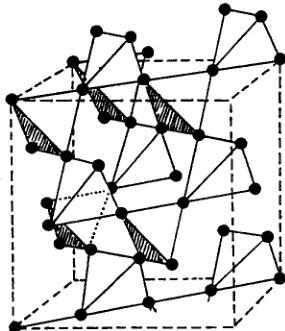
This magnetic structure sheds light on some aspects of the non trivial magnetic behaviour of the modified pyrochlore family \( [1-5] \) . In this structure, the basic unit is formed by a tetrahedron of corner sharing octahedra, the corners of the tetrahedron being occupied by the bivalent and trivalent magnetic ions (Fig. 4). This cationic organization implies triangles of metallic ions and, therefore, a topological spin frustration \( [13] \) . It
Table 4. Refined magnetic moments at 4.2 K (in \( \mu \) B).
| Atom (x, y, z) | Mx | My | Mz | M |
| Fe3+ (0 00) | 3.86 (7) | 1.00 (9) | 1.07 (10) | 4.13 (8) |
| Fe2+ (0.1975, 1/4, 0.2682) | 0 | 3.12 (9) | 0 | 3.12 (9) |
Table 5. Partial magnetic dipolar energies in \( NH_{4}Fe^{II} \) \( Fe^{III}F_{6} \) . \( E_{M_{1},M_{2}} \) represents the energy of the \( M_{1} \) ion in a \( M_{2} \) surrounding.
| M1-M2 | EM1-M2(J·m−1) |
| Fe3+-Fe3+ | -4.80 |
| Fe2+-Fe2+ | -2.07 |
| Fe2+-Fe3+ | -3.55 |
| Fe3+-Fe2+ | -3.24 |

Fig. 3. (00 1) Projection of the magnetic structure of \( NH_{4}Fe_{2}F_{6} \) . Iron atoms have the same symbolism that in Fig. 2. + and - indicates the orientation of the moment respective to the projection plane.

Fig. 4. Tetrahedral magnetic sublattice of 3d ions in the pyrochlore structure (from (4)).
was assumed that this property and the randomness of the distribution of the 3d ions on their sites (which leads to the Fd3m cubic symmetry) were sufficient to lead to a spin glass like behaviour [2–3]. However, some recent experimental work [4, 5] using neutron diffraction and very low field susceptibility reveals fundamental differences from the classical spin glasses, particularly for the instability of the field cooled susceptibility curves. Actually, the results are better analyzed in terms of clusters and domains.
In the case of \( NH_{4}Fe_{2}F_{6} \) , the influence of randomness on the magnetic properties disappears and only topological frustration effects remain. This is the very situation predicted by Villain [3]: a canted antiferromagnet structure must appear when a 2:2 order arises at the corners of the cationic tetrahedron. In \( NH_{4}Fe^{III}Fe^{III}F_{6} \) , canting appears only on the \( Fe^{3+} \) sublattice; \( Fe^{2+} \) can be highly anisotropic, and the b direction of the \( Fe^{2+} \) moments is probably not due only to dipolar interactions, but there might be an influence of dipolar interactions on the \( Fe^{3+} \) system. It may be assumed that \( Fe^{3+} \) coupling governs the magnetic behaviour of this compound, owing to both the strong \( d^{5}-d^{5} \) magnetic exchange and dipolar energies. In the ordered cationic tetrahedron, when the antiferromagnetic order between \( Fe^{3+} \) ions is established, \( Fe^{2+} \) ions cannot simultaneously satisfy antiferromagnetic interactions (14, 15) with both \( Fe^{3+} \) of the triangle. It is then frustrated. Consequently, it may be thought that \( Fe^{2+}-Fe^{3+} \) magnetic interactions are weak and are responsible for the low Neel temperature of this compound.
This study allows the respective influence of the frustrating topology and of the cationic randomness on the spin glass behaviour in the pyrochlore family to be clarified. If there is cationic order, magnetic frustration occurs without any spin glass characteristics. Cationic disorder is necessary to induce this property.
REFERENCES
- D. Babel, Z. Anorg, Allgem. Che., 387, 161 (1972).
1a. G. Ferey, R. de Pape & B. Boucher, Acta Cryst. B34, 1084 (1978).
-
W. Kurtz & S. Roth, Physica 86–88 B. 715 (1977).
-
J. Villain, Z. Physik B33, 31 (1979) and private communication.
-
L. Bevaart, P.M.H.L Tegelaar, A.J. Van Duyneveldt & M. Steiner, Phys. Rev. B26, 6150 (1982).
-
M. Alba, J. Hamman, C. Jacoboni & C. Pappa, Phys. Letters 89A(8), 423 (1982).
-
G. Ferey, M. Leblanc & R. de Pape, J. Solid State Chem. 40, 1 (1980) and references therein.
-
H.M. Rietveld, J. Applied Cryst. 2, 65 (1969).
-
A.W. Hewat, Harwell Report AERE – R 7350 (1973).
-
G. Bacon, Neutron Diffraction, Oxford Clarendon Press (1975).
-
R.E. Watson & J. Freeman, Acta Cryst. 14, 27 (1961).
-
A.W. Hewat, Acta Cryst. A35, 248 (1979).
-
E.F. Bertaut, in Magnetism III Rado et Shull Ed., 149 (1963).
-
G. Toulouse, Comm. Phys. 2, 115 (1977).
-
J.B. Goodenough, Magnetism and the chemical Bond, Interscience, J. Wiley and Sons, New York (1963).
-
J. Kanamori, J. Phys. Chem solids 10, 87 (1959).