| Transition Temperature | 2.4 K |
|---|---|
| Experiment Temperature | 1.3 K |
| Parent Space Group | Pm-3m (#221) |
| Magnetic Space Group | Camca (#64.479) |
| Magnetic Point Group | mmm1' (8.2.25) |
| Lattice Parameters | 16.55840 16.55840 8.27920 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1016/0304-8853(85)90382-8 |
| Reference | J. Effantin, J. Rossat-Mignod, P. Burlet, H. Bartholin, S. Kunii and T. Kasuya, Journal of Magnetism and Magnetic Materials (1985) 47-48 145-148. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Ce1_1 | Ce | -0.2 | 0.2 | 0.0 | 0.28 |
| Ce1_2 | Ce | -0.2 | -0.2 | 0.0 | 0.28 |
Title
MAGNETIC PHASE DIAGRAM OF CeB\(_{6}\)
Authors
J.M. EFFANTIN, J. ROSSAT-MIGNOD, P. BURLET DN/DRF, Centre d'Etudes Nucléaires de Grenoble, 85 X, 38041 Grenoble cedex, France
H. BARTHOLIN Lab. P.C., Université de Toulon, 83130 La Garde, France
S. KUNII and T. KASUYA Department of Physics, Tohoku University, Sendai, Japan
Materials Studied
CeB\(_{6}\) (Cerium hexaboride), specifically single crystals with enriched \(^{11}\)B.
Key Information
- Crystal structure / space group: CsCl structure.
- Magnetic ordering type and temperature:
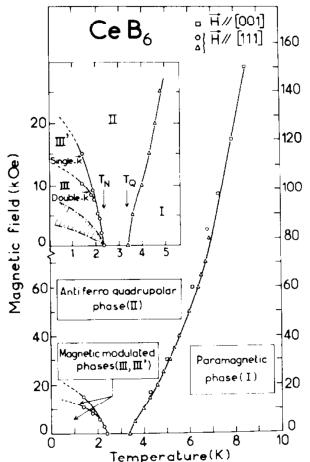
- Phase I (Paramagnetic): \(T > T_{Q} = 3.2\) K (in zero field). Exhibits logarithmic electrical resistivity, dense Kondo compound behavior.
- Phase II (Antiferroquadrupolar (AFQ) order): \(T_{N} = 2.4 \, K < T < T_{Q}\) (in zero field). No magnetic ordering in zero field, but magnetic field induces an antiferromagnetic component.
- Phase III (Magnetic ordering): \(T < T_{N}\). Double-k commensurate magnetic structure.
- Phase III': An additional phase observed when a magnetic field is applied along [111], corresponding to a collinear k-k' structure.
- Propagation vector(s):
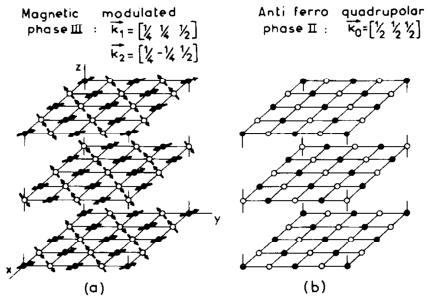
- Phase III (Magnetic): \( \kappa_{1} = [1/4 \bar{1}/4 1/2] \), \( \kappa_{2} = [1/4 1/4 1/2] \), \( \kappa_{1}^{\prime} = [1/4 1/4 0] \) and \( \kappa_{2}^{\prime} = [1/4 \bar{1}/4 0] \). This is clarified as a double-k commensurate structure of wave vector \( k = [1/4\ 1/4\ 1/2] \).
- Phase II (AFQ): \( \boldsymbol{k}_{0} = [1/2\ 1/2\ 1/2] \).
- Magnetic moments:
- Phase III (T=1.3 K, zero field, powder): Amplitudes of modulation \( A_{k}=(0.20\pm0.04)\mu_{\mathrm{B}} \) and \( A_{k^{\prime}}=(0.18\pm0.04)\mu_{\mathrm{B}} \). Ordered moment \( m_{0}=(0.28\pm0.06)\mu_{\mathrm{B}} \).
- Phase III' (T=1.5 K, H=10 kOe, H along [111]): Amplitudes \( A_{k_{2}}=(0.25\pm0.03)\mu_{\mathrm{B}} \) and \( A_{k_{2}^{\prime}}=(0.12\pm0.03)\mu_{\mathrm{B}} \). Antiferromagnetic components of ordered moments: \( (0.26\pm0.05)\mu_{\mathrm{B}} \) and \( (0.08\pm0.05)\mu_{\mathrm{B}} \).
- Phase II (induced AF component): Less than \( 0.07\mu_{B} \) in zero field. Less than \( 0.05\mu_{B} \) for other symmetry points under field.
- Saturation moment (high field): About \( 1\mu_{B} \) at H = 150 kOe and T = 0.6 K.
- Lattice parameters: Not available.
- Any other critical measured values:
- Kondo temperature \( T_{\mathbf{K}} \approx 1 \) K.
- \( \Gamma_{8} \) ground state separated by >500 K from \( \Gamma_{7} \) excited level.
- Maximum magnetic field investigated: H = 200 kOe.
- Temperature range investigated: T = 1.3 K to 55 K.
- Field-induced AF component in Phase II saturates at H = 60 kOe (T = 2.6 K) and disappears at T = 6.3 K (H = 84 kOe).
Synthesis Method
Single crystals of CeB\(_{6}\) with enriched \(^{11}\)B were prepared by the floating zone method.
Abstract
The magnetic field–temperature phase diagram of CeB\(_{6}\) has been investigated up to H = 200 kOe by high field magnetization and neutron scattering experiments.
We establish that CeB\(_{6}\) develops first an antiferroquadrupolar structure before to undergo a magnetic ordering. The magnetic ordering is a double-k commensurate structure of wave vector \( k = [1/4\ 1/4\ 1/2] \). This complex ordering is the consequence of the antiferroquadrupolar order of wave vector \( k = [1/2\ 1/2\ 1/2] \).
Main Content Summary
Cerium hexaboride (CeB\(_{6}\)) is a dense Kondo compound crystallizing in a CsCl structure, known for its unusual magnetic phase diagram with three distinct phases. Phase I is paramagnetic with Kondo behavior (\(T_{\mathbf{K}} \approx 1\) K). Phase II, existing between \(T_{N}\) and \(T_{Q}\) (3.2 K in zero field), shows no magnetic ordering in zero field but its transition temperature is strongly field-dependent. Phase III, below \(T_{N}\) (2.4 K in zero field), exhibits a complex magnetic ordering described by multiple wave vectors. The study aimed to clarify the nature and structure of phases II and III, and the interplay between the dense Kondo state and f-f interactions.
Experimental investigations involved high-field magnetization measurements up to 200 kOe and neutron scattering experiments on single crystals of \(^{11}\)B-enriched CeB\(_{6}\). Magnetization curves along the [001] direction helped determine the I/II phase transition line. Powder diffraction patterns in zero field were used to accurately determine the ordered moment values in phase III, yielding \(m_{0}=(0.28\pm0.06)\mu_{\mathrm{B}}\) for the primary wave vectors \(k_{1}=\langle1/4\ 1/4\ 1/2\rangle\) and \(k^{\prime}_{1}=\langle1/4\ 1/4\ 0\rangle\). An additional phase, III', was observed with a field along [111], characterized by a collinear k-k' structure and distinct moment values on different cerium sublattices.
Crucially, neutron diffraction experiments in phase II under an applied magnetic field (H = 76 kOe along \( [\overline{1}\overline{1}1] \)) revealed an induced antiferromagnetic component with a wave vector \( \boldsymbol{k}_{0} = [1/2\ 1/2\ 1/2] \). This signal was absent in zero field, saturated at higher fields, and disappeared at higher temperatures, consistent with previous NMR findings. This field-induced ordering in phase II strongly suggests the presence of an antiferroquadrupolar (AFQ) order at \(T_{Q}=3.2\ K\), where the \( \Gamma_{8} \) ground state splits into two doublets with alternating quadrupolar moments.
The magnetic ordering in phase III is interpreted as a double-k commensurate structure, which is a direct consequence of the underlying AFQ order in phase II. The AFQ ordering with \( \boldsymbol{k}_{0}=[1/2\ 1/2\ 1/2] \) makes the previously identified four wave vectors effectively reduce to a double-k structure, accounting for the second-order nature of the magnetic transition. The magnetic moments, with a value of \(m_{0}=(0.28\pm0.06)\mu_{B}\), lie within the (001) plane in a non-collinear arrangement, with moments on the A-sublattice along [110] and on the B-sublattice along [110]. The \( \Gamma_{8} \) ground state, confirmed by other studies, plays a significant role, with the Kondo effect reducing the ordered moments.
Conclusion
The high field magnetization and neutron scattering experiments, reported in this paper, have allowed us to clarify the unusual magnetic phase diagram of CeB\(_{6}\). The main phase of the phase diagram is actually phase II which corresponds to an antiferroquadrupolar ordering of wave vector \( k = [1/2\ 1/2\ 1/2] \). At lower temperatures, CeB\(_{6}\) develops a magnetic ordering, corresponding to phase III, with a double-k commensurate structure of wave vector \( k = [1/4\ 1/4\ 1/2] \). In phase I, CeB\(_{6}\) exhibits a typical dense Kondo behaviour which is certainly enhanced by the larger degeneracy of the \( \Gamma_{8} \) ground state. Therefore the magnetic properties of CeB\(_{6}\) are dominated by the interplay of single site virtual fluctuations of Kondo type ( \( T_{K} \) ) and of quadrupolar ( \( T_{Q} \) ) and magnetic ( \( T_{N} \) ) intersite interactions. In CeB\(_{6}\), \( T_{K} \) and \( T_{Q} \) are of the same order of magnitude giving rise to a Kondo reduced AFQ ordering, but they dominate \( T_{N} \). This is particularly demonstrated by the huge increase of \( T_{Q} \) and of the specific heat anomaly with the applied field. Such a behaviour can be hardly understood with a classical mean field treatment within a \( \Gamma_{8} \) ground state. We believe that the dense Kondo state prevents the indirect interactions to establish the AFQ ordering, as it does for the magnetic ordering when only a spin S = 1/2 doublet is considered. So in zero field \( T_{Q} \) and the ordered quadrupolar moment are reduced; but with increasing magnetic field the Kondo state is progressively suppressed and so the AFQ ordering can develop at higher temperatures.
MAGNETIC PHASE DIAGRAM OF C \( \epsilon \) B \( _{6} \)
J.M. EFFANTIN, J. ROSSAT-MIGNOD, P. BURLET
DN/DRF, Centre d'Etudes Nucléaires de Grenoble, 85 X, 38041 Grenoble cedex, France
H. BARTHOLIN
Lab. P.C., Université de Toulon, 83130 La Garde, France
S. KUNII and T. KASUYA
Department of Physics, Tohoku University, Sendai, Japan
The magnetic field–temperature phase diagram of \( CeB_{6} \) has been investigated up to H = 200 kOe by high field magnetization and neutron scattering experiments.
We establish that \( CeB_{6} \) develops first an antiferroquadrupolar structure before to undergo a magnetic ordering. The magnetic ordering is a double-k commensurate structure of wave vector \( k = [1/4\ 1/4\ 1/2] \) . This complex ordering is the consequence of the antifcrroquadrupolar order of wave vector \( k = [1/2\ 1/2\ 1/2] \) .
1. Introduction
Cerium hexaboride, a monovalent metal, crystallizes in a CsCl structure in which boron octaedra replace Cl atoms. The interaction between the 4f electron of a trivalent cerium atom, and the electrons of the conduction band, with a 5d character on cerium sites, gives rise to a typical dense Kondo compound behaviour and to a very unusual magnetic phase diagram [1]. Three distinct phases have been reported:
i) in phase I (\(T > T_{Q} = 3.2\) K in zero field) electrical resistivity exhibits a logarithmic behaviour with \(T_{\mathbf{K}} \approx 1\) K;
ii) in phase II ( \( T_{N} = 2.4 \, K < T < T_{Q} \) in zero field) NMR [2] and neutron experiments [3,4] give no evidence for any magnetic ordering in zero field, while the I/II transition temperature is strongly dependent on the magnetic field;
iii) in phase III \( (T < T_{N}) \) the magnetic ordering corresponds to a modulation by four wave vectors belonging to two different starts [5,3]: \( \kappa_{1} = [1/4 \bar{1}/4 1/2] \) , \( \kappa_{2} = [1/4 1/4 1/2] \) , \( \kappa_{1}^{\prime} = [1/4 1/4 0] \) and \( \kappa_{2}^{\prime} = [1/4 \bar{1}/4 0] \) , but surprisingly the II/III transition is second order.
High field magnetic measurements and a neutron study have been undertaken to determine the nature and the structure of phases II and III, and to identify the respective contribution of the dense Kondo state and of unconventional f-f interactions in the behaviour of \( CeB_{6} \) .
2. Experimental
Single crystals of \( CeB_{6} \) with enriched \( {}^{11}B \) were prepared by the floating zone method [6].
Neutron measurements were carried out at the Siloe reactor at C.E.N.-Grenoble. A filtered neutron wavelength of 2.4 Å, from a graphite monochromator was used for a power experiment on the DN1 three-axis spectrometer. A wavelength of 0.99 Å from a copper monochromator was used for the single crystal experiment on the DN3 two-axis spectrometer, equipped with a moving up counter arm; the single crystal was placed in a cryomagnetic system.
Magnetization measurements were carried out at the S.N.C.I. by an extraction method.
3. Experimental results
3.1. Magnetization results
Magnetization curves for a field along the [001] direction were collected up to 200 kOe between T = 4.2
and 55 K. The line of transition between phase I and phase II, determined from the first inflexion of the magnetization curve, is reported in fig. 1.
3.2. Phase III
In order to determine the ordered moment value in phase III from measurements avoiding any extinction effects, two powder diffraction patterns have been recorded in zero field at T=1.3 and 4.2 K. As the directions of the magnetic modulations have been unambiguously determined by previous single crystal measurements [3], we collected data only for the magnetic peaks \( [1/4\ 1/4\ 1/2] \) and \( [1/4\ 1/4\ 0] \) in order to compensate the weakness of the signal by a longer counting time.
The amplitudes of the modulation of wave vectors \( k_{1}=\langle1/4\ 1/4\ 1/2\rangle \) and \( k^{\prime}_{1}=\langle1/4\ 1/4\ 0\rangle \) were found equal within the experimental accuracy. The normalization to the intensity of the [100] and [110] nuclear peaks gives a value of the magnetic amplitude at T=1.3 K: \( A_{k}=(0.20\pm0.04)\mu_{\mathrm{B}} \) and \( A_{k^{\prime}}=(0.18\pm0.04)\mu_{\mathrm{B}} \) . For the structure of phase III proposed in section 4.3, this gives a rather low value of the ordered moment \( m_{0}=(0.28\pm0.06)\mu_{\mathrm{B}} \) .
These powder experiments allow us also to correct from extinction effects (which appear in fact to be very

Fig. 1. Magnetic phase diagram of \( CeB_{6} \) obtained for a magnetic field applied along [001] and [111].
small) our previous data obtained on the single crystal. With field applied along [111] an additional phase III', corresponding to a collinear \( k-k' \) structure, is obtained [3]. It contains two kinds of cerium atoms with different moment values. In this phase III', the amplitude of the modulation by \( k_{2}=[1/4\ \overline{1}/4\ 1/2] \) and \( k_{2}^{\prime}=[1/4\ \overline{1}/4\ 0] \) are respectively \( A_{k_{2}}=(0.25\pm0.03)\mu_{\mathrm{B}} \) and \( A_{k_{2}^{\prime}}=(0.12\pm0.03)\mu_{\mathrm{B}} \) at \( T=1.5\ K \) and \( H=10\ kOe \) ; then in the magnetic structure proposed in section 4.3 the antiferromagnetic component of the ordered moments has two distinct values: \( (0.26\pm0.05)\mu_{\mathrm{B}} \) and \( (0.08\pm0.05)\mu_{\mathrm{B}} \) .
3.3. Phase II
Previous neutron diffraction results in zero field [3] did not succeed, in phase II, to give evidence for any magnetic ordering corresponding to a modulation with an amplitude larger than \( 0.07\mu_{B} \) . Nevertheless NMR measurements [2], reveal that at the phase I/phase II transition, a simple line splitting occurs which decreases with decreasing field, indicating in phase II the existence of an induced ordering.
A magnetic field H = 76 kOe was applied along the vertical \( [\overline{1}\overline{1}1] \) direction of the crystal; scans along various symmetry directions and intensity measurements at high symmetry points of the Brillouin zone were performed at T = 1.3 K. The comparison with the same measurements at the same field in the paramagnetic phase indicates that an additional intensity exists for the scattering vectors \( [1/2\ \overline{1}/2\ \overline{1}/2] \) , \( [3/2\ 3/2\ 1/2] \) and \( [3/2\ \overline{3}/2\ \overline{5}/2] \) giving evidence for an ordering with a wave vector \( \boldsymbol{k}_{0} = [1/2\ 1/2\ 1/2] \) . For the other symmetry points the magnetic amplitude, if it exists, was estimated to be less than \( 0.05\mu_{B} \) .
The observed signal at \( Q - [3/2 \ \overline{3}/2 \ \overline{5}/2] \) decreases with decreasing field and disappears in zero field, it saturates at about H = 60 kOe at T = 2.6 K and disappears in increasing temperature at T = 6.3 K for H = 84 kOe. This is in excellent agreement with the behaviour found by NMR measurements. So in phase II the magnetic field induces an antiferromagnetic component with a wave vector \( k_{0} = [1/2 \ 1/2 \ 1/2] \) .
4. Discussion
4.1. Nature of the paramagnetic ground state
The nature of the 4f ground state level in \( CeB_{6} \) was a controversial subject. Nevertheless recent neutron inelastic scattering [7] and specific heat [8] measurements confirmed the previously proposed [9] level scheme with
a \( \Gamma_{8} \) ground state separated by more than 500 K from the \( \Gamma_{7} \) excited level. Then \( CeB_{6} \) is the first example of a Kondo effect within a \( \Gamma_{8} \) quartet and actually this effect strongly reduces, at low temperatures, the ordered moment in phase III ( \( m_{0} \approx 0.28\mu_{B} \) ) and the saturation value reached in high field (about \( 1\mu_{B} \) at H = 150 kOe and T = 0.6 K) [11].
4.2. Quadrupolar ordering
The evidence in phase II of an antiferromagnetic component with a wave-vector \( \boldsymbol{k}_{0}=[1/2\ 1/2\ 1/2] \) induced by a magnetic field reveals the existence of two kinds of cerium ions, which differenciate in zero field only by the value of their magnetic susceptibility. Such a result can only be accounted for if an antiferroquadrupolar (AFQ) order builds up at the phase II–phase III transition. So at \( T_{Q}=3.2\ K \) the \( \Gamma_{8} \) ground state splits into two doublets characterized by quadrupolar moments Q and -Q and exhibiting an antisotropic magnetic susceptibility. The ordering consists of an alternating sequence, along the three cubic axes, of A and B cerium ions with quadrupolar moments \( \langle Q\rangle_{A}=Q \) and \( \langle Q\rangle_{B}=-Q \) (fig. 2b).
4.3. Magnetic ordering
The moment distribution \( m(\boldsymbol{R}_{n}) \) in phase III is given by adding the four Fourier components:
\[ \boldsymbol{m}(\boldsymbol{R}_{n})=\sum_{\substack{\boldsymbol{k}=\pm\boldsymbol{k}_{1},\pm\boldsymbol{k}_{2},\\ \pm\boldsymbol{k}_{1}^{\prime},\pm\boldsymbol{k}_{2}^{\prime}.}}\boldsymbol{m}_{\boldsymbol{k}}\mathrm{e}^{\mathrm{i}\boldsymbol{k}\cdot\boldsymbol{R}_{n}}, \]
where \( \boldsymbol{m}_{k}=(A_{k}/2)\mathrm{e}^{\mathrm{i}\phi_{k}}\boldsymbol{u}_{k},\boldsymbol{u}_{k} \) are unit vectors giving the polarization of the magnetic modulation and have

Fig. 2. (a) Magnetic structure of the phase III; (b) antiferroquadrupolar structure of phase II.
been found [3] to be \( u_{k_{1}}=1/\sqrt{2} \) [110] for \( k_{1} \) and \( k_{1}^{\prime} \) and \( u_{k_{2}}=1/\sqrt{2} \) [110] for \( k_{2} \) and \( k_{2}^{\prime} \) , the amplitudes \( A_{k} \) are equal [3] for the four involved wave vectors.
Only one magnetic structure is consistent with the AFQ ordering of wave vector \( \boldsymbol{k}_{0}=[1/2\ 1/2\ 2] \) . It corresponds to the following combination of Fourier components (fig. 2a):
\[ \begin{aligned}m(\boldsymbol{R}_{n})=&A_{k}\left\{\left[\cos(\boldsymbol{k}_{1}\cdot\boldsymbol{R}_{n}+\pi/4)\right.\right.\\&\left.\left.\quad+\cos(\boldsymbol{k}_{1}^{\prime}\cdot\boldsymbol{R}_{n}-\pi/4)\right]\boldsymbol{u}_{k_{1}}\right.\\&+\left[\cos(\boldsymbol{k}_{2}\cdot\boldsymbol{R}_{n}+3\pi/4)\right.\\&\left.\left.+\cos(\boldsymbol{k}_{2}^{\prime}\cdot\boldsymbol{R}_{n}+\pi/4)\right]\boldsymbol{u}_{k_{2}}\right\}.\end{aligned} \]
In such a model the magnetic moments have a value \( m_{0}=A_{k}\sqrt{2}=(0.28\pm0.06)\mu_{B} \) and lie within the (001) plane with a non-collinear arrangement; the magnetic moments of the two cerium sublattices of the AFQ structure order along their own directions. The ordering is described by the wave vectors \( k_{1} \) and \( k_{1}^{\prime} \) for cerium on the A-sublattice ( \( m_{A} \) along the [110] direction) and by wave vectors \( k_{2} \) and \( k_{2}^{\prime} \) for the B-sublattice ( \( m_{B} \) along the [110] direction). Actually the AFQ ordering makes the wave vectors \( k_{1}=[1/4\ 1/4\ 1/2] \) and \( k_{2}=1/4\ \bar{1}/4\ 1/2 \) equivalent to \( k_{1}^{\prime}=[1/4\ 1/4\ 0] \) and \( k_{2}^{\prime}=[1/4\ \bar{1}/4\ 0] \) , respectively, because \( k_{1}^{\prime}=k_{1}+k_{0} \) and \( k_{2}^{\prime}=k_{2}+k_{0} \) . Then the magnetic ordering in \( CeB_{6} \) corresponds only to a double-k structure which accounts for the second-order character of the magnetic phase transition. A similar double-k structure, associated with the wave vectors \( k_{1} \) and \( k_{2} \) , has also been found in \( PrB_{6} \) [10]. Such a structure is believed to arise from the anisotropic part of the indirect f-f interaction which is expected to be more important for light rare earths.
When a magnetic field is applied along the \( [1\bar{1}1] \) direction, involving a large field component in the plane of the moments, a new phase III' is reached corresponding to a single-k structure. In this phase the antiferromagnetic components are perpendicular to the field; on one sublattice they have the same value as in phase III, but on the other sublattice the moment value is reduced because the moments are flipped away from the easy axis defined by the quadrupolar ordering.
5. Conclusion
The high field magnetization and neutron scattering experiments, reported in this paper, have allowed us to clarify the unusual magnetic phase diagram of \( CeB_{6} \) . The main phase of the phase diagram is actually phase II which corresponds to an antiferroquadrupolar order.
ing of wave vector \( k = [1/2\ 1/2\ 1/2] \) . At lower temperatures, \( CeB_{6} \) develops a magnetic ordering, corresponding to phase III, with a double-k commensurate structure of wave vector \( k = [1/4\ 1/4\ 1/2] \) . In phase I, \( CeB_{6} \) exhibits a typical dense Kondo behaviour which is certainly enhanced by the larger degeneracy of the \( \Gamma_{8} \) ground state. Therefore the magnetic properties of \( CeB_{6} \) are dominated by the interplay of single site virtual fluctuations of Kondo type ( \( T_{K} \) ) and of quadrupolar ( \( T_{Q} \) ) and magnetic ( \( T_{N} \) ) intersite interactions. In \( CeB_{6} \) , \( T_{K} \) and \( T_{Q} \) are of the same order of magnitude giving rise to a Kondo reduced AFQ ordering, but they dominate \( T_{N} \) . This is particularly demonstrated by the huge increase of \( T_{Q} \) and of the specific heat anomaly with the applied field. Such a behaviour can be hardly understood with a classical mean field treatment within a \( \Gamma_{8} \) ground state. We believe that the dense Kondo state prevents the indirect interactions to establish the AFQ ordering, as it does for the magnetic ordering when only a spin S = 1/2 doublet is considered. So in zero field \( T_{Q} \) and the ordered quadrupolar moment are reduced; but with increasing magnetic field the Kondo state is progressively suppressed and so the AFQ ordering can develop at higher temperatures.
References
[1] T. Kasuya, K. Takegahara, Y. Aoki, T. Suzuki, S. Kunii, M. Sera, N. Sato, T. Fujita, T. Goto, A. Tamaki and T.
Komatsubara, in: Proc. Intern. Conf. on Valence Instabilities, eds. P. Wachter and H. Boppart (North-Holland, Amsterdam, 1982) p. 359.
[2] M. Kawakami, K. Mizuno, S. Kunii, T. Kasuya, H. Enokiya and K. Kume, J. Magn. Magn. Mat. 30 (1982) 201. M. Takigawa, H. Yasuoka, T. Tanaka and Y. Ishizawa, J. Phys. Soc. Japan 52 (1983) 728.
[3] J.M. Effantin, P. Burlet, J. Rossat-Mignod, S. Kunii and T. Kasuya, in: Proc. Intern. Conf. on Valence Instabilities, ed. P. Wachter (North-Holland, Amsterdam, 1982) p. 559.
[4] S. Horn, F. Steglich, M. Loewenhaupt, H. Scheuer. W. Felsch and K. Winzer, Z. Phys. B42 (1981) 125.
[5] J. Rossat-Mignod, P. Burlet, T. Kasuya, S. Kunii and T. Komatsubara, Solid State Commun. 39 (1981) 471.
[6] M. Kawakami, S. Kunii, T. Komatsubara and T. Kasuya, Solid State Commun. 36 (1980) 435.
[7] M. Loewenhaupt and J.M. Carpenter, I.P.N.S. Progr. Rep., Argonne (1983) p. 132.
[8] Y. Peysson, C. Ayache, B. Salce, J. Rossat-Mignod, S. Kunii and T. Kasuya. J. Magn. Magn. Mat. 47&48 (1985) 63.
[9] J. Rossat-Mignod, P. Burlet, S. Quezel, J.M. Effantin, D. Delacôte, H. Bartholin, O. Vogt and D. Ravot, J. Magn. Magn. Mat. 31–34 (1983) 402.
[10] J.M. Effantin, P. Burlet, J. Rossat-Mignoud, S. Kunii and T. Kasuya, to be published.
[11] N. Sato, T. Komatsubara, S. Kunii, T. Suzuki and T. Kasuya, Valence Fluctuations in Solids, eds. L.M. Falicov, W. Hanke and M.B. Maple (North-Holland, Amsterdam, 1981) p. 259.