| Transition Temperature | 3.2 K |
|---|---|
| Experiment Temperature | 1.2 K |
| Parent Space Group | Pm-3m (#221) |
| Magnetic Space Group | PIa-3 (#205.36) |
| Magnetic Point Group | m-31' (29.2.110) |
| Lattice Parameters | 6.75400 6.75400 6.75400 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1016/0038-1098(72)90586-8 |
| Reference | R. Chamard-Bois, N. Nhung, J. Yakinthos, M. Wintenberger, Solid State Communications (1972) 10 685 - 689 |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Ho1 | Ho | 3. | 3. | 3. | 5.20 |
Title
STRUCTURES MAGNETIQUES DES COMPOSES EQUIATOMIQUES TERRES RARES-RHODIUM T Rh (T = Dy, Ho, Er)
Authors
R. Chamard-Bois, Nguyen van Nhung, J. Yakinthos, et Mme M. Wintenberger Laboratoire de Diffraction Neutronique, CEN–G, Cedex 85, 38–Grenoble-Gare, France
Materials Studied
- DyRh
- HoRh
- ErRh
- General composition: TRh (where T = Dy, Ho, Er)
- Mentioned for context: TbRh, FeRh, DyCu
Key Information
- Crystal structure / space group: Cubique de type CsCl; Pm3m.
- Magnetic ordering type and temperature:
- DyRh: Ferromagnetic below T_C = 4.8 K.
- HoRh: Antiferromagnetic below T_N = 3.2 K.
- ErRh: Antiferromagnetic below T_N = 3.3 K.
- Propagation vector(s):
- For ErRh and HoRh: \( k = [0, 0, \frac{1}{2}] \)
- Magnetic moments:
- DyRh: \( \mu_{Dy} = 7,1 \pm 1 \mu_{B} \) (assuming Rh moment is zero).
- HoRh: \( \mu_{Ho} = 5,2 \pm 0.3 \mu_{B} \) (assuming Rh moment is zero).
- ErRh: \( \mu_{Er} = 6,1 \pm 0,3 \mu_{B} \) (assuming Rh moment is zero).
- Possible Rh moment in DyRh: ~0.5 \( \mu_{B} \) (estimated, not definitively measured).
- Lattice parameters:
- DyRh: \( a = 3,394 \pm 0,005 \) Å
- HoRh: \( a = 3,377 \pm 0,005 \) Å
- ErRh: \( a = 3,361 \pm 0,005 \) Å
- (For comparison, Dwight's values: DyRh: \( a = 3,403 \pm 0,002 \) Å, HoRh: \( a = 3,388 \pm 0,002 \) Å, ErRh: \( a = 3,372 \pm 0,002 \) Å)
- Any other critical measured values:
- Neutron scattering lengths: \( b_{Dy} = 1,69 \times 10^{-12} \) cm, \( b_{Rh} = 0,59 \times 10^{-12} \) cm, \( b_{Ho} = 0,85 \times 10^{-12} \) cm.
- R-factor for HoRh: ~4%.
- Dipolar anisotropy for HoRh (collinear case): \( \Delta W = 2,83 \times 10^{-16} \) erg/atome ( \( W_{ox} = -0.945 \times 10^{-16} \) erg/atome).
Synthesis Method
The alloys were prepared by melting the constituent elements in a high-frequency furnace equipped with a horizontal copper boat cooled by water circulation. To ensure effective quenching, small quantities of the product were used. The purity of the compounds was controlled by X-ray diffraction using the Debye–Scherrer method.
Abstract
Neutron diffraction on powdered samples shows that the antiferromagnetic structures of ErRh and HoRh may be described by a propagation vector \( k\ (0\ 0\frac{1}{2}) \) or by some related multiaxial configurations. The rare earth magnetic moments in these compounds and in ferromagnetic DyRh are evaluated.
Main Content Summary
The paper investigates the magnetic structures of equiatomic rare earth-rhodium compounds (TRh, where T = Dy, Ho, Er) using neutron diffraction on powdered samples. These compounds crystallize in the cubic CsCl structure (Pm3m). Previous studies indicated that TbRh and DyRh are ferromagnetic, while HoRh and ErRh are antiferromagnetic below their respective ordering temperatures.
The samples were prepared by melting constituent elements in a high-frequency furnace, and their purity was verified by X-ray diffraction. Lattice parameters were measured for DyRh (\( a = 3.394 \pm 0.005 \) Å), HoRh (\( a = 3.377 \pm 0.005 \) Å), and ErRh (\( a = 3.361 \pm 0.005 \) Å), which were slightly lower than previously reported values.
For DyRh, neutron diffraction at 1.2 K confirmed ferromagnetic ordering, with a calculated dysprosium magnetic moment of \( 7.1 \pm 1 \mu_B \). The possibility of rhodium polarization was considered, but due to the limitations of powder diffraction and measurement precision, it could not be definitively confirmed, suggesting that polarized neutron studies on single crystals would be necessary.
For HoRh, neutron diffraction at 1.2 K revealed an antiferromagnetic structure characterized by a propagation vector \( k = [0, 0, \frac{1}{2}] \). While a collinear model with spins perpendicular to the z-axis provided a good fit to the data, yielding a holmium moment of \( 5.2 \pm 0.3 \mu_B \), crystal field studies suggested that moments aligned along a ternary axis would be energetically more favorable. Consequently, the authors proposed and discussed two distinct non-collinear, multiaxial configurations (one cubic and one monoclinic) that are consistent with the observed diffraction pattern and have the same isotropic magnetic coupling and dipolar energy as the collinear model, aligning with the crystal field predictions.
Similarly, ErRh exhibited an antiferromagnetic structure at 1.2 K with the same propagation vector \( k = [0, 0, \frac{1}{2}] \). The erbium magnetic moment was determined to be \( 6.1 \pm 0.3 \mu_B \). This value is in agreement with crystal field studies, which favor a spin direction along a quaternary axis, compatible with a collinear configuration where moments lie within the xy plane.
Conclusion
Neutron diffraction on powdered samples shows that the antiferromagnetic structures of ErRh and HoRh may be described by a propagation vector \( k\ (0\ 0\frac{1}{2}) \) or by some related multiaxial configurations. The rare earth magnetic moments in these compounds and in ferromagnetic DyRh are evaluated.
STRUCTURES MAGNETIQUES DES COMPOSES EQUIATOMIQUES TERRES RARES-RHODIUM
T Rh (T = Dy, Ho, Er)
R. Chamard-Bois, Nguyen van Nhung, J. Yakinthos, et Mme M. Wintenberger
Laboratoire de Diffraction Neutronique, CEN–G, Cedex 85, 38–Grenoble-Gare, France
(Reçu le 14 janvier 1972 par E.F. Bertaut)
Par diffraction neutronique sur poudre, on observe des structures antiferromagnétiques correspondant au vecteur de propagation \( (0\ 0\frac{1}{2}) \) pour ErRh et HoRh; on discute les configurations non colinéaires possibles. On évalue les moments pour ces deux composés et pour DyRh ferromagnétique.
1. INTRODUCTION
LES COMPOSÉS TRh dans lesquels T = terres rares allant du samarium au lutécium cristallisent dans la structure cubique de type CsCl; \( ^{1} \) cette structure appartient au groupe Pm3m. Les atomes de terres rares et de rhodium occupent deux sites de même symétrie. Les propriétés magnétiques de certains de ces alliages ont été étudiées récemment; \( ^{2} \) alors que TbRh et DyRh sont ferromagnétiques au-dessous de 19,2 K et 4,8 K, HoRh et ErRh deviennent antiferromagnétiques au-dessous de 3,2 et 3,3 K respectivement.
2. PREPARATION
Pour les besoins de la diffraction neutronique, nous avons préparé ces alliages par fusion des éléments constituants dans un four haute fréquence à barquette horizontale de cuivre refroidie par une circulation d'eau; pour être efficace, la trempe doit être effectuée sur de faibles quantités de produit. La pureté des composés a été contrôlée par rayons X par la méthode Debye–Scherrer. Les paramètres des mailles cristallines sont \( a = 3,394 \pm 0,005 \) Å pour DyRh, \( a = 3,377 \pm 0,005 \) Å pour HoRh et \( a = 3,361 \pm 0,005 \) Å pour ErRh; ces valeurs sont toutes légèrement inférieures à celles données par Dwight qui sont \( a = 3,403 \pm 0,002 \) Å, \( a = 3,388 \pm 0,002 \) Å et \( a = 3,372 \pm 0,002 \) Å respectivement, la différence pouvant provenir des conditions de préparation.
3. ETUDE DE DyRh
L'absorption importante des neutrons par le dysprosium oblige à diluer l'alliage dans de la poudre d'aluminium. A la température ordinaire, le diagramme observé s'interprète par la diffusion nucléaire cohérente des neutrons en prenant pour longueur de Fermi \( b_{Dy} = 1,69 \times 10^{-12} \) cm et \( b_{Rh} = 0,59 \times 10^{-12} \) cm. A la température de l'hélium pompé (T = 1,2 K), on observe un accroissement des valeurs des intensités des raies, caractéristique de l'établissement de l'ordre ferromagnétique des moments. En supposant le dysprosium seul porteur de moment, le moment ainsi calculé est \( \mu_{Dy} = 7,1 \pm 1 \mu_{B} \) , comparable à celui observé par mesure magnétique sous un champ de 27 koe alors que l'aimantation n'est pas saturée.
Il se peut qu'il existe une polarisation des atomes de rhodium par les moments de la terre rare comme cela a été inféré dans le cas de \( FeRh^{3} \) par la mesure de l'accroissement de la raie (100) et de la saturation magnétique. Pour nous prononcer nous devons évaluer indépendamment \( (\mu_{Dy} f_{Dy} - \mu_{Rh} f_{Rh})^{2} \) et \( (\mu_{Rh} f_{Rh})^{2} \) . En
adoptant pour \( f_{Rh} \) les valeurs déterminées à l'aide d'un monocristal de FeRh, \( ^{4} \) on peut estimer à environ 4% la modification de l'intensité magnétique de la raie (110) apportée par un moment de rhodium de 0,5 \( \mu_{B} \) ; ceci est très inférieur à la précision de mesure de l'accroissement de la raie (110), proche de la raie (111) de l'aluminium. Seule une étude aux neutrons polarisés sur monocristal pourrait permettre de mettre en évidence un changement dans l'état électronique du rhodium.
4. ETUDE DE HoRh
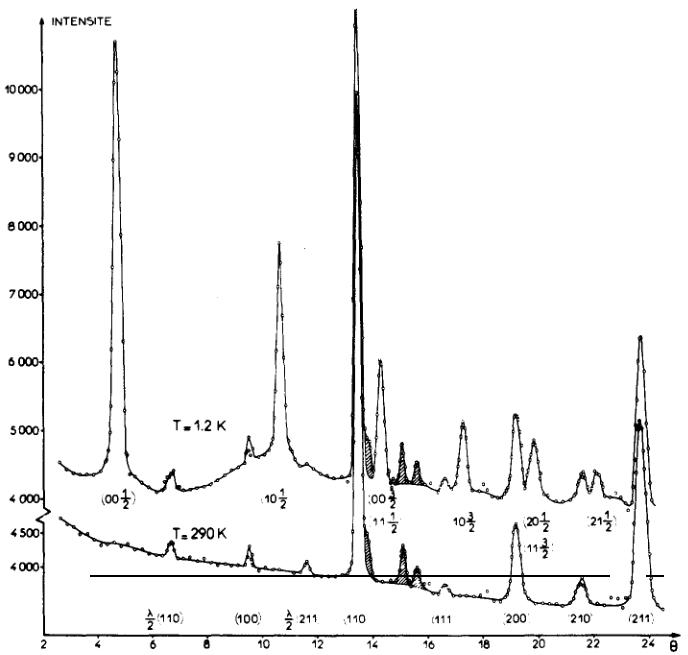
Les diagrammes de diffraction neutronique enregistrés à l'ambiance et à T = 1,2 K sont représentés sur la Fig. 1. Les valeurs observées des raies intenses caractéristiques du cube centré \( [h + k + l = 2n; (110), (200), (211) \ldots] \) sont en bon accord avec les valeurs calculées en prenant pour longueurs de Fermi \( b_{Ho} = 0,85 \times 10^{-12} \) cm et \( b_{Rh} = 0,59 \times 10^{-12} \) cm. Les valeurs observées des raies faibles, caractéristiques de l'ordre des atomes d'holmium et de rhodium \( [h + k + l = 2n + 1; (100), (111), (210) \ldots] \) sont entachées d'une erreur trop importante pour être prises en considération dans le facteur de normalisation.
La plus petite maille qui permette l'indexation des raies de surstructure caractéristiques de l'ordre antiferromagnétique des atomes d'holmium est une maille quadratique \( (a, a, 2a) \) ; le vecteur de propagation \( k = [0, 0, \frac{1}{2}] \) de la structure ainsi observée peut être compris à partir d'interactions indirectes de type Ruderman–Kittel. \( ^{5} \) Les valeurs des intensités observées sont en bon accord avec celles calculées en supposant un modèle colinéaire dont la direction des spins est perpendiculaire à l'axe oz (Tableau 1). En utilisant le facteur de forme calculé par Blume, Freeman et Watson, \( ^{6} \) le moment moyen trouvé est de 5,2 \( \pm \) 0.3 \( \mu_{B} \) et le facteur de véracité
\[ \frac{\sum\mid l_{obs}-l_{cal}\mid}{\sum l_{cal}} \]
de l'ordre de 4%.
Cependant l'étude du champ cristallin \( ^{2} \) indique que l'énergie de l'état ordonné doit être plus basse lorsque le moment est porté par l'axe ternaire. Comme cela a été montré dans l'étude de DyCu, \( ^{7} \) une maille magnétique cubique de coté 2a convient également à l'interprétation du diagramme, les conditions d'extinction assignant alors aux moments situés sur les sommets opposés du cube d'être dirigés en sens contraire.
Attribuons à chaque moment trois composantes \( S_{x} \) , \( S_{y} \) , \( S_{z} \) de même module \( S/\sqrt{3} \) : pour que chaque contribution soit analogue à celle d'une configuration colinéaire dans le plan de base xy, il suffit que les composantes se propagent avec conservation dusigne lorsqu'il s'agit de l'axe de même nom et changement de signe pour l'un des deux axes restants. L'intensité d'une raie \( \left|hkl\right| \) peut se calculer comme la somme des intensités dues à \( S_{x}^{2} \) , \( S_{y}^{2} \) et \( S_{z}^{2} \) , car en sommant sur les réflexions d'un triplet \( \left|hkl\right| \) , les termes rectangles de type \( S_{x} \cdot S_{y} \) s'annulent.
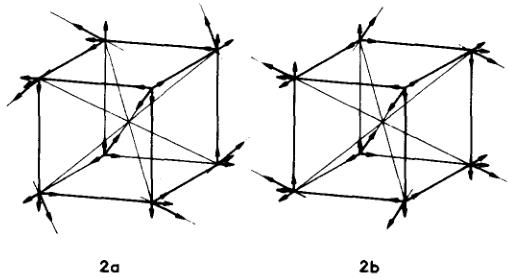
Compte tenu des restrictions ci-dessus, il n'existe que deux configurations distinctes cristallographiquement. Si la composante \( S_{x} \) garde le même signe en passant d'un atome à son voisin le long de 0x et 0y, et alterne le long de 0z, on notera le mode de propagation de la composante (00π); les modes de propagation possibles pour cette composante sont alors (00π) et (0π0). Le premier type de configuration possible correspond à un clangerent de signe des composantes sur chaque axe; pour \( S_{x} \) (0π0), \( S_{y} \) (00π), \( S_{z} \) (π00), la structure obtenue est de symétrie cubique [Fig. 2(a)], son groupe de Shubnikov étant \( l_{p} \) 3a. Le second type de configuration possible, obtenue en changeant de signe deux composantes sur un même axe, par exemple \( S_{x} \) (0π0), \( S_{y} \left( \pi 00 \right) \) , \( S_{z} \left( \pi 00 \right) \) , appartient au groupe de Shubnikov \( C_{p} \) 2/m [Fig. 2(b)]. Seule une expérience sur monocristal monodomaine permettrait de distinguer ces deux configurations.
Comme dans le cas de DyCu, \( ^{7} \) on peut montrer que, d'une part l'énergie de couplage magnétique isotrope et d'autre part l'énergie dipolaire des configurations envisagées ci-dessus sont les mêmes que celles de la configuration colinéaire avec des moments dans le plan xy. En utilisant la formule indiquée par Bertaut, \( ^{8} \) nous avons calculé l'anisotropie dipolaire dans le cas colinéaire et trouvé \( \Delta W = 2,83 \times 10^{-16} \) erg/atome ( \( W_{ox} = -0.945 \times 10^{-16} \) erg/atome).

FIG. 1. Diagrammes de diffraction neutronique enregistrés à température ambiante et à T = 1,2 K pour HoRh; les raies hachurées proviennent du cryostat.

FIG. 2. Structures magnétiques non colinéaires cubique (2a) et monoclinique (2b).
Tableau 1. Valeurs des intensité calculées et observées d'une part des raies nucléaires à température ambiante et d'autre part des raies magnétiques à 1,2 K pour HoRh.
| T = 290 K | T = 1,2 K | ||||
| h k l | INcell | INobs | h k l | IMcell | IMobs |
| 1 0 0 | 0,40 | 0,25 | 0 0 1/2 | 3,78 | 4,03 |
| 1 1 0 | 24,88 | 25,28 | 1 0 1/2 | 7,37 | 7,57 |
| 1 1 1 | 0,54 | 0,60 | (1 1 1/2 | 8,63 | 8,89 |
| 2 0 0 | 12,44 | 12,26 | (0 0 3/2 | ||
| 2 1 0 | 1,62 | 2,89 | 1 0 3/2 | 7,72 | 7,46 |
| 2 1 1 | 49,76 | 49,54 | (2 0 1/2 | 10,13 | 9,80 |
| (1 1 3/2 | |||||
| 2 1 1/2 | 6,96 | 6,52 | |||
Tableau 2. Valeurs des intensités calculées et observées d'une part des raies nucléaires à température ambianteet d'autre part des raies magnétiques à 1,2 K pour ErRh.
| T = 290 K | T = 1,2 K | ||||
| h k l | INcal | INobs | h k l | IMcal | IMobs |
| 1 0 0 | 0,24 | 0 0 1/2 | 5,08 | 4,88 | |
| 1 1 0 | 22,85 | 23,01 | 1 0 1/2 | 9,62 | 9,84 |
| 1 1 1 | 0,32 | (1 1 1/2 | 10,48 | 10,69 | |
| 2 0 0 | 11,43 | 15,04 | (0 0 3/2 | ||
| 2 l 0 | 0,96 | 1 0 3/2 | 9,25 | 8,52 | |
| 2 l 1 | 45,70 | 41,91 | (2 0 1/2 | 11,48 | 10,60 |
| (1 1 3/2 | |||||
Compte tenu de la direction de moment favorisée par le champ cristallin, les structures multiaxiales proposées sont celles d'énergie diplaire minimum
5. ETUDE DE ErRh
Le diagramme de diffraction neutronique est semblable à celui de HoRh; les valeurs des intensités des raies nucléaires et magnétiques sont consignées dans le tableau 2. Le moment des atomes d'erbium vaut \( 6,1 \pm 0,3 \mu_{B} \) , ceci en supposant le moment du rhodium nul. Cette valeur est en bon accord avec l'étude du champ cristallin, \( ^{2} \) lequel favorise une direction de spin suivant un axe quaternaire, compatible avec une configuration colinéaire à moments dans le plan xy.
REFERENCES
-
DWIGHT A.E., CONNER R.A. and DOWNER Jr. J.W., Acta Crystallogr., 18, 837 (1965).
-
CHAMARD-BOIS R., NGUYEN VAN NHUNG and PIERRE J., Phys. Status Solidi (b) 49 (1972).
-
BERTAUT E.F., DE BERGEVIN F. and ROULT G., C.r. heb. séanc. Acad. Sci., Paris, 256, 1688 (1963).
-
SHIRANE G., NATHANS R., PICKART S.J. and ALPERIN H.A., Proc. Int. Conf. on Magnetism, 223 (1964).
-
PIERRE J., Solid State Commun., 7, 165 (1969); Proc 8th Rare Earth Conf. Reno (Nevada) 102 (1970).
-
BLUME M., FREEMAN A.J. and WATSON R.E., J. Chem. Phys., 37, 1245 (1962).
-
WINTENBERGER M., CHAMARD-BOIS R., BELAKHOVSKY M. and PIERRE J., Phys. Status Solidi (b) 48, 705 (1971).
-
BERTAUT E.F., Magnetism,(edited by RADO G.T. and SUHL H.) Vol. III p. 199. Academic Press (1963).
Neutron diffraction on powdered samples shows that the antiferromagnetic structures of \( ErRh \) and \( HorRh \) may be described by a propagation vector \( k\ (0\ 0\frac{1}{2}) \) or by some related multiaxial configurations. The rare earth magnetic moments in these compounds and in ferromagnetic DyRh are evaluated.