| Transition Temperature | 290 K |
|---|---|
| Experiment Temperature | 77 K |
| Parent Space Group | Fm-3m (#225) |
| Magnetic Space Group | Ic41/acd (#142.570) |
| Magnetic Point Group | 4/mmm1' (15.2.54) |
| Lattice Parameters | 8.52600 8.52600 8.52600 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1103/PhysRev.138.A584 |
| Reference | B. van Laar, PHYSICAL REVIEW (1965) 138 A584 - A587 |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Co1 | Co | -0.325 | -0.325 | 0.888 | 1.00 |
Title
Multi-Spin-Axis Structure for CoO†
Authors
B. VAN LAAR Reactor Centrum Nederland, Pelten, The Netherlands
Materials Studied
CoO (Cobalt Oxide) Specifically, the sample was prepared from Merck CoO, and chemical analysis showed the composition to be CoO\(_{0.97}\).
Key Information
- Crystal structure / space group:
- Approximately cubic (NaCl type) in the antiferromagnetic state, with a small crystallographic distortion.
- CoO becomes tetragonal with c/a < 1 below the Néel temperature.
- The proposed tetragonal unit cell is body-centered with an 'a' axis equal to one-half the face diagonal of the pseudocubic cell.
- Space group: I4\(_{1}\)/acd (D\(_{4h}^{20}\)) for the tetragonal system.
- Magnetic ordering type and temperature (T_N, T_C):
- Antiferromagnetic state.
- Data collected at liquid-nitrogen temperature (77 K).
- Néel temperature (T_N) is mentioned as the temperature below which crystallographic distortion occurs, but no specific value is given.
- Propagation vector(s): The magnetic intensities are indexed with h, k, l all odd, corresponding to a doubled unit cell edge, implying a propagation vector of the type (1/2, 1/2, 1/2) in the pseudocubic cell.
- Magnetic moments:
- Magnetic moment of the Co\(^{++}\) ion at 77 K was deduced to be 3.52 μ\(_{B}\).
- Lattice parameters:
- Tetragonal distortion: c/a = 0.988.
- Any other critical measured values:
- Angle between the spin axis and the c axis for the collinear model (derived from new data): (27.4 ± 0.5)°. (Older data by Roth gave 11.5°).
- Neutron wavelength used: 1.273 Å.
- Nuclear scattering amplitude of Co: bCo\(_{0}\) = 0.245 × 10\(^{-12}\) cm.
- Nuclear scattering amplitude of O: b\(_{0}\) = 0.577 × 10\(^{-12}\) cm.
- Debye-Waller factor: 2B = 0.74 × 10\(^{-16}\) cm\(^{2}\).
Synthesis Method
The sample of CoO was prepared from Merck CoO by heating to 950°C in a nitrogen atmosphere. Chemical analysis showed the composition to be CoO\(_{0.97}\).
Abstract
New intensity data from CoO in the antiferromagnetic state have been obtained with a high-resolution neutron diffractometer. These improved data can be interpreted by a collinear spin structure with an angle of \( 27.4^{\circ} \) between the spin axis and the c axis, as compared with the older data of Roth which gave this angle as \( 11.5^{\circ} \). Alternatively a multi-spin-axis model is proposed which explains the intensity data equally well. This model is related to the collinear model B proposed by Li and has a tetragonal spin superstructure in conformity with the tetragonal crystallographic deformation below the Néel temperature.
Main Content Summary
The paper addresses the long-standing problem of the spin arrangement in antiferromagnetic CoO, which, unlike other transition metal monoxides (MnO, FeO, NiO), exhibits a tetragonal crystallographic distortion (c/a < 1) below its Néel temperature, yet previous neutron diffraction studies by Roth suggested a spin axis inconsistent with this symmetry. The author obtained new, high-resolution neutron diffraction data for CoO at liquid-nitrogen temperature, which allowed for the separation of previously unresolved diffraction peaks like {113} and {311}.
Initially, the new data were analyzed assuming a single-spin-axis (collinear) model. This analysis indicated a spin axis in the (1\(\bar{1}\)0) plane, making an angle of (27.4 ± 0.5)° with the c-axis. This significantly differs from Roth's earlier finding of 11.5°. However, this collinear model was rejected because it would imply a spin structure similar to rhombohedral MnO, contradicting CoO's observed tetragonal distortion. Furthermore, explaining this large angle (27.4°) with existing theories (Nagamiya and Motizuki) would require an improbably high ratio of anisotropy constants.
Given the shortcomings of the collinear model, the paper proposes a new multi-spin-axis structure. This model, detailed with specific direction cosines for the spins of four independent atoms, perfectly fits the observed neutron diffraction intensities, including the previously problematic ratios of {311}/{113} and {331}/{313} peaks. Crucially, this multi-spin model is strictly tetragonal, aligning perfectly with the observed tetragonal crystallographic deformation (c/a = 0.988) of CoO. The magnetic moment of the Co\(^{++}\) ion at 77 K was determined to be 3.52 μ\(_{B}\).
Finally, the paper discusses the symmetry in the antiferromagnetic state, proposing a body-centered tetragonal unit cell with space group I4\(_{1}\)/acd (D\(_{4h}^{20}\)). This space group allows for the Co atoms to be placed in positions that do not restrict their spin directions along or perpendicular to the c-axis, accommodating the proposed multi-spin structure. The multi-spin-axis model is presented as a more probable description of CoO's magnetic structure due to its consistency with the crystallographic symmetry.
Conclusion
The paper concludes that the proposed multi-spin-axis model for CoO is more probable than the previously suggested collinear model. This preference stems from the multi-spin model's strict tetragonal spin structure, which is in conformity with the observed tetragonal crystallographic deformation of CoO (c/a = 0.988). The collinear model, while fitting the powder intensities, would imply a spin structure nearly identical to rhombohedral MnO, contradicting CoO's known crystallographic distortion. The multi-spin-axis structure is related to Li's model B, specifically in the arrangement of the z components of the spins. The symmetry in the antiferromagnetic state is identified as tetragonal, with a body-centered unit cell and the space group I4\(_{1}\)/acd (D\(_{4h}^{20}\)).
Multi-Spin-Axis Structure for CoO†
B. VAN LAAR
Reactor Centrum Nederland, Pelten, The Netherlands
(Received 20 November 1964)
New intensity data from CoO in the antiferromagnetic state have been obtained with a high-resolution neutron diffractometer. These improved data can be interpreted by a collinear spin structure with an angle of \( 27.4^{\circ} \) between the spin axis and the c axis, as compared with the older data of Roth which gave this angle as \( 11.5^{\circ} \) . Alternatively a multi-spin-axis model is proposed which explains the intensity data equally well. This model is related to the collinear model B proposed by Li and has a tetragonal spin superstructure in conformity with the tetragonal crystallographic deformation below the Néel temperature.
INTRODUCTION
THE arrangement of atomic spins in the antiferromagnetic state of MnO, FeO, CoO, and NiO was described by Shull, Strauser, and Wollan \( ^{1} \) in 1951 and by Roth \( ^{2} \) in 1958. In the antiferromagnetic state these oxides are approximately cubic (NaCl type). Their neutron diffraction patterns in the antiferromagnetic (af) state can be indexed with a doubled unit cell edge. The reflection conditions \( h_{1}, k, l \) , all even for the nuclear intensities and \( h_{2}, k, l \) , all odd for the magnetic intensities, are those for a fcc magnetic unit cell in which each spin has an antiparallel partner at \( \pm\left(\frac{1}{2}, \frac{1}{2}, \frac{1}{2}\right) \) . Since in this arrangement next-nearest neighbors have antiparallel spins, the existence of a superexchange interaction is directly evident.
It has been shown by Li \( ^{a} \) that for a single-spin-axis arrangement the four face-centered sublattices can be correlated in two different ways in order to fulfill this condition. These two possibilities are model A and model B, as designated by Li in his paper. The principal difference between the two possibilities is that model A is compatible with a rhombohedral deformation while model B is compatible with a tetragonal deformation.
In the antiferromagnetic state the oxides are not cubic; there is a small crystallographic distortion (Rooksby, \( ^{4} \) Tombs and Rooksby \( ^{6} \) ). MnO and NiO become rhombohedral with \( \alpha>60^{\circ} \) . FeO becomes rhombohedral with \( \alpha<60^{\circ} \) and CoO becomes tetragonal with c/a<1.
From neutron diffraction data both Shull et al. and Roth rejected model B and accepted model A, based on ferromagnetic sheets of moments, parallel to (111) planes with signs alternating in adjacent sheets. Roth, who had the most accurate data, derived for the spin directions: (a) in MnO and NiO the spin axis is in the (111) plane; (b) in FeO the spin axis is along the [111] axis; (c) in CoO the spin axis is parallel to [117], thus making an angle of \( 11^{\circ}30' \) with the c axis. Evidently the arrangement of moments is consistent with the crystallographic distortion, except in the case of CoO.
Nagamiya and Motizuki, \( ^{6} \) who modified a theory of Kanamori, \( ^{7} \) tried to explain the tetragonal deformation of CoO by assuming a balancing between cubic anisotropy and trigonal dipolar anisotropy, characterized respectively by the constants K and T. To explain an angle of \( 10^{\circ} \) between the tetragonal c axis and the spin axis a ratio of T/K as large as 0.3 had to be assumed, which they did not consider impossible.
The interpretation of Roth's diffraction data was complicated by the lack of reliable values for the \( Co^{++} \) form factor on which the calculated angle of deviation is strongly dependent. Due to the limited resolving power of his neutron diffractometer, Roth was able to measure only the intensity of the peaks of the cubic forms \( \{hkl\} \) but he recognized that additional information might be obtained from the separate intensities \( \{hkl\} \) and \( \{hlk\} \) . As the resolving power of the diffractometer at the High Flux Reactor in Petten is high enough to separate these intensities, CoO has been reinvestigated to obtain more reliable information about the spin arrangement.
EXPERIMENTAL
The sample of CoO was prepared from Merck CoO by heating to \( 950^{\circ} \) C in a nitrogen atmosphere. Chemical analysis showed the composition to be \( CoO_{0.97} \) . Neutron diffraction data were collected at liquid-nitrogen temperature from a sample contained in a cylindrical aluminium sample holder with a diameter of 20 mm and a wall thickness of 0.05 mm. The neutron wavelength was 1.273 Å. Soller slits of \( 5\frac{1}{2} \) angular divergence were mounted between the reactor and the copper monochromator. The slits in front of the \( BF_{3} \) detector had an angular divergence of 5'.
RESULTS AND DISCUSSION
Single-Spin-Axis Structure
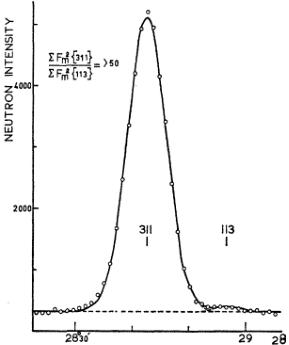
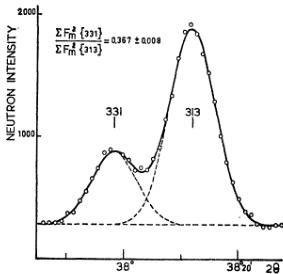
Although the separation of the peaks \( \{113\} \) and \( \{311\} \) , and also \( \{331\} \) and \( \{313\} \) is not complete (the
angular distances are \( 14' \) and \( 15' \) in \( 2\Theta \) , it is quite simple, by means of a computer program, to obtain the relative intensities, which are given in Table I. The peaks are shown in Figs. 1 and 2.
TABLE I. Comparison of the observed ratios of the intensities from \( \{hkl\} \) and \( \{hkl\} \) with those calculated from different models. The second part of the table refers to the collinear model with two different values for the angle of deviation; the third part refers to the multispin models, proposed by Roth.
| \( \Sigma F_{m}^{a}(311) \) | \( \Sigma F_{m}^{a}(331) \) | |
| \( \Sigma F_{m}^{a}(113) \) | \( \Sigma F_{m}^{a}(313) \) | |
| Observed | >50 | 0.367±0.008 |
| \( A[11.5^{\circ}] \) | 32 | 0.64 |
| \( A[27.4^{\circ}] \) | 158 | 0.366 |
| I | 0.55 | 0.86 |
| J | 1.99 | 0.03 |
| K | 1.20 | 0.36 |
| R | 1.20 | 0.36 |
| T | 1.20 | 0.36 |
| U | 2.06 | 0.88 |
| V | 2.15 | 0.82 |
| Multi-spin-axis structure proposed in this paper | 158 | 0.366 |
From the almost complete absence of the \( \{113\} \) peak a rough indication of the direction of the antiferromagnetic axis is obtained if the existence of a single-spin-axis model is assumed. A much more sensitive determination is possible from the ratio of the intensities \( \{331\} \) and \( \{313\} \) . Combining these criteria shows unambiguously that the spin axis is situated in the \( (1\bar{1}0) \) plane and that the angle of deviation from the c axis is \( (27.4\pm0.5)^{\circ} \) .
This model would imply that there is hardly any difference between the CoO and the MnO structures; in MnO the spins are in the (111) planes; in CoO they are tipped out of these planes by an angle of \( 8^{\circ} \) . Two important objections can be made; however, (1) the distortion from cubic symmetry below the Néel tem-
FIG. 1. Neutron diffraction peaks \( \{311\} \) and \( \{113\} \) .

FIG. 2. Neutron diffraction peaks \( \{331\} \) and \( \{313\} \) .

perature is tetragonal for CoO and rhombohedral for MnO, although according to this model their spin structures would be nearly equal; (2) to explain the angle of deviation of \( 27.4^{\circ} \) by means of the theory of Nagamiya and Motizuki a ratio of T/K of 0.55 has to be assumed, which is very improbable.
Rejecting the collinear model for CoO for these reasons, the only other possibility for the CoO structure is a noncollinear model.
Multi-Spin-Axis Structure
In a multi-spin-axis structure the four antiferromagnetic fc sublattices are independent. Therefore the direction of the spins of four atoms has to be determined, the spin of each of these atoms generating eight other spin directions [four parallel spins due to the face-centering and then again four antiparallel spins at \( +(\frac{1}{2},\frac{1}{2},\frac{1}{2}) \) ]. These four independent atoms are taken at \( (0,0,0) \) ; \( (\frac{1}{4},0,\frac{1}{4}) \) ; \( (\frac{1}{4},\frac{3}{4},\frac{1}{2}) \) ; \( (0,\frac{3}{4},\frac{3}{4}) \) . The magnetic structure factor is then given by:
\[ \mathbf{F}_{m}=8\mu\mathbf{c}_{0}++f\mathbf{c}_{0}++\left[\frac{e\mathbf{\gamma}}{2m c^{2}}\right] \]
\[ \begin{aligned}\times\left\{\mathbf{q}_{1}+\mathbf{q}_{2}\exp\left[\frac{h+l}{2\pi i}-\right]+\mathbf{q}_{3}\exp\left[\frac{h+3k+2l}{4}\right]\right.\\\left.+\mathbf{q}_{4}\exp\left[\frac{3k+3l}{4}\right]\right\}.\end{aligned} \]
\[ \mathbf{q}_{i}=\varepsilon(\varepsilon\cdot\mathbf{k}_{i})-\mathbf{k}_{i}. \]
In this expression \(e\) and \(m\) are the electron charge and mass, \(\gamma\) is the magnetic moment of the neutron expressed in nuclear magnetons, \(\mu_{\mathrm{Co}^{++}}\) is the magnetic moment of the \(\mathrm{Co}^{++}\) ion expressed in Bohr magnetons, \(f_{\mathrm{Co}^{++}}\) is form factor for the magnetic scattering by the \(\mathrm{Co}^{++}\) ion, \(\varepsilon\) is the scattering vector and \(\mathbf{k}_{i}\) is a unit vector in the direction of the magnetic moment of the \(\mathrm{Co}^{++}\) ion.
Roth \( ^{8} \) proposed seven multispin models for CoO (designated I, J, K, R, T, U, and V). From the present data it is found that all of these can be rejected since
TABLE II. Multi-spin-axis structure of CoO.
| Atom | Direction cosines of spins | ||
| \( \alpha \) | \( \beta \) | \( \gamma \) | |
| 1. 0, 0, 0 | -0.325 | -0.325 | +0.888 |
| 2. \( \frac{1}{2} \) , 0, \( \frac{1}{2} \) | +0.325 | -0.325 | -0.888 |
| 3. \( \frac{1}{2} \) , \( \frac{3}{2} \) , \( \frac{1}{2} \) | +0.325 | +0.325 | +0.888 |
| 4. 0, \( \frac{3}{2} \) , \( \frac{1}{2}\) | -0.325 | +0.325 | -0.888 |
they give too low a value for the ratio of the \( \{311\} \) and the \( \{113\} \) intensity (Table I).
A model, fitting the intensities perfectly well, is given in Table II. This model leads to exactly the same powder intensities as the collinear model A with an angle of deviation of \( 27.4^{\circ} \) ( \( \alpha = -0.325 \) , \( \beta = -0.325 \) , \( \gamma = +0.888 \) ), but while the multispin model gives exactly the same intensity for all members of a form \( \{hkl\} \) , in model A only one quarter of the possible reflections accounts for the full intensity.
A survey of calculated and observed structure factors is given in Table III. In the calculation of \( \Sigma(F_{m}^{2}/64\rho^{2}) \) from the observed intensities, the \( Co^{++} \) form factor given by Scatturin \( ^{9} \) was used. The magnetic moment of the \( Co^{++} \) ion at \( 77^{\circ}K \) was deduced to be \( 3.52\mu_{B} \) , which is about 10% less than the value reported by Roth, who
TABLE III. Comparison of calculated and observed intensities. \( CoO_{0.965} \) ; \( bCo_{0}=0.245\times10^{-12} \) cm; \( b_{0}=0.577\times10^{-12} \) cm; \( \mu_{Co}=3.52\mu_{B} \) ; \( 2B=0.74\times10^{-16} \) cm \( ^{2} \) . The good fit between the calculated and observed nuclear scattering confirms the reliability of the above-mentioned value of the nuclear scattering amplitude of Co, first reported by Roth in his paper on CoO, then by the same author in \( Co_{4}O_{4} \) . This value is considerably smaller than the usually tabulated value of \( 0.28\times10^{-12} \) cm, given by Shull and Wollan. \( ^{b} \)
| {hkl} | Nuclear scattering | |
| Calculated | \( \Sigma F_{n}^{2}/(\times10^{40}) \) | |
| 222 | 796.8 | 810±20 |
| 400 | 2633.6 | 2600±30 |
| 004 | 1316.8 | 1320±20 |
| 440 | 2633.6 | 2650±40 |
| 404 | 5267.2 | 5280±50 |
| 444 | 5267.2 | 5200±50 |
| Magnetic scattering | ||
| {hkl} | Calculated | Observed |
| 111 | 31.4 | 32.1±0.7 |
| 311 | 50.7 | 50.1±1.0 |
| 113 | 0.3 | 18.5±0.4 |
| 331 | 18.3 | 50.4±1.0 |
| 313 | 50.1 | 68.9±1.4 |
| 511 | 61.4 | |
| 333 | 31.4 | 106.0±2.0 |
| 115 | 14.9 | |
| 531 | 63.9 | |
| 513 | 24.6 | 109.0±4.0 |
| 315 | 16.3 | |
\( ^{a} \) W. L. Roth, J. Phys. Chem. Solids 25, 1 (1964). \( ^{b} \) C. G. Shull and E. O. Wollan, Phys. Rev. 81, 527 (1951).
\( ^{9} \) V. Scatturin, L. Corliss, N. Elliot, and J. Hastings, Acta Cryst. 14, 19 (1961).


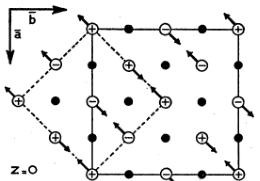
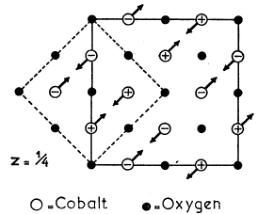
FIG. 3. Multi-spin-axis structure of CoO as proposed in this paper. The plus or minus signs designate the z components of the spins pointing up and down into the paper. The arrows represent the projection of the spins on the a-b plane. The layers \( z=\frac{1}{2} \) and \( z=\frac{3}{4} \) are constructed by reversing the spin directions in the layers \( z=0 \) and \( z=\frac{1}{2} \) , respectively. The drawn lines represent the pseudocubic F cell, the dotted lines the tetragonal I cell as discussed in the text.
obtained this result from averaged data of runs at 77 and 4.2°K.
Although it is not possible to make a choice between the two models from powder data, the multispin model is attractive in that the spin structure is strictly tetragonal in conformity with the observed deformation (which amounts to c/a=0.988 in the sample used in this investigation).
As there are no conclusive arguments against a multispin axis model, this model seems to be more probable than the collinear model, proposed by Roth.
The multispin axis structure that is obtained (Fig. 3) is related to \( L^{3} \) s model B in the sense that the z components of the spins are arranged according to this model.
Symmetry in the Antiferromagnetic State
As the symmetry in the antiferromagnetic (af) state is no longer cubic but tetragonal, it should be possible to find the proper spacegroup in the tetragonal system. The tetragonal unit cell is body-centered with an a axis equal to one-half the face diagonal of the pseudocubic cell. The cell volume is one-half that of the pseudocubic cell and the cell contains 16 CoO units.
There are no I groups with two sixteenfold positions in which all coordinates are fixed by symmetry; the group \( I4_{1}/acd(D_{4h}^{20}) \) is the only one with one sixteenfold fixed position. Selecting this group we have available for Co the position 16c on the centers of symmetry and for O the position 16e (with x=0) on the twofold axes. The Co atoms cannot be sited on the twofold axes as
this would restrict the direction of the Co spins along the c axis, or perpendicular to this axis.
It should be noted that in the tetragonal state the oxygen atoms are no longer required by symmetry to be exactly halfway between the Co atoms. In the nuclear intensities, however, no evidence was found for a deviation.
ACKNOWLEDGMENTS
The author is grateful to Professor Dr. J. A. Goedkoop and Dr. B. O. Loopstra for numerous discussions, to Dr. E. H. P. Cordfunke for the preparation and analysis of the sample and to Dr. W. L. Roth for the suggestion of the problem.
PHYSICAL REVIEW
VOLUME 138, NUMBER 2A
19 APRIL 1965
Master Equation for Ising Model \( ^{*} \)
S. P. HEIMS
Department of Physics, Brandeis University, Wallham, Massachusetts (Received 29 October 1964)
A spin system with unperturbed Hamiltonian \( 3C_{0}=\frac{1}{2}\sum B_{jk}\sigma_{x}^{j}\sigma_{x}^{k}-\gamma H\sum\sigma_{x}^{j} \) relaxing via the spin-lattice coupling \( G=\frac{1}{2}\sum C_{jk}\sigma_{x}^{j}(\sigma_{y}^{k}+\sigma_{x}^{k}) \) is studied by means of the general density-matrix theory of magnetic relaxation. By making some assumptions about the magnitude and time constants of the lattice correlation functions \( (C_{ij}(t)C_{kl}(0)) \) , a master equation is obtained. It agrees at high temperatures with a master equation previously suggested by Glauber for the one-dimensional nearest-neighbor case. At high temperatures the magnetic moment relaxes with a single relaxation time, and the spin pair-correlation functions satisfy a closed set of equations. At low temperatures, however, the equations for the magnetization and the correlation functions are coupled to higher-order moments.
INTRODUCTION
A MASTER equation to describe the time-dependent behavior for a one-dimensional Ising model has been proposed by Glauber. \( ^{1} \) The master equation of Glauber is based on a simple stochastic model. The equation leads to explicit solutions for the magnetization and for correlation functions; it is constructed to yield also the correct equilibrium distribution.
Another, perhaps more fundamental, approach to obtaining a master equation begins with the quantum-mechanical Liouville equation for an explicit Hamiltonian. This approach has several advantages: (1) The physical assumptions and approximations going into the master equation can be clearly stated, and therefore also the physical circumstances to which it corresponds are more evident. (2) Generalizations of the master equation, which include off-diagonal elements of the density matrix, can be obtained. (3) The equation is equally valid for the one-, two-, or three-dimensional Ising model, and is not restricted to nearest-neighbor coupling. The two- and three-dimensional Ising models are of particular interest because for those cases the system can undergo a phase transition.
There is already in existence a general theory of the time-dependent behavior for a spin system, which interacts with a heat reservoir, presumably consisting of the lattice vibrations and other coordinates of the solid. In the theory first developed by Bloch, \( ^{2} \) and extended and refined by others, \( ^{3} \) the Liouville equation for the combined system of spins and “lattice” is the starting point. Mostly the theory has been applied to single or weakly coupled spins, but it can equally well be applied to a many-particle system if that system can be solved exactly. In this note the general theory will be applied to the special case of the Ising model spin system (with arbitrary range and sign of interaction), with an additional interaction causing transitions. The master equation obtained will be shown to agree in the one-dimensional case with Glauber’s at high temperatures (relative to J/k) and zero magnetic field, but not at low temperatures or finite field strengths.
DERIVATION OF MASTER EQUATION
The total Hamiltonian to be considered is
\[ \Im\mathcal{C}=\Im\mathcal{C}_{s}+\Im\mathcal{L}_{L}+G, \quad (1) \]
where \( 3C_{s} \) and \( 3C_{L} \) depend only on spin and lattice coordinates, respectively, and G depends on both. The “lattice” (i.e., all degrees of freedom other than the spins of interest) will be regarded as a thermal reservoir. Consequently the detailed form of \( 3C_{L} \) is not needed. For \( 3C_{s} \) the following explicit form is taken:
\[ \Im\mathcal{C}_{s}=\frac{1}{2}\sum_{j}^{N}\sum_{k}^{N}B_{j k}\sigma_{x}^{j}\sigma_{x}^{k}-\gamma H\sum_{j}\sigma_{x}^{j}, \quad (2) \]