| Transition Temperature | 4 K |
|---|---|
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | Pnma (#62) |
| Magnetic Space Group | P212121 (#19.25) |
| Magnetic Point Group | 222 (6.1.17) |
| Lattice Parameters | 5.59570 7.62900 5.30090 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1103/physrevlett.101.097205 |
| Reference | Y. Tokunaga, S. Iguchi, T. Arima and Y. Tokura, Physical Review Letters (2008) 101. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Dy1 | Dy | 1. | 0.0 | 0.0 | 1.00 |
| Fe1 | Fe | 1. | 0.3 | 0.0 | 1.04 |
Title
Magnetic-Field-Induced Ferroelectric State in DyFeO_{3}
Authors
Y. Tokunaga, \( ^{1} \) S. Iguchi, \( ^{2} \) T. Arima, \( ^{3} \) and Y. Tokura \( ^{1,2,4,5} \)
\( ^{1} \) Multiferroics Project, ERATO, Japan Science and Technology Agency (JST), Wako, Saitama 351-0198, Japan \( ^{2} \) Department of Applied Physics, University of Tokyo, Bunkyo-ku, Tokyo 113-8656, Japan \( ^{3} \) Institute of Multidisciplinary Research for Advanced Materials, Tohoku University, Sendai 980-8577, Japan \( ^{4} \) Correlated Electron Research Center (CERC), National Institute of Advanced Industrial Science and Technology (AIST), Tsukuba, Ibaraki 305-8562, Japan \( ^{5} \) Cross-Correlated Materials Research Group (CMRG), ASI, RIKEN, Wako, Saitama 351-0198, Japan
Materials Studied
- \( DyFeO_{3} \) (single crystal)
Key Information
- Crystal structure / space group:
- Orthorhombic, \( Pbnm \) setting.
- Magnetic point group: \( m'm'm' \) (below \( T_{N}^{Dy} \) in the linear-ME phase, \( H < H_{r}^{Fe} \)).
- Magnetic point group: \( m'm'2 \) (in the H-induced multiferroic phase, \( H > H_{r}^{Fe} \)).
- Magnetic ordering type and temperature:
- \( Fe^{3+} \) spins: G-type antiferromagnetic (AFM) order below \( T_{N}^{Fe} \sim 645 \) K.
- Fe spin reorientation transition at \( T_{r} \sim 37 \) K (from \( G_{x}A_{y}F_{z} \) to \( A_{x}G_{y}C_{z} \)).
- Dy moments: AFM ordering below \( T_{N}^{Dy} \sim 4 \) K (or \( \sim 3.8 \) K in low H). Configuration is \( G_{x}A_{y} \).
- Propagation vector(s): Not explicitly stated, but commensurate ordering implied by Bertaut notation.
- Magnetic moments:
- Weak ferromagnetic (WFM) component along c-axis: \( [\geq 0.5\mu_{B}/formula unit (f.u.)] \) in the H-induced multiferroic phase.
- Dy moments: Ising nature.
- Lattice parameters: Not available.
- Any other critical measured values:
- Linear-ME tensor component: \( \alpha_{zz} \sim 2.4 \times 10^{-2} \) esu (CGS dimensionless unit) at 3 K (for \( H < H_{r}^{Fe} \)).
- Electric polarization: \( P (\geq 0.2\muC/cm^{2}) \) along the c-axis in the H-induced multiferroic phase.
- Spontaneous P: \( \sim 0.15 \mu C/cm^{2} \) at 3 K (extrapolated from \( H > H_{f}^{Fe} \) region).
- Magnetic field for Fe spin reorientation / multiferroic phase induction: \( H_{r}^{Fe} \sim 24 \) kOe at 3 K, \( \sim 32 \) kOe at 2.5 K.
- P-E hysteresis loop frequency for complete reversal: \( f < 10 \) Hz.
Synthesis Method
A single crystal of \( DyFeO_{3} \) was grown by a floating-zone method in a flow of oxygen. The orientation of the single crystal was determined using back-reflection x-ray Laue photographs. Thin plates with wide faces perpendicular to the crystallographic a, b, or c axis in \( Pbnm \) setting were cut from the single-crystalline rod. Typical dimensions of the plates were \( 3 \times 3 \times 0.1 \, mm^{3} \). Each wide face was mechanically polished to obtain a flat smooth surface. Electrodes were formed on both sides of the plate by a heat-treatment type silver paste to create a capacitor structure.
Abstract
Versatile and gigantic magnetoelectric (ME) phenomena have been found for a single crystal of \( DyFeO_{3} \). Below the antiferromagnetic ordering temperature of Dy moments, a linear-ME tensor component as large as \( \alpha_{zz} \sim 2.4 \times 10^{-2} \) esu is observed. It is also revealed that application of magnetic field along the c axis induces a multiferroic (weakly ferromagnetic and ferroelectric) phase with magnetization \( [\geq 0.5\mu_{B}/formula unit (f.u.)] \) and electric polarization ( \( \geq 0.2\muC/cm^{2} \) ) both along the c axis. Exchange striction working between adjacent \( Fe^{3+} \) and \( Dy^{3+} \) layers with the respective layered antiferromagnetic components is proposed as the origin of the ferroelectric polarization in the multiferroic phase.
Main Content Summary
The paper investigates the magnetoelectric (ME) properties of a single crystal of \( DyFeO_{3} \), focusing on the emergence of a magnetic-field-induced ferroelectric state. The authors highlight the rarity of multiferroic materials exhibiting both large electric polarization (P) and strong ME coupling, noting that spin-driven ferroelectrics, while showing strong coupling, often have small P. They introduce \( DyFeO_{3} \) as a candidate, where the existence of a linear-ME effect below the Dy ordering temperature was predicted but not extensively reported.
The experimental setup involved growing a single crystal of \( DyFeO_{3} \) using a floating-zone method, followed by precise cutting, polishing, and electrode application to prepare samples for magnetic and electric measurements. Magnetization (M) was measured with a SQUID magnetometer, and electric polarization (P) was determined by integrating displacement current or using a Sawyer-Tower bridge for P-E hysteresis loops. The magnetic properties of \( DyFeO_{3} \) were characterized, revealing a G-type antiferromagnetic order of Fe spins below \( T_{N}^{Fe} \sim 645 \) K, with a reorientation transition at \( T_{r} \sim 37 \) K. Below \( T_{N}^{Dy} \sim 4 \) K, Dy moments order antiferromagnetically in a \( G_{x}A_{y} \) configuration. Crucially, applying a magnetic field \( H > H_{r}^{Fe} \) along the c-axis causes a reorientation of Fe spins, inducing a weak ferromagnetic (WFM) component along the c-axis.
The study reports two significant ME phenomena. First, below \( T_{N}^{Dy} \), a very large linear-ME tensor component \( \alpha_{zz} \sim 2.4 \times 10^{-2} \) esu is observed along the c-axis for magnetic fields below \( H_{r}^{Fe} \). This value is stated to be the largest ever reported among single-phase ME compounds. Second, and more importantly, the application of a magnetic field \( H (\geq 24 \, \text{kOe}) \) along the c-axis induces a multiferroic phase. In this phase, both magnetization \( [\geq 0.5\mu_{B}/f.u.] \) and electric polarization \( (\geq 0.2\muC/cm^{2}) \) are observed along the c-axis, indicating the coexistence of weak ferromagnetism and ferroelectricity. The spontaneous polarization in this H-induced state is estimated to be \( \sim 0.15 \mu C/cm^{2} \) at 3 K, which is comparable to other spin-driven ferroelectrics.
The authors propose exchange striction between adjacent \( Fe^{3+} \) and \( Dy^{3+} \) layers as the microscopic origin of the ferroelectric polarization in the H-induced multiferroic phase. This mechanism differs from the inverse Dzyaloshinskii-Moriya interaction typically found in spiral magnets. The magnetic point group \( m'm'2 \) in this phase allows for both spontaneous P and M along the c-axis. The reversal of P is attributed to a change in the phase of the layered-AFM spin modulation of \( Dy^{3+} \) moments, requiring relatively slow dynamics for complete reversal (f < 10 Hz). The retention property of P demonstrates its conservation even when the magnetic field crosses the phase boundary, suggesting a quasicontinuity between the linear-ME and H-induced multiferroic phases.
Conclusion
In summary, we have studied the ME properties of \( DyFeO_{3} \). A very large linear-ME tensor component \( \alpha_{zz} \sim 2.4 \times 10^{-2} \) is observed below \( T_{N}^{Dy} (\sim 4 \, \text{K}) \). More importantly, we show that \( DyFeO_{3} \) is a new class of multiferroics with \( M \parallel c \) and \( P \parallel c \) in the application of \( H (\geq 24 \, \text{kOe}) \) along the c axis. The exchange striction working between adjacent \( Fe^{3+} \) and \( Dy^{3+} \) layers with the layered-AFM components is a possible origin of the FE polarization in the H-induced multiferroic phase.
Magnetic-Field-Induced Ferroelectric State in DyFeO_{3}
Y. Tokunaga, \( ^{1} \) S. Iguchi, \( ^{2} \) T. Arima, \( ^{3} \) and Y. Tokura \( ^{1,2,4,5} \)
\( ^{1} \) Multiferroics Project, ERATO, Japan Science and Technology Agency (JST), Wako, Saitama 351-0198, Japan
\( ^{2} \) Department of Applied Physics, University of Tokyo, Bunkyo-ku, Tokyo 113-8656, Japan
\( ^{3} \) Institute of Multidisciplinary Research for Advanced Materials, Tohoku University, Sendai 980-8577, Japan
\( ^{4} \) Correlated Electron Research Center (CERC), National Institute of Advanced Industrial Science and Technology (AIST), Tsukuba, Ibaraki 305-8562, Japan
\( ^{5} \) Cross-Correlated Materials Research Group (CMRG), ASI, RIKEN, Wako, Saitama 351-0198, Japan (Received 2 June 2008; published 29 August 2008)
Versatile and gigantic magnetoelectric (ME) phenomena have been found for a single crystal of \( DyFeO_{3} \) . Below the antiferromagnetic ordering temperature of Dy moments, a linear-ME tensor component as large as \( \alpha_{zz} \sim 2.4 \times 10^{-2} \) esu is observed. It is also revealed that application of magnetic field along the c axis induces a multiferroic (weakly ferromagnetic and ferroelectric) phase with magnetization \( [\geq 0.5\mu_{B}/formula unit (f.u.)] \) and electric polarization ( \( \geq 0.2\muC/cm^{2} \) ) both along the c axis. Exchange striction working between adjacent \( Fe^{3+} \) and \( Dy^{3+} \) layers with the respective layered antiferromagnetic components is proposed as the origin of the ferroelectric polarization in the multiferroic phase.
DOI: 10.1103/PhysRevLett.101.097205
Materials, which possess two or more ferroic orders, such as concurrent (anti)ferromagnetic and ferroelectric (FE) orders, are called multiferroics. Among these materials, FE (anti)ferromagnets have been extensively studied in recent years because of possible technical applications, e.g., to storage devices \( [1-4] \) . Although some materials are reported as multiferroics, very few of them exhibit both large electric polarization (P) and strong magnetoelectric (ME) coupling. To attain the large ME coupling, it is advantageous that the origin of the P is magnetic. In fact, the large ME coupling is reported for the spiral magnets such as orthorhombic \( RMnO_{3}(R = Tb, Dy, etc.) \) \( [5,6] \) , \( CoCr_{2}O_{4} \) \( [7] \) , \( MnWO_{4} \) \( [8] \) , some hexaferrites \( [9-11] \) , etc. These materials show the P below the spiral spin order transition, which can be easily modified by the application of a magnetic field (H). The inverse effect of Dzyaloshinskii-Moriya (DM) interaction is proposed as a microscopic origin of the \( P[12,13] \) . However, the P of these materials is generally small, typically of the order of \( 10^{-2} \muC/cm^{2} \) or less, except for some RMnO \( _{3} \) systems \( [6] \) . Note, incidentally, that the well-known multiferroic \( BiFeO_{3} \) \( [3] \) shows the ferroelectricity arising from the \( Bi^{3+} \) lone-pair \( 6s^{2} \) , but not of the magnetic origin.
As other examples of the ME perovskite, a large linear-ME component is known for orthorhombic \( DyAlO_{3} \) and \( DyCoO_{3} \) with \( Dy^{3+} \) as the A-site cation [14–16]. In these materials, Dy moments with Ising nature align antiferromagnetically in the configuration of \( G_{x}A_{y} \) in Bertaut's notation [17] below \( T_{N}^{Dy} \sim 3.5 \) K. The Ising axis is confined in the ab-plane and its orientation is \( \sim 30^{\circ} \) off the b axis. The magnetic point group in this state is \( m'm'm' \) and thus allows ME tensor components of \( \alpha_{xx} \) , \( \alpha_{yy} \) , and \( \alpha_{zz} \) [14–16,18]. It is noteworthy that both Al and Co are diamagnetic at the ground state and have no magnetic contribution to the ME effect in these materials. Thus,
PACS numbers: 75.80.+q, 77.80.Fm
these materials do not have spontaneous P or magnetization (M), while hosting the large ME coupling. To establish a FE ferromagnetic state, it may be useful to further introduce magnetic ions in the perovskite B sites and utilize their magnetic order.
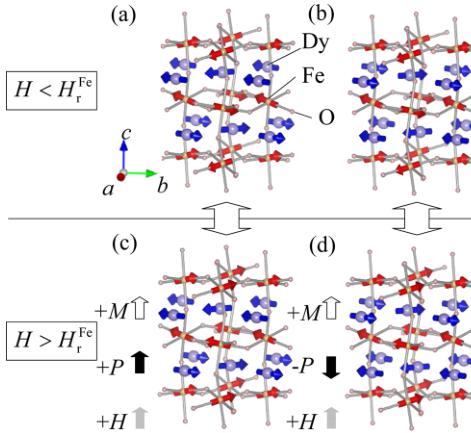
For \( DyFeO_{3} \) investigated in this study, the existence of the linear-ME effect below \( T_{N}^{Dy} \) was predicted in 1970s [19] from the viewpoint of the magnetic symmetry. In \( DyFeO_{3} \) , Dy moments order in the same configuration as those in \( DyAlO_{3} \) and \( DyCoO_{3} $ , while Fe ions (S = 5/2) show the antiferromagnetic (AFM) order [see Fig. 1(a)]. The proposed magnetic point group below \( T_{N}^{Dy} \) is 222, and hence the ME tensor components \( \alpha_{xx} \) , \( \alpha_{yy} \) , and a \( _{zz} \) are allowed. However, a possibly large ME effect has not been reported as yet. It was reported in literature [20] that the application of \( H = H_{F}^{Fe} \) along the c axis causes reorientation of Fe spins so as to produce a weak ferromagnetic (WFM) component along the c axis [see Fig. 1(c) or 1(d)]. Here we report on the large linear-ME effects as well as a H-induced FE state for a single crystal of \( DyFeO_{3} \) .
A single crystal of \( DyFeO_{3} \) was grown by a floating-zone method in a flow of oxygen. The orientation of the single crystal was determined by using back-reflection x-ray Laue photographs. Thin plates with wide faces perpendicular to the crystallographic a, b, or c axis in \( Pbnm \) setting were cut from the single-crystalline rod. Typical dimensions of the plates were \( 3 \times 3 \times 0.1 \, mm^{3} \) . Each wide face was mechanically polished to obtain the flat smooth surface. Electrodes were formed on the both sides of the plate by a heat-treatment type silver paste to make a capacitor structure. M was measured by a superconducting quantum interference device magnetometer (MPMS, Quantum Design). P was measured by integrating displacement current as sweeping temperature (T) or H with use of an electrometer (model 6517, Keithley). The P-E

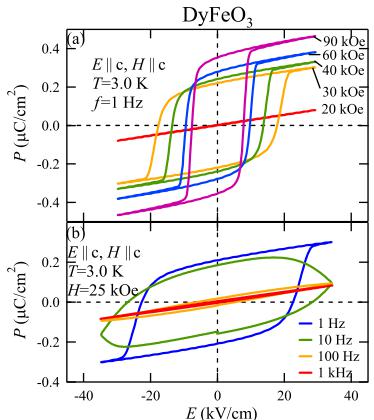
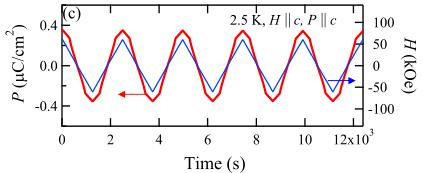
FIG. 1 (color online). Schematic of magnetic structures of \( DyFeO_{3} \) below \( T_{N}^{Fe} \) . (a),(b) Magnetic structures for the linear-ME phase ( \( H < H_{r}^{Fe} \) along the c axis). The magnetic configuration is \( G_{x}A_{y} \) for Dy moments and \( A_{x}G_{y}C_{z} \) for Fe spins. The phase of AFM order of Dy moments is different between (a) and (b). (c),(d) Magnetic structures for multiferroic phase ( \( H > H_{r}^{Fe} \) along the c axis). Magnetic configuration is \( G_{x}A_{y} \) for Dy moments and \( G_{x}A_{y}F_{z} \) for Fe spins. The phase of AFM order of Dy moments is a different between (c) and (d). (c) and (d) have opposite sign of P (see text).
hysteresis loop was measured by a Sawyer-Tower bridge (FCE, Toyo Technica).
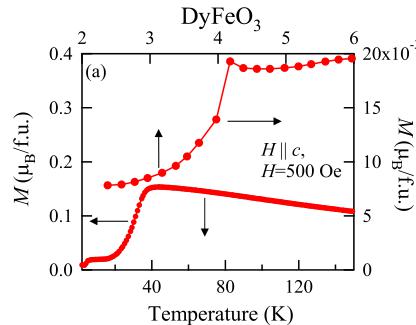
Figure 2(a) shows the T dependence of M of DyFeO_{3} along the c axis measured in H = 500 Oe. The G-type AFM order of Fe spins is set in below \( T_{N}^{Fe} \sim 645 \) K, while the G-type component directs toward the a axis ( \( G_{x} \) ). Because of DM interaction, canted components, i.e., A-type and WFM components, arise along the b and c axis, respectively ( \( G_{x}A_{y}F_{z} \) ) [12,21]. In lowering T, the G-type component of Fe spins reorients toward the b axis at \( T_{r} \sim 37 \) K, thus the magnetic configuration changes to \( A_{x}G_{y}C_{z} \) and the WFM component disappears [see Fig. 2(a)] [21], contrary to the case of other rare-earth orthoferrites which show a reorientation transition from \( G_{x}A_{y}F_{z} \) to \( F_{x}C_{y}G_{z} \) [22]. On further cooling, the M shows another anomaly at around \( T_{N}^{Dy} \sim 4 \) K [Fig. 2(a) on the upper and right-hand scales] which corresponds to the AFM ordering of Dy moments in the \( G_{x}A_{y} \) configuration [Fig. 1(a) or 1(b)]. Below \( T_{r} \) , application of \( H > H_{r}^{Fe} \) along the c axis causes the change of the configuration of Fe spins so as to produce the WFM component along the c axis [from \( A_{x}G_{y}C_{z} \) to \( G_{x}A_{y}F_{z} \) ; see Figs. 1(a) and 1(c)]. This transition occurs both for the \( T > T_{N}^{Dy} \) and \( T < T_{N}^{Dy} \) , while \( H_{r}^{Fe} \) increase steeply as the T decreases below \( T_{N}^{Dy} \) .
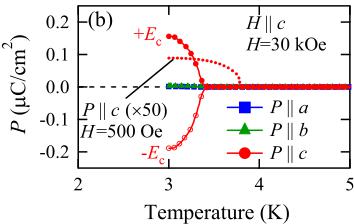
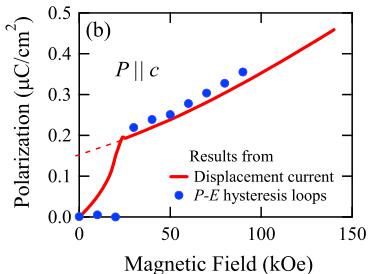
Figure 2(b) shows the H-induced P along the \(a\), \(b\), and \(c\) axes in \(H = 30\) kOe (\(>H_{\mathrm{r}}^{\mathrm{Fe}}\) at 3 K) applied along the \(c\) axis measured after ME cooling down to 3 K at \(H =\)


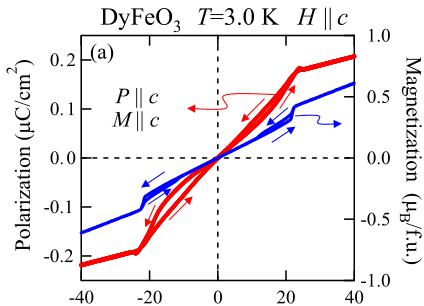
FIG. 2 (color online). T dependence of M and P in H applied along the c axis for DyFeO_{3}. (a) M measured in H = 500 Oe in the temperature range of 2.4 K < T < 6 K (the upper abscissa) and 2.4 K < T < 150 K (the lower one), respectively. (b) P along the a, b, and c axes in H = 30 kOe ( \( >H_{r}^{Fe} \) ; indicated by filled rectangles, triangles, and circles, respectively). Dotted line shows T dependence of P magnified by a factor of 50 along the c axis in H = 500 Oe ( \( 30 kOe applied along the c axis and \( E = \pm 2 \) kV/cm along the respective axes. A large P is observed only along the c axis with a polarity depending on the sign of poling E. As increasing T, P monotonically decreases and becomes zero at around \( T_{N}^{Dy} \) , suggesting that the ordered moments of Dy should contribute to this P. A slight difference in the transition temperatures seen in the T dependence of M and P arises from their H dependence. In fact, \( P \parallel c \) measured in \( H(H = 500 \, \text{Oe} (< H_{\text{r}}^{\text{Fe}} \text{ below } T_{\text{N}}^{\text{Dy}}) \) along the c axis) shows a higher transition temperature ( \( \sim 3.8 \, K \) ; see a dotted line in Fig. 2(b)). Figure 3 shows the \( H(H \parallel c) \) dependence of M and P along the c axis at 3 K. The ME poling was executed under \( E \parallel c \) of about \( +2 \, kV/cm \) and \( H \parallel c \) of \( +30 \, kOe \) . M along the c axis is 1 order of magnitude smaller than M along the a and b axes, since the Dy moments show the strong magnetic anisotropy, lying in the ab-plane. Therefore, the M along the c axis almost linearly depends on H, but shows a small jump at \( H_{r}^{Fe} \) . As increasing H, P increases monotonically from zero, then shows a small drop at around the \( H_{r}^{Fe} \sim 24 \) kOe, while changing its slope above \( H_{r}^{Fe} \) . The P continues to increase with H nonlinearly, at least, up to H = 140 kOe. FIG. 3 (color online). (a) \( H(H \parallel c) \) dependence of M and P measured along the c axis at T = 3 K. (b) H dependence of the residual P obtained by P-E hysteresis loops (filled circles) and the displacement current measurement (solid line). [see Fig. 3(b)]. With changing the sign of H, the sign of P is also reversed. We also confirmed that the relative direction between P and H was reversed by changing the sign of either the H or E in the poling procedures (not shown). As for \( H < H_{f}^{Fe} \) , although the magnetic point group allows the existence of \( \alpha_{xx} \) , \( \alpha_{yy} \) , and \( \alpha_{zz} \) , only the \( \alpha_{zz} \) component has a large value. The value of \( \alpha_{zz} \) calculated from the slope of the P-H curve at 3 K is \( \sim2.4 \times 10^{-2} \) in CGS dimensionless unit. This is 2 orders of magnitude larger than those reported for \( Cr_{2}O_{3} \) and the largest value ever reported among the single-phase ME compounds, while the components \( \alpha_{xx} \) and \( \alpha_{yy} \) are under the detection limit (less than \( 10^{-4} \) ). The anomalous behavior of P coupled with the change of the Fe spin configuration suggests that the ME effect in this system depends not only on the magnetic structure of Dy but also on that of Fe. Upon the emergence of the WFM state at \( H = H_{f}^{Fe} \) , G-type components of Fe spins rotate by \( 90^{\circ} \) in the ab plane and M shows a positive jump, while the P at \( H_{f}^{Fe} \) shows a small negative jump. It is important to note that the extrapolated value of P in the region of \( H > H_{f}^{Fe} \) toward H = 0 is nonzero [ \( \sim 0.15 \mu C/cm^{2} \) at 3 K; see a dashed line in Fig. 3(b)]. This means that a spontaneous P exists along the c-axis in \( H > H_{f}^{Fe} \) . The coexistence of the spontaneous P and the weak ferromagnetism in \( H > H_{f}^{Fe} \) indicates that this phase is not a linear-ME phase but can be rather viewed as a multiferroic one. The value of spontaneous P is quite large as the spin-driven ferroelectrics and comparable to those reported for orthomanganites such as \( DyMnO_{3} \) [6] and \( DyMn_{2}O_{5} \) [23]. Figure 4(a) shows the P-E hysteresis loops measured at 3 K with the E-sweep frequency (f) of 1 Hz in \( H \parallel c \) . Above \( H > H_{f}^{Fe} \) , the sign of P in \( H > H_{f}^{Fe} \) is reversed directly by the application of E. The coercive field decreases monotonically as H increases. The H dependence of the residual P obtained from P-E hysteresis is consistent with that measured by displacement current measurement apart from the linear-ME region ( \( H < H_{f}^{Fe} \) ), where P is too hard to be reversed directly by E up to 30 kV/cm [see Fig. 3(b)]. Here, we propose the exchange striction as a possible microscopic origin of the spontaneous P in the \( H > H_{f}^{Fe} \) multiferroic phase. For this FE state, the magnetic structure of Dy is \( G_{x}A_{y} \) and that of Fe is \( G_{x}A_{y}F_{z} \) [see Fig. 1(c)]. The magnetic point group is expected to be \( m'm'2 \) [19], which allows the existence of both the spontaneous P and M along the c axis as well as the linear-ME tensor components \( \alpha_{xx} \) , \( \alpha_{yy} \) , and \( \alpha_{zz} \) [18,19]. The fact that the directional relation between P and \( M(P \parallel M) \) is different from those reported in other transverse-spiral magnets manifests FIG. 4 (color online). (a) H dependence of the P-E hysteresis measured under H || c and E || c configuration with f = 1 Hz at T = 3 K. (b) f dependence of the P-E hysteresis in H = 25 kOe at T = 3 K. (c) The retention property of P against sweeping of H taken at T = 2.5 K. H is swept between +60 kOe and -60 kOe after ME-cooling from 10 to 2.5 K with E = +15 kV/cm and H = +60 kOe. that the origin of the spontaneous P in this phase is different from that of the inverse DM interaction model [13]. As shown in Fig. 1(c), the ferromagnetic sheets formed by Fe and Dy stack along the c axis; both of Dy and Fe moments (spins) possess the \( A_{y} \) components. As for the y component, the spins on a Fe layer become parallel to the moments on the one of the nearest neighbor layer of Dy and antiparallel to that on the other nearest neighbor layer. As a result, Dy layers should displace cooperatively toward Fe layers with antiparallel spins via the exchange striction, and, accordingly, the P along the c axis should be generated. For reversal of P, therefore, it is necessary to change the phase (0 or \( \pi \) ) of layered-AFM spin modulation of either Dy or Fe, i.e., to reverse the moment (spin) of each \( Dy^{3+} \) ( \( Fe^{3+} \) ). It should be noted that in \( H > H_{r}^{Fe} \) the phase (0 or \( \pi \) ) of AFM modulation (intralayer component) of Fe is fixed so as to produce WFM components in the H direction because of the DM interaction. Thus, the E-induced reversal of P in this state can be ascribed to the change of the phase of layered-AFM spin modulation of \( Dy^{3+} \) moments, i.e., reversal of each Ising moment of the \( Dy^{3+} \) [see Fig. 1(d)]. Figure 4(b) shows the P-E hysteresis loops measured with varying the E-sweeping speed (frequency f) at H = 25 kOe applied along the c axis. Complete reversal of P is attained only when f < 10 Hz, which suggests the relatively slow dynamics of the nucleation process of FE domains with opposite electric polarity (or excitation of AFM kinks of Ising Dy moments) and/or their domain wall (or kink) motion. Such a slow dynamics may result from the difficulty in reversing large Ising moments of Dy. Figure 4(c) shows the retention property of P against sweeping of H at 2.5 K. H was swept between +60 kOe and -60 kOe after ME-cooling from 10 to 2.5 K with \( E = +15 kV/cm \) and \( H = +60 kOe \) . Once the sample is poled by the appropriate ME-cooling procedure, the sign of ME coupling and the magnitude of P are conserved even if H gets across the phase boundary ( \( H = H_{r}^{Fe}(\sim32 kOe \) at 2.5 K)) repeatedly, while changing the polarity across H = 0. This suggests quasicontinuity of P between the low-H linear-ME phase and the H-induced multiferroic phase, although the phase change at \( H = H_{r}^{Fe} \) is of first order in nature. Note that the H direction here is perpendicular to the Ising axis of the Dy moments. Thus, what is conserved during the H-sweeping process is the phase (0 or \( \pi \) ) of AFM modulation of Dy moments. In other words, magnetic structure changes either from (c) to (a) or from (d) to (b) as shown in Fig. 1, as the H decreases from \( +H > H_{r}^{Fe} \) and crosses \( H_{r}^{Fe} \) . Note that the initial phase of AFM modulation of Dy moments is determined by the sign of H and E in the ME poling procedure. On the other hand, the phase of AFM modulation of Fe spins in the H-induced WFM phase is determined uniquely by the direction of H via the DM interaction irrespective of the phase of AFM modulation of Dy moments or the ME poling procedure. Thus, when the direction of H is reversed, the phase of AFM modulation of Fe spins is reversed so as to align WFM components in the direction of H, while the phase of Dy-moment modulation remains intact. Therefore the sign of the spontaneous P is reversed as shown in Fig. 4(c). In summary, we have studied the ME properties of \( DyFeO_{3} \) . A very large linear-ME tensor component \( \alpha_{zz} \sim 2.4 \times 10^{-2} \) is observed below \( T_{N}^{Dy} (\sim 4 \, \text{K}) \) . More importantly, we show that \( DyFeO_{3} \) is a new class of multiferroics with \( M \parallel c \) and \( P \parallel c \) in the application of \( H (\geq 24 \, \text{kOe}) \) along the c axis. The exchange striction working between adjacent \( Fe^{3+} \) and \( Dy^{3+} \) layers with the layered-AFM components is a possible origin of the FE polarization in the H-induced multiferroic phase. The authors thank N. Furukawa, Y. Taguchi, and S. Horiuchi for useful discussions and comments. This work was in part supported by Grant-in-Aids for Scientific Research from the MEXT (No. 20340086, 20046004, and 20740186), Japan. [1] M. Fiebig, J. Phys. D 38, R123 (2005). [2] S.-W. Cheong and M. Mostvoy, Nature Mater. 6, 13 (2007). [3] R. Ramesh and N. A. Spaldin, Nature Mater. 6, 21 (2007). [4] Y. Tokura, J. Magn. Magn. Mater. 310, 1145 (2007). [5] T. Kimura et al., Nature (London) 426, 55 (2003). [6] T. Goto et al., Phys. Rev. Lett. 92, 257201 (2004). [7] Y. Yamasaki et al., Phys. Rev. Lett. 96, 207204 (2006). [8] K. Taniguchi et al., Phys. Rev. Lett. 97, 097203 (2006). [9] T. Kimura et al., Phys. Rev. Lett. 94, 137201 (2005). [10] S. Ishiwata et al., Science 319, 1643 (2008). [11] K. Taniguchi et al., Appl. Phys. Express 1, 031301 (2008). [12] I. Dzyaloshinskii, J. Phys. Chem. Solids 4, 241 (1958); T. Moriya, Phys. Rev. 120, 91 (1960). [13] H. Katsura et al., Phys. Rev. Lett. 95, 057205 (2005). [14] L. M. Holmes et al., Phys. Rev. B 5, 138 (1972). [15] L. M. Holmes and L. G. Van Uitert, Phys. Rev. B 5, 147 (1972). [16] G. Velleaud and M. Mercier, Solid State Commun. 17, 237 (1975). [17] E. F. Bertaut, in Magnetism, edited by G. T. Rado and H. Suhl (Academic, New York, 1963), Vol. 3, p. 149. [18] A. S. Borovik-Romanov and H. Grimmer, in International Tables for Crystallography, edited by A. Authier (Kluwer Academic, Dordrecht, 2003), Vol. D, p. 137. [19] T. Yamaguchi and T. Tsushima, Phys. Rev. B 8, 5187 (1973). [20] C. E. Johnson et al., J. Magn. Magn. Mater. 15, 557 (1980). [21] G. Gorodetsky et al., J. Appl. Phys. 39, 1371 (1968). [22] R. L. White, J. Appl. Phys. 40, 1061 (1969). [23] D. Higashiyama et al., Phys. Rev. B 70, 174405 (2004).