| Experiment Temperature | 5 K |
|---|---|
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | Pnma (#62) |
| Magnetic Space Group | Pn'ma' (#62.448) |
| Magnetic Point Group | m'm'm (8.4.27) |
| Lattice Parameters | 5.62780 7.47670 5.25070 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1039/c4dt02503b |
| Reference | H. James, B.J. Kennedy, T.A. Whittle and M. Avdeev, Dalton Trans. (2014) 43 17085-17089. |
Title
Structural and magnetic studies of perovskite \( YCr_{0.5}Mn_{0.5}O_{3} \)
Authors
Hannah James\( ^{a} \), Brendan J. Kennedy\( ^{*a} \), Thomas A. Whittle\( ^{a} \) and Maxim Avdeev\( ^{b} \)
\( ^{a} \) School of Chemistry, The University of Sydney, Sydney, NSW 2006, Australia. E-mail: brendan.kennedy@sydney.edu.au; Tel: +61 2 9351 2769 \( ^{b} \) Australian Nuclear Science and Technology Organisation, Lucas Heights, NSW 2234, Australia
Materials Studied
\( YCr_{0.5}Mn_{0.5}O_{3} \) (Also mentions \( Y_{2}O_{3} \) as a minor impurity phase)
Key Information
- Crystal structure / space group: Orthorhombic space group \( Pbnm \) (at room temperature). The Cr and Mn cations are disordered on the octahedral sites. The structure exhibits cooperative tilting of the corner-sharing \( (\mathrm{MnCr})\mathrm{O}_{6} \) octahedra, described as \( a^{-}a^{-}c^{+} \) in Glazer's nomenclature.
- Magnetic ordering type and temperature:
- Magnetic ordering observed near 75 K (divergence of ZFC/FC susceptibilities).
- Antiferromagnetic ground state (indicated by negative Weiss constant).
- Ferrimagnetic behavior (from hysteresis loops at 4 K and rapid increase in field-cooled susceptibility).
- Low temperature neutron diffraction reveals a G-type antiferromagnetic arrangement.
- Presence of a ferromagnetic component along the b-axis.
- Magnetic model: \( \Gamma5 \) CxFyAz, with propagation vector \( k(0,0,0) \).
- Propagation vector(s): \( k(0,0,0) \)
- Magnetic moments:
- Effective magnetic moment (\( \mu_{eff} \)): \( 4.12\mu_{B} \) (from Curie-Weiss fit above 150 K).
- Expected moment for 1:1 mixture of \( Cr^{3+} \) (\( d^{3} \)) and \( Mn^{3+} \) (\( d^{4} \)): \( 4.39\mu_{B} \).
- Determined components of magnetic moment at 5 K:
- a-axis: 0.63(3) \( \mu_{B} \)
- b-axis: 0.25(14) \( \mu_{B} \)
- c-axis: 1.83(2) \( \mu_{B} \)
- Total magnetic moment at 5 K: 1.95(3) \( \mu_{B} \) (approximately 0.65 of the full moment).
- Lattice parameters: (Orthorhombic \( Pbnm \) at room temperature)
- \( a = 5.25074(8) \) Å
- \( b = 5.62780(10) \) Å
- \( c = 7.47670(10) \) Å
- Volume = 220.937(6) Å\( ^{3} \)
- Any other critical measured values:
- Weiss constant (\( \theta \)): -57 K.
- Bond Valence Sum (BVS): Mn = 3.19, Cr = 2.90.
- Pseudo-tetragonal distortion: \( \sqrt{2}b/c = 1.06 \).
- Rietveld refinement parameters (room temperature): \( R_{p} = 5.40 \), \( R_{wp} = 4.16 \), \( \chi^{2} = 2.08 \).
- Rietveld refinement parameters (5 K): \( R_{p} = 4.53\% \), \( R_{wp} = 5.93\% \), \( R_{mag} = 6.14\% \), \( \chi^{2} = 3.10 \).
Synthesis Method
A 5 g sample of \( YCr_{0.5}Mn_{0.5}O_{3} \) was prepared by solid-state synthesis using stoichiometric quantities of \( Y_{2}O_{3} \), \( Cr_{2}O_{3} \), and \( Mn_{2}O_{3} \). 1. The oxides were dried. 2. Stoichiometric quantities were mixed in an agate mortar and pestle under acetone. 3. The mixture was heated overnight in air at 1173 K. 4. After regrinding, it was heated at 1473 K for 24 hours in a muffle furnace. 5. The powder was reground, pressed into pellets, and heated at 1673 K for 96 hours. This step involved periodic regrinding and pelleting until the X-ray diffraction pattern no longer changed. 6. The sample was slowly cooled to room temperature in the furnace over approximately 5 hours. The final product was black.
Abstract
The structure of \( YCr_{0.5}Mn_{0.5}O_{6} \), established from Rietveld refinement of powder neutron diffraction data, contains Cr and Mn that are disordered on the octahedral sites. The structure is best described in the orthorhombic space group \( Pbnm \). Low temperature neutron diffraction data reveal a G-type antiferromagnetic type arrangement, with a ferromagnetic component along the b-axis, indicating that the Cr and Mn couple ferro (or possibly ferri) magnetically to each other.
Main Content Summary
This study investigates the structural and magnetic properties of the perovskite \( YCr_{0.5}Mn_{0.5}O_{3} \) using powder neutron diffraction (NPD) and magnetic measurements. The primary goal was to resolve the controversy regarding the ordering of Cr and Mn cations, as previous X-ray diffraction (XRD) studies by different groups suggested either a disordered or an ordered arrangement. Due to the similar X-ray scattering factors of \( Cr^{3+} \) and \( Mn^{3+} \), NPD was employed, which offers significantly different scattering lengths for these ions, making it ideal for distinguishing their distribution.
Room temperature NPD data unequivocally confirmed that the Cr and Mn cations are disordered on the octahedral sites, with the structure best described in the orthorhombic space group \( Pbnm \). Rietveld refinement of the NPD data provided precise lattice parameters: \( a = 5.25074(8) \) Å, \( b = 5.62780(10) \) Å, and \( c = 7.47670(10) \) Å. The structure exhibits a Jahn-Teller-like distortion associated with the \( Mn^{3+} \) cation, evidenced by distorted \( (\mathrm{MnCr})\mathrm{O}_{6} \) octahedra with four short and two long bonds. Bond Valence Sum calculations further supported the trivalent state of both Cr and Mn.
Magnetic measurements revealed a divergence between zero-field-cooled (ZFC) and field-cooled (FC) susceptibilities near 75 K, indicating magnetic ordering. The inverse susceptibility above 150 K followed Curie-Weiss behavior, yielding an effective magnetic moment of \( 4.12\mu_{B} \) and a negative Weiss constant of -57 K, consistent with an antiferromagnetic ground state. However, the rapid increase in FC susceptibility and clear hysteresis loops observed at 4 K pointed towards ferrimagnetic behavior. An unusual crossover from positive to negative values in ZFC measurements was attributed to magnetic compensation between different local magnetic couplings.
Low-temperature neutron diffraction data confirmed the presence of magnetic scattering, which could be indexed with a propagation vector \( k(0,0,0) \), implying that the magnetic unit cell is commensurate with the chemical unit cell. Representational analysis identified the \( \Gamma5 \) CxFyAz model as the best description of the magnetic structure. This model corresponds to a G-type antiferromagnetic arrangement, where the strongest antiferromagnetic component is along the c-axis, accompanied by a small ferromagnetic component along the b-axis. The refined magnetic moments at 5 K were 0.63(3) \( \mu_{B} \) along a, 0.25(14) \( \mu_{B} \) along b, and 1.83(2) \( \mu_{B} \) along c, resulting in a total moment of 1.95(3) \( \mu_{B} \). The presence of a ferromagnetic component, even in the disordered structure, suggests ferro- or ferri-magnetic coupling between Cr and Mn.
Conclusion
Neutron diffraction measurements show that the structure of the perovskite \( YCr_{0.5}Mn_{0.5}O_{6} \) is adequately described in the orthorhombic space group \( Pbnm \), in which the \( Cr^{3+} \) and \( Mn^{3+} \) cations randomly occupy the octahedral sites. Whilst it is possible altering the conditions used to prepare the sample can alter the degree of disorder, the neutron data demonstrate that the previous suggestion of ordering of the \( Cr^{3+} \) and \( Mn^{3+} \) cations is incorrect. Magnetic susceptibility measurements confirm the presence of magnetic ordering. Low temperature neutron diffraction data reveal that the strongest magnetic exchange is indicative of a G-type antiferromagnetic type arrangement. These data reveal the presence of a ferromagnetic component along the b-axis, indicating that the Cr and Mn couple ferro (or possibly ferri) magnetically to each other.
PAPER

CrossMark
Cite this: Dalton Trans., 2014, 43, 17085
Received 17th August 2014, Accepted 22nd September 2014 DOI: 10.1039/c4dt02503b
www.rcs.org/datton
Structural and magnetic studies of perovskite \( YCr_{0.5}Mn_{0.5}O_{3} \)
Hannah James, \( ^{a} \) Brendan J. Kennedy, \( ^{*a} \) Thomas A. Whittle \( ^{a} \) and Maxim Avdeev \( ^{b} \)
The structure of \( YCr_{0.5}Mn_{0.5}O_{6} \) , established from Rietveld refinement of powder neutron diffraction data, contains Cr and Mn that are disordered on the octahedral sites. The structure is best described in the orthorhombic space group \( Pbnm \) . Low temperature neutron diffraction data reveal a G-type antiferromagnetic type arrangement, with a ferromagnetic component along the b-axis, indicating that the Cr and Mn couple ferro (or possibly ferri) magnetically to each other.
Introduction
The complex interplay between the spin, orbit, lattice and charge degrees of freedom in doped manganese perovskites results in examples of unique and fascinating phenomena, including colossal magnetoresistance, magnetocaloric response and multiferroic behaviour. \( ^{1} \) Orbital ordering in \( Mn^{3+} \) perovskites is a consequence of a Jahn–Teller type distortion, \( ^{2} \) that is also evident in \( Cu^{2+} \) (3d \( ^{9} \) ) perovskites, where it is related to the observed superconducting behaviour.
The title oxide \( Y_{2}CrMnO_{6} \) has recently become of interest, however the structure of this is not well established. Liu and co-workers \( ^{3} \) described it as having an orthorhombic structure in space group \( Pnma \) (an alternate setting of \( Pbnm \) ) where the \( Cr^{3+} \) and \( Mn^{3+} \) cations are disordered on the octahedral sites. If the two cations are disordered it is best to describe this as \( YCr_{0.5}Mn_{0.5}O_{3} $ to emphasise the disorder. Independently Hao and co-workers \( ^{4,5} \) argued that the \( Cr^{3+} \) and \( Mn^{3+} \) \( C_{2} \) cations were ordered, suggesting two monoclinic structures initially in \( P2_{1}/n \) but later revising this to \( P2_{1}/b \) . The cation ordered arrangement is best represented by the formula \( Y_{2}CrMnO_{6} \) . These two monoclinic structures differ in the arrangement of the \( Cr^{3+} \) and \( Mn^{3+} \) , cations, the former having a rock-salt like ordering whereas the latter has a layered ordered arrangement. Both \( Liu^{3} \) and \( HaO^{4,5} \) relied on X-ray diffraction to establish the structure of \( YCr_{0.5}Mn_{0.5}O_{3} \( . The applicability of this approach is questionable since the electron configuration of \) Cr^{3+} \( and \) Mn^{3+} $ differ by a single electron; consequently \( Cr^{3+} \) and \( Mn^{3+} \) are practically indistinguishable when investigated using conventional X-ray diffraction methods. Ordering of cations in perovskites typically requires a significant difference in the ionic size and/or charge of the cations \( ^{6} \) as illustrated in \( Sr_{2}NiWO_{6} \) \( ^{7} \) . Charge ordering occurs in oxides such as \( Ba_{2}Bi^{III}Bi^{VO_{6}} \) . \( ^{8} \) Orbital ordering can also occur leading to a lowering of symmetry as illustrated in the vanadates \( AVO_{3} \) . \( ^{9} \) Cation ordering, irrespective of its origin, is often associated with unusual electronic properties \( ^{10} \) and the ferrimagnetism reported for \( YCr_{0.5}Mn_{0.5}O_{3}M \) may provide evidence of this. Whilst there are numerous examples of cation ordering in perovskite-type oxides, \( ^{6} \) ordering of \( Cr^{3+} \) and \( Mn^{3+} \) in a perovskite would be exceptional, given the similarity in the size and charge of these two cations and would be a unique example of orbital effects inducing chemical ordering. Given the absence of any well known examples of such ordering there is a need to establish if such ordering does indeed occur.
In the present paper we have utilised powder neutron diffraction to establish a precise and accurate structure of \( YCr_{0.5}Mn_{0.5}O_{5} \) . Whilst the X-ray scattering factors of \( Cr^{3+} \) and \( Mn^{3+} \) , are extremely similar the neutron scattering lengths are dramatically different; Mn has a coherent scattering factor of -3.73 fm and Cr has a coherent scattering factor of 3.635 fm. The magnetic structure of \( YCr_{0.5}Mn_{0.5}O_{4} \) has also been investigated.
Experimental
A 5 g sample of \( YCr_{0.5}Mn_{0.5}O_{3}\mathrm{~w a s~prepared~by~the~solid~state~synthesis~of~}Y_{2}O_{3} \) , \( Cr_{2}O_{3} \) and \( Mn_{2}O_{3} \) . After drying the oxides, stoichiometric quantities of \( Y_{2}O_{3} \) , \( Cr_{2}O_{3}~and~Mn_{2}O_{3} \) were mixed in an agate mortar and pestle under acetone. The resulting mixture was transferred to an alumina boat and then heated overnight in air at 1173 K, and then, after regrinding, at 1473 K for 24 hours using a muffle furnace. The powder was reground, pressed into pellets at heated at 1673 K for 96 hours with periodically re-grounding and pelleting until the powder
X-ray diffraction pattern no longer changed. The sample was cooled to room temperature in the furnace over a period of \( \sim \) 5 hours. The final product was black.
Magnetic measurements were conducted between 4 K and 300 K under both field cooled and zero field cooled conditions with a measuring magnetic field of 1 kOe using a Quantum Design Physical Properties Measurement System. Magnetic hysteresis loops were measured at 5 K.
X-ray diffraction data were collected on a PANalytical X'Pert Pro MPD X-ray diffractometer (45 kV, 40 mA). Data were collected for a \( 2\theta \) range of 5 to \( 120^{\circ} \) using \( CuK_{\alpha} \) radiation. Neutron powder diffraction data were measured using the high resolution powder diffractometer Echidna at ANSTO's OPAL facility at Lucas Heights using wavelengths of 1.622 or \( 2.439 \AA \) . \( ^{11} \)
Results and discussion
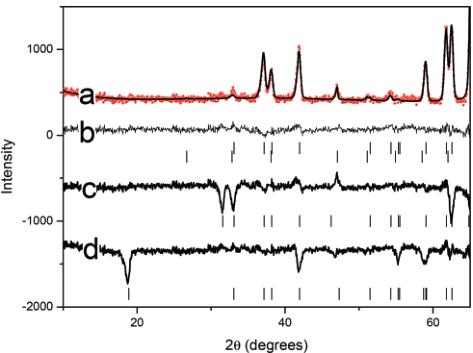
A polycrystalline sample of \( YCr_{0.5}Mn_{0.5}O_{3} \) was prepared as described by Hao et al. \( ^{4} \) The extent of cation disorder in perovskites can be influenced by the highest temperature used to prepare the sample and the rate of cooling, with rapid cooling tending to stabilise disordered structures. The present sample was heated to 1673 K, the same maximum temperature employed by Hao et al. \( ^{4} \) and the sample was slowly cooled. The structure of this was initially investigated using powder X-ray diffraction (XRD) data. As described by Liu et al. \( ^{3} \) and Hao et al. \( ^{4} \) Rietveld refinement assuming a disordered arrangement of the Cr and Mn cations in the orthorhombic Pbnm space group was successful. Examination of the data revealed a weak peak near \( 2\theta = 30^{\circ} \) that was identified as coming from the presence of a small amount of \( Y_{2}O_{3} \) , Liu et al. noted that high pressure was required to eliminate the formation of this phase. \( ^{3} \) Models in the two monoclinic models described by Hao et al. ( \( P2_{1}/n \) and \( P2_{1}/b \) ) \( ^{4,5} \) were also tested and these gave comparable quality fits to the XRD data, reflecting the similarity in the X-ray scattering factors of \( Cr^{3+} \) and \( Mn^{3+} \) . The same cannot be said for the neutron powder diffraction (NPD) data. Fig. 1 illustrates a portion of the powder neutron diffraction pattern for \( YCr_{0.5}Mn_{0.5}O_{3} $ recorded at room temperature.  Fig. 1 Portion of the neutron diffraction pattern recorded for \( YCr_{0.5}Mn_{0.5}O_{3}\ at room temperature using \lambda = 2.44 \AA \) neutrons. The top trace (a) is the observed data (symbols) and the fit (solid line) to this in the orthorhombic space group Pbnm. Below this trace (b) is the difference between the observed and calculated profiles in (a) and the tick markers for the (upper) orthorhombic phase and (lower) \( Y_{2}O_{3} \) phases. Trace (c) is the difference between the observed data and the best fit in \( P2_{1}/n \) , and immediately below are the tick marks showing the positions of the Bragg reflections in \( P2_{1}/n \) . Trace (d) is the difference between the observed data and the best fit in \( P2_{1}b \) , and immediately below are the tick marks showing the positions of the Bragg reflections in \( \overline{P2_{1}b} \) . Although the fits using the monoclinic models allowed for the presence of trace amounts of \( Y_{2}O_{3} \) the tick marks for this phase are not shown below traces (c) and (d) for clarity.
The models for the \( P2_{1}/b \) and \( P2_{1}/n \) symmetries both calculate significant intensity in peaks when there is none present, making it clear that they are not appropriate. Conversely the fit obtained using the disordered model in Pbnm contains no significant discrepancies. It should be noted that in the refinement of the Pbnm model the atomic displacement parameter of the disordered Cr/Mn site was fixed at \( 0.5 \times 10^{-2} \) Å \( ^{3} \) . The 1:1 mixture of Cr and Mn gives this site an effective neutron scattering length of close to zero.
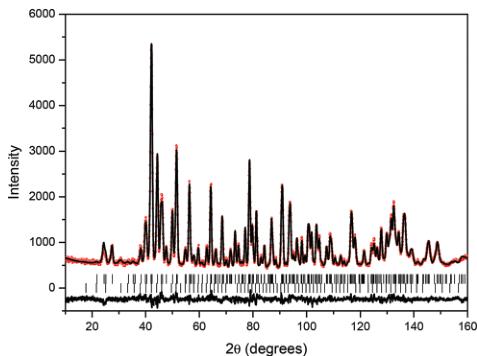
The refined structural parameters, obtained using a combination of the 1.62 and 2.44 Å neutron data sets are summarised in Table 1, whilst the fit to the 1.62 Å pattern is shown in Fig. 2. The unit cell parameters in the orthorhombic Pbnm
Table 1 Refined structural parameters for \( YCr_{0.5}Mn_{0.5}O_{3}s \) using neutron diffraction data. \( a = 5.25074(8) \) b = 5.62780(10) c = 7.47670(10) Å. Volume = 220.937(6) Å \( ^{3} \) . \( R_{p} = 5.40 R_{wp} = 4.16 \) and \( \chi^{2} = 2.08 \)
| Name | x | y | z | Ui/Ue \( \times \) 100 |
| Y | 0.01702(20) | 0.57255(19) | 0.25 | 0.860(27) |
| Cr | 0 | 0 | 0 | 0.5 \( ^{a} \) |
| Mn | 0 | 0 | 0 | 0.5 \( ^{a} \) |
| O1 | -0.10690(24) | -0.03501(25) | 0.25 | 0.79 \( ^{b} \) |
| O2 | 0.19654(18) | 0.31212(20) | 0.05396(13) | 1.02 \( ^{b} \) |
| U \( ^{11} \) | U \( ^{22} \) | U \( ^{33} \) | U \( ^{12} \) | |
| O1 | 0.89(8) | 1.16(8) | 0.32(7) | 0.67(6) |
| O2 | 0.52(4) | 1.83(6) | 0.71(5) | -0.15(4) |
\( ^{a} \) Fixed at \( 0.5 \times 10^{-2} \) . \( ^{b} \) Anisotropic displacement parameters were employed for the oxygen atoms, whilst that of the disordered Cr/Mn cations was fixed.

Fig. 2 Observed calculated and difference neutron diffraction profiles for \( YCr_{0.5}Mn_{0.5}O_{3} \) at room temperature using \( \lambda = 1.62 \AA \) neutrons. The structure was refined in the orthorhombic space group Pbnm. The lower set of tick marks are from \( Y_{2}O_{3} \) .
model are related to the unit cell length of the ideal cubic perovskite \( a_{0} \) as \( a \sim \sqrt{2}a_{0}b \sim \sqrt{2}a_{0}c \sim 2a_{0} \) with the expansion in the cell being a consequence of cooperative tilting of the corner sharing \( (\mathrm{MnCr})\mathrm{O}_{6} \) octahedra. The tilting in Pbnm is described as \( a^{-}a^{-}c^{+} \) in Glazer's nomenclature. The coordination of the \( (\mathrm{MnCr})\mathrm{O}_{6} \) octahedra is highly distorted with four short and two long \( (\mathrm{MnCr})-\mathrm{O} \) bonds \( (\mathrm{MnCr})-\mathrm{O}(1) \) 1.9616(4)Å and \( (\mathrm{MnCr})-\mathrm{O}(2) \) 1.9544(10) and 2.0768(11)Å. This reflects the presence of a Jahn-Teller like distortion associated with the \( Mn^{3+} \) cation. That both the Mn and Cr cations are trivalent was verified by Bond Valence calculations that gave a BVS of 3.19 for Mn and 2.90 for Cr. The distortion of the \( (\mathrm{MnCr})\mathrm{O}_{6} \) octahe-dra is associated with the large pseudo-tetragonal distortion of the unit cell with \( \sqrt{2}b/c = 1.06 \) , This is smaller than the distortion in \( YMnO_{3} \) , 1.11, \( ^{12} \) that only contains \( Mn^{3+} \) but is larger than that seen in the \( Mn^{4+} \) perovskite \( CaMnO_{3} \) \( b/c = 1.00 \) \( ^{13} \) or the \( Cr^{3+} \) containing oxide \( YCrO_{3} \) \( b/c = 1.04 \) . \( ^{14} \) A similar large distortion of both the \( BO_{6} \) octahedra and cell metric was observed in \( Sr_{2}MnSbO_{6} \) where extensive disorder of the \( Mn^{3+} \) and \( Sb^{5+} \) cations occurs. \( ^{15} \)

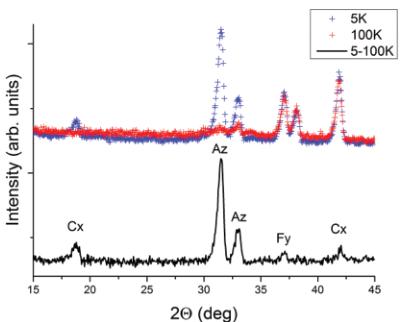
Fig. 4 Neutron powder diffraction data collected at 5 K and 100 K and the difference (blue and red symbols and black solid line, respectively). The letters indicate magnetic peaks associated with a particular magnetic ordering mode in the \( CxFyA_{Z} \) model.
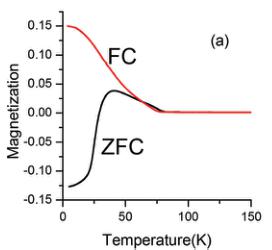
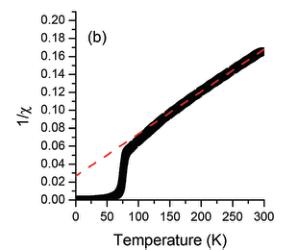
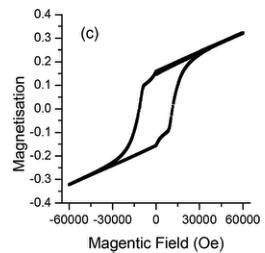
Magnetic measurements of \( YCr_{0.5}Mn_{0.5}O_{3} \( reveal a divergence of the zero field cooled and field cooled susceptibilities near 75 K as observed previously. Above 150 K the inverse susceptibilities display Curie-Weiss type behaviour with an effective magnetic moment of \) \mu_{eff} = 4.12\mu_{B} \( with a negative Weiss constant of \) \theta = -57 \( K indicative of an antiferromagnetic ground state, although the rapid increase in the field cooled susceptibility is suggestive of ferrimagnetism. The observed magnetic moment and Weiss constant are in excellent agreement with the results described by Liu et al. ( \) 4.53\mu_{B} \( and \) -59 K respectively) and the moment is close to the value expected for a 1:1 mixture of ) Cr^{3+} \( ( \) d^{3} \( ) and \) Mn^{3+} \( ( \) d^{4} $ ), \( 4.39\mu_{B} $ . The magnetization (M) vs. applied magnetic field (H) measurements at 4 K showed clear hysteresis loops, depicting ferrimagnetic behaviour. An unusual feature of Fig. 3 is the crossover from positive to negative values during the ZFC measurements. As locally \( d^{4}_{HS}-d^{4}_{HS} \) , \( d^{4}_{HS}-d^{3} \) , and \( d^{3}-d^{3} \) pairs are expected to couple via superexchange ferro-, ferro-, and antiferromagnetically, respectively, this is believed to be a consequence of magnetic compensation between the \( Mn^{3+}-Mn^{3+} \) and \( Mn^{3+}-Cr^{3+} \) contact



Fig. 3 (a) Temperature dependence of the field-cooled (FC) and zero-field-cooled (ZFC) magnetization of \( YMn_{0.5}Cr_{0.5}O_{3} \) was measured at magnetic field of 1 kOe. (b) Temperature dependence of the inverse (FC) molar magnetic susceptibility. The dashed line is a linear fit to the high temperature region. (c) Magnetization as a function of applied magnetic field for \( YMn_{0.5}Cr_{0.5}O_{3} at 5 K \) .

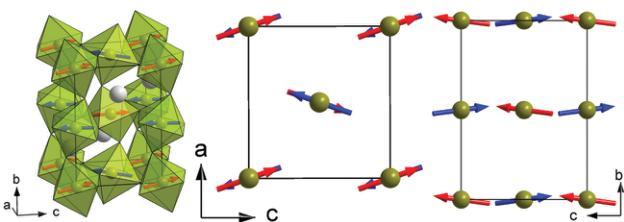
Fig. 5 General view of the crystal and magnetic structure of Y(Cr_{0.5}Mn_{0.5})O_{3} (left) and projections along b- (middle) and a-axes (right) (in Pnma setting).
rich domains with the moment aligned antiparallel to each other. We note that the effect of compensation was not observed by \( Liu^{3} \) as it is clearly highly dependent on the sample preparation protocol determining Mn and Cr distribution uniformly over the sample.
Neutron diffraction measurements at low temperatures showed the presence of magnetic scattering, Fig. 4. All the magnetic peaks were indexed by a chemical unit cell i.e. with the propagation vector \( k(0,0,0) \) . Representational analysis performed with BasiReps for the (4a) Wyckoff site of the space group 62 in the standard Pnma setting revealed AxGyCz, GxAyFz, CxFyAz, and FxCgYz possible ordering models (irreducible representations \( \Gamma1 \) , \( \Gamma3 \) , \( \Gamma5 \) , and \( \Gamma7 \) , respectively). Data examination showed that the best magnetic model is unambiguously \( \Gamma5 \) CxFyAz. The structure is best described as G-type, where the AFM component is along c-axis, containing a small ferromagnetic component along the b-axis, see Fig. 5.

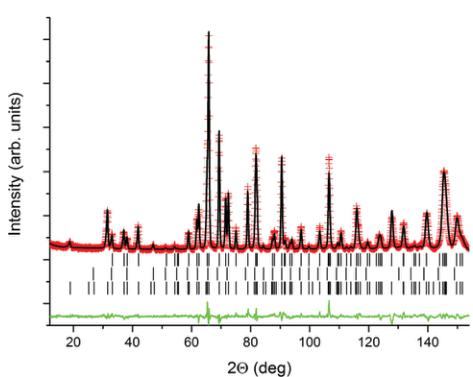
Fig. 6 The Rietveld plot for \( Y(\mathrm{Cr}_{0.5}\mathrm{Mn}_{0.5})\mathrm{O}_{3} \) refined against NPD data collected at 5 K. The red crosses and black and green solid lines indicate the observed and calculated patterns and their difference, respectively. The tick marks from top to bottom indicate the position of the diffraction peaks of the nuclear structures of \( Y(\mathrm{Cr}_{0.5}\mathrm{Mn}_{0.5})O_{3} \) , \( Y_{2}O_{3} \) (0.53(5)wt.%), and magnetic structure of \( Y(\mathrm{Cr}_{0.5}\mathrm{Mn}_{0.4})\mathrm{O}_{3} \) . \( R_{p} = 4.53\% \) , \( R_{wp} = 5.93\% \) , \( R_{mag} = 6.14\% \) , \( \chi^{2} = 3.10 \) .
In the modelling of the magnetic site it was assumed that the reduction of the moment from the full moment of S = 3/2 \( Cr^{3+} \) and \( S = 2~Mn^{3+} \) is the same for both cations. The final Rietveld plot is shown in Fig. 6. The determined components of magnetic moment along a-, b-, and c-axes are 0.63(3), 0.25(14), 1.83(2) \( \mu_{B} \) , respectively yielding the total moment of 1.95(3) \( \mu_{B} \) which is \( \sim0.65 \) of the full moment. The moment reduction is not surprising as locally some \( Mn^{3+} \) and \( Cr^{3+} \) atoms will have a combination of the nearest magnetic neighbours with interactions of varying strength or even type (AFM/FM).
Finally, the model indeed allows ferromagnetic component (along b-axis) and then we have two options: either Cr and Mn are coupled ferro- or ferri- to each other. The data does not allow these options to be distinguished. That such coupling can exist in the disordered model was overlooked by Hiu et al. \( ^{4,5} \)
Conclusions
Neutron diffraction measurements show that the structure of the perovskite \( YCr_{0.5}Mn_{0.5}O_{6} \) is adequately described in the orthorhombic space group \( Pbnm \) , in which the \( Cr^{3+} \) and \( Mn^{3+} \) cations randomly occupy the octahedral sites. Whilst it is possible altering the conditions used to prepare the sample can alter the degree of disorder, the neutron data demonstrate that the previous suggestion of ordering of the \( Cr^{3+} \) and \( Mn^{3+} \) cations is incorrect. Magnetic susceptibility measurements confirm the presence of magnetic ordering. Low temperature neutron diffraction data reveal that the strongest magnetic exchange is indicative of a G-type antiferromagnetic type arrangement. These data reveal the presence of a ferromagnetic component along the b-axis, indicating that the Cr and Mn couple ferro (or possibly ferri) magnetically to each other.
Acknowledgements
We acknowledge the Australian Research Council and the Australian Institute of Nuclear Science and Engineering for support of this work.
References
1 J. M. D. Coey, M. Viret and S. von Molnar, Adv. Phys., 1999, 48, 167–293.
2 Z. Popovic and S. Satpathy, Phys. Rev. Lett., 2002, 88, 197201.
3 F. Y. Liu, J. J. Li, Q. L. Li, Y. Wang, X. D. Zhao, Y. J. Hua, C. T. Wang and X. Y. Liu, Dalton Trans., 2014, 43, 1691–1698.
4 L. Yang, Q. Y. Duanmu, L. Hao, Z. F. Zhang, X. P. Wang, Y. Y. Wei and H. Zhu, J. Alloys Comp., 2013, 570, 41–45.
5 L. Hao, L. Yang, M. H. Lee, T. H. Lin, Z. F. Zhang, X. N. Xie and H. Zhu, J. Alloys Compd., 2014, 601, 14–18.
6 M. T. Anderson, K. B. Greenwood, G. A. Taylor and K. R. Poeppelmeier, Prog. Solid State Chem., 1993, 22, 197–233.
7 Q. D. Zhou, B. J. Kennedy, C. J. Howard, M. M. Elcombe and A. J. Studer, Chem. Mater., 2005, 17, 5357–5365.
8 B. J. Kennedy, C. J. Howard, K. S. Knight, Z. M. Zhang and Q. D. Zhou, Acta Crystallogr., Sect. B: Struct. Sci., 2006, 62, 537–546.
9 S. Miyasaka, Y. Okimoto, M. Iwama and Y. Tokura, Phys. Rev. B: Condens. Matter, 2003, 68, 100406.
10 K. L. Kobayashi, T. Kimura, H. Sawada, K. Terakura and Y. Tokura, Nature, 1998, 395, 677–680.
11 K. D. Liss, B. Hunter, M. Hagen, T. Noakes and S. Kennedy, Physica B, 2006, 385–86, 1010–1012.
12 J. A. Alonso, M. J. Martinez-Lope, M. T. Casais and M. T. Fernandez-Diaz, Inorg. Chem., 2000, 39, 917–923.
13 Q. D. Zhou and B. J. Kennedy, J. Phys. Chem. Solids, 2006, 67, 1595–1598.
14 K. Sardar, M. R. Lees, R. J. Kashtiban, J. Sloan and R. I. Walton, Chem. Mater., 2011, 23, 48–56.
15 M. Cheah, P. J. Saines and B. J. Kennedy, J. Solid State Chem., 2006, 179, 1775–1781.