| Transition Temperature | 720 K |
|---|---|
| Experiment Temperature | 4.2 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | Pcmn (#62) |
| Magnetic Space Group | Pn'm'a (#62.446) |
| Magnetic Point Group | m'm'm (8.4.27) |
| Lattice Parameters | 5.64000 14.68000 5.39000 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1143/JPSJ.24.446 |
| Reference | Takayoshi Takeda, Yasuo Yamaguchi, Shoichi Tomiyoshi, Masahiro Fukase, Mitsuo Sugimoto, Hiroshi Watanabe, J. Phys. Soc. Jpn. (1968) 24 446 - 452 |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Fe1 | Fe | 0.0 | 0.0 | 4.5 | 4.50 |
| Fe2 | Fe | 0.0 | 0.0 | -4.5 | 4.50 |
Magnetic Structure of Ca₂Fe₂O₅
Takayoshi TAKEDA, Yasuo YAMAGUCHI and Shoichi TOMIYOSHI
The Research Institute for Iron, Steel and Other Metals, Tohoku University, Sendai
Masahiro Fukase
Konishiroku Photo Industries Company Limited, Hino, Tokyo
Mitsuo Sugimoto
The Institute for Physical and Chemical Research, Komagome, Tokyo
and
Hiroshi WATANABE
The Research Institute for Iron, Steel and Other Metals, Tohoku University,Sendai and
The Institute for Physical and Chemical Research, Komagome, Tokyo (Received September 14, 1967)
Magnetic measurements indicate that \( Ca_{2}Fe_{2}O_{5} \) is an antiferromagnet, with weak parasitic ferromagnetism. The lattice, with the space group \( P_{emn}-D_{6h}^{2} \) , can be considered as an oxygen deficient perovskite. The magnetic structure as determined from a neutron diffraction study is of G-type, and \( Fe^{3+} \) spins are directed approximately along c-axis.
§ 1. Introduction
The crystal structure of \( Ca_{2}Fe_{2}O_{5} \) has been studied by Bertaut et al. \( ^{1,2} \) . It is orthorhombic and the space group is \( P_{cmn}-D_{6h}^{2} \) . The lattice constants, according to these authors, are: \( a=5.64 \) , \( b=14.68 \) and \( c=5.39\ \AA \) . Subsequently Smith \( ^{3} \) confirmed Bertaut et al.'s results.
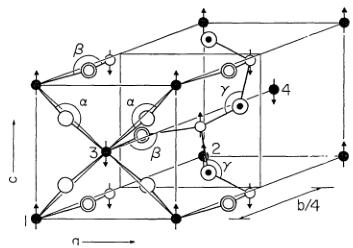
There are two types of iron sites, \( Fe_{I} \) and \( Fe_{II} \) , which alternate along the b-axis. \( Fe_{I} \) is an octahedral site surrounded by \( 6O^{2-} \) , while \( Fe_{II} \) is a tetrahedral site surrounded by \( 4O^{2-} \) ions. The crystal lattice can be regarded as a deformed, oxygen-deficient perovskite. The unit cell of this lattice is made up of four unit cells of primitive perovskite cells stacked in the b-direction. \( ^{*} \) Hence the magnetic structure of this antiferromagnetic compound has been considered as of G-type, on the analogy of the magnetic structure usually met with in \( Fe^{3+} \) containing perovskite oxides. In G-type structure, near-neighboring \( Fe^{3+} \) ions have always opposite spins. Then the two sublattices, \( Fe_{I} \) and \( Fe_{II} \) , are antiferromagnetic within each of them as well as to each other. (Fig. 1)
Geller et al. \( ^{5} \) studied the Fe \( ^{57} \) Mössbauer effect

Fig. 1. Crystal structure and proposed magnetic structure of Ca₂Fe₂O₅.
\[ a=5.64,b=14.68and c=5.39\mathring{\mathrm{A}}. \]
\[ \bullet\quad\mathrm{Fe}_{\mathrm{I}}\quad\textcircled{\cdot}\quad\mathrm{O}_{\mathrm{I}}\quad(b=0) \]
\[ \textcircled{\circ}\quad\mathrm{O}_{\mathrm{II}}\quad(b=0.133) \]
\[ \textcircled{\cdot}\quad\mathrm{Fe}_{\mathrm{II}}\quad\textcircled{\cdot}\quad\mathrm{O}_{\mathrm{III}}\quad(b=1/4) \]
Center of inversion at FeI, and mirror plane at b=1/4.
\[ \alpha=167^{\circ}\quad\mathrm{Fe}_{\mathrm{I}}-\mathrm{O}_{\mathrm{I}}\quad1.96_{8}\mathring{\mathrm{A}} \]
\[ \beta=147^{\circ}\quad\mathrm{Fe}_{\mathrm{I}}-\mathrm{O}_{\mathrm{II}}\quad1.97_{7}\mathring{\mathrm{A}} \]
\[ \gamma=132^{\circ}\quad\mathrm{Fe}_{\mathrm{II}}-\mathrm{O}_{\mathrm{II}}\quad1.88_{4}\mathring{\mathrm{A}} \]
\[ \mathrm{Fe}_{\mathrm{II}}-\mathrm{O}_{\mathrm{III}}\quad1.85_{8}\mathring{\mathrm{A}}\mathrm{and}1.85_{9}\mathring{\mathrm{A}} \]
of \( Ca_{2}Fe_{2}O_{5} \) and of compounds in which \( Fe^{3+} \) are partially replaced by \( Ga^{3+} \) or \( Sc^{3+} \) . These ions were expected, and actually found, to go into one of the two sublattices preferentially ( \( Ga^{3+} \) to \( Fe_{II} \) , and \( Sc^{3+} \) to \( Fe_{I} \) ), so that it was expected that the substituted compound should become ferrimagnetic if each of the sublattices had nonzero moment. But since this was not the case, they concluded that the magnetic structure was of
G-type, as has been expected above. In a subsequent study of the Mössbauer effect with linearly polarized \( \gamma \) rays, Gonser et al. \( ^{6)} \) suggested that the spin direction was along the c-axis.
In order to ascertain these considerations, a neutron diffraction experiment was performed with the TOG neutron diffractometer at JRR-3. The spin direction was investigated as well as the antiferromagnetic structure. On the basis of the proposed structure, occurrence of weak parasitic ferromagnetism was expected. This was borne out by a thermomagnetic study.
§ 2. Neutron Diffraction Study
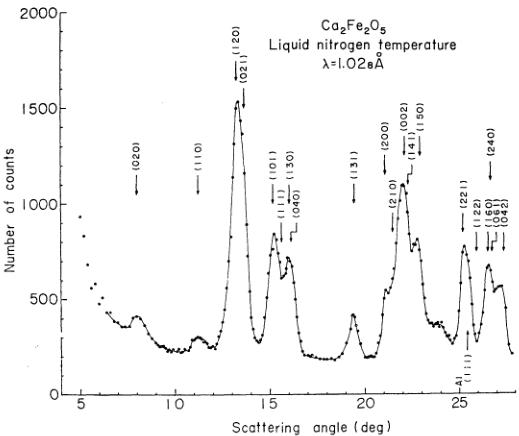
Powdered samples were sintered from constituent compounds, \( CaCO_{3} \) and \( Fe_{2}O_{3} \) , at about \( 1200^{\circ}C \) in air for 3 hrs, and then annealed at \( 1150^{\circ}C \) for 3 hrs. Small amounts of ferromagnetic impurities, if any, were removed by this annealing process. X-ray diffraction pattern was taken, and it was found that both line positions and line intensities were in complete conformity with Bertaut et al.'s. \( ^{1,2} \) Neutron diffraction patterns were taken with TOG neutron diffractometer installed at JRR-3 of JAERI. The pattern taken at liquid nitrogen temperature is shown in Fig. 2. All the existing lines could be indexed on the basis of the chemical unit cell, except for some amount of contamination with Al, mainly from the aluminum sample holder. Observed magnetic intensity was deduced from the difference pattern between the liquid nitrogen temperature run and

Fig. 2. Neutron diffraction pattern of \( Ca_{2}Fe_{2}O_{5} \) at liquid nitrogen temperature.
a run taken at \( 480^{\circ} \) C. Theoretical intensity was calculated using the atomic parameters given by Bertaut et al. \( ^{2} \) and with the aid of NEAC 2230 computer at Tohoku University, and the form factor of \( Mn^{2+} \) by Shull, Strauser and Wollan \( ^{7} \) was used. In Table I comparison between observed and calculated intensities is given on the basis of the G-type antiferromagnetic structure. Here the \( Fe^{3+} \) spins are assumed to be directed along c-axis. For other posibilties we will discuss later on. Because of the large lattice constants, most of the peaks consist of a number of lines which are not separable. For the determination of the scale value, we have chosen the peak including the line (101) as the reference, since this peak contains fairly strong nuclear intensity and relatively small magnetic intensity. Agreement between observed and calculated intensities is on the whole good. Although the Mössbauer effect measurements by Geller et al. \( ^{5} \) and Gonser et al. \( ^{6} \) showed that the internal fields for the two crystallographic sites (4a and 4c) were different, it was suspected that the \( Fe^{3+} \) moments had the same value. In order to check this point, we sought (100) peak carefully, without finding any intensity. So within the experimental error, \( Fe^{3+} \) moments could be assumed to be the same for the different crystallographic sites. They were found to be \( 4.5 \pm 0.2 \mu_{B} \) .
Although the G-type antiferromagnetic struc-
Table I. Comparison between observed and calculated intensities of the powder neutron diffraction data of \( Ca_{2}Fe_{2}O_{5} \) taken at liquid nitrogen temperature. \( Fe^{3+} \) atomic moments are assumed to be equal to \( 4.54 \mu_{B} \) for both of the crystallographic sites. For the model for theoretical intensity, see text. \( Fe^{3+} \) moments are assumed to be along c-axis.
| khl(Pcmn) | 2θ(deg) | Theoretical intensity | Experimental intensity | |||||||
| Nuc. | Mag. | Total | Nuc. | Mag. | Total | |||||
| 020 | 8.03 | 13.15 | 13.15 | 0 | 0 | 13.15 | 12.2 | 0 | 12.2 | |
| 100 | 10.46 | 0 | 11.63 | 0.28 | 0 | 0.86 | 12.49 | 11.9 | 0 | 11.9 |
| 110 | 11.20 | 11.63 | 0 | |||||||
| 011 | 11.66 | 0 | 0.59 | |||||||
| 120 | 13.20 | 0 | 0 | 118.03 | 158.32 | 158.32 | 0 | 158.3 | 158.3 | |
| 021 | 13.59 | 0 | 40.28 | |||||||
| 101 | 15.16 | 50.66 | 94.37 | 0.24 | 5.63 | 100.00 | 100 | |||
| 111 | 15.68 | 7.56 | 3.76 | |||||||
| 130 | 15.98 | 15.38 | 0 | |||||||
| 040 | 16.10 | 19.81 | 0 | |||||||
| 031 | 16.31 | 0 | 1.20 | |||||||
| 121 | 17.18 | 0.96 | 0.44 | |||||||
| 140 | 19.24 | 0 | 9.99 | 0.13 | 2.88 | 12.87 | 11.1 | 4.8 | 15.9 | |
| 131 | 19.41 | 9.99 | 2.73 | |||||||
| 041 | 19.51 | 0 | 0.03 | |||||||
| 200 | 21.00 | 24.34 | 142.93 | 0 | 12.28 | 155.21 | 149.6 | 18.9 | 168.5 | |
| 210 | 21.39 | 0 | 5.60 | |||||||
| 002 | 21.99 | 38.18 | 0 | |||||||
| 141 | 22.18 | 33.77 | 0.26 | |||||||
| 012 | 22.36 | 0.40 | 0 | |||||||
| 220 | 22.52 | 3.65 | 0 | |||||||
| 150 | 22.76 | 29.28 | 0 | |||||||
| 051 | 23.00 | 0 | 0.63 | |||||||
| 022 | 23.44 | 8.83 | 0 | |||||||
| 201 | 23.74 | 3.63 | 0.88 | |||||||
| 211 | 24.08 | 0.07 | 0.43 | |||||||
| 060 | 24.25 | 0.30 | 0 | |||||||
| 230 | 24.28 | 0 | 3.74 | |||||||
| 102 | 24.40 | 0.34 | 0.10 | |||||||
| 112 | 24.74 | 0.13 | 0.65 | |||||||
| 221 | 25.10 | 5.55 | 11.01 | 21.80 | 30.73 | 41.73 | 11.8 | 31.0 | 48.9 | |
| 032 | 25.15 | 0.22 | 0 | |||||||
| 151 | 25.32 | 4.88 | 1.44 | |||||||
| 122 | 25.73 | 0.35 | 7.49 | |||||||
| 111(A1) | 25.40 | 6.1 | ||||||||
| 160 | 26.48 | 0 | 42.71 | 15.85 | 30.58 | 73.29 | 39.9 | 27.3 | 67.4 | |
| 240 | 26.58 | 13.12 | 0 | |||||||
| 061 | 26.68 | 0 | 13.49 | |||||||
| 231 | 26.71 | 2.18 | 0.32 | |||||||
| 132 | 27.30 | 16.29 | 0.92 | |||||||
| 042 | 27.37 | 11.12 | 0 | |||||||
ture is certainly reasonable both from the standpoint of the crystallographic nature of this substance as well as from its compatibility with the neutron diffraction data, a ferrimagnetic model was also tested in which \( Fe_{I} \) and \( Fe_{II} \) moments point in the opposite directions. For this model the structure factor is
\[ S=4f(\mathrm{Fe}_{\mathrm{I}})-4f(\mathrm{Fe}_{\mathrm{II}})(-1)^{k/2}\cos2\pi h x\cos2\pi l z \]
for \( h+1 \) even and k even, and
\[ S=4f(\mathrm{Fe}_{\mathrm{II}})(-1)^{k/2}\sin2\pi h x\sin2\pi l z \]
for \( h+1 \) odd and k even. The former examples are:
\[ (020):\quad S=4(f(\mathrm{Fe}_{\mathrm{I}})+f(\mathrm{Fe}_{\mathrm{II}})), \]
and
\[ (121):\quad S=4f(\mathrm{Fe}_{\mathrm{I}})+3.385f(\mathrm{Fe}_{\mathrm{II}}). \]
The latter examples are:
\[ (120):\quad S=1.748f(\mathrm{Fe}_{\mathrm{II}}) \]
and
\[ (021):\quad S=1.355f(\mathrm{Fe}_{\mathrm{II}}). \]
Hence there should be big magnetic intensities in (020) and (121), while (120) and (021) magnetic intensities should not be so large. The actually
Table II. Calculated Intensity of the powder diffraction data of \( Ca_{2}Fe_{2}O_{5} \) taken at liquid nitrogen temperature. \( Fe^{3+} \) moments are assumed to be along a or b direction. Calculations are based on the G-type antiferromagnetic model.
| hkl | Intensity (Nuc.+Mag.) | Experimental intensity | |||
| Saμ=4.55μB | Sbμ=4.78μB | ||||
| 120 | 44.29 | 158.32 | 78.86 | 158.32 | 158.3 |
| 021 | 114.03 | 79.47 | |||
| 101 | 50.23 | 100.00 | 49.12 | 100.00 | 100.0 |
| 111 | 11.49 | 14.55 | |||
| 130 | 15.16 | 14.74 | |||
| 040 | 19.54 | 19.00 | |||
| 031 | 2.17 | 1.05 | |||
| 121 | 1.40 | 1.53 | |||
| 221 | 13.39 | 43.46 | 32.60 | 65.46 | 48.9 |
| 032 | 0.22 | 0.21 | |||
| 151 | 6.25 | 5.36 | |||
| 122 | 23.60 | 27.29 | |||
| 160 | 13.21 | 73.83 | 2.66 | 49.15 | 67.4 |
| 240 | 12.94 | 12.58 | |||
| 061 | 16.12 | 2.95 | |||
| 231 | 2.29 | 2.41 | |||
| 132 | 18.30 | 17.88 | |||
| 042 | 10.97 | 10.67 | |||
observed intensities, however, are in violent disagreement with this situation, so that the ferrimagnetic model is apparently improbable.
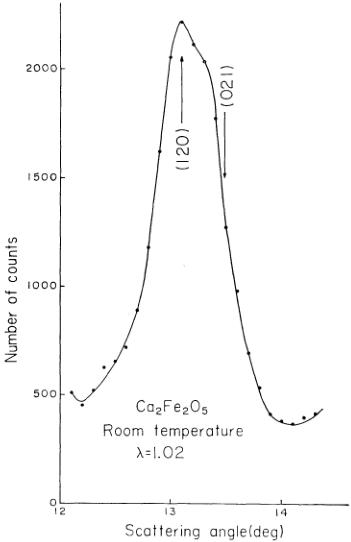
The spin direction is more difficult to determine. In Table II we have shown the result of calculation similar to that given in Table I, but the spin direction is assumed to be along a or b axis. Spin//a is more consistent with experiment than spin//b, since in the latter case the calculated intensity for the peak including (221) line is too strong, while that including (160) is too small. Then we have to compare spin//a with spin//c. The compatibilities of these two models with experiment are about the same. So we decided to measure the shape of the (120)+(021) peak carefully, in order to choose a better one out of them. As can be seen from the tables, (120) intensity is bigger than (021) intensity for spin//c, and the situation is reversed for spin//a. The measurement was done at room temperature with the sample in a cassette with a smaller diameter (15 mm) and with a higher counting statistics. This was meant to increase the resolution. Actually we could obtain an asymmetrical shape of the peak as shown in Fig. 3. The data show that spin//c is more favorable.
The above conclusion of the spin direction is in

Fig. 3. Line profile of the \( (120)+(021) \) peak at room temperature.
accord with that of the polarized Mössbauer data by Gonser et al. \( ^{8} \) In the course of preparing the manuscript, we have become aware of an abstract of Corliss et al.'s neutron work \( ^{8} \) who reported the same result as above. Their moment value, \( 4.4 \mu_{B} \) , is also fairly close to ours.
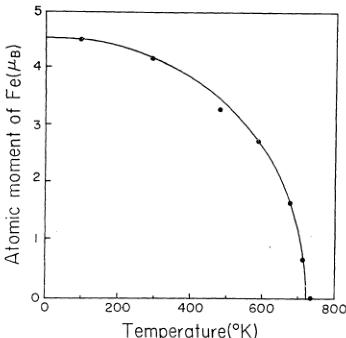
The temperature dependence of the \( (120)+(021) \) peak intensity was measured up to the Néel temperature, \( T_{N} \) . This is shown in Fig. 4. \( T_{N} \)

Fig. 4. Temperature dependence of the \( Fe^{3+} \) atomic moment as deduced from the \( (120)+(021) \) peak intensity.
\( =720^{\circ}K \) in the present experiment, as compared to \( 730^{\circ}K \) by Corliss et al. \( ^{8)} \) The curve in the figure is a Brillouin fit to the experimental points, with spin 5/2.
§ 3. Magnetic Study
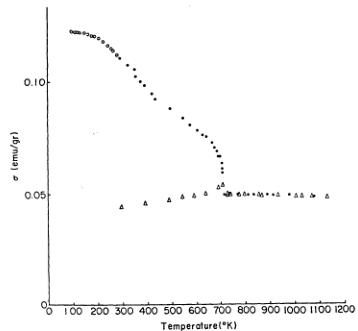
As stated above, \( Ca_{9}Fe_{9}O_{5} \) is an antiferromagnetic with \( T_{N}=720^{\circ}K \) . Its thermomagnetic curve, however, shows that it has a thermoema-

Fig. 5. Thermomagnetic curve of \( Ca_{9}Fe_{9}O_{5} \) under the field of \( H=3950~Oe \) , \( \triangle \) experimental point measured during heating. ● and ○ experimental points measured during cooling under a magnetic field.
nent magnetization if it is cooled from above \( T_{N} \) under a magnetic field. In Fig. 5, one can see the magnetization during cooling under a magnetic field is by far greater than that during heating. After this treatment the magnetization (hysteresis curve) is shifted along the magnetization axis. The phenomenon is much the same as has been observed in many orthoferrites with the perovskite-type structure. \( ^{9)} \) This anomalous shift is due to an extremely large coercive force brought about by the smallness of the net magnetization.
The origin of the weak ferromagnetism is considered to be the Dzyaloshinskii-Moriya interaction. \( ^{10)} \) Consideration of the symmetry elements leads to the following relation between the spin components \( S_{i} \) (for numbering of spins, see Fig. 1):
\[ \left.\begin{array}{l}S_{1z}^{(2)}=\varepsilon S_{1z}^{(1)},\quad S_{1y}^{(2)}=-\varepsilon S_{1y}^{(1)},\quad S_{1z}^{(2)}=\varepsilon S_{1z}^{(1)},\\ S_{1y}^{(3)}=-\varepsilon^{\prime}S_{1y}^{(1)},\quad S_{1y}^{(3)}=\varepsilon^{\prime}S_{1y}^{(1)},\quad S_{1z}^{(3)}=\varepsilon^{\prime}S_{1z}^{(1)},\\ S_{1z}^{(4)}=-\varepsilon\varepsilon^{\prime}S_{1z}^{(1)},\quad S_{1y}^{(4)}=-\varepsilon\varepsilon^{\prime}S_{1y}^{(1)},\quad S_{1z}^{(4)}=\varepsilon\varepsilon^{\prime}S_{1z}^{(1)},\end{array}\right\} \quad (1) \]
where \( \varepsilon \) and \( \varepsilon' \) take the values \( \pm1 \) . The components of the net moment vector
\[ m_{\mathrm{I}}=S_{\mathrm{I}}^{(1)}+S_{\mathrm{I}}^{(2)}+S_{\mathrm{I}}^{(3)}+S_{\mathrm{I}}^{(4)} \]
can be written as:
\[ \left.\begin{array}{l}m_{\mathrm{I}x}=(1+\varepsilon)(1-\varepsilon^{\prime})S_{\mathrm{I}x}^{(1)},\\ m_{\mathrm{I}y}=(1-\varepsilon)(1+\varepsilon^{\prime})S_{\mathrm{I}y}^{(1)},\\ m_{\mathrm{I}z}=(1+\varepsilon)(1+\varepsilon^{\prime})S_{\mathrm{I}z}^{(1)}.\end{array}\right\} \quad (2) \]
As the magnetic structure is of G-type, \( S_{\mathrm{I}}^{(1)}\sim S_{\mathrm{I}}^{(2)}\sim-S_{\mathrm{I}}^{(3)}\sim-S_{\mathrm{I}}^{(4)} \) , so that the vector
\[ l_{\mathrm{I}}=S_{\mathrm{I}}^{(1)}+S_{\mathrm{I}}^{(1)}-S_{\mathrm{I}}^{(1)}-S_{\mathrm{I}}^{(4)} \]
should have a non-zero absolute value. From (1) it follows that:
\[ \left.\begin{array}{l}l_{\mathrm{I}x}=(1+\varepsilon)(1+\varepsilon^{\prime})S_{\mathrm{I}x},\\ l_{\mathrm{I}y}=(1-\varepsilon)(1-\varepsilon^{\prime})S_{\mathrm{I}y},\\ l_{\mathrm{I}z}=(1+\varepsilon)(1-\varepsilon^{\prime})S_{\mathrm{I}z}.\end{array}\right\} \quad (3) \]
The case \( \varepsilon=-1 \) , \( \varepsilon^{\prime}=+1 \) is inhibited, because, then, all of the components of l in (3) vanish. Hence we have three cases:
(1) \( \varepsilon=\varepsilon^{\prime}=+1 \)
From (3) we have \( I_{1x}=4S_{1x} \) and \( I_{1y}=I_{1z}=0 \) so that the approximate spin direction is along the a-axis. From (2) \( m_{1x}=m_{1y}=0 \) , \( m_{1z}=4S_{1z} \) and a small moment appears in the c-direction.
(2) \( \varepsilon=1,\varepsilon^{\prime}=-1. \)
\( I_{1z}=I_{1y}=0 \) , \( I_{1z}=4S_{1z} \) , so that the approximate spin direction is along the c-axis. From (2) \( m_{1z}=4S_{1z} \) , \( m_{1y}=m_{1z}=0 \) and a small moment appears in the a-direction
(3) \( \varepsilon=\varepsilon^{\prime}=-1 \)
\( I_{1x}=I_{1z}=0 \) , \( I_{1y}=4S_{1y} \) , so that the approximate spin direction is along the b-axis. From (2) \( m_{1x}=m_{1y}=m_{1z}=0 \) and no net moment appears. The same argument holds for \( Fe_{II} \) spins.
The neutron diffraction result is consistent with this consideration, case (2) being realized.
§ 4. Relation to the Mössbauer Effect Studies
As stated above, the result that the spins are directed along the c-axis is consistent with the Mössbauer effect measurement by Gonser et al. \( ^{6} \) . It is interesting now to compare the observed quadrupole interaction with the calculated value on the basis of the established spin direction.
Gonser et al.'s \( ^{6)} \) data on polycrystalline samples showed that the quadrupole interaction in \( Ca_{2}Fe_{2}O_{5} \) is negative for octahedral ( \( Fe_{I} \) ) sites, while it is positive for tetrahedral ( \( Fe_{II} \) ) sites. This has been confirmed by Wittmann et al. \( ^{11)} \) . On the other hand, an electronic computer calculation has been made of the electric field gradient tensor for each site of Fe by Wittmann \( ^{12)} \) and by Hudson et al. \( ^{13)} \) independently. Both the Fe atoms have been considered to be in the \( Fe^{3+} \) state, which is spherically symmetric. Therefore the calculation has been made on the assumption that the major contribution to the quadrupole interaction was the field gradient due to the surrounding atoms. The results of the calculation by these two authors coincided with each other, as they should, except for detailed figures. The calculated \( q_{z} \) (or the electric field gradient along c-axis) for both sites were positive. Now to the \( 0^{th} \) through \( 2^{nd} \) order perturbation theory of the hyperfine interaction the difference of the separations of the peaks
\[ (6-5)-(2-1)=4\Delta E \]
is related to \( q_{z} \) by the following formula:
\[ 4\Delta E=e Q q_{z}, \quad (4) \]
Q being the quadrupole moment of the \( Fe^{57} \) nucleus and e the electronic charge. \( ^{14)} \) The relation (4) is modified if the \( 3^{rd} \) and \( 4^{th} \) order perturbations are taken into account, \( ^{15)} \) but the effect is small in the present case, and can be neglected. The result of the calculation that the value of \( q_{z} \) for \( Fe_{I} \) is positive is therefore in disagreement with that of the experiment that \( \Delta E \) for \( Fe_{I} \) is negative.
The reason for the disagreement may be considered as partly due to the point change approximation and partly to negligence of the covalent character of Fe ions. The internal fields for Fe(I) and Fe(II) sites are 555 and 505 kOe at \( 0^{\circ}K^{11} \) or 534 and 467 kOe at \( 5^{\circ}K,^{12)} \) respectively. These values are considerably lower than those found in compounds with completely ionic character, eg \( FeF_{3} \) , whose internal field is 622 kOe at \( 4^{\circ}K,^{16)} \) . Also the atomic moment of Fe found in \( Ca_{2}Fe_{2}O_{5} \) in the present study, \( 4.5 \mu_{B} \) , is lower than the \( Fe^{3+} \) value of \( 5 \mu_{B} \) . These may be regarded as indications that the compound is not purely ionic.
After completion of the present manuscript, a paper on the neutron diffraction study on \( Ca_{2}Fe_{2}O_{5} \) by Friedman et al. \( ^{[17]} \) has appeared. Their conclusion on the magnetic structure is the same as ours.
Acknowledgements
The authors would like to express their hearty thanks to Dr. H. Yamamoto for his valuable discussion. Also they are indebted to Mr. Y. Sato for his technical assistance in the neutron diffraction experiment. A part of the expenditure for the present study has been defrayed from the Scientific Research Funds of the Ministry of Education.
References
1) E. F. Bertaut, P. Blum et G. Magnano: CR Acad. Sci. 244 (1957) 2944.
2) E. F. Bertaut, P. Blum et A. Sagnières: Acta cryst. 12 (1959) 149.
3) D. K. Smith: Acta cryst. 15 (1962) 1146.
4) T. Hirone: J. appl. Phys. 36 Part 2 (1965) 988.
5) S. Geller, R. W. Grant, U. Gonser, H. Wiedersich and G. P. Espinosa: Phys. Letters 20 (1966) 115.
6) U. Gonser, R. W. Grant, H. Wiedersich and S. Geller: Appl. Phys. Letters 9 (1966) 18.
7) C. G. Shull, W. A. Strauser and E. O. Wollan: Phys. Rev. 83 (1951) 333.
8) L. M. Corliss, J. M. Hastings, W. Kunnmann and E. Banks: Acta crystall. 21 (1966) Suppl. A. 95.
9) H. Forestier and G. Guiot-Guillain: CR Acad. Sci. 230 (1950) 1844; R. C. Sherwood, J. P. Remeika and H. J. Williams: J. appl. Phys. 30 (1959) 217; R. M. Bozorth V. Kramer and J. P.
Remeika: Phys. Rev. Letters 1 (1958) 3; H. Watanabe: J. Phys. Soc. Japan 14 (1959) 511.
10) I. E. Dzyaloshinskii: Soviet Physics -JETP 5 (1957) 1259; T. Moriya: Phys. Rev. 120 (1960) 91.
11) F. Wittmann und F. Pobell: Z. Naturforsch. 21a (1966) 831.
12) F. Wittmann: Phys. Letters 24A (1967) 252.
13) A. Hudson and H. J. Whitfield: J. Chem. Soc.
(A) (1967) 376.
14) G. K. Wertheim: Phys. Rev. 121 (1961) 63; Mös- sbauer Effect (Academic Press, N. Y., 1964)
15) S. S. Hafner, B. J. Evans and G. M. Kalvius: Solid State Commun. 5 (1967) 17.
16) D. N. E. Buchanan and G. K. Wertheim: Bull. Amer. Phys. Soc. 7 (1962) 227.
17) Z. Friedman, H. Shaked and S. Shtrikman: Phys. Letters 25A (1967) 9.