| Transition Temperature | 8.5 K |
|---|---|
| Experiment Temperature | 2 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | Pbcn (#60) |
| Magnetic Space Group | Pb'cn (#60.419) |
| Magnetic Point Group | m'mm (8.3.26) |
| Lattice Parameters | 6.79230 10.35660 6.05500 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1103/physrevb.82.014411 |
| Reference | B.C. Melot, B. Paden, R. Seshadri, E. Suard, G. Nenert, A. Dixit and G. Lawes, Physical Review B (2010) 82. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Co1 | Co | 3.1 | 0.0 | 0.8 | 3.20 |
Magnetic structure and susceptibility of CoSe_{2}O_{5}: An antiferromagnetic chain compound
Brent C. Melot, Brian Paden, and Ram Seshadri
Materials Department and Materials Research Laboratory, University of California, Santa Barbara, California 93106, USA
Emmanuelle Suard and Gwilherm Nénert Institute Laue Langevin, F-38042 Grenoble, France
Ambesh Dixit and Gavin Lawes
Department of Physics and Astronomy, Wayne State University, Detroit, Michigan 48201, USA (Received 25 March 2009; revised manuscript received 12 April 2010; published 13 July 2010)
\( CoSe_{2}O_{5} \) has a crystal structure consisting of zigzag chains of edge shared \( CoO_{6} \) octahedra running along the c axis with the chains separated by \( Se_{2}O_{5}^{2-} \) units. Magnetic-susceptibility measurements indicate a transition at 8.5 K to an ordered state. We investigate the nature of this magnetic order using magnetization and specific-heat measurements, in addition to powder neutron diffraction. A transition to long-range antiferromagnetic order is found below \( T_{N}=8.5 \) K as identified by magnetic-susceptibility and heat-capacity measurements, and the emergence of magnetic Bragg reflections with a propagation vector k=0. The low-field magnetic-susceptibility data indicate the presence of weak ferromagnetism in the antiferromagnetic ordered state which saturates in very small fields. Heat-capacity measurements at low temperatures indicate that only about half the configurational entropy is released at \( T_{N} \) . The functional form of the heat capacity below \( T_{N} \) suggests the presence of a gap of 6.5 K in the magnon dispersion. The refined magnetic structure shows that the moments align perpendicular to the c axis, and tilting alternately by \( +14^{\circ} \) and \( -14^{\circ} \) with respect to the a axis.
DOI: 10.1103/PhysRevB.82.014411
PACS number(s): 75.50.Ee
I. INTRODUCTION
Materials with reduced crystallographic dimensionality are of great interest because their physics is dominated by strong interplay between charge, lattice, and magnetic degrees of freedom. \( ^{1,2} \) From the perspective of magnetism, chains of spins are especially interesting because of the possibility of competing nearest- and next-nearest-neighbor exchange interactions. \( ^{3} \) Examples of recently studied compounds with magnetic chains include those showing geometric frustration, magnetoelectric coupling, and possible quantum tunneling of the magnetization, as exemplified by \( Ca_{3}Co_{2}O_{6} \) , \( ^{4-6} \) \( MnWO_{4} \) , \( ^{7} \) and \( LiCu_{2}O_{2} \) . \( ^{3,8} \)
Here we report a detailed magnetic study of polycrystalline \( CoSe_{2}O_{5} \) , an orthorhombic compound crystallizing in the \( Pbcn \) space group, comprising chains of edge sharing \( CoO_{6} \) octahedra that zigzag along the c axis. Each chain is bound together by \( Se_{2}O_{5}^{2-} \) units via shared oxygen atoms at the corners of the octahedra. The diselenite units can be visualized as two trigonal pyramids of \( SeO_{3} \) which share a corner and contain two lone pairs of electrons which point in antiparallel directions. This compound and its structure were reported by Harrison et al. \( ^{9} \) but no reports on the properties have been made so far. We were particularly interested in this compound because of its chain structure and the presence of symmetry reducing lone pairs.
We have used a combination of magnetic-susceptibility and magnetization measurements, specific-heat measurements, and low-temperature powder neutron diffraction to characterize the nature of the magnetic ground state below \( T_{N}=8.5 \) K and at low-magnetic fields. We suggest the presence of more complex magnetic structures in the presence of large fields and point to the presence of a 6.5 K gap in the magnon dispersion from heat-capacity measurements.
II. EXPERIMENTAL METHODS
\( CoSe_{2}O_{5} \) was prepared following the reported hydrothermal procedure. \( ^{9} \) \( SeO_{2} \) (5.0 g, Cerac, 99.99%) was dissolved in 15 cm \( ^{3} \) of water and combined with \( CoSO_{4}\cdot xH_{2}O \) (2.0 g, Sigma-Aldrich, 98%). The mixture was sealed in a 23 mL poly(tetrafluoroethylene)-lined pressure vessel (Parr Instruments) and heated to 200 °C for 48 h. The resulting product consisted of dark purple single crystals averaging 1.5 mm × 1.5 mm × 0.5 mm.
\( ZnSe_{2}O_{5} \) , a nonmagnetic analog to the title compound, was also prepared in order to estimate the lattice contribution to the specific heat. \( SeO_{2} \) (0.7317 g, Cerac, 99.99%) was ground in an agate mortar with \( ZnO \) (0.2683 g, Sigma-Aldrich, 98%), sealed in a quartz tube and heated at \( 350\ ^{\circ}C \) for 48 h. \( ^{10} \) The resulting product consisted of an off-white polycrystalline powder.
Temperature dependence of the dc magnetization was measured on well-ground powder samples using a Quantum Design magnetic property measurement system (MPMS) 5XL superconducting quantum interference device magnetometer. Powders were preferred for magnetization measurements since the shape and dimensions of the available single crystals made them difficult to align with respect to the field direction. The specific-heat data were collected on a 9.5 mg single crystal using the semiadiabatic technique as implemented in a Quantum Design physical property measurement system, under zero applied field as well as under a 10 kOe field. The measurement on nonmagnetic \( ZnSe_{2}O_{5} \) was made by mixing the compound with equal parts by mass of Ag powder and pressing into a pellet in order to improve thermal coupling. The contribution from Ag was measured separately and subtracted.
Neutron-diffraction data were collected on a sample of well-ground single crystals at the D2B powder diffracto-

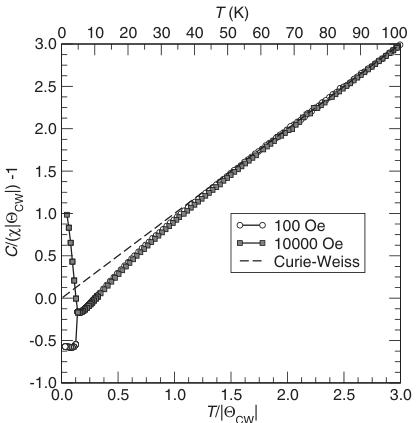
FIG. 1. FC dc magnetic susceptibility of polycrystalline \( CoSe_{2}O_{5} \) acquired under magnetic fields of 100 and 10 000 Oe. The data have been scaled as indicated in the text to emphasize deviations from Curie-Weiss behavior.
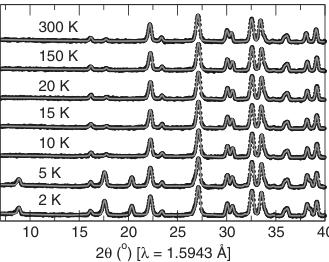
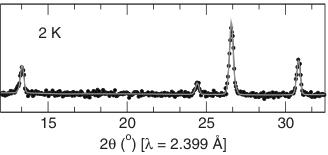
meter at the Institut Laue-Langevin (ILL), France \( ^{11} \) using a wavelength of 1.5949 Å. The precise wavelength of the incident neutrons was refined against the data obtained at 300 K by fixing the cell parameters to the values determined from a room-temperature x-ray diffraction pattern collected on a Philips XPERT MPD diffractometer operated at 45 kV and 40 mA. In order to achieve a better fit to the lowest-lying magnetic reflections, a diffraction pattern was also collected at 2 K using a wavelength of 2.399 Å.
III. RESULTS AND DISCUSSION
The high-temperature region (350–400 K) of the inverse susceptibility was fit to the Curie-Weiss equation, \( C/(T - \Theta_{CW}) \) , to obtain the effective moment \( \mu_{eff} \) from the Curie constant and the Curie-Weiss intercept \( \Theta_{CW} \) . A Curie-Weiss temperature of -34 K and an effective moment of \( 5.19\mu_{B} \) were extracted from the fits to the data collected under a 100 Oe field. This effective moment can be compared to the value of \( 5.2\mu_{B} \) expected for octahedrally coordinated \( Co^{2+} \) (Refs. 12 and 13) ( \( d^{7} \) , \( f_{2g}^{5}e_{g}^{2} \) , S=3/2, and L=3) where the spin and orbital contributions to the effective moment are completely decoupled from one another as obtained using the relationship \( ^{14} \) \( \mu_{L+5}=\sqrt{4S(S+1)+L(L+1)} \) .
Using the values of C and \( \Theta_{CW} \) from the fit to the high-temperature susceptibility, we display in Fig. 1 a plot of the scaled field-cooled (FC) susceptibility of \( CoSe_{2}O_{5} \) in a manner that emphasizes deviations from Curie-Weiss behavior. The scaling is performed by plotting \( C/(\chi[\Theta_{CW}])-1 \) as a function of \( T/|\Theta_{CW}| \) , for which Curie-Weiss behavior should yield a straight line through the origin (indicated by the dashed line). The purpose of such scaling has been discussed in prior work. \( ^{15} \) Deviations from Curie-Weiss behavior start at temperatures near 34 K (note that the frustration index \( ^{16} \) \( f=|\Theta_{CW}|/T \) can be read from the inverse of the x axis). At \( T_{N} \)

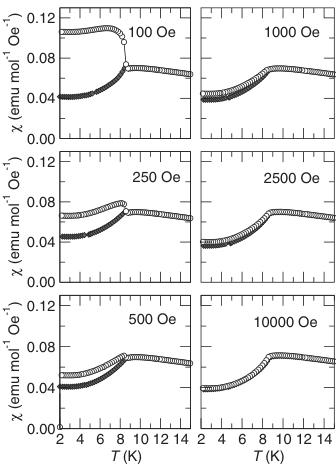
FIG. 2. (a) FC (open symbols) and ZFC (closed symbols) magnetic susceptibility of a powder sample of \( CoSe_{2}O_{5} \) acquired under increasing strengths of the external magnetic field. At 8.5 K, the system orders to an antiferromagnetic state. A weak-ferromagnetic component is found in low-field data, suggested from the separating ZFC and FC traces. Note also that the magnetic ordering temperature is not field dependent.
near 8.5 K, there is a sharp transition to an ordered ground state.
The ordering temperature of 8.5 K is smaller than \( \Theta_{CW} \) as is commonly found in systems with reduced crystallographic dimensionality. One of the advantages of the scaling used in Fig. 1 is that systems with purely antiferromagnetic ordering display positive deviations from the Curie-Weiss line. In contrast, systems with ferromagnetic interactions or more generally, uncompensated magnetic ordering, display negative deviations, reaching a limiting value of -1 for the case \( \chi \rightarrow \infty \) . \( ^{15} \) While the FC susceptibility under a 10 000 Oe field clearly attains a ground state that is completely compensated and antiferromagnetic, the lower field measurement obtained at 100 Oe while also resulting in a transition near 8.5 K, results in a ground state that retains some uncompensated moment rather than being purely antiferromagnetic.
To better understand the nature of the 8.5 K transition, we show in Fig. 2 the temperature dependence of the magnetic susceptibility for a powder sample of \( CoSe_{2}O_{5} \) collected under different magnetic fields. When measured in fields smaller than 1000 Oe, a sharp jump in the susceptibility is observed below 8.5 K. Such a jump would not be expected for an antiferromagnet with complete cancellation of the magnetic moment within the unit cell. Instead, we attribute the jump to the presence of weak ferromagnetism that can be found in systems with a canted antiferromagnetic spin structure. \( ^{[17]} \) The weak ferromagnetism is an intrinsic property of the material since there is no change in the ordering temperature as a function of field and no magnetic impurities were detected in the powder neutron-diffraction data as will be discussed in the following. Additionally, we find that the

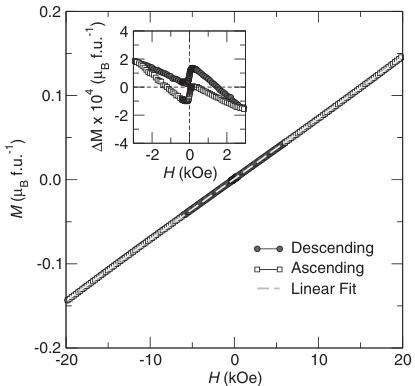
FIG. 3. Isothermal magnetization curve as a function of the applied field. The inset depicts \( \Delta M \) which is obtained by subtracting as explained in the text, at T=2 K. At low fields, the weak-ferromagnetic component displays a somewhat S-shaped trace which saturates quickly in fields near H=100 Oe.
contribution from the weak ferromagnetism can be minimized by application of sufficiently large fields. Indeed, magnetic measurements under fields ranging from 1000 to 10 000 Oe display the characteristic, somewhat rounded downturn expected for a well-compensated antiferromagnet.
From Fig. 2 we see that the separation between the zero-field-cooled (ZFC) and FC susceptibility corresponding to the weak-ferromagnetic component is gradually reduced with increasing field strength as the weak ferromagnetism saturates and the antiferromagnetism begins to dominate the susceptibility. By fitting a straight line to measurements of M vs H at T=2 K and subtracting this straight line from the 2 K magnetization, we obtain plots of \( \Delta M \) as a function of the ascending and descending magnetic fields at T=2 K displayed in Fig. 3. The resulting trace shows a small maximum near \( H=0 \) , which indicates the ferromagnetic component has a saturation value around \( 2 \times 10^{-4} \mu_{B}/Co \) .
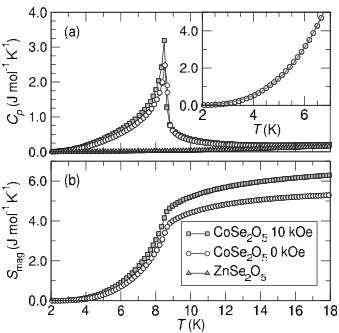
The temperature dependence of the specific heat \( C_{p} \) of \( CoSe_{2}O_{5} \) shown in Fig. 4(a) exhibits a \( \lambda \) -type anomaly at around 8.5 K corresponding to the transition to long-range magnetic order observed in the susceptibility and in the

FIG. 4. (a) Temperature dependence of the specific heat of \( CoSe_{2}O_{5} \) measured on a 9.5 mg single crystal under zero field, and with a H=10 kOe field applied along the b axis of the crystal. A nonmagnetic analog, \( ZnSe_{2}O_{5} \) , was also measured in order to obtain the lattice contribution to the specific heat. Note the large width of the ordering peak and the release of entropy well above the transition temperature of 8.5 K. The inset depicts the fit (solid line) to the experimental data (symbols) as described in the text. (b) Entropy released due to the magnetic ordering, obtained by integration of the magnetic heat capacity.
neutron-diffraction data. Measurements on nonmagnetic \( ZnSe_{2}O_{5} \) give an estimate of the lattice contribution using a three-term expansion with the best fit yielding a Debye temperature, \( \Theta_{D} \) , of 222 K. An estimate of the change in entropy associated with the magnetic transition can be obtained by integrating \( C_{p,\mathrm{magn}}/T \) defined between the specific-heat data of \( CoSe_{2}O_{5} \) and \( ZnSe_{2}O_{5} \) [Fig. 4(b)]. The change in entropy due to the magnetic transition, thus determined, was \( 5.3\ J\ mol^{-1}\ K^{-1} \) which is smaller than the value of \( 11.5\ J\ mol^{-1}\ K^{-1} \) predicted by the Boltzmann equation \( [\Delta S = R\ \ln(2S + 1) \) and \( S = 3/2] \) .
The relatively large temperature range (nearly 15 K) over which the 8.5 K ordering takes place is consistent with the large range of temperature over which the deviation from Curie-Weiss behavior commences in the magnetic susceptibility. This is also a characteristic of the reduced dimensionality of the system. In contrast, in three-dimensional antiferromagnets such as the rutile difluorides of Fe, Co, and Ni, the \( \lambda \) anomaly has a width of only a few Kelvin. \( ^{18} \)
TABLE I. Summary of the results of Rietveld structure refinement of variable temperature neutron-diffraction data. The employed neutron wavelength \( \lambda \) is indicated.
| 300 K ( \( \lambda=1.6 \) Å) | 2 K ( \( \lambda=1.6 \) Å) | 2 K ( \( \lambda=2.4 \) Å) | |
| a ( \( \textup{\AA} \) ) | 6.7920 \( ^{\textup{a}} \) | 6.7923(3) | 6.7928(3) |
| b ( \( \textup{\AA} \) ) | 10.3687 \( ^{\textup{a}} \) | 10.3566(4) | 10.3578(5) |
| c ( \( \textup{\AA} \) ) | 6.0759 \( ^{\textup{a}} \) | 6.0550(2) | 6.0556(3) |
| M ( \( \mu_{B} \) ) | 3.1(2) | 3.3(2) | |
| V ( \( \textup{\AA}^{3} \) ) | 427.899 \( ^{\textup{a}} \) | 425.941(3) | 426.063(4) |
| \( R_{\textup{nuc.}} \) (%) | 4.5 | 3.3 | 2.6 |
| \( R_{\textup{mag.}} \) (%) | 5.5 | 4.5 |
\( ^{a} \) Fixed from the room-temperature Rietveld refinement of laboratory XRD data. See text.
TABLE II. Atomic positions from Rietveld refinements carried out on data acquired at 300 and 2 K using 1.6 Å neutrons. All error bars on the atomic positions were less than \( 4 \times 10^{-4} \) .
| 300 K | 2 K | |||||
| x | y | z | x | y | z | |
| Co | 0 | 0.9395 | \( \frac{3}{4} \) | 0 | 0.9389 | \( \frac{3}{4} \) |
| Se | 0.6314 | 0.1544 | 0.9685 | 0.6312 | 0.1542 | 0.9686 |
| O1 | 0.8060 | 0.2093 | 0.3420 | 0.8055 | 0.2089 | 0.3408 |
| O2 | \( \frac{1}{2} \) | 0.9312 | \( \frac{1}{4} \) | \( \frac{1}{2} \) | 0.9317 | \( \frac{1}{4} \) |
| O3 | 0.8402 | 0.9331 | 0.4519 | 0.8397 | 0.9333 | 0.4526 |
The specific heat was also measured with a field of 10 000 Oe applied along b axis. As seen in Fig. 4(a) there is very little change in the character of the transition as might be expected for a small reorientation of the spin axis. It should also be noted that the entropy is slightly increased to a value of \( 6.3 \, J mol^{-1} \, K^{-1} \) , closer to the predicted value of \( 11.5 \, J mol^{-1} \, K^{-1} \) .
A fit to the specific heat below the transition temperature could not be obtained using only the \( T^{3} \) term as expected for a typical insulating antiferromagnet. Instead, the best fit to the data was found when an exponential term was included, using \( C_{p,\mathrm{mag}} \propto T^{3} \exp(-\Delta / k_{B} T) \) . \( ^{19,20} \) This result reflects the presence of low-energy magnetic excitations in the magnon dispersion with a gap, \( \Delta \) , determined here to be 6.5 K in zero field and 5.8 K under 10 kOe. The size of the gap in this system is on the order of the energies associated with the spin-orbit splitting of the lowest-lying electronic states of octahedral \( Co^{2+} \) as determined by ab initio calculations, \( ^{21} \) although other microscopic origins for the gap are also possible.
The nuclear and magnetic structure of \( CoSe_{2}O_{5} \) were refined using the Rietveld method as implemented in the FULLPROF software suite. \( ^{22} \) The peak shape was described using the Thompson-Coex-Hastings pseudo-Voigt function, and the background was fit by interpolation between regions showing no Bragg reflections. The crystal structures were analyzed based on the model proposed by Harrison et al., \( ^{9} \) although it should be noted that we use the standard setting of space-group number 60 ( \( Pbc_{n} \) ) instead of the alternate Pnab description used in the original work. A summary of key refinement results is shown in Tables I and II. For the magnetic structure, group theoretical analysis was performed using representational analysis as implemented in the program SARAH (Ref. 23) to determine all of the possible spin configurations which were compatible with the crystal symmetry.
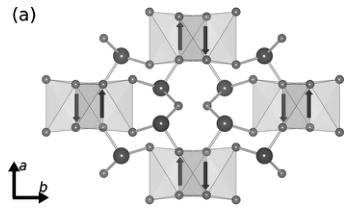
The thermal evolution of the neutron-diffraction patterns collected from 300 to 2 K are shown in Fig. 5. Three magnetic reflections appear below 10 K in the patterns obtained at 2.4 Å at 8°, 17°, and 20°. These three peaks could only be fit simultaneously by using the basis vectors of the irreducible representation \( \Gamma_{4} \) (Table III). The resulting magnetic structure associated with \( \Gamma_{4} \) refined from the 2.4 Å data is illustrated in Fig. 6. The propagation vector consistent with the neutron-diffraction data is k=0. Each chain of Co moments align antiferromagnetically down the length of the chain and with respect to the neighboring chains. The moments tilt in the ac plane, forming alternately, angles of \( +14^{\circ} \) and \( -14^{\circ} \) with respect to the a axis. The moments have no component along b. The magnetic moment on every Co atoms refined to a value of \( 3.2\mu_{B} \) at 2 K using the \( \lambda=2.399 \) Å neutron-diffraction data. This value corresponds to the three unpaired spins per Co atom in the ordered antiferromagnetic structure with a small contribution from the orbital moment. Clarke and co-workers have described the moment on other octahedral \( Co^{2+} \) containing compounds as being composed of a spin moment which has been reduced by covalency and some orbital contribution obtained by mixing of excited states of \( E_{g} \) symmetry. While the refined moment is smaller than observed for other \( Co^{2+} \) containing complexes, this may be explained by considering that the irregular octahedral environment reduces the symmetry of the octahedral environment from the \( T_{1g} \) ground state and thereby decreases the contribution from the orbital moment. \( ^{24,25} \)
To summarize our understanding of \( CoSe_{2}O_{5} \) , we note that magnetic-susceptibility measurements under small fields


FIG. 5. Top panel—low-angle region of the powder neutron-diffraction patterns of \( CoSe_{2}O_{5} \) (D2B, ILL) obtained for \( \lambda = 1.5949 \) Å. Bottom panel—low-angle region of the powder neutron-diffraction patterns for \( \lambda = 2.399 \) Å meant to emphasize the fit to the magnetic reflections. Note the development of magnetic Bragg peaks in the 5 and 2 K patterns.
TABLE III. Basis vectors for the space group Pbcn with \( k_{19} = (0,0,0) \) . The atoms of the nonprimitive basis are defined according to 1: \( (0,0.9389, \frac{3}{4}) \) , 2: \( (\frac{1}{2},0.5611, \frac{1}{4}) \) , 3: \( (0,0.0611, \frac{1}{4}) \) , and 4: \( (\frac{1}{2},0.4389, \frac{3}{4}) \) .
| IR | BV | Atom | BV components | ||
| \( m_{\parallel a} \) | \( m_{\parallel b} \) | \( m_{\parallel c} \) | |||
| \( \Gamma_{4} \) | \( \psi_{1} \) | 1 | 2 | 0 | 0 |
| 2 | 2 | 0 | 0 | ||
| 3 | -2 | 0 | 0 | ||
| \( \psi_{2} \) | 4 | -2 | 0 | 0 | |
| 1 | 0 | 0 | 2 | ||
| 2 | 0 | 0 | -2 | ||
| 3 | 0 | 0 | -2 | ||
| 4 | 0 | 0 | 2 | ||
(less than 5000 Oe) reveal a ZFC-FC separation that suggests weak ferromagnetism overlaid on the antiferromagnetic crystal structure. The weak ferromagnetism is not expected from the completely compensated antiferromagnetic structure that we determine to be most consistent with the low-temperature powder neutron diffraction data. However, we note that the estimated saturation magnetization of the weak-antiferromagnetic component \( \mathcal{O}(10^{-4}\mu_{B}) \) per Co atom, is significantly smaller than what can be resolved with powder neutron diffraction. ZFC-FC separation of the kind observed at low fields in Fig. 2 has been attributed to intrinsic weak ferromagnetism in a number of systems as a consequence of the Dzyaloshinskii-Moriya interaction (DM). \( ^{26-30} \) Spin canting leading to weak ferromagnetism in the absence of the DM interaction has also been observed previously in \( Ba_{2}Cu_{3}O_{4}Cl_{2} \) . \( ^{31} \) The weak ferromagnetism could also arise from local disordering of the spin structure as a result of a combination of competing interactions and the reduced dimensionality. Such disorder would not necessarily generate extra Bragg reflections in the neutron-diffraction data due to the lack of long-range coherency.
IV. CONCLUSIONS
We have examined the magnetic properties of \( CoSe_{2}O_{5} \) using neutron-diffraction, magnetization, magnetic-
(a)

(b)

FIG. 6. Magnetic structure of \( CoSe_{2}O_{5} \) as determined from Rietveld refinements of the neutron-diffraction pattern obtained using a \( \lambda=2.4 \) Å at 2 K. (a) View down the c axis of the Pbcn structure. (b) View down the b axis. The small light gray atoms are oxygen while the larger and darker gray atoms are selenium.
susceptibility, and specific-heat measurements. We show that below the magnetic ordering temperature, the magnetic chains arrange their moments antiferromagnetically down the length of the chain and with respect to neighboring chains. The magnetic order in small fields is found to additionally exhibit signatures of weak ferromagnetism. We also find evidence in the heat capacity of a gap of 6.5 K in the magnon dispersion, that is unrelated, based on the energy scale, to the weak ferromagnetism but may still be relevant for understanding the magnetic ground state of \( CoSe_{2}O_{5} \) . All evidence points to a rich H-T phase diagram.
ACKNOWLEDGMENTS
We gratefully acknowledge discussions with Simon J. Clarke, Nicola Spaldin, and P. A. Pincus. Support for this work came from the National Science Foundation through a Career Award to R.S. (Grant No. DMR 0449354) and to G.L. (Grant No. DMR 06044823), and for the use of MRSEC facilities at UCSB (Grant No. DMR 0520415).
\( ^{1} \) S.-W. Cheong and M. Mostovoy, Nature Mater. 6, 13 (2007).
\( ^{2} \) T. Kimura, Annu. Rev. Mater. Res. 37, 387 (2007).
\( ^{3} \) S. Park, Y. J. Choi, C. L. Zhang, and S.-W. Cheong, Phys. Rev. Lett. 98, 057601 (2007).
\( ^{4} \) V. Hardy, S. Lambert, M. R. Lees, and D. McK. Paul, Phys. Rev. B 68, 014424 (2003).
\( ^{5} \) A. Maignan, V. Hardy, S. Hébert, M. Drillon, M. R. Lees, O. Petrenko, D. McK. Paul, and D. Khomskii, J. Mater. Chem. 14, 1231 (2004).
\( ^{6} \) Y. J. Choi, H. T. Yi, S. Lee, Q. Huang, V. Kiryukhin, and S.-W.
Cheong, Phys. Rev. Lett. 100, 047601 (2008).
\( ^{7} \) K. Taniguchi, N. Abe, T. Takenobu, Y. Iwasa, and T. Arima, Phys. Rev. Lett. 97, 097203 (2006).
\( ^{8} \) T. Masuda, A. Zheludev, B. Roessli, A. Bush, M. Markina, and A. Vasiliev, Phys. Rev. B 72, 014405 (2005).
\( ^{9} \) W. T. A. Harrison, A. V. P. McManus, and A. K. Cheetham, Acta Crystallogr., Sect. C: Cryst. Struct. Commun. 48, 412 (1992).
\( ^{10} \) G. Meunier and M. Bertaud, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem. 30, 2840 (1974).
\( ^{11} \) A. W. Hewat and S. Heathman, Acta Crystallogr., Sect. C: Cryst.
Struct. Commun. 40, C364 (1984).
\( ^{12} \) T. Jo and T. Shishidou, J. Phys. Soc. Jpn. 67, 2505 (1998).
\( ^{13} \) J. Kanamori, Prog. Theor. Phys. 17, 197 (1957).
\( ^{14} \) M. C. Day and J. Selbin, Theoretical Inorganic Chemistry, 2nd ed. (Reinhold, New York, 1960).
\( ^{15} \) B. C. Melot, J. E. Drewes, R. Seshadri, E. M. Stoudenmire, and A. P. Ramirez, J. Phys.: Condens. Matter 21, 216007 (2009).
\( ^{16} \) A. P. Ramirez, Annu. Rev. Mater. Sci. 24, 453 (1994).
\( ^{17} \) T. Moriya, Phys. Rev. 120, 91 (1960).
\( ^{18} \) J. W. Stout and E. Catalano, Phys. Rev. 92, 1575 (1953).
\( ^{19} \) A. Tari, The Specific Heat of Matter at Low Temperatures (Imperial College Press, Covent Garden, London, England, 2003).
\( ^{20} \) J. C. Lashley, R. Stevens, M. K. Crawford, J. Boerio-Goates, B. F. Woodfield, Y. Qiu, J. W. Lynn, P. A. Goddard, and R. A. Fisher, Phys. Rev. B 78, 104406 (2008).
\( ^{21} \) K. Fink, C. Wang, and V. Staemmler, Inorg. Chem. 38, 3847 (1999).
\( ^{22} \) J. Rodríguez-Carvajal, Physica B 192, 55 (1993).
\( ^{23} \) A. S. Wills, Physica B 276-278, 680 (2000).
\( ^{24} \) C. F. Smura, Ph.D. thesis, University of Oxford, 2008.
\( ^{25} \) S. J. C. Herkelrath, Ph.D. thesis, University of Oxford, 2009.
\( ^{26} \) P. Marchukov, R. Geick, C. Brotzeller, W. Treutmann, E. G. Rudashevsky, and A. M. Balbashov, Phys. Rev. B 48, 13538 (1993).
\( ^{27} \) W. M. Reiff, J. H. Zhang, H. Tam, J. P. Attfield, and C. C. Torardi, J. Solid State Chem. 130, 147 (1997).
\( ^{28} \) Y. Ma, X. M. Chen, and Y. Q. Lin, J. Appl. Phys. 103, 124111 (2008).
\( ^{29} \) L. B. Steren, M. Tovar, and S. B. Oseroff, Phys. Rev. B 46, 2874 (1992).
\( ^{30} \) K. Tezuka, M. Inamura, Y. Hinatsu, Y. Shimojo, and Y. Morii, J. Solid State Chem. 145, 705 (1999).
\( ^{31} \) K.-H. Müller and M. Wolf, J. Appl. Phys. 87, 6022 (2000).