| Transition Temperature | 2.49 K |
|---|---|
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | Ia-3d (#230) |
| Magnetic Space Group | Ia-3d' (#230.148) |
| Magnetic Point Group | m-3m' (32.4.121) |
| Lattice Parameters | 12.376 12.376 12.376 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1103/physrev.138.a176 |
| Reference | J.M. Hastings, L.M. Corliss and C.G. Windsor, Physical Review (1965) 138 A176-A177. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Dy1 | Dy | -9.0 | 0.0 | 0.0 | 9.00 |
perimental points for the hyperfine fields at the rare-earth nuclei in \( Fe_{2}Dy,^{17}Fe_{2}Er,^{18} \) and \( Fe_{2}Tm,^{19} \) Of course
\( ^{17} \) E. Bauminger, L. Grodzins, and A. J. Freeman, Rev. Mod. Phys. 36, 392 (1964).
\( ^{18} \) R. L. Cohen and J. H. Wernick, Phys. Rev. 134, B503 (1964).
\( ^{19} \) R. L. Cohen, Phys. Rev. 134, A94 (1964).
these are intermetallic compounds rather than dilute substitutional solid solutions, and thus not quite comparable to the other data. If cubic crystal field effects are important the fields given by Eq. (2) can be regarded only as upper limits.
PHYSICAL REVIEW
VOLUME 138, NUMBER 1A
5 APRIL 1965
Antiferromagnetic Structure of Dysprosium Aluminum Garnet \( ^{*} \)
J. M. HASTINGS AND L. M. CORLISS Brookhaven National Laboratory, Upton, New York
AND
C. G. WINDSOR† Yale University, New Haven, Connecticut (Received 13 November 1964)
The low-temperature antiferromagnetic structure of \( Dy_{2}Al_{8}O_{18} \) (DAG) has been established by means of neutron diffraction. The spin arrangement consists of six interpenetrating substructures directed along \( \pm X \) , \( \pm Y \) , \( \pm Z \) , as predicted by Wolf and co-workers. The observed value of the \( Dy^{+8} \) moment is \( 9.0 \pm 0.5 \mu_{B} \) , in agreement with the g value obtained from esr measurements.
INTRODUCTION
In a series of elegant papers, Wolf and co-workers \( ^{1-4} \) have presented evidence that dysprosium aluminum garnet (DAG) behaves like a three-dimensional Ising antiferromagnet in which dipolar forces account for more than half of the interaction energy.
Electron-spin-resonance measurements \( ^{1} \) on \( Dy^{+3} \) in yttrium aluminum garnet have shown that the general form of the spectrum is that of a Kramers-doublet ground state. This reduction to an effective spin of \( s^{\prime}=\frac{1}{2} \) is caused by crystal-field effects. The measured g values below \( 4^{\circ}K \) are highly anisotropic with \( g_{1}=0 \) and \( g_{11}=18.2 \) , where the parallel axis refers to one of the three cubic axes depending on the location of the ion in the unit cell. Specific heat and susceptibility measurements on DAG indicated a transition to an antiferromagnetic state at \( T_{N}=2.49^{\circ}K \) . Whereas no resonance can be obtained for \( Dy^{+3} \) in pure DAG, the expected similarity in the crystal field leads one to suppose that the ionic g tensor will be the same as in the dilute solid solutions and that, in the antiferromagnetic state, DAG can be regarded as a three-
\( ^{*} \) Research performed, in part, under the auspices of the U. S. Atomic Energy Commission.
† Present address: Solid State Division, Atomic Energy Research Establishment, Harwell, Berks., England.
\( ^{1} \) M. Ball, M. T. Hutchings, M. J. M. Leask, and W. P. Wolf, in Proceedings of the Eighth International Conference on Low-Temperature Physics, London, 1962 (Butterworth Scientific Publication, Ltd., London, 1963).
\( ^{2} \) M. Ball, M. J. M. Leask, W. P. Wolf, and A. F. G. Wyatt, J. Appl. Phys. 34, 1104 (1963).
\( ^{3} \) M. Ball, W. P. Wolf, and A. F. G. Wyatt, J. Appl Phys. 35, 937 (1964).
\( ^{4} \) W. P. Wolf and A. F. G. Wyatt, Phys. Rev. Letters 13, 368 (1964).
dimensional Ising model; i.e., three orthogonal, interpenetrating substructures of Ising spins. Assuming that the dominant ordering forces are magnetic dipole interactions, Wolf and co-workers \( ^{2-4} \) have been able to account for the susceptibility and specific heat measurements semiquantitatively.
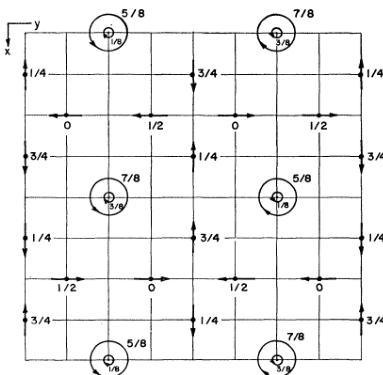
The magnetic structure \( ^{1} \) assumed in computing the susceptibility below the Néel temperature was the one having the lowest dipolar energy subject to the condition of cubic symmetry. This structure is shown in

FIG. 1. Spin arrangement in DAG. Dy \( ^{18} \) ions are in special positions 24(c) of space group Ia3d. The numbers in the figure give the height above the Z=0 plane. Spins pointing along the Z axis are indicated as current loops in a right-hand sense.
Fig. 1, in which the arrows indicate the direction of Dy \( ^{+3} \) magnetic moments. This structure is seen to consist of antiferromagnetic chains directed along the three cubic axes. Another structure considered was one in which the antiferromagnetic chains along X, Y, and Z were replaced by ferromagnetic ones. The dipolar energy of the latter arrangement is some 30% higher than the former. All other simple structures have even higher energies. We undertook a neutron diffraction study of DAG in order to test the validity of the final model obtained by this very plausible, though necessarily indirect, line of reasoning.
EXPERIMENTAL
Neutron diffraction patterns were obtained at room temperature, 4.2°K, and at 1.35°K. The crystal structure of DAG belongs to the space group Ia3d, with eight molecules per unit cell. The metal atoms are in special positions but the oxygen atoms require the fixing of three parameters. The values of the oxygen parameters given by Prince \( ^{6} \) for the analogous com-
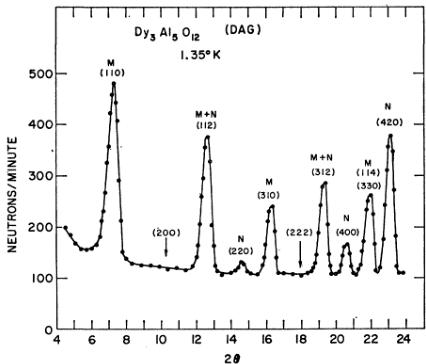
TABLE I. Intensities for DAG at 1.35°K.
| hkl | Nuclear | I_{cable} | Total | I_{obs} |
| 110 | 0 | 560 | 560 | 568 |
| 200 | 0 | 0 | 0 | 0 |
| 112 | 104 | 237 | 341 | 333 |
| 220 | 20.7 | 0 | 20.7 | 19.6 |
| 310 | 0 | 161 | 161 | 158 |
| 222 | 0 | 0 | 0 | 0 |
| 312 | 57.7 | 116.7 | 174 | 184 |
| 400 | 62.7 | 0 | 62.7 | 58.7 |
| 114,330 | 0 | 152 | 152 | 147 |
| 420 | 259 | 0 | 259 | 262 |
\( ^{a} \) Magnetic intensities calculated for \( \mu_{Dy}=9.0\mu_{B} \)
pound, yttrium aluminum garnet, gave excellent agreement between calculated and observed integrated intensities for the nuclear peaks. The pattern at \( 1.35^{\circ}K \) , given in Fig. 2, showed a number of new peaks, indicating a transition to an antiferromagnetic state. The new reflections can be indexed on the original chemical unit cell. The indexing of the magnetic peaks, as well as the intensity calculations shown in Table I, agree with predictions from the model of Fig. 1 and eliminate the alternative model with ferromagnetic chains.
Intensity calculations for DAG were made using the spherical-form-factor calculations of Blume, Freeman, and Watson. \( ^{6} \) The extreme anisotropy of the g tensor, resulting from crystal field effects, suggests that some modification of the form factor would be required. Estimates by Blume \( ^{7} \) for the \( \pm15/2 \) ground state

FIG. 2. Diffraction pattern of DAG at 1.35°K. Magnetic and nuclear reflections are indicated by the symbols M and N.
indicate that the spin density is indeed noncollinear but that theo ver-all effect on the intensities is within the experimental uncertainty of our data.
It is of interest to consider the DAG problem from the point of view of magnetic symmetry. Since the chemical space group is Ia3d, and since no superstructure is observed below the Néel point, the highest possible magnetic symmetry in the antiferromagnetic state can be described by the magnetic groups derived from Ia3d by addition of the time reversal operation. In the notation of Belov et al. \( ^{8} \) , these are Ia3d, Ia'3d, Ia3d', and Ia'3d'; the group Ia3'd is a gray group and properly describes the paramagnetic state. If a spin with arbitrary x, y, and z components is placed on one of the 24(c) Dy \( ^{+3} \) sites, and the remaining spins are generated by application of the magnetic symmetry operations, contradictions are obtained for alternative group operations unless the spins are directed along the cube edges. Furthermore, only two self-consistent structures are possible. The first of these belongs to Ia3d', and is, in fact, the arrangement shown in Fig. 1. The second, belonging to Ia'3d, is the ferromagnetic chain model discussed above in connection with the dipolar energy calculations. \( ^{9} \)
ACKNOWLEDGMENTS
We wish to thank Professor W. P. Wolf of Yale University for bringing this problem to our attention and for valuable discussions. We are indebted to S. Mroczkowski of the same institution for preparation of the specimen used in this work.