| Transition Temperature | 9.5 K |
|---|---|
| Experiment Temperature | 1.5 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | Pnma (#62) |
| Magnetic Space Group | P21'21'21 (#19.27) |
| Magnetic Point Group | 2'2'2 (6.3.19) |
| Lattice Parameters | 7.64760 6.88550 14.60580 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1021/ic802410p |
| Reference | S. Vilminot, G. Andre and M. Kurmoo, Inorganic Chemistry (2009) 48 2687-2692. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Cu1 | Cu | 0.7 | 0.0 | 0.7 | 0.99 |
| Cu2 | Cu | 0.0 | 0.0 | 0.0 | 0.00 |
| Cu3 | Cu | 0.7 | 0.0 | 0.7 | 0.99 |
Magnetic Properties and Magnetic Structure of \( Cu^{II}_{3}MoV_{2}O_{9} \)
Serge Vilminot, \( ^{*} \) \( ^{\dagger} \) Gilles André, \( ^{\ddagger} \) and Mohamedally Kurmoo \( ^{*} \) \( ^{\S} \)
Groupe des Matériaux Inorganiques, IPCMS, UMR 7504 (CNRS-UDS), 23 rue du Loess, BP 43, 67034 Strasbourg Cedex 2, France, Laboratoire Léon Brillouin, CEA-CNRS, CEA Saclay, 91191 Gif sur Yvette Cedex, France, and Laboratoire de Chimie de Coordination Organique, CNRS-UMR 7140, Université de Strasbourg, Institut Le Bel, 4 rue Blaise Pascal, 67000 Strasbourg Cedex 01, France
Received December 18, 2008
The magnetic properties and the low-temperature nuclear and magnetic structures of \( Cu_{3}Mo_{2}O_{9} \) are reported. It consists of magnetic chains of oxygen-bridged vertex-shared \( Cu_{4} \) tetrahedra connected into a 3D network by bridging \( MoO_{4} \) . Each chain is a segment of the pyrochlore structure. The magnetic properties are dominated by antiferromagnetic coupling and show a low-dimensional behavior with a broad maximum at 20 K. At 9.5 K, long-range antiferromagnetic ordering with a small canting is observed. The magnetic structure determination from neutron diffraction resolves only the orientations and magnitude \( (1.0(1)\mu_{\mathrm{B}} \) per Cu) of the moments of two of the three crystallographically independent atoms. The third appears not to contribute to the long-range ordering. Geometric frustration may be responsible for the randomness. It is a unique antiferromagnet with eight sublattices (two sets of four) in the ac plane, leaving the canting to be only possible along the b axis.
Introduction
One of the major interests in the field of magnetism is the understanding of the way magnetic moments on carriers are ordered in the solids. \( ^{1} \) Neutron scattering studies give a clear view of this in most cases, but in a few cases, this is not possible. \( ^{2} \) Among the difficult cases are those with structures where degenerate magnetic arrangements are possible, and these can be due to geometrical frustration. \( ^{3} \) There are several known geometrical frustrated structures, and the most studied are the kagome and pyrochlore systems. These are derived from the spinels (ABB'X \( _{4} \) ), where if the tetrahedral site (A) is vacant the pyrochlore results, and when one of the octahedra (B) of the latter is absent, the kagome is the final 2D network. Considerable efforts are being devoted to the understanding of their magnetic properties and magnetic structures. \( ^{4} \) We and others have recently been studying metal hydroxides containing tetrahedral anionic moieties, such as sulfate, selenate, and molybdate, and in these compounds, different types of structures are obtained where frustration appears to be present as a result of the \( \mu_{3} \) -bridging OH. \( ^{4-7} \) Neutron studies of these materials revealed features that have not been observed before, for example, the coexistence of short-range and long-range magnetic ordering, triple chains where the moments in the central part are random, and a cycloidal magnetic structure with a periodicity of seven. \( ^{6} \) During the course of the study of the Lindgrenite mineral,
\( \mathrm{Cu}_{3}(\mathrm{OH})_{2}(\mathrm{MoO}_{4})_{2} \) , prepared in our laboratory, we observed its transformation to \( Cu_{3}Mo_{2}O_{9} \) upon dehydration at \( 410\;^{\circ}C \) . Different groups have reported its nuclear structure. It consists of three independent copper atoms forming chains of \( Cu_{4} \) at the corners of tetrahedra, and adjacent tetrahedra share one vertex. \( ^{8-10} \) The structure is therefore a segment of a pyrochlore. \( MoO_{4} \) units bridge these chains to form the 3D network. The lack of any study of its magnetic properties and magnetic structure prompted us to complete this part. Here, we report our finding of a unique eight-sublattice antiferromagnet consisting of ordering of only two of the three independent copper moments and random orientation for the third.
Experimental Section
Synthesis. The starting material Lindgrenite, \( \mathrm{Cu_{3}(OH)_{2}(MoO_{4})_{2}} \) , was prepared as described in the literature. \( ^{7} \) \( Cu_{3}Mo_{2}O_{9} \) was prepared as a brown-orange powder by heating Lindgrenite in a flow of air between 370 and 410 °C. The transformation is quite effective, with only the loss of one molecule of water as follows:
\[ \mathrm{Cu_{3}(OH)_{2}(MoO_{4})_{2}\longrightarrow Cu_{3}Mo_{2}O_{9}+H_{2}O\uparrow} \]
As the structure was already known from X-ray analysis of the single-crystal diffraction data, it was not necessary to obtain a single crystal for our study.
Characterizations. Infrared spectra were recorded with a Digilab Excalibur Series FTIR spectrometer by transmission through KBr pellets containing 1% of the crystals. Powder X-ray diffraction patterns were recorded using a D5000 Siemens diffractometer (Cu \( K\alpha_{1} \) , 1.5406 Å), equipped with a front monochromator. Magnetic susceptibility measurements were performed in the range 2–300 K by means of a Quantum Design MPMS-XL SQUID magnetometer.
The neutron diffraction experiments were performed at the Laboratoire Léon Brillouin (CEA Saclay) using the multidetector (800 cells) G4.1 ( \( \lambda = 2.4226 \) Å) diffractometer for the determination of the magnetic structure and the thermal evolution study of the low-temperature patterns. Six diffraction patterns were recorded
(5) (a) Vilminot, S.; Richard-Plouet, M.; André, G.; Swierczynski, D.; Bourée-Vigneron, F.; Marino, E.; Guillot, M. Cryst. Eng. 2002, 5, 177. (b) Vilminot, S.; Richard-Plouet, M.; André, G.; Swierzczynski, D.; Bourée-Vigneron, F.; Kurmoo, M. Inorg. Chem. 2003, 42, 6859. (c) Ben Salah, M.; Vilminot, S.; André, G.; Richard-Plouet, M.; Bourée-Vigneron, F.; Mhiri, T.; Kurmoo, M. Chem.—Eur. J. 2004, 10, 2048. (d) Ben Salah, M.; Vilminot, S.; Mhiri, T.; Kurmoo, M. Eur. J. Inorg. Chem. 2004, 2272. (e) Ben Salah, M.; Vilminot, S.; André, G.; Richard-Plouetz, M.; Mhiri, T.; Takagi, S.; Kurmoo, M. Chem. Mater. 2005, 17, 2612. (f) Ben Salah, M.; Vilminot, S.; André, G.; Richard-Plouett, M.; Bourée-Vigneron, F.; Mhiri, T.; Kurmoon, M. J. Am. Chem. Soc. 2006, 128, 7972. (g) Vilminot, S.; Richard-Plouet, M.; André, G.; Swicrzczynski, D.; Bourée-Vigneron, F.; Kurmoo, M. Dalton Trans. 2006, 1455. (h) Vilminot, S.; André, G.; Bourée-Vigneron, F.; Richard-Plouet, M.; Kurmoo, M. Inorg. Chem. 2007, 46, 10079.
(6) Vilminot, S.; André, G.; Bourée-Vigneron, F.; Richardson-Plouet, M.; Kurmoo, M. Inorg. Chem. 2001, 46, 10079.
(7) (a) Vilminot, S.; André, G.; Richard-Plouet, M.; Bourée- Vigneron, F.; Kurmoo, M. Inorg. Chem. 2006, 45, 10938–10946. (b) Vilminot, S.; André, G.; Bourée-Vigneron, F.; Baker, P. J.; Blundell, S. J.; Kurmoo, M. J. Am. Chem. Soc. 2008, 130, 13490–13499. (c) Shores, M. P.; Bartlett, B. M.; Nocera, D. G. J. Am. Chem. Soc. 2005, 127, 17986.
(8) Kihlborg, L.; Norrestam, R.; Olivecrona, B. Acta Crystallogr. 1971, B27, 2066–2070.
(9) Kihlborg, L.; Norrestam, R. Acta Crystallogr. 1972, B28, 3097.
(10) Reichelt, W.; Steiner, U. Acta Crystallogr. 1997, C53, 1371–1373.
in the \( 2\theta \) range \( 3-82.9^{\circ} \) , at different temperatures between 1.5 and 12 K. The powder sample was set in a cylindrical vanadium can and held in a liquid helium cryostat. Nuclear and magnetic structures were refined using the FULLPROF program. \( ^{[11]} \) The nuclear scattering lengths \( (b_{\mathrm{Cu}} = 0.7718 \times 10^{-12} \, \mathrm{cm}, b_{\mathrm{Mo}} = 0.6715 \times 10^{-12} \, \mathrm{cm}, \text{and } b_{\mathrm{O}} = 0.5803 \times 10^{-12} \, \mathrm{cm}) \) and copper magnetic form factor were those included in this program.
Results and Discussion
Synthesis. The preparation of molybdates of transition metals has been performed using different techniques such as hydrothermal, refluxing suspensions of solid precursors, thermal treatment at \( 900\ ^{\circ}C \) of a mixture of oxides in sealed silica tubes, and chemical transport of the oxides using \( Br_{2} \) . \( ^{8-10} \) The latter two approaches employ CuO and \( MoO_{3} \) as starting materials. The thermal dehydration of \( \mathrm{Cu_{3}(OH)_{2}-(MoO_{4})_{2}} \) followed by annealing to \( Cu_{3}Mo_{2}O_{9} \) using a low-temperature solid-to-solid reaction is a new procedure, and it results in powder only. \( ^{7} \) Consequently, large quantities can be prepared, which makes it suitable for powder neutron diffraction studies. The fact that \( \mathrm{Cu_{3}(OH)_{2}(MoO_{4})_{2} \) and \( Cu_{3}Mo_{2}O_{9} \) have the same 3:2 Cu/Mo ratio explains the possible transformation.
X-Ray Powder Diffraction. The X-ray powder diffraction (XRD) pattern of \( Cu_{3}Mo_{2}O_{9} \) agrees with that of JCPDS file number 24–55. However, the space group has been changed from the first reported, \( Pna2_{1} \) , to that of the two recently reported, \( Pnma \) , \( ^{9,10} \) in orthorhombic symmetry (see later). Refinement of the unit cell parameters from the powder data yields the following values: \( a = 7.661(2) \) , \( b = 6.857(2) \) , \( c = 14.605(3) \) Å, and \( V = 767.2(6) \) Å \( ^{3} \) . All of the diffraction lines were indexed with the unit cell parameters.
Infrared Spectroscopy. The infrared spectrum of \( Cu_{3}Mo_{2}O_{9} \) reveals the presence of strong sharp bands below \( 1000\ cm^{-1} \) , at 966, 939, 900, 816, 774, 718, and \( 526\ cm^{-1} \) (Figure S1, Supporting Information); two medium intensity bands at 400 and \( 318\ cm^{-1} \) ; and very weak broad bands around \( 3500\ cm^{-1} \) . The latter bands are related to water absorbed in the KBr. According to Nakamoto, \( ^{12} \) the vibration bands of the \( MoO_{4}^{2-} \) tetrahedron in solution appear at \( 897\ cm^{-1} \) ( \( \nu_{1} \) ), \( 317\ cm^{-1} \) ( \( \nu_{2} \) or \( \nu_{4} \) ), and \( 837\ cm^{-1} \) ( \( \nu_{3} \) ). If the local symmetry is lowered, the number of infrared-active vibrations increases to three for \( \nu_{3} \) ; in addition, \( \nu_{1} \) becomes infrared-active. Therefore, we have attributed the band at \( 966\ cm^{-1} \) to \( \nu_{1} \) and those at 939, 900, and \( 816\ cm^{-1} \) to \( \nu_{3} \) . The band at \( 318\ cm^{-1} \) is very close to the value expected for \( \nu_{4} \) , \( 317\ cm^{-1} \) . According to the variations of the line positions with the mass of the central atom, its oxidation state, the mass of the Y atom for an \( XY_{6} \) octahedron, and the evolution between square pyramid and octahedron, we have tried assigning the remaining vibration bands. In the structure of \( Cu_{3}Mo_{2}O_{9} \) , two copper ions are in an octahedral environment (Cu1 and Cu3), and one is in a square pyramid.
Table 1. Summary of the Neutron Powder Data Collection at 1.5 K and Structural and Magnetic Refinements of \( Cu_{3}Mo_{2}O_{9} \)
| a ( \( \textup{\AA} \) ) | 7.6476(4) | 2 \( \theta \) range/step (deg) | 3.0-82.9/0.1 |
| b ( \( \textup{\AA} \) ) | 6.8855(3) | number of parameters | 41 |
| c ( \( \textup{\AA} \) ) | 14.6058(7) | R \( _{\textup{p}} \) (%) | 6.22 |
| V ( \( \textup{\AA}^{3} \) ) | 769.1(1) | R \( _{\textup{wp}} \) (%) | 6.96 |
| Z | 4 | R \( _{\textup{B}} \) (%) | 1.86 |
| space group | P \( \textup{nma} \) (No. 62) | R \( _{\textup{F}} \) (%) | 1.34 |
| D \( _{\textup{calcd}} \) (g cm \( ^{-3} \) ) | 4.55 | R \( _{\textup{magn}} \) (%) | 12.8 |
| radiation \( \lambda \) ( \( \textup{\AA} \) ) | 2.4226 |
Table 2. Fractional Atomic Coordinates for \( Cu_{3}Mo_{2}O_{9} \) Obtained from Neutron Powder Diffraction Data at 1.5 K
| atom | x/a | y/b | z/c |
| Mo1 | 0.2657(10) | 0.25 | 0.1688(7) |
| Mo2 | 0.1568(11) | 0.75 | 0.3859(8) |
| Cu1 | 0 | 0 | 0 |
| Cu2 | 0.1614(8) | 0.75 | 0.1426(4) |
| Cu3 | 0.2055(8) | 0.25 | 0.4372(5) |
| O1 | 0.0886(10) | 0.75 | 0.0149(6) |
| O2 | 0.2080(13) | 0.75 | 0.2701(8) |
| O3 | 0.4361(15) | 0.75 | 0.0957(11) |
| O4 | 0.2490(7) | 0.9636(8) | 0.4394(4) |
| O5 | 0.1407(7) | 0.0396(10) | 0.1375(3) |
| O6 | 0.3037(10) | 0.25 | 0.2852(7) |
| O7 | 0.4699(13) | 0.25 | 0.1104(9) |
environment (Cu2). We propose to assign the bands at 774 and \( 718\ cm^{-1} \) to those of the square pyramid and the band at \( 526\ cm^{-1} \) to the \( \nu_{3} \) vibration of the octahedra. The bands at 400 and also the one at \( 318\ cm^{-1} \) can be attributed to some Cu—O vibrations. Table S1 (Supporting Information) summarizes the observed IR bands and their assignments.
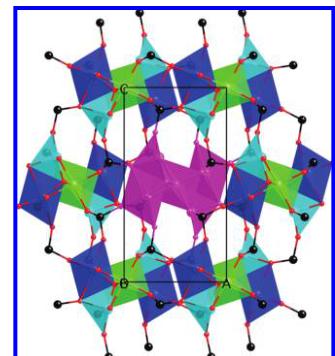
Structure Description. In agreement with the XRD and the single-crystal data of Reichelt and Steiner at room temperature, \( ^{10} \) the neutron diffraction patterns at all temperatures can be indexed and refined (Tables 1 and 2). As the structure at all temperatures remains the same as that described, we will only give a brief description and highlight the relevant parts pertaining to the magnetic properties and magnetic structure that will follow. There are three independent copper atoms with two different coordination geometries, distorted octahedron for Cu1 and Cu3 and square pyramid for Cu2. The three centers share edges with one another, and Cu1 connects to neighboring Cu1 via one oxygen atom. Cu1 and Cu3 form a chain of triangles consisting of two Cu1's and one Cu3 running along the c axis (Figure 2), while Cu2 sits on top of each triangular unit. The result is a chain of corner-sharing \( Cu_{4}O_{4} \) cubanes where the copper atoms are at the corners of a distorted tetrahedron with distances of 2.95–3.43 Å.
The \( MoO_{4} \) tetrahedra connect these chains through corner-sharing (Figure 1). Cu1 octahedra are corner-shared with two other Cu1 octahedra and edge-shared with one Mo1 tetrahedron, two Mo2 tetrahedra, one Cu2 pyramid, and two Cu3 octahedra; that is, Cu1 is surrounded by eight polyhedra. The situation is simpler for Cu2 with four neighbors (two Cu1, one Cu3, and one Mo2) and for Cu3 with five neighbors (two Cu1, one Cu2, one Mo1, and one Mo2). Concerning the two independent \( MoO_{4} \) tetrahedra, Mo1 is connected to four copper polyhedra (one Cu1, one Cu2, and two Cu3) and Mo2 to six (two Cu1, two Cu2, and two Cu3). \( Cu_{3}Mo_{2}O_{9} \) indeed exhibits a peculiar structure involving many links between the tetrahedra, pyramids, and octahedra. \( MoO_{4} \)

Figure 1. Projection of the crystal structure along the b axis, showing the parallel chains of copper (Cu1, green; Cu2, turquoise; Cu3, blue) connected by \( MoO_{4} \) (black). The central chain is highlighted in purple.

Figure 2. A single chain of \( Cu_{4} \) tetrahedra with the interatomic distances.
tetrahedra are quite regular with mean Mo–O distances of 1.774 and 1.766 Å for Mo1 and Mo2, respectively (Table S2, Supporting Information). Cu1 exhibits the compressed octahedral coordination as mentioned by Steiner and Reichelt, \( ^{10} \) with axial Cu–O distances of 1.863 Å and equatorial ones of 2.129 and 2.295 Å. These authors attributed the compression to lattice strain. Cu2 is surrounded by five oxygen atoms defining a slightly distorted square pyramid, with basal Cu–O distances between 1.896 and 2.002 Å, mean Cu–O = 1.962 Å, and an axial length of 2.210 Å. For Cu3, the environment can be considered 5-fold (square pyramid) or 6-fold (distorted octahedron by including Cu–O3 = 2.556 Å) according to the limit chosen for Cu–O distances. Bond-valence calculations (Table S3, Supporting Information) yield results very similar to the calculations performed on X-ray single-crystal data but do not allow one to choose between a 5- or 6-fold environment for Cu3. \( ^{13} \) The oxygen atoms are of the \( \mu_{2} \) or \( \mu_{3} \) type except O1, which is \( \mu_{4} \) . From a knowledge of the geometries adopted by the individual components and the valences of the metals, the compound should be regarded as \( \mathrm{Cu_{3}O(MoO_{4})_{2}} \) . Considering the Cu–O–Cu angles whose values dictate the sign of the magnetic exchange coupling, it is established that the exchange coupling is antiferromagnetic for angles higher than 96° and ferromagnetic for lower values. For the present case, the Cu1–O1–Cu1 angle of 135.1° can be related to

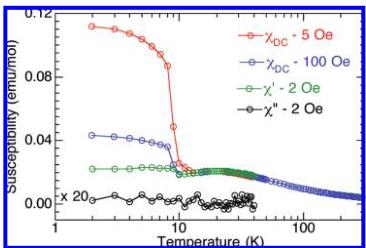
Figure 3. Temperature dependence of the ac and dc magnetic susceptibilities.

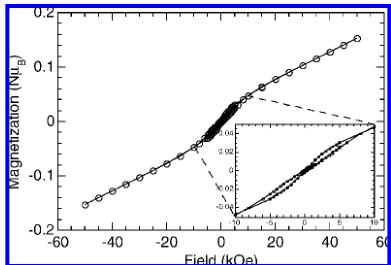
Figure 4. Isothermal magnetization at 2 K.
antiferromagnetic coupling between the corner-shared octahedra. For all other cases, two Cu–O–Cu bridges are involved, with one value lower than the limit \( (83.0-92.3^{\circ}) \) and the other one higher \( (102.5-109.2^{\circ}) \) . Therefore, it is not possible to predict the sign of the exchange coupling unambiguously.
Magnetic Properties. In the paramagnetic region \( (T > 50\;\mathrm{K}) \) , the susceptibility follows a Curie–Weiss law, \( \chi = C/(T - \theta) \) , with \( C = 1.36(1) \) emu K/mol (or 0.45(1) emu K/mol Cu) and \( \theta = -43(2) \) K. The effective moment per copper is therefore \( 1.9\;\mu_{B} \) , which is within the experimentally observed range of 1.8–2.1 for Cu(II). The average g value is 2.199. Below 50 K, the susceptibility exhibits a broad maximum centered at around 20 K. It then increases sharply at 9.5 K (Figure 3). The broad maximum at 20 K is probably related to 1D or 2D short-range antiferromagnetic correlation, whereas the sharp increase is spontaneous magnetization due to 3D magnetic ordering. The same features are evidenced for the real part of the ac susceptibilities. The absence of an anomaly in the corresponding imaginary part suggests antiferromagnetic ordering below \( T_{N} \sim 10 \) K with possibly a small canting. The sudden increase in the dc susceptibility is in agreement with a canting of the moments. The isothermal magnetization versus applied field recorded at 2 K reveals a linear evolution above \( H = 6\;kOe \) to only a fraction of the expected saturation value at 50 kOe. Between -6 and +6 kOe, a very narrow constricted hysteresis loop is observed with a coercive field around 150 Oe (Figure 4). Extrapolating the linear dependent part of the isothermal magnetization above 6 kOe, we estimated a remanent magnetization of \( 0.015\;\mu_{B} \) , from which we calculated a canting angle of \( 0.26^{\circ} \) by assuming the expected saturation.

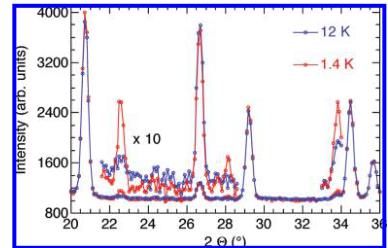
Figure 5. Part of the observed neutron diffraction patterns recorded below (red) and above (blue) \( T_{N} \) .
value of \( 3 \times 1.1 \mu_{B} \) . It is quite interesting to note that, within a tetrahedron of copper atoms, although the angles Cu1–O–Cu1 (134°), Cu1–O–Cu2 (102° and 88°), Cu1–O–Cu3 (103° and 91°), and Cu2–O–Cu3 (109° and 83°) define both ferromagnetic and antiferromagnetic interactions, the antiferromagnetic one dominates. \( ^{14} \) Interchain interactions through the O–Mo–O connections will not be negligible at low temperatures, and all of these pathways will need to be considered in any model. Due to the large number of pathways, it is not realistic to propose one definitive model.
Magnetic Structure Determination. A comparison of the neutron powder data recorded at 1.5 K (below \( T_{N} \) ) and 12 K (above \( T_{N} \) ) reveals very few modifications. Figure 5 zooms in on the \( 2\theta \) region at \( 20-36^{\circ} \) . Five weak magnetic contributions appear at 1.5 K compared to 12 K at 20.65 (101), 22.5 (011), 28.1 (012), 29.1 (111), and \( 33.7^{\circ} \) (112). Among them, only the line at \( 28.1^{\circ} \) is purely magnetic, corresponding to an extinction of the nuclear space group Pnma. The weak intensities could be related to the nature of the magnetic ion, \( Cu^{2+} \) , with a theoretical magnetic moment of \( 1\mu_{B} \) . The observation of additional peaks, which are extinct in the Pnma space group, suggests an antiferromagnetic ordering of the moments. Furthermore, the absence of any superlattice reflections suggests a propagation vector \( k=(0\ 0\ 0) \) .
To determine the magnetic structure, we used Bertaut's representation analysis method applied to the Pnma space group, a \( k = (0 \ 0 \ 0) \) propagation vector, and Wyckoff positions (4a) for Cu1 and (4c) for Cu2 and Cu3. \( ^{15} \) Eight one-dimensional irreducible representations (IRs), \( \Gamma_{1}-\Gamma_{8} \) , are associated with the basis vectors (magnetic structures) for Cu2 and Cu3, while only four, \( \Gamma_{2} \) , \( \Gamma_{4} \) , \( \Gamma_{6} \) , and \( \Gamma_{8} \) , are associated with Cu1. \( ^{16,17} \) If the combination of IRs is not forbidden, one usually starts the determination using the same IR for all magnetic atoms. However, it clearly appears that there is no magnetic model resulting from \( \Gamma_{2} \) , \( \Gamma_{4} \) , $ \Gamma_{6}
Table 3. Basis Functions of the Irreducible Representations, \( \Gamma_{5} \) and \( \Gamma_{6} \)
| IR | moment | CuN1 | CuN2 | CuN3 | CuN4 |
| \( \Gamma_{6} \) Cu1 | \( M_{x}, M_{y}, M_{z} \) | + + + | + + - | - + - | - + + |
| \( \Gamma_{6} \) Cu3 (or Cu2) | \( M_{x}, M_{y}, M_{z} \) | 0 + 0 | 0 + 0 | 0 + 0 | 0 + 0 |
| \( \Gamma_{5} \) Cu3 (or Cu2) | \( M_{x}, M_{z}, M_{z} \) | + 0 + | + 0 - | - 0 - | - 0 + |
\( ^{a} \) Cu11 (0, 0, 0); Cu12 (1/2, 0, 1/2); Cu13 (0, 1/2, 0); Cu14 (1/2, 1/2, 1/2); Cu3 (or Cu2)1 (x, y, z), Cu3 (or Cu2)2 (1/2 - x, -y, 1/2 + z); Cu3 (or Cu2)3 (-x, 1/2 + y, -z); Cu3 (or Cu2)4 (1/2 + x, 1/2 - y, 1/2 - z). N = 1, 2, and 3.

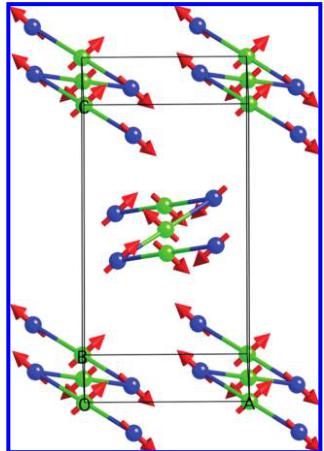
Figure 6. Perspective view of the magnetic structure along the b axis.
IRs for the three copper atoms that allows all of the observed magnetic lines to be calculated. Therefore, the problem appears to be much more complicated, and following through with trials using different combinations of IRs, we finally find that a model using \( \Gamma_{6} \) for Cu1 and \( \Gamma_{5} \) for Cu2 and Cu3 yields all expected magnetic lines. The choice of the model was suggested by their comparison, as shown in Table 3. It is to be noted that all possible models that do not involve a ferromagnetic model have been checked.
For \( \Gamma_{6} \) (Cu1), it appears that the component along the b axis must be zero; otherwise, the model corresponds to a ferromagnet. For \( \Gamma_{5} \) , the IR imposes a zero value. We started the refinements by using independent values for \( M_{x} \) and \( M_{z} \) for the three atoms. It results in values of the moment components that are much below the corresponding standard deviations for Cu2. Therefore, \( M_{x} \) and \( M_{z} \) for Cu2 have been set to zero. Further refinements for Cu1 and Cu3 yield an improved \( R_{magn} \) value when using the same components for Cu1 and Cu3 instead of independent ones, 12.8 and 13.1%, respectively. As the polyhedra around Cu1 and Cu3 are edge-shared, the magnetic coupling can be better described with a model having the same components. At 1.5 K, the almost similar values of \( M_{x}=0.7(2)\mu_{B} \) and \( M_{z}=0.7(2)\mu_{B} \) giving \( M_{total}=1.0(1)\mu_{B} \) are obtained for both Cu1 and Cu3. The value of \( 1.0\mu_{B} \) for the total moment is close to that expected for copper. This means that the moment for Cu2 is random or idle. It was interestingly requested by one of the reviewers to define the term “random or idle” in the context of “paramagnetic and glassy”. In our opinion, there is order of

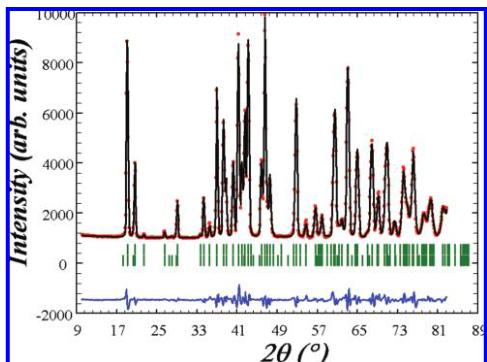
Figure 7. Observed (red circles) and calculated (black line) profiles of the neutron powder diffraction pattern of \( Cu_{5}Mo_{2}O_{9} \) obtained on the G4.1 diffractometer ( \( \lambda = 2.4226 \) Å) at 1.5 K with the position of the Bragg reflections (short vertical green lines) and the difference between observed and calculated profiles (blue lines).

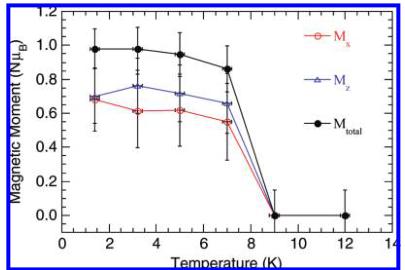
Figure 8. Temperature dependence of the components and the total of the magnetic moments.
the moment, but the coherent length may be short. This is seen as additional background scattering at low angles. However, it is not easy to estimate the coherent length from the limited data. We will therefore be inclined to think a glassy state is a more appropriate description. Figure 6 shows the magnetic structure (the molybdenum and Cu2 atoms have been omitted for clarity). Inside the zigzag chains of Cu1 and Cu3 atoms, the magnetic moment rotates counterclockwise by nearly \( 90^{\circ} \) in the ac plane from one copper to the next one along the b axis, with an antiferromagnetic distribution. Moreover, the moments of the copper along the chain containing Cu1 at (1/2, 1/2, 1/2) are rotated by nearly \( 90^{\circ} \) from those in the chains at the corner of the unit cell (i.e., Cu1 at (0, 0, 0)). The canting angle observed in the magnetic measurements is too small to be resolvable in the neutron magnetic structure. Figure 7 shows the observed and calculated diffraction patterns. The same model has been used to refine the magnetic structure for the other measuring temperatures, and Figure 8 shows the evolution of the magnetic components (Table 4).
This antiferromagnetic magnetic structure is quite particular. It is one where there are eight magnetic sublattices, two sets of four in which the moments are oriented at \( 90^{\circ} \) to each other. The moments of both sets lie in the ac plane.
Table 4. Components of the Magnetic Moments of \( Cu_{3}Mo_{2}O_{9} \) at 1.5 K (the moments of Cu2 atoms do not order)
| atom | x/a | y/b | z/c | M_{x} (\mu_{\mathrm{B}}) | M_{z} (\mu_{\mathrm{B}}) | M_{\mathrm{total}} (\mu_{\mathrm{B}}) |
| Cu11 | 0 | 0 | 0 | 0.7(2) | 0.7(2) | 1.0(1) |
| Cu12 | 0.5 | 0 | 0.5 | 0.7(2) | -0.7(2) | 1.0(1) |
| Cu13 | 0 | 0.5 | 0 | -0.7(2) | -0.7(2) | 1.1(1) |
| Cu14 | 0.5 | 0.5 | 0.5 | -0.7(2) | 0.7(2) | 1.0 |
| Cu31 | 0.20538 | 0.25 | 0.43718 | 0.7(2) | 0.7(2) | 1 |
| Cu32 | 0.29452 | 0.75 | 0.93718 | 0.7(2) | -0.7(2) | 0.1(1) |
| Cu33 | 0.79452 | 0.75 | 0.56282 | -0.7(2) | -0.7(2) | |
| Cu34 | 0.70548 | 0.25 | 0.06282 | -0.7(2) | 0.7(2) | 0.1(1) |
Within each set of four, the moments cancel each other, resulting in a zero moment, as they are of the same crystallographic copper site with equal moments. Though there is an angle between the moments of the two different sets, there is no resultant moment within the ac plane. This leaves the b axis as the only axis along which the observed canting may be oriented. This unique magnetic structure will not be possible with an observed moment on \( Cu_{2} \) . How the magnetic frustration within each tetrahedron is responsible for this unique magnetic structure is an interesting exercise deserving a full theoretical study.
Conclusion
The formation of edge- and vertex-sharing polyhedra in \( Cu_{3}Mo_{2}O_{9} \) resulted in one-dimensional Cu–O–Cu chains bridged by -O–Mo–O– into a 3D network. The magnetic exchange is dominated by overall antiferromagnetism, which is displayed by a broad maximum at 20 K in the susceptibility. Long-range antiferromagnetic ordering sets in below 9.5 K. The neutron diffraction reveals ordering of only two of the three moments, while the third remains random. Magnetic frustration, believed to be present within the \( Cu_{4} \) tetrahedra, may be responsible for the randomness of Cu2 and also for a unique magnetic structure with eight sublattices lying in the ac plane and a canting inferred to lie along the b axis.
Acknowledgment. This work was funded by the CNRS (France) and the CEA (France).
Supporting Information Available: Details of crystallographic data and infrared spectrum. This material is available free of charge via the Internet at http://pubs.acs.org.
IC802410P