| Transition Temperature | 26 K |
|---|---|
| Experiment Temperature | 1.5 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | Pca21 (#29) |
| Magnetic Space Group | Pc'a21' (#29.101) |
| Magnetic Point Group | m'm2' (7.3.22) |
| Lattice Parameters | 8.76030 8.69360 12.34660 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1080/00150199708222187 |
| Reference | O. Crottaz, P. Schobinger-Papamantellos, E. Suard, C. Ritter, S. Gentil, J.-P. Rivera and H. Schmid, Ferroelectrics (1997) 204 45-55. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Mn1 | Mn | 5.3 | 0.0 | 1.13 | 5.42 |
| Mn2 | Mn | 0.0 | 0.0 | -3.8 | 3.80 |
| Mn3 | Mn | 0.0 | 0.0 | 3.8 | 3.80 |
This article was downloaded by: [Moskow State Univ Bibliote] On: 29 December 2013, At: 04:36 Publisher: Taylor & Francis Informa Ltd Registered in England and Wales Registered Number: 1072954 Registered office: Mortimer House, 37-41 Mortimer Street, London W1T 3JH, UK

Ferroelectrics
Publication details, including instructions for authors and subscription information: http://www.tandfonline.com/loi/gfer20
Magnetic ordering of \( Mn_{3}B_{7}O_{13}X \) (X = Cl, Br, I) boracites determined by magnetic measurements and neutron diffraction
O. Crottaz \( ^{a} \) , P. Schobinger-Papamantellos \( ^{b} \) , E. Suard \( ^{c} \) , C. Ritter \( ^{c} \) , S. Gentil \( ^{a} \) , J.-P. Rivera \( ^{a} \) & H. Schmid \( ^{a} \)
\( ^{a} \) Department of Inorganic, Analytical and Applied Chemistry, University of Geneva, CH-1211, Geneva, 4, Switzerland
\( ^{b} \) Laboratorium für Kristallographie ETHZ, CH-8092, Zurich, Switzerland
\( ^{c} \) Institut Laue-Langevin, B. P. 156, 38042, Grenoble, Cedex, 9, France
Published online: 26 Oct 2011.
To cite this article: O. Crottaz, P. Schobinger-Papamantellos, E. Suard, C. Ritter, S. Gentil, J.-P. Rivera & H. Schmid (1997) Magnetic ordering of \( Mn_{3}B_{7}O_{13}X \) (X=Cl, Br, I) boracites determined by magnetic measurements and neutron diffraction, Ferroelectrics, 204:1, 45-55, DOI: 10.1080/00150199708222187
To link to this article: http://dx.doi.org/10.1080/00150199708222187
PLEASE SCROLL DOWN FOR ARTICLE
Taylor & Francis makes every effort to ensure the accuracy of all the information (the "Content") contained in the publications on our platform. However, Taylor & Francis, our agents, and our licensors make no representations or warranties whatsoever as to the accuracy, completeness, or suitability for any purpose of the Content. Any opinions and views expressed in this publication are the opinions and views of the authors, and are not the views of or endorsed by Taylor & Francis. The accuracy of the Content should not be relied upon and should be independently verified with primary sources of information. Taylor and Francis shall not be liable for any losses, actions, claims, proceedings, demands, costs, expenses, damages, and other liabilities whatsoever or howsoever caused arising directly or indirectly in connection with, in relation to or arising out of the use of the Content.
This article may be used for research, teaching, and private study purposes. Any substantial or systematic reproduction, redistribution, reselling, loan, sub-licensing, systematic supply, or distribution in any form to anyone is expressly forbidden. Terms & Conditions of access and use can be found at http://www.tandfonline.com/page/terms-and-conditions
MAGNETIC ORDERING OF Mn₃B₇O₁₃X (X = Cl, Br, I) BORACITES DETERMINED BY MAGNETIC MEASUREMENTS AND NEUTRON DIFFRACTION
O. CROTTAZ \( ^{a} \) , P. SCHOBINGER-PAPAMANTELLOS \( ^{b} \) , E. SUARD \( ^{c} \) , C. RITTER \( ^{c} \) , S. GENTIL \( ^{a} \) , J.-P. RIVERA \( ^{a} \) and H. SCHMID \( ^{a} \)
\( ^{a} \) Department of Inorganic, Analytical and Applied Chemistry, University of Geneva, CH-1211 Geneva 4, Switzerland; \( ^{b} \) Laboratorium für Kristallographie ETHZ, CH-8092 Zurich, Switzerland; \( ^{c} \) Institut Laue-Langevin, B.P. 156, 38042 Grenoble Cedex 9, France
(Received in final form 15 May 1997)
A new method for the preparation of \( Mn_{3}^{II}B_{7}O_{13}I \) powder sample, used for neutron diffraction, is presented. Magnetization measurements on powder samples of \( Mn_{3}B_{7}O_{13}X \) (X = Cl, Br, I) have shown that their Néel temperatures are \( 11\pm0.5 \) K for \( Mn_{3}B_{7}O_{13}Cl \) , \( 14\pm0.5 \) K for \( Mn_{3}B_{7}O_{19}B_{7} \) and \( 26\pm0.5 \) K for \( Mn_{3}B_{7}O_{11}I \) . The crystal and the magnetic structures of \( Mn_{3}B_{7}O_{13}I \) have been investigated by neutron diffraction. The neutron diffraction pattern in the paramagnetic phase at 35 K was refined in space group \( Pca2_{1}1' \) . The neutron diffraction data confirm the onset of magnetic ordering at 26 K. The magnetic structure has been determined at 1.5 K in the magnetic space group \( Pc'a2_{1}' \) . The magnetic moments of the three manganese sites order with a two-dimensional canted spin arrangement. The moments of two sites point along c with \( \mu_{z}(\mathrm{Mn2}) = \mu_{z}(\mathrm{Mn3}) = 3.8(2)\mu_{B}/\mathrm{atom} \) while the \( \mathrm{Mn(1)} \) site has a magnetic moment of 5.4(2) \( \mu_{B}/\mathrm{atom} \) located in the (101) orthorhombic plane, forming an angle of 12.0(3) degrees with the a direction. The effect of the antiferromagnetic/ferromagnetic compromise on the Mn–I–Mn pathways is discussed.
Keywords: Manganese iodine boracite; neutron diffraction; Néel temperature; magnetic phase transition; magnetic structure
1. INTRODUCTION
Manganese iodine boracite \( Mn_{3}B_{7}O_{13}I \) is a member of the boracite family with general formula \( M_{3}B_{7}O_{13}X \) (hereafter M-X) where M denotes usually a divalent transition metal ion and X a halogen ion. Mn-I undergoes a first
order ferroelastic/ferroelectric phase transition from a cubic \( (c) \) \( (F\overline{4}3c1^{\prime}) \) to an orthorhombic phase \( (o) \) \( (Pca2_{1}1^{\prime}) \) at \( 407~K^{[1]} \) , associated with a doubling of the primitive cell and a threefold splitting of the Mn positions (lettering c/o is used hereafter). The crystal structure of both phases has recently been determined in a single crystal X-ray diffraction study \( ^{[2,3]} \) .
The magnetic structures have so far been determined for the boracites \( Ni-Br^{[4]} \) , \( Ni-Cl^{[5]} \) , \( Co-Cl^{[6]} \) , \( Co-Br^{[7]} \) and \( Co-I^{[8]} \) . They are characterized by the formation of tetrahedral \( Metal_{3} \) -Halogen groups with a frustrated triangular spin arrangement. It was of interest to extend this study to the magnetic ordering of other members of the boracite family for allowing a comparison between the magnetic structures with different \( M^{2+} \) ions and for gaining a better understanding of the frustration process with the two step ordering observed in \( Ni-Br^{[4]} \) , \( Co-Br^{[7]} \) and \( Co-I[8] \) .
Previous magnetic measurements \( ^{[9]} \) report the existence of magnetic order below \( T_{N}=5.0 \) K for Mn-Cl, 7.6 K for Mn-Br and 5.8 K for Mn-I. However, these temperatures seem to be inconsistent with the usual trend of the boracites showing an increase of the ordering temperatures when going from chlorine to iodine boracites \( ^{[10]} \) . To clarify the magnetic behaviour of these compounds magnetic measurements were made on powder samples by means of a vibrating sample magnetometer (VSM). For Mn-I the magnetic structure has been determined by neutron diffraction on a powder sample. The results obtained by these two methods are the subject of the present paper.
2. SYNTHESIS
The Mn−I, Mn−Br and Mn−Cl powders used for the VSM measurements were prepared by chemical vapor transport, using the so-called “three crucible method” \( ^{[11,12]} \) . Approximately 100 mg of tiny crystals were obtained in this way and carefully ground to a powder before being fixed on the magnetometer’s sample holder.
Because of the large absorption cross section of natural B for neutrons, \( {}^{11}B \) enriched \( B_{2}O_{3} \) was used as starting product for preparing the \( Mn_{3}^{11}B_{7}O_{13}I \) powder ( \( \sim3~cm^{3} \) ) for neutron diffraction experiment. Although it was possible to use the three crucible method with \( {}^{11}B_{2}O_{3} \) (instead of \( B_{2}O_{3} \) as usually) and to grind the crystals obtained, this has the disadvantage that only a small amount of sample is obtained in each synthesis. Consequently, a modification of the method was used. This implies mixing of the starting products ( \( MnO, {}^{11}B_{2}O_{3} \) , and \( MnX_{2} \) ) in a
single crucible. The composition of the mixture is based on the stoichiometry of the reaction with an excess of 15% of halide. The temperature was set to \( 870^{\circ} \) C for 48 h. If some water is introduced into the ampoule (for activating the local transport reaction) it has been observed that small parts of the quartz crucible tend to break. It was also observed that this leads to the formation of impurities, such as \( Mn_{2}O_{3} \) and of a borosilicate (the composition of which has not yet been determined) on the interface between the powder and the quartz crucible. This problem was solved by using thoroughly dried products.
3. MAGNETIC MEASUREMENTS WITH THE VSM MAGNETOMETER
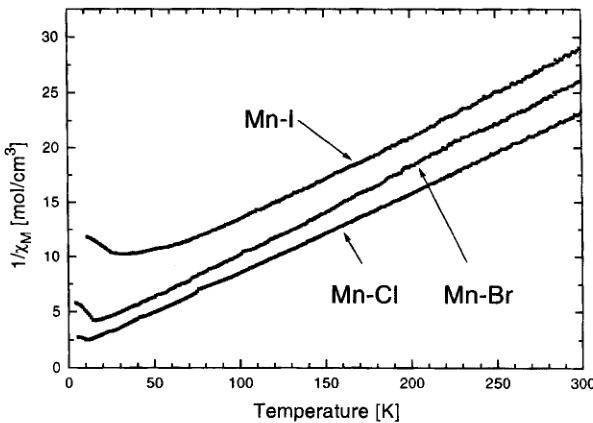
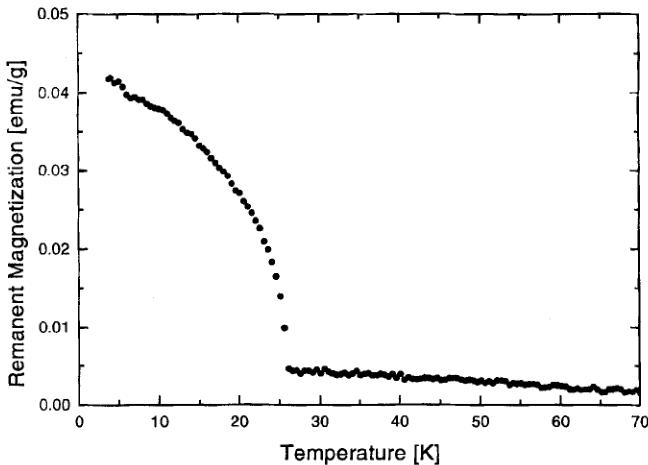
As already stated above, the previously reported Néel temperatures for the manganese boracite series \( [9] \) seem incorrect because they are not increasing in the sense \( Cl \rightarrow Br \rightarrow I \) . Consequently, prior to the neutron diffraction study, magnetization measurements were carried out on a VSM magnetometer. Results obtained are summarized in Table I. As expected, the Néel temperature increases when going from the chlorine boracite via the bromine to the iodine boracite. The \( \mu_{Br} \) values in the paramagnetic state are close to the spin only \( M = 2\sqrt{S(S + 1)}\mu_{B} = 5.92\mu_{B}/Mn^{2+} \) , indicating that no important orbital contribution is present. The Curie-Weiss temperatures \( \theta \) are all negative, indicating antiferromagnetic interactions between the paramagnetic ions (see Fig. 1). The remanent magnetization of Mn-I boracite as a function of the temperature is shown in Figure 2. Good agreement is obtained between the Néel temperatures observed by this method and those by a) neutron data (see next section), b) SQUID
TABLE I Effective magnetic moments, Curie-Weiss temperatures \( \theta \) [K] and Néel temperatures [K] of three manganese boracites. Values in parentheses are esd's on the fitting of the linear part of the curve
| Compound | \( \mu_{\text{eff}}[\mu_{\text{B}}](\sqrt{8 \text{ CM}}) \) | Curie-Weiss temperature [K] | Néel temperature [K] |
| Mn-Cl | 6.03(1) | -16.2(2) | 11±0.5 |
| Mn-Br | 5.76(1) | -26.7(3) | 14±0.5 |
| Mn-I | 5.92(1) | -78.7(7) | 26±0.5 |
Néel temperature of Mn-I obtained from measurement of the remanent magnetization, for Mn Br and Mn-Cl from susceptibility measurements, their real value may be slightly different due to the applied magnetic field.

FIGURE 1 Reciprocal magnetic susceptibilities versus temperature of powders of \( Mn_{3}B_{7}O_{13}Cl \) , \( Mn_{3}B_{7}O_{13}Br \) and \( Mn_{3}B_{7}O_{13}I \) boracite. The applied magnetic field is 9.5 kOe. The Néel temperatures are \( 11\pm0.5 \) K for \( Mn_{3}B_{7}O_{13}Cl \) , \( 14\pm0.5 \) K for \( Mn_{3}B_{7}O_{12}Br \) and \( 26\pm0.5 \) K for \( Mn_{3}B_{7}O_{11}I \) .

FIGURE 2 Remanent magnetization of \( Mn_{3}B_{7}O_{13}I \) boracite versus temperature. The Néel temperature is equal to \( 26\pm0.5 \) K. The cooling was made with an applied field of 9.5 kOe. Measurement made on heating with zero field applied.
magnetometer, magnetoelectric effect, magnetic birefringence \( ^{[13]} \) and c) specific heat measurements \( ^{[14]} \) .
4. NEUTRON DIFFRACTION
Neutron diffraction was performed at the “Institut Laue-Langevin” in Grenoble, using the D1B ( \( \lambda=2.5200 \) Å) and D2B diffractometers ( \( \lambda=1.59432 \) Å). The data collection was made at 295 K and in the range 1.5–35 K. The step increment on the diffraction angle was 0.2° on the D1B diffractometer and 0.05° on the high resolution D2B diffractometer. The data analysis was carried out by the Fullprof Rietveld Line-Profile Analysis Program \( ^{[15]} \) .
4.1. Nuclear Structure at 35 K
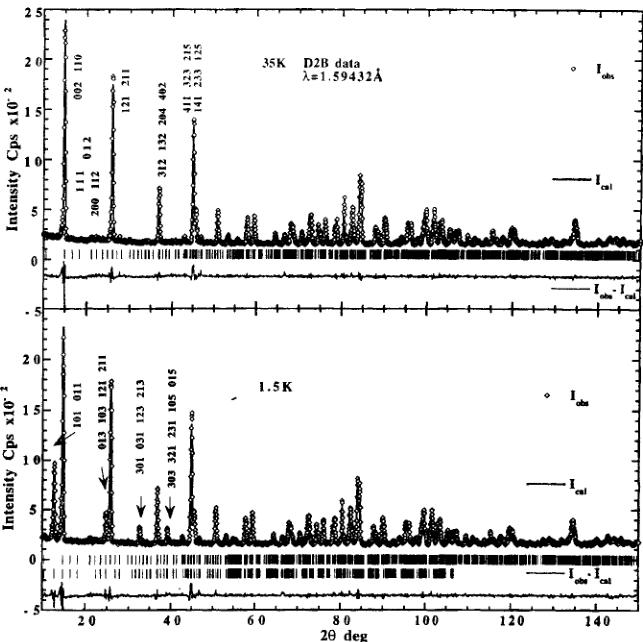
The crystal structure of the paramagnetic phase of Mn-I was refined at 35 K in space group \( Pca2_{1}1' \) (Fig. 3) using the high resolution D2B data. The refinement of the model was based on the X-ray starting parameter values. Cell parameters, atomic positions and reliability factors are summarized in Table II. These atomic positions were in turn used for the refinements of the magnetic phase.
4.2. Magnetic Structure
The 1.5 K neutron diffraction pattern (D2B) indicates the presence of additional magnetic lines at reciprocal lattice positions of the nuclear cell (Fig. 3). The observed reflection conditions suggest the magnetic space group \( Pc^{\prime}a2_{1}^{\prime} \) which allows a ferromagnetic moment along b and a three dimensional canted arrangement with the magnetic modes \( C_{x}(++--) \) , \( F_{y}(++++) \) , \( A_{z}(+--+) \) for each of the three manganese 4(a) sites: 1) x, y, z; 2) -x, -y, (1/2) + z; 3) (1/2) + x, -y, z; 4) (1/2) -x, y, (1/2) + z. This space group is the same as the one of other weakly ferromagnetic/ferroelectric orthorhombic boracites for which the magnetic structures have been determined (Ni-Br \( ^{[4]} \) , Ni-Cl \( ^{[5]} \) , Co-Br \( ^{[7]} \) Co-I \( ^{[8]} \) ) and is in agreement with the magnetic point group \( m^{\prime}m2^{\prime} \) determined by using a SQUID magnetometer and magnetoelectric effect measurements \( ^{[13]} \) . Refinements were made using all data collected with D1B and D2B diffractometers in the range 1.5–26 K. Since the magnetic reflections are relatively weak compared to the nuclear ones a better estimation of the

FIGURE 3 Observed, calculated and difference neutron powder diffraction diagram of orthorhombic \( Mn_{3}B_{7}O_{13}I \) boracite. D2B data. a) in the paramagnetic state at 35 K. Only nuclear contributions are observed on this diagram. b) in the magnetically ordered state at 1.5 K. Both nuclear and magnetic contributions are observed on this diagram. Indexing refers to magnetic reflections.
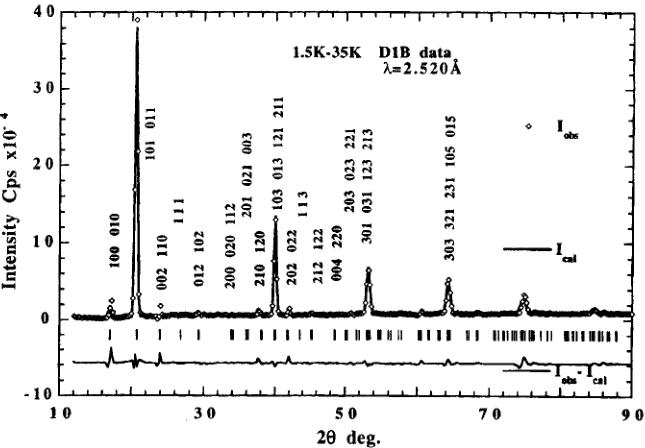
magnetic moment values was obtained by using difference diagrams between the magnetically ordered state at 1.5 K and the paramagnetic state at 35 K (Fig. 4). Due to the fact that the difference diagram 1.5–35 K of D2B data shows a "missfit" at the positions of nuclear peaks we preferably used the D1B difference diagram to obtain more correct values of the magnetic moments. The fact that weak ferromagnetic contributions, overlapping with allowed nuclear peaks, are not observed indicates that these are either very weak or their contributions cancel in the structure factor. Refinements carried out in space group \( Pca^{\prime}2_{1}^{\prime} \) gave higher values of the reliability factors ( \( R_{Magnetic}=14.3 \) instead of 12.6 in \( Pc^{\prime}a2_{1}^{\prime} \) ). The refined parameters are given in Table III and correspond to a two-dimensional canted
TABLE II Refined structural parameters of \( Mn_{3}B_{7}O_{13}I \) in the paramagnetic state at 35 K. Data collection on the D2B diffractometer. Space group \( Pca2_{1}1' \) . All atoms occupy site 4(a). Cell parameters (in Å) are \( a=8.7603(2) \) , \( b=8.6936(2) \) , \( c=12.3466(3) \) .
| Atom | x | y | z |
| Mn1 | 0.758(2) | 0.240(3) | 0.252(2) |
| Mn2 | 0.494(2) | 0.517(2) | 0.512(3) |
| Mn3 | -0.006(2) | 0.014(2) | 0.511(2) |
| I | 0.750(1) | 0.243(2) | 0.50870 |
| B1 | 0.499(1) | 0.500(1) | 0.258(1) |
| B2 | 0.256(1) | 0.250(2) | 0.506(1) |
| B3 | 0.000(1) | -0.005(1) | 0.260(2) |
| B4 | 0.4434(9) | 0.251(2) | 0.354(1) |
| B5 | 0.243(1) | 0.398(2) | 0.181(2) |
| B6 | 0.907(1) | 0.746(2) | 0.830(1) |
| B7 | 0.758(1) | 0.906(2) | 0.679(2) |
| O1 | 0.2282(9) | 0.246(2) | 0.247(1) |
| O2 | 0.532(2) | 0.329(2) | 0.281(2) |
| O3 | 0.379(1) | 0.329(1) | 0.439(2) |
| O4 | 0.971(2) | 0.156(1) | 0.284(2) |
| O5 | 0.326(2) | 0.359(1) | 0.078(2) |
| O6 | 0.159(2) | 0.971(2) | 0.234(2) |
| O7 | 0.141(1) | 0.174(1) | 0.436(2) |
| O8 | 0.335(2) | 0.514(1) | 0.236(2) |
| O9 | 0.181(2) | 0.125(1) | 0.074(2) |
| O10 | 0.952(1) | 0.594(2) | 0.851(2) |
| O11 | 0.535(1) | 0.909(2) | 0.857(1) |
| O12 | 0.913(2) | 0.540(1) | 0.664(2) |
| O13 | 0.597(2) | 0.945(1) | 0.667(2) |
\( R_{p} \) : 6.60, \( R_{wp} \) : 8.65, \( \mathrm{Chi}^{2} \) : 1.81, \( R_{Bragg} \) : 4.76.

FIGURE 4 Observed, calculated and difference neutron powder diagram of orthorhombic \( Mn_{3}B_{7}O_{13}I \) obtained by subtracting the 35 K nuclear data from the data in the magnetic state at 1.5 K. D1B diffractometer. Only magnetic contributions are observed on this diagram.
TABLE III Refined parameters of the magnetic structure of Mn–I at 1.5 K using 1.5–35 K difference diagram. Data collection on the D1B diffractometer. Magnetic space group \( Pc^{\prime}a2_{1}^{\prime} \) . Cell parameters (in Å) are \( a=8.760(4) \) , \( b=8.691(4) \) , \( c=12.380(4) \) (on the normal 1.5 K diagram cell parameters are \( a=8.7600(2) \) , \( b=8.6928(2) \) , \( c=12.3458(3) \) ).
| Atom | \( \mu_{x}[\mu_{B}] \) | \( \mu_{y}[\mu_{B}] \) | \( \mu_{z}[\mu_{B}] \) | \( \mu_{Total}[\mu_{B}] \) |
| Mn1 | 5.3(2) | 0 | 1.13(9) | 5.4(2) |
| Mn2 | 0 | 0 | -3.8(2) \( ^{*} \) | 3.8(2) |
| Mn3 | 0 | 0 | 3.8(2) \( ^{*} \) | 3.8(2) \( ^{*} \) |
\( R_{p} \) : 5.40, \( R_{wp} \) : 5.66, \( \mathrm{Chi}^{2} \) : 1.46, Magnetic R-factor: 12.6, *Constraints to opposed values. Within the \( 3\sigma \) limit the values of the magnetic moments can be compared with 4.6 \( \mu_{B} \) in \( MnI_{2} \) \( ^{[18]} \) and 5.0 in \( MnO \) \( ^{[19]} \) .
arrangement (see Fig. 5). The ferromagnetism along y is, within \( 3\sigma \) , equal to zero. In fact a small value can be refined for \( \mu_{y} \) of the Mn(2) and Mn(3) sites but their values cancel within 1.5 sigma. As the introduction of these parameters increases a lot the sigma values on the other parameters they were set equal to zero in the final refinement.
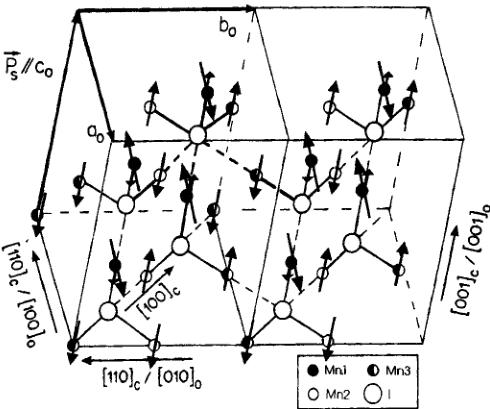
Analogously to Ni–Br \( ^{[4]} \) and Co–Br \( ^{[7]} \) among the three metal sites only two types of magnetic moment value are observed in Mn–I. The first type consists in the Mn(2) and Mn(3) ions which form mutually perpendicular Mn(2)–I–Mn(3) chains in the (001) \( _{o} \) plane. These two sites have the value

FIGURE 5 The two-dimensionally canted arrangement of magnetic moments of \( Mn_{3}B_{7}O_{13}I \) at 1.5 K. The small solid circles represent \( \mathrm{Mn}(1) \) , open circles \( \mathrm{Mn}(2) \) and half-solid circles \( \mathrm{Mn}(3) \) sites. Large open circles represent I atoms. The \( (c) \) and \( (o) \) subscripts indicate cubic and orthorhombic directions respectively. The magnetic moments of \( \mathrm{Mn}(1) \) are in the \( (101)_{o} \) plane.
of 3.8(2) \( \mu_{B}/atom \) along c. The second type consists in the \( \mathrm{Mn}(1) \) ions, forming \( \mathrm{Mn}(1)-\mathrm{I}-\mathrm{Mn}(1) \) chains along the \( [001]_{o} \) direction. Their magnetic moments of 5.4(2) \( \mu_{B} \) deviate by 12.0(3)° from the a axis in the \( (101)_{o} \) plane (see Fig. 5). The moment value is within the 3 \( \sigma \) limit close to the spin only value 2 S of 5.0 \( \mu_{B}/Mn^{2+} \) .
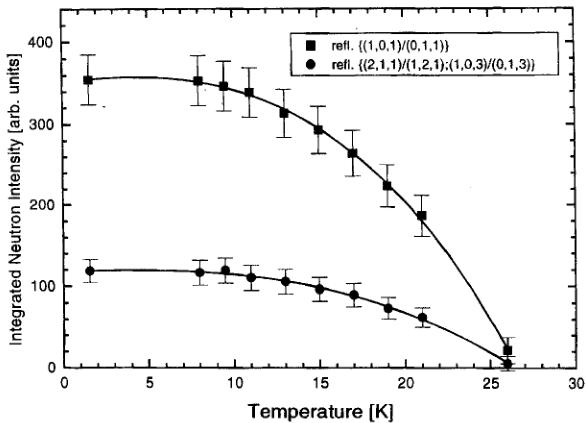
4.3. Temperature Dependence of the Magnetic Intensities
The temperature dependence of the two dominating magnetic peaks is shown in Figure 6. In agreement with measurements using other methods (see item 3) the Néel temperature is found to be 26 K, with the phase transition being of second order. It is interesting to note that in Co – Br a shoulder in the intensity versus temperature curve has been observed \( ^{[7]} \) which is also reflected in a Schottky anomaly, detected in the specific heat \( ^{[16]} \) , while in Mn–I, where no Schottky anomaly is detected in the specific heat measurements \( ^{[14]} \) the intensity versus temperature curve shows no anomaly.
5. CONCLUSION
Magnetization and neutron diffraction measurements on \( Mn_{3}B_{7}O_{13}I \) show clearly the appearance of a magnetically ordered phase below \( T_{N\acute{e}el}=26~K \) .

FIGURE 6 Temperature dependence of the integrated neutron intensity of the two strongest orthorhombic magnetic reflections of \( Mn_{3}B_{7}O_{13}I \) .
Although the magnetic structure can be described in the same magnetic group \( Pc^{\prime}a2_{1}^{\prime} \) found for Ni–Br and Co–Br boracites, the arrangement of the magnetic moments is rather different. In the latter compounds the three \( M^{2+} \) sublattices display canted moments perpendicular to each other. This canted arrangement is related to the two step onset of magnetic order: at higher temperatures, due to the frustration of the antiferromagnetic interactions between Metal (2) and Metal (3), only one site orders.
In Mn–I the temperature dependence of the magnetic moments shows that all sites order at the same temperature. In fact, according to Goodenough \( ^{[17]} \) the superexchange interaction tendency for two \( d^{5} \) cations via an intermediate oxygen or chlorine ion is antiferromagnetic, both for the \( 180^{\circ} \) and \( 90^{\circ} \) pathway. However, the \( 90^{\circ} \) interaction is rather weak. A similar tendency can be expected for the interaction via an iodine ion. Indeed, we observe for Mn–I that the two mutually perpendicular \( 180^{\circ} \) Mn(2)–I–Mn(3) chains, along \( \langle110\rangle_{o} \) and \( \langle1\overline{1}0\rangle_{o} \) , couple fully antiferromagnetically and the \( 180^{\circ} \) Mn(1)–I–Mn(1) chains along \( \langle001\rangle_{o} \) are also dominantly antiferromagnetism but with a canting, leading to a local small ferromagnetic component along \( \langle001\rangle_{o} \) . This strong antiferromagnetic coupling on the \( 180^{\circ} \) pathways is a general feature of the magnetic structures of boracites \( ^{[4-7]} \) . Note that an antiferromagnetic ordering both for the \( 180^{\circ} \) and \( 90^{\circ}\rangle \) interactions can not be realized fully since the Mn(2)–I–Mn(3) chains are mutually perpendicular. Since the \( 90^{\circ} \) interactions are weaker than the \( 180^{\circ} \) ones the structure orders with \( 180^{\circ} \) antiferromagnetic arrangement and with 1/2 of the \( 90^{\circ} \) interactions ferromagnetic and 1/2 antiferromagnetic. Thus it seems likely that the frustration effect is essentially lifted by the antiferromagnetic/ferromagnetic compromise on the \( 90^{\circ} \) Mn–I–Mn pathways.
Acknowledgements
The authors are grateful to the Swiss National Science Foundation for support and to the Fonds Mark Birkigt for enabling the presentation at the \( 3^{rd} \) International Conference on Magnetoelectric Interaction Phenomena in Crystals, Novgorod (Russia), Sept. 16–29, 1996 and to R. Boutellier for technical help.
References
[1] Schmid, H. and Tippmann, H. (1978). Ferroelectrics, 20, 21.
[2] Crotiaz, O., Kubel, F. and Schmid, H. (1995). J. Solid State Chem., 120, 60.
[3] Kubel, F. and Crotiaz, O. (1996). Z. Kristallogr., 211, 926.
[4] Mao, S. Y., Kubel, F., Schmid, H., Schobinger, P. and Fischer, P. (1993). Ferroelectrics, 146, 81.
[5] Ye, Z.-G., Schobinger-Papamantellos, P., Mao, S.-Y., Ritter, C., Suard, E. and Schmid, H. "MEIPIC 3", Sept. 16–20, 1996, Novgorod (Russia), Ferroelectrics, in press.
[6] Schobinger-Papamantellos, P., Ye, Z.-G., Suard, E., Ritter, C. and Schmid, H. To be published.
[7] Schobinger-Papamantellos, P., Fischer, P., Kubel, F. and Schmid, H. (1994). Ferroelectrics, 162, 93.
[8] Clin, M., Schmid, H., Schobinger, P. and Fischer, P. (1991). Phase Transitions, 33, 149.
[9] Muller, J. (1970). Thèse de 3ème cycle, Université de Grenoble.
[10] Tolédano, P., Schmid, H., Clin, M. and Rivera, J.-P. (1985). Phys. Rev. B, 32, 6006.
[11] Schmid, H. (1965). Phys. Chem. Solids, 26, 973.
[12] Schmid, H. and Tippmann, H. (1979). J. Cryst. Growth, 46, 723.
[13] Crottaz, O., Rivera, J.-P., Revaz, B. and Schmid, H. "MEIPIC 3", Sept. 16–20. 1996, Novgorod (Russia), Ferroelectrics, in press.
\[ [14]\quad Schnelle,W.,Crottaz,O.,Gmelin,E.andSchmid,H.to be published. \]
[15] Rodriguez-Carvajal, J. (1993). Physica B, 192, 55.
[16] Clin, M., Dai, W., Gmelin, E. and Schmid, H. (1990). Ferroelectrics, 108, 201.
[17] Goodenough, J. B. (1963) "Magnetism and the Chemical Bond" Figure 43, p. 181, Wiley New-York.
[18] Cable, J. W., Wilkinson, M. K., Wollan, E. O. and Kochler, W. C. (1962). Phys. Rev., 125, 1860.
[19] Roth, W. L. (1958). Phys. Rev., 110, 1333.